Abstract
We show a separation result between on the one hand models of concurrency that contain solutions to the consensus problem, where many identical concurrent processes must reach agreement; and on the other hand models with monotonic parallel composition, where processes always have the possibility to act independently of other processes in their environment. Our definitions and proofs are easy to instantiate in order to obtain particular separation results. We illustrate this point by strengthening several results from the literature, and proving some new ones. Highlights include a separation between unreliable and reliable broadcast \(\pi \), between the \(\rho \)-calculus and cc-pi, and between the full psi-calculi framework and its restriction to monotonic assertion logics.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
There is today a plethora of modelling formalisms for concurrent programs, focusing on different aspects and using different kinds of semantics. In order to compare two such formalisms it is natural to investigate their expressive power. If a certain behaviour can be expressed in one formalism but not in another we say that the behaviour separates the formalisms.
In this paper we present a simple method for separation results between transition systems with parallel composition, based on little more than whether parallel components may act independently or not. This allows us to strengthen several known separation results, and obtain new ones with pleasingly little effort. Our inspiration and examples come from process calculi, but we believe the arguments to be simple and general enough to be applicable to other models of concurrency also. The proof strategy is based on a simplification of the leader election problem which we call the consensus problem. It can be intuitively formulated as follows:
n observationally equivalent greasers walk into a bar. The greasers may, possibly after conferring with each other, non-deterministically declare that either Elvis Presley or Jerry Lee Lewis is the greatest singer of all time. Once either Elvis or Jerry has been declared, the other may not be declared; otherwise a bar fight will break out. A solution to the consensus problem is to find a process P, representing a greaser, such that no matter what n is, both Elvis and Jerry are possible outcomes and it can be guaranteed that a fight will never break out. Such a solution we call a consensus process.
In this paper, we show that the consensus problem is unsolvable with monotonic composition. The most natural example, and a mainstay in process calculi, is a parallel operator | on processes that admits independent behaviour via the rule


This says that whatever P can do alone it can also do if Q sits inert at its side. There can additionally be other rules for interaction between P and Q; a parallel operator counts as monotonic if the rule par holds, i.e. if a parallel context cannot hinder a transition. Examples of the myriad transition systems with monotonic parallel composition operators include CCS, the \(\pi \)-calculus, the \(\rho \)-calculus [1], and the fusion calculus [2]. Developments that include transition priorities may use non-monotonic composition; for example a high priority transition in Q may mean that P cannot take any transition in parallel with Q.
We exhibit several examples of transition systems where parallel composition does not satisfy par, and where consensus processes can indeed be expressed: the broadcast \(\pi \)-calculus [3], CCS with priorities [4], cc-pi [5], TPL [6], and some instances of psi-calculi [7]. We also exhibit two sets of criteria on encodings that both preserve the property of being a consensus process. It then follows immediately that there can exist no encoding of these languages satisfying our criteria if we only use monotonic composition in the target language. By this approach we strengthen the separation results from [3, 8, 9]. We also obtain several hitherto unseen results; highlights are a separation between unreliable broadcast (where messages may be lost) and reliable broadcast (where they may not), a separation between concurrent constraint formalisms based on whether inconsistent stores are reachable, and between the full psi-calculi framework [7] and its restriction to monotonic assertion logics (where connectivity between channels cannot decrease).
In order to increase confidence in the correctness of our developments, we have mechanised the proofs of our main results in the interactive theorem prover Isabelle/HOL [10]. The proof scripts are available online [11].
Our work is in the tradition of leader election-based separation results of Bougé [12] and Palamidessi [13]. In the leader election problem, n parallel processes must reach agreement among themselves to elect one (and only one) of them to act as their leader. In particular we are inspired by Ene and Muntean’s separation between the \(\pi \)-calculus and the broadcast \(\pi \)-calculus [3]. They show that if the n participants are allowed to differ only by alpha-renaming and are not allowed to know n in advance, the \(\pi \)-calculus cannot solve the leader election problem, but the broadcast \(\pi \)-calculus can. Hence there can be no encoding from broadcast \(\pi \) to \(\pi \), if we require that the encoding translates leader election systems into leader election systems. Their proof relies on the fact that the \(\pi \)-calculus allows local synchronisation independently of the environment via its monotonic parallel operator; hence the election can be split into two cliques that independently reach different election results. By contrast, the global synchronisation imposed by broadcast communication precludes such behaviour and allows the leader election problem to be solved. Variations of this argument have been used to show separation results between process calculi with priorities and their unprioritised counterparts [8, 9].
The consensus problem we consider is reminiscent of — yet distinct from — the well-studied binary distributed consensus problem in distributed computing (see e.g. [14]). Both problems are concerned with n parallel processes reaching agreement on some value. Our problem formulation is stronger in the sense that the participants do not a priori know the value of n, while in distributed consensus n is known. Intuitively we may think of this as our formulation allowing for additional greasers to enter the bar while the discussion is still ongoing, while distributed consensus requires that everyone is present at the start. On the other hand, our formulation is weaker in the sense that we do not insist on eventual termination, so crash failures are not a concern; we accept solutions that may crash or livelock as long as disagreement is avoided.
The main message of this paper is a method to obtain separation results, and it is presented so that it can be understood without knowledge of any particular process calculus, or indeed without any background in process calculi at all. In applications and examples, while we do give brief informal introductions to most languages under consideration, we will often use process calculi without formally defining them: divulging all details would seriously bog down the presentation with background material that is independent of our main message. The unacquainted reader is referred to the cited literature on the particular calculi for background; alternatively, she may safely skip examples pertaining to areas where she lacks background.
2 Definitions
2.1 Transition Systems and Composition
We consider the standard notion of non-labelled transition systems:
Definition 1
(Transition Systems). A transition system is a tuple  where
where
-
1.
\(\mathcal {P}\) is a set of processes, ranged over by P, Q, R, S, T, and
-
2.
 is called the transition relation.
is called the transition relation.
We write  , and let
, and let  denote the reflexive and transitive closure of
denote the reflexive and transitive closure of  .
.
Definition 2
(Composition). Let  be a transition system. A function \(\otimes : \mathcal {P} \times \mathcal {P} \rightarrow \mathcal {P}\) is a composition if \((\mathcal {P},\otimes )\) is a commutative semigroup, i.e. if it is associative and commutative. For \(n>1\) we write \(P^n_{\otimes }\) to mean \(P \otimes P \otimes \cdots \otimes P\) where P occurs n times.
be a transition system. A function \(\otimes : \mathcal {P} \times \mathcal {P} \rightarrow \mathcal {P}\) is a composition if \((\mathcal {P},\otimes )\) is a commutative semigroup, i.e. if it is associative and commutative. For \(n>1\) we write \(P^n_{\otimes }\) to mean \(P \otimes P \otimes \cdots \otimes P\) where P occurs n times.
Definition 3
(Monotonic Composition). A composition is monotonic if for all \(P,Q,R \in \mathcal {P}\),  implies
implies  . A composition that is not monotonic is called non-monotonic.
. A composition that is not monotonic is called non-monotonic.
Most examples discussed in this paper are on languages with a parallel operator denoted | as part of their syntax; unless otherwise specified, this is the composition that we have in mind. But formally \(\otimes \) need not be part of the process syntax. This makes our results applicable in non-algebraic models of concurrency. It also strengthens our separation results since we do not insist that the parallel operator is translated homomorphically. For example, consider \(\otimes \) as the disjoint union of place-transition nets. This operation is monotonic since any enabled transition will still be enabled if another net is put on its side. On the other hand, if \(\otimes \) is ordinary (non disjoint) union it is non-monotonic, since a transition can become disabled by adding a precondition without a token.
2.2 Consensus Processes
We will separate transition systems based on their ability to represent consensus processes. The idea is that P is an f, g-consensus process, where f, g are process predicates, if arbitrarily many copies of P in parallel can reach a state where f holds or a state where g holds, but once either has been reached the other cannot be reached. This captures the intuitive notion of consensus: that the participants can never disagree about whether f or g holds.
Definition 4
(Process Predicates). A process predicate of a transition system  is a function \(f : \mathcal {P} \rightarrow \mathbb {B}\).
is a function \(f : \mathcal {P} \rightarrow \mathbb {B}\).
A predicate f is
-
\(P,\otimes \) -extensible if f(Q) implies \(f(P\otimes Q)\);
-
\(P,\otimes \) -stable if for all \(P',n\) such that
 , f is \(P',\otimes \)-extensible.
, f is \(P',\otimes \)-extensible.
If the choice of \(\otimes \) is clear from the context we often write P-stable to mean \(P,\otimes \)-stable. Intuitively it means that for all n, the composition with any derivative of \(P^n_\otimes \) preserves f. Stable predicates are used to signal consensus; in this context stability means that once a clique of greasers decide to declare for either Elvis or Jerry, their decision remains firm in the presence of other greasers who did not partake in the decision.
Definition 5
(Consensus Process). Let  be a transition system with composition \(\otimes \). A process P is an f,g-consensus process over
\(\otimes \) if f, g are P-stable predicates such that for all \(n>1\):
be a transition system with composition \(\otimes \). A process P is an f,g-consensus process over
\(\otimes \) if f, g are P-stable predicates such that for all \(n>1\):
-
1.
(can choose f) there exists \(P'\) such that
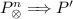 and \(f(P')\) holds;
and \(f(P')\) holds; -
2.
(can choose g) there exists \(P'\) such that
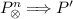 and \(g(P')\) holds; and
and \(g(P')\) holds; and -
3.
(no conflict) whenever
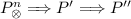 , \(f(P')\) implies \(\lnot g(P'')\), and \(g(P')\) implies \(\lnot f(P'')\)
, \(f(P')\) implies \(\lnot g(P'')\), and \(g(P')\) implies \(\lnot f(P'')\)
We say that a process P is a consensus process over \(\otimes \) if there are f, g such that P is an f, g-consensus process over \(\otimes \).
When the choice of \(\otimes \) is clear from the context or irrelevant, we will often write consensus process to mean consensus process over \(\otimes \).
To continue the informal example of place-transition nets: with disjoint union there exists no consensus process. This is a consequence of Theorem 15 in Sect. 3 since disjoint union is monotonic. With ordinary union we have a trivial consensus process: a net where a place with one token is precondition for two different transitions with postconditions f and g. Since union is idempotent \(P^n_{\cup } = P\) (in other words, taking any number of greasers results in just the one greaser), and the three requirements above are satisfied.
Note that our requirements are weak in the sense that we allow P to diverge and to reach a deadlocked state. In this sense a consensus process is not of much practical use. We could add more requirements to make it more realistic, but using weak requirements strengthens our separation results: non-monotonic composition cannot solve consensus even if we admit “solutions” that do not always terminate with a result. Note that all examples of consensus processes that we exhibit in this paper are guaranteed to eventually reach consensus, and all save for Examples 8 and 9 are guaranteed to eventually terminate. In those two examples, there are other consensus processes that do terminate.
2.3 Examples of Consensus Processes
Example 6
(Test-and-set).
A multiset of anonymous threads run on a CPU with two shared memory cells x, y, both initially set to 0. The threads have the following two instructions, both of which are executed atomically:
Let P(n) be a process that runs the following instruction sequence, where z is a private memory cell:
Then \(\{P(1),P(2)\}\) is a consensus process over multiset union for predicates \(y=1\) and \(y=2\). What makes this possible is that the \(\text{ test-and-set }\) instruction allows processes to detect whether or not they won the initial data race on x. The winner then writes her value of choice to y, while the losers all terminate.
Below, we show several examples of process calculi whose parallel operators are non-monotonic composition operators that can express consensus processes. Note that the requisite that composition is associative and commutative means that for applications to process calculi, we consider processes to be implicitly quotiented by structural congruence.
For predicates we will often use barbs, denoted \(\downarrow _{x}\). We write \(P\downarrow _{x}\) to mean that the process P offers a potential synchronisation on the channel x to the environment.
Example 7
(Broadcast \(\pi \) ). In broadcast \(\pi \) [3], a sender process \(\overline{a}\, x \) sends x on the channel a; when this happens, every listener \(a(z).P\) on channel a instantly receives x and continues as \(P[z :=\! x]\). The following is a consensus process over | in (asynchronous) broadcast \(\pi \):
where the process predicates are \(\downarrow _{x}\) and \(\downarrow _{y}\). The idea is that consensus is reached on whichever of x or y gets sent on a first. Further outputs on a can happen, but are immaterial since nobody listens. We use the non-labelled semantics for broadcast \(\pi \) given in [9].
Example 8
(CBS). In the broadcast calculus CBS as presented in [15], there are no channels; all messages are broadcast on the same unnamed ether. This example illustrates how to use predicates other than barbs in consensus processes, suggesting a way to connect our work to Gorla’s criteria on correct encodings [16], where barbs are absent. CBS offers a guarded choice operator \( x?p\; \& \;a!q\) that works as follows: if the environment broadcasts a message b, the process receives it and proceeds as \(p[x :=\! b]\). It may alternatively broadcast a to the environment and proceed as q. We can exploit this operator to define a consensus process over | in CBS as follows:
Here \(\varOmega \) is a divergent process, \(\checkmark \) is the successful process, and 0 is a process with no outgoing transitions. The process predicates are “the process has diverged” and “the process has reached success”.
Example 9
(CCS with Priorities). In CCS with priorities [4], underlined actions have high priority and no low-priority action can be taken if a high-priority action is possible. Let \(P(x) = \tau .(\underline{x} \;|\;\text{ fix }\; X.(\underline{\tau }.X))\). The process
is an \(\downarrow _{x}\),\(\downarrow _{y}\)-consensus process over | in CCS with priorities. The intuition is that once a choice has been made between x and y, all further choices are blocked because the process \(\text{ fix }\; X.(\underline{\tau }.X)\) takes precedence indefinitely.
Example 10
(cc-pi). cc-pi [5] is a calculus for specifying and negotiating quality of service requirements. It combines and extends elements of the name passing and concurrent constraint programming paradigms. The cc-pi agent \(\mathbf {tell}\; c\) can take a step that consists in adding the constraint c to the constraint store; however, this step may only be performed if the resulting constraint store is consistent.
Let \(c,c'\) be two constraints such that their composition \(c \times c'\) is inconsistent. Then the process
is a consensus process over | in cc-pi, with process predicates \(\mathord \vdash \,c\) (meaning that the store implies c) and \(\mathord \vdash \,c'\).
Example 11
(Psi-calculi). Psi-calculi [7] is a family of pi-calculus extensions that is parameterised on assertions. Assertions are facts about the environment in which processes execute. They may occur as part of the process syntax, and influence which transitions may be taken.
Consider a psi-calculus that has assertions \(\varPsi , \varPsi '\) that disable all further transitions. Further, let this psi-calculus have two distinct conditions \(\phi ,\phi '\) such that \(\varPsi \vdash \phi \) and \(\varPsi ' \vdash \phi '\). Then
is a consensus process over |, where the predicates are \(\mathord \vdash \,\phi \) and \(\mathord \vdash \,\phi '\). There will only ever be one transition; this transition will also unguard assertions such that exactly one of \(\mathord \vdash \,\phi \) and \(\mathord \vdash \,\phi '\) holds. Note that the assertion logic for this psi-calculus is non-monotonic.
Example 12
(FAP). The calculus FAP [9] is a minimal fragment of CCS with priorities that contains only input, output, nil and parallel composition. Output does not have continuations, but can have either high or low priority; \(\underline{\overline{x}}\) denotes high priority output on channel x, which preempts synchronisations involving low priority outputs \(\overline{y}\) on all names y. Let \(P(x) = a.b.(x \;|\;\overline{\underline{c}})\). Then the following is a consensus process in FAP for predicates \(\downarrow _{x}\) and \(\downarrow _{y}\).
Initially, the only available transition is a synchronisation on a, in which either P(x) or P(y) takes a step. At this point the choice between x and y has already been made, but not yet communicated with the world. The synchronisation on b acts as a lock (which is initially unlocked) to make sure no other choice has already been communicated. Once a process has communicated its choice, it initiates a chain reaction of synchronisations on c, which closes all locks by consuming all the available outputs on b. After that, the remaining participants may still choose between taking steps from either P(x) and P(y), yet a conflict is avoided because the locks prevent this choice from being communicated by exposing x or y.
Example 13
(CPG). CPG [8] augments CCS with priority guards \(U:\alpha .P\), where \(\alpha \) is an action and U is a set of actions. The intuition is that \(U:\alpha .P\) may act as \(\alpha .P\) unless the environment offers an action in U. In the latter case \(U:\alpha .P\) is blocked from proceeding until the environment ceases to offer actions from U. A consensus process in CPG with predicates \(\downarrow _{x}\) and \(\downarrow _{y}\) can be written
where \(P(x) = \{u\} : a.(\overline{u} | \overline{x})\). The intuition is that once a synchronisation on a where either P(x) or P(y) participates has been performed, all other processes are blocked from doing so by the offer being made on u.
Example 14
(TPL). Hennessy and Regan’s Temporal Process Language [6] (TPL for short) extends CCS with a notion of discrete time. The main addition is the prefix \(\sigma . P\), meaning that P will execute after one unit of time has passed. The time model of TPL assumes that time can only pass when there are no possible synchronisations; this is a common feature of timed calculi known as the maximal progress assumption. Formally,  can only happen if
can only happen if  . The effect of the \(\sigma \)-transition on P is to consume all top-level \(\sigma \) prefixes — this means that TPL assumes all agents to have synchronised clocks.
. The effect of the \(\sigma \)-transition on P is to consume all top-level \(\sigma \) prefixes — this means that TPL assumes all agents to have synchronised clocks.
We define a non-labelled transition relation for TPL as  . The following is an \(\downarrow _{x},\downarrow _{y}\)-consensus process over | in TPL:
. The following is an \(\downarrow _{x},\downarrow _{y}\)-consensus process over | in TPL:
Intuitively, a synchronisation on a means that the sender waives the choice between \(\downarrow _{x}\) and \(\downarrow _{y}\). These synchronisations continue until all but one process have waived. At that point no further synchronisations are possible, and time passes for the one remaining process, unguarding the choice between \(\overline{x}\) and \(\overline{y}\).
3 A Method for Separation Results
In expressiveness it is common to distinguish absolute expressiveness, where languages are compared based on their ability to solve certain problems; and relative expressiveness, where languages are compared based on whether it is possible to define an encoding between them satisfying certain quality criteria. The following theorem yields an absolute expressiveness result:
Theorem 15
Let  be a transition system with monotonic composition \(\otimes \). Then there is no consensus process over \(\otimes \).
be a transition system with monotonic composition \(\otimes \). Then there is no consensus process over \(\otimes \).
Proof
(Mechanised in Isabelle). By contradiction. Assume that P is an f, g-consensus process over \(\otimes \), and let \(n>1\). By Definition 5.1–2 there exists \(P',P''\) such that  and
and  , where \(f(P')\) and \(g(P'')\). By monotonicity of \(\otimes \), we get
, where \(f(P')\) and \(g(P'')\). By monotonicity of \(\otimes \), we get  and
and  . Hence
. Hence  . By the definition of stability we get \(f(P' \otimes P'')\) and \(g(P' \otimes P'')\), contradicting Definition 5.3.
. By the definition of stability we get \(f(P' \otimes P'')\) and \(g(P' \otimes P'')\), contradicting Definition 5.3.
The main use of this theorem is to obtain relative separation results between a source language \(\mathcal {S}\) and a target language \(\mathcal {T}\), by the following method:
-
1.
Exhibit a consensus process in \(\mathcal {S}\).
-
2.
Show that the composition under consideration in \(\mathcal {T}\) is monotonic.
-
3.
Obtain non-encodability of \(\mathcal {S}\) in \(\mathcal {T}\) by applying the corollaries of Theorem 15 to be introduced in Sects. 3.1 and 3.2.
The two corollaries yield non-encodability with two different kinds of encodings: uniform and observation-respecting. The rest of this section is devoted to defining them, and proving that they map consensus processes to consensus processes.
3.1 Uniform Encodings
We here consider a weakening of the criteria used by Ene and Muntean [3] to separate the \(\pi \)-calculus and the broadcast \(\pi \)-calculus.
Definition 16
(Invariant Predicates). A process predicate f is P-invariant if for all \(Q,Q'\) such that  and f(Q) it holds that \(f(Q')\).
and f(Q) it holds that \(f(Q')\).
Definition 17
(Uniform Encoding)
A relation \(\prec \) on states is f-preserving if \(P \prec Q\) and f(P) implies f(Q). An encoding \(\llbracket \cdot \rrbracket : \mathcal {P} \Rightarrow \mathcal {Q}\) between transition systems  and
and  is \(f,g,\otimes _\mathcal {P},\otimes _\mathcal {Q}\)
-uniform for the predicates \(f,g : \mathcal {P} \Rightarrow \mathbb {B}\) and composition operators \(\otimes _\mathcal {P},\otimes _\mathcal {Q}\) if there exists \(\hat{f},\hat{g}: \mathcal {Q} \Rightarrow \mathbb {B}\) with an \(\hat{f},\hat{g}\)-preserving relation \(\prec \) and:
is \(f,g,\otimes _\mathcal {P},\otimes _\mathcal {Q}\)
-uniform for the predicates \(f,g : \mathcal {P} \Rightarrow \mathbb {B}\) and composition operators \(\otimes _\mathcal {P},\otimes _\mathcal {Q}\) if there exists \(\hat{f},\hat{g}: \mathcal {Q} \Rightarrow \mathbb {B}\) with an \(\hat{f},\hat{g}\)-preserving relation \(\prec \) and:
-
1.
 implies
implies  for some \(Q'\).
for some \(Q'\). -
2.
If
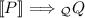 then there exists \(P',Q'\) such that
then there exists \(P',Q'\) such that  and
and  .
. -
3.
If f is P-stable then \(\hat{f}\) is \(\llbracket P \rrbracket \)-stable, if f is P-invariant then \(\hat{f}\) is \(\llbracket P \rrbracket \)-invariant, and f(P) iff \(\hat{f}(\llbracket P \rrbracket )\).
-
4.
If g is P-stable then \(\hat{g}\) is \(\llbracket P \rrbracket \)-stable, if g is P-invariant then \(\hat{g}\) is \(\llbracket P \rrbracket \)-invariant, and g(P) iff \(\hat{g}(\llbracket P \rrbracket )\).
-
5.
\(\llbracket P \otimes _\mathcal {P} P' \rrbracket = \llbracket P \rrbracket \otimes _\mathcal {Q} \llbracket P' \rrbracket \).
Clauses 17.1 and 17.2 are called operational correspondence, and capture the intuition that an encoding should preserve and reflect the source language’s transition behaviour. The role of the relation \(\prec \) is to perform garbage collection of junk terms that the encoding may produce. In the literature on relative expressiveness a behavioural equivalence is typically used for the same purpose; we do not insist on equivalences since weaker conditions yield stronger separation results. The extra catch-up transition from Q in Clause 17.2 allows for the encoding to mimic behaviour with protocols whose intermediary states have no direct counterpart in the target language.
Clauses 17.3 and 17.4 state that the process predicates used to signal consensus in the source language must have some corresponding predicates in the target language.
Clause 17.5 states that the encoding must be strongly compositional w.r.t. the composition operators under consideration. This requisite captures the intuition that the encoding must preserve the degree of distribution of the source language.
Definition 18
(Power-invariant Predicates). A process predicate f is \(P,\otimes \) -power-invariant if for all n, f is \(P^n_\otimes \)-invariant.
Thus power-invariance means that for all derivatives of \(P^n_{\otimes }\), if f becomes true it stays true.
Theorem 19
If P is an f, g-consensus process over \(\otimes _\mathcal {P}\), and if \(\llbracket \cdot \rrbracket \) is an \(f,g,\otimes _\mathcal {P},\otimes _\mathcal {Q}\)-uniform encoding, and if f, g are \(P,\otimes _\mathcal {P}\)-power-invariant, then \(\llbracket P \rrbracket \) is an \(\hat{f},\hat{g},\otimes _\mathcal {Q}\)-consensus process.
Proof
(Mechanised in Isabelle). We discharge each clause of Definition 5 as follows:
-
1.
By the definition of consensus process, for all \(n>1\) there exists \(P'\) such that
 and \(f(P')\). Since \(\llbracket \cdot \rrbracket \) is uniform there exists Q such that
and \(f(P')\). Since \(\llbracket \cdot \rrbracket \) is uniform there exists Q such that  . By definition of uniform encoding we get \(\hat{f}(\llbracket P' \rrbracket )\), and since \(\llbracket P' \rrbracket \prec Q\), \(\hat{f}(Q)\) follows.
. By definition of uniform encoding we get \(\hat{f}(\llbracket P' \rrbracket )\), and since \(\llbracket P' \rrbracket \prec Q\), \(\hat{f}(Q)\) follows. -
2.
The same, except substitute g for f.
-
3.
By contradiction. Assume
 with \(\hat{f}(Q)\) and \(\hat{g}(Q')\). By uniformity of \(\llbracket \cdot \rrbracket \) there exists \(P',Q''\) such that
with \(\hat{f}(Q)\) and \(\hat{g}(Q')\). By uniformity of \(\llbracket \cdot \rrbracket \) there exists \(P',Q''\) such that  and
and 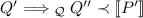 . By invariance, we get \(\hat{f}(Q'')\) and \(\hat{g}(Q'')\); since \(Q'' \prec \llbracket P' \rrbracket \) we get \(\hat{f}(\llbracket P' \rrbracket )\) and \(\hat{g}(\llbracket P' \rrbracket )\). By uniformity of \(\llbracket \cdot \rrbracket \) it then follows that \(f(P')\) and \(g(P')\), contradicting Definition 5.3.
. By invariance, we get \(\hat{f}(Q'')\) and \(\hat{g}(Q'')\); since \(Q'' \prec \llbracket P' \rrbracket \) we get \(\hat{f}(\llbracket P' \rrbracket )\) and \(\hat{g}(\llbracket P' \rrbracket )\). By uniformity of \(\llbracket \cdot \rrbracket \) it then follows that \(f(P')\) and \(g(P')\), contradicting Definition 5.3.
Corollary 20
If there exists an f, g-consensus process P over \(\otimes _\mathcal {P}\), and if \(\otimes _\mathcal {Q}\) is a monotonic composition, and if f, g are \(P,\otimes _\mathcal {P}\)-power-invariant, then there is no \(f,g,\otimes _\mathcal {P},\otimes _\mathcal {Q}\)-uniform encoding from \(\mathcal {P}\) to \(\mathcal {Q}\).
Remark 21
The invariance side conditions imposed on all process predicates used in this section are necessary to prevent a scenario where \(\hat{f}\) or \(\hat{g}\) may hold in some intermediate state of the target language, but ceases to hold once a state corresponding to a source language state is reached.
In practice this restriction is not severe. Of the consensus processes we consider in this paper, all but one satisfy it. The exception is the consensus process for broadcast \(\pi \) from Example 7, where the output \(\overline{x}\) that signals consensus is non-blocking; hence it may take the transition  , causing the predicate \(\downarrow _{x}\) to no longer hold. Fortunately, the example can be adjusted so that \(\downarrow _{x}\) and \(\downarrow _{y}\) are power-invariant by simply replicating the consensus signals:
, causing the predicate \(\downarrow _{x}\) to no longer hold. Fortunately, the example can be adjusted so that \(\downarrow _{x}\) and \(\downarrow _{y}\) are power-invariant by simply replicating the consensus signals:
3.2 Observation-Respecting Encodings
Definition 22
(Computations). Given a transition system  , the computations, ranged over by \(\mathcal {C}\), are finite or infinite sequences of processes such that for every process P in \(\mathcal {C}\) that has a successor Q, it holds that
, the computations, ranged over by \(\mathcal {C}\), are finite or infinite sequences of processes such that for every process P in \(\mathcal {C}\) that has a successor Q, it holds that  . A computation is maximal if it cannot be extended, i.e. either the computation is infinite or there are no transitions from the tail.
. A computation is maximal if it cannot be extended, i.e. either the computation is infinite or there are no transitions from the tail.
We overload process predicates so that we may also apply them to computations. Let \(f(\mathcal {C})\), where \(\mathcal {C} = P_0,P_1,\dots \) mean that there exists i such that \(f(P_i)\).
Definition 23
(Observation-respecting Encodings). An encoding \(\llbracket \cdot \rrbracket : \mathcal {P} \Rightarrow \mathcal {Q}\) between transition systems  and
and  is \(f,g,\otimes _\mathcal {P},\otimes _\mathcal {Q}\)
-respecting for the predicates \(f,g : \mathcal {P} \Rightarrow \mathbb {B}\) and composition operators \(\otimes _\mathcal {P},\otimes _\mathcal {Q}\) if there are predicates \(\hat{f},\hat{g} : \mathcal {Q} \Rightarrow \mathbb {B}\) such that
is \(f,g,\otimes _\mathcal {P},\otimes _\mathcal {Q}\)
-respecting for the predicates \(f,g : \mathcal {P} \Rightarrow \mathbb {B}\) and composition operators \(\otimes _\mathcal {P},\otimes _\mathcal {Q}\) if there are predicates \(\hat{f},\hat{g} : \mathcal {Q} \Rightarrow \mathbb {B}\) such that
-
1.
For every maximal computation \(\mathcal {C}\) starting from P, there exists a maximal computation \(\mathcal {C'}\) starting from \(\llbracket P \rrbracket \) such that \(f(\mathcal {C})\) iff \(\hat{f}(\mathcal {C'})\), and \(g(\mathcal {C})\) iff \(\hat{g}(\mathcal {C'})\).
-
2.
For every maximal computation \(\mathcal {C}\) starting from \(\llbracket P \rrbracket \), there exists a maximal computation \(\mathcal {C'}\) starting from P such that if \(\hat{f}(\mathcal {C})\) then \(f(\mathcal {C}')\), and if \(\hat{g}(\mathcal {C})\) then \(g(\mathcal {C}')\).
-
3.
If f is P-stable then \(\hat{f}\) is \(\llbracket P \rrbracket \)-stable.
-
4.
If g is P-stable then \(\hat{g}\) is \(\llbracket P \rrbracket \)-stable.
-
5.
\(\llbracket P \otimes _\mathcal {P} P' \rrbracket = \llbracket P \rrbracket \otimes _\mathcal {Q} \llbracket P' \rrbracket \).
This set of criteria is a simplification of the criteria considered in [9], where the term observation-respecting is used with a similar meaning.Footnote 1 The intuition behind Clauses 23.1 and 23.2 is that a process and its encoding should have computations with the same observable behaviour. This requisite is often formulated in terms of the computations having the same barbs, but since we are only interested in observing the predicates f, g used to signal consensus we require no more. Clause 23.2 allows target language computations to mimic only a subset of its corresponding source language computation’s observables; this means that we admit encodings that may introduce divergence and other failures.
The remaining criteria are similar to the criteria used for uniform encodings, with the notable exception that we do not require invariant predicates in this section.
Theorem 24
If P is an f, g-consensus process over \(\otimes _\mathcal {P}\), and if \(\llbracket \cdot \rrbracket \) is an \(f,g,\otimes _\mathcal {P},\otimes _\mathcal {Q}\)-respecting encoding, then \(\llbracket P \rrbracket \) is an \(\hat{f},\hat{g}\)-consensus process over \(\otimes _\mathcal {Q}\).
Proof
(Mechanised in Isabelle). We discharge each clause of Definition 5 as follows:
-
1.
By the definition of consensus process, for all \(n>1\) there exists \(P'\) such that
 and \(f(P')\). Then for all maximal computations \(\mathcal {C}\) from \(P^n_{\otimes _\mathcal {P}}\) through \(P'\) (of which there must be at least one), \(f(\mathcal {C})\) holds. Since \(\llbracket \cdot \rrbracket \) is f, g-respecting there exists \(\mathcal {C}'\) starting from \(\llbracket P \rrbracket ^n_{\otimes _\mathcal {Q}}\) such that \(\hat{f}(\mathcal {C}')\).
and \(f(P')\). Then for all maximal computations \(\mathcal {C}\) from \(P^n_{\otimes _\mathcal {P}}\) through \(P'\) (of which there must be at least one), \(f(\mathcal {C})\) holds. Since \(\llbracket \cdot \rrbracket \) is f, g-respecting there exists \(\mathcal {C}'\) starting from \(\llbracket P \rrbracket ^n_{\otimes _\mathcal {Q}}\) such that \(\hat{f}(\mathcal {C}')\). -
2.
The same, except substitute g for f.
-
3.
By contradiction. Assume
 with \(\hat{f}(Q)\) and \(\hat{g}(Q')\). Then for all maximal computations \(\mathcal {C}\) from \(\llbracket P \rrbracket ^n_{\otimes _\mathcal {Q}}\) through Q and \(Q'\) (of which there must be at least one), \(\hat{f}(\mathcal {C})\) and \(\hat{g}(\mathcal {C})\) holds. Since \(\llbracket \cdot \rrbracket \) is f, g-respecting there exists \(\mathcal {C}'\) starting from \(P^n_{\otimes _\mathcal {P}}\) such that \(f(\mathcal {C}')\) and \(g(\mathcal {C'})\). Then \(P^n_{\otimes _\mathcal {P}}\) cannot be a consensus process and we have a contradiction.
with \(\hat{f}(Q)\) and \(\hat{g}(Q')\). Then for all maximal computations \(\mathcal {C}\) from \(\llbracket P \rrbracket ^n_{\otimes _\mathcal {Q}}\) through Q and \(Q'\) (of which there must be at least one), \(\hat{f}(\mathcal {C})\) and \(\hat{g}(\mathcal {C})\) holds. Since \(\llbracket \cdot \rrbracket \) is f, g-respecting there exists \(\mathcal {C}'\) starting from \(P^n_{\otimes _\mathcal {P}}\) such that \(f(\mathcal {C}')\) and \(g(\mathcal {C'})\). Then \(P^n_{\otimes _\mathcal {P}}\) cannot be a consensus process and we have a contradiction.
Corollary 25
If there exists an f, g-consensus process over \(\otimes _\mathcal {P}\), and if \(\otimes _\mathcal {Q}\) is a monotonic composition, then there is no \(f,g,\otimes _\mathcal {P},\otimes _\mathcal {Q}\)-respecting encoding from \(\mathcal {P}\) to \(\mathcal {Q}\).
3.3 Comparing the Criteria
All separation results presented in this paper apply to both uniform and observation-respecting encodings. This may lead the reader to wonder whether the criteria are in fact equivalent; in this section we demonstrate that this is not the case by exhibiting counterexamples.
Consider the transition systems \(\mathcal {L}_1,\mathcal {L}_2,\mathcal {L}_3\) whose states and transitions are shown in Fig. 1. For state predicates we will use explicit sets of states. We identify a set S with its membership function \(\lambda x. x \in S\).
We assume that each of \(\mathcal {L}_1,\mathcal {L}_2,\mathcal {L}_3\) additionally has an unreachable junk state \(\bot \) where all predicates under consideration implicitly hold. For \(\otimes \) we use the function \(\lambda (x,y). \bot \) that maps every pair of states to the junk state. Note that this means that all predicates are stable, and renders all our requisites on encodings that concern composition trivially satisfied; hence we ignore composition for the remainder of this section.
There is a \({\{B\}},{\{C\}}\)-respecting encoding from \(\mathcal {L}_1\) to \(\mathcal {L}_3\): choose \({\{I\}},{\{J\}}\) as target language predicates, and map A, B, C respectively to H, I, J. However, there can be no \({\{B\}},{\{C\}}\)-uniform encoding from \(\mathcal {L}_1\) to \(\mathcal {L}_3\) since no choice of target language predicates can simultaneously satisfy all conjuncts of Definition 17.3–4. The reason is that B and C must be mapped to different states, and since \(\{B\}\) and \(\{C\}\) are invariant the corresponding predicates in \(\mathcal {L}_3\) must also be invariant, meaning they must both hold in K and thus cannot be disjoint.
There is an \({\{E\}},{\{F\}}\)-uniform encoding from \(\mathcal {L}_2\) to \(\mathcal {L}_1\): we may choose target language predicates \({\{B\}}\) and \({\{C\}}\), and let the encoding map G to A. However, there can be no \({\{E\}},{\{F\}}\)-respecting encoding because unlike \(\mathcal {L}_2\), there are no maximal computations in \(\mathcal {L}_1\) where neither predicate holds.
4 Applications
In this section, we demonstrate the applicability of the method described in Sect. 3 by using it to strengthen several separation results from the literature, and obtain several new separation results.
4.1 Strengthened Results from the Literature
Recall from Example 7 that broadcast \(\pi \) can express consensus processes. Since our requirements on encodings are weaker than Ene and Muntean’s, we strengthen their result that there is no uniform encoding from broadcast \(\pi \) to \(\pi \) [3]. More precisely, our notion of uniform encoding is weaker in the following ways:
-
They require operational correspondence of labelled transitions, whereas we only require operational correspondence of non-labelled transitions.
-
They require that \(\llbracket P \rrbracket \sigma = \llbracket P\sigma \rrbracket \) for all substitutions \(\sigma \), whereas we make no such requirement.
-
They do not admit the use of a behavioural equivalence or preorder for garbage collection in the definition of operational correspondence.
-
They require that \(\llbracket P \;|\;Q \rrbracket = \llbracket P \rrbracket \;|\;\llbracket Q \rrbracket \), whereas we require only that \(\llbracket P \;|\;Q \rrbracket = \llbracket P \rrbracket \otimes \llbracket Q \rrbracket \) for some monotonic composition \(\otimes \). For an example, our result also holds if we translate parallel composition with a context, i.e. \(\llbracket P \;|\;Q \rrbracket = C[\llbracket P \rrbracket ,\llbracket Q \rrbracket ]\), where the choice of C may depend on P and Q, given that the context is monotonic, associative and commutative.
From the consensus process exhibited in Example 12, we recover the result of Versari et al. [9] that there is no observation-respecting encoding of FAP in the \(\pi \)-calculus. Again, we achieve a strengthening by not insisting on homomorphic translation of parallel composition. A further strengthening is achieved since they require that observables used to signal the result of a leader election be exactly preserved by the translation, whereas our criteria allow the encoding to use a different signalling mechanism entirely.
From the consensus process exhibited in Example 13, we recover the result of Phillips [8] that the \(\pi \)-calculus has no observation-respecting encoding of CPG. We achieve a strengthening by relaxing their requirements on homomorphic translation of parallel composition, and their requisite that \(\llbracket P \rrbracket \sigma = \llbracket P\sigma \rrbracket \) for all substitutions \(\sigma \).
4.2 Reliable and Unreliable Broadcast
By reliable broadcast we mean that everyone who can listen to a broadcast must listen; this is the communication model of CBS, broadcast \(\pi \) and others. By contrast unreliable broadcast means that each potential listener may non-deterministically either hear the broadcast or not; this is the communication model used in CMN [17], broadcast psi-calculi [18] and others. It has been observed by Fehnker et al. that reliable broadcast is more practical for protocol verification, because without it we cannot prove any guarantees about eventual successful message delivery [19]. In this section, we lend additional support to their preference by showing that reliable broadcast is strictly more expressive than unreliable broadcast.
In order to obtain a separation, it suffices to observe that reliable broadcast requires non-monotonic parallel composition, but unreliable broadcast does not. For a slightly informal example, the labelled semantics of broadcast \(\pi \) as presented in [20] contains a rule that looks like this:


An unreliable version of broadcast \(\pi \) is obtained by replacing this rule with the usual \(\textsc {Par}\) rule:


Since transitions are considered up to alpha-equivalence of bound names this rule is monotonic parallel; it follows immediately by Corollaries 20 and 25 that there is no observation-respecting or uniform encoding of (reliable) broadcast \(\pi \) in unreliable broadcast \(\pi \).
Corollary 26
There is no \(\downarrow _{x},\downarrow _{y},|,|\)-respecting or -uniform encoding from broadcast \(\pi \) to unreliable broadcast \(\pi \).
However, an encoding in the other direction is possible. It is homomorphic on all operators except input, which is encoded as
Intuitively, the encoding mimics message loss by receiving the message, then pretending it never happened. This encoding enjoys a very tight operational correspondence:
Theorem 27
For all processes P of unreliable broadcast \(\pi \) it holds that:
-
1.
If \(\alpha \) is not an input action, then
-
(a)
If
 then
then  .
. -
(b)
If
 then there exists \(P''\) such that
then there exists \(P''\) such that  and \(\llbracket P'' \rrbracket = P'\).
and \(\llbracket P'' \rrbracket = P'\).
-
(a)
-
2.
If
 then
then 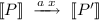 .
. -
3.
If
 then either \(P' = \llbracket P \rrbracket \) or there exists \(P''\) such that
then either \(P' = \llbracket P \rrbracket \) or there exists \(P''\) such that  and \(\llbracket P'' \rrbracket = P'\).
and \(\llbracket P'' \rrbracket = P'\).
Proof
The proof of each clause is by induction on the derivation of the transition. The clauses must be proved in reverse order: the derivation of an output or \(\tau \) may have premises that depend on the derivation of inputs, but not the other way around.
Hence reliable broadcast communication is strictly more expressive than unreliable broadcast communication. Finally, note that Ene and Muntean’s study of the expressiveness of point-to-point versus broadcast communication [3] applies only to reliable broadcast communication; hence the relative expressiveness of point-to-point communication and unreliable broadcast is still an open problem.
4.3 Consistency in Concurrent Constraint Formalisms
In Example 10 we exhibited a consensus process in cc-pi [5], that relies on the fact that cc-pi forbids steps that would lead to an inconsistent constraint store. The \(\rho \)-calculus [1] handles inconsistency in a different way: failure (denoted \(\bot \)) may be reached; once reached, it can be detected and any further computation may be aborted. Since there is no need to check the environment for potential inconsistencies when taking steps in the \(\rho \)-calculus, its parallel operator is monotonic; a separation between the \(\rho \)-calculus and cc-pi follows immediately.
Corollary 28
There is no \(\mathord \vdash \,c,\mathord \vdash \,c',|,\wedge \)-respecting or -uniform encoding from cc-pi to the \(\rho \)-calculus, where \(c,c'\) are consistent but \(c \times c'\) is not.
\(\wedge \) is \(\rho \)-calculus notation for the parallel operator. This result illustrates that insisting on consistent stores increases the expressive power of concurrent constraint formalisms.
4.4 Psi-Calculi with Non-monotonic and Monotonic Logics
The psi-calculi framework [7] is parameterised on an arbitrary logic, whose judgements are of the form \(\varPsi \vdash \varphi \). Here \(\varPsi \) ranges over assertions and \(\varphi \) ranges over conditions, and \(\vdash \) is the entailment relation; all three are parameters that may be chosen freely when instantiating the framework. Assertions may occur in processes, and influence the behaviour of processes in two ways. First, they influence the evaluation of guards in conditions. For an example, the agent  may take a transition to \((\!|\varPsi |\!) \;|\;P'\) iff
may take a transition to \((\!|\varPsi |\!) \;|\;P'\) iff  and \(\varPsi \vdash \varphi \).
and \(\varPsi \vdash \varphi \).
Assertions also influence which prefixes are deemed to be channel equivalent, i.e. which prefixes represent the same communication channel for the purposes of synchronisation. For an example, the agent \((\!|\varPsi |\!) \;|\;\underline{a}(x).P \;|\;\overline{b}\, y \) may take a transition to \((\!|\varPsi |\!) \;|\;P[x :=\! y]\) iff  , where the condition
, where the condition  is pronounced “a is channel equivalent to b”.
is pronounced “a is channel equivalent to b”.
Another parameter is the binary operator \(\otimes \) on assertions, called composition. It determines the influence of parallel assertions upon each other. Let us return to the example above, where  , and suppose \(P' \equiv (\!|\varPsi '|\!) \;|\;P''\). Only unguarded assertions influence behaviour; so now that \((\!|\varPsi '|\!)\) has become unguarded, further transitions from \(P''\) with preconditions \(\varphi \) will require that \(\varPsi \otimes \varPsi ' \vdash \varphi \) rather than \(\varPsi \vdash \varphi \).
, and suppose \(P' \equiv (\!|\varPsi '|\!) \;|\;P''\). Only unguarded assertions influence behaviour; so now that \((\!|\varPsi '|\!)\) has become unguarded, further transitions from \(P''\) with preconditions \(\varphi \) will require that \(\varPsi \otimes \varPsi ' \vdash \varphi \) rather than \(\varPsi \vdash \varphi \).
A psi-calculus is monotonic if its logic is monotonic, i.e. if for all \(\varPsi ,\varPsi ',\varphi \) it holds that \(\varPsi \vdash \varphi \) implies \(\varPsi \otimes \varPsi ' \vdash \varphi \). Intuitively this means that once a condition becomes true, it will remain true forever. Hence, in a monotonic psi-calculus, adding more assertions to a process may only increase its possible behaviours, and never decrease it. By contrast, in a non-monotonic psi-calculus it may be the case that adding an assertion removes behaviour, if doing so causes the retraction of a condition that was necessary for some transition.
Previous results indicate that monotonic and non-monotonic psi-calculi are fundamentally different beasts: monotonic psi-calculi admit a far simpler treatment of weak equivalences than their non-monotonic counterparts [21], and non-monotonic psi-calculi allow priorities to be encoded [22]. Here, we lend weight to this intuition by obtaining a formal separation result.
Recall the consensus process for non-monotonic psi-calculi from Example 11. We obtain a separation between monotonic and non-monotonic psi-calculi by observing that monotonic psi-calculi have monotonic parallel composition. The rule


is not in general valid in a non-monotonic calculus, because it may be the case that Q contains assertions that retract the necessary conditions for the transition  . However, in monotonic psi-calculi it can be derived, since if P itself already contains all necessary assertions for the derivation, then by monotonicity no assertions in Q may invalidate it. Hence
. However, in monotonic psi-calculi it can be derived, since if P itself already contains all necessary assertions for the derivation, then by monotonicity no assertions in Q may invalidate it. Hence
Corollary 29
There is no \(\mathord \vdash \,\varphi ,\mathord \vdash \,\varphi ',|,|\)-respecting or -uniform encoding from the psi-calculus of Example 11 into a psi-calculus with a monotonic logic.
4.5 Explicit Fusion with Mismatch
The \(\pi \)-calculus is sometimes presented with a mismatch operator \([x\!\!\ne \!\!y]P\), that may behave as P as long as x and y are different. Clearly the \(\pi \)-calculus parallel operator remains monotonic if we add mismatch, since the equality of these names depends on nothing but themselves. However, if we add a mismatch operator to the explicit fusion calculus [23] the situation is different. The explicit fusion calculus has monotonic parallel composition, but with the mismatch operator added, parallel composition becomes non-monotonic: two names that differ in P may be equivalent in \(P \;|\;Q\) if Q fuses them. Indeed, we may then write an \(\downarrow _{a},\downarrow _{b}\)-consensus process as follows:
In light of the thus obtained separation between explicit fusion with and without mismatch, and the separation between \(\rho \)-calculus and cc-pi obtained in Sect. 4.3, an interesting direction for future work would be to revisit Victor and Parrow’s result that the \(\rho \)-calculus can be encoded in the fusion calculus [2]. As a concluding remark, the authors note that “the question whether more complex constraint systems can be handled in the same way is largely open” [2, p. 469]; the results in this paper suggest that constraint systems allowing only consistent stores are beyond the reach of the fusion calculus. It would be interesting to investigate if adding mismatch allows a good encoding of such constraint systems.
4.6 SCCS: Beyond Monotonic Composition
In this section we consider SCCS [24] as a non-trivial example of a language where the product operator \(\times \) is non-monotonic, yet there is no reasonable consensus process over \(\times \). To our minds, a reasonable consensus process should use predicates f, g that are stable under strong bisimulation, i.e. f(P) and \(P \sim Q\) implies f(Q), and analogously for g. Using predicates that are not stable under bisimulation would mean that an observer cannot distinguish between states where f holds and where it does not, which would rather defeat the intuition that f, g signal consensus to the outside world.
SCCS is a variant of CCS where all parallel processes proceed in lockstep, rather than asynchronously as in CCS. It is parameterised on a commutative monoid \((Act,\cdot )\) of actions, ranged over by \(\alpha ,\beta \). The derivation rule that can infer transitions from \(P \times Q\) is the product rule:


SCCS also has a process 0, called inaction, with no outgoing transitions. An immediate consequence of this is that \(0 \times P\) also has no outgoing transitions, since the product rule is inapplicable. Hence \(0 \times P \sim 0\), where \(\sim \) is strong bisimulation.
There are two reasonable ways to define a non-labelled transition relation  from the standard LTS for SCCS: we can either let it be
from the standard LTS for SCCS: we can either let it be  , where 1 is the identity of the action monoid, or
, where 1 is the identity of the action monoid, or  . What follows is independent of which one we choose.
. What follows is independent of which one we choose.
We say that Q
may deadlock if there is \(Q'\) such that  and \(Q' \sim 0\).
and \(Q' \sim 0\).
Theorem 30
Suppose that f, g are stable under strong bisimulation. Then there is no f, g-consensus process over \(\times \) in SCCS.
Proof
By contradiction; suppose Q is an f, g-consensus process over \(\times \), and fix \(n>1\). We proceed by case analysis on whether \(Q^n_\times \) may deadlock.
-
Suppose that \(Q^n_\times \) may deadlock. By the definition of consensus processes we have that there is \(Q'\) such that
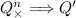 and \(f(Q')\); analogously there is \(Q''\) such that
and \(f(Q')\); analogously there is \(Q''\) such that  and \(g(Q'')\). Since \(Q^n_\times \) may deadlock we also have that
and \(g(Q'')\). Since \(Q^n_\times \) may deadlock we also have that 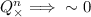 ; by Q-stability of f, g and since f, g are stable under \(\sim \), it follows that \(f(Q' \times 0) = f(0)\) and \(g(Q'' \times 0) = g(0)\). Hence, \(Q^n_\times \) may reach a (deadlocked) state where both f and g holds, which contradicts the definition of consensus process.
; by Q-stability of f, g and since f, g are stable under \(\sim \), it follows that \(f(Q' \times 0) = f(0)\) and \(g(Q'' \times 0) = g(0)\). Hence, \(Q^n_\times \) may reach a (deadlocked) state where both f and g holds, which contradicts the definition of consensus process. -
Suppose that \(Q^n_\times \) may not deadlock. By definition of consensus processes there exists \(R_0,\dots ,R_i,S_0,\dots ,S_j\) such that
 and
and  , where \(f(R_i)\) and \(g(S_j)\). Without loss of generality we may assume that \(i \le j\). Since \(Q^n_\times \) may not deadlock there is \(R_{i+1},\dots ,R_j\) such that
, where \(f(R_i)\) and \(g(S_j)\). Without loss of generality we may assume that \(i \le j\). Since \(Q^n_\times \) may not deadlock there is \(R_{i+1},\dots ,R_j\) such that  . By applying the product rule j times we get
. By applying the product rule j times we get  . By Q-stability we have \(f(R_i \times S_i)\) and \(g(R_j \times S_j)\), contradicting Definition 5.3.
. By Q-stability we have \(f(R_i \times S_i)\) and \(g(R_j \times S_j)\), contradicting Definition 5.3.
Intuitively, \(\times \) alone cannot express consensus processes since despite its non-monotonicity, it affords no way for one operand to constrain the behaviour of the other — unless it stops the world by unguarding 0, but in a stopped world we cannot observe what the consensus is. In SCCS the capability to constrain the behaviour of others is instead found in the interplay between the product and restriction operators. Theorem 30 does not contradict Holmer’s result that there is a fully abstract encoding from CBS to SCCS [25]; what it does mean is that if we insist on encodings that satisfy \(\llbracket P \;|\;Q \rrbracket = \llbracket P \rrbracket \times \llbracket Q \rrbracket \), Holmer’s encodability result becomes a separation result.
4.7 Maximal Progress in Timed Calculi
In this section we revisit the result of Corradini et al. [26] that TPL is strictly more expressive than Moller and Toft’s loose Temporal CCS [27] (abbreviated lTCCS). Our result has fewer conditions on how the encoding preserves semantics.
Recall from Exampe 14 that by using the maximal progress assumption of TPL [6] we may write a consensus process. Some calculi eschew the maximal progress assumption, and allow time to pass even if there are synchronisations that could happen; lTCCS is an example. There are two main technical differences from TPL:
-
lTCCS uses an explicit time domain ranged over by s, t, and has a prefix (t).P, meaning that P will execute after t units of time have passed.
-
A transition labelled t represents the passage of t time units. Every process may always take a t-transition.
Analogously with TPL, the non-labelled transition relation for lTCCS is the union of the \(\tau \) transitions and the time elapsing steps. The parallel operator of lTCCS is non-monotonic — clocks are synchronised, as modelled by the only rule for inferring t-transitions from \(P \;|\;Q\):


Nonetheless, there is no consensus process in lTCCS:
Theorem 31
There exists no consensus process over | in lTCCS.
Proof
(Sketch). By contradiction. Assume P is an f, g-consensus process and fix \(n > 1\). We have that  and
and  such that \(f(P')\) and \(g(P'')\). Then there exists R, S such that there is a transition sequence from \(P^{2n}\) that goes through both \(P' \;|\;R\) and \(S \;|\;P''\), where
such that \(f(P')\) and \(g(P'')\). Then there exists R, S such that there is a transition sequence from \(P^{2n}\) that goes through both \(P' \;|\;R\) and \(S \;|\;P''\), where  and
and  . By P-stability of f, g we obtain a contradiction with the definition of consensus process.
. By P-stability of f, g we obtain a contradiction with the definition of consensus process.
Note that the transition sequences from \(P^n\) to \(P'\) must be inferred from synchronisations interspersed with time elapsing, i.e. it performs an action sequence with labels \(\widetilde{\alpha } = \widetilde{\tau }s_0\widetilde{\tau }s_1\dots \widetilde{\tau }s_n\widetilde{\tau }\). The transition to \(P''\) analogously looks like \(\widetilde{\beta } = \widetilde{\tau }t_0\widetilde{\tau }t_1\dots \widetilde{\tau }t_n\widetilde{\tau }\).
A transition sequence from \(P^{2n} = P^n \;|\;P^n\) containing both \(P' \;|\;R\) and \(S \;|\;P''\) is then constructed via the following algorithm:
-
1.
Perform all \(\tau \) steps occurring before the first time steps of \(\widetilde{\alpha },\widetilde{\beta }\), applied respectively to the LHS and RHS of the outermost parallel operator.
-
2.
If \(s_0 \le t_0\), perform an \(s_0\)-step. Then iterate these steps for \(\widetilde{\alpha } = \widetilde{\tau }s_1\dots \widetilde{\tau }s_n\widetilde{\tau }\) and \(\widetilde{\beta } = t_0'\widetilde{\tau }t_1\dots \widetilde{\tau }t_n\widetilde{\tau }\), where \(t_0 = s_0 + t_0'\), until both sequences are empty. If \(t_0 < s_0\) do the same except swap \(\widetilde{\alpha },\widetilde{\beta }\) and s, t.
When \(\widetilde{\alpha }\) is empty, the LHS of the resulting process is exactly \(P'\). When \(\widetilde{\beta }\) is empty the RHS is exactly \(P''\).
Corollary 32
There is no \(\downarrow _{x},\downarrow _{y},|,|\)-respecting or -uniform encoding from TPL to lTCCS.
Intuitively the separation holds because with maximal progress, processes can gain information about other processes through the passage of time. A process offering a synchronisation on a will know, once time passes, that no other process was willing to meet the offer. When time may pass at any time, processes learn nothing from its passage.
Corradini et al. [26] exhibit an encoding in the reverse direction that is fully abstract wrt. strong bisimulation. They then show that there can be no encoding \(\llbracket \cdot \rrbracket \) from lTCCS to TPL such that \(\llbracket P \rrbracket \sim \llbracket Q \rrbracket \) implies \(P \sim Q\), if we additionally require that the encoding preserves labelled transitions exactly, i.e.  implies
implies  . For a separation result, this is a very strong semantic correspondence that rules out a priori any encoding that uses a non-trivial protocol. From Corollary 32 we obtain a separation result for encodings with a significantly weaker semantic correspondence, at the expense of requiring homomorphic translation of the parallel operator.
. For a separation result, this is a very strong semantic correspondence that rules out a priori any encoding that uses a non-trivial protocol. From Corollary 32 we obtain a separation result for encodings with a significantly weaker semantic correspondence, at the expense of requiring homomorphic translation of the parallel operator.
5 Isabelle Implementation
In order to obtain increased confidence in the correctness of our developments, we have formally proved Theorems 15, 19 and 24 and their Corollaries 20 and 25 in the interactive theorem prover Isabelle/HOL [10]. The proof scripts are available online [11]. This accounts for all the results presented in this paper that do not pertain to particular languages; mechanising those proofs would require that we first mechanise the languages under consideration, an arduous task that would justify a paper of its own.
Our mechanisation consists of 1000 lines of code and took less than a week in total to develop, meaning that the marginal cost of mechanising these results has been rather small. Perhaps surprisingly, the most challenging work was the proof of a technical lemma concerning computations: namely, that for every process P there is a maximal computation starting from P. We have chosen to mechanise computations using Lochbihler’s formalisation of coinductive lists [28]. This allows us to handle finite and infinite computations in a uniform way, and grants access to the powerful proof technique of coinduction. Since we do not have a concrete transition system to work with, obtaining a witness to the existence of a maximal computation is problematic. We achieve this using iteration over the Hilbert choice function \(\epsilon \), which given a predicate A returns an arbitrary witness to the predicate if one exists (using the axiom of choice). We then prove by coinduction that the sequence \(P_0,P_1,\dots \) is a maximal computation from P, where \(P_0 = P\), and  , and the candidate predicate is the set of all such iterations from P. It is unclear to us if a proof exists that avoids using the axiom of choice, at least if we insist on carrying out the proof in an abstract setting.
, and the candidate predicate is the set of all such iterations from P. It is unclear to us if a proof exists that avoids using the axiom of choice, at least if we insist on carrying out the proof in an abstract setting.
Isabelle’s locale mechanism [29] allows us to define a local context that states what constants must be defined and what axioms they must satisfy. The proofs of our main results are carried out in this context. A locale may be interpreted by instantiating the constants of the locale with concrete transition systems, and showing that they satisfy the axioms; Isabelle then automatically generates concrete instances of all theorems proven in the abstract within the locale. This means that our Isabelle developments are easy to re-use and build upon.
6 Conclusion
We have defined a method for separation results between non-monotonic and monotonic composition operators, based on their ability or inability to express consensus processes. We have demonstrated the wide applicability of our method by improving on several results from the literature, and exhibiting several novel separation results. Machine-checked proofs of our main results yield high confidence in the correctness of the method.
The idea of providing methods for separation results without committing to the precise languages under comparison has been previously introduced by Gorla [16], who offers two methods. One is for separation between languages that contain inert P such that \(P \;|\;P\) may take transitions, and those that do not; the other is for separation between languages based on their matching degree (the least upper bound on how many names must match to yield a transition), where greater matching degrees lead to greater expressiveness. These methods allow many well-known separation results from the literature to be proved in a simple and uniform way. However, Gorla’s methods are not applicable to the separation results considered in this paper.
Palamidessi’s result that mixed choice \(\pi \)-calculus is more expressive than separate choice \(\pi \)-calculus [30] was derived using leader election-based techniques; Peters and Nestmann achieved a stronger version of the same result by abstracting away from leader election and focusing instead on the problem of breaking symmetries in general [31]. Similarly to our work, Peters and Nestmann can then drop Palamidessi’s requirement that the translation respects substitutions, i.e. that for all \(P,\sigma \) it holds that \(\llbracket P \rrbracket \sigma = \llbracket P\theta \rrbracket \) for some substitution \(\theta \).
While our criteria on encodings and the languages under consideration are remarkably weak, different criteria may of course yield different results. For an example, there is an encoding of CBS into CCS due to Prasad [32], so clearly our separation results cannot hold if we weaken our criteria so that they are compatible with his. Prasad’s encoding works by introducing a handler for every parallel operator that is responsible for distributing transmitted messages to the left, right and to the environment. These three activities are performed on distinct channels, so the encoding of a subterm will differ depending on whether it occurs to the left or to the right of the innermost parallel operator, meaning that it is not a composition in our sense. Further, neither \(\llbracket P \rrbracket \) nor \(\llbracket Q \rrbracket \) occur as subterms of \(\llbracket P \;|\;Q \rrbracket \), so the encoding is not compositional in the sense of Gorla [16].
Traditionally, many separation results have been proven with homomorphic translation of the parallel operator as a criterion. This is usually justified by the intuition that an encoding should preserve the degree of distribution of the source language. We agree with this intuition. Our criterion that \(\llbracket P \;|\;Q \rrbracket = \llbracket P \rrbracket \otimes \llbracket Q \rrbracket \) for some monotonic composition \(\otimes \) is weaker, and can be seen as a less syntactic way to state that the degree of distribution should be preserved.
Another way to obtain a weaker criterion that still guarantees preservation of the degree of distribution has been proposed by Peters et al. [33]. Their approach is more focused on syntactic distributability, and more specifically tailored towards process calculi. It assumes that the process languages have a syntax where subprocesses can be composed with operators in an algebraic manner, and have capabilities, i.e. parts of a process that are removed when it transitions (such as prefixes in process calculi). Distributability is then a syntactic property of processes, where (roughly stated) a process is distributable into its set of top-level capabilities. An encoding preserves distributability if whenever a source process is distributable into some components, the target process is distributable into the same number of components, where each component of the target process is behaviourally equivalent to a corresponding component of the source process.
Hence our approach offers more flexibility in the kind of languages it can be applied to, and in designing encodings that are semantically but not syntactically distributable. For example, a normal form of a \(\pi \)-calculus process P is an equivalent process on the form \(\varSigma _i\;\alpha _i.P_i\), where each \(P_i\) is also on normal form. An encoding that translates every agent of the finite fragment of the \(\pi \)-calculus to its normal form would satisfy our criterion that parallel must be translated by monotonic composition, but does not preserve the degree of distribution in the sense of Peters et. al. On the other hand, they do not insist on associativity and commutativity of the contexts that parallel translates into, which offers some flexibility in designing encodings that is not available with our criteria. For future work, it would be interesting to investigate if a fruitful synthesis can be achieved.
References
Niehren, J., Smolka, G.: A confluent relational calculus for higher-order programming with constraints. In: Jouannaud, J.-P. (ed.) CCL 1994. LNCS, vol. 845, pp. 89–104. Springer, Heidelberg (1994)
Victor, B., Parrow, J.: Concurrent constraints in the fusion calculus. In: Larsen, K.G., Skyum, S., Winskel, G. (eds.) ICALP 1998. LNCS, vol. 1443, pp. 455–469. Springer, Heidelberg (1998)
Ene, C., Muntean, T.: Expressiveness of point-to-point versus broadcast communications. In: Ciobanu, G., Păun, G. (eds.) FCT 1999. LNCS, vol. 1684, pp. 258–268. Springer, Heidelberg (1999)
Cleaveland, R., Hennessy, M.: Priorities in process algebras. In: LICS, pp. 193–202. IEEE Computer Society (1988)
Buscemi, M.G., Montanari, U.: CC-Pi: a constraint-based language for specifying service level agreements. In: De Nicola, R. (ed.) ESOP 2007. LNCS, vol. 4421, pp. 18–32. Springer, Heidelberg (2007)
Hennessy, M., Regan, T.: A process algebra for timed systems. Inf. Comput. 117, 221–239 (1995)
Bengtson, J., Johansson, M., Parrow, J., Victor, B.: Psi-calculi: mobile processes, nominal data, and logic. In: Proceedings of LICS 2009, pp. 39–48. IEEE (2009)
Phillips, I.: CCS with priority guards. In: Larsen, K.G., Nielsen, M. (eds.) CONCUR 2001. LNCS, vol. 2154, pp. 305–320. Springer, Heidelberg (2001)
Versari, C., Busi, N., Gorrieri, R.: On the expressive power of global and local priority in process calculi. In: Caires, L., Vasconcelos, V.T. (eds.) CONCUR 2007. LNCS, vol. 4703, pp. 241–255. Springer, Heidelberg (2007)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: a Proof Assistant for Higher-Order Logic. Lecture Notes in Computer Science, vol. 2283. Springer, Heidelberg (2002)
Åman Pohjola, J.: The expressive power of monotonic parallel composition. http://www.it.uu.se/research/group/mobility/theorem/monopar.tgz. Isabelle 2014/HOL formalisation of the definitions, theorems and proofs
Bougé, L.: On the existence of symmetric algorithms to find leaders in networks of communicating sequential processes. Acta Inf. 25, 179–201 (1988)
Palamidessi, C.: Comparing the expressive power of the synchronous and the asynchronous \(\pi \)-calculus. In: Proceedings of the 24th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. POPL 1997, 256–265. ACM, New York (1997)
Fischer, M.J., Lynch, N.A., Paterson, M.S.: Impossibility of distributed consensus with one faulty process. J. ACM 32, 374–382 (1985)
Prasad, K.V.S.: A calculus of broadcasting systems. Science of Computer Programming 25, 285–327 (1995)
Gorla, D.: Towards a Unified Approach to Encodability and Separation Results for Process Calculi. In: van Breugel, F., Chechik, M. (eds.) CONCUR 2008. LNCS, vol. 5201, pp. 492–507. Springer, Heidelberg (2008)
Merro, M.: An observational theory for mobile ad hoc networks (full version). J. Inf. Comput. 207, 194–208 (2009)
Borgström, J., Huang, S., Johansson, M., Raabjerg, P., Victor, B., Åman Pohjola, J., Parrow, J.: Broadcast Psi-calculi with an application to wireless protocols. In: Barthe, G., Pardo, A., Schneider, G. (eds.) SEFM 2011. LNCS, vol. 7041, pp. 74–89. Springer, Heidelberg (2011)
Fehnker, A., van Glabbeek, R.J., Höfner, P., McIver, A., Portmann, M., Tan, W.L.: A process algebra for wireless mesh networks used for modelling, verifying and analysing AODV. CoRR abs/1312.7645 (2013)
Ene, C., Muntean, T.: A broadcast-based calculus for communicating systems. In: Proceedings of the 15th International Parallel & Distributed Processing Symposium, IPDPS 2001, Computer Society, p. 149. IEEE, Washington, DC (2001)
Johansson, M., Bengtson, J., Parrow, J., Victor, B.: Weak equivalences in Psi-calculi. In: LICS, pp. 322–331. IEEE Computer Society (2010)
Åman Pohjola, J., Parrow, J.: Priorities without priorities: representing preemption in Psi-calculi. In: Borgström, J., Crafa, S. (eds.) Proceedings Combined 21st International Workshop on Expressiveness in Concurrency, EXPRESS 2014, and 11th Workshop on Structural Operational Semantics, SOS 2014, Rome, Italy, 1st. vol. 160, EPTCS, 2–15 September 2014
Gardner, P., Wischik, L.: Explicit fusions. In: Nielsen, M., Rovan, B. (eds.) MFCS 2000. LNCS, vol. 1893, pp. 373–382. Springer, Heidelberg (2000)
Milner, R.: Calculi for synchrony and asynchrony. Theor. Comput. Sci. 25, 267–310 (1983)
Holmer, U.: Interpreting broadcast communication in SCCS. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 188–201. Springer, Heidelberg (1993)
Corradini, F., D’Ortenzio, D., Inverardi, P.: On the relationships among four timed process algebras. Fundam. Inf. 38, 377–395 (1999)
Moller, F., Tofts, C.: Relating processes with respect to speed. In: Baeten, J.C., Groote, J.F. (eds.) CONCUR ’91. Lecture Notes in Computer Science, vol. 527, pp. 424–438. Springer, Berlin Heidelberg (1991)
Lochbihler, A.: Coinductive. Archive of Formal Proofs 2010 (2010)
Ballarin, C.: Locales: a module system for mathematical theories. J. Autom. Reasoning 52, 123–153 (2014)
Palamidessi, C.: Comparing the expressive power of the synchronous and asynchronous pi-calculi. Math. Struct. Comput. Sci. 13, 685–719 (2003)
Peters, K., Nestmann, U.: Breaking symmetries. In: Fröschle, S.B., Valencia, F.D. (eds.) Proceedings 17th International Workshop on Expressiveness in Concurrency, EXPRESS 2010, Paris, France, 30 August 2010, vol. 41, pp. 136–150. EPTCS (2010)
Prasad, K.V.S.: Broadcast calculus interpreted in CCS upto bisimulation. Electr. Notes Theor. Comput. Sci. 52, 83–100 (2001)
Peters, K., Nestmann, U., Goltz, U.: On distributability in process calculi. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 310–329. Springer, Heidelberg (2013)
Acknowledgments
We are grateful to the anonymous reviewers for their many constructive comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Åman Pohjola, J., Parrow, J. (2016). The Expressive Power of Monotonic Parallel Composition. In: Thiemann, P. (eds) Programming Languages and Systems. ESOP 2016. Lecture Notes in Computer Science(), vol 9632. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49498-1_30
Download citation
DOI: https://doi.org/10.1007/978-3-662-49498-1_30
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49497-4
Online ISBN: 978-3-662-49498-1
eBook Packages: Computer ScienceComputer Science (R0)


 is called the transition relation.
is called the transition relation. , f is
, f is 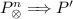 and
and 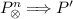 and
and 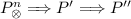 ,
,  implies
implies  for some
for some 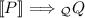 then there exists
then there exists  and
and  .
. and
and  . By definition of uniform encoding we get
. By definition of uniform encoding we get  with
with  and
and 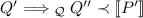 . By invariance, we get
. By invariance, we get  and
and  with
with 

 then
then  .
. then there exists
then there exists  and
and  then
then 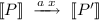 .
. then either
then either  and
and 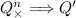 and
and  and
and 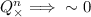 ; by Q-stability of f, g and since f, g are stable under
; by Q-stability of f, g and since f, g are stable under  and
and  , where
, where  . By applying the product rule j times we get
. By applying the product rule j times we get  . By Q-stability we have
. By Q-stability we have 