Abstract
We give an event structures based true-concurrency characterization of deep inference proofs. The method is general to all deep inference systems that can be expressed as term rewriting systems. This delivers three consequences in a spectrum from theoretical to practical: the event structure characterization (i) provides a qualification of proof identity akin to proof nets for multiplicative linear logic and to atomic flows for classical logic; (ii) provides a concurrency theoretic interpretation for applications in logic programming; (iii) reduces the length of the proofs, and thereby extends the margin of proof search applications.
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Deep inference [4] proofs are sequences of inference rule instances, which are essentially term rewrites of a rewriting system. The sequential construction of deep inference derivations imposes a total order structure that is beneficial in simplifying certain aspects of the proof theoretical analysis, for example, in an inductive argument for proving cut-elimination. However, such a bureaucratic view of derivations [6] also veils other aspects of proofs, and this has important implications. For example, at the more theoretical end of the spectrum, the causal dependence of the deduction components becomes hidden by the total order structure, and as a result of this, the derivations that are identical in terms of their deductive essence become presented as distinct syntactic objects.
To see this on an example, consider the following three proofs of the same multiplicative linear logic formula. While the first two proofs are identical with respect to their inference steps, they differ in the order of these steps, and thus they are depicted as syntactically distinct objects. On the other hand, the third proof is shorter, although it results in the same proof net [2] as the first two proofs. Moreover, from a computational point of view, the sequentiality of some of the rule instances in the first two proofs is redundant as the sequentiality does not imply a causal dependence; for example, the instances of the rule \({\mathsf {ai}{\downarrow }}\) are causally independent from each other.

In this respect, the lack of a formal mechanism that can identify the independence and causality in the derivations poses a problem. This problem was previously addressed by generalizing the deep inference formalism syntactically to partially capture some of the concurrency in derivations [6]. Here, we present an alternative approach via a labelled event structure (LES) characterization that provides a true-concurrency interpretation of deep inference derivations.
Event structures is a model of concurrency [14, 16], where the concurrent events are described with a partial order relation that formalizes their causal dependency, and nondeterminism is captured by a conflict relation, which is a symmetric irreflexive relation of events. In a proof search perspective, this corresponds to inference rules that are applicable in the same state, but are in conflict with each other in the sense that application of one of them instead of the other results in a different state space ahead. Figure 1 depicts in the middle the event structure for the example derivations above. There, the conflict-free structure on the left characterizes the two proofs on the left as well as two others, whereas the one on the right describes the single proof on the right and no other.
In the following, by relaxing the total order in deep inference derivations at incremental steps and by generalizing the approach in [7], we associate each formula an event structure, and show the correspondence between their conflict-free sub-structures and deep inference derivations. For the presentation, we use the multiplicative linear logic system \({\mathsf {MLS}}\), which is the simplest meaningful deep inference system. However, the methods should generalize to all the deep inference systems that can be expressed as term rewriting systems.
Our results provide a qualification of identity of proofs with respect to event structures, where all the derivations that only differ with respect to permutations of their inference rules are identified by a unique structure. Moreover, the event structure interpretation of derivations makes it possible to consider applications in logic programming that can exploit the true-concurrent nature of the derivations. This has also implications in proof search as a controlled use of concurrency becomes instrumental in reducing the length of the proofs, and thereby extends the margin of proof search applications.
2 Deep Inference
We use the term rewriting notation of deep inference systems modulo equational theories [10]. Other common representations for deep inference systems and derivations can be trivially obtained from the term rewriting notation without any loss of information.
Formulae (or structures) are defined in the usual way. For example, the multiplicative linear logic formulae P, Q, R, ... are generated by

where a stands for any atom; negation is defined on the atoms as a (non-identical) involution  , thus dual atom occurences, as a and
, thus dual atom occurences, as a and  , can appear in the formulae. \(\mathsf {1}\) and \(\bot \) are the units one and bottom, which are special atoms. Different kind of brackets are used to enhance readability, and they can be ignored.
, can appear in the formulae. \(\mathsf {1}\) and \(\bot \) are the units one and bottom, which are special atoms. Different kind of brackets are used to enhance readability, and they can be ignored.
Formulae are considered to be equivalent modulo a congruence relation. Within the term rewriting setting, term rewriting rules are applied modulo this relation. For multiplicative linear logic, we use the smallest congruence relation induced by the equational system consisting of the equations for associativity and commutativity for multiplicative disjunction and multiplicative conjunction.
Remark 1
We define negation only on atoms. This is not a limitation because of De Morgan laws. In deep inference systems in the literature, often the congruence relation includes equalities for the units of the logic. Here, we carry these equalities to the inference system to make their role in deduction more explicit.
Example 1
With respect to the congruence relation on the formulae, we have  and we can denote both formulae with
and we can denote both formulae with  .
.
Inference rules are rewriting rules. We define system \({\mathsf {MLS}}\) for multiplicative linear logic as the term rewiting system below, where r , t, u are generic terms that can match any formula, and x is a special term that can only match atoms.

A rule instance of the form  is defined by a rule \(\rho \), a function \(\mu \) that uniquely indicates the position of the redex, and a function \(\phi \) that assigns a substitution \(\sigma \). The rule instance is then given by an application of a rule \(\rho \) at the redex uniquely identified by \(\mu \) with a substitution \(\sigma \) such that \(\sigma \) provides a matching for the redex subterm \(R'\) of R with the left-hand side of the rule. That is, with \(\rho : l \rightarrow r\) and \(\mu (R) = R'\) and \(R' = l \sigma \), we get the contractum \(\mu (T) = r \sigma \). We call the triple \((\rho , \mu , \phi )\) an action. We denote actions with \(\mathsf {a}, \mathsf {b}, \mathsf {c},\ldots \)
is defined by a rule \(\rho \), a function \(\mu \) that uniquely indicates the position of the redex, and a function \(\phi \) that assigns a substitution \(\sigma \). The rule instance is then given by an application of a rule \(\rho \) at the redex uniquely identified by \(\mu \) with a substitution \(\sigma \) such that \(\sigma \) provides a matching for the redex subterm \(R'\) of R with the left-hand side of the rule. That is, with \(\rho : l \rightarrow r\) and \(\mu (R) = R'\) and \(R' = l \sigma \), we get the contractum \(\mu (T) = r \sigma \). We call the triple \((\rho , \mu , \phi )\) an action. We denote actions with \(\mathsf {a}, \mathsf {b}, \mathsf {c},\ldots \)
A derivation \(\varDelta \) is a formula or a finite chain of instances of rule instances. The left-most structure in a derivation is the premise, and the right-most formula is the conclusion. A derivation \(\varDelta \) whose premise is T, conclusion is R, and inference rules are in  is written as \(R \mathop {\longrightarrow }\limits ^{\varDelta } T\). A \({\mathsf {MLS}}\) proof \(\varPi \) is a derivation whose premise is the unit \(\mathsf {1}\). A derivation can also be written as the pair of the conclusion and the sequence of actions of the derivations, e.g.,
is written as \(R \mathop {\longrightarrow }\limits ^{\varDelta } T\). A \({\mathsf {MLS}}\) proof \(\varPi \) is a derivation whose premise is the unit \(\mathsf {1}\). A derivation can also be written as the pair of the conclusion and the sequence of actions of the derivations, e.g.,  .
.
Example 2
Consider the proof of the formula  below, where we denote the redexes with shading.
below, where we denote the redexes with shading.

We then write this derivation as 
Below, we associate to every formula a labelled event structure. Events correspond to instances of inference rules. In a LES events are partially ordered and there is a conflict relation amongst the events. The partial order relation provides a representation of independence and causality between these events, which can be, for example, due to resource production and consumption relationships, or modifications of structures as it is the case below. The conflict relation here represents the nondeterminism in the system. Events that are not in conflict can take place in a way, which respects the order determined by the partial order. Labelled event structures that we formally define below thus provide a computational model for logical expressions and their derivations. This results in a characterization of concurrency, given by the partial order and conflict relations that deliver the independence and causality relationships in the inference steps.
Definition 1
A labelled event structure is a structure \( (E, \le , \#, \mathcal {L} , \ell )\, , \) where
-
(i)
E is a set of events;
-
(ii)
\(\le \; \subseteq E^2\) is a partial order such that for every \(\mathsf {e} \in E\) the set \(\{ \mathsf {e'} \in E \; | \; \mathsf {e'} \le \mathsf {e} \, \}\) is finite;
-
(iii)
the conflict relation \(\# \, \subseteq E^2\) is a symmetric and irreflexive relation such that if \( \mathsf {e} \, \# \,\mathsf {e'} \) and \(\mathsf {e'} \le \, \mathsf {e''}\,\), then \(\mathsf {e} \, \# \, \mathsf {e''}\), for every \(\mathsf {e}, \mathsf {e'}, \mathsf {e''} \in E\,\);
-
(iv)
\(\mathcal {L}\) is a set of labels;
-
(v)
\(\ell : E \rightarrow \mathcal {L}\) is a labeling function.
Example 3
Figure 1 depicts the LES for the formula  .
.
3 Event Structures of Proofs
We associate to every formula an event structure that characterizes the independence and causality of the rule instances. We first associate to each formula a labelled transition system. We define labelled transition systems in the usual way, and denote states with s and transitions with t. Given a transition system, a path with length k is a sequence  of transitions such that
of transitions such that  or equivalently \(t_i = (s_{i-1},s_i, a)\) for \(i = 1, 2, \ldots \) and the initial state \( s_I = s_0\). We distinguish the transitions from rewrites with the notation \(\twoheadrightarrow \); rewrites and derivations are denoted with \(\rightarrow \) and \(\longrightarrow \).
or equivalently \(t_i = (s_{i-1},s_i, a)\) for \(i = 1, 2, \ldots \) and the initial state \( s_I = s_0\). We distinguish the transitions from rewrites with the notation \(\twoheadrightarrow \); rewrites and derivations are denoted with \(\rightarrow \) and \(\longrightarrow \).
Definition 2
Given a formula R and a set \(\mathcal {A}\) of actions of system \({\mathsf {MLS}}\) as defined above, \({\mathsf {TS}} {[\![} R {]\!]} = (\mathcal {S}, s_I, \mathcal {A}, \twoheadrightarrow )\) is the reachable transition system with the set of states \(\mathcal {S}\) such that  where \(\varDelta , \varDelta ' \in \mathcal {S}\) iff
where \(\varDelta , \varDelta ' \in \mathcal {S}\) iff
-
\(s_I = R \in \mathcal {S}\) is the initial state;
-
for some structure T, derivation \(\varDelta \) has the shape \(R \mathop {\longrightarrow }\limits ^{\varDelta } T\);
-
for some structure Q, there exists \(T \mathop {\rightarrow }\limits ^{\mathsf {a}} Q\) with \(\mathsf {a} = (\rho , \sigma ,\mu ) \in \mathcal {A}\);
-
\(\varDelta '\) is the derivation \(R \mathop {\longrightarrow }\limits ^{\varDelta } T \mathop {\rightarrow }\limits ^{\mathsf {a}} Q\;\).
We then write \(\varDelta \mathop {\twoheadrightarrow }\limits ^{\mathsf {a}} \varDelta '\;\).
For any formula R, \({\mathsf {TS}} {[\![} R {]\!]} \) is acyclic, because transitions result in bigger derivations. For a formula R, \({\mathsf {TS}} {[\![} R {]\!]} \) overlaps with the state space of the derivations with R in the conclusion; each state of \({\mathsf {TS}} {[\![} R {]\!]} \) is a reachable derivation.
As a first step towards observing the independence and the causality in the derivations, we consider two derivations equivalent if they have the same premise and conclusion. The following definition serves this purpose.
Definition 3
Let \(\mathcal {D}\) be the set of derivations, and R and T be formulae. \(\approx \; \subset \mathcal {D}^2\) is the least equivalence relation such that \(\varDelta \approx \varDelta '\) iff we have that
 denotes the equivalence class of the derivation \(\varDelta \) under \(\approx \). The set \(\mathcal {D}/\!\!\approx \,\), the set of equivalence classes of derivations under \(\approx \,\), is called the set of abstract derivations. The elements of \(\mathcal {D}/\!\!\approx \,\) are denoted by \(\delta \).
denotes the equivalence class of the derivation \(\varDelta \) under \(\approx \). The set \(\mathcal {D}/\!\!\approx \,\), the set of equivalence classes of derivations under \(\approx \,\), is called the set of abstract derivations. The elements of \(\mathcal {D}/\!\!\approx \,\) are denoted by \(\delta \).
Example 4
Consider the two derivations \(\varDelta \) and \(\varDelta '\) below with \(\varDelta \approx \varDelta '\).

Proposition 1
For any two states \(\varDelta \) and \(\varDelta '\) of \({\mathsf {TS}} {[\![} R {]\!]} \), if \(\varDelta \approx \varDelta '\) then for all \(\varDelta \mathop {\twoheadrightarrow }\limits ^{\mathsf {a}} \varDelta ''\) in \({\mathsf {TS}} {[\![} R {]\!]} \), there exists a transition \(\varDelta ' \mathop {\twoheadrightarrow }\limits ^{\mathsf {a}} \varDelta '''\) in \({\mathsf {TS}} {[\![} R {]\!]} \) with \(\varDelta '' \approx \varDelta '''\,\).
Proof
Because \(\varDelta ''\) and \(\varDelta '''\) have the same premises, same inference rules can be applied to the premises of these two derivations.
We now redefine transition systems that are associated with the formulae such that they respect the equivalence of derivations induced by the relation \(\approx \).
Definition 4
Given a formula R and a  , let
, let  be the transition system such that (i) \({s_I}_\approx = R\,;\;\,\) (ii) \(\mathcal {S}_\approx = \mathcal {S}/\!\approx \,;\;\,\) (iii)
be the transition system such that (i) \({s_I}_\approx = R\,;\;\,\) (ii) \(\mathcal {S}_\approx = \mathcal {S}/\!\approx \,;\;\,\) (iii)  where
where  .
.
As a result of this definition, transition systems are not trees anymore, but they are graphs. For the case of system \({\mathsf {MLS}}\), because each inference rule results in an incremental step in a terminating computation, the \({\mathsf {TS}}_\approx {[\![} R {]\!]}\) graphs are acyclic. However, \({\mathsf {TS}}_\approx {[\![} R {]\!]}\) graphs can in general be cyclic, for example, if the deductive system involves a cut rule or a contraction rule.
Definition 5
Let R be a formula and  be a finite path in \({\mathsf {TS}}_\approx {[\![} R {]\!]}\). \(\tau \) is an abstract path yielding \(\delta _h\), if, for all \(1 \le i \le h\), \(t_i = (\delta _{i - 1} , \delta _i, a_i )\).
be a finite path in \({\mathsf {TS}}_\approx {[\![} R {]\!]}\). \(\tau \) is an abstract path yielding \(\delta _h\), if, for all \(1 \le i \le h\), \(t_i = (\delta _{i - 1} , \delta _i, a_i )\).
The intuition behind abstract paths can be better understood from the point of view of their transitions: given \(\delta \mathop {\twoheadrightarrow }\limits ^{\mathsf {a}} \delta '\), we have that \(\delta \) is the equivalence class of derivations with a premise T and conclusion R, and we have \(T \mathop {\rightarrow }\limits ^{\mathsf {a}} Q\) such that \(\delta '\) is the equivalence class of derivations with a premise Q and conclusion R. Because \({\mathsf {TS}} {[\![} R {]\!]} \) is by definition reachable, \({\mathsf {TS}}_\approx {[\![} R {]\!]}\) is also reachable.
Definition 6
Given a formula R and \({\mathsf {TS}}_\approx {[\![} R {]\!]}\), let the relation  be such that \((\mathsf {a} , \mathsf {a'}, \delta , \delta ', \delta '', \delta ''') \in \diamondsuit \) iff \((\delta , \delta ', \mathsf {a})\), \((\delta , \delta '', \mathsf {a'})\), \((\delta ', \delta ''', \mathsf {a'})\), and \((\delta '', \delta ''', \mathsf {a})\) are in \({\mathsf {TS}}_\approx {[\![} R {]\!]}\). We call \(\diamondsuit \) the diamond relation of \({\mathsf {TS}}_\approx {[\![} R {]\!]}\).
be such that \((\mathsf {a} , \mathsf {a'}, \delta , \delta ', \delta '', \delta ''') \in \diamondsuit \) iff \((\delta , \delta ', \mathsf {a})\), \((\delta , \delta '', \mathsf {a'})\), \((\delta ', \delta ''', \mathsf {a'})\), and \((\delta '', \delta ''', \mathsf {a})\) are in \({\mathsf {TS}}_\approx {[\![} R {]\!]}\). We call \(\diamondsuit \) the diamond relation of \({\mathsf {TS}}_\approx {[\![} R {]\!]}\).
The diamond relation corresponds to the permutability of the inference rules over each other in the standard deep inference notation, e.g., [15]. With this definition, we do not distinguish anymore the derivations that differ only in the permutations of their inference rules. Below, we thus propagate the diamond relation to paths, and this way establish an equivalence relation on the paths.
Example 5
For an \({\mathsf {MLS}}\) derivation with formula R in the conclusion, let \(\delta \), \(\delta '\), \(\delta ''\) and \(\delta '''\) be equivalence classes of derivations such that we have the graph in Fig. 2 with  and
and  . Then we have \((\mathsf {a},\mathsf {a}', \delta , \delta ', \delta '', \delta ''')\), where \(\phi _1\) maps \(\sigma _1\) to
. Then we have \((\mathsf {a},\mathsf {a}', \delta , \delta ', \delta '', \delta ''')\), where \(\phi _1\) maps \(\sigma _1\) to  , and \(\phi _2\) maps \(\sigma _2\) to
, and \(\phi _2\) maps \(\sigma _2\) to  and
and  on the left and on the right, respectively.
on the left and on the right, respectively.
With the following definition we propagate the diamond relation from derivations to paths, and this way prepare the grounds for defining a transition system whose states are paths rather than derivations.
Definition 7
Given  and its diamond relation \(\diamondsuit \), the relation \(\backsimeq \) is the least equivalence relation such that, for any two paths
and its diamond relation \(\diamondsuit \), the relation \(\backsimeq \) is the least equivalence relation such that, for any two paths

if \(\, ( \mathsf {a} , \mathsf {a'} , \delta , \delta ' , \delta '' , \delta ''' ) \in \diamondsuit \), then \(\tau _1 \backsimeq \tau _2\).
Proposition 2
Given finite paths \(\tau _1\) and \(\tau _2\) in \({\mathsf {TS}}_\approx {[\![} R {]\!]}\), if \(\tau _1 \backsimeq \tau _2\), then they both yield the same state in \({\mathsf {TS}}_\approx {[\![} R {]\!]}\).
The labelled event structure for a formula R is obtained from a transition system defined on paths such that all paths reaching a certain state belong to the same equivalence class induced by \(\backsimeq \,\). Below we define this transition system based on the \({\mathsf {TS}}_\approx {[\![} R {]\!]}\) and the equivalence relation \(\backsimeq \) on its paths.
Definition 8
Given an \({\mathsf {MLS}}\) formula R and  ,
,  is the transition system such that
is the transition system such that
-
(i)
\(\mathcal {S}_\simeq = \mathcal {T} / \! \simeq \), where \(\mathcal {T}\) is the set of finite paths in \({\mathsf {TS}}_\approx {[\![} R {]\!]}\) and \(\simeq \) is the equivalence relation on its paths induced by the diamond relation \(\diamondsuit \) of \({\mathsf {TS}}_\approx {[\![} R {]\!]}\). Elements of \(\mathcal {S}_\simeq \) are denoted by \(\pi \,\);
-
(ii)
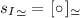 ;
; -
(iii)
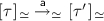 iff
iff 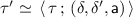 where \((\delta , \delta ', \mathsf {a}) \in \; \rightarrow _{\approx }\).
where \((\delta , \delta ', \mathsf {a}) \in \; \rightarrow _{\approx }\).
Proposition 3
For every formula R, \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) is reachable and acyclic.
Proof
\({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) is obtained from \({\mathsf {TS}}_\approx {[\![} R {]\!]}\) which is reachable. Because each transition transforms an abstract path to a syntactically bigger abstract path, \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) is acyclic.
Example 6
The transition system \(\mathsf {TS}_\simeq \) associated to the formula  is depicted in Fig. 3.
is depicted in Fig. 3.
A LES of a formula R is obtained from \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\,\) by extracting the transitions denoting the same events. To obtain this information, we propagate the diamond relation of the transition systems \(\mathsf {TS}_\approx \) to the transition systems \(\mathsf {TS}_\simeq \), that is, from the equivalence classes of derivations to the equivalence classes of paths.
Definition 9
Given a formula R and the diamond relation \(\diamondsuit \) of \({\mathsf {TS}}_\approx {[\![} R {]\!]}\,\), we define  for \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) as the relation such that, for some abstract paths \(\tau ,\tau ' ,\tau '', \tau '''\), we have \(( \mathsf {a} , \mathsf {a'} , [\tau ]_\simeq , [\tau ']_\simeq , [\tau '']_\simeq , [\tau ''']_\simeq ) \in \diamondsuit _\simeq \) iff
for \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) as the relation such that, for some abstract paths \(\tau ,\tau ' ,\tau '', \tau '''\), we have \(( \mathsf {a} , \mathsf {a'} , [\tau ]_\simeq , [\tau ']_\simeq , [\tau '']_\simeq , [\tau ''']_\simeq ) \in \diamondsuit _\simeq \) iff

and \((\mathsf {a} , \mathsf {a'}, \delta , \delta ', \delta '', \delta ''') \in \diamondsuit \) for some states \(\delta , \delta ', \delta ''\) and \(\delta '''\) of \({\mathsf {TS}}_\approx {[\![} R {]\!]}\,\).
Definition 10
Given  and its diamond relation
and its diamond relation  , the relation \(\, \sim \;\) is the least equivalence relation on \(\, t, t'\in \; \rightarrow _\simeq \, \) such that
, the relation \(\, \sim \;\) is the least equivalence relation on \(\, t, t'\in \; \rightarrow _\simeq \, \) such that
and there exists  such that
such that 
Intuitively, two transitions are in \(\sim \) if they represent the same event.
Example 7
Let \(\tau \) be an abstract path that leads to a derivation with the formula  at the premise. Then we have
at the premise. Then we have

We then have  . Then we have \(t \sim t'\) for
. Then we have \(t \sim t'\) for

Definition 11
Given a formula R and  , let
, let  be the labelled event structure such that
be the labelled event structure such that
-
(i)
\(E = \; \rightarrow _\simeq \!/\! \sim \,\);
-
(ii)
\(\le \) is the reflexive closure of <, which is defined as follows: for all \(\mathsf {e}, \mathsf {e'} \in E\), \(\mathsf {e} < \mathsf {e'}\) iff
 and
and 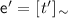 , and for every path \(\tau \) in \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) and for every \(t''' \in \; \rightarrow _\simeq \) such that
, and for every path \(\tau \) in \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) and for every \(t''' \in \; \rightarrow _\simeq \) such that 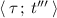 is a path and \(t''' \sim t'\), there exists \(t'' \sim t\) such that
is a path and \(t''' \sim t'\), there exists \(t'' \sim t\) such that 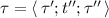 for some \(\tau ', \tau ''\,\);
for some \(\tau ', \tau ''\,\); -
(iii)
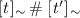 iff for every path \(\tau \) in \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) and for every \(t'', t''' \in \, \rightarrow _\simeq \) such that \(t \sim t''\) and \(t' \sim t'''\), if \(t''\) appears in \(\tau \), then \(t'''\) does not appear in \(\tau \);
iff for every path \(\tau \) in \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) and for every \(t'', t''' \in \, \rightarrow _\simeq \) such that \(t \sim t''\) and \(t' \sim t'''\), if \(t''\) appears in \(\tau \), then \(t'''\) does not appear in \(\tau \); -
(iv)
 .
.
The partial order relation of a LES provides a representation of independence and causality between different events. The events that are left unordered by \(\le \) are independent, thus their ordering in execution with respect to each other does not affect the behavior of the system. In deep inference derivations, this independence corresponds to the permutability of the instances of the inference rules: the independent rule instances can be applied to a formula in any order as their instances do not create a conflict for their mutual applicability. In contrast, the events that are ordered by the relation \(\le \) follow a chain of causality, that is, for an event \(\mathsf {e}\), all events \(\mathsf {e'} < \mathsf {e}\), the execution of \(\mathsf {e}\) is impossible without the prior execution of \(\mathsf {e'}\). For the deep inference proofs such a causal dependence is a consequence of the structural relations that are modified by the instances of the inference rules that make a rule instance necessary prior to another one.
The relation \(\#\) is an irreflexive relation on events that expresses conflicting situations in execution. If \(e \,\# \,e'\), then event e and \(e'\) are competing for resources, thus execution of e conflicts with the execution of \(e'\), and vice versa, which requires a choice of one over the other. In the deep inference proofs, this corresponds to the different choices in the construction of derivations due to multiple rule instances that can be applicable to a formula at each inference step.
Example 8
The \(\mathsf {LES}\) associated to the formula  is depicted in Fig. 1, where we abbreviate events with their labels.
is depicted in Fig. 1, where we abbreviate events with their labels.
The notions of LES result in a concurrent model of all the possible derivations of formula, which we characterize with the definitions below.
Definition 12
Given a \(\mathsf {LES}\)  , for an event \(\mathsf {e} \in E\), \({\lfloor } \mathsf {e} {\rfloor }\) denotes the set \(\{ \mathsf {e'} \in E \; | \; \mathsf {e'} < \mathsf {e} \, \}\) of causes of event \(\mathsf {e}\).
, for an event \(\mathsf {e} \in E\), \({\lfloor } \mathsf {e} {\rfloor }\) denotes the set \(\{ \mathsf {e'} \in E \; | \; \mathsf {e'} < \mathsf {e} \, \}\) of causes of event \(\mathsf {e}\).
The causes of an event \(\mathsf {e}\) is the set that collects those events that event \(\mathsf {e}\) requires in order to take place. In the deep inference derivations, the causes of a rule instance at an inference step is the set of rule instances that modify the formula in such a way that makes that rule instance possible. Configurations, that we define below, collect such causally related events that are not in conflict, while preserving the information on the independence of different causes.
Definition 13
Given a \(\mathsf {LES}\) \(( E , \le , \# , L, \ell )\),  is a configuration iff
is a configuration iff
-
(i)
for all
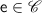 we have that
we have that  ;
; -
(ii)
for all
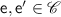 , it is not the case that \(\mathsf {e} \, \# \, \mathsf {e'}\).
, it is not the case that \(\mathsf {e} \, \# \, \mathsf {e'}\).
Definition 14
Given a \(\mathsf {LES}\) \(( E , \le , \# , L, \ell )\), and one of its configurations  , we say that event \(\mathsf {e}\) is enabled at
, we say that event \(\mathsf {e}\) is enabled at  (denoted by
(denoted by  ) if and only if
) if and only if
(i)  ; (ii)
; (ii)  ; (iii) \(\mathsf {e'} \, \# \, \mathsf {e}\) implies
; (iii) \(\mathsf {e'} \, \# \, \mathsf {e}\) implies  .
.
Example 9
Consider the LES in Fig. 1. Let us abbreviate the events with their labels. We have that  , and there exists a configuration
, and there exists a configuration 
 such that
such that  .
.
Informally, an event \(\mathsf {e}\) is enabled at a configuration  if it is not in
if it is not in  , all the events on which it depends are in
, all the events on which it depends are in  and it does not conflict with any event in
and it does not conflict with any event in  . Let us now define securings, which are serializations of events in configurations.
. Let us now define securings, which are serializations of events in configurations.
Definition 15
Given a \(\mathsf {LES}\) \(( E , \le , \# , L , \ell )\) and a finite sequence of events  , \(\mathsf {S}\) is a securing for
, \(\mathsf {S}\) is a securing for  if and only if
if and only if  is a configuration and, for all \(1 \le i \le h\), \(\{ e_1, \ldots , e_{i-1} \} \vartriangleright e_i\,\).
is a configuration and, for all \(1 \le i \le h\), \(\{ e_1, \ldots , e_{i-1} \} \vartriangleright e_i\,\).
Example 10
From the LES in Fig. 1, we can read nine derivations, which can be read as the securings in  , obtained from four configurations in Fig. 4. The first two derivations do not result in a proof.
, obtained from four configurations in Fig. 4. The first two derivations do not result in a proof.

Four configurations obtained from the LES depicted in Fig. 1.
The following results are analogous to the results on search spaces of multiset rewriting encodings in multiplicative exponential linear logic in deep inference [8], following the discussions above with respect to the ideas presented in [3, 14, 16]. They demonstrate, for any \({\mathsf {MLS}}\) formula R, the formal correspondence between the transition systems \({\mathsf {TS}} {[\![} R {]\!]} \) and the \({\mathsf {LES}} {[\![} R {]\!]}\).
Theorem 1
Given a formula R,  and a securing \(\mathsf {S}\) in \({\mathsf {LES}} {[\![} R {]\!]}\), there is a path \(R \mathop {\twoheadrightarrow }\limits ^{\ell (\mathsf {S})} \varDelta \) in \({\mathsf {TS}} {[\![} R {]\!]} \).
and a securing \(\mathsf {S}\) in \({\mathsf {LES}} {[\![} R {]\!]}\), there is a path \(R \mathop {\twoheadrightarrow }\limits ^{\ell (\mathsf {S})} \varDelta \) in \({\mathsf {TS}} {[\![} R {]\!]} \).
Theorem 2
Given a formula R and a path  in \({\mathsf {TS}} {[\![} R {]\!]} \), there is a securing \(\mathsf {S}\) in
in \({\mathsf {TS}} {[\![} R {]\!]} \), there is a securing \(\mathsf {S}\) in  such that
such that  .
.
For an exposure of the relationship between transition systems, labelled event structures, and other models for concurrency, we refer the reader to [14, 16].
4 From Deep Inference Derivations to Configurations
A configuration in a LES of a formula can be considered as a canonical representation of a set of derivations with the same premise and conclusion, which however differ in their orders of the rule instances due to permutations. Conversely, inference rules in a derivation can be permuted to obtain other derivations that have the same premise and conclusion. Below by exploiting this observation, we introduce an algorithm for obtaining configurations from \({\mathsf {MLS}}\) derivations.
Definition 16
We denote labels that range over actions with letters \(\mathsf {a},\mathsf {b},\mathsf {c}, \ldots \) Let \(\varDelta \) be an \({\mathsf {MLS}}\) derivation such that each subformula in \(\varDelta \) is labeled with the special action \(\epsilon \) as a subscript and each inference rule modifies these labels as described below. The function \(\psi \) on \(\varDelta \) is defined as follows. If \(\varDelta \) is a formula then \(\psi (\varDelta ) = \emptyset \). Otherwise, if \(\varDelta \) is of the form \(R \mathop {\rightarrow }\limits ^{\rho } R' \mathop {\longrightarrow }\limits ^{\varDelta '} T\) and the instance of the rule \(\rho \) with its action \(\mathsf {a}\) is an instance of
-
 with
with 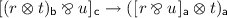 then
then  ;
; -
 with
with  then
then 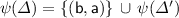 ;
; -
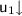 with
with  then
then  ;
; -
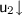 with
with 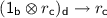 then
then 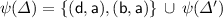 .
.
Given a derivation \(\varDelta \) with a formula R in the conclusion, a constraint set of \(\varDelta \) for R (\(\mathcal {C}_{R,\varDelta }\)) is given with \(\psi (\varDelta )\).
Function \(\psi \) extracts the production and consumption relationships between rule instances, and this way provides a canonical representation of all derivations that are different from the input derivation only with respect to rule permutations. This is because each action at each inference step modifies, annihilates or produces a subformula that has been introduced by another. By keeping track of these relationships as a representation of causality, we obtain a configuration.
Example 11
We label the derivation below according to Definition 16 and apply function \(\psi \). We obtain the set \(\mathcal {C} = \mathcal {C}_4\), which provides a canonical representation of four derivations. Any of these four derivations delivers the same set \(\mathcal {C}\).

Remark 2
There can be cases in derivations due to identical subformulae with different labels, which correspond to different configurations. For example, consider the instance below, which can result in two different constraint sets due to the choice of the redex of the \({\mathsf {ai}{\downarrow }}\) rule. This nondeterminism is due to the choice of the redex of the rule instance at the inference step.

Proposition 4
For any derivation \(\varDelta \), \(\psi (\varDelta )\) terminates in linear time in the number of atoms in \(\varDelta \).
Proposition 5
Let R be a multiplicative linear logic formula with a derivation \(\varDelta \) and \(\mathcal {C}_{R,\varDelta }\) be their constraint set. \(\mathcal {C}_{R,\varDelta }\) is irreflexive and antisymetric.
Proof
Follows from an inspection of the steps of function \(\psi \) in Definition 16: none of the actions introduces a constraint of the form (x, x), and the inductive steps of \(\psi \) introduce a new action as the second of a pair (x, y) at each step.
Definition 17
Let R be a multiplicative linear logic formula with a derivation \(\varDelta \) and \(\mathcal {C}_{R,\varDelta }\) be the constraint set. The concurrent derivation of \(\varDelta \) for R, and denoted with \(\mathsf {Con}_{R,\varDelta }\), is the transitive reflexive closure of \(\mathcal {C}_{R,\varDelta }\).
Remark 3
For any constraint set \(\mathcal {C}_{R,\varDelta }\), \(\mathsf {Con}_{R,\varDelta }\) is a partial order.
Definition 18
A linearization \(\mathsf {Lin}\) of a concurrent derivation \(\mathsf {Con}_{R,\varDelta }\) is a strict total order of the actions of \(\mathsf {Con}_{R,\varDelta }\) such that \(\mathsf {Con}_{R,\varDelta } \subseteq \mathsf {Lin}\). Given a linearization \(\mathsf {Lin}\) of \(\mathsf {Con}_{R,\varDelta }\), the derivation induced by \(\mathsf {Lin}\) is the derivation with R in the conclusion, constructed by applying the actions of \(\mathsf {Lin}\) with respect to their order.
Theorem 3
For a derivation \(R \mathop {\longrightarrow }\limits ^{\varDelta } T\) in \({\mathsf {MLS}}\), any derivation \(\varDelta '\) induced by a linearization \(\mathsf {Lin}\) of \(\mathsf {Con}_{R,\varDelta }\) has the premise T. In other words, if \(\varDelta '\) is a derivation induced by a linearization \(\mathsf {Lin}\) of \(\mathsf {Con}_{R,\varDelta }\) then it has the premise T.
Proof
Proof by induction on the length of \(\varDelta \). If \(k =0\), then \(\mathcal {C} = \emptyset \), hence \(\mathsf {Lin} = \emptyset \). Then the only linearization of \(\mathsf {Con}_{R,\varDelta }\) is \(R = T\).
For the inductive case, let \(\varDelta \) be of the form \(R \mathop {\longrightarrow }\limits ^{\varDelta _k} T' \mathop {\rightarrow }\limits ^{\rho } T \). Let \(\psi (\varDelta _k) = \mathcal {C}_k\) and \(\mathsf {Con}_{R,\varDelta _k}\) be the corresponding concurrent derivation. By induction hypothesis, any derivation \({\varDelta '_k}\) induced by a linearization \(\mathsf {Lin}_k\) of \(\mathsf {Con}_{R,\varDelta _k}\) has the premise \(T'\) and by applying \(\rho \) to \(T'\) we obtain T. Let \({\varDelta '_k}\) be  . For any \(\rho \in {\mathsf {MLS}}\) and its action \(\mathsf {a}\), we have that, for \(\mathsf {a}_i, \mathsf {a}_j \in \{\mathsf {a}_1,\ldots , \mathsf {a}_k\}\), \(\mathcal {C}\) is given by
. For any \(\rho \in {\mathsf {MLS}}\) and its action \(\mathsf {a}\), we have that, for \(\mathsf {a}_i, \mathsf {a}_j \in \{\mathsf {a}_1,\ldots , \mathsf {a}_k\}\), \(\mathcal {C}\) is given by
-
(a)
either \( \psi (\varDelta ) = \{ ( \mathsf {a}_i , \mathsf {a}) , ( \mathsf {a}_j , \mathsf {a}) \} \, \cup \, \mathcal {C}_k\),
-
(b)
or \(\psi (\varDelta ) = \{ ( \mathsf {a}_i , \mathsf {a}) \} \, \cup \, \mathcal {C}_k\).
We proceed as in case (a) since the case (b) follows from (a). Let \(\mathsf {Con}_{R,\varDelta }\) be the concurrent derivation obtained from \(\mathcal {C}\), that is, \(\mathsf {Con}_{R,\varDelta }\) is the reflexive transitive closure of \(\mathcal {C}\). By induction hypothesis, for any linearization of \(\mathsf {Con}_{R,\varDelta _k}\), we have that  is a derivation with T at the premise.
is a derivation with T at the premise.
In any linearization \(\mathsf {Lin}\) of \(\mathsf {Con}_{R,\varDelta }\) we have that either \((\mathsf {a}_i , \mathsf {a_j} )\) or \((\mathsf {a}_j , \mathsf {a_i} )\). Let us assume the former (since otherwise we have an analogous case). Given that \(( \mathsf {a}_j , \mathsf {a}) \in \, \mathcal {C}\), the redex of \(\mathsf {a}\) is not modified by any \(\mathsf {a}_n \in \{\mathsf {a}_{j+1} , \ldots , \mathsf {a}_k \}\), which implies that for any derivation  induced by a linearization of \(\mathsf {Con}_{R,\varDelta _k}\), the linearizations induced by \(\mathsf {Con}_{R,\varDelta }\) are enumerated by all the derivations where \(\mathsf {a}\) is applied anywhere after \(\mathsf {a}_j\). Because no action \(\mathsf {a}_n \in \{\mathsf {a}_{j+1} , \ldots , \mathsf {a}_k \}\) modifies the redex of \(\mathsf {a}\), the derivation has the premise T.
induced by a linearization of \(\mathsf {Con}_{R,\varDelta _k}\), the linearizations induced by \(\mathsf {Con}_{R,\varDelta }\) are enumerated by all the derivations where \(\mathsf {a}\) is applied anywhere after \(\mathsf {a}_j\). Because no action \(\mathsf {a}_n \in \{\mathsf {a}_{j+1} , \ldots , \mathsf {a}_k \}\) modifies the redex of \(\mathsf {a}\), the derivation has the premise T.
Corollary 1
For any \({\mathsf {MLS}}\) formula R and derivation \(R \mathop {\longrightarrow }\limits ^{\varDelta } T\), \(\mathsf {Con}_{R,\varDelta }\) is a configuration in \({\mathsf {LES}} {[\![} R {]\!]}\).
5 From Concurrent Derivations to Proof Search
Because of the exponential blow up in proof search that is a consequence of hard complexity bounds [7, 11], the margin of successful applications are determined by the interplay between the breadth of the search space, nondeterminism and length of proofs. In general, deep inference provides short proofs due to a more immediate access to subformulae [1, 9]. However, the greater nondeterminism and resulting large breadth of search space hinders broad proof search applications that benefit from these short proofs. In [9], we have provided a formal method that reduces nondeterminism in deep inference proof search, and this way provides a more immediate access to shorter proofs. Below, we demonstrate that this method together with the true-concurrency characterization above provides a means to simultaneously reduce nondeterminism and proof length. This is because an untamed introduction of concurrency can result in an excessive increase in the breadth of the search space. However, a formal mechanism such as the following can provide control on search-space-breadth due to concurrency.
Definition 19
Given a formula R, \({\mathsf {at}} \, R\) is the set of the atoms in R.
Example 12
For  , we have \({\mathsf {at}} \, R = \{ a, \lnot {a}, b,\lnot {b}, \bot \}\).
, we have \({\mathsf {at}} \, R = \{ a, \lnot {a}, b,\lnot {b}, \bot \}\).
Definition 20
[9] Consider the switch rule.

We say that an instance of switch is an instance of interaction switch \(\mathsf {(is)}\) iff
-
(i)
r and u are matched to formulae R and U such that \({\mathsf {at}}\, \overline{R} \, \cap \, {\mathsf {at}}\, U \ne \emptyset \), that is, R and U contain complementary atoms.
-
(ii)
u is matched to formula that is a conjunction or an atom different from \(\bot \).
-
(iii)
r is matched to formula that is a disjunction or an atom different from \(\mathsf {1}\).
Definition 21
[9] System \({\mathsf {MLSi} }\) is the system obtained by replacing the switch rule in system \({\mathsf {MLS}}\) with the interaction switch rule.
Example 13
Consider the formula  with the transition system \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) depicted in Fig. 3 and \({\mathsf {LES}} {[\![} R {]\!]}\) depicted in Fig. 1. By using system \({\mathsf {MLSi} }\) instead of system \({\mathsf {MLS}}\) we obtain \(\mathsf {TS}'_\simeq ({R})\) and \(\mathsf {LES}'({R})\) depicted in Fig. 5, which prune the two \({\mathsf {MLS}}\) derivations that do not result in a proof.
with the transition system \({\mathsf {TS}}_\simeq {[\![} R {]\!]}\) depicted in Fig. 3 and \({\mathsf {LES}} {[\![} R {]\!]}\) depicted in Fig. 1. By using system \({\mathsf {MLSi} }\) instead of system \({\mathsf {MLS}}\) we obtain \(\mathsf {TS}'_\simeq ({R})\) and \(\mathsf {LES}'({R})\) depicted in Fig. 5, which prune the two \({\mathsf {MLS}}\) derivations that do not result in a proof.
Theorem 4
[9] Systems \({\mathsf {MLS}}\) and \({\mathsf {MLSi} }\) prove the same formulae, that is, system \({\mathsf {MLSi} }\) is complete for multiplicative linear logic.
Example 14
In systems \({\mathsf {MLS}}\) and \({\mathsf {MLSi} }\) the shortest proof of  has length three as illustrated in Fig. 1. However, by resorting to the causally independent true-concurrent characterization of derivations we can obtain proofs of length two by composing rules in parallel as hinted in Fig. 5. Below we first apply the composition of the causally independent rules \(\mathsf {s}\) and \({\mathsf {ai}{\downarrow }}\), and then the composition of the rules \({\mathsf {u}_2{\downarrow }}\) and \({\mathsf {ai}{\downarrow }}\).
has length three as illustrated in Fig. 1. However, by resorting to the causally independent true-concurrent characterization of derivations we can obtain proofs of length two by composing rules in parallel as hinted in Fig. 5. Below we first apply the composition of the causally independent rules \(\mathsf {s}\) and \({\mathsf {ai}{\downarrow }}\), and then the composition of the rules \({\mathsf {u}_2{\downarrow }}\) and \({\mathsf {ai}{\downarrow }}\).

6 Discussion
The partial order representation of derivations provides a canonical representation of the derivations that differ only with respect to permutation of inference rules, but that are in essence identical. Such a characterization provides a qualification of identity of proofs with respect to rule permutations, while distinguishing proofs that differ in the inference steps that they take. A similar characterization is provided, for example, by proof nets for the case of multiplicative linear logic [2]. However, proof nets lack any information about the deductive steps performed in the proof. In contrast, in our approach, proofs that have identical proof nets can be distinguished with respect to their different configurations that result from distinct inference strategies. This aspect, which is illustrated in Fig. 4 and Example 10, is one of the contributions of this paper. Such considerations are also addressed by atomic flows for classical logic [5, 6].
The event structure characterization of derivations exploits the independence and causality of rule instances such that the rule instances that are not causally dependent become partially ordered. This partial order characterization relaxes their total order representation in the standard deep inference syntax, which is in fact recognized as a bureaucratic constraint rather than a logical requirement [6]. As a result of the event structure characterization, our method reveals the true-concurrent nature of derivations, which should find applications in logic programming. Within the computation as proof search paradigm that uses deductive systems as a framework for logic programming [12, 13], such a true concurrent interpretation of proof construction should broaden the potential applications.
As we have demonstrated in the previous section, the true-concurrency characterization of the derivations provides a point of view of the rule instances that exposes their independence in proof search. This in return provides a means for concurrent application of inference rules in a way that reduces the length of the proofs. Although uncontrolled use of concurrency can result in an excessive increase in the breadth of search space, introducing control by means of other orthogonal methods for reducing nondeterminism [9] should result in improvement in proof search applications.
Topics of further investigation include carrying these methods to other logics with deep inference systems within a more general framework, and their exploration with respect to applications in logic programming and proof search.
References
Bruscoli, P., Guglielmi, A.: On the proof complexity of deep inference. ACM Trans. Computat. Logic 2(14), 1–34 (2009)
Girard, J.-Y.: Linear logic: Its syntax and semantics. In: Girard, J.-Y., Lafont, Y., Regnier, L. (eds.) Advances in Linear Logic (Proceedings of the Workshop on Linear Logic, Cornell University), vol. 222. Cambridge University Press (1995)
Guglielmi, A.: Abstract Logic Programming in Linear Logic Independence and Causality in a First Order Calculus. Ph.D. thesis, Universita di Pisa (1996)
Guglielmi, A.: A system of interaction and structure. ACM Trans. Comput. Logic 8(1), 1–64 (2007)
Guglielmi, A., Gundersen, T.: Normalisation control in deep inference via atomic flows. Log. Methods Comput. Sci. 4(1:9), 1–36 (2008)
Guglielmi, A., Gundersen, T., Parigot, M.: A proof calculus which reduces syntactic bureaucracy. In: Proceedings of the International Conference on Rewriting Techniques and Applications 2010 (Edinburgh), pp. 135–150. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik 2010 LIPIcs (2010)
Kahramanoğulları, O.: System BV is NP-complete. Ann. Pure Appl. Logic 152(1–3), 107–121 (2008)
Kahramanoğulları, O.: On linear logic planning and concurrency. Inform. Comput. 207(11), 1229–1258 (2009)
Kahramanoğulları, O.: Interaction and depth against nondeterminism in proof search. Log. Methods Comput. Sci. 10(2:5), 1–49 (2014)
Kahramanoğulları, O.: Maude as a platform for designing and implementing deep inference systems. In: Proceedings of the Eighth International Workshop on Rule-Based Programming, RULE 2007. ENTCS, vol. 219, pp. 35–50. Elsevier (2008)
Kanovich, M.: The multiplicative fragment of linear logic is NP-complete. Technical Report X-91-13, Institute for Language, Logic, and Information (1991)
Miller, D.: Forum: a multiple-conclusion specification logic. Theor. Comput. Sci. 165, 201–232 (1996)
Miller, D.: Overview of linear logic programming. In: Ehrhard, T., Girard, J.-Y., Ruet, P., Scott, P. (eds.) Linear Logic in Computer Science. London Mathematical Society Lecture Note, vol. 316. Cambridge University Press, Cambridge (2004)
Sassone, V., Nielsen, M., Winskel, G.: Models for concurrency: towards a classification. Theor. Comput. Sci. 170(1–2), 297–348 (1996)
Strassburger, L., Guglielmi, A.: A system of interaction and structure IV: The exponentials anddecomposition. ACM Trans. Comp. Logic 12(4), 1–39 (2011)
Winskel, G., Nielsen, M.: Models for concurrency. In: Abramsky, S., Gabbay, D.M., Maibaum, T.S.E. (eds.) Handbook of Logic in Computer Science, vol. 4, pp. 1–148. Oxford University Press, Oxford (1995)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Kahramanoğulları, O. (2016). True Concurrency of Deep Inference Proofs. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds) Logic, Language, Information, and Computation. WoLLIC 2016. Lecture Notes in Computer Science(), vol 9803. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-52921-8_16
Download citation
DOI: https://doi.org/10.1007/978-3-662-52921-8_16
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-52920-1
Online ISBN: 978-3-662-52921-8
eBook Packages: Computer ScienceComputer Science (R0)





 . The symbol
. The symbol 
 in the transition system
in the transition system 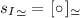 ;
;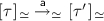 iff
iff 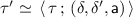 where
where 
 and the pathways that result in seven distinct
and the pathways that result in seven distinct  and
and 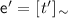 , and for every path
, and for every path 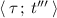 is a path and
is a path and 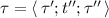 for some
for some 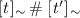 iff for every path
iff for every path  .
.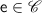 we have that
we have that  ;
;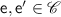 , it is not the case that
, it is not the case that 
 with
with 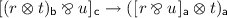 then
then  ;
; with
with  then
then 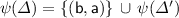 ;
;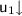 with
with  then
then  ;
;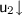 with
with 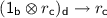 then
then 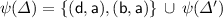 .
.