Abstract
We initiate the study of multi-user (mu) security of authenticated encryption (AE) schemes as a way to rigorously formulate, and answer, questions about the “randomized nonce” mechanism proposed for the use of the AE scheme GCM in TLS 1.3. We (1) Give definitions of mu ind (indistinguishability) and mu kr (key recovery) security for AE (2) Characterize the intent of nonce randomization as being improved mu security as a defense against mass surveillance (3) Cast the method as a (new) AE scheme RGCM (4) Analyze and compare the mu security of both GCM and RGCM in the model where the underlying block cipher is ideal, showing that the mu security of the latter is indeed superior in many practical contexts to that of the former, and (5) Propose an alternative AE scheme XGCM having the same efficiency as RGCM but better mu security and a more simple and modular design.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Traditionally, security definitions were single-user, meaning there was a single target key. Consideration of the multi-user setting began with public-key encryption [3]. In this setting, there are many users, each with their own key, and the target is to violate security under some key. This is, first, simply more realistic, reflecting real usage, but is now even more relevant from the mass-surveillance perspective. This paper initiates a study of the multi-user security of authenticated encryption. Our motivation comes from TLS 1.3.
AE. The form of authenticated encryption (AE) we consider is nonce-based [28]. The encryption algorithm \(\mathsf {\mathsf {AE}.Enc}\) takes key  , nonce \(N\), message \(M\) and header \(H\) to deterministically return a ciphertext
, nonce \(N\), message \(M\) and header \(H\) to deterministically return a ciphertext  . The requirement formalized in [28] is to provide privacy of \(M\), and authenticity of both \(M\) and \(H\), as long as a nonce is not re-used. The formalization refers to only one target key, meaning is in the single user (su) setting.
. The requirement formalized in [28] is to provide privacy of \(M\), and authenticity of both \(M\) and \(H\), as long as a nonce is not re-used. The formalization refers to only one target key, meaning is in the single user (su) setting.
There are many AE schemes (provably) meeting this security requirement. One simple way to obtain them is via generic composition of privacy-only encryption schemes with MACs [5, 26]. There are also dedicated schemes such as OCB [22, 29, 31], CCM [11] and GCM [12, 24]. The last, with AES, is used in TLS 1.3.
Multi-user Security of AE. We formalize multi-user (mu) security of an authenticated-encryption scheme \(\mathsf {AE}\). The game picks an adversary-determined number \(u\) of independent target keys  . The adversary gets an encryption oracle that takes an index \(i\in [1..u]\), a message, nonce and header, and returns either an encryption of these under
. The adversary gets an encryption oracle that takes an index \(i\in [1..u]\), a message, nonce and header, and returns either an encryption of these under  or a random string of the same length. It also gets a verification oracle that takes i, a ciphertext, nonce and header, and indicates whether or not decryption is valid. Security is required as long as the adversary does not re-use a nonce for a particular user. That is, it is fine to obtain encryptions under the same nonce for different keys, just not under the same key. When \(u=1\), we get a definition equivalent to (but formulated slightly differently from) the (single-user) definition of [28].
or a random string of the same length. It also gets a verification oracle that takes i, a ciphertext, nonce and header, and indicates whether or not decryption is valid. Security is required as long as the adversary does not re-use a nonce for a particular user. That is, it is fine to obtain encryptions under the same nonce for different keys, just not under the same key. When \(u=1\), we get a definition equivalent to (but formulated slightly differently from) the (single-user) definition of [28].
Besides this usual goal (which we call indistinguishability), we also formalize a mu key-recovery goal. Again the game picks target keys  and gives the adversary an encryption oracle. This time time the latter is always true, meaning it takes an index \(i\in [1..u]\), a message, nonce and header, and returns an encryption of these under
and gives the adversary an encryption oracle. This time time the latter is always true, meaning it takes an index \(i\in [1..u]\), a message, nonce and header, and returns an encryption of these under  . The adversary also gets a verification oracle, and, to win, must find one of the target keys. A key-recovery attack is much more damaging than a distinguishing attack, and is the threat of greatest concern to practioners. Key recovery security is usually dismissed by theoreticians as being implied by indistinguishability, but this view misses the fact that the quantitative security of a scheme, in terms of bounds on adversary advantage, can be very different for the two metrics, making it worthwhile to consider key recovery security separately and additionally.
. The adversary also gets a verification oracle, and, to win, must find one of the target keys. A key-recovery attack is much more damaging than a distinguishing attack, and is the threat of greatest concern to practioners. Key recovery security is usually dismissed by theoreticians as being implied by indistinguishability, but this view misses the fact that the quantitative security of a scheme, in terms of bounds on adversary advantage, can be very different for the two metrics, making it worthwhile to consider key recovery security separately and additionally.
We give our definitions in the ideal-cipher model. (Standard-model definitions follow because this is just the special case where scheme algorithms and adversaries make no queries to the ideal cipher.) For all the schemes we consider, the assumption that the underlying blockcipher is a PRP suffices to prove security. The reason we use the ideal-cipher model is that adversary queries to the ideal cipher give a clear and rigorous way to measure the offline computation being performed in an attack. Also in some cases we get better bounds.
Multi-user security is not qualitatively different from single-user security. A hybrid argument shows that the latter implies the former. But the two could be quantitatively quite different, and this has important practical implications. In the hybrid reduction, there is a loss of a factor \(u\) in adversary advantage. Thus, the mu advantage of an adversary could be as much as \(u\) times its su advantage. This is the worst case. But it could be a lot less, degrading much more slowly with \(u\). This would be better.
AE in TLS 1.3. As the protocol underlying https, TLS is the basis for secure communication on the Internet, used millions of times a day. The existing versions up to TLS 1.2 have however been subject to many attacks. The effort to create a new and (hopefully) better version, TLS 1.3, is currently underway. TLS (of whatever version) begins with a handshake. This is an authenticated key exchange that establishes a shared session key, called the traffic secret, between client and server. This step will not be our concern. After the handshake, data is authenticated and encrypted within the so-called record layer, using an authenticated encryption scheme \(\mathsf {AE}\) that is keyed by a key  derived from the traffic secret. The currently proposed choice of \(\mathsf {AE}\) is AES-GCM.
derived from the traffic secret. The currently proposed choice of \(\mathsf {AE}\) is AES-GCM.
The most natural way to use \(\mathsf {AE}\) in the record layer is directly, meaning the data message \(M\) is simply encrypted via  , where \(N\) is a nonce (in TLS 1.3 this is a sequence number that is known to the receiver) and \(H\) is the header. This is not what TLS 1.3 proposes. Instead, they randomize the nonce, computing
, where \(N\) is a nonce (in TLS 1.3 this is a sequence number that is known to the receiver) and \(H\) is the header. This is not what TLS 1.3 proposes. Instead, they randomize the nonce, computing  , where the randomizer \(L\) is also derived from the traffic secret. (It is thus known to the receiver, enabling decryption.) Why do this? Brian Smith gave the following motivation on the TLS 1.3 mailing list [33]:
, where the randomizer \(L\) is also derived from the traffic secret. (It is thus known to the receiver, enabling decryption.) Why do this? Brian Smith gave the following motivation on the TLS 1.3 mailing list [33]:
... massively parallel attacks on many keys at once seem like the most promising way to break AES-128. It seems bad to have popular endpoints encrypting the same plaintext block with the same nonce with different keys. That seems like exactly the recipe for making such attacks succeed. It seems like it would be better, instead, to require that the initial nonces to be calculated from the key block established during key agreement ... This ... should prevent any such massively-parallel attack from working.
In this paper, we aim to understand and formalize the threat alluded to here, and then assess to what extent one can prove that nonce-randomization guarantees security. In particular, we suggest that the formal cryptographic goal underlying nonce randomization and Smith’s comment is improved multi-user security. In our model, the “massively parallel attack” is a key-search attack that finds the GCM key of some user out of \(u\) target users —here we are referring to the basic GCM scheme, in the absence of nonce randomization— in time \(2^{\kappa }/u\) where \(\kappa \) is the key length of the underlying block cipher, \(\kappa =128\) for AES. The attack picks some \(N,M,H\) and for each \(i\in [1..u]\) obtains from its encryption oracle the encryption \(C_i\) of these quantities under  . Now, it goes through all possible \(\kappa \)-bit keys \(L\), for each computing \(C_L\leftarrow \mathsf {\mathsf {AE}.Enc}(L,N,M,H)\), and returning \(L\) if \(C_L=C_i\) for some i. Note that the attack needs a single computation of \(\mathsf {\mathsf {AE}.Enc}\) for each \(L\), not one per user, which is why the running time is \(2^{\kappa }/u\). Given NSA computing capabilities, the fear of the TLS 1.3 designers is that this attack may be feasible for them for large \(u\), and thus a mass-surveillance threat. Nonce randomization is a candidate way to circumvent the attack. The question this raises is whether nonce randomization works. To answer this in a rigorous way, we abstract out a (new) AE scheme and then use our definitions of mu security.
. Now, it goes through all possible \(\kappa \)-bit keys \(L\), for each computing \(C_L\leftarrow \mathsf {\mathsf {AE}.Enc}(L,N,M,H)\), and returning \(L\) if \(C_L=C_i\) for some i. Note that the attack needs a single computation of \(\mathsf {\mathsf {AE}.Enc}\) for each \(L\), not one per user, which is why the running time is \(2^{\kappa }/u\). Given NSA computing capabilities, the fear of the TLS 1.3 designers is that this attack may be feasible for them for large \(u\), and thus a mass-surveillance threat. Nonce randomization is a candidate way to circumvent the attack. The question this raises is whether nonce randomization works. To answer this in a rigorous way, we abstract out a (new) AE scheme and then use our definitions of mu security.
RGCM. In TLS 1.3, nonce randomization is viewed as a way to use GCM in the record layer. We take a different perspective. We view the method as defining a new AE scheme that we call RGCM. In this scheme, the randomizer is part of the key. This view is appropriate because the randomizer was derived from the traffic secret just like the base key, and has the security necessary to be used as a key, and the randomizer is also static across the session, just like the base key. While GCM has a key whose length is the key length \(\kappa \) of the underlying block cipher (\(\kappa =128\) for AES), RGCM has a key of length \(\kappa +\nu \), where \(\nu \) is the length of the randomizer (\(\nu =96\) for GCM in TLS 1.3). Nonces are assumed to also have length \(\nu \) so that xoring the nonce with the randomizer makes sense.
Results. With this perspective, we are looking at two AE schemes, GCM and RGCM. We can now divorce ourselves of TLS details and analyze them as AE schemes to determine the quantitative mu security of both. The number \(p\) of adversary queries to the ideal cipher is the central parameter, capturing the offline computational effort of the adversary. As before \(u\) is the number of users, and we let \(m\) denote the total number of bits encrypted, meaning the sum of the lengths of all messages in queries.
Let us first discuss mu security under key recovery, where the picture is clearer. Roughly, we show that key recovery for GCM needs \(p= 2^{\kappa }/u\) while for RGCM it needs \(p= 2^{\kappa +\nu }/um\). We expect \(m\) to be quite a bit less than \(2^{\nu }\) —in the current schemes, \(\nu = 96\)— so the effort to recover a key is significantly higher for RGCM than for GCM. This says that nonce randomization works, meaning it does increase mu security as targeted by the TLS 1.3 designers, at least for key recovery.
For mu-ind security, the picture is more complex. We distinguish the case of passive attacks, where the adversary does not query its verification oracle, and active attacks, where it does. In the passive case, RGCM still emerges as superior, but in the active case, the two schemes become comparable. Also, our bounds in the ind case are complex, and interesting terms get swamped by collision terms. We stress that the bounds here may not be tight, so the picture we are seeing could reflect limitations of our analysis techniques rather than the inherent security of the schemes. Obtaining better (and ideally tight) bounds is an interesting open question.
XGCM. Even if under some metrics superior to GCM, RGCM performs considerably worse than expected from an AE with key length \(\kappa +\nu \), and the natural question is, why not use some standard scheme or construction paradigm rather than “roll your own” with RGCM? The most obvious choice is AES256-GCM. Our analysis of GCM shows that AES256-GCM has good enough mu security, simply due to the larger key size. However, AES256-GCM is slower than AES-RGCM, and a scheme using AES itself would be preferable. We suggest and analyze XGCM, derived simply as GCM with the blockcipher \(\textsc {E}{:\,}\{0,1\}^{\kappa }\times \{0,1\}^{\lambda }\rightarrow \{0,1\}^{\lambda }\) replaced by \(\textsc {EX}{:\,}\{0,1\}^{\kappa +\lambda } \times \{0,1\}^{\lambda } \rightarrow \{0,1\}^{\lambda }\), defined by \(\textsc {EX}(K\Vert L,X) = L{\oplus }\textsc {E}(K,L{\oplus }X)\). This transform of a blockcipher uses the Even-Mansour technique [13]. It was suggested by Rivest as a key-extension method for DES and first analyzed by Kilian and Rogaway [19]. Our analysis implies that, with AES parameters, the mu security of XGCM is better than that of RGCM. Its performance is however essentially the same as that of GCM or RGCM. While it would be a viable alternative for AES-RGCM in TLS 1.3, it does require non-black-box changes to the implementation of AES-GCM, whereas for AES-RGCM the change is only the randomization of the nonce input.
Related Work. GCM was proposed by McGrew and Viega (MV) [24] and standardized by NIST as [12]. MV [24] prove single-user security assuming PRP-security of the underlying blockcipher. While the original scheme allows variable-length nonces [24], IOM [18] showed that the security proof of MV was flawed in this case and the claimed security bounds did not hold. They provide a corrected proof, which was later improved by NOMI [27]. In this paper we only consider fixed-length nonces. We prove security in the mu setting in the ideal cipher model.
Key-recovery security of symmetric encryption schemes was defined in [30] for the single-user, privacy-only setting. We extend their definition to the mu, authenticated encryption setting.
BMMRT [1] and FGMP [14] analyze the record layer of TLS 1.3 relative to the goal of providing a secure channel, under an appropriate formalization of the latter. These works assume that AES-GCM is a secure AE scheme. Our work is not attempting to analyze the record layer. It is analyzing the security of GCM and RGCM as stand-alone AE schemes, with emphasis on their mu security.
We are seeing increased interest in multi-user security, further reflected in this paper. BCK [4] considered mu security for PRFs as an intermediate step in the analysis of the cascade construction. Multi-user security of PRFs and PRPs (blockciphers) has been further considered in [2, 25, 34]. The first work that highlighted mu security as a goal and targeted quantitative security improvements seems to have been BBM [3], the primitive here being public-key encryption. Multi-user security for signatures was considered by GMS [16] and has been the subject of renewed interest in [8, 20]. Further works involving multi-user security include [9, 10, 17], and, in the cryptanalytic context, [15].
2 Preliminaries
We let \(\varepsilon \) denote the empty string. If Z is a string then |Z| denotes its length and Z[1..i] denotes bits 1 through i of Z. If  is a finite set, we let
is a finite set, we let  denote picking an element of
denote picking an element of  uniformly at random and assigning it to x. Algorithms may be randomized unless otherwise indicated. Running time is worst case. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with random coins r on inputs \(x_1,\ldots \) and assigning the output to y. We let
uniformly at random and assigning it to x. Algorithms may be randomized unless otherwise indicated. Running time is worst case. If A is an algorithm, we let \(y \leftarrow A(x_1,\ldots ;r)\) denote running A with random coins r on inputs \(x_1,\ldots \) and assigning the output to y. We let  be the result of picking r at random and letting \(y \leftarrow A(x_1,\ldots ;r)\). We let \([A(x_1,\ldots )]\) denote the set of all possible outputs of A when invoked with inputs \(x_1,\ldots \).
be the result of picking r at random and letting \(y \leftarrow A(x_1,\ldots ;r)\). We let \([A(x_1,\ldots )]\) denote the set of all possible outputs of A when invoked with inputs \(x_1,\ldots \).
We use the code-based game-playing framework of BR [6]. (See Fig. 1 for an example.) By \(\Pr [\mathrm {G}]\) we denote the probability that the execution of game \(\mathrm {G}\) results in the game returning \(\mathsf {true}\). In games, integer variables, set variables and boolean variables are assumed initialized, respectively, to 0, the empty set, and \(\mathsf {false}\).
A family of functions \(\mathsf {F}{:\,}\mathsf {F}.\mathsf {Keys} \times \mathsf {F}.\mathsf {Dom}\rightarrow \mathsf {F}.\mathsf {Rng}\) is a two-argument function that takes a key K in the key space \(\mathsf {F}.\mathsf {Keys}\), an input x in the domain \(\mathsf {F}.\mathsf {Dom}\) and returns an output \(\mathsf {F}(K,x)\) in the range \(\mathsf {F}.\mathsf {Rng}\). In the ROM, \(\mathsf {F}\) takes an oracle \(\mathsf {RO}\). We say \(\mathsf {F}\) has key length \(\mathsf {F}.\mathsf {kl}\) if \(\mathsf {F}.\mathsf {Keys}=\{0,1\}^{\mathsf {F}.\mathsf {kl}}\); output length \(\mathsf {F}.\mathsf {ol}\) if \(\mathsf {F}.\mathsf {Rng}=\{0,1\}^{\mathsf {F}.\mathsf {ol}}\); and input length \(\mathsf {F}.\mathsf {il}\) if \(\mathsf {F}.\mathsf {Dom}=\{0,1\}^{\mathsf {F}.\mathsf {il}}\).
We say that \(\mathsf {F}{:\,}\{0,1\}^{\mathsf {F}.\mathsf {kl}}\times \{0,1\}^{\mathsf {F}.\mathsf {il}}\rightarrow \{0,1\}^{\mathsf {F}.\mathsf {ol}}\) is a block cipher if \(\mathsf {F}.\mathsf {il}=\mathsf {F}.\mathsf {ol}\) and \(\mathsf {F}(K,\cdot ) {:\,}\{0,1\}^{\mathsf {F}.\mathsf {il}}\rightarrow \{0,1\}^{\mathsf {F}.\mathsf {ol}}\) is a permutation for each K in \(\{0,1\}^{\mathsf {F}.\mathsf {kl}}\). We denote by \(\mathsf {F}^{-1}(K,\cdot )\) the inverse of \(\mathsf {F}(K,\cdot )\).
Let \(\mathsf {H}{:\,}\mathsf {H}.\mathsf {Keys} \times (\{0,1\}^*\times \{0,1\}^*) \rightarrow \{0,1\}^{\mathsf {H}.\mathsf {ol}}\) be a family of functions with domain \(\mathsf {H}.\mathsf {Dom} = \{0,1\}^* \times \{0,1\}^*\). Let \(\epsilon {:\,}{{\mathbb N}} \times {{\mathbb N}} \rightarrow [0,1]\) be a function. Somewhat extending [21], we say that \(\mathsf {H}\) is \(\epsilon \) -almost XOR-universal if for all distinct \((M_1,H_1),(M_2,H_2)\in \mathsf {H}.\mathsf {Dom}\) and all \(s\in \{0,1\}^{\mathsf {H}.\mathsf {ol}}\), we have

3 Multi-user Security of Symmetric Encryption
We consider symmetric encryption in a multi-user setting. We give two definitions of security. The first, an indistinguishability-style definition, extendsP Rogaway’s single-user definition [28] to the multi-user setting, and represents a very strong requirement. We also define security against key recovery, representing the goal the attacker would most like to achieve and the most common target of cryptanalysis. We will see that the security bounds for these notions can differ. Since our analyses will be in the ideal-cipher model, the definitions are given directly in that model.
Syntax. A symmetric encryption scheme \(\mathsf {AE}\) specifies a deterministic encryption algorithm \(\mathsf {\mathsf {AE}.Enc}{:\,}\{0,1\}^{\mathsf {\mathsf {AE}.kl}} \times \mathsf {\mathsf {AE}.NS}\times \{0,1\}^* \times \{0,1\}^* \rightarrow \{0,1\}^*\) that takes a key  , a nonce \(N\in \mathsf {\mathsf {AE}.NS}\), a message \(M\in \{0,1\}^*\) and a header \(H\in \{0,1\}^*\) to return a ciphertext
, a nonce \(N\in \mathsf {\mathsf {AE}.NS}\), a message \(M\in \{0,1\}^*\) and a header \(H\in \{0,1\}^*\) to return a ciphertext  . Here \(\mathsf {\mathsf {AE}.kl}\in {{\mathbb N}} \) is the key length of the scheme, \(\mathsf {\mathsf {AE}.NS}\) is the nonce space and \(\mathsf {\mathsf {AE}.cl}{:\,}{{\mathbb N}} \rightarrow {{\mathbb N}} \) is the ciphertext length function. The oracles represent a cipher \(\textsc {E}{:\,}\{0,1\}^{\mathsf {AE}.\mathsf {ckl}}\times \{0,1\}^{\mathsf {AE}.\mathsf {bl}}\rightarrow \{0,1\}^{\mathsf {AE}.\mathsf {bl}}\) and its inverse \(\textsc {E}^{-1}\). In the security games this cipher will be chosen at random, meaning be ideal. We view the key length \(\mathsf {AE}.\mathsf {ckl}\) and block length \(\mathsf {AE}.\mathsf {bl}\) of the cipher as further parameters of \(\mathsf {AE}\) itself. Also specified is a deterministic decryption algorithm \(\mathsf {\mathsf {AE}.Dec}{:\,}\{0,1\}^{\mathsf {\mathsf {AE}.kl}}\times \mathsf {\mathsf {AE}.NS}\times \{0,1\}^* \times \{0,1\}^* \rightarrow \{0,1\}^*\cup \{\bot \}\) that takes
. Here \(\mathsf {\mathsf {AE}.kl}\in {{\mathbb N}} \) is the key length of the scheme, \(\mathsf {\mathsf {AE}.NS}\) is the nonce space and \(\mathsf {\mathsf {AE}.cl}{:\,}{{\mathbb N}} \rightarrow {{\mathbb N}} \) is the ciphertext length function. The oracles represent a cipher \(\textsc {E}{:\,}\{0,1\}^{\mathsf {AE}.\mathsf {ckl}}\times \{0,1\}^{\mathsf {AE}.\mathsf {bl}}\rightarrow \{0,1\}^{\mathsf {AE}.\mathsf {bl}}\) and its inverse \(\textsc {E}^{-1}\). In the security games this cipher will be chosen at random, meaning be ideal. We view the key length \(\mathsf {AE}.\mathsf {ckl}\) and block length \(\mathsf {AE}.\mathsf {bl}\) of the cipher as further parameters of \(\mathsf {AE}\) itself. Also specified is a deterministic decryption algorithm \(\mathsf {\mathsf {AE}.Dec}{:\,}\{0,1\}^{\mathsf {\mathsf {AE}.kl}}\times \mathsf {\mathsf {AE}.NS}\times \{0,1\}^* \times \{0,1\}^* \rightarrow \{0,1\}^*\cup \{\bot \}\) that takes  and returns
and returns  . Correctness requires that
. Correctness requires that  for all \(M,H\in \{0,1\}^*\), all \(N\in \mathsf {\mathsf {AE}.NS}\) and all
for all \(M,H\in \{0,1\}^*\), all \(N\in \mathsf {\mathsf {AE}.NS}\) and all  .
.
Indistinguishability Security. We extend Rogaway’s definition of indistinguishability security for authenticated encryption [28], which is in the single-user setting, to the multi-user setting. The formalization is based on game \(\mathbf {G}^\mathrm{mu\text{- }ind}_{\mathsf {AE}}(A)\) of Fig. 1, associated to encryption scheme \(\mathsf {AE}\) and adversary \(A\). The game initially samples a random bit challenge b, with \(b=1\) indicating it is in “real” mode and \(b=0\) that it is in “ideal” mode. As per our conventions noted in Sect. 2, the sets U, V are assumed initialized to the empty set, and the integer v is assumed initialized to 0. Now the adversary \(A\) has access to an oracle \(\textsc {New}\) that creates new user instances. \(A\) also has access to an encryption oracle \(\textsc {Enc}\) that takes a user instance identifier i, a nonce \(N\in \mathsf {\mathsf {AE}.NS}\), a message \(M\), and a header \(H\). The oracle either returns a uniformly random bit string of length \(\mathsf {\mathsf {AE}.cl}\) that depends only on the length of \(M\) (for \(b=0\)), or an encryption under \(\mathsf {\mathsf {AE}.Enc}\) using the key of user i (for \(b=1\)). The oracle checks that \(A\) does not re-use nonces for a user instance, and that it is invoked only for user instances that exist. Analogously, there is a verification oracle \(\textsc {Vf}\) that takes user instance i, nonce \(N\in \mathsf {\mathsf {AE}.NS}\), ciphertext \(C\), and header \(H\). Oracle \(\textsc {Vf}\) always accepts ciphertexts generated by \(\textsc {Enc}\) for the same i, \(N\), and \(H\), rejects all other ciphertexts for \(b=0\), and uses the decryption algorithm \(\mathsf {\mathsf {AE}.Dec}\) to check the validity of the ciphertext for \(b=1\). As a last step, the adversary outputs a bit \(b'\) that can be viewed as a guess for b. The advantage of adversary \(A\) in breaking the mu-ind security of \(\mathsf {AE}\) is defined as \(\mathsf {Adv}^\mathrm{mu\text{- }ind}_{\mathsf {AE}}(A) = 2\Pr [\mathbf {G}^\mathrm{mu\text{- }ind}_{\mathsf {AE}}(A)]- 1\).
The ideal-cipher oracles \(\textsc {E}\) and \(\textsc {E}^{-1}\) are given to the adversary, the encryption algorithm and the decryption algorithm, where the inputs are \(L\in \{0,1\}^{\mathsf {AE}.\mathsf {ckl}}\) and \(x,y\in \{0,1\}^{\mathsf {AE}.\mathsf {bl}}\). The oracles are defined using lazy sampling. The description of game \(\mathbf {G}^\mathrm{mu\text{- }ind}_{\mathsf {AE}}\) in Fig. 1 uses some notation that we introduce here and use also elsewhere. First of all, \(T[\cdot ,\cdot ]\) describes a map \(\{0,1\}^*\times \{0,1\}^*\rightarrow \{0,1\}^*\) that is initially \(\bot \) everywhere, with new values defined during the game. By im\(T[\cdot ,\cdot ]\) we denote the set \(\{ z \in \{0,1\}^* : \exists x,y\in \{0,1\}^* \text { with } T[x,y]=z \}\) and by supp\(T[\cdot ,\cdot ]\) the set \(\{ (x,y) \in \{0,1\}^*\times \{0,1\}^*: T[x,y] \not = \bot \}\). Both terms are also used in the obvious sense in settings where one of the inputs is fixed. (In Fig. 1, this input is L.) Finally, for a subset \(A \subset B\), the notation \(\overline{A}\) refers to the complement \(B \setminus A\) in B. We use this notation in places when the superset B is clear from the context. (In Fig. 1, the set B is \(\{0,1\}^{\mathsf {AE}.\mathsf {bl}}\).)
Definitions of mu security for authenticated encryption in the standard model are obtained as a special case, namely by restricting attention to schemes and adversaries that do not make use of the \(\textsc {E}\) and \(\textsc {E}^{-1}\) oracles.
One can further strengthen the security of the above ind definition by considering nonce-misuse resistance as defined by Rogaway and Shrimpton [32]. This requires changing the condition \((i,N)\in U\) in oracle \(\textsc {Enc}\) to only prevent queries where nonce and message (or even nonce, message, and header) are repeated. We do not use such a stronger definition in this work because GCM does not achieve it.
We say that an adversary is passive if it makes no queries to its \(\textsc {Vf}\) oracle. In some cases we will get better bounds for passive adversaries.
Rogaway’s definition of indistinguishability security for authenticated encryption (in the su setting) [28] gives the adversary a decryption oracle, while we give it a verification oracle. The latter is simpler and our definition can be shown equivalent to one with a decryption oracle by the technique of BN [5].
Key-Recovery Security. The qualitatively weaker requirement of key-recovery security can sometimes be established with better bounds than ind, which is of practical importance since violating key recovery is much more damaging that violating ind. The formalization is based on game \(\mathbf {G}^\mathrm{mu\text{- }kr}_{\mathsf {AE}}(A)\) of Fig. 2, associated to encryption scheme \(\mathsf {AE}\) and adversary \(A\). The goal of the adversary \(A\) is simply to output the key of any honest user. It again has access to oracles \(\textsc {New}\), \(\textsc {Enc}\), \(\textsc {Vf}\), \(\textsc {E}\), and \(\textsc {E}^{-1}\). Oracles \(\textsc {Enc}\) and \(\textsc {Vf}\) are defined to always return the values as determined by the scheme \(\mathsf {AE}\). Adversary \(A\) wins if it outputs any one of the keys that was generated using the \(\textsc {New}\) oracle. The advantage of \(A\) in breaking the mu-kr security of \(\mathsf {AE}\) is defined as \(\mathsf {Adv}^\mathrm{mu\text{- }kr}_{\mathsf {AE}}(A) \ = \ \Pr [\mathbf {G}^\mathrm{mu\text{- }kr}_{\mathsf {AE}}(A)]\).
4 The Schemes
We present a symmetric encryption scheme we call \(\mathsf {CAU}\), for Counter-Mode with a AXU hash function. GCM is a special case. This allows us to divorce our results and analyses from some details of GCM (namely, the particular, polynomial-evaluation based hash function) making them both simpler and more general.
The TLS Working Group introduced a specific usage mode of GCM in recent draft versions of TLS 1.3 in which material, obtained in the handshake key derivation phase, is used to mask the nonce. We take a different perspective and view this as a new symmetric encryption scheme whose generalized version we specify here as \(\mathsf {RCAU}\). Finally we specify \(\mathsf {XCAU}\), our own variant that better achieves the same goals.
CAU. Let \(\kappa ,\lambda ,\nu \ge 1\) be integers such that \(\nu \le \lambda -2\), where \(\kappa \) is referred to as the cipher key length, \(\lambda \) as the block length and \(\nu \) as the nonce length. Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be an \(\epsilon \)-XOR universal hash function. We associate to these the symmetric encryption scheme \(\mathsf {CAU}= \mathbf {CAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\) —here \(\mathbf {CAU}\) is a transform taking \(\mathsf {H},\kappa ,\lambda ,\nu \) and returning a symmetric encryption scheme that we are denoting \(\mathsf {CAU}\)— whose encryption and decryption algorithms are specified in Fig. 3. The scheme has key length \(\mathsf {\mathsf {CAU}.kl}= \kappa \), cipher key length \(\mathsf {\mathsf {CAU}.ckl}= \kappa \) and block length \(\mathsf {\mathsf {CAU}.bl}= \lambda \). It has nonce space \(\mathsf {\mathsf {CAU}.NS}= \{0,1\}^{\nu }\) and ciphertext length function \(\mathsf {\mathsf {CAU}.cl}(\cdot )\) defined by \(\mathsf {\mathsf {CAU}.cl}(m) = m + \lambda \). Explanations follow.
The algorithms \(\mathsf {\mathsf {CAU}.Enc}\) and \(\mathsf {\mathsf {CAU}.Dec}\) are given access to oracles that represent a cipher \(\textsc {E}{:\,}\{0,1\}^{\kappa }\times \{0,1\}^{\lambda }\rightarrow \{0,1\}^{\lambda }\) and its inverse \(\textsc {E}^{-1}\). In the security games the cipher will be chosen at random, meaning be ideal. In practice, it will be instantiated by a block cipher, usually \(\mathsf {AES}\).
\(\mathsf {CAU}\) is an encrypt-then-mac scheme [5]. Encryption is counter-mode of the block cipher. The MAC is a Carter-Wegman MAC based on the AXU function family \(\mathsf {H}\). Some optimizations are performed over and above generic encrypt-then-mac to use the same key for both parts. The name stands for “Counter Almost Universal.”
In the description of Fig. 3, the plaintext \(M\) is first partitioned into \(\ell = \lceil |M|/\lambda \rceil \) plaintext blocks \(M_1,\dots ,M_\ell \). The first \(\ell -1\) blocks have length \(\lambda \). The final block \(M_{\ell }\) has length \(1\le r \le \lambda \). The value G defined as  is later used as a key for the hash function \(\mathsf {H}\). The loop then computes the counter mode encryption. Here and in the rest of the paper we use the following notation. If Z is a \(\lambda \) bit string and \(j\ge 0\) is an integer then we let
is later used as a key for the hash function \(\mathsf {H}\). The loop then computes the counter mode encryption. Here and in the rest of the paper we use the following notation. If Z is a \(\lambda \) bit string and \(j\ge 0\) is an integer then we let
where \(\langle 1+j\rangle \) is the representation of the integer \((1+j) \bmod 2^{\lambda -\nu }\) as a \((\lambda -\nu )\)-bit string. Thus, in the scheme, \(Y+i = N\Vert \langle 1+i\rangle \). Function \(\mathrm {msb}_n\), which is needed to compute the final and possibly incomplete ciphertext block \(C_\ell \), maps a string of length \(\ge n\) to its n-bit prefix. The final step in the scheme is then to compute the function \(\mathsf {H}\) on \(H\) and \(C= C_1\Vert \dots \Vert C_\ell \) and xor it to the output of the block cipher on input Y. To simplify the technical descriptions in our proofs, we define the ciphertext as consisting of the tag prepended to the output of the counter-mode encryption.
GCM, as proposed by McGrew and Viega [24] and standardized by NIST [12], is obtained by instantiating the block cipher with \(\mathsf {AES}\), so that \(\lambda = \kappa = 128\). The nonce length (in the standardized version) is \(\nu = 96\). The hash function \(\mathsf {H}\) is based on polynomial evaluation. The specifics do not matter for us. For our security analysis, all we need is that \(\mathsf {H}\) is an \(\epsilon \)-almost XOR-universal hash function (according to our definition of Sect. 2) for some \(\epsilon {:\,}{{\mathbb N}} \times {{\mathbb N}} \rightarrow [0,1]\). McGrew and Viega [24, Lemma 2] show that \(\mathsf {H}\) has this property for \(\epsilon (m,n) = (\lceil m/\lambda \rceil + \lceil n/\lambda \rceil + 1) / 2^{\lambda }\).
\(\mathsf {CAU}\) has fixed-length nonces, reflecting the standardized version of GCM in which \(\nu = 96\). While the original scheme allows variable-length nonces [24], IOM [18] showed that the original security proof was flawed for variable-length nonces and the claimed security bounds did not hold.
RCAU. The TLS Working Group introduced a specific usage mode of GCM in recent draft versions of TLS 1.3 to prevent the scheme from evaluating the block cipher on the same inputs in each session. This countermeasure is described as computing an additional \(\nu \) bits of key material in the key derivation phase, and using these to mask the \(\nu \)-bit nonce given to GCM.
In order to analyze the effectiveness of this countermeasure, we take a different perspective, casting the method as specifying a new symmetric encryption scheme in which the mask becomes part of the key. Formally, as before, let \(\kappa ,\lambda ,\nu \ge 1\) be integers representing the cipher key length, block length and nonce length, where \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be an \(\epsilon \)-XOR universal hash function. We associate to these the symmetric encryption scheme \(\mathsf {RCAU}= \mathbf {RCAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\) whose encryption and decryption algorithms are specified in Fig. 4. The scheme has key length \(\mathsf {\mathsf {RCAU}.kl}= \kappa +\nu \), cipher key length \(\mathsf {\mathsf {RCAU}.ckl}= \kappa \) and block length \(\mathsf {\mathsf {RCAU}.bl}= \lambda \). It has nonce space \(\mathsf {\mathsf {RCAU}.NS}= \{0,1\}^{\nu }\) and ciphertext length function \(\mathsf {\mathsf {RCAU}.cl}(\cdot )\) defined by \(\mathsf {\mathsf {RCAU}.cl}(m) = m + \lambda \). Note that the key length is \(\kappa +\nu \), while that of \(\mathsf {CAU}\) was \(\kappa \). The definition of \(Y+i\) is as per (1), so \(Y+i = (N\oplus L) \Vert \langle 1+i\rangle \).
XCAU. We suggest a different scheme to achieve the multi-user security goal targeted by \(\mathsf {RCAU}\). Recall that if \(\textsc {E}{:\,}\{0,1\}^{\kappa }\times \{0,1\}^{\lambda }\rightarrow \{0,1\}^{\lambda }\) is a block cipher than \(\textsc {EX}{:\,}\{0,1\}^{\kappa +\lambda } \times \{0,1\}^{\lambda } \rightarrow \{0,1\}^{\lambda }\) is the block cipher defined by \(\textsc {EX}(K\Vert L,X) = L{\oplus }\textsc {E}(K,L{\oplus }X)\). This can be viewed as strengthening \(\textsc {E}\) using an Even-Mansour technique [13]. This was suggested by Rivest as a key-extension method for DES and first analyzed by Kilian and Rogaway [19]. We then simply use \(\textsc {EX}\) in place of \(\textsc {E}\) in the basic \(\mathsf {CAU}\). Formally, as before, let \(\kappa ,\lambda ,\nu \ge 1\) be integers representing the cipher key length, block length and nonce length, where \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be an \(\epsilon \)-XOR universal hash function. We associate to these the symmetric encryption scheme \(\mathsf {XCAU}= \mathbf {XCAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\) whose encryption and decryption algorithms are specified in Fig. 5. The scheme has key length \(\mathsf {\mathsf {XCAU}.kl}= \kappa +\lambda \), cipher key length \(\mathsf {\mathsf {XCAU}.ckl}= \kappa \) and block length \(\mathsf {\mathsf {XCAU}.bl}= \lambda \). It has nonce space \(\mathsf {\mathsf {XCAU}.NS}= \{0,1\}^{\nu }\) and ciphertext length function \(\mathsf {\mathsf {XCAU}.cl}(\cdot )\) defined by \(\mathsf {\mathsf {XCAU}.cl}(m) = m + \lambda \). Note that the key length is \(\kappa +\lambda \), while that of \(\mathsf {RCAU}\) was \(\kappa +\nu \). The definition of \(Y+i\) is as per (1), so \(Y+i = N\Vert \langle 1+i\rangle \).
Our analysis of this scheme builds on the work of Kilian and Rogaway, but analyzes the construction directly in the multi-user setting. We believe that the bounds can be further improved along the lines of Mouha and Luykx’s work [25], but this does not affect the terms we are most interested in.
5 Key-Recovery Security
The multi-user security differences between the schemes are most easily seen in the case of security against key recovery, so we start there.
5.1 Security of CAU
We show that the multi-user kr advantage scales linearly in the number of adversarial evaluations of the ideal cipher (corresponding to offline evaluations of the blockcipher in practice) and the number of user instances. We give both an upper bound (security proof) and lower bound (attack) on the kr-advantage to show this, beginning with the former.
Theorem 1
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be a family of functions. Let \(\mathsf {CAU}= \mathbf {CAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\) oracle and \(p\) queries to its \(\textsc {E}\) and \(\textsc {E}^{-1}\) oracles. Then
Intermediate games for decoupling the oracles \(\textsc {E}/\textsc {E}^{-1}\) and \(\textsc {RF}\) in the proof of Theorem 1.
Proof
We use the code-based game-playing technique of BR [6]. Without loss of generality, we assume that the adversary \(A\) does not input invalid user identifiers \(i \notin \{1,\dots ,v\}\) to \(\textsc {Enc}\) or \(\textsc {Vf}\), and does not re-use nonces in encryption queries. We also assume that \(A\) does not verify correct ciphertexts they obtained from \(\textsc {Enc}\) at its \(\textsc {Vf}\) oracle. These restrictions allow us to simplify the descriptions of the games, and any arbitrary adversary \(A\) can be translated into an adversary \(A'\) that adheres to these restrictions and makes at most the same number of queries as \(A\). Our proof proceeds in a sequence of games.
The first step in the proof is to rewrite game \(\mathbf {G}^\mathrm{mu\text{- }kr}_{\mathsf {CAU}}(A)\) syntactically by introducing an additional oracle \(\textsc {RF}\) that implements the forward evaluation of the ideal cipher for the algorithms \(\mathsf {\mathsf {CAU}.Enc}\) and \(\mathsf {\mathsf {CAU}.Dec}\). This is sufficient as encryption and decryption in CAU never query \(\textsc {E}^{-1}\). We call this game \(\mathrm {G}_0\), but do not explicitly describe as it is obtained easily from \(\mathbf {G}^\mathrm{mu\text{- }kr}_{\mathsf {CAU}}(A)\).
We then rewrite the game in the form of \(\mathrm {G}_1\), which is described in Fig. 6 and basically obtained by a syntactic modification of the oracles \(\textsc {E}\), \(\textsc {E}^{-1}\), and \(\textsc {RF}\). In more detail, oracle \(\textsc {RF}\) samples the ideal cipher for the keys used in the encryption using the map \(U[\cdot ,\cdot ]\). The oracles \(\textsc {E}\) and \(\textsc {E}^{-1}\) are adapted such that, for keys used in the game, they sample the map \(T[\cdot ,\cdot ]\) consistently with \(U[\cdot ,\cdot ]\). We introduce a flag \(\mathsf {bad}\) that is set when the adversary \(A\) queries one of the oracles \(\textsc {E}\) or \(\textsc {E}^{-1}\) with a key that is also used in the oracle \(\textsc {RF}\).
The next game \(\mathrm {G}_2\) modifies the way in which the responses for the \(\textsc {E}\), \(\textsc {E}^{-1}\), and \(\textsc {RF}\) oracles are determined. In particular, we break the consistency between \(\textsc {E}\) and \(\textsc {E}^{-1}\) on the one hand, and \(\textsc {RF}\) on the other hand, by sampling the oracle responses independently. Since all changes appear only after \(\mathsf {bad}\) has been set, we can relate the games using the Fundamental Lemma from Bellare and Rogaway [6] and proceed by bounding the probability of setting \(\mathsf {bad}\). This probability is in fact bounded by \(up/ 2^{\kappa }\). As all computations while \(\mathsf {bad}\) is not set are independent of the values  , the maximal probability of the adversary to guess one of these uniformly random values is \(u/ 2^{\kappa }\) in each of its \(p\) queries to \(\textsc {E}\) and \(\textsc {E}^{-1}\).
, the maximal probability of the adversary to guess one of these uniformly random values is \(u/ 2^{\kappa }\) in each of its \(p\) queries to \(\textsc {E}\) and \(\textsc {E}^{-1}\).
The keys in \(\mathrm {G}_2\) only serve as labels, the game is independent of their actual values. The only remaining step is to compute the probability of guessing any one of the \(u\) keys that are chosen at random without collision, which is also incorporated into the advantage. In more detail:
which concludes the proof. \(\square \)
Adversary \(A_{u,p_e}\) used in Theorem 2.
Next we show that the security bound proven in Theorem 1 is (almost) tight. We describe an attack (adversary) that achieves the described bound up to a (for realistic parameters small) factor. The adversary is shown in Fig. 7. It is parameterized by a number \(u\) of users and an (even) number \(p_e\) of queries to \(\textsc {E}\). It first encrypts a short message \(0^{2\lambda }\) for each of the \(u\) users. Next, it queries the \(\textsc {E}\) oracle on the value \(0^{\lambda -2}10\), the first block that is used for masking actual plaintext, for up to \(p_e\) different keys. As soon as it finds a matching key \(L\) for the first block, it simply evaluates \(\textsc {E}(L, {0^{\lambda -2}11})\) and checks for consistency with the second block. If the check succeeds, the adversary outputs the key \(L\), otherwise it tries further keys.
The described attack strategy extends to any application of CAU in which the nonces used in the scheme are the same in each session. As TLS 1.3 uses the sequence number to compute the nonces, a version without the nonce randomization technique would be susceptible to this attack.
Theorem 2
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be a family of functions. Let \(\mathsf {CAU}= \mathbf {CAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(u\ge 1\) be an integer and \(p_e\ge 2\) an even integer. Associate to them the adversary \(A_{u,p_e}\) described in Fig. 7, which makes \(u\) queries to \(\textsc {New}\), \(q_e=u\) queries to \(\textsc {Enc}\) of length \(2\lambda \) bits, no queries to \(\textsc {Vf}\), \(p_e\) queries to \(\textsc {E}\), and no queries to \(\textsc {E}^{-1}\). Then
where
This means that the advantage of \(A_{u,p_e}\) scales (almost) linearly with the number of users, and in fact, for values \(u,p_e\) such that \(up_e/2^{\kappa +1} \le 1\), the advantage is lower bounded by \(\mu \cdot (1 - 1/e) \cdot \frac{p_eu}{2^{\kappa +1}}\). The proof we give can be improved in terms of tightness, for instance, we allow the attack to completely fail if only a single collision occurs between honest users’ keys. In particular the factor \((1 - u(u-1) / 2^{\kappa +1})\) could be improved especially for large \(u\).
Proof
(Theorem 2 ). The probability for any of the \(u=q_e\) keys to collide is at most \(u(u-1)/2^{\kappa +1}\). In the subsequent steps we compute the probabilities based on the assumption that no user keys generated within \(\textsc {New}\) collide, which is correct with probability at least \(1-u(u-1)/2^{\kappa +1}\). In more detail, given that we have no collisions of user keys, the adversary uses at least \(p_e/2\) attempts to guess any one of \(u=q_e\) (uniformly random, without collision) keys from a set of size \(2^\kappa \). The probability for each honest user’s key to be among the adversary’s guesses is \(p_e/2^{\kappa +1}\), and so the overall probability for any one of the adversary’s attempts to succeed is
We still need to bound the probability of false positives, that is, keys that were not sampled in a \(\textsc {New}\) oracle but coincide with the block cipher outputs, and therefore lead to a wrong guess: The probability that the ideal cipher for a specific “wrong” key (out of \(2^\kappa -u)\) coincides with the ideal cipher for each of the \(u\) “correct” keys on both inputs \(0^{\nu }\Vert 0^{\lambda -\nu -2}\Vert 10\) and \(0^{\nu }\Vert 0^{\lambda -\nu -2}\Vert 11\) is \(2^{-\lambda }(2^\lambda -1)^{-1}\). The existence of such a colliding key can be bounded using the Union Bound to be at most \(u(2^{\kappa }-u)/(2^{\lambda }(2^\lambda -1))\), so the probability that no such collision exists is at least \(1 - u(2^{\kappa }-u)/(2^{\lambda }(2^\lambda -1))\). Overall, we obtain the stated bound. \(\square \)
Evaluating the formula for realistic values for GCM in TLS 1.3, we set \(\kappa = 128\). We allow the adversary to make \(p_e=2^{64}\) evaluations of the block cipher. We estimate the number of TLS sessions per day as \(2^{40}\), which leaves us a security margin of roughly \(2^{24}\). While this means that on expectation the attack still needs \(2^{24}\) days to recover a single key, it is important to recall that this estimate is obtained under the strong assumption that AES behaves like an ideal cipher.
5.2 Security of RCAU
RCAU aims to avoid the attack strategy described in Sect. 5.1 by randomizing the nonce before it is used in the block cipher. Here we assess whether the measure succeeds, again first upper bounding adversary advantage via a proof, then lower bounding it via an attack.
In contrast to the bound for \(\mathsf {CAU}\), the bound for \(\mathsf {RCAU}\) depends on more parameters. This is caused by the more intricate “decoupling” of the \(\textsc {E}/\textsc {E}^{-1}\) and \(\textsc {RF}\) oracles.
Theorem 3
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be a family of functions. Let \(\mathsf {RCAU}= \mathbf {RCAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\) oracle, \(q_e\) queries to its \(\textsc {Enc}\) oracle with messages of length at most \(\ell _\mathrm {bit}\) bits, \(q_v\) queries to its \(\textsc {Vf}\) oracle of length at most \(\ell _\mathrm {bit}+\lambda \) bits, \(p_e\) queries to its \(\textsc {E}\) oracle, and \(p_i\) queries to its \(\textsc {E}^{-1}\) oracle. Then
where \(\ell _\mathrm {blk}= \lceil \ell _\mathrm {bit}/\lambda \rceil + 1\).
Proof
As in Theorem 1, we restrict our attention to adversaries \(A\) that do not use invalid user identifiers, that do not re-use nonces, and that do not verify ciphertexts obtained from the \(\textsc {Enc}\) oracle. As in the proof of Theorem 1, we now aim at “decoupling” the oracles \(\textsc {E}\)/\(\textsc {E}^{-1}\) and \(\textsc {RF}\), but this time we have to be cautious: we cannot just “give up” when the adversary “guesses” one of the users keys in calls to \(\textsc {E}\)/\(\textsc {E}^{-1}\); this would ruin our bound. The first step is as above to introduce an auxiliary map \(U[\cdot ,\cdot ]\) in addition to \(T[\cdot ,\cdot ]\), but keep the maps synchronized. The change from \(\mathbf {G}^\mathrm{mu\text{- }kr}_{\mathsf {RCAU}}(A)\) to \(\mathrm {G}_0\) is therefore only syntactic. Intuitively, the lazy sampling of the block cipher is now performed using both maps, where \(T[\cdot ,\cdot ]\) is filled in calls to \(\textsc {E}\) and \(\textsc {E}^{-1}\), and \(U[\cdot ,\cdot ]\) is filled in \(\textsc {RF}\). The oracles make sure that the maps stay consistent.
In game \(\mathrm {G}_1\), described in detail in Fig. 8, we first change the way in which the responses are sampled, but still in an equivalent way, namely we first attempt to sample consistently only for \(T[\cdot ,\cdot ]\) and then check for consistency with \(U[\cdot ,\cdot ]\). If this fails, we set \(\mathsf {bad}\leftarrow \mathsf {true}\) and re-sample with the correct distribution. Additionally, we set \(\mathsf {bad}\leftarrow \mathsf {true}\) whenever we need to answer for either \(T[\cdot ,\cdot ]\) or \(U[\cdot ,\cdot ]\) and the answer is already defined by the respective other map. Game \(\mathrm {G}_1\) is equivalent to \(\mathrm {G}_0\). The proof is further complicated by the fact that \(\mathsf {RCAU}\) derives the key for \(\mathsf {H}\) as  and this query is therefore not randomized. As a consequence, we have to treat the queries with value \(0^{\lambda }\) independently of the other queries, and keep the maps \(T[\cdot ,0^{\lambda }]\) and \(U[\cdot ,0^{\lambda }]\) consistent for the next proof steps.
and this query is therefore not randomized. As a consequence, we have to treat the queries with value \(0^{\lambda }\) independently of the other queries, and keep the maps \(T[\cdot ,0^{\lambda }]\) and \(U[\cdot ,0^{\lambda }]\) consistent for the next proof steps.
In game \(\mathrm {G}_2\) we modify the behavior of the oracles \(\textsc {E}\), \(\textsc {E}^{-1}\), and \(\textsc {RF}\) to not re-sample to avoid inconsistencies with the other oracles. Also, we do not enforce consistency between  and
and  for values that are defined already in one of the maps; we sample a fresh value in a map independently of whether the point is already defined in the other map. As both modifications occur only after the flag \(\mathsf {bad}\) has been set, we can use the Fundamental Lemma to relate the advantages of an adversary in games \(\mathrm {G}_1\) and \(\mathrm {G}_2\).
for values that are defined already in one of the maps; we sample a fresh value in a map independently of whether the point is already defined in the other map. As both modifications occur only after the flag \(\mathsf {bad}\) has been set, we can use the Fundamental Lemma to relate the advantages of an adversary in games \(\mathrm {G}_1\) and \(\mathrm {G}_2\).
Intermediate games for decoupling the oracles \(\textsc {E}/\textsc {E}^{-1}\) and \(\textsc {RF}\) in the proof of Theorem 3.
To bound the probability for the flag \(\mathsf {bad}\) to be set in games \(\mathrm {G}_1\) or \(\mathrm {G}_2\), respectively, we begin with the following observation: As long as \(\mathsf {bad}\) is not set, each row  or
or  for a specific key
for a specific key  is sampled without collisions within this row, but independently of any other row, and also mutually independent between
is sampled without collisions within this row, but independently of any other row, and also mutually independent between  and
and  . This is the case because the only other way of defining a value for those maps is either re-sampling or copying from the other map; in both cases we set the flag \(\mathsf {bad}\). Furthermore, we observe that all operations that occur before the flag \(\mathsf {bad}\) is set are independent of the actual values of the keys
. This is the case because the only other way of defining a value for those maps is either re-sampling or copying from the other map; in both cases we set the flag \(\mathsf {bad}\). Furthermore, we observe that all operations that occur before the flag \(\mathsf {bad}\) is set are independent of the actual values of the keys  . Given these insights, we now analyze the probabilities for setting the \(\mathsf {bad}\) flag at the different code points, first for \(\textsc {E}\) and \(\textsc {E}^{-1}\):
. Given these insights, we now analyze the probabilities for setting the \(\mathsf {bad}\) flag at the different code points, first for \(\textsc {E}\) and \(\textsc {E}^{-1}\):
-
The probability of enforcing re-sampling in \(\textsc {E}\) or \(\textsc {E}^{-1}\) is analyzed as follows: For a particular key
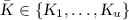 for which m blocks have been defined through queries to \(\textsc {RF}\), the probability of sampling a value that collides is at most \(m / (2^\lambda - p)\), as we choose uniformly from \(2^\lambda - p\) values. The expected number of blocks for the key \(L\) in the query is \(u(\ell _\mathrm {blk}(q_e+ q_v)+1) / 2^\kappa \), which leads to an overall probability of \(u(\ell _\mathrm {blk}(q_e+ q_v) + 1) / (2^{\kappa }(2^\lambda - p))\) for each query.
for which m blocks have been defined through queries to \(\textsc {RF}\), the probability of sampling a value that collides is at most \(m / (2^\lambda - p)\), as we choose uniformly from \(2^\lambda - p\) values. The expected number of blocks for the key \(L\) in the query is \(u(\ell _\mathrm {blk}(q_e+ q_v)+1) / 2^\kappa \), which leads to an overall probability of \(u(\ell _\mathrm {blk}(q_e+ q_v) + 1) / (2^{\kappa }(2^\lambda - p))\) for each query. -
The probability of enforcing that a value be copied (that is, the final “Else” statement becomes active) in \(\textsc {E}\) is bounded by \(u(\ell _\mathrm {blk}(q_e+ q_v) + 1) / 2^{\kappa +\nu }\) for each of the \(p\) queries. This is computed analogously to above: executing the “Else” statement means that the adversary guessed a combination of a \(\kappa \)-bit key and a \(\nu \)-bit mask value.
-
Finally, the probability for copying a value in \(\textsc {E}^{-1}\) is bounded by the term \(1 / 2^{-\kappa }\). The reason is that it corresponds to guessing a the key for a specific user.
We obtain the bounds \(up(\ell _\mathrm {blk}(q_e+ q_v) + 1) / (2^\kappa (2^\lambda - p))\), \(up_e(\ell _\mathrm {blk}(q_e+ q_v) + 1)/2^{\kappa +\nu }\), and \(p_i/ 2^{-\kappa }\) as the adversary makes at most \(p_e\) queries to \(\textsc {E}\), \(p_i\) queries to \(\textsc {E}^{-1}\), and \(p=p_e+p_i\) queries accumulated.
We proceed by analyzing the probabilities for \(\textsc {RF}\) analogously:
-
With respect to enforcing re-sampling in \(\textsc {RF}\), for a key \(L\) for which m blocks have been defined, the probability of sampling a colliding value is \(m / (2^\lambda - q_e- q_v)\). This leads to an overall probability of at most \(p/ (2^{\kappa }(2^\lambda - q_e- q_v))\).
-
The probability of enforcing that a value be copied (that is, the final “Else” statement becomes active) in \(\textsc {RF}\) is bounded by \(u(\ell _\mathrm {blk}(q_e+ q_v) +1) p/ 2^{\kappa +\nu }\). The reason is that for a particular key \(L\) for which m blocks have been defined through queries to \(\textsc {E}\) and \(\textsc {E}^{-1}\), the probability that an query to \(\textsc {RF}\) as done by \(\mathsf {\mathsf {CAU}.Enc}^\textsc {RF}\) uses the same input is bounded by \(m / 2^\nu \). This leads to a probability of \(p/ 2^{\kappa +\nu }\).
Since the encryption and decryption algorithms overall make \(u(\ell _\mathrm {blk}(q_e+ q_v) + 1)\) queries to \(\textsc {RF}\), we obtain the bounds \(up(\ell _\mathrm {blk}(q_e+ q_v) + 1) / (2^\kappa (2^{\lambda } - q_e- q_v))\) and \(up(\ell _\mathrm {blk}(q_e+q_v)+1) / 2^{\kappa +\nu }\).
Finally, as in \(\mathrm {G}_2\) the oracles \(\textsc {E}\) and \(\textsc {E}^{-1}\) are independent of the oracle \(\textsc {RF}\) that is used in \(\mathsf {RCAU}\), the probability of guessing a key is \(u/2^\kappa \). All these terms together comprise the bound in the theorem statement. \(\square \)
For realistic parameters, the bound in Theorem 3 means that the “best” attack for passive adversaries is now the inversion of a block observed while eavesdropping. In contrast to the attack analyzed in Sect. 5.1, this attack does not scale in the mass surveillance scenario, because the adversary has to target one specific ciphertext block.
Adversary \(A_{p_i}\) used in Theorem 4.
In more detail, the adversary strategy \(A\) analyzed in the below lemma and specified in detail in Fig. 9 proceeds as follows. First obtain an encryption of \(0^{2\lambda }\) from an honest user. Then brute-force the key by decrypting the first ciphertext block using \(\textsc {E}^{-1}\), checking whether the output satisfies the structure \(N\Vert 0^{\lambda -\nu -2}10\). In case this structure is observed, verify the key by checking if the next block is consistent with an evaluation of \(\textsc {E}\) with the same key and plaintext \(N\Vert 0^{\lambda -\nu -2}11\).
Since the described attack strategy applies independently of how the nonces are chosen (prior to the randomization) as long as the value is predictable, the lower bound also applies to the scheme as used in the latest draft of TLS 1.3.
Theorem 4
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be a family of functions. Let \(\mathsf {RCAU}= \mathbf {RCAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(p_i\ge 2\) an even integer and the adversary \(A_{p_i}\) as described in Fig. 9, which makes 1 query to each \(\textsc {New}\) and \(\textsc {Enc}\) (the latter of length \(2\lambda \) bits), no queries to \(\textsc {Vf}\), \(p_i\) queries to \(\textsc {E}^{-1}\), and no queries to \(\textsc {E}\). Then
with
Proof
Let  be the key sampled during the invocation of \(\textsc {New}\) in the game. The probability for the block cipher on a key
be the key sampled during the invocation of \(\textsc {New}\) in the game. The probability for the block cipher on a key  to satisfy the first condition is \(2^{\nu -\lambda }\), since in the first invocation of \(\textsc {E}^{-1}\) the value is sampled uniformly at random and \(\lambda -\nu \) bits have to match. The second invocation of \(\textsc {E}^{-1}\) has to lead to the correct outcome \(N\Vert 0^{\lambda -\nu -2}11\), the value is drawn uniformly at random from the remaining \(2^\lambda -1\) values not equal to the outcome of the first query. There are \(2^\kappa \) keys, so by the Union Bound the probability of any key
to satisfy the first condition is \(2^{\nu -\lambda }\), since in the first invocation of \(\textsc {E}^{-1}\) the value is sampled uniformly at random and \(\lambda -\nu \) bits have to match. The second invocation of \(\textsc {E}^{-1}\) has to lead to the correct outcome \(N\Vert 0^{\lambda -\nu -2}11\), the value is drawn uniformly at random from the remaining \(2^\lambda -1\) values not equal to the outcome of the first query. There are \(2^\kappa \) keys, so by the Union Bound the probability of any key  to lead to an admissible pattern on the first two blocks is bounded by \((2^\kappa -1)2^\nu /(2^\lambda (2^\lambda -1))\).
to lead to an admissible pattern on the first two blocks is bounded by \((2^\kappa -1)2^\nu /(2^\lambda (2^\lambda -1))\).
In the event that no key  satisfies the above condition, this advantage of adversary \(A_{p_i}\) is simply the probability of guessing a uniformly random key of \(\kappa \) bits in \(p_i/2\) attempts, as for each key \(A_{p_i}\) spends at most 2 queries. This completes the proof. \(\square \)
satisfies the above condition, this advantage of adversary \(A_{p_i}\) is simply the probability of guessing a uniformly random key of \(\kappa \) bits in \(p_i/2\) attempts, as for each key \(A_{p_i}\) spends at most 2 queries. This completes the proof. \(\square \)
The attack analyzed in Theorem 4 is considerably harder to mount than the one analyzed in Theorem 2, because the queries in the Theorem 2 attack can be preprocessed and apply to all observed communication sessions equally, whereas in the Theorem 4 attack the queries have to be made for a particular session under attack. Still, in the following Sect. 5.3, we show that at low computational cost for the honest parties, the Theorem 4 attack can be made considerably harder.
5.3 Security of XCAU
The term \(p_i/2^\kappa \) in the bound for RCAU originates in the fact that only the input of the block cipher is masked, and inversion queries by the adversaries are not hindered. In the scheme XCAU, an advantage beyond the randomization of the input to derive the hash function key is that the output of the block cipher is masked, which restricts the power of inversion queries to the block cipher considerably.
Our analysis of XCAU is based on combining the analysis of DESX-like input and output whitening in a multi-user setting, and then prove the security of XCAU along the lines of Theorem 8. We first prove a multi-user bound for the DESX-like construction. The security goal is described by the games in Fig. 10.
Theorem 5
Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\), \(q_2\) queries to its \(\textsc {RF}\) oracle per user, \(p\) queries to its \(\textsc {E}\) oracle and \(\textsc {E}^{-1}\) oracles. Then
Proof
We introduce two intermediate games \(\mathrm {G}_0\) and \(\mathrm {G}_1\) in Fig. 11. Game \(\mathrm {G}_0\) is equivalent to game \(\mathrm {R}(A)\); the introduction of the additional map \(U[\cdot ,\cdot ]\) is only syntactic as we make sure that it stays consistent with \(T[\cdot ,\cdot ]\) throughout. We also modify the procedures for sampling new values for the maps \(U[\cdot ,\cdot ]\) and \(T[\cdot ,\cdot ]\) such that first we sample a new value such that it is consistent only with the respective map, then check whether it is consistent with the other map, and re-sample consistently if we determine that it is not. In \(\mathrm {G}_1\), the map \(U[\cdot ,\cdot ]\) is completely independent of the map \(T[\cdot ,\cdot ]\). Both \(\mathrm {G}_0\) and \(\mathrm {G}_1\) set the flag \(\mathsf {bad}\) on occasions where the sampling creates inconsistencies between \(U[\cdot ,\cdot ]\) and \(T[\cdot ,\cdot ]\).
Modification of the sampling algorithm. In \(\mathrm {G}_0\), the values are sampled to keep consistency between \(U[\cdot ,\cdot ]\) and \(T[\cdot ,\cdot ]\), with the flag \(\mathsf {bad}\) set if attempted independent sampling leads to inconsistencies. In \(\mathrm {G}_1\), the maps \(U[\cdot ,\cdot ]\) and \(T[\cdot ,\cdot ]\) are sampled independently, making \(\textsc {RF}\) an independent ideal cipher.
The probability of setting the \(\mathsf {bad}\) flag in \(\mathrm {G}_2\) and \(\mathrm {G}_3\) can be bounded as follows. We first observe that besides the \(\mathsf {bad}\) flag, \(\mathrm {G}_3\) is equivalent to \(\mathrm {S}\). For both \(\mathrm {G}_2\) and \(\mathrm {G}_3\), as long as \(\mathsf {bad}\) is not set, all outputs are uniformly distributed among the values that are valid for the respective oracle and key. Moreover, xoring  to all inputs or outputs modifies each concrete permutation; however, the distribution of a uniformly random permutation remains unchanged by this operation. Following the definition of Maurer [23], this means that both games \(\mathrm {G}_2\) and \(\mathrm {G}_3\) with the respective flags \(\mathsf {bad}\) are conditionally equivalent to the game \(\mathrm {S}\). (In other words, conditioned on \(\mathsf {bad}=\mathsf {false}\), the outputs of the games are distributed exactly as in \(\mathrm {S}\).)
to all inputs or outputs modifies each concrete permutation; however, the distribution of a uniformly random permutation remains unchanged by this operation. Following the definition of Maurer [23], this means that both games \(\mathrm {G}_2\) and \(\mathrm {G}_3\) with the respective flags \(\mathsf {bad}\) are conditionally equivalent to the game \(\mathrm {S}\). (In other words, conditioned on \(\mathsf {bad}=\mathsf {false}\), the outputs of the games are distributed exactly as in \(\mathrm {S}\).)
Subsequently, we can employ Maurer’s result [23, Theorem 1] to bound the distinguishing advantage between \(\mathrm {G}_2\) and \(\mathrm {G}_3\) by the advantage of the best non-adaptive distinguisher. As the adversary makes at most \(p\) queries to its \(\textsc {E}\) and \(\textsc {E}^{-1}\) oracles, and \(uq_2\) queries to its \(\textsc {RF}\) oracle, there are \(u\cdot q_2 \cdot p\) possible combinations of queries that may provoke the flag \(\mathsf {bad}\) to be set, and each case appears with probability \(2^{-\lambda -\kappa -1}\). We conclude the proof via the Union Bound. \(\square \)
Analogously to the previous results on CAU and RCAU, we now analyze the key-recovery security of XCAU.
Theorem 6
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be a family of functions. Let \(\mathsf {XCAU}= \mathbf {XCAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\) oracle, \(q_e\) queries to its \(\textsc {Enc}\) oracle with messages of length at most \(\ell _\mathrm {bit}\) bits, \(q_v\) queries to its \(\textsc {Vf}\) oracle with messages of length at most \(\ell _\mathrm {bit}+\lambda \) bits, and \(p\) queries to its \(\textsc {E}\) and \(\textsc {E}^{-1}\) oracles. Assume furthermore that \(q_e\le 2^{\nu }\), and \(\ell _\mathrm {bit}\le \lambda (2^{\lambda -\nu }-2)\). Then, with \(\ell _\mathrm {blk}= \lceil \ell _\mathrm {bit}/\lambda \rceil + 1\),
Proof
As in Theorems 1 and 3, we restrict our attention to adversaries \(A\) that do not use invalid user identifiers, that do not re-use nonces, and that do not verify ciphertexts obtained from the \(\textsc {Enc}\) oracle. The first step in this proof is to rewrite the game as \(\mathrm {G}_0\) in the same way as in the previous proofs; the scheme is changed to use the oracle \(\textsc {RF}\) that is, however, kept consistent with \(\textsc {E}\) and \(\textsc {E}^{-1}\). The game is described in Fig. 12.
The next game \(\mathrm {G}_1\) is again a syntactic modification from \(\mathrm {G}_0\). The change is that we replace \(\mathsf {XCAU}\), which uses the original block cipher and applies the input and output whitening for the block cipher as a part of the encryption and decryption procedures, by \(\mathsf {CAU}\) instantiated with a block cipher with key length \(\lambda +\kappa \). Consequently, we rewrite the oracle \(\textsc {RF}\) to perform the input and output whitening.
In the next game \(\mathrm {G}_2\), the oracles \(\textsc {E}\) and \(\textsc {E}^{-1}\), and the oracle \(\textsc {RF}\) are based on different maps \(T[\cdot ,\cdot ]\) (for \(\textsc {E}\) and \(\textsc {E}^{-1}\)) and \(U[\cdot ,\cdot ]\) (for \(\textsc {RF}\)), but the oracles are defined to keep them consistent. This is achieved by first sampling them independently, but then re-sampling in case an inconsistency occurs. Should that be the case, the flag \(\mathsf {bad}\) is set. Apart from this flag, games \(\mathrm {G}_1\) and \(\mathrm {G}_2\) are equivalent. We do not describe the game \(\mathrm {G}_2\) explicitly, but remark that it is obtained by verbatim replacement of the oracles \(\textsc {E}\), \(\textsc {E}^{-1}\), and \(\textsc {RF}\) in game \(\mathrm {G}_1\) by the ones described in game \(\mathrm {G}_0\) in Fig. 11. In the next game \(\mathrm {G}_3\), the re-sampling procedure keeping the oracles consistent is abandoned, which means that the oracles \(\textsc {RF}\) and \(\textsc {E}\) together with \(\textsc {E}^{-1}\) are independent. Like \(\mathrm {G}_2\), game \(\mathrm {G}_3\) is obtained by replacing the oracles \(\textsc {E}\), \(\textsc {E}^{-1}\), and \(\textsc {RF}\) by the ones in game \(\mathrm {G}_1\) in Fig. 11.
The probability of setting the \(\mathsf {bad}\) flag in \(\mathrm {G}_2\) and \(\mathrm {G}_3\) can be bounded using Theorem 5. More technically, we describe an adversary \(B= B(A)\) that emulates oracles to \(A\) as follows: Queries \(\textsc {New}\), \(\textsc {E}\), and \(\textsc {E}^{-1}\) by \(B\) are responded by \(B\) performing the same query in its game. Queries \(\textsc {Enc}\) and \(\textsc {Dec}\) are responded by \(B\) emulating the respective oracles using the oracle \(\textsc {RF}\) in its game to evaluate \(\mathsf {\mathsf {CAU}.Enc}\) and \(\mathsf {\mathsf {CAU}.Dec}\). The view of \(A\) is the same in \(\mathrm {G}_2\) and in the game \(\mathrm {R}(B(A))\), and in \(\mathrm {G}_3\) and the game \(\mathrm {S}(B(A))\), respectively. The numbers of queries \(u\) to the \(\textsc {New}\) oracle and \(p\) to the \(\textsc {E}\) and \(\textsc {E}^{-1}\) oracles are preserved by \(B\). At most \(q_e\) queries of length at most \(\ell _\mathrm {bit}\) to \(\textsc {Enc}\) and at most \(q_v\) queries of length at most \(\ell _\mathrm {bit}+\lambda \) to \(\textsc {Vf}\) translate into at most \(\ell _\mathrm {blk}(q_e+q_v) + 1\) queries to \(\textsc {RF}\) in the game played by \(B\). Using Theorem 5, this means that the probability of setting \(\mathsf {bad}\) can be bounded by \(up(\ell _\mathrm {blk}(q_e+q_v) + 1) / 2^{\lambda +\kappa +1}\).
All that remains to be done is bounding the probability of \(A\) guessing any key in \(\mathrm {G}_3\). As in this game, similarly to the previous proofs, the keys used to reference values in \(U[\cdot ,\cdot ]\) is only used as an index to the table and is unrelated to all values that \(A\) observes in the game, the guessing probability is at most \(u/2^\kappa \). This concludes the proof. \(\square \)
6 Indistinguishability Security
In this section we prove the multi-user indistinguishability security bounds for CAU, RCAU, and XCAU, all in the ideal cipher model. All proofs in this section are deferred to the full version of this paper [7].
6.1 Preparation: A Lemma on CAU
We begin with a multi-user analysis of CAU which models the block cipher as a uniform random permutation and is useful in the subsequent proofs. The analysis is related to the ones of MV [24], IOM [18], and NOMI [27], with the main difference that they proved single-user security, while we directly prove multi-user security. We formalize the random-permutation model using our game \(\mathbf {G}^\mathrm{mu\text{- }ind}_{ \text {CAU} }\) while considering only adversaries that do not make use of the oracles \(\textsc {E}\) and \(\textsc {E}^{-1}\).
Lemma 7
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be an \(\epsilon \)-almost XOR-universal hash function, for some \(\epsilon {:\,}{{\mathbb N}} \times {{\mathbb N}} \rightarrow [0,1]\). Let \(\mathsf {CAU}= \mathbf {CAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\) oracle, \(q_e\) queries to its \(\textsc {Enc}\) oracle with messages of length at most \(\ell _\mathrm {bit}\) bits, and \(q_v\) queries to its \(\textsc {Vf}\) oracle with messages of length at most \(\ell _\mathrm {bit}+\lambda \) bits,Footnote 1. In particular, \(A\) does not use the \(\textsc {E}\) and \(\textsc {E}^{-1}\) oracles. Assume furthermore that \(q_e\le 2^{\nu }\) and \(\ell _\mathrm {bit}\le \lambda (2^{\lambda -\nu }-2)\). Then
for \(\ell _\mathrm {blk}= \lceil \ell _\mathrm {bit}/\lambda \rceil + 1\) and where the AEAD headers are restricted to \(\ell _\mathrm {head}\) bits.
6.2 Security of CAU
We now prove the multi-user indistinguishability security of plain CAU in the ideal-cipher model.
Theorem 8
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be an \(\epsilon \)-almost XOR-universal hash function, for some \(\epsilon {:\,}{{\mathbb N}} \times {{\mathbb N}} \rightarrow [0,1]\). Let \(\mathsf {CAU}= \mathbf {CAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\) oracle, \(q_e\) queries to its \(\textsc {Enc}\) oracle with messages of length at most \(\ell _\mathrm {bit}\) bits, \(q_v\) queries to its \(\textsc {Vf}\) oracle with messages of length at most \(\ell _\mathrm {bit}+\lambda \) bits, and \(p\) queries to its \(\textsc {E}\) and \(\textsc {E}^{-1}\) oracles. Assume furthermore that \(q_e\le 2^{\nu }\) and \(\ell _\mathrm {bit}\le \lambda (2^{\lambda -\nu }-2)\). Then
for \(\ell _\mathrm {blk}= \lceil \ell _\mathrm {bit}/\lambda \rceil + 1\) and where the AEAD headers are restricted to \(\ell _\mathrm {head}\) bits.
The first term originates from the advantage of the adversary in guessing a user’s key in a query to the ideal cipher. This term grows linearly in the number of honest sessions, and it also grows linearly in the number of adversary calls to the ideal cipher. We show below in Theorem 2 that a term of this size is inevitable by proving the effectiveness of an attack. The second term stems from a PRF/PRP-switching in the proof of counter mode. The third term stems from a potential collision of honest-user keys, and the final term from the authentication using the AUH-based MAC.
6.3 Security of RCAU
In terms of bounds for RCAU, we first show a simple corollary proving that the same bounds as for \(\mathsf {CAU}\) also apply for \(\mathsf {RCAU}\). This follows immediately by a reduction that randomizes the nonces.
Corollary 9
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be an \(\epsilon \)-almost XOR-universal hash function, for some \(\epsilon {:\,}{{\mathbb N}} \times {{\mathbb N}} \rightarrow [0,1]\). Let \(\mathsf {RCAU}= \mathbf {RCAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\) oracle, \(q_e\) queries to its \(\textsc {Enc}\) oracle with messages of length at most \(\ell _\mathrm {bit}\) bits, \(q_v\) queries to its \(\textsc {Vf}\) oracle with messages of length \(\ell _\mathrm {bit}+\lambda \) bits, \(p_e\) queries to its \(\textsc {E}\) oracle, \(p_i\) queries to its \(\textsc {E}^{-1}\) oracle, and \(p= p_e+ p_i\). Assume furthermore that \(q_e\le 2^{\nu }\), and \(\ell _\mathrm {bit}\le \lambda (2^{\lambda -\nu }-2)\). (For brevity we write \(q=q_e+q_v\).) Then
for \(\ell _\mathrm {blk}= \lceil \ell _\mathrm {bit}/\lambda \rceil + 1\) and where the AEAD headers are restricted to \(\ell _\mathrm {head}\) bits.
We prove a stronger bound for the advantage of a passive adversary that does not use its \(\textsc {Vf}\) oracle in a non-trivial way. The bound differs from the one proven above significantly: we show that for passive adversaries we can replace the term \(up/2^\kappa \) in the bound for \(\mathsf {CAU}\) by terms that are smaller for realistic parameters. The proof does, however, not extend to active adversaries that make use of the \(\textsc {Vf}\) oracle: In fact, \(\mathsf {RCAU}\) evaluates the block cipher, in each session, on the fixed value \(0^{\lambda }\) to obtain the key for \(\mathsf {H}\), and our analysis of the authenticity guarantee requires that this key be uniformly random. This requirement is of course not fulfilled if the adversary evaluated the block cipher on the value \(0^{\lambda }\) for the respective key.
In the result for RCAU, we explicitly distinguish between the numbers for evaluation \(p_e\) and inversion \(p_i\) queries for the block cipher, with \(p= p_e+ p_i\).
Theorem 10
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be a family of functions. Let \(\mathsf {RCAU}= \mathbf {RCAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\) oracle, \(q_e\) queries to its \(\textsc {Enc}\) oracle with messages of length at most \(\ell _\mathrm {bit}\) bits, \(q_v\) queries to its \(\textsc {Vf}\) oracle with messages of length \(\ell _\mathrm {bit}+\lambda \) bits, \(p_e\) queries to its \(\textsc {E}\) oracle, \(p_i\) queries to its \(\textsc {E}^{-1}\) oracle, and \(p= p_e+ p_i\). Assume furthermore that \(q_e\le 2^{\nu }\), and \(\ell _\mathrm {bit}\le \lambda (2^{\lambda -\nu }-2)\). (For brevity we write \(q=q_e+q_v\).) Then
for \(\ell _\mathrm {blk}= \lceil \ell _\mathrm {bit}/\lambda \rceil + 1\), and for an adversary \(A\) making \(q_v= 0\) verification queries.
In comparison with the bound proven in Theorem 8, the major difference in Eq. (4) is that the term \(up/ 2^\kappa \) is replaced by the four terms \(up(\ell _\mathrm {blk}(q_e+ q_v) + 1) / 2^{\kappa +\nu }\), \(up(\ell _\mathrm {blk}(q_e+ q_v) + 1) / 2^\kappa (2^\lambda - u)\), \(up(\ell _\mathrm {blk}(q_e+ q_v) + 1) / 2^\kappa (2^\lambda - q_e- q_v)\) and \(p_i/ 2^{\kappa }\). This is an improvement because for the values used in TLS 1.3 it is reasonable to assume \(\ell _\mathrm {blk}(q_e+ q_v) + 1 \ll 2^{96}\) as well as \(q_e+q_v,p\ll 2^{96}\), and the term \(p_i/2^\kappa \) does not scale with \(u\). Unfortunately, our proof does not support a similar statement for active attacks.
We stress that the term \(up/2^\kappa \) in Eq. (3) does, unlike the one in Theorem 8, not immediately corresponds to a matching attack on the use of the scheme within the TLS protocol. The reason is that such an attack would require sending a great amount of crafted ciphertexts within the TLS session, but TLS tears down a session and discards the keys after the first failure in MAC verification. Therefore, it is conceivable that the scheme as used within TLS achieves considerably better security against active attacks than our above bound suggests. Moreover, such an attack would be inherently active and not suitable for mass surveillance.
6.4 Security of XCAU
To analyze the indistinguishability security of XCAU, we combine the results of Theorem 5 and Lemma 7. The proof is almost the same as the one for Theorem 8, but the step of “decoupling” the \(\textsc {E}\)/\(\textsc {E}^{-1}\) and \(\textsc {RF}\) oracles makes use of the results in Theorem 5. Most notably and in contrast to RCAU, the bound does not contain a term of the type \(p_i/2^\kappa \), and applies to active adversaries as well.
Theorem 11
Let \(\kappa ,\lambda ,\nu \ge 1\) be such that \(\nu \le \lambda -2\). Let \(\mathsf {H}{:\,}\{0,1\}^{\lambda } \times (\{0,1\}^* \times \{0,1\}^*) \rightarrow \{0,1\}^{\lambda }\) be an \(\epsilon \)-almost XOR-universal hash function, for some \(\epsilon {:\,}{{\mathbb N}} \times {{\mathbb N}} \rightarrow [0,1]\). Let \(\mathsf {XCAU}= \mathbf {XCAU}[\mathsf {H},\kappa ,\lambda ,\nu ]\). Let \(A\) be an adversary that makes at most \(u\) queries to its \(\textsc {New}\) oracle, \(q_e\) queries to its \(\textsc {Enc}\) oracle with messages of length at most \(\ell _\mathrm {bit}\) bits, \(q_v\) queries to its \(\textsc {Vf}\) oracle with messages of length at most \(\ell _\mathrm {bit}+\lambda \) bits, and \(p\) queries to its \(\textsc {E}\) and \(\textsc {E}^{-1}\) oracles. Assume furthermore that \(q_e\le 2^{\nu }\) and \(\ell _\mathrm {bit}\le \lambda (2^{\lambda -\nu }-2)\). Then
for \(\ell _\mathrm {blk}= \lceil \ell _\mathrm {bit}/\lambda \rceil + 1\), and with headers of length at most \(\lambda \ell _\mathrm {head}\) bits.
7 Conclusion
TLS 1.2 is the most widely used cryptographic protocol in the Internet, but due to issues with both performance and security, it will soon be replaced by its successor, TLS 1.3. Given that the bulk of Internet traffic will likely be protected by TLS 1.3 in the next years, it is extremely important that the security of the protocol is well-understood. Facing the threat of mass surveillance and the expected great number of TLS 1.3 sessions, the TLS Working Group has introduced a nonce-randomization technique to improve the resilience of TLS 1.3 against such attacks.
We show that the proposed technique can be understood as a key-length extension for AE; it essentially extends the 128-bit key of AES-GCM to a 224-bit key. We first describe the authenticated encryption CAU (Counter mode Almost Universal) as an abstraction of GCM. We then describe the scheme with randomized nonces as its variant RCAU and analyze it in the multi-user setting, where we show that it improves the resilience against (passive) mass surveillance as intended by the designers. We also show, however, that the AE does not perform as well as one might expect from an AE with a 224-bit key, especially in presence of active attacks. One alternative would be to simply increase the key size by, e.g., switching to an AES-256-based mode; this achieves better security but also impacts performance.
We suggest a new encryption mode that we call XCAU. The mode uses an additional 128-bit key (256 bits in total) to randomize the inputs and outputs of the block cipher (here AES) as in DESX. The mode is almost as efficient as the mode RCAU used in TLS 1.3, only adding two 128-bit xor operations for each call to the block cipher over plain CAU, our abstraction for GCM. We show that, still, its security is improved over RCAU in two ways. The security bounds we prove for security of XCAU against active attacks scale significantly better in the number \(u\) of users than those for RCAU, this stems mostly from the fact that all inputs to the block cipher are randomized. Furthermore, the whitening of the block-cipher output allows to remove the (for realistic parameters largest) term \(p_i/2^{\kappa }\) from the security bound. (It should be noted, however, that this term is not worrisome for realistic parameters.) The fact that the implementation of XCAU, in contrast to that of RCAU, requires non-black-box changes to the libraries implementing CAU, however, makes adoption in the currently developed standard TLS 1.3 difficult.
Notes
- 1.
The ciphertext contains an \(\lambda \)-bit MAC tag, so the length of the contained plaintext is \(\ell _\mathrm {bit}\) bits.
References
Badertscher, C., Matt, C., Maurer, U., Rogaway, P., Tackmann, B.: Augmented secure channels and the goal of the TLS 1.3 record layer. In: AU, M.-H., et al. (eds.) ProvSec 2015. LNCS, vol. 9451, pp. 85–104. Springer, Heidelberg (2015). doi:10.1007/978-3-319-26059-4_5
Bellare, M., Bernstein, D.J., Tessaro, S.: Hash-function based PRFs: AMAC and its multi-user security. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 566–595. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_22
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000)
Bellare, M., Canetti, R., Krawczyk, H.: Pseudorandom functions revisited: the cascade construction and its concrete security. In: 37th FOCS, pp. 514–523. IEEE Computer Society Press, October 1996
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 531–545. Springer, Heidelberg (2000)
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006)
Bellare, M., Tackmann, B.: The multi-user security of authenticated encryption: AES-GCM in TLS 1.3. Cryptology ePrint Archive, Report 2016/564 (2016). http://eprint.iacr.org/
Bernstein, D.J.: Multi-user Schnorr security, revisited. Cryptology ePrint Archive, Report 2015/996 (2015). http://eprint.iacr.org/2015/996
Boyarsky, M.K.: Public-key cryptography and password protocols: the multi-user case. In: ACM CCS 1999, pp. 63–72. ACM Press, November 1999
Dodis, Y., Lee, P.J., Yum, D.H.: Optimistic fair exchange in a multi-user setting. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 118–133. Springer, Heidelberg (2007)
Dworkin, M.: Recommendation for block cipher modes of operation: the CCM mode for authentication and confidentiality. NIST Special, Publication 800-38C, May 2004
Dworkin, M.: Recommendation for block cipher modes of operation: Galois/Counter Mode (GCM) and GMAC. NIST Special, Publication 800-38D, November 2007
Even, S., Mansour, Y.: A construction of a cipher from a single pseudorandom permutation. J. Cryptol. 10(3), 151–162 (1997)
Fischlin, M., Günther, F., Marson, G.A., Paterson, K.G.: Data is a stream: security of stream-based channels. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 545–564. Springer, Heidelberg (2015)
Fouque, P.-A., Joux, A., Mavromati, C.: Multi-user collisions: applications to discrete logarithm, even-mansour and PRINCE. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 420–438. Springer, Heidelberg (2014)
Galbraith, S., Malone-Lee, J., Smart, N.P.: Public key signatures in the multi-user setting. Inf. Process. Lett. 83(5), 263–266 (2002)
Huang, Q., Yang, G., Wong, D.S., Susilo, W.: Efficient optimistic fair exchange secure in the multi-user setting and chosen-key model without random oracles. In: Malkin, T. (ed.) CT-RSA 2008. LNCS, vol. 4964, pp. 106–120. Springer, Heidelberg (2008)
Iwata, T., Ohashi, K., Minematsu, K.: Breaking and repairing GCM security proofs. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 31–49. Springer, Heidelberg (2012)
Kilian, J., Rogaway, P.: How to protect DES against exhaustive key search (an analysis of DESX). J. Cryptol. 14(1), 17–35 (2001)
Kiltz, E., Masny, D., Pan, J.: Optimal security proofs for signatures from identification schemes. Cryptology ePrint Archive, Report 2016/191 (2016). http://eprint.iacr.org/
Krawczyk, H.: LFSR-based hashing and authentication. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 129–139. Springer, Heidelberg (1994)
Krovetz, T., Rogaway, P.: The software performance of authenticated-encryption modes. In: Joux, A. (ed.) FSE 2011. LNCS, vol. 6733, pp. 306–327. Springer, Heidelberg (2011)
Maurer, U.M.: Indistinguishability of random systems. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 110–132. Springer, Heidelberg (2002)
McGrew, D.A., Viega, J.: The security and performance of the Galois/Counter Mode (GCM) of operation. In: Canteaut, A., Viswanathan, K. (eds.) INDOCRYPT 2004. LNCS, vol. 3348, pp. 343–355. Springer, Heidelberg (2004)
Mouha, N., Luykx, A.: Multi-key security: the even-mansour construction revisited. In: Gennaro, R., Robshaw, M.J.B. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 209–223. Springer, Heidelberg (2015)
Namprempre, C., Rogaway, P., Shrimpton, T.: Reconsidering generic composition. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 257–274. Springer, Heidelberg (2014)
Niwa, Y., Ohashi, K., Minematsu, K., Iwata, T.: GCM security bounds reconsidered. In: Leander, G. (ed.) FSE 2015. LNCS, vol. 9054, pp. 385–407. Springer, Heidelberg (2015)
Rogaway, P.: Authenticated-encryption with associated-data. In: Atluri, V. (ed.) ACM CCS 2002, pp. 98–107. ACM Press, November 2002
Rogaway, P.: Efficient instantiations of tweakable blockciphers and refinements to modes OCB and PMAC. In: Lee, P.J. (ed.) ASIACRYPT 2004. LNCS, vol. 3329, pp. 16–31. Springer, Heidelberg (2004)
Rogaway, P., Bellare, M.: Robust computational secret sharing and a unified account of classical secret-sharing goals. In: Ning, P., di Vimercati, S.D.C., Syverson, P.F. (eds.) ACM CCS 2007, pp. 172–184. ACM Press, October 2007
Rogaway, P., Bellare, M., Black, J., Krovetz, T.: OCB: a block-cipher mode of operation for efficient authenticated encryption. In: ACM CCS 2001, pp. 196–205. ACM Press, November 2001
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006)
Smith, B.: Pull request: removing the AEAD explicit IV. Mail to IETF TLS Working Group, March 2015
Tessaro, S.: Optimally secure block ciphers from ideal primitives. In: Iwata, T., et al. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 437–462. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48800-3_18
Acknowledgments
Bellare was supported in part by NSF grants CNS-1526801 and CNS-1228890, ERC Project ERCC FP7/615074 and a gift from Microsoft. Tackmann was supported in part by the Swiss National Science Foundation (SNF) via Fellowship No. P2EZP2_155566 and by NSF grant CNS-1228890.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Bellare, M., Tackmann, B. (2016). The Multi-user Security of Authenticated Encryption: AES-GCM in TLS 1.3. In: Robshaw, M., Katz, J. (eds) Advances in Cryptology – CRYPTO 2016. CRYPTO 2016. Lecture Notes in Computer Science(), vol 9814. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53018-4_10
Download citation
DOI: https://doi.org/10.1007/978-3-662-53018-4_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53017-7
Online ISBN: 978-3-662-53018-4
eBook Packages: Computer ScienceComputer Science (R0)













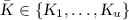 for which m blocks have been defined through queries to
for which m blocks have been defined through queries to 


