Abstract
Application Programming Interfaces (APIs) to cryptographic tokens like smartcards and Hardware Security Modules (HSMs) provide users with commands to manage and use cryptographic keys stored on trusted hardware. Their design is mainly guided by industrial standards with only informal security promises.
In this paper we propose cryptographic models for the security of such APIs. The key feature of our approach is that it enables modular analysis. Specifically, we show that a secure cryptographic API can be obtained by combining a secure API for key-management together with secure implementations of, for instance, encryption or message authentication. Our models are the first to provide such compositional guarantees while considering realistic adversaries that can adaptively corrupt keys stored on tokens. We also provide a proof of concept instantiation (from a deterministic authenticated-encryption scheme) of the key-management portion of cryptographic API.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Key management, i.e. the secure creation, storage, backup, and destruction of keys, has long been identified as a major challenge in all practical uses of cryptography. To achieve high levels of security, in practice one commonly relies on physical protection: store cryptographic keys inside a tamper-resistant device, called a cryptographic token, and only allow access to the keys (e.g. for performing cryptographic operations) indirectly through an Application Programming Interface (API). Tokens are widely deployed in practice and range from smart cards and USB sticks to powerful Hardware Security Modules (HSMs). They are used to generate and store keys for certification authorities, to accelerate SSL/TLS connections and they form the backbone of interbank communication networks.
A user with access to the token may use the API to perform—securely on the token—cryptographic operations, such as encryption or authentication of user-provided data, using the stored keys. A key feature of such APIs is their support for key management across tokens. We focus on wrapping, the mechanism to transport keys between devices by encrypting them under an already shared key. Finally, the API prevents insecure or unauthorized use of keys, typically based on attributes and policies. Through their APIs, the overall distributed architecture provides an increased level of security for keys, simplifies access control through flexible key-management, and enables modular application development.
The design and analysis of key-management APIs mainly follows industrial standards, notably PCKS#11 [23], that are geared towards specifying functionality and interoperability. The standards typically lack a clearly defined security goal, let alone a rigorous analysis that any security claim is reasonably met. As a result, proper deployment relies strongly on best practices (undocumented in the public domain); moreover, tokens are subject to regular successful attacks [2–4, 7]. This raises the question whether the security of cryptographic APIs can be captured and compartmentalized, taking into account the reality that some keys will leak.
The main symmetric operation employed in key-management, namely the key-wrapping primitive, is fairly well understood through appropriate models and efficient implementations [15, 21, 22]. However, the security of the overall design of cryptographic APIs is a far more complicated problem, that only recently received attention [5, 17, 18]. None of the existing models is entirely satisfactory: they are either too specific [5, 17]; underspecified while imposing unnecessary restrictions on how PKCS#11 can be used [18]; or avoid the highly relevant issue of adaptive key corruption [5, 17]. We provide a more in-depth comparison later in the paper (Sect. 6). Our model naturally and unsurprisingly shares various modelling choices with past work: We keep track of the information concerning which key encrypts which key using a graph; we maintain information about keys, handles and attributes in a similar way. Our focus is on the modular analysis where the key-management component can be analyzed separately from the cryptographic schemes that use the keys, and all of this in a reasonable corruption model.
Our Contributions. We give a formal syntax and security model for cryptographic APIs, reflecting concepts distilled from PKCS#11. We have aimed for a level of abstraction that allows for common deployment “best practices” (e.g. hierachical layering of managed keys based upon their intended use), without being overly tied to any particular implementation. Our formalism captures the core symmetric functionalities exposed by cryptographic APIs. Specifically, management and exporting/importing of cryptographic keys via the API; and cryptographic operations (e.g. encryption) performed under the managed keys, on behalf of applications requesting these operations via the API.
To foster modular analysis, we establish security goals for the key-management system (the abstract “back end” whose state is affected by key-management API calls). These goals are agnostic toward the particular cryptographic operations the keys will support. The primitives underlying the cryptographic operations exposed by the API are also are treated abstractly, as are their corresponding security notions.
Our key technical result shows that—as one would hope and expect—composing a secure key-management system with a secure primitive yields a secure overall system, provided certain conditions are met. Remarkably, our composition result holds while allowing adaptive corruptions of managed keys; we discuss later how we overcome the well-documented difficulties associated to merging composition and adaptive security in a single framework.
We also show how to instantiate a secure key-management system based upon deterministic authenticated-encryption (DAE). The DAE primitive was previously proposed as a method for secure “key-wrapping”, loosely the symmetric encryption of key \(K_1\) (and its associated data) under another key \(K_2\), ostensibly for the purpose of transporting \(K_1\) between devices that share \(K_2\). We build upon this functionality to deliver a (minimal) secure key-management component of a cryptographic API, specifically one with hierarchical layering of keys. Below, we discuss these contributions in greater detail.
Our Syntax and Security Model. Our syntax for a cryptographic API abstractly captures the following abilities: (1) to create keys with specified attributes on a named token; (2) to wrap, and subsequently unwrap, a managed key for external transport between tokens; (3) to transport keys directly from one token to another (without (un)wrapping); and (4) to run (non-key-management) cryptographic primitives on user-provided inputs, under user-indicated keys. These operations are all subject to the policy enforced by the token. We include this dependency on the policy in our model, but leave it unspecified.
The security model exposes these capabilities to adversaries who, speaking informally, attempt to “break” the token by sequences of API calls. In particular, an adversary can create, wrap, and unwrap keys as it wishes, and use these keys in the supported cryptographic primitives. The realistic multi-token setting is captured by allowing the adversary to cause direct transfers of keys between tokens (modeling secure injection of a single key into several tokens, say during the manufacturing process, or by security officers), and by allowing it to corrupt individual keys adaptively. The latter capability models the real possibility that some keys leak, due to for instance partial security breaches or successful cryptanalysis.
Security with respect to our model will demand that all managed keys that are not compromised (directly, or indirectly by clever API calls) can be used securely by the cryptographic primitives. Our focus on the exported primitives, instead of individual keys, highlights the raison d’être of cryptographic tokens: they should guarantee the security of the operations performed with the keys that they store.
One salient feature of our model is its generality. Instead of providing a model only for say an encryption API, we work with an abstract (symmetric) cryptographic primitive. In brief, we start with an abstract security definition for arbitrary (symmetric) primitives and lift it to the setting of APIs. Our general treatment has the benefit that the resulting security definition can be instantiated for APIs that export a large class of symmetric primitives (including all of the usual ones).
Composition Theorem. The main technical contribution of this paper is a modular treatment for cryptographic APIs. As a first step, we isolate the core common component shared by cryptographic tokens, namely key-management, and provide a separate security model for it. Essentially, we define a key-management API (or KM-API, in short) to be a cryptographic API that allows only key-management operations. We define security of a KM-API to mean that any key that is not trivially compromised (directly or indirectly) is indistinguishable from random.
Next, we show how to compose a KM-API and an arbitrary (abstract) primitive. We require common sense syntactic restrictions to ensure the composition is meaningful (e.g. that the space of keys managed by the KM-API fits the one of the symmetric primitives). More importantly, the design that we propose requires that each key is used for either key-management or for keying the primitive, but not for both. Many of the existent attacks on APIs are the result of careless enforcement of this separation of key roles. Technically, we enforce this requirement via a mechanism from the PKCS#11 standard—the security of our construction essentially confirms the validity of this mechanism.
In a nutshell, to each key an attribute is associated making the key either \(\mathsf {external}\) or not.
We ensure the attribute has the desired effect by requiring that it is sticky. This notion formalizes an integrity property for attributes informally defined by PKCS#11. It guarantees that once set, the value of an attribute cannot be changed. The following theorem establishes the security of our design, allowing for the two components to be designed and analyzed separately.
Theorem 1
(Informal). If CA is a secure KM-API and P is a secure primitive then the composition of CA and P (as above) is a secure cryptographic API that exports P.
Importantly, the composition theorem is for a setting where adversaries can adaptively corrupt keys. Our models rely on game-based definitions, which is the main tool that we use to reconcile composition and adaptive corruption, two features that raise well-known problems in settings based on simulation [6, 20].
Construction Based on Deterministic Authenticated Encryption. We show that a secure KM-API can be built upon DAE schemes. In particular, we show that when the wrapping and unwrapping functionalities are implemented by a secure DAE scheme, one can securely instantiate a KM-API for an abstract “back end” that enforces hierachical layering of keys. Keys at the lowest layer of the hierarchy are used only to key the cryptographic primitives (we call these external keys), and keys above this are used only to wrap keys at lower layers (we call these internal keys). Whether a key is external or internal is specified in that key’s attributes. To wrap external key \(K_1\) under internal key \(K_2\), the encryption algorithm of a DAE scheme is used, and the attributes of key \(K_2\) serve as the associated data. (Of course, the KM-API only allows calling applications to indicate which keys are to be involved, not the actual key values.) The design of our proposed API ensures that the API policy will enforce layering.
Extensions. Our ultimate goal is to provide usable security models that should facilitate the analysis of security tokens in realistic scenarios. In this paper, for simplicity we restricted attention to the symmetric aspect of APIs only; moreover our security definition for cryptographic APIs only concerns the primitives they export. We do not address other properties that can be enforced by token policies, e.g. that internal policies may restrict operations to authenticated users that log-in to the token. Such policies play important roles in the logic of applications that rely on tokens. Nonetheless, we believe our model provides a suitable starting point for further extension. Indeed, we already incorporate attributes and use a very simple policy to enforce the security of our composition. We leave identifying and formalizing the intended semantics for other PKCS#11 attributes and extending to public-key functionality as an open problem.
2 Cryptographic Primitives
In this section we provide an abstract framework for cryptographic primitives that captures common goals such as encryption and message authentication. Our abstraction is tailored specifically for its subsequent use in defining (Sect. 3) and constructing (Sect. 4) cryptographic APIs. Thus, while our abstraction is rather general the choices regarding to what to abstract and what to make explicit in our framework are strongly motivated by the later context.
Standard notions of encryption and authentication (e.g., IND-CPA and EUF-CMA) are usually defined based on a single key and corruption of this single key is seldom considered: it typically renders the game trivial (either the adversary wins easily, or winning is information theoretically impossible). Adding explicit corruption to the single-key security model facilitates moving to the multi-key scenario (that is needed in the more general API setting). There are also true multi-key definitions in the literature (e.g. for key-dependent message security), but for technical reasons we require a modular multi-key definition that is induced by a single-key one.
Syntax. A primitive \({\mathsf {P}}\) is defined by a pair of stateless, randomized algorithms \(({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\). Algorithm \({\mathsf {Kg}}_{\mathsf {P}}\) takes as input some parameter \(\mathsf {pm}\) and generates a key from some set \({{\mathsf {Keys}}}_\mathsf {pm}\); here the distribution may depend on the parameter (e.g. which key length to use). Algorithm \({\mathsf {Alg}}_{\mathsf {P}}\) implements the functionality of the primitive, taking as input both a key and a primary input \(\mathsf {in}\), and producing an output \(\mathsf {out}\). Without loss of generality, the definition of the primitive requires only a single formal algorithm. If some functionality is naturally implemented using several algorithms (e.g. one for encryption and decryption each) these can all be “packed” inside \({\mathsf {Alg}}_{\mathsf {P}}\) by tagging the input to \({\mathsf {Alg}}_{\mathsf {P}}\) with a label that indicates which of the natural algorithms is to be executed. This means that our framework also captures a situation where multiple “types” of primitives (e.g. both encryption and a MAC) need to be supported, as all relevant algorithms can be neatly packed in the single \({\mathsf {Alg}}_{\mathsf {P}}\) (for which several distinct security notions can be defined, e.g. one for confidentiality and one for authenticity).
Correctness. Correctness is usually defined as a requirement on a sequence of calls that involve the algorithms that define a primitive. For instance encrypting an arbitrary message and subsequently decrypting the ciphertext (under the same key) should return the original message. Definition 1 captures this idea in the context of arbitrary primitives. For generality, the definition is formulated in a setting with multiple keys.
We consider an adversary that can create keys of its choice for the primitive (using oracle \({\textsc {new}}\)), and can invoke the algorithms of the primitive, via oracle \({\textsc {alg}}\) using the index i of a key \(K_i\). The experiment maintains a list \(\mathrm {tr}\) that records the execution trace: the occurrence of triple (i, x, y) in the trace indicates that \({\mathsf {Alg}}_{\mathsf {P}}\) was invoked on key \(K_i\), with input x and returning y. The correctness of \({\mathsf {P}}\) is captured by a predicate \(\mathsf {corr}_{\mathsf {P}}\) applied to the execution trace. Usually \(\mathsf {corr}_{\mathsf {P}}\) will be monotone: initially, for the empty trace, it will be \(\mathsf {true}\) and, once set to \(\mathsf {false}\), it will remain \(\mathsf {false}\).
Definition 1
Let \(({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\) implement a primitive \({\mathsf {P}}\) with \({{\mathsf {Keys}}}\supseteq \bigcup _{\mathsf {pm}}[{{\mathsf {Keys}}}_\mathsf {pm}]\). Let \(\mathsf {corr}_{\mathsf {P}}\) be a correctness predicate and \(\mathcal {A}\) an adversary, then the incorrectness advantage of \(\mathcal {A}\) against \(({\mathsf {Kg}}_{\mathsf {P}}, {\mathsf {Alg}}_{\mathsf {P}})\) with respect to \(\mathsf {corr}_{\mathsf {P}}\) is defined as
for the experiment \({\mathbf {Exp}^{{\mathsf {corr}_{\mathsf {P}}}}_{{\mathsf {P}}}} (\mathcal {A})\) as given in Fig. 1.
We call \({\mathsf {P}}\) correct with respect to \(\mathsf {corr}_{\mathsf {P}}\) iff for all (terminating) adversaries the advantage is 0.
Security. Next, we introduce a formalism for specifying security notions for symmetric primitives. We first consider the case of a single key (which we associate with index 1) and then extend the formalism to the case of multiple keys.
Single-Key Scenario. A security notion for primitive \({\mathsf {P}}\) is given by four algorithms \(\sec =({\mathsf {setup}},{{\mathsf {chal}}_{0}},{{\mathsf {chal}}_{1}},{{\mathsf {chal}}_{\mathrm {aux}}})\). Informally, these algorithms define two experiments \({\mathbf {Exp}^{{{\mathsf {1sec}(\mathsf {pm})}\text{- }{0}}}_{{\mathsf {P}}}}\) and \({\mathbf {Exp}^{{{\mathsf {1sec}(\mathsf {pm})}\text{- }{1}}}_{{\mathsf {P}}}}\) which characterize security in terms of an adversary that tries to distinguish between the two. Both experiments maintain a state \(\mathrm {st}\) initialized via the algorithm \({\mathsf {setup}}\).
In experiment \({\mathbf {Exp}^{{{\mathsf {1sec}(\mathsf {pm})}\text{- }{b}}}_{{\mathsf {P}}}}(\mathcal {A})\) (b is either 0 or 1), the adversary has access to the algorithm \({\mathsf {Alg}}_{\mathsf {P}}\) only indirectly through its challenge oracle \({{\textsc {chal}}_{b}}\) and the auxiliary oracle \({{\textsc {chal}}_{\mathrm {aux}}}\). The behavior of these oracles is defined by the algorithm \({{\mathsf {chal}}_{x}}\) (for the relevant \(x\in \{0,1,\mathrm {aux}\}\)) which has both access to the game’s state and oracle access to the actual primitive algorithm \({\mathsf {Alg}}_{\mathsf {P}}\). Our formalization generalizes many of the standard definitions for security of cryptographic primitives, where an adversary needs to distinguish between two “worlds” (modeled here by oracles \({{\textsc {chal}}_{b}}\) with \(b=0,1\)). For example, to define indistinguishability under chosen-plaintext attack for probabilistic symmetric encryption schemes, we would instantiate oracle \({{\textsc {chal}}_{b}}\) with a left-right oracle that receives a pair of messages \(m_0,m_1\), checks that they have the same length, and returns an encryption of \(m_b\). Oracle \({{\textsc {chal}}_{aux}}\) would allow the adversary to see encryptions of whatever messages it wants. Security under chosen-ciphertext attacks can be captured by letting oracle \({{\textsc {chal}}_{aux}}\) also answer decryption queries.
Without loss of generality we assume \({{\mathsf {chal}}_{x}}\) makes at most one call to \({\mathsf {Alg}}_{\mathsf {P}}\). The state of the game allows the algorithm \({{\mathsf {chal}}_{x}}\) to suppress or modify the output of \({\mathsf {Alg}}_{\mathsf {P}}\), for instance to avoid the decryption of a challenge ciphertext being made available directly to the adversary. Of course, how a sequence of calls to a \({{\mathsf {chal}}_{b}}\) and \({{\mathsf {chal}}_{\mathrm {aux}}}\) interact with each other is specific to the security game.
Our model allows the adversary to corrupt the secret key. The distinction between the algorithm \({{\mathsf {chal}}_{b}}\) and the oracle \({{\textsc {chal}}_{b}}\) as an interface to \({{\mathsf {chal}}_{b}}\) allows us to deal with corruptions explicitly: if the key is corrupted, the interface \({{\textsc {chal}}_{b}}\) will suppress the output of the algorithm \({{\mathsf {chal}}_{b}}\). We record if the key is used in some challenge oracle \({{\textsc {chal}}_{b}}\) in set H and record its corruption using set C and then prevent trivial wins by appropriate checks.
The experiments \({\mathbf {Exp}^{{{\mathsf {1sec}(\mathsf {pm})}\text{- }{b}}}_{{\mathsf {P}}}}(\mathcal {A})\) for the single key security notion \(\mathsf {1sec}\) defined by the tuple \(({\mathsf {setup}},{{\mathsf {chal}}_{0}},{{\mathsf {chal}}_{1}},{{\mathsf {chal}}_{\mathrm {aux}}})\) for primitive \({\mathsf {P}}=({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\). The single key in the system has implicit index 1 and is generated using parameter \(\mathsf {pm}\) selected by the adversary from a set of possible parameters.
Multi-Key Scenario. When utilized within tokens, primitives are effectively in a multi-key setting. Looking ahead, our definition for cryptographic API security essentially bootstraps from the security of primitives in a standalone scenario as described above to when used in this more complex scenarios.
3 Cryptographic APIs
A cryptographic API is an interface between an untrusted usage environment, and a trusted environment that stores cryptographic objects (e.g. keys) and carries out cryptographic operations (e.g. encryption). In practice, the trusted environment is instantiated as a hardware token, or a hardware security module; we will simply refer to the trusted environment as the token. A user may request, via the cryptographic API, that the token carry out cryptographic operations on the user’s behalf. In typical scenarios, the user will also control which key or keys are to be used, by specifying one or more handles to these keys. However, the cryptographic value of the key (as stored on the token) should remain hidden from the user and the outside world in general.
To protect the confidentiality and proper usage of exported and imported keys, tokens employ key wrapping and unwrapping mechanisms. Oftentimes there are multiple tokens in the same cryptologic ecosystem. In this case, keys may be exported from one trusted token to another (via the API). Thus our abstraction includes (a minimal set of) explicit key management functions, and an interface to use some specific cryptographic primitive.
The ultimate goal of a cryptographic API is the correct and secure implementation of some cryptographic primitive and our main target in this section are appropriate definitions of correctness (Definition 3) and security (Definition 5). These definitions build on the abstract notion of a cryptographic primitive from Sect. 2.
As explained in the introduction, the focal point of this paper is on those aspects associated to key-management, shared by cryptographic APIs. For instance, when wrapping a key, the expectation is that after unwrapping the original, wrapped key emerges (correctness) and that this key has not leaked (security), e.g. as a result of the wrapping. We provide a separate set of notions relevant for the key management part of a cryptographic API (Definitions 4, 6, and 7).
3.1 Modeling and Syntax
Tokens, Handles, Keys, and Attributes. Formally, we model a token \(t\) as having some abstract state \(s\in {{\mathsf {States}}}\) plus a number of associated handles. For simplicity, we assume the token identity \(t\) is a (unique) natural number and let the token’s initial state consist of this identity only. When API calls to the token are being made, its state might evolve arbitrarily.
Handles are part of some set \({{\mathsf {Handles}}}\) (that itself can be thought of as some fixed, finite subset of \(\{0,1\}^*\)). Each handle belongs to a unique token, identified by \(\mathsf {tkn}({h})\), and points to an actual cryptographic key value, denoted \(h.\mathsf {key}\). Since the key will be stored on the token \(\mathsf {tkn}({h})\), the value represented by \(h.\mathsf {key}\) depends on the token’s state. Since this state is not static, \(h.\mathsf {key}\) could change over time. The different notation, \(\mathsf {tkn}({h})\) versus \(h.\mathsf {key}\), captures the distinction between immutable properties associated to a handle (possibly for bookkeeping within a cryptographic game) and changeable quantities that are associated to it directly by the API.
The association between a handle and a cryptographic key is annotated by an attribute, denoted \(h.\mathsf {attr}\). For instance, an attribute could indicate that the handle points to a 128-bit AES key to be used in some specific mode of operation only, say CBC-MAC.
Like the key, the attribute will be stored on the cryptographic token (and could change over time). We will assume that \(h.\mathsf {attr} \in {{\mathsf {Attributes}}}\), where \({{\mathsf {Attributes}}}\) is some fixed set of possible attributes. Note that the abstraction to a single attribute only is without loss of generality, as one can capture say the more traditional setting of many Boolean attributes by a single attribute (in this case a true/false vector).
Our model is purposefully abstract, but it is worth bearing in mind typical implementations as used in practice. For instance, PKCS #11 reliance on ‘objects’ implies that a token’s state will contain a mapping between handles and key–attribute pairs, plus additional information that helps the token to maintain the security policy. Thus, for most APIs it will be possible to write the state explicitly in the form \(s=({\tilde{s}},(h\mapsto (\mathsf {key},a))_h)\), where for each handle \(h\), the mapping \(h\mapsto (\mathsf {key},a)\) indicates the associated key and attribute pair (so \(h.\mathsf {key}=\mathsf {key}\) and \(h.\mathsf {attr}=a\)), and the state \({\tilde{s}}\) contains a snapshot of the token’s past I/O only (which in principle could be made public without compromising core cryptographic security).
The Application Programming Interface (API). Each token runs an API that allows the outside world to interface with the keys present on the token. Definition 2 lists the procedures supported by our abstract API. Intuitively, each of the API procedures has a clearly specified objective. For instance, there is an API call \({{\mathsf {\mathsf {CA}.new}}}(t, a)\) that is supposed to create a new key on the token \(t\) and returns a fresh handle \(h\) such that \(h.\mathsf {key}\) is this newly generated key and \(h.\mathsf {attr}=a\). Here freshness is global and means that the handle does not yet occur elsewhere, so that a handle can uniquely be associated to a token (explicitly embedding the token identity in the handle could facilitate global freshness). While the syntax thus guarantees uniqueness of the handles returned by the API calls, there is no guarantee that API calls behave as intended (other than possibly implied by the correctness properties introduced later).
Definition 2
A cryptographic API \(\mathsf {CA}\) exporting a primitive \({\mathsf {P}}\) (cf. Sect. 2) is defined by the following tuple of algorithms.
-
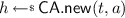 creates and returns a fresh handle on token \(t\), so \(\mathsf {tkn}({h})=t\); the intention is that \(h.\mathsf {attr}=a\) and \(h.\mathsf {key}\) is a newly generated key, drawn from some set \({{\mathsf {Keys}}}\) according to a distribution that could for instance depend on \(a\).
creates and returns a fresh handle on token \(t\), so \(\mathsf {tkn}({h})=t\); the intention is that \(h.\mathsf {attr}=a\) and \(h.\mathsf {key}\) is a newly generated key, drawn from some set \({{\mathsf {Keys}}}\) according to a distribution that could for instance depend on \(a\). -
 creates and returns a fresh handle on token \(t\), so \(\mathsf {tkn}({h})=t\); the intention is that \(h.\mathsf {attr}=a\) and \(h.\mathsf {key}=\mathsf {key}\).
creates and returns a fresh handle on token \(t\), so \(\mathsf {tkn}({h})=t\); the intention is that \(h.\mathsf {attr}=a\) and \(h.\mathsf {key}=\mathsf {key}\). -
 takes as input two handles and runs on the first handle’s token \(\mathsf {tkn}({h_1})\). It returns some \(w\in {{\mathsf {CWraps}}}\), where \({{\mathsf {CWraps}}}\) is the space of all wraps. Supposedly \(w\) is a wrap of \(h_2.\mathsf {key}\) tied to \(h_2.\mathsf {attr}\) under key \(h_1.\mathsf {key}\).
takes as input two handles and runs on the first handle’s token \(\mathsf {tkn}({h_1})\). It returns some \(w\in {{\mathsf {CWraps}}}\), where \({{\mathsf {CWraps}}}\) is the space of all wraps. Supposedly \(w\) is a wrap of \(h_2.\mathsf {key}\) tied to \(h_2.\mathsf {attr}\) under key \(h_1.\mathsf {key}\). -
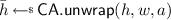 takes as input a handle to use for unwrapping, a wrap and an attribute string. If unwrapping succeeds, a fresh handle \(\bar{h}\) is created on \(\mathsf {tkn}({h})\) and returned. The intention is that \(\bar{h}.\mathsf {attr}=a\) and \(\bar{h}.\mathsf {key}\) equals the key that was wrapped under \(h.\mathsf {key}\).
takes as input a handle to use for unwrapping, a wrap and an attribute string. If unwrapping succeeds, a fresh handle \(\bar{h}\) is created on \(\mathsf {tkn}({h})\) and returned. The intention is that \(\bar{h}.\mathsf {attr}=a\) and \(\bar{h}.\mathsf {key}\) equals the key that was wrapped under \(h.\mathsf {key}\). -
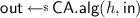 intends to evaluate the primitive \({\mathsf {Alg}}_{\mathsf {P}}\) on key \(h.\mathsf {key}\) and input \(\mathsf {in}\), returning \(\mathsf {out}\).
intends to evaluate the primitive \({\mathsf {Alg}}_{\mathsf {P}}\) on key \(h.\mathsf {key}\) and input \(\mathsf {in}\), returning \(\mathsf {out}\).
Any call may result in an API error \(\perp _\mathrm {api}\). An API for key-management only may omit the procedure \({{\mathsf {\mathsf {CA}.alg}}}\).
All of the above commands, but the \({{\mathsf {\mathsf {CA}.create}}}\), reflect the typical interface available to the user of a token. We use \({{\mathsf {\mathsf {CA}.create}}}\) as an abstraction of (often non-cryptographic) mechanisms for transferring keys from one token to another. For example, in the production phase the same cryptographic key may be injected in several devices (which are to be used by the same company).
The procedures of the API directly manipulate the state of one token only, where the relevant token is either made explicit by the API call (\({{\mathsf {\mathsf {CA}.new}}}\) and \({{\mathsf {\mathsf {CA}.create}}}\)), or it follows from the handles involved (e.g. \({{\mathsf {\mathsf {CA}.wrap}}}(h_1,h_2)\) can affect the state of \(\mathsf {tkn}({h_1})\)). We could make this manipulation explicit by keeping track of the token’s state as input and output of each of the API’s procedures etc. For readability, we keep the state of the token implicit and only stress that the commands may not depend on, or modify, the state of another token.
Policies and Attributes. To protect the security of the keys the API will enforce a policy. For instance, an API may forbid usage of a key intended for authentication to be used for encryption. To indicate that an operation is not allowed, an API call can return a policy error message (distinct from possible error messages resulting for instance from decrypting an invalid ciphertext). For simplicity, we will model all possible policy errors with a singleFootnote 1 symbol \(\perp _\mathrm {api}\).
We will not give a formal definition of what constitutes a policy. Actually, the level of abstraction of our model makes it somewhat cumbersome to pin down an exact, yet general concept of a policy. In a practical, multi-token setting, the use of attributes is useful to enforce consistent yet efficient implementation of a policy across tokens. We will see a concrete example of this in Sect. 4 (see Definition 8).
An API can also use the token’s state for this decision (e.g. to prevent wrapping a sensitive key under a key that is somehow deemed insecure or to avoid circularity). For instance, a token could keep track of all the calls (with responses) ever made to it (note that, with the exception of the \(\mathsf {key}\) value of \({{\mathsf {\mathsf {CA}.create}}}\) queries, this information can all be made public). If only a single token exists, this leads to a complete history of the API’s use, which suffices to implement (albeit inefficiently) a meaningful security policy (cf. [5]).
Enforcing Meaning. So far our syntax does not formally give any guarantees that \(h.\mathsf {key}\) and \(h.\mathsf {attr}\) are used by the API in an explicit, meaningful way. The generality of our notion of state would allow an API to for instance declare some key as \(h.\mathsf {key}\) but in fact use a completely different cryptographic value throughout. The KSW definitions, which use a similar abstract state as our work, share this problem, but leave it unaddressed.
Since working completely abstractly (e.g. making no assumptions on states) seems to easily lead to difficulties without obvious gains we make explicit assumptions regarding the implementations. Our upcoming correctness notion deals with the wrapping mechanism as a means to transfer keys from token to token. Notice that wrapping involves \(h.\mathsf {key}\) where \(h\) is the ‘source’ handle, and only implicitly involves the associated key. Since, we would like to reflect that the actual key is transferred we need to make explicit the assumption that wraps are linked to actual cryptographic keys. Along similar lines, we make explicit the assumption that the cryptographic operations exported by the API make use of actual keys. The assumption is useful to define and analyze the composition between an API for key-management with actual primitives. Moreover, we will use the attributes to create a policy separating keys that can be used by the primitive and those that cannot. This slight loss of generality enables simpler definitions and analysis and still reflects virtually all designs commonly used in practice.
3.2 Correctness of a Cryptographic API
In this section we present a definition of correctness for a cryptographic API. Much of the discussion and formalization is relevant to the latter sections where we define security since both for correctness and security we explain how to lift the definitions of Sect. 2 from primitives to primitives exported by the APIs.
The main difficulty is an important difference between the interfaces that an adversary has against a primitive and against a primitive exported by an API. In Sect. 2, primitive correctness is modeled as a predicate on the execution trace of an adversary, where the trace keeps track of both the keys that are generated and of the cryptographic operations that the adversary executes with these keys. Crucially, the trace only included the indexes of the keys and not their cryptographic values. In contrast, an adversary against the API refers to the underlying keys using the handles provided by the API. Notice that the difference goes further, in that several handles may point to the same cryptographic key.
To bridge this gap we introduce a mapping that associates to each handle some index. The map \(\mathsf {idx}\) that we introduce reflects the idea that handles with same index have associated the same cryptographic key.Footnote 2 Formally, when defining the oracles used by an adversary to interact with a cryptographic API, we explicitly keep track of the indexes associated to handles—we explain below our modeling. We then lift the definitions from primitives to primitives exported by APIs by (essentially) replacing the handles with their associated index in the execution trace. We detail below our approach.
Indexing Handles by Equivalence Classes. To each handle \(h\) we will assign an index \(\mathsf {idx}(h)\in \mathbb {N}\) as soon as the handle is created following some key-management operation. This indexing induces an equivalence relation: two handles \(h_1\) and \(h_2\) are equivalent iff \(\mathsf {idx}(h_1)=\mathsf {idx}(h_2)\). We aim to ensure that if two handles are expected to have the same associated cryptographic key then they should belong to the same class. Notice that we aim to maintain this property globally, i.e. the mapping handles to indexes is “system wide” and is not restricted to one particular token.
Oracles used in experiments \({\mathbf {Exp}^{{\mathsf {corr}_{\mathsf {P}}}}_{\mathsf {CA}[{\mathsf {P}}]}} (\mathcal {A})\) and \({\mathbf {Exp}^{{\mathsf {corr}_\mathsf {km}}}_{\mathsf {CA}}} (\mathcal {A})\) that define the correctness of a crypto API \(\mathsf {CA}\). The boxed line is only relevant for the experiment involving \(\mathsf {corr}_\mathsf {km}\).
Formal Definitions. Our formal definitions of correctness for key-management (Fig. 5) and primitive-exporting APIs (Fig. 4) use the oracles in Fig. 3 to model the interaction of an adversary with the API via key-management commands. Each oracle reflects the behavior of the API and contains the bookkeeping that we do to maintain and assign equivalence classes to handles. The games where these oracles are used maintain a global variable i (initially 0) that counts the number of equivalence classes.
The only way to create a new equivalence class is through the \({{\textsc {new}}}\) oracle: whenever oracle \({{\textsc {new}}}\) is called successfully (i.e. does not return \(\perp _\mathrm {api}\)) we increment i and assign it as the index of the handle that is returned. Handles can be added to the equivalence classes through calling either the \({{\textsc {transfer}}}\) or the \({{\textsc {unwrap}}}\) oracle.
The \({{\textsc {transfer}}}\) oracle is used, as explained earlier, for bootstrapping purposes: to create a wrap on one token and then unwrap it on another one, the two tokens already need to contain the same key. Oracle \({{\textsc {transfer}}}\) models this ability: handle \(\bar{h}\) pointing to the transferred key has the same index as \(h\) which points to the original key.
Dealing with handles created via unwrapping requires some more bookkeeping. We use set W (initially empty) to maintain all wraps created by the \({{\textsc {wrap}}}\) oracle, together with the handles involved: we add \((h_1,h_2,w)\) to W if w was the result of wrapping (the key associated to) \(h_2\) under (the key associated to) \(h_1\). When calling \({{\textsc {unwrap}}}(h,w,a)\) we use W to test whether \(w\) was created by wrapping some \(h_2\) under a handle \(h_1\) equivalent to \(h\) (the set S contains all such \(h_2\)). If this is the case (S is not empty), then the newly returned handle is equivalent to \(h_2\) and is therefore assigned the same index. In case a wrap w was created multiple times, the lowest applicable index is used (if the key-management component is secure, it should not be possible to create identical wraps under non-equivalent handles). If S is empty, the wrap \(w\) is adversarially generated and, since we do not wish to consider dishonest adversaries for defining the correctness of a cryptographic API, we set the flag \(bad\) to force an adversarial loss.
Valid Traces. The calls that the adversary makes to the algorithm \({{\mathsf {\mathsf {CA}.alg}}}\) (through its oracle \({{\textsc {alg}}}\)) are recorded in a similar way as done in the experiment for primitive correctness (Fig. 1). To account for the possibility that the same key is used via equivalent handles, we identify the key used in the cryptographic operation by the index of the handle. For an \({{\textsc {alg}}}\) call, this derived index neatly matches the index of the algorithm used in our multi-key primitive definition.
The experiment \({\mathbf {Exp}^{{\mathsf {corr}_{\mathsf {P}}}}_{\mathsf {CA}[{\mathsf {P}}]}} (\mathcal {A})\) for defining the correctness of a crypto API \(\mathsf {CA}\) that exports primitive \({\mathsf {P}}\) based on correctness predicate \(\mathsf {corr}_{\mathsf {P}}\). An adversary additionally has access to the oracles \(\mathcal {O}\) given in Fig. 3.
Definition 3
Let API \(\mathsf {CA}[{\mathsf {P}}]\) implement a primitive \({\mathsf {P}}\) and let \(\mathsf {corr}_{\mathsf {P}}\) be a correctness predicate. Then the incorrectness advantage of \(\mathcal {A}\) against \(\mathsf {CA}[{\mathsf {P}}]\) with respect to \(\mathsf {corr}_{\mathsf {P}}\) is defined as
for the experiment \({\mathbf {Exp}^{{\mathsf {corr}_{\mathsf {P}}}}_{\mathsf {CA}[{\mathsf {P}}]}} (\mathcal {A})\) as given in Fig. 4. We call \(\mathsf {CA}[{\mathsf {P}}]\) correct with respect to \(\mathsf {corr}_{\mathsf {P}}\) iff for all (terminating) adversaries the advantage is 0.
Note that correctness only really implies consistency, it does not incorporate robustness. There is no guarantee that a successfully wrapped key can in fact be unwrapped at all, or that a primitive API call will result in an evaluation of the primitive. In both cases, the policy might well result in \(\perp _\mathrm {api}\), in which case the correctness game effectively ignores the output of the corresponding call. As an extreme example, the cryptographic API that always returns \(\perp _\mathrm {api}\) is considered correct.
3.3 Correctness of an API’s Key Management
For the correctness definition above, we only looked directly at the final primitive calls, ignoring the cryptographic key values. However, intuitively if two handles are equivalent, one might expect that the associated cryptographic keys are identical. This intuition is captured by the experiment described in Fig. 5, where an adversary tries to find a handle pointing to a key distinct from the key associated to the handle’s index.
The experiment \({\mathbf {Exp}^{{\mathsf {corr}_\mathsf {km}}}_{\mathsf {CA}}} (\mathcal {A})\) for defining the correctness of the key management component of a cryptographic API \(\mathsf {CA}\). An adversary has access to the oracles \(\mathcal {O}\) given in Fig. 3.
Definition 4
(Correctness of the Key Management). Let \(\mathsf {CA}\) be a key management API and \(\mathcal {A}\) an adversary. Then the advantage of \(\mathcal {A}\) against \(\mathsf {CA}\)’s key correctness is defined as
for the experiment \({\mathbf {Exp}^{{\mathsf {corr}_\mathsf {km}}}_{\mathsf {CA}}} (\mathcal {A})\) as given in Fig. 5. We call \(\mathsf {CA}\) key-correct iff for all (terminating) adversaries the advantage is 0.
Note that correctness of the key management component of a cryptographic API does not relate to the attribute. For deployed systems, it is common that equivalent handles are associated using different attributes; moreover, these attributes might change over time. Nonetheless, some attributes should not easily be changed by an adversary. For example, it should not be possible to change an attribute that declares a key as “sensitive” (a PKCS#11 term).
This relates to the well-known notion of stickyness, for which we provide a formal definition later on (Definition 7).
Cryptographic Key Wrap Assumption. Definition 2 mentions that \({{\mathsf {\mathsf {CA}.wrap}}}\) is supposed to wrap \(h_2.\mathsf {key}\) tied to \(h_2.\mathsf {attr}\) under key \(h_1.\mathsf {key}\). Implicitly, this assumes that knowledge of both w and \(h_1.\mathsf {key}\) suffices to determine \(h_2.\mathsf {key}\) as well. For most schemes used in practice this is indeed the case, however it does not follow logically from our abstract syntax (even when taking into account correctness of the key management component).Footnote 3 Assumption 2 formalizes the idea that an honestly, successfully generated wrap \(w\leftarrow {{\mathsf {\mathsf {CA}.wrap}}}(h_1, h_2)\) contains sufficient information to recover the wrapped key \(h_2.\mathsf {key}\), provided one knows the actual key \(h_1.\mathsf {key}\) used for wrapping, and the attributes \(h_1.\mathsf {attr}, h_2.\mathsf {attr}\) associated to the handles in the wrapping command.
Henceforth, we will restrict our attention to schemes satisfying the key wrap assumption (which has direct consequences for the security notion we consider in the upcoming sections).
Assumption 2
(Key Wrap Assumption). A cryptographic API \(\mathsf {CA}\) satisfies the key wrap assumption iff there exists an extractor U that extracts keys from wraps. Specifically, for all \(w\leftarrow {{\mathsf {\mathsf {CA}.wrap}}}(h_1, h_2), w\ne \perp _\mathrm {api}\) with, at the time of calling, \(\mathsf {key}_1=h_1.\mathsf {key}\) and \(\mathsf {key}_2=h_2.\mathsf {key}\) it holds that \(U(w,\mathsf {key}_1,h_1.\mathsf {attr},h_2.\mathsf {attr})\) outputs \(\mathsf {key}_2\) with probability 1.
3.4 Security of a Cryptographic API
We will consider three types of security. Our primary concern is the security of the exported primitive (Definition 5), of secondary concern are security of keys managed internally by the API (Definition 6) and the integrity of the attributes (Definition 7). The various security experiments to define these notions rely on a set of common oracles, given in Fig. 6. With the exception of \({{\textsc {corrupt}}}\) and \({{\textsc {attrib}}}\), the oracles match those for the correctness game (as given in Fig. 3), but with more elaborate internal bookkeeping, whose reasoning is explained below. The oracles \({{\textsc {new}}}\) and \({{\textsc {unwrap}}}\) contain a macro \({\mathsf {initclass}}\) that will be defined depending on the game.
Oracles common to the security experiments \({\mathbf {Exp}^{{{\sec }\text{- }{b}}}_{\mathsf {CA}[{\mathsf {P}}]}}(\mathcal {A})\), \({\mathbf {Exp}^{{{\mathsf {km}}\text{- }{b}}}_{\mathsf {CA}}}(\mathcal {A})\), and \({\mathbf {Exp}^{{{\mathsf {sticky}}}}_{\mathsf {CA}}} (\mathcal {A})\), for a crypto API \(\mathsf {CA}\) that exports \({\mathsf {P}}=({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\). The macro \({\mathsf {initclass}}\) is defined separately for each of the experiments.
Corrupt and Compromised Handles. We have explained earlier in the context of the correctness game for APIs that “honest” wrap/unwrap queries induce an equivalence relation on handles, and how the equivalence class of a handle can be represented (and maintained) by an index. For defining the security of APIs we also have to take into account adversaries that may be actively trying to subvert the system. In addition to dishonest API calls (e.g. asking for unwrappings of adversarially created wraps), we will also model corruptions of handles. When an adversary corrupts a handle, the associated cryptographic key is returned to the adversary. Note that the API itself is not aware of corruptions. Moreover, corruptions and (dishonest API) calls tend to reinforce each other, which we model by compromised handles, namely those handles for which an adversary can reasonably be assumed to know the corresponding key. The notion of corrupt and compromised handles is based on ideas similar to those used by Cachin and Chandran [5], and Kremer et al. [18].
Corruptions. The premise of cryptographic APIs is that keys should be kept secret and are stored securely—an adversary does not have access to cryptographic keys. Yet, in practice keys that are initially stored securely on HSMs might be exported to weaker tokens that can be breached physically (e.g. by means of side-channel analysis or fault injection). As a result, the adversary can learn these keys. Such leakage of keys is modeled by corruptions: an adversary can issue a corruption request of a handle to learn the associated key. In general, one cannot guarantee security for handles that have been corrupted (cf. the primitive’s security game). Moreover, corruption of a handle automatically leads to corruption of the equivalence class of that handle (as equivalent handles are presumed to point to identical cryptographic keys). We let C be the set of indices corresponding to handles that have been corrupted directly by the adversary through making a corruption query.
Compromised Handles. An adversary could issue a query \({{\textsc {wrap}}}(h_1,h_2)\), receiving a wrap \(w\ne \perp _\mathrm {api}\) as a result. Subsequent corruption of \(h_1\) might then also compromise \(h_2\). Indeed, Assumption 2 states that knowledge of a wrapping key suffices to unwrap (and learn) a wrapped key, making the compromise of \(h_2\) inevitable. Thus, the corruption of a small set of keys could lead to the compromise of a much larger set.
We let L(C) be the set of indices corresponding to compromised handles (where \(C\subseteq L(C)\)). To identify precisely the set L(C) of compromised equivalence classes, we keep track of which key (handle) wraps which key by means of a directed graph (V, E). The vertices of the graph are defined by the equivalence classes associated to the handles (so a subset of the natural numbers). There is an edge from i to j iff for some handles \(h_1,h_2\) with \(\mathsf {idx}(h_1)=i\) and \(\mathsf {idx}(h_2)=j\) the adversary has issued a query \({{\textsc {wrap}}}(h_1,h_2)\), receiving \(w\ne \perp _\mathrm {api}\) as a result. For a given graph (V, E) and corrupted set \(C \subseteq V\), we define L(C) as the set of all vertices that can be reached from C (including C itself).
Dishonest Wraps. Since a wrap is just a bitstring, an adversary can try to unwrap some w that has not been produced by the API itself (i.e., \(S=\emptyset \) in \({{\textsc {unwrap}}}(h,w,a)\)). If unwrapping succeeds and returns a fresh handle, the security game needs to associate this handle to some equivalence class. We will consider two options.
Firstly, the unwrapping could have been performed under a handle that has not been compromised (intuitively, this corresponds to a wrapping forgery). In that case, the handle returned by the unwrapping will be assumed to create a new equivalence class. Technically, w is now a wrap of a handle in this new class i under \(\mathsf {idx}(h)\), yet we do not add a corresponding edge \((\mathsf {idx}(h), i)\) to E. Adding this edge would have resulted in the new class being compromised as a result of the corruption of \(\mathsf {idx}(h)\), so that an adversary could no longer win the primitive game based on the newly introduced equivalence class. Since the new class is effectively the result of a successfully forged wrap (as \(S=\emptyset \)), we prefer the stronger definition (i.e. without adding an edge to E) where an adversary might benefit from a forged wrap.
Secondly, the unwrapping could have been called using a compromised handle. Since the adversary knows the key corresponding to the compromised handle, creation of such wraps is likely feasible; moreover, the adversary can be assumed to know the key corresponding to the handle being returned. To simplify matters, we will use the equivalence class 0 for all handles that result from unwrapping under compromised handles. The set C of corrupt handles initially contains the class 0. The index class 0 is special as there are no correctness guarantees for it: if \(\mathsf {idx}(h_1) = \mathsf {idx}(h_2) = 0\), it is quite possible that \(h_1.\mathsf {key} \ne h_2.\mathsf {key}\).
Incorporating the Primitive’s Security Game. Intuitively, an adversary breaks a cryptographic API, exporting a primitive \({\mathsf {P}}\), if and only if he manages to win the primitive’s security game. Formally, in order to express an adversary’s advantage against the cryptographic API in terms of the abstract security game for the primitive itself, we would need to interpret an adversary’s actions against a cryptographic API as that of an adversary directly playing the abstract primitive game.
As in the correctness game, we use the equivalence to associate handles in the API game with keys in the primitive game. Whenever a new equivalence class is created, the API game creates a new instance of the primitive game by calling  (the macro \({\mathsf {initclass}}\) takes care of this).
(the macro \({\mathsf {initclass}}\) takes care of this).
For the API’s challenge oracle we want to draw on the challenge algorithms from the primitive game. These algorithms themselves expect an oracle that implements the primitive. In the API’s game the challenge oracle can use the API primitive interface. If the API outputs \(\perp _\mathrm {api}\) we suppress the output of the challenge oracle and regard the challenge call as not having taken place in the primitive’s game (note that the call might still have had an effect on the API’s state).
As in the multi-key primitive game, at the end of the game we check whether the adversary caused a breach by challenging on corrupt (or in this case compromised) key or not. As mentioned before, an alternative (and stronger) formulation would maintain \(L(C) \cap H = \emptyset \) as invariant by suppressing any query that would cause a breach of the invariant (possibly allowing for those queries that the API already caught). However, our formalism is easier to specify and simplifies an already complex model without materially changing its meaning.
Note that if a cryptographic API exports several different primitives, each with their own security notion, one can consider several security notions for the cryptographic API. One could modify the \({{\mathsf {chal}}}_\mathrm {aux}\) algorithm to model joint security.
The security experiment \({\mathbf {Exp}^{{{\sec }\text{- }{b}}}_{\mathsf {CA}[{\mathsf {P}}]}}(\mathcal {A})\) for a crypto API \(\mathsf {CA}\) that exports \({\mathsf {P}}=({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\) with security notion \(\sec =({\mathsf {setup}},{{\mathsf {chal}}_{0}},{{\mathsf {chal}}_{1}},{{\mathsf {chal}}_{\mathrm {aux}}})\). The adversary additionally has access to the oracles defined in Fig. 6 (which is where the macro \({\mathsf {initclass}}\) is used).
Definition 5
Let API \(\mathsf {CA}[{\mathsf {P}}]\) export primitive \({\mathsf {P}}\) and let \(\sec =({\mathsf {setup}},{{\mathsf {chal}}_{0}},{{\mathsf {chal}}_{1}},{{\mathsf {chal}}_{\mathrm {aux}}})\) be a security notion for \({\mathsf {P}}\). Then the advantage of an adversary \(\mathcal {A}\) against \(\mathsf {CA}[{\mathsf {P}}]\) is defined by
for the experiments \({\mathbf {Exp}^{{{\sec }\text{- }{b}}}_{\mathsf {CA}[{\mathsf {P}}]}}(\mathcal {A})\) as given in Fig. 7.
3.5 Security of an API’s Key Management
When concentrating on the security of the exported primitive, we ignored confidentiality of cryptographic keys and authenticity of associated attributes. However, for the key-management component of a cryptographic API these are important properties and we capture these with Definitions 6 and 7, respectively.
We define the security of a key-management API via the experiment \({\mathbf {Exp}^{{{\mathsf {km}}\text{- }{b}}}_{\mathsf {CA}}}(\mathcal {A})\) as given in Fig. 8. Here, the goal of an adversary is to distinguish real keys managed by the API from fake ones generated at random. As usual, we capture this idea via a challenge oracle parametrized by a bit b which the adversary needs to determine. When called with handle h as input, the oracle returns the real key associated with h or a fake key (depending on b). In the process the adversary controls the key-management API which we model via the oracles in Fig. 6. We impose only minimal restrictions to prevent trivial wins. As before, we assume that for all compromised handles, the adversary knows the corresponding (real) key, making a win trivial (we can exclude these wins at the end by imposing that \(H\cap L(C) = \emptyset \) as before).
Moreover, notice that under the key wrap assumption (Assumption 2), if a handle has been used to wrap another key, an adverary may easily distinguish between the key and a random one by unwrapping: the operation would always succeed with the real key and would fail with the fake one. We call an index tainted if one of the keys with that index is compromised, or has been used in a wrapping operation.
We write T(C) for the class of tainted indexes: the adversary loses (the experiment returns 0) if it challenges a key that belongs to a tainted class.
Definition 6
Let API \(\mathsf {CA}\) be a key management API. Then the advantage of an adversary \(\mathcal {A}\) against \(\mathsf {CA}\) is defined by
for the experiments \({\mathbf {Exp}^{{{\mathsf {km}}\text{- }{b}}}_{\mathsf {CA}}}(\mathcal {A})\) as given in Fig. 8.
The security experiment \({\mathbf {Exp}^{{{\mathsf {km}}\text{- }{b}}}_{\mathsf {CA}}}(\mathcal {A})\) for a key-management API \(\mathsf {CA}\), relative to generator \({\mathsf {Kg}}\). The adversary additionally has access to the oracles defined in Fig. 6.
Our notion of secure key management differs from existing ones, e.g. KSW describe a fake game where the challenge key is not directly revealed, but instead wraps based on fake keys are given to an adversary. We believe that our notion is the natural one: in the key agreement literature (including KEMs) distinguishing between real and random keys is standard. Our notion of secure key management has some beneficial implications: indistinguishability of keys (privacy) implies correctness, to some extent.Footnote 4 See the full version of this paper.
Remark 1
A useful observation is that key-management security with respect to adversaries that make polynomially many challenge queries can be reduced via a hybrid argument to security against an adversary that makes a single challenge query. Specifically, for any adversary \(\mathcal {A}\) that makes \(q_c\) challenge queries, there is an adversary \(\mathcal {B}\) that makes a single challenge query so that \(\mathbf {Adv}^{{\mathsf {km}}}_{\mathsf {CA}} (\mathcal {A}) \le q_c \cdot \mathbf {Adv}^{{\mathsf {km}}}_{\mathsf {CA}} (\mathcal {B})\).
3.6 Stickyness: Attribute Security
In general, attributes associated to a handle may evolve over time. For instance, an attribute might indicate whether its handle has been used to perform a wrap operation or not. Initially this will not be true, but once it has occurred, it will be and should remain true. Existing API attacks show the importance of the integrity of critical parts of the attribute (e.g. to prevent a handle from being used for two conflicting purposes). In PKCS# 11 parlance, a binary attribute is sticky iff it cannot be unset. We model this by a stickyness game defined for an arbitrary predicate over the attribute space. Our notion of stickyness allows no change whatsoever (i.e. a predicate that is initially not set will have to remain unset). Note that, as expected, there are no guarantees for index 0.
Oracles for defining experiment \({\mathbf {Exp}^{{{{\pi }\text{- }}{\mathsf {sticky}}}}_{\mathsf {CA}}} (\mathcal {A})\) for the partial authenticity of attributes in a cryptographic API. The adversary additionally has access to the oracles defined in Fig. 6.
Definition 7
Let \(\mathsf {CA}\) be a cryptographic API with attribute space \({{\mathsf {Attributes}}}\). Let \(\pi : {{\mathsf {Attributes}}}\rightarrow \{0,1\}\) be a predicate on the attribute space. Then the advantage of an adversary \(\mathcal {A}\) against the stickyness of \(\pi \) equals \(\mathbf {Pr}\left[ {{\mathbf {Exp}^{{{{\pi }\text{- }}{\mathsf {sticky}}}}_{\mathsf {CA}}} (\mathcal {A})=\mathsf {true}}\right] \) with the experiment as given in Fig. 9.
In the next section we exhibit one particular predicate which specifies whether the key is intended for key management or for other cryptographic operations. These two possibilities are modelled through a predicate \(\mathsf {external}\) applied to attributes: the predicate is set if the key is intended for cryptographic operations other than key management.
Remark 2
In this section we have defined secrecy of keys via indistinguishability from random ones. This may seem like a questionable choice, since API keys are usually used to accomplish some cryptographic task, and any such use immediately gives rise to a distinguishing attack. This result can be understood by drawing a useful analogy with the area of key-exchange protocols. There, security is also defined via indistinguishability, even though keys are used later to achieve some other task (i.e. implement a secure channel). The composition of a good key exchange with a secure implementation of secure channels should yield a secure channel establishment protocol.
Similarly, one should understand the model of this section as a steppingstone towards the modular analysis of cryptographic APIs of the next section. There, we show how to combine a key-management API secure in the sense defined in this section with arbitrary (symmetric) primitives to yield a secure cryptographic API. The security of the latter is defined by asking that all of the cryptographic tasks implemented by the cryptographic API meet their (standard) game-based security notion.
4 The Power of Key Management
In this section we show how to compose, generically, a key-management API with an arbitrary primitive. First we identify some compatibility conditions that permit the composition of the two components. Informally, these require that the keys of the API are of one of two types. Internal keys are used exclusively for key management (i.e. wrapping other keys). External keys are used exclusively for keying the primitives exported by the API. Whether a key is internal or external follows from the attribute associated to the handle through a predicate \(\mathsf {external}\). Below, we write \(h.\mathsf {external}\) for the value of the \(\mathsf {external}\) predicate associated to handle \(h\).
Definition 8
Let \(\mathsf {CA}=({{\mathsf {\mathsf {CA}.init}}},{{\mathsf {\mathsf {CA}.new}}},{{\mathsf {\mathsf {CA}.create}}},{{\mathsf {\mathsf {CA}.key}}},{{\mathsf {\mathsf {CA}.wrap}}},\) \({{\mathsf {\mathsf {CA}.unwrap}}})\) be a key-management API and let \({\mathsf {P}}=({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\) be the implementation of an arbitrary primitive with key space \({{\mathsf {Keys}}}\). We say that \(\mathsf {CA}\) and \({\mathsf {P}}\) are compatible if:
-
1.
there exists an easy to compute predicate \(\mathsf {external}\) on the attribute space \({{\mathsf {Attributes}}}\), denoted \(h.\mathsf {external}\) for a particular handle \(h\);
-
2.
if \(h_1.\mathsf {external}=\mathsf {true}\) (at call time) then both \({{\mathsf {\mathsf {CA}.wrap}}}(h_1,h_2)\) and \({{\mathsf {\mathsf {CA}.unwrap}}}(h_1,w)\) return \(\perp _\mathrm {api}\);
-
3.
if \(h.\mathsf {external}=\mathsf {true}\) then \(h.\mathsf {key}\in {{\mathsf {Keys}}}\).
An abstract primitive \({\mathsf {P}}\) and a compatible key-management API \(\mathsf {CA}\) can be composed in a generic fashion by exploiting the predicate \(\mathsf {external}\), leading to a cryptographic API \([\mathsf {CA};{\mathsf {P}}]\) as formalized in Definition 9 below. Correctness of \([\mathsf {CA};{\mathsf {P}}]\) follows from correctness of its two constituent components (Theorem 3). Our main composition result (Theorem 4) states that if both components are secure and, additionally, the \(\mathsf {external}\) predicate is sticky, then the composition yields a secure cryptographic API exporting \({\mathsf {P}}\). We formalize our construction in the following definition.
Definition 9
(Construction of \([\mathsf {CA};{\mathsf {P}}]\) ). Let \(\mathsf {CA}\) be a key management API defined by algorithms \(({{\mathsf {\mathsf {CA}.init}}},{{\mathsf {\mathsf {CA}.new}}},{{\mathsf {\mathsf {CA}.create}}},{{\mathsf {\mathsf {CA}.key}}},{{\mathsf {\mathsf {CA}.wrap}}},{{\mathsf {\mathsf {CA}.unwrap}}})\), and let \({\mathsf {P}}=({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\) be a compatible primitive. We define the composition of key management API \(\mathsf {CA}\) and the primitive \({\mathsf {P}}\) as
where \({{\mathsf {\mathsf {CA}.alg}}}(h,x)\) simply returns \({\mathsf {Alg}}_{\mathsf {P}}(h.\mathsf {key},x)\) if \(h.\mathsf {external}=\mathsf {true}\) and returns \(\perp _\mathrm {api}\) otherwise (note that a call \({{\mathsf {\mathsf {CA}.alg}}}(h,x)\) does not change the API’s state).
The following theorem states that if the components are correct, the result of the composition is also correct.
Theorem 3
(Correctness of \([\mathsf {CA};{\mathsf {P}}]\) ). Let \(\mathsf {CA}\) be a key-management API and let \({\mathsf {P}}=({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\) be a compatible primitive with correctness notion defined by the predicate \(\mathsf {corr}_{\mathsf {P}}\). Then
Then correctness of both \(\mathsf {CA}\) and \({\mathsf {P}}\) implies correctness of \([\mathsf {CA};{\mathsf {P}}]\).
Proof
Consider the game \({\mathbf {Exp}^{{\mathsf {corr}_{\mathsf {P}}}}_{[\mathsf {CA}; {\mathsf {P}}]}} \) with \({{\mathsf {\mathsf {CA}.alg}}}\) specified for the construction at hand. The resulting oracle \({{\textsc {alg}}}\) is specified in Fig. 10 (without the boxed statement). Adding the boxed statement provides an identical game, unless at some point \(h.\mathsf {key}\ne {{\mathsf {key}}}(\mathsf {idx}(h))\). This event is exactly the event that triggers a win in the key-management’s correctness game (the \(bad\) flags in the cryptographic API game and the key management game coincide). Furthermore, when considering the overall correctness game using \({{\textsc {alg}}}\) with boxed statement included, a win can be syntactically mapped to a win in the primitive’s correctness game, concluding the proof. \(\square \)
Compatibility of a key-management API \(\mathsf {CA}\) and a primitive \(({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\) only involved the set from which the primitive’s keys are drawn. While for correctness this suffices, for security the way keys are distributed matters as well. Recall that \({\mathsf {Kg}}_{\mathsf {P}}\) takes as input a parameter \(\mathsf {pm}\), whereas a \({{\textsc {new}}}\) call to the key-management API takes as input an attribute \(a\). Let \(\mathsf {a2pm}\) be a function that maps attributes to parameters (or  ). Let \({\mathsf {Kg}}\) take in an attribute such that for all attributes \(a\) for which the predicate external is set, it holds that \({\mathsf {Kg}}(a)={\mathsf {Kg}}_{\mathsf {P}}(\mathsf {a2pm}(a))\) (i.e. the output distributions of the two algorithms match).
). Let \({\mathsf {Kg}}\) take in an attribute such that for all attributes \(a\) for which the predicate external is set, it holds that \({\mathsf {Kg}}(a)={\mathsf {Kg}}_{\mathsf {P}}(\mathsf {a2pm}(a))\) (i.e. the output distributions of the two algorithms match).
The following theorem establishes that composing a secure key management API with a compatible secure primitive yields a secure cryptograhpic API. The proof of the theorem is in the full version of the paper.
Theorem 4
(Security of \([\mathsf {CA};{\mathsf {P}}]\) ). Let \(\mathsf {CA}\) be a key-management API and let \({\mathsf {P}}=({\mathsf {Kg}}_{\mathsf {P}},{\mathsf {Alg}}_{\mathsf {P}})\) be a compatible primitive with security notion defined by the tuple of algorithms \(({\mathsf {setup}},{{\mathsf {chal}}_{0}},{{\mathsf {chal}}_{1}},{{\mathsf {chal}}_{\mathrm {aux}}})\). Then for any adversary \(\mathcal {A}\) against the security of the cryptographic API \([\mathsf {CA};{\mathsf {P}}]\), there exist efficient reductions \(\mathcal {B}_1\), \(\mathcal {B}_2\), and \(\mathcal {B}_3\) such that
where \(\mathbf {Adv}^{{{\mathsf {sticky}}}}_{\mathsf {CA}} \) refers to \(\mathsf {external}\), \(\mathbf {Adv}^{{\mathsf {km}}}_{\mathsf {CA}} \) is relative to \({\mathsf {Kg}}\) defined above, and \(q_e\) is an upper bound on the number of non-zero index classes that ever contain a handle with attribute \(\mathsf {external}\) set (in the game played by \(\mathcal {A}\)).
Remark 3
To avoid being tied down to a particular cryptographic interface, we have developed an abstract framework for arbitrary security games. One nice side-effect of our choice is that we can treat (modularly) settings where APIs leak “fingerprints" of their external keys via their attributes. Specifically, we can treat these fingerprints as an additional functionality of the abstract primitive (instead of an attribute). Obviously the actual primitive needs to be proven secure in the presence of fingerprints.
5 Instantiating a KM-API
We now show how to instantiate a KM-API from a DAE scheme. This KM-API enforces a “leveled” key hierarchy. The bottom level will contain keys for one or more (unspecified) cryptographic primitives. The top level will contain keys for a DAE scheme. Our KM-API will enforce the following policy: top-level keys may only be used to (un)wrap keys at the bottom level, and bottom-level keys may not (un)wrap any key. Intuitively, keys on the bottom should only be used with their associated cryptographic primitive.
DAE Schemes. A deterministic authenticated encryption scheme (DAE) is a tuple \(\varPi =(\mathcal {K},\mathcal {E},\mathcal {D})\). The first component \(\mathcal {K}\subseteq \{0,1\}^*\) is the set of encryption keys. The encryption algorithm \(\mathcal {E}\) and decryption algorithm \(\mathcal {D}\) both take an input in \(\mathcal {K}\times \{0,1\}^* \times \{0,1\}^*\) and return either a string or a distinguished value \(\bot \). We write \(\mathcal {E}_K^V(X)\) for \(\mathcal {E}(K,V,X)\) and \(\mathcal {D}_K^V(Y)\) for \(\mathcal {D}(K,V,Y)\). We assume there are an associated data space \(\mathcal {V}\subseteq \{0,1\}^*\) and a message space \(\mathcal {X}\subseteq \{0,1\}^*\), such that \(X \in \mathcal {X}\Rightarrow \{0,1\}^{|X|} \subset \mathcal {X}\) and \(\mathcal {E}_K^V(X) \in \{0,1\}^*\) iff \(V \in \mathcal {V}\) and \(X \in \mathcal {X}\).
Our convention is that \(\mathcal {E}_K^V(\bot )=\mathcal {D}_K^V(\bot )=\bot \) for all \(K\in \mathcal {K},V\in \mathcal {V}\). We require that \(\mathcal {D}\) and \(\mathcal {E}\) are each others inverses on their range excluding \(\bot \): for all \(K \in \mathcal {K}, V \in \mathcal {V}, Y \in \{0,1\}^*\), if there is an X such \(\mathcal {E}_K^V(X)=Y\) then we require that \(\mathcal {D}_K^V(Y)=X\) (correctness), moreover if no such X exists, then we require that \(\mathcal {D}_K^V(Y)=\bot \) (tidyness).
We require \(\mathcal {E}\) to be length-regular with stretch \(\tau :\mathbb {N} \times \mathbb {N} \rightarrow \mathbb {N}\), meaning that for all \(K \in \mathcal {K}, V \in \mathcal {V}, X \in \mathcal {X}\) it holds that \(|\mathcal {E}_K^V(X)| = |X| + \tau (|V|,|X|)\). Consequently, ciphertext lengths can only on the lengths of V and X.
The experiments \({\mathbf {Exp}^{{{\ell \text{- }\mathsf {dae\text{- }crpt}}\text{- }{b}}}_{\varPi }}(\mathcal {A})\) for defining left-or-right DAE security with adaptive key-corruption. To prevent trivial wins, we make the following assumptions on the adversary: (1) it does not ask (i, V, Y) to its \(\textsc {Dec}\)-oracle if some previous \(\textsc {Enc}\)-oracle query (i, V, X) returned Y, or if some previous \(\textsc {LR}\)-oracle query \((i,V,X_0,X_1)\) returned Y; (2) it does not ask (i, V, X) to its \(\textsc {Enc}\)-oracle if some previous \(\textsc {Dec}\)-oracle query (i, V, Y) returned X; (3) if (i, V, X) is ever asked to the \(\textsc {Enc}\)-oracle, then no query of the form \((i,V,X,\cdot )\) or \((i,V,\cdot ,X)\) is ever made to the \(\textsc {LR}\)-oracle, and vice versa.
DAE Scheme Security. For integer \(\ell \ge 1\) we define the advantage of adversary \(\mathcal {A}\) in the \(\ell \) -key left-or-right DAE with corruptions experiment as
where the probability is over the experiment in Fig. 11 and the coins of \(\mathcal {A}\). Without loss of generality, we assume that the adversary does not repeat any query, and that it does not ask queries that are outside of the implied domains of its oracles.
As a special case of this, we also define the advantage of adverary \(\mathcal {A}\) in the \(\ell \)-key left-or-right DAE experiment as
where \({\mathbf {Exp}^{{{\ell \text{- }\mathsf {dae}}\text{- }{b}}}_{\varPi }}\) is defined by modifying Fig. 11 to no longer include the \(\textsc {Enc}\) or \(\textsc {Reveal}\) oracles, the sets I, C, and any references to these. The applicable restrictions on adversarial behavior carry over.
We note that this notion differs from the DAE security notion first given by Rogaway and Shrimpton [22]. We use a left-or-right version, more along the lines of Gennaro and Halevi [15] because it suits our needs better.
A standard “hybrid argument” provides a proof of the following theorem, along with the description of the claimed adversary \(\mathcal {B}\). We omit this proof.
Theorem 5
[1-key left-or-right DAE implies \(\ell \)-key left-or-right DAE with corruptions.] Fix an integer \(\ell \ge 1\). Let \(\varPi =(\mathcal {K},\mathcal {E},\mathcal {D})\) be a DAE scheme with associated-data space \(\mathcal {V}\), message space \(\mathcal {X}\), and ciphertext-expansion function e. Let \(\mathcal {A}\) be an adversary compatible with the \(\ell \)-key DAE advantage notion. Let \(\mathcal {A}\) ask \(q_i\) \(\textsc {LR}\)-queries of the form \((i,\cdot ,\cdot ,\cdot )\) and \(p_i\) \(\textsc {Dec}\)-queries of the form \((i,\cdot ,\cdot )\), and have time-complexity t. Then there is an adversary \(\mathcal {B}\) that makes black-box use of \(\mathcal {A}\) such that
where \(\mathcal {B}\) asks at most \(\max _{i}\{q_i\}\) \(\textsc {LR}\)-queries and \(\max _{i}\{p_i\}\) \(\textsc {Dec}\)-queries.
Building a KM-API from a DAE Scheme. Assume that there exists an easy to compute predicate \(\mathsf {external}\) on the attribute space \({{\mathsf {Attributes}}}\subseteq \{0,1\}^*\), and assume that sampling attributes for which the predicate holds, respectively does not hold, both are easy. Recall that, as before, for a particular handle \(h\), we use the shorthand \(h.\mathsf {external}\) for the predicate evaluated on \(h.\mathsf {attr}\).
Let \({\mathsf {Kg}}_{\mathsf {P}}\) be the key generation for some primitive with key space \({{\mathsf {Keys}}}\) and let \(\mathsf {pm}\) be a function that maps attributes to parameters (or  ). Let \(\varPi =(\mathcal {K},\mathcal {E},\mathcal {D})\) be a DAE-scheme with associated-data space \(\mathcal {V}={{\mathsf {Attributes}}}\) and message-space \(\mathcal {X}\) that contains \({{\mathsf {Keys}}}\). Define \({\mathsf {Kg}}:{{\mathsf {Attributes}}}\rightarrow {{\mathsf {Keys}}}\cup \mathcal {K}\) to be the algorithm that, on input an attribute \(a\) that satisfies \(\mathsf {external}\), samples from \({{\mathsf {Keys}}}\) according to \({\mathsf {Kg}}_{\mathsf {P}}(\mathsf {pm}(a))\) and otherwise samples uniformly from \(\mathcal {K}\).
). Let \(\varPi =(\mathcal {K},\mathcal {E},\mathcal {D})\) be a DAE-scheme with associated-data space \(\mathcal {V}={{\mathsf {Attributes}}}\) and message-space \(\mathcal {X}\) that contains \({{\mathsf {Keys}}}\). Define \({\mathsf {Kg}}:{{\mathsf {Attributes}}}\rightarrow {{\mathsf {Keys}}}\cup \mathcal {K}\) to be the algorithm that, on input an attribute \(a\) that satisfies \(\mathsf {external}\), samples from \({{\mathsf {Keys}}}\) according to \({\mathsf {Kg}}_{\mathsf {P}}(\mathsf {pm}(a))\) and otherwise samples uniformly from \(\mathcal {K}\).
Before specifying the algorithms that comprise our KM-API, let us detail our assumptions on the state of tokens with its scope. We assume that all tokens have state of the form \(s=({\tilde{s}},(h\mapsto (\mathsf {key},a))_h)\), where for each handle \(h\), the mapping \(h\mapsto (\mathsf {key},a)\) indicates the associated key and attribute pair (so \(h.\mathsf {key}=\mathsf {key}\) and \(h.\mathsf {attr}=a\)), and the state \({\tilde{s}}\) contains a snapshot of the token’s past I/O only. Let \(\mathsf {fresh}\) be a mechanism that creates fresh (unique) handles on a per token basis.
With all of this established, the algorithms of our KM-API are defined as follows:
-
\({{\mathsf {\mathsf {CA}.new}}}(t, a)\): Create a fresh handle \(h\) on token \(t\) by calling \(\mathsf {fresh}(t)\). Sample
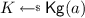 and update the state of token \(t\) to reflect the new mapping \(h\mapsto (K,a)\). Return \(h\).
and update the state of token \(t\) to reflect the new mapping \(h\mapsto (K,a)\). Return \(h\). -
\({{\mathsf {\mathsf {CA}.create}}}(t, K ,a)\): Create a fresh handle \(h\) on token \(t\) by calling \(\mathsf {fresh}(t)\) and update the state on token \(t\) to reflect the new mapping \(h\mapsto (K,a)\). Return \(h\).
-
\({{\mathsf {\mathsf {CA}.wrap}}}(h_1,h_2)\): If \(h_1.\mathsf {external}\vee \lnot h_2.\mathsf {external}\) then return \(\perp _\mathrm {api}\). Otherwise, \(w\leftarrow \mathcal {E}_{h_1.\mathsf {key}}^{h_2.\mathsf {attr}}(h_2.\mathsf {key})\). Return \(w\).
-
\({{\mathsf {\mathsf {CA}.unwrap}}}(h, w,a)\): If \(h.\mathsf {external}\) return \(\perp _\mathrm {api}\). Compute \(K \leftarrow \mathcal {D}_{h.\mathsf {key}}^{a}(w)\). If \(K = \bot \) then return \(\perp _\mathrm {api}\). Otherwise, create a fresh handle \(\bar{h}\) and update the state on token \(\mathsf {tkn}({h})\) to reflect the new mapping \(\bar{h}\mapsto (K,a)\). Return \(\bar{h}\).
Theorem 6
Fix a nonempty set \({{\mathsf {Keys}}}\). Let \(\varPi =(\mathcal {K},\mathcal {E},\mathcal {D})\) be a DAE-scheme with associated-data space \(\mathcal {V}={{\mathsf {Attributes}}}\) and message-space \(\mathcal {X}\) that contains \({{\mathsf {Keys}}}\). Let \(\mathsf {CA}\) be the KM-API just described, and let \(\mathcal {A}\) be an efficient KM-API adversary asking a single challenge query. Let \(q_{n}\) be the number of \({{\textsc {new}}}\)-oracle queries made by \(\mathcal {A}\) in its execution, and let \(\ell \le q_{n}\) be the number of these that produce an internal key. Then there exist efficient adversaries \(\mathcal {B}, \mathcal {F}\) for the \(\ell \)-key DAE with corruptions experiment such that
6 Related Work
Symbolic Models for API Security. Given that many attacks against APIs rely on logical flaws rather than weak cryptography a large body of work addresses their security using symbolic models. The first set of attacks were discovered by Longley and Rigby [19], Bond [3], and Clulow [7]. More recently, Cortier et al. [8], Delaune et al. [13], and Bortolozzo et al. [4] uncovered further vulnerabilities by using automated tools. Security models and proofs of security include the work of Courant and Monin who use Coq to analyze a variant of IBM CCA API [11] and Cortier et al. [8]. Fröschle and Steel [14] and Cortier and Steel [9] analyze a fragment of the of PKCS#11 standard. Newer models consider key-management that employs asymmetric cryptographic [12] and revocation of keys [10]. While symbolic models are suitable for finding attacks, security proofs are less meaningful—in particular they do not a priori imply security with respect to the types of stronger computational models that we develop in this paper.
The Cachin–Chandran Model [5]. This is the first computational security model for a cryptographic API. The model is based on a particular design that relies on a centrally located server which keeps track of all key-management operations (how realistic the presence of such a server is in the distributed environment in which tokens typically operate is unclear).
The security model is intrinsically stated in terms of this suggested implementation of an API by hardwiring into the syntax of what constitutes an API their specific implementation choices (e.g. how and when certain attributes change, how and what information the overall internal state of the token should maintain). Clearly this severely restricts the model’s applicability. For example, the security of the wrap scheme is hardwired into the model and essentially demands that the wrap operation be implemented with a probabilistic scheme—schemes employing a deterministic wrapping mechanism would be ruled insecure under the model (in particular our key-management scheme is not captured as our tokens need not keep track, internally, of the attributes associated to keys).
From a security perspective, just like in our model, the adversary has access to the full interface of the token and aims to break the cryptographic functionality that the token provides. Yet, there are three aspects—we believe shortcomings—of the Cachin–Chandran model on which our model significantly improves. Firstly, as stated already, the Cachin–Chandran model rules out (either explicitly or by implication) some very reasonable and secure implementations of a cryptographic API. Secondly, aliasing issues caused by the possibility that a key can have multiple distinct handles pointing to it are sidestepped in the Cachin–Chandran model (essentially, unwrapping of wraps that were not previously created is not permitted). Finally, the corruption model considered in the Cachin–Chandran model is restricted to users, which implies that an adversary can then act on that user’s behalf. However, there are no further implications to the experiment, as acting on behalf of a user does not give access to any keys. Consequently, the notion of corrupted or compromised keys is absent in the Cachin–Chandran model.
Our model makes only minimal assumptions about the inner-workings of a cryptographic API (it allows but certainly does not impose a central server for the implementation). Our security model carefully keeps track of the equivalence classes on handles that the wrap/unwrap operations give rise to. More importantly, we explicitly allow for adaptive corruption of API keys and demand that any other key that is not directly or indirectly affected by corruptions stays secure.
The Kremer–Steel–Warinschi Model [18]. The KSW computational modelFootnote 5 fixes some of the shortcomings of the Cachin–Chandran model. In particular, it presents definitions for the syntax and security of an encryption-exporting API not driven by any particular implementation and allowing adaptive corruption of keys. The syntax is single token and the security requirements imposed are incompatible with PKCS#11 implementations: all attributes need to be sticky, whereas PKCS#11 mandates that some attributes change during operations. Interestingly, while the Cachin-Chandran model imposes that wrapping be implemented with a probabilistic encryption scheme, the modelling choice adopted by the KSW model enforces wrapping to be deterministic. Perhaps worse, the high level of abstraction led to underspecified, malformed definitions.Footnote 6
In contrast, we consider a multi-token environment and only surface minimal assumptions that avoid the underspecification in the KSW model. Our security notion is more relaxed. For example, for key-management APIs we only demand that the application keys are secret, which allows for both probabilistic and deterministic solutions to the key-wrap problem. Crucially, we show that our notion of security for key-management APIs is composable, whereas no such result is known to hold for the KSW model.
Universally Composable Key-Management[17]. This paper is, in spirit, closest to ours. It aims to provide a compositional framework where key-management can be analyzed separately from the other cryptographic operations that tokens may export. The formalization relies on the universal composability framework (as refined by Hofheinz and Shoup [16]) and consists of an ideal key-management functionality which, as usual, should be emulated by a secure implementation. The framework naturally encompasses multi-token scenarios which are simply distributed implementations of the functionality and should guarantee the desired guarantee: the implementation can replace the functionality in any other scenario.
Since the underlying definitional framework relies on simulation, the model does not tolerate well adversaries that adaptively corrupt keys (we discuss this issue below), so the adversary is only allowed static corruptions. An additional issue is that in simulation based settings keys cannot be freely passed around between functionalities. The solution adopted here employs a cumbersome capability-based mechanism to model the interaction between key-management and other cryptographic operations. The key-management functionality is not fully agnostic of the primitive in which the managed keys are to be used. Furthermore, the key-management functionality has hardwired a wrapping algorithm (which needs to be deterministic, authenticated and secure against related-key attacks).
We avoid all of these shortcomings. Our construction is mostly oblivious to the primitive in which keys are used and allows various instantiations where wrapping can be either probabilistic or deterministic. Our use of game-based definitions enables the proof of the composition theorem even with adaptive corruptions.
Computationally Sound API Analysis. Recently, Scerri and Stanley-Oakes have proposed an approach for the analysis of key-management APIs [24] using the framework of Bana and Comon-Lundh [1]. This framework allows to model and reason about cryptographic systems using a high-level of abstraction and then use a general theorem that links the results with security in a standard computational model. The approach used by Scerri and Stanley-Oakes is similar to ours in that they treat the key-management component of APIs separately and retrieve the security of the overall API through a composition theorem that considers the use of API keys in symmetric encryption. That work provides a more detailed treatment of API policies and benefits from the simple, axiomatic way of reasoning about security of protocols. The main drawback is that the adversary is only allowed a constant number of queries to the API.
7 Conclusion
We propose models that capture the core security guarantees that cryptographic and key-management APIs should provide. Our treatment is general, in that we do not consider a particular primitive (or primitives) but rely on an abstraction that allows multiple instantiations. Our work opens several interesting research avenues. We currently treat policies abstractly, and only indicate their influence on tokens as part of our execution model. It would be interesting to investigate further additional guarantees for tokens that relate to secure policy enforcement. For example, useful policies may attempt to ensure that certain keys are used only by certain users and only for a restricted set of operations. Such guarantees can be defined and analyzed in an extension of our model that incorporates the notion of token users and formalizes the type of restrictions envisioned by the policy. In this paper we consider only the management of symmetric keys. It would be useful to extend our treatment to include private keys for the asymmetric cryptographic primitives that are part of a standard PKCS#11 interface.
Notes
- 1.
An extension of our model could consider a more fine-grained level of errors, identifying why an operation results in an error.
- 2.
Notice that the converse implication is not necessarily true.
- 3.
As an example, a scheme could effectively share the key over multiple wraps, where unwrapping fails (outputs \(\perp _\mathrm {api}\)) unless sufficient shares (wraps) have been received: no single wrap will allow extraction of the key.
- 4.
For information theoretic adversaries the lemma is worthless.
- 5.
The paper also introduces two other related models: an idealized and a symbolic one.
- 6.
For example, the formalization crucially relies on the notation \(s[{{\mathsf {key}}}(h)\mathop {\mapsto }\limits ^{\$} k_0]\) which indicates some state \(s\) in which \({{\mathsf {key}}}(h)\) has been replaced with the randomly chosen \(k_0\). However, given the abstract notion of state, it is unclear what this state change even means. For instance, if another handle points to the same key, does that handle’s key also get affected? Is the state change persistent? Is \(k_0\) drawn anew each time?.
References
Bana, G., Comon-Lundh, H.: Towards unconditional soundness: computationally complete symbolic attacker. In: Degano, P., Guttman, J.D. (eds.) POST 2012 (ETAPS 2012). LNCS, vol. 7215, pp. 189–208. Springer, Heidelberg (2012)
Bardou, R., Focardi, R., Kawamoto, Y., Simionato, L., Steel, G., Tsay, J.-K.: Efficient padding oracle attacks on cryptographic hardware. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 608–625. Springer, Heidelberg (2012)
Bond, M.: Attacks on cryptoprocessor transaction sets. In: Koç, Ç.K., Naccache, D., Paar, C. (eds.) CHES 2001. LNCS, vol. 2162, pp. 220–234. Springer, Heidelberg (2001)
Bortolozzo, M., Centenaro, M., Focardi, R., Steel, G.: Attacking and fixing PKCS#11 security tokens. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 2010, pp. 260–269. ACM Press, October 2010
Cachin, C., Chandran, N.: A secure cryptographic token interface. In: Proceedings of 22th IEEE Computer Security Foundations Symposium (CSF 2009), pp. 141–153. IEEE Computer Society Press (2009)
Canetti, R., Feige, U., Goldreich, O., Naor, M.: Adaptively secure multi-party computation. In: 28th ACM STOC, pp. 639–648. ACM Press, May 1996
Clulow, J.: On the security of PKCS#11. In: Walter, C.D., Koç, Ç.K., Paar, C. (eds.) CHES 2003. LNCS, vol. 2779, pp. 411–425. Springer, Heidelberg (2003)
Cortier, V., Keighren, G., Steel, G.: Automatic analysis of the security of XOR-based key management schemes. In: Grumberg, O., Huth, M. (eds.) TACAS 2007. LNCS, vol. 4424, pp. 538–552. Springer, Heidelberg (2007)
Cortier, V., Steel, G.: A generic security API for symmetric key management on cryptographic devices. In: Backes, M., Ning, P. (eds.) ESORICS 2009. LNCS, vol. 5789, pp. 605–620. Springer, Heidelberg (2009)
Cortier, V., Steel, G., Wiedling, C.: Revoke and let live: a secure key revocation api for cryptographic devices. In: Yu, T., Danezis, G., Gligor, V.D. (eds.) ACM CCS 2012, pp. 918–928. ACM Press, October 2012
Courant, J., Monin, J.F.: Defending a bank with a proof assistant. In: WITS, pp. 87–98 (2006)
Daubignard, M., Lubicz, D., Steel, G.: A secure key management interface with asymmetric cryptography. In: Abadi, M., Kremer, S. (eds.) POST 2014 (ETAPS 2014). LNCS, vol. 8414, pp. 63–82. Springer, Heidelberg (2014)
Delaune, S., Kremer, S., Steel, G.: Formal analysis of PKCS#11. In: Proceedings of 21th IEEE Computer Security Foundations Symposium (CSF 2008), pp. 331–344. IEEE Computer Society Press (2008)
Fröschle, S., Steel, G.: Analysing PKCS#11 key management APIs with unbounded fresh data. In: Degano, P., Viganò, L. (eds.) ARSPA-WITS 2009. LNCS, vol. 5511, pp. 92–106. Springer, Heidelberg (2009)
Gennaro, R., Halevi, S.: More on key wrapping. In: Jacobson Jr., M.J., Rijmen, V., Safavi-Naini, R. (eds.) SAC 2009. LNCS, vol. 5867, pp. 53–70. Springer, Heidelberg (2009)
Hofheinz, D., Shoup, V.: GNUC: a new universal composability framework. J. Cryptol. 28(3), 423–508 (2015)
Kremer, S., Künnemann, R., Steel, G.: Universally composable key-management. In: Crampton, J., Jajodia, S., Mayes, K. (eds.) ESORICS 2013. LNCS, vol. 8134, pp. 327–344. Springer, Heidelberg (2013)
Kremer, S., Steel, G., Warinschi, B.: Security for key management interfaces. In: Proceedings of 24th IEEE Computer Security Foundations Symposium (CSF 2011), pp. 266–280. IEEE Computer Society Press (2011)
Longley, D., Rigby, S.: An automatic search for security flaws in key management schemes. Comput. Secur. 11(1), 75–89 (1992)
Nielsen, J.B.: Separating random oracle proofs from complexity theoretic proofs: the non-committing encryption case. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 111–126. Springer, Heidelberg (2002)
Osaki, Y., Iwata, T.: Further more on key wrapping. IEICE Trans. 95–A(1), 8–20 (2012)
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006)
RSA Security Inc: PKCS#11: cryptographic token interface standard, June 2004
Scerri, G., Stanley-Oakes, R.: Analysis of key wrapping APIs: generic policies, computational security. In: Proceedings of 29th IEEE Computer Security Foundations Symposium (CSF 2016). IEEE Computer Society Press (2016)
Acknowledgements
This work was supported in part by European Union Seventh Framework Programme (FP7/2007-2013) grant agreement 609611 (PRACTICE), and ERC Advanced Grant ERC-2010AdG-267188-CRIPTO. It was also supported by National Science Foundation grant CNS-1319061.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Shrimpton, T., Stam, M., Warinschi, B. (2016). A Modular Treatment of Cryptographic APIs: The Symmetric-Key Case. In: Robshaw, M., Katz, J. (eds) Advances in Cryptology – CRYPTO 2016. CRYPTO 2016. Lecture Notes in Computer Science(), vol 9814. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53018-4_11
Download citation
DOI: https://doi.org/10.1007/978-3-662-53018-4_11
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53017-7
Online ISBN: 978-3-662-53018-4
eBook Packages: Computer ScienceComputer Science (R0)




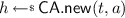 creates and returns a fresh handle on token
creates and returns a fresh handle on token  creates and returns a fresh handle on token
creates and returns a fresh handle on token  takes as input two handles and runs on the first handle’s token
takes as input two handles and runs on the first handle’s token 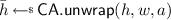 takes as input a handle to use for unwrapping, a wrap and an attribute string. If unwrapping succeeds, a fresh handle
takes as input a handle to use for unwrapping, a wrap and an attribute string. If unwrapping succeeds, a fresh handle 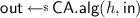 intends to evaluate the primitive
intends to evaluate the primitive 








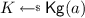 and update the state of token
and update the state of token