Abstract
In this paper, we analyze the security of round-reduced versions of the Keccak hash function family. Based on the work pioneered by Aumasson and Meier, and Dinur et al., we formalize and develop a technique named linear structure, which allows linearization of the underlying permutation of Keccak for up to 3 rounds with large number of variable spaces. As a direct application, it extends the best zero-sum distinguishers by 2 rounds without increasing the complexities. We also apply linear structures to preimage attacks against Keccak. By carefully studying the properties of the underlying Sbox, we show bilinear structures and find ways to convert the information on the output bits to linear functions on input bits. These findings, combined with linear structures, lead us to preimage attacks against up to 4-round Keccak with reduced complexities. An interesting feature of such preimage attacks is low complexities for small variants. As extreme examples, we can now find preimages of 3-round SHAKE128 with complexity 1, as well as the first practical solutions to two 3-round instances of Keccak challenge. Both zero-sum distinguishers and preimage attacks are verified by implementations. It is noted that the attacks here are still far from threatening the security of the full 24-round Keccak.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The Keccak sponge function family [6] was designed by Bertoni et al. as one of the 64 proposals submitted to the SHA-3 competition [24] in October 2008. It won in October 2012 after intense competition, and was subsequently standardized by the U.S. National Institute of Standards and Technology (NIST) as Secure Hash Algorithm-3 [25] (SHA-3) in August 2015. As such, Keccak has received intensive security analysis, since the design was made public in 2008, against the traditional security notions such as collision, preimage, and second-preimage resistance, as well as distinguishers of the underlying permutations and securities under some message authentication code, stream cipher, and authenticated cipher modes.
Up to date, the best collision attacks are reduced up to 4 out of 24 rounds of Keccak-224/256 with practical complexities [12, 14], and up to 5 rounds of Keccak-256 with theoretical complexities [13], by differential attacks. Practical preimage attacks are up to 2 rounds, by the approaches of meet-in-the-middle [23] and SAT solvers [21]. Theoretical preimage attacks work up to 7 / 8 / 9 rounds for Keccak-224/256/512 respectively with small time complexity gains over bruteforce [3, 11, 20]. There were mainly two types of distinguishers against the underlying permutation of Keccak (named Keccak-f), i.e., zero-sum distinguishers [2, 9] and those involving high probability differentials [17, 19]. These distinguishers work for 9 rounds in [2], 8 rounds in [19] with practical complexities, and up to 15 rounds with theoretical complexities bounded by \(2^{800}\) (birthday bound) for the 1600-bit Keccak-f permutation. Besides these, there are also attacks in other security settings, we are not listing them all as they are less relevant with our work here.
To promote security analysis with practical complexities, the Keccak team has been organizing the “Keccak Crunchy Crypto Collision and Preimage Contest” [4] (we will call it Keccak Challenge for short) and offering cash prizes for the winners. To make it feasible, the instances are set to be round-reduced variants of Keccak with capacity \(c=160\) and the output truncated to 160 bits for collisions and 80 bits for preimages, so the theoretical complexities for both are \(2^{80}\), which is relatively small but yet beyond PC’s capability. Instances have been solved for up to 4 and 2 rounds for collisions and preimages, respectively.
Our Contributions. In this paper, we focus on security analysis of Keccak with respective to two security notions, i.e., distinguisher of round-reduced versions of the underlying permutation Keccak-f, and preimage of round-reduced variants of the Keccak hash function family. Firstly, we review the zero-sum distinguisher by Aumasson and Meier [2]. Zero-sum distinguishers finds a set of input to the permutation, whose sum is zero and the set of corresponding output sums to zero at the same time. This distinguisher makes use of the property of low algebraic degrees 2 and 3 of the Sbox and its inverse used in Keccak-f, which is the only non-linear step of the round function. The attack starts from the middle of the permutation, and extends freely towards both forward and backward directions of the permutations. By setting up initial values of the middle starting point, one can bypass one round without increasing the algebraic degrees. Similar idea was extended to bypass one round by Dinur et al. [15] for key recovery attacks in keyed settings. In this paper, we formalize this idea as linear structures and extend the free starting rounds to 3 by combining properties of the linear layers and Sbox of the Keccak-f round function, and generally increase the attacked rounds of the zero-sum distinguishers by Aumasson and Meier by 2 without increasing the complexities. Notably, we extend the practically attacked rounds from 9 to 11. Furthermore, the 12-round Keccak-f permutations can be distinguished with complexity \(2^{65}\) or \(2^{82}\). This is of special interests since the 12-round Keccak-f permutation variants are used in the CAESAR candidates Keyak [8] and Ketje [7]. Nevertheless, we stress here that this distinguisher does not affect the security of Keyak or Ketje. A summary of the comparisons of our results with the previous ones is shown in Table 1. Our results are verified by an implementation of the 11-round distinguisher with time and data complexity \(2^{33}\), with all the 1600 bits of the output summing to zero with certainty. Note that Table 1 does not include the distinguishers with complexities \(\ge 2^{800}\), such as [9, 16]. In the Keccak reference [6, Page 61], the designers mentioned that “Only structural distinguishers on f that have non-zero advantage below \(2^{800}\) queries can possibly qualify as a threat for the security of a sponge function that uses it.” This is a birthday bound with regard to the size of the permutation.
The second contributions of this paper are improved preimage attacks. In contrast to the meet-in-the-middle and SAT solver techniques used previously, we adopt the techniques of linear structures and find preimages by linearizing the Keccak round functions and converting the preimage finding problems to that of solving systems of linear equations. This technique leads to attacks on up to 4-round Keccak with reduced complexities. The complexities of 3-round preimages are so significantly reduced that enables us to find preimages of SHAKE128 (a variant of Keccak \([r = 1344, c = 256]\) adapted by SHA-3) practically, and to solve two of 3-round preimage instances and a near-preimage with only two bits difference of 4-round preimage instance of the Keccak Challenge. The summary of our preimage attacks together with the previous best ones is shown in Table 2. Note that Table 2 does not include small optimizations of exhaustive search, such as [3, 11]. In this table, by variant 128 we mean SHAKE128 (M, 128). Different with the attacks of [20] which outperform exhaustive search by a larger factor as the hash size becomes larger, our attacks outperform exhaustive search by a larger factor as the hash size (or the capacity) becomes smaller.
Both improved zero-sum distinguishers and preimage attacks are possible thanks to the technique linear structures. By exploiting the properties of the Sbox used in Keccak, we find ways to linearize both the Sbox itself and its inverse. Combining with properties of the linear layer of the Keccak round function, we are able to find linear subspaces with large dimension by setting proper initial values. A nice property of these linear structures is that the algebraic degrees can be kept the same for up to 3 rounds, i.e., output bits of 3-round Keccak-f can be expressed as linear combinations of input bits. As a special feature of the linear structure, complexities of our attacks reduce significantly when the targets are Keccak instances with small capacities. In such cases, the number of required constraints derived from pre-set constants is small and the degree of freedom left is relatively large, and hence leads to faster attacks. As extreme examples, we can find preimages of 3-round SHAKE128 (M, 128) and solve the 3-round Keccak \([r = 1440, c = 160, \ell = 80]\) instance of Keccak Challenge with complexity 1.
Organization. The rest of the paper is organized as follows. Section 2 gives the details of the Keccak hash function family, followed by the properties of the Sbox in Sect. 3. The linear structure is introduced in Sect. 4. Its applications of zero-sum distinguishers and preimages attacks are presented in Sects. 5 and 6, respectively. Section 7 concludes the paper.
2 Definition of Keccak
2.1 The Sponge Function
The Keccak hash function follows the sponge construction, as depicted in Fig. 1. The message M is padded and split into blocks of r bits each. Beginning with an initial value (IV), the first r bits of b-bit state is XORed with the message block, followed by the application of the permutation f. This step is repeated until all message blocks are processed. Then the first r bits are outputted, r more bits can be obtained after an additional application of f, and this process is repeated until all required digest bits are obtained. The number of iterations is determined by the requested number of digest bits \(\ell \). Finally the output is truncated to its first \(\ell \) bits.
The sponge function [5]
The Keccak state [6]
2.2 The Keccak Hash Functions
To define the Keccak hash function family, the designers give the details of the underlying permutation f, as well as parameters set of \((r,c,\ell )\). The IV is set to be all “0”s. The underlying permutation of the Keccak hash function is chosen in a set of seven Keccak-f permutations, denoted Keccak-f [b], where \(b\in \{25, 50, 100, 200, 400, 800, 1600\}\) is the width of the permutation. The default version of Keccak-f is of size \(b = 1600\) bits, which can be represented as \(5\times 5\) 64-bit lanes as depicted in Fig. 2, denoted as A[x, y] with x for the index of column and y for the index of row. In what follows, indexes of x and y are from the set \(\{0,1,2,3,4\}\) and they are working in modulo 5 without other specification. The underlying permutation Keccak-f [1600] consists of 24 identical round functions up to a difference of constant addition. The round function R consists of five operations (\(\theta \) goes first):

-
\({\theta }:\) \(A[x,y] = A[x,y] \oplus \bigoplus _{j = 0}^4(A[x-1,j] \oplus (A[x+1,j] \lll 1))\), for \(x,y = 0, \ldots , 4\).
-
\({\rho }:\) \(A[x,y] = A[x,y]\lll r[x,y]\), for \(x,y = 0, \ldots , 4\).
-
\({\pi }:\) \(A[y,2x+3y] = A[x,y]\), for \(x,y = 0, \ldots , 4\).
-
\({\chi }:\) \( A[x,y] = A[x,y] \oplus ((\sim A[x+1,y]) \& A[x+2,y])\), for \(x,y = 0, \ldots , 4\).
-
\({\iota }:\) \(A[0,0] = A[0,0] \oplus RC\).
Here “\(\oplus \)” denotes for bit-wise XOR, “\(\lll \)” for bit rotation towards MSB of the 64-bit word, “\(\sim \)” for bit negation of 64-bit word, “ ” for bit-wise logic AND, “r[x, y]” for lane dependent rotation constants presented in Table 3, and “RC” for round-dependent round constants. We ignore the details of RC since it does not affect our attacks to be presented.
” for bit-wise logic AND, “r[x, y]” for lane dependent rotation constants presented in Table 3, and “RC” for round-dependent round constants. We ignore the details of RC since it does not affect our attacks to be presented.
Without other specifications, Keccak-f hereinafter refers to Keccak-f [1600].
2.3 Instances of Keccak and SHA-3
The hash function Keccak \([r, c, \ell ]\) refers to the instance of the Keccak sponge function family with parameters capacity c, bitrate r and output length \(\ell \). The official versions of Keccak have \(r=1600-c\) and \(c = 2\ell \), where \(\ell \in \{224, 256, 384, 512\}\), called Keccak-224, Keccak-256, Keccak-384, and Keccak-512. The padding rule of Keccak is of the form \(M10^*1\), i.e., it pads a single bit “1” followed by a smallest non-negative number of “0”, then a bit “1”, such that the bit length of the padded message becomes multiple of r.
The SHA-3 standard takes mainly the four default instances of Keccak with digest sizes 224, 256, 384, 512. The only difference is the padding rule. These four SHA-3 instances pad the message with two bits “01” before applying the Keccak padding rule, so the padded message becomes \(M0110^*1\), i.e., it pads M by three bits “011”, followed by a smallest non-negative number of “0”s, then a bit “1”, such that the padded message is of multiple of r bits. Generally, all our analysis results in this paper on Keccak applies to SHA-3, under the same parameters \((r, c, \ell )\), possibly with an increment of the complexities by at most \(2^2\) due to the two extra padding bits.
The SHA-3 family also includes two extendable-output functions (XOFs), called SHAKE128 and SHAKE256. More exactly, these instances SHAKE128 \((M, \ell )\) and SHAKE256 \((M, \ell )\) are defined from Keccak \([r=1344, c=256]\) and Keccak \([r=1088, c=512]\) by appending a four-bit suffix “1111” to the message, for any output length \(\ell \). Our preimage attacks on Keccak-256 also applies to SHAKE256 (M, 256). We will only consider preimage attacks on SHAKE128 (M, 128).
3 Properties of the Sbox \(\chi \)
In this section, we discuss the properties of the Sbox \(\chi \), which will be used to construct distinguishers on Keccak-f permutation in Sect. 5, and to mount preimage attacks on Keccak in Sect. 6.
3.1 Setting up Linear Equations from the Output of \(\chi \)
Bilinear Structure. We show in this section that given t consecutive bits out of the 5 output bits of \(\chi \), one can set up at least \(t-1\) linear equations on the 5 input bits due to the bilinear structure of the \(\chi \). Hereinafter, we may also refer to the \(\chi \) operation by Sbox.
The algebraic normal form of \(\chi \) mapping 5-bit \(a = a_0a_1a_2a_3a_4\) into 5-bit \(b = b_0b_1b_2b_3b_4\) can be written as \(b_i = a_i \oplus (a_{i+1} \oplus 1) \cdot a_{i+2}\), i.e.,
Then, we show that given two consecutive bits of the output of \(\chi \), one linear equation can be set up on the input bits. Without loss of generality, assume that \(b_{0}\) and \(b_{1}\) are known. By (2), we have
and thus according to (1) we obtain
Given three consecutive bits of the output of \(\chi \), to say \(b_{0}\), \(b_{1}\) and \(b_{2}\), an additional linear equation can be similarly set up:
Generally, the input a and output b of \(\chi \) satisfy \(F(a,b)=0\) with \(F(a,b)=aSb+Ta+Qb\), for some \(5\times 5\) binary matrices S, T, Q.
Given four output bits of \(\chi \), any bit of the input can be represented as a linear function on the unknown bit of the output, and one can naturally set up four linear equations on the input bits by eliminating the unknown output bit. It is clear that given all the five output bits of \(\chi \), the input bits are all determined. We summarize in Table 4 the number of linear equations on the input bits that can set up for given t consecutive bits of the output of \(\chi \).
3.2 Setting up More Linear Equations
As explained above, given t bits of the output of \(\chi \), for \(t=4\) or 5, one can set up t linear equations on the input of \(\chi \), and for \(t<4\), one can set up \(t-1\) linear equations. Here we present two more methods for setting up one or more extra linear equations on input bits when less than 4 bits of the output are known.
The first method is to guess the value of an input bit. We obtain two extra linear equations at cost of doubling the operations needed. For example, if a single bit \(b_0\) of the output is known, no linear equation could be set with previous methods. However, here we can guess the input bit \(a_1\) so that the equation \(b_0 = a_0 \oplus (a_1 \oplus 1) \cdot a_2\) becomes linear. Together with the guess of \(a_1\) itself, we obtain in total two more linear equations. The cost is that there are 2 choices of the guess, so we obtained the two extra linear equations with the cost of an increase of time complexity by a factor of 2. This is generally true when the number of known output bits is less than 4, as summarized in Setting 1.
Setting 1
When the number of known output bits is in the range [1, 3], a guess of an input bit leads to two extra linear equations on the input bits, by the cost of doubling the time complexity.
The second method is to make use of the probabilistic equation \(b_i=a_i\) which holds with probability 0.75, due to the fact that \(b_i = a_i \oplus (a_{i+1}\oplus 1) \cdot a_{i+2}\) and \((a_{i+1} \oplus 1) \cdot a_{i+2}\) is 0 with probability 0.75 assuming uniformly distributed \(a_{i+1}\) and \(a_{i+2}\), as summarized in Setting 2. This method will result in time complexity increase by a factor \(0.75^{-1} = 2^{0.415}\).
Setting 2
\(b_i = a_i\) of the \(\chi \) holds with probability 0.75 when input bit \(a_j\)’s are uniformly distributed, for all \(i \in \{0,\ldots , 4\}\).
3.3 Linearizing the Inverse of \(\chi \)
The inverse \(\chi ^{-1}\) \(:b\mapsto a\) has algebraic degree 3, and its algebraic normal form can be written as
where \(0\le i\le 4\) and the indexes are operated on modulo 5, that is,
It is obvious to note
Setting 3
If there is a single unknown output bit \(b_j\) of \(\chi \) and all other output bits are constants, then all input bits \(a_i\) can be expressed as linear combination of \(b_j\).
If we impose \(b_3=0\) and \(b_4=1\), then we have
and thus all \(a_i\)’s are linear on \(b_0\) and \(b_2\). That’s, for \(b_3=0\), \(b_4=1\) and any fixed \(b_1\), the algebraic degree of \(\chi ^{-1}\) becomes 1.
If we further impose \(b_1=1\), then we have
so all inputs bits \(a_i\)’s become linear combinations of \(b_i\)’s. Similar property holds when \(b_1 = 0\). This is summarized as:
Setting 4
When \(b_{j+3}=0\), \(b_{j+4} = 1\), and \(b_{j+1}\) is known (either 0 or 1), then all inputs bits \(a_i\)’s can be written as linear combinations of \(b_i\)’s, for all \(j \in \{0,\ldots , 4\}\).
4 The Linear Structures
In this section, we review the previous work, and formalize the idea of linear structure. We show linearization of Keccak-f permutation for up to 3 rounds. Our distinguisher and preimage attacks using linear structures depend directly on the space size of the variables of these linear structures, i.e., more variable bits result in lower attack complexities. We show in details how the largest space size possible could be obtained in each scenario.
4.1 Techniques for Keeping 2 Rounds Being Linear
In [15], Dinur et al. exploited a method for keeping the first round of Keccak-f being linear and used it to analyze the security of keyed variants of Keccak. Here we restate and formalize their technique. Let \({A[1,i]}\), \(i=0,1,2,3\), be variables and \({A[1,4]=\bigoplus _{i=0}^{3}A[1,i]}\oplus \alpha \) with any constant \(\alpha \) so that variables in each column sum to a constant. Then, as shown in Fig. 3, we can see how the variables affect the internal state under the transformation of Keccak-f round function  . In Fig. 3 and hereinafter, the 2-tuple number “x, y” denotes the position of a lane at the initial state, and we track its position under the \(\pi \) function, where \(0\le x, y\le 4\). All bits of the lanes with orange slashes have algebraic degree 1, those of the lanes in orange have algebraic degree at most 1, and the other lanes are all constants. Note the algebraic degrees will not be affected by the linear operations \(\theta \), \(\rho \), \(\pi \), and \(\iota \). The only non-linear operation is the \(\chi \), and its degree is 2 or 3 in forward or backward directions, respectively. As shown in the third state in Fig. 3, each row contains a single bit of degree 1 and the other 4 bits are constants. Since the only possibility for \(\chi \) to increase the algebraic degree is through two neighbouring bits due to the term \((a_{i+1}\oplus 1) \cdot a_{i+2}\), the algebraic degree of the state bits remains at most 1 after \(\chi \), i.e., after one round function R. The size of free variables can be at most 4 lanes, i.e., \(64\times 4=256\) bits.
. In Fig. 3 and hereinafter, the 2-tuple number “x, y” denotes the position of a lane at the initial state, and we track its position under the \(\pi \) function, where \(0\le x, y\le 4\). All bits of the lanes with orange slashes have algebraic degree 1, those of the lanes in orange have algebraic degree at most 1, and the other lanes are all constants. Note the algebraic degrees will not be affected by the linear operations \(\theta \), \(\rho \), \(\pi \), and \(\iota \). The only non-linear operation is the \(\chi \), and its degree is 2 or 3 in forward or backward directions, respectively. As shown in the third state in Fig. 3, each row contains a single bit of degree 1 and the other 4 bits are constants. Since the only possibility for \(\chi \) to increase the algebraic degree is through two neighbouring bits due to the term \((a_{i+1}\oplus 1) \cdot a_{i+2}\), the algebraic degree of the state bits remains at most 1 after \(\chi \), i.e., after one round function R. The size of free variables can be at most 4 lanes, i.e., \(64\times 4=256\) bits.
Noting that the only nonlinear part of R is \(\chi \) which operates on each 5-bit row. Since there is at most 1 variable in each row as in the first state in Fig. 3, the inverse function \(\chi ^{-1}\) is linear on these variables due to Setting 3. Thus, the first inverse round \(\textsf {R} ^{-1}\) is linear on these variables. This property was first used to construct zero-sum distinguishers on Keccak-f in [2].
Increasing the Degrees of Freedom up to 512 for 2 Rounds. Let \({A[i,j]}\) for \(i=0,2\) and \(j=0,1,2,3\) be variables and \({A[i,4]=\bigoplus _{j=0}^{3}A[i,j]}\oplus \alpha _i\) with constants \(\alpha _i\) for \(i=0,2\). Figure 4 shows how the variables propagate in one round R for \(\alpha _0=0\) and  . The bits of the lanes in gray (resp. lightgray) are set to all 1’s (resp. 0’s), and the bits of white lanes are set to arbitrary constants. The lanes with orange slashes or orange have algebraic degree at most 1 as above. Since there are at most two variables in each row input to \(\chi \) and the variables are not adjacent, the outputs of \(\chi \) are all linear on these variables. Therefore, the algebraic degree of the state bits in these variables remains 1 after the first round of Keccak-f permutation, and the size of free variables can achieve at most \(64\times 4\times 2=512\). This is also true for other constants \(\alpha _i\).
. The bits of the lanes in gray (resp. lightgray) are set to all 1’s (resp. 0’s), and the bits of white lanes are set to arbitrary constants. The lanes with orange slashes or orange have algebraic degree at most 1 as above. Since there are at most two variables in each row input to \(\chi \) and the variables are not adjacent, the outputs of \(\chi \) are all linear on these variables. Therefore, the algebraic degree of the state bits in these variables remains 1 after the first round of Keccak-f permutation, and the size of free variables can achieve at most \(64\times 4\times 2=512\). This is also true for other constants \(\alpha _i\).
To keep the algebraic degrees to be at most one when \(\chi ^{-1}\) is applied (inverting one round) to the 512 variables in the first state of Fig. 4, according to Setting 4, we restrict the bits of gray lanes to be all ones and the bits of lightgray lanes to be all zeros, where the bits in gray and lightgray lanes respectively correspond to \(b_{i+4}\)’s and \(b_{i+3}\)’s in Setting 4. Note that the step \(\iota \) only adds a constant to the first lane and thus it does not affect the gray and lightgray lanes. In this case, the first inverse round \(\textsf {R} ^{-1}\) is linear on these 512 variables.
4.2 How to Keep 3 Rounds Being Linear
Based on the technique above, in this section we describe a technique for keeping an additional forward round of Keccak-f being linear.
Let A[i, j] with \(i=0,2\) and \(j=0,1,2\) be variables. In what follows, we show how to impose some conditions on the input bits such that all the output bits after two rounds forward are linear. To make sure that the variables do not affect the values of the other bits after step \(\theta \) of the first round, i.e., keeping the sum of all columns to be zero constants, we impose the following \(2\times 64\) equations:
The values of white lanes are set in such a way that the value of the gray and lightgray lanes remained unchanged after step \(\theta \) of the first round, as shown in Fig. 5. The steps \(\rho \) and \(\pi \) are respectively shifts of the bits in the same lanes and permutations of the positions of the lanes. After the steps \(\chi \) and \(\iota \), the lane at column 0 and row 0 equals \(A[0,0] \oplus A[2,2]_{\lll 43}\), the other lanes in orange remain unchanged up to constants, and the white lanes are all constants. To make sure that the variables do not propagate after step \(\theta \) of the second round, we impose \(3\times 64\) more equations:
Note that this result is still valid when constants are XORed to the above three equations. Since this linear system has in total \(5\times 64=320\) equations and \(6\times 64=384\) variables, there remains 64 degrees of freedom. As shown in Fig. 5, we can see that after the second round all the output bits are linear since no adjacent bits contain variables before step \(\chi \) of the second round.
To ensure that the inverse function \(\chi ^{-1}\) is linear, we restrict the bits of lanes A[4, j] with \(j=0,1,2\) to be all ones and the bits of lanes A[3, j] with \(j=0,1,2\) to be all zeros as in Setting 4.
Increasing the Degrees of Freedom to up to 128. Similarly, we can increase the degrees of freedom from 64 to 128 by setting A[i, j] with \(i=0,2\) and \(j=0,1,2,3\) be variables and imposing some conditions on the input bits as shown in Fig. 6. We build a linear system of \(6\times 64=384\) equations on \(8\times 64=512\) variables which has 128 degrees of freedom and satisfies that the output bits after the second round are all linear. To ensure that the inverse function \(\chi ^{-1}\) is linear, we restrict the bits of lanes A[4, j] with \(j=0,1,2,3\) to be all ones and the bits of lanes A[3, j] with \(j=0,1,2,3\) to be all zeros.
Increasing the Degrees of Freedom to up to 194. We further extend the degrees of freedom to 194 by setting A[i, j] with \(i=0,2\) and \(j=0,1,\cdots ,4\) be variables and imposing some conditions on the input bits as shown in Fig. 7. We build a linear system of \(7\times 64=448\) equations on \(10\times 64=640\) variables which has 194 degrees of freedom and satisfies that the output bits after the second round are all linear. Note that there are two linear equations linearly dependent on the other equations, so the degree of freedom is 194 instead of 192. To ensure that the inverse function \(\chi ^{-1}\) is linear, we restrict the bits of lanes A[4, j] with \(j=0,1,\cdots ,4\) to be all ones and the bits of lanes A[3, j] with \(j=0,1,\cdots ,4\) to be all zeros.
In summary, we found linear structures of Keccak-f permutation reduced to 2 rounds with degree of freedom up to 512, and 3 rounds with degree of freedom up to 194.
5 Zero-Sum Distinguishers
A zero-sum distinguisher for a function is a method to find a set of values summing to zero such that their respective images also sum to zero. That is, it is a method to find a set S such that \(\sum _{x\in S}{x}=0\) and \(\sum _{x\in S}{f(x)}=0\) for the function f. It is well known that the d-th order derivative of a polynomial with degree at most d is a constant. For a Boolean function of algebraic degree at most d, its d-th order derivative is also a constant. Thus the outputs of a Boolean function of degree at most d sum to zero when the inputs take over a linear space of dimension at least \(d+1\).
The Keccak-f permutation is the core function of Keccak and SHA-3. The known method for constructing zero-sum distinguishers on Keccak-f permutation, exploits the fact that adding a round in Keccak-f only doubles the degree of the algebraic expression of the output bits in terms of the input bits, and only triples the degree of the algebraic expression of the input bits in terms of the output bits. This is due to that the algebraic degree of one Keccak-f round is 2 and the algebraic degree of one inverse round is 3. The real zero-sum distinguisher starts from some middle round of the Keccak-f permutation, and extends n rounds forward and m rounds backward. So the algebraic degree of n forward rounds \(\textsf {R} ^n\) is bounded by \(2^n\), and m backward rounds \(\textsf {R} ^{-m}\) by \(3^{m}\). With a linear space \(S_M\) from the middle round of size at least \(2^{1+\max (2^n,3^m)}\), one can be ensured that both input and output sum to zero, i.e., \(\sum _{x \in S_M} \textsf {R} ^{n}(x) = 0\) and \(\sum _{x \in S_M} \textsf {R} ^{-m}(x) = 0\). The desired input space S of the \((m+n)\)-round distinguisher can be obtained by \(S = \{\textsf {R} ^{-m}(x) ~|~ x \in S_M\}\).
The attack has been extended in two different directions, finding better bounds of the algebraic degrees of \(\textsf {R} ^n\) and \(\textsf {R} ^{-m}\) [9, 16], and inserting rounds in the starting point in the middle [2]. Our improved zero-sum distinguisher is in line with the second approach. Aumasson and Meier showed in [2] that one round could be inserted for free. This is achieved by carefully choosing the set \(S_M\) so that the algebraic degree keeps to be 1 after one round. It becomes obvious to note the linear structures presented in Sect. 4 could be used here to extend the number of free rounds to three, i.e., with linear structures as \(S_M\) (similar to the way how initial structures are used in MITM preimage attacks [1, 18]), the algebraic degrees of one backward round \(\textsf {R} ^{-1}\) and two forward rounds \(\textsf {R} ^{2}\) are kept to be 1.
As such, with the same complexity \(2^{1+ \max (2^n,3^m)}\), our improved distinguisher works for \((m+n+3)\) rounds, i.e., \((m+1)\) rounds backward and \((n+2)\) rounds forward. In Table 1, we summarize our results with the best combinations of m and n. Note the number of attacked rounds is limited by the size of \(S_M\), a.k.a., the size of the linear structures. For instance, the largest space we found for 3-round linear structure is \(2^{194}\), so the distinguisher works for all combinations of m and n such that \(2^{1+\max (2^n,3^m)} \le 2^{194}\). When \(m=4\) (5 rounds backward) and \(n=7\) (9 rounds forward), as stated in the last entry of the third column of Table 1, the attack applies to \(m+n+3=14\) rounds with time/data complexity \(2^{1+\max (2^n,3^m)} = 2^{1+\max (2^7,3^4)} = 2^{129} \le 2^{194}\).
As a trade-off, the size of linear structure could be larger for less rounds, e.g., up to \(2^{512}\) for 2 rounds. So the distinguisher works as below
While there is one free round less, we can afford larger complexities, e.g., with \(m=5\) and \(n=8\), we can distinguish \(m+n+2 = 15\) rounds with complexity \(2^{1+\max (2^n,3^m)} = 2^{257}\). Results of other choices of (m, n) are listed in the second column of Table 1.
As a direct application to the 12-round Keccak-f permutation used in the CAESAR candidate Keyak [8], the 3-round linear structure is large enough and the choice of \((m=3,n=6)\) results in attack complexity \(2^{65}\). Ketje [7] uses a 12-round Keccak-f permutation reduced to 400 bits (denoted as Keccak-\(p[400,n_r=12]\)), by reducing the length of lanes from 64 to 16 bits. When we project the zero-sum distinguisher to this small variant, the maximum sizes of linear structures are reduced to \(512/4=128\) and \(192/4=48\) bits respectively for 2 and 3 rounds. While the size for the 3-round linear structure is insufficient for distinguishing 12 rounds, the 128-bit 2-round linear structure makes it eligible with complexity \(2^{82}\). We note that though our distinguishers work for 12-round Keccak-f, they do not result in attacks in settings of authenticated cipher against Keyak or Ketje.
In summary our improved zero-sum distinguishers work for up to 15 rounds, and for up to 11 rounds with practical complexities.
Experiments. We have made an experiment for verifying our distinguishers on Keccak-f permutation reduced to 7 rounds in the forward direction. We use the structure with degrees of freedom up to 64 as shown in Sect. 4.2. Note that all the bits of the 7-round output have algebraic degree at most \(2^{7-2}=32\) for this structure. It is sufficient to use a 33 dimensional space. In our experiment, 31 out of those 64 variables are first randomly valued and fixed, then the outputs are summed over all the possible values of the rest input variables. It turns out that all the 1600 bits of this sum are zeros.
6 Preimage Attacks
In this section, we exploit algebraic techniques to mount preimage attacks on several variants of Keccak based on the properties of the Sbox \(\chi \) and the linear structures of Keccak-f permutation. The preimage attacks on SHA-3 are the same except that the time complexity may be at most \(2^2\) larger in some cases due to the two extra padding bits. In general, here we find preimages of message with length \(\le r-2\) bits by setting the (\(r-1\))-th bit of the input state to be 1 so that the padded message is one block, unless the degree of freedom is insufficient. We choose the message in such a way that the internal states of the first few rounds follow linear structures as presented in Sect. 4 and the \(\chi \) of the last round is inverted by the methods presented in Sect. 3. To achieve smallest possible time complexities, we will use different linear structures, and different methods inverting the \(\chi \) for each instance of Keccak. Note, the first \(r-1\) bits of the input to Keccak-f can be chosen freely by choosing the proper message bit values. However, the last \(c=b-r\) bits could not be chosen since there is no addition of message bits, so we can only choose “variables” of linear structures from the first \(r-1\) bits, and this is why we must use different linear structures for different instances. In what follows, we present the preimage attacks by showing the choice of linear structures, ways to invert the Sbox, followed by a complexity analysis of each instance attacked. The basic idea of our attacks is to set up and solve linear equations. The complexity in this section is measured by the number of times for solving the linear system of equations.
6.1 Preimage Attacks on 2-Round Keccak
First we discuss the preimage attacks on Keccak reduced to 2 rounds. They follow 1-round linear structures, plus 1-round inversion of the Sbox. These attacks adopt some similar ideas of meet-in-the-middle [23], while they exploit the linear structures of Keccak. For 2-round Keccak-512, we execute the attack as follows (depicted in Fig. 8):
-
1.
Invert the first 320 bits of a given hash value h through
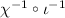 . Note these bits form the full output of the 64 Sboxes in the first row, so the corresponding input bits can be fully determined.
. Note these bits form the full output of the 64 Sboxes in the first row, so the corresponding input bits can be fully determined. -
2.
Randomly guess the values of the lanes in white of the state input to the first round, as shown in Fig. 8, where the 1024 bits of the lanes in lightgray are set to all zeros and the last bit of A[3, 1] is set to 1 such that the state input to the first round satisfies the padding rule;
-
3.
For each guess, we set \(A[0,1]=A[0,0]+\alpha _0\) and \(A[2,1]=A[2,0]+\alpha _2\) with random constants \(\alpha _0, \alpha _2\), build a linear system between A[0, 0], A[2, 0] and the recovered 320 input bits of the \(\chi \) in the second round, then solve this system and check whether the resulted hash value is correct.
Since A[0, 0] and A[2, 0] have 128 bits, so we have a complexity gain over bruteforce of \(2^{128}\), i.e., \(2^{512-128} = 2^{384}\) for 2-round Keccak-512 preimage attack. Note the degree of freedom in our setting is sufficient to find a preimage eventually. There are 128 bits from A[0, 0] and A[2, 0], 319 bits from white lanes, and 128 bits from \(\alpha _0\) and \(\alpha _2\), which sums to 575 bits, larger than the required 512 bits.
For the 2-round Keccak-384, the attack is similar to that for Keccak-512, except that we can construct linear structure from \(r=1600-2\times 384-1=831\) bits instead of 575 bits for Keccak-512. We can obtain a linear structure of 256-bit variables from (A[0, 0], A[0, 1], A[2, 0], A[2, 1]) with \(A[0,2] = A[0,0] \oplus A[0,1] \oplus \alpha _0\) and \(A[2,2] = A[2,0] \oplus A[2,1] \oplus \alpha _2\), hence a linear system of 256-bit equations, as shown in Fig. 9. For generating a message satisfying the padding rule, we just need a solution with the last bit of A[2, 2] being 1. Therefore, the time complexity of this attack is \(2^{384-256+1} = 2^{129}\).
Noting that we can obtain 4 linear equations on the input bits given 4 output bits of the 5-bit Sbox \(\chi \). We can also apply the above preimage attack to 2-round Keccak-256, by solving the system of linear equations just once, i.e., with time complexity 1. As a feature of sponge functions, all other variants with digest size less than 256 bits could be attacked in exactly the same way by randomly presetting the extra digest bits not outputted.
6.2 Preimage Attacks on 3-Round Keccak
Next, we show preimage attacks on several instances of Keccak reduced to 3 rounds.
Preimage attacks on 3-round \({{{\mathbf {\mathtt{{SHAKE128.}}}}}}\) SHAKE128 (M, \(\ell \)) is an instance of SHA-3 standard defined from Keccak \([r=1344,c=256]\), with unlimited output length \(\ell \). We focus on the preimage attack on SHAKE128 (M, 128), denoted by SHAKE128 hereinafter for simplicity.
Similar to that in Sect. 4.2, we set A[i, j] with \(i=0,2\) and \(j=0,1,2,3\) being variables, and impose some conditions on the input bits such that all the output bits after two rounds are linear, as shown in Fig. 10. A[0, 4] is set to any constant such that M is a legal message. The lanes in gray and lightgray are set to all ones and all zeros. To make sure that all the output bits after two rounds are linear, we require:

All these \(6\times 64\) linear equations are linearly independent and thus have \(2^{128}\) solutions. We expect that there is one solution matching the given 128-bit hash value. Since  is linear, the bits input to \(\chi \) of the last round are all linear on the variables. For SHAKE128, the first two output bits of each 5 bits of the 64 Sboxes \(\chi \) in the first row of the last round are known. According to the properties of \(\chi \) as shown in Table 4, we can set up 1 linear equation for each Sbox, hence 64 linear equations in total between the input bits to the Sboxes of the last round and hash value. There are two methods to obtain extra 64 linear equations, as shown in Sect. 3.1, including guess-and-determine technique in Setting 1 and probabilistic linearization in Setting 2. For the former, we guess 32 bits input to \(\chi \) of the last round and obtain 64 more linear equations, which will find the correct solution in \(2^{32}\). For the latter, we exploit the probabilistic equations \(b_i=a_i\)’s each of which holds with probability 0.75. Since we have 64 probabilistic equations, the total probability of this system is \(0.75^{64}=2^{-26.6}\). We can expect a correct solution from \(2^{26.6}\) such systems which can be obtained by changing the values of A[0, 4]. Thus the complexity of this attack is \(2^{26.6}\).
is linear, the bits input to \(\chi \) of the last round are all linear on the variables. For SHAKE128, the first two output bits of each 5 bits of the 64 Sboxes \(\chi \) in the first row of the last round are known. According to the properties of \(\chi \) as shown in Table 4, we can set up 1 linear equation for each Sbox, hence 64 linear equations in total between the input bits to the Sboxes of the last round and hash value. There are two methods to obtain extra 64 linear equations, as shown in Sect. 3.1, including guess-and-determine technique in Setting 1 and probabilistic linearization in Setting 2. For the former, we guess 32 bits input to \(\chi \) of the last round and obtain 64 more linear equations, which will find the correct solution in \(2^{32}\). For the latter, we exploit the probabilistic equations \(b_i=a_i\)’s each of which holds with probability 0.75. Since we have 64 probabilistic equations, the total probability of this system is \(0.75^{64}=2^{-26.6}\). We can expect a correct solution from \(2^{26.6}\) such systems which can be obtained by changing the values of A[0, 4]. Thus the complexity of this attack is \(2^{26.6}\).
Preimage attacks on 3-round Keccak \({\mathbf {[r = 1440, c = 160, \ell = 80].}}\) Similar techniques as presented previously allow us to find solutions for the 3-round preimage challenge with width 1600 in the Keccak Challenge [4]. As shown in Fig. 11, we set the lanes with orange slashes of the first state to be variables. The 31st bit of A[2, 4] is set to 1 for ensuring that the state input to the first round complies with the padding. Finally, we get 161 degrees of freedom such that the bits input to \(\chi \) of the last round are all linear. The sketch of the processing is shown in Fig. 11. According to the properties of \(\chi \) as presented in Sect. 3.1, we can set up 16 linear equations between the bits input to the last \(\chi \) and hash value. We can obtain extra \(2\times 64\) linear equations by guessing 64 bits input to the last \(\chi \). Now, we build a linear system of \(16+2\times 64=144\) equations on 161 variables. Therefore, we immediately get correct solutions for any given hash value by solving this system. A solution for the 3-round preimage challenge with width 1600 is listed as below, where the message has length 1438 and each 64-bit word is expressed in hexadecimal.

Preimage attacks on 3-round Keccak \({\mathbf {[r = 640, c = 160, \ell = 80].}}\) Similar techniques also allow us to find solutions for the 3-round preimage challenge with width 800. The sketch of the attack is shown in Fig. 12. To keep two rounds being linear, the six lanes with orange slashes of input state are expressed by 64 variables for any fixed values of auxiliary variables, and the two lanes with red grid, A[3, 0] and A[4, 3], are represented by 32 auxiliary variables. We set up 64 linear equations on 64 variables for a given 80-bit hash value by guessing 8 bits of the variables, and expect a correct preimage for \(2^{16}\) tries. The time complexity of this attack is \(2^{24}\). As a matter of fact, the time complexity can be further cut down to \(2^7\) by applying a similar attack as described in Sect. 6.4. A solution for the 3-round preimage challenge with width 800 is listed as below, where the message has length 638.

Preimage Attacks on 3-Round Keccak -
224 and Keccak -
256 . Since the rates r of Keccak-224 and Keccak-256 are much smaller than that of SHAKE128, there are less choices of constant part when keeping two rounds being linear with as many degrees of freedom as possible. For Keccak-256, we use 384 variables A[i, j], \(i=0,2,j=0,1,2\), out of which there will be 64 independent variables after forcing the sum of variables in column 0, 2 of the input to \(\theta \) in the first round, and in column 0, 1, 2 of the input to the \(\theta \) in the second round to be constants as depicted in Fig. 13, i.e., the size of this linear structure is \(2^{64}\). However, it is insufficient to match a 256-bit hash value by 64-bit variables. To get enough choices for the state input to the first round, we set the constant part by using 128 auxiliary variables A[3, 0] and A[4, 2] such that the linear structure remains linear after two rounds for any fixed values of auxiliary variables. As depicted in Fig. 13, we required that the gray and lightgray lanes of the state after step \(\theta \) of the first round are respectively ones and zeros. To achieve this, we first fix the values of A[0, 3] and A[3, 0], and then set up 192 linear equations,  and \(\bigoplus _{j = 0}^4(A[i-1,j] \oplus (A[i+1,j] \lll 1))=0, i=3\), which implies that A[4, 2] is determined by A[3, 0]. To make sure that the variables do not affect the other bits after step \(\theta \) of the second round, we impose 192 more equations according to the value of A[1, 2]. Finally, the six lanes with orange slashes of input state can be expressed by 64 variables for any fixed values of auxiliary variables, and the two lanes with red grid can be represented by 64 auxiliary variables. As usual, we can set up 64 linear equations on these 64 variables for a given 256-bit hash value. Since there are \(2^{64}\) choices for variable lanes, \(2^{64}\) choices for auxiliary variable lanes, and \(2^{128}\) choices for constant lanes, we have \(2^{256}\) choices for the state input to the first round, and we expect a correct solution. The time complexity of this attack is \(2^{192}\).
and \(\bigoplus _{j = 0}^4(A[i-1,j] \oplus (A[i+1,j] \lll 1))=0, i=3\), which implies that A[4, 2] is determined by A[3, 0]. To make sure that the variables do not affect the other bits after step \(\theta \) of the second round, we impose 192 more equations according to the value of A[1, 2]. Finally, the six lanes with orange slashes of input state can be expressed by 64 variables for any fixed values of auxiliary variables, and the two lanes with red grid can be represented by 64 auxiliary variables. As usual, we can set up 64 linear equations on these 64 variables for a given 256-bit hash value. Since there are \(2^{64}\) choices for variable lanes, \(2^{64}\) choices for auxiliary variable lanes, and \(2^{128}\) choices for constant lanes, we have \(2^{256}\) choices for the state input to the first round, and we expect a correct solution. The time complexity of this attack is \(2^{192}\).
The preimage attack on Keccak-224 is similar, as shown in Fig. 14. To keep two rounds being linear, the eight lanes with orange slashes of input state are expressed by 128 variables for any fixed values of auxiliary variables, and the four lanes with red grid are represented by 64 auxiliary variables. We set up 128 linear equations on 128 variables for a given 224-bit hash value (half solutions correspond to legal messages), and expect a correct preimage for \(2^{97}\) tries. The time complexity of this attack is \(2^{97}\).
6.3 Preimage Attacks on 3-Round Keccak-384/512 and 4-round Keccak-224/256
For 3-round Keccak-512, on one hand, we have 128 variables such that the bits input to step \(\chi \) of the second round are all linear, as depicted in Fig. 8; on the other hand, we can directly inverse 320 bits through  from a given hash value, each bit of which is a sum of 11 bits of the output of the second round. Since
from a given hash value, each bit of which is a sum of 11 bits of the output of the second round. Since  just permutate the positions of the bits and \(\iota \) just add a constant to the first lane, they do not increase the nonlinear terms, and thus we neglect these steps in the last one and a half rounds.
just permutate the positions of the bits and \(\iota \) just add a constant to the first lane, they do not increase the nonlinear terms, and thus we neglect these steps in the last one and a half rounds.

The expressions of \(\theta \) and \(\chi \) are given as follows,
Since the bits input to step \(\chi \) of the second round are all linear, each output bit of the second round is quadratic and the quadratic part is a product of two linear combinations. Note that the quadratic parts of B[x][y][z] and \(B[x-1][y][z]\) share a common factor \(A[x+1][y][z]\) according to (14). We linearize C[x][y][z] by guessing 10 bits input to step \(\chi \). That is, we obtain \(11=1+10\) linear equations and match 1 bit of the hash value. As such, we can match \(\lfloor \frac{128}{11}\rfloor =11\) bits of the hash value since we have 128 variables. The time complexity of this preimage attack is \(2^{501}\).
For 3-round Keccak-384, we set the last bit of A[2, 2] to be 1 and have 255 variables such that the bits input to step \(\chi \) of the second round are all linear, as depicted in Fig. 9, and thus the time complexity of the preimage attack is \(2^{384-\lfloor \frac{255}{11}\rfloor }=2^{361}\).
For Keccak-224/256, we cannot inverse the hash value through \(\chi ^{-1}\) as Keccak-384/512, but we can set up the equations such as \(a_0=b_0\) for \(b_1=1\) according to (6). Since we have 127 and 64 variables such that the bits input to step \(\chi \) of the third round are all linear, as depicted in Figs. 14 and 13, the time complexities for 4-round Keccak-224/256 are respectively \(2^{213}\) and \(2^{251}\).
Improved Preimage Attacks on 3-Round Keccak -
384 and Keccak -
512 . In the above attacks, we assume that all the guessed linear combinations are linearly independent. It is possible to cut down the time complexity if elaborately choose linearly dependent ones, since there will be more degrees of freedom for guessing more linear combinations to match more bits of the hash value. For 3-round Keccak-384/512, we can further improve the attacks by this method. Since we can inverse 320 bits of through  from a given hash value, we can choose the bits which share a sum of one column (according to the property of \(\theta \)) or common linear parts in quadratic terms (according to the property of \(\chi \)).
from a given hash value, we can choose the bits which share a sum of one column (according to the property of \(\theta \)) or common linear parts in quadratic terms (according to the property of \(\chi \)).
By (14), \(B[x-1][y][z]\) and B[x][y][z] are linear after guessing the value of \(A[x+1][y][z]\) for \(0\le y\le 4\). It is also true that \(B[x+1][y][z-1]\) and \(B[x+2][y][z-1]\) are linear after guessing the value of \(A[x+3][y][z-1]\) for \(0\le y\le 4\). This means that after guessing the above 10 bits input to step \(\chi \), we not only linearize C[x][y][z], but also obtain an extra equation:
the quadratic part of which only appears in \(B[x+1][y+1][z]\). Thus we can set up 2 extra linear equations and match one more bit of the hash value by guessing one more bit. Totally we set up 13 linear equations and match two bits of the given hash value.
Then we consider another two equations:
Again, we can set up another 8 linear equations and match two more bits of the hash value by guessing 6 more bits.
Generally, we can match \(2\lfloor \frac{t-5}{8}\rfloor \) bits of a given hash value if we have t variables. For 3-round Keccak-384/512, we have 255 and 128 variables, and thus match 62 and 30 bits respectively. Therefore, the time complexities of this improved preimage attack are respectively \(2^{322}\) and \(2^{482}\) for 3-round Keccak-384/512.
6.4 Improved Preimage Attacks on SHAKE128
The idea presented in Sect. 6.3 also applies to SHAKE128. In this section we extend it to improve the preimage attacks on SHAKE128.
Instead of linearizing 2 rounds forward, we linearize 2 rounds by combining one round forward and one round backward as discussed in Sect. 4.1, and we have 512 variables such that these two rounds are linear. To make sure that the state input to the first round corresponds to a legal message, we set up 262 linear equations such that the last 256 bits are all zeros and the following last 6 bits are all ones. Then there remains 250 degrees of freedom such that the bits input to step \(\chi \) of the third round are all linear.
For 3-round SHAKE128, we set up 64 linear equations between these 250 variables and a given hash value as the same way done in Sect. 6.2, and then obtain extra \(2\times 64\) linear equations by guessing 64 bits input to step \(\chi \) of the third round. Each solution of this linear system corresponds to a preimage of the given hash value. Therefore, the time complexity of this attack is 1.
For 4-round SHAKE128, given a 128-bit hash value, we expect 32 zeros and 32 ones among its last 64 bits (\(b_1\)’s), and thus we can set up a linear system, which matches 22 bits (\(b_0\)’s) of the hash value, by guessing 220 bits input to step \(\chi \) of the third round. This attack gives a correct preimage in \(2^{106}\).
6.5 Preimage Attacks on 4-Round Keccak \([r = 1440, C = 160, \ell = 80]\)
A similar attack as proposed in Sect. 6.4 also applies to Keccak \([r = 1440, c = 160, \ell = 80]\). In stead, we use two rounds forward and one round backward for linearization. As shown in Sect. 4.2, we have 194 degrees of freedom for such 3-round linear structure. To make sure that the state input to the first round corresponds to a legal message, we set up 161 linear equations such that the last 161 bits are fixed. Then there remains 33 degrees of freedom such that the bits input to step \(\chi \) of the fourth round are all linear. Given an 80-bit hash value of 4-round Keccak \([r = 1440, c = 160, \ell = 80]\), we can set up 16 linear equations by (6), and set up 17 probabilistic equations using \(b_i=a_i\). This attack gives a correct two-block preimage in \(2^{47+17\times 0.42}\approx 2^{54}\). We estimate that the computations of the whole attack need approximately \(2^{20}\) CPU core hours. We run this attack in less than \(2^{10}\) CPU core hours, and find a 78-bit matched preimage of length 2874 for the 4-round Keccak preimage challenge with width 1600.

7 Conclusions
In conclusion, we have described the linear structures of Keccak-f and exploited them to analyze the security of Keccak, including zero-sum distinguishers on Keccak-f permutation and preimage attacks on Keccak. Our distinguishers work on Keccak-f reduced to up to 15 rounds, and are practical for up to 11 rounds. These results improve the previously best known distinguishers by two more rounds with the same complexities. Our preimage attacks work on all variants of Keccak reduced to up to 4 rounds except for 4-round Keccak-384/512, much faster than the exhaustive search. Specially, in terms of practical preimage attacks, we could find the preimage by solving a small linear system just once for 2-round Keccak-224/256 and 3-round SHAKE128. With these techniques, we have found preimages for 3-round Keccak Challenge with widths 1600 and 800, and a 78-bit matched preimage for 4-round Keccak Challenge with width 1600. It will be interesting to see applications of linear structures to other Keccak-like ciphers or functions.
References
Aoki, K., Guo, J., Matusiewicz, K., Sasaki, Y., Wang, L.: Preimages for step-reduced SHA-2. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 578–597. Springer, Heidelberg (2009). doi:10.1007/978-3-642-10366-7_34
Aumasson, J.P., Meier, W.: Zero-sum distinguishers for reduced Keccak-f and for the core functions of Luffa and Hamsi (2009). https://131002.net/data/papers/AM09.pdf
Bernstein, D.J.: Second Preimages for 6 (7?(8??)) Rounds of Keccak. NIST mailing list (2010)
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: Keccak crunchy crypto collision and pre-image contest. http://keccak.noekeon.org/crunchy_contest.html
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: Cryptographic sponge functions, January 2011. http://sponge.noekeon.org/CSF-0.1.pdf
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: The Keccak reference, Version 3.0, January 2011. http://keccak.noekeon.org
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G., Van Keer, R.: CAESAR submission: KETJE v1, March 2014. http://ketje.noekeon.org
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G., Van Keer, R.: CAESAR submission: Keyak v2, December 2015. http://keyak.noekeon.org/
Boura, C., Canteaut, A., Cannière, C.: Higher-order differential properties of Keccak and Luffa. In: Joux, A. (ed.) FSE 2011. LNCS, vol. 6733, pp. 252–269. Springer, Heidelberg (2011). doi:10.1007/978-3-642-21702-9_15
Canteaut, A. (ed.): FSE 2012. LNCS, vol. 7549. Springer, Heidelberg (2012)
Chang, D., Kumar, A., Morawiecki, P., Sanadhya, S.K.: 1st and 2nd preimage attacks on 7, 8 and 9 rounds of Keccak-224,256,384,512. In: SHA-3 Workshop, August 2014
Dinur, I., Dunkelman, O., Shamir, A.: New attacks on Keccak-224 and Keccak-256. In: Canteaut, A. (ed.) FSE 2012. LNCS, vol. 7549, pp. 442–461. Springer, Heidelberg (2012). doi:10.1007/978-3-642-34047-5_25
Dinur, I., Dunkelman, O., Shamir, A.: Collision attacks on up to 5 rounds of SHA-3 using generalized internal differentials. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 219–240. Springer, Heidelberg (2014). doi:10.1007/978-3-662-43933-3_12
Dinur, I., Dunkelman, O., Shamir, A.: Improved practical attacks on round-reduced Keccak. J. Cryptol. 27(2), 183–209 (2014)
Dinur, I., Morawiecki, P., Pieprzyk, J., Srebrny, M., Straus, M.: Cube attacks and cube-attack-like cryptanalysis on the round-reduced Keccak sponge function. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 733–761. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46800-5_28
Duan, M., Lai, X.: Improved zero-sum distinguisher for full round Keccak-f permutation. Cryptology ePrint Archive, Report 2011/023 (2011). http://eprint.iacr.org/
Duc, Alexandre, Guo, Jian, Peyrin, Thomas, Wei, Lei: Unaligned rebound attack: application to Keccak. In: [10] 402–421
Guo, J., Ling, S., Rechberger, C., Wang, H.: Advanced meet-in-the-middle preimage attacks: first results on full tiger, and improved results on MD4 and SHA-2. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 56–75. Springer, Heidelberg (2010). doi:10.1007/978-3-642-17373-8_4
Jean, J., Nikolić, I.: Internal differential boomerangs: practical analysis of the round-reduced Keccak- \(f\) permutation. In: Leander, G. (ed.) FSE 2015. LNCS, vol. 9054, pp. 537–556. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48116-5_26
Morawiecki, P., Pieprzyk, J., Srebrny, M.: Rotational Cryptanalysis of Round-Reduced Keccak. In: [22] 241–262
Morawiecki, P., Srebrny, M.: A SAT-based preimage analysis of reduced Keccak hash functions. Inf. Process. Lett. 113(10–11), 392–397 (2013)
Morawiecki, P., Pieprzyk, J., Srebrny, M.: Rotational cryptanalysis of round-reduced Keccak. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 241–262. Springer, Heidelberg (2014). doi:10.1007/978-3-662-43933-3_13
Naya-Plasencia, M., Röck, A., Meier, W.: Practical analysis of reduced-round Keccak. In: Bernstein, D.J., Chatterjee, S. (eds.) INDOCRYPT 2011. LNCS, vol. 7107, pp. 236–254. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25578-6_18
NIST: SHA-3 COMPETITION (2007–2012). http://csrc.nist.gov/groups/ST/hash/sha-3/index.html
The U.S. National Institute of Standards and Technology: SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions . Federal Information Processing Standard, FIPS 202, 5th August 2015
Acknowledgement
We are grateful to Florian Mendel, Lei Wang, and anonymous reviewers of ASIACRYPT 2016 for their fruitful discussions and helpful comments. The second author was supported by the National Natural Science Foundation of China (Grant Nos. 61672516, 61303258, 61379139 and 11526215) and the Strategic Priority Research Program of the Chinese Academy of Sciences under Grant XDA06010701.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Guo, J., Liu, M., Song, L. (2016). Linear Structures: Applications to Cryptanalysis of Round-Reduced Keccak . In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10031. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53887-6_9
Download citation
DOI: https://doi.org/10.1007/978-3-662-53887-6_9
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53886-9
Online ISBN: 978-3-662-53887-6
eBook Packages: Computer ScienceComputer Science (R0)












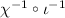 . Note these bits form the full output of the 64 Sboxes in the first row, so the corresponding input bits can be fully determined.
. Note these bits form the full output of the 64 Sboxes in the first row, so the corresponding input bits can be fully determined.





