Abstract
KDM\([\mathcal {F}]\)-CCA secure public-key encryption (PKE) protects the security of message f(sk), with \(f\in \mathcal {F}\), that is computed directly from the secret key, even if the adversary has access to a decryption oracle. An efficient KDM\([\mathcal {F}_{\text {aff}}]\)-CCA secure PKE scheme for affine functions was proposed by Lu, Li and Jia (LLJ, EuroCrypt2015). We point out that their security proof cannot go through based on the DDH assumption.
In this paper, we introduce a new concept Authenticated Encryption with Auxiliary-Input \(\mathsf {AIAE}\) and define for it new security notions dealing with related-key attacks, namely IND-RKA security and weak INT-RKA security. We also construct such an \(\mathsf {AIAE}\) w.r.t. a set of restricted affine functions from the DDH assumption. With our \(\mathsf {AIAE}\),
-
we construct the first efficient KDM\([\mathcal {F}_{\text {aff}}]\)-CCA secure PKE w.r.t. affine functions with compact ciphertexts, which consist only of a constant number of group elements;
-
we construct the first efficient KDM\([\mathcal {F}_{\text {poly}}^d]\)-CCA secure PKE w.r.t. polynomial functions of bounded degree d with almost compact ciphertexts, and the number of group elements in a ciphertext is polynomial in d, independent of the security parameter.
Our PKEs are both based on the DDH & DCR assumptions, free of NIZK and free of pairing.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Public-key encryption
- Key-dependent messages
- Chosen-ciphertext security
- Authenticated encryption
- Related-key attack
1 Introduction
Traditional Chosen-Ciphertext Attack (CCA) security of a public-key encryption (PKE) scheme considers the security of messages chosen by an adversary, even if the adversary obtains the public key pk, challenge ciphertexts of the messages, and has access to a decryption oracle (which provides decryption services to the adversary but refuses to decrypt the challenge ciphertexts). Note that the adversary cannot compute messages directly from secret keys, since it does not possess the secret keys. Therefore, CCA security does not cover the corner, where messages closely depend on the secret keys, say the secret keys themselves or functions of the secret keys. This issue was first identified in [GM84]. Later the security of key-dependent messages was formalized as KDM-security [BRS02]. KDM-security is an important notion, and has found wide applications, like hard disk encryption [BHHO08], cryptographic protocols [CL01], etc.
KDM-security w.r.t. a set of functions \({\mathcal {F}}\) is denoted by KDM\([\mathcal {F}]\)-security. The larger \(\mathcal {F}\) is, the stronger the security is. Roughly speaking, n-KDM\([\mathcal {F}]\)-security of PKE considers such a scenario: an adversary is given public keys \((pk_1, pk_2, \cdots , pk_n)\) of n users and an encryption oracle. Whenever the adversary queries a function \(f\in \mathcal {F}\), the encryption oracle will always reply with an encryption of a constant say 0, or always reply with an encryption of \(f(sk_1, sk_2, \cdots , sk_n)\). If the adversary cannot tell which case it is, the PKE is n-KDM\([\mathcal {F}]\)-CPA secure. If the adversary has also access to a decryption oracle in the scenario, then KDM\([\mathcal {F}]\)-CPA security is improved to KDM\([\mathcal {F}]\)-CCA security. Obviously, KDM-CCA security notion is stronger than KDM-CPA.
KDM[\(\mathcal {F}\)]-CPA Security. The BHHO scheme [BHHO08] was the first PKE achieving KDM\([\mathcal {F}_{\text {aff}}]\)-CPA security based on the Decisional Diffie-Hellman (DDH) assumption, where \(\mathcal {F}_{\text {aff}}\) denotes the set of affine functions. It was later generalized by Brakerski and Goldwasser [BG10] to KDM\([\mathcal {F}_{\text {aff}}]\)-CPA secure PKE schemes based on the Subgroup Indistinguishability Assumption (including the QR and the DCR assumptions). These schemes have incompact ciphertexts containing \(O(\ell )\) group elements, where \(\ell \) denotes the security parameter.
A variant of Regev’s scheme [Reg05] was shown to be KDM\([\mathcal {F}_{\text {aff}}]\)-CPA secure and has compacter ciphertexts by Applebaum et al. [ACPS09].
Barak et al. [BHHI10] proposed KDM-CPA secure PKE w.r.t. a very large function set, i.e., the function set of boolean circuits of bounded size \(p = p(\ell )\). However, their scheme is inflexible and highly impractical, since its encryption algorithm depends on the bound p and the number of users, and the ciphertext contains a garbled circuit of size at least \(p = p(\ell )\).
Brakerski et al. [BGK11] amplified the BHHO scheme to KDM\([\mathcal {F}_{\text {poly}}^d]\)-CPA security w.r.t. the set of polynomial functions of bounded degree d. However, their ciphertext contains \(O(\ell ^{d+1})\) group elements.
It is Malkin et al. [MTY11] who designed the first efficient PKE scheme achieving KDM\([\mathcal {F}_{\text {poly}}^d]\)-CPA security. Their ciphertext contains only O(d) group elements, thus d can be polynomial in \(\ell \) in their case. The function set \(\mathcal {F}_{\text {poly}}^d\) is characterized by a polynomial-size Modular Arithmetic Circuit in [MTY11].
KDM \([\mathcal {F}]\) -CCA Security. KDM\([\mathcal {F}]\)-CCA security of PKE is far more difficult to design than KDM\([\mathcal {F}]\)-CPA security. Camenisch et al. [CCS09] gave the first solution, following Naor-Yung’s paradigm, which needs a KDM-CPA secure PKE, a CCA-secure PKE and a non-interactive zero-knowledge (NIZK) proving that the two PKEs encrypt the same message.
NIZK is not practical in general, except Groth-Sahai proofs [GS08]. When following [CCS09]’s approach, the only possible way to get an efficient KDM-CCA secure PKE, is using Groth-Sahai proofs together with an efficient KDM-CPA secure PKE. However, many existing efficient KDM-CPA secure schemes, such as [ACPS09, MTY11], are not based on pairing-friendly groups, thus not compatible with Groth-Sahai’s efficient NIZK.
Another work by Galindo et al. [GHV12] is based on the Matrix DDH assumption over pairing-friendly groups. Their scheme has compact ciphertexts, but only obtains a bounded form of KDM-CCA security, i.e., the number of encryption queries is limited to be linear in the size of the secret key.
To get an efficient KDM-CCA secure PKE, Hofheinz [Hof13] proposed another approach, which uses a new tool called “lossy algebraic filter”. His work results in the first PKE enjoying both KDM-CCA security and compact ciphertexts (consisting only of a constant number of group elements). However, the function set \(\mathcal {F}_{\text {circ}}\) only consists of selection functions \(f(sk_1, \cdots , sk_n)=sk_i\) and constant functions.
It is quite challenging to enlarge \(\mathcal {F}\) for KDM\([\mathcal {F}]\)-CCA security while still keeping PKE efficient. One effort was recently made by Lu, Li and Jia [LLJ15], who proposed the first efficient KDM\([\mathcal {F}_{\text {aff}}]\)-CCA secure PKE with compact ciphertexts. We call their construction the LLJ scheme. There is an essential building block called “Authenticated Encryption” (\(\overline{\textsf {AE}}\)) in their scheme. The KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security heavily relies on a so-called INT-\(\mathcal {F}_{\text {aff}}\)-RKA security of \(\overline{\textsf {AE}}\). INT-\(\mathcal {F}_{\text {aff}}\)-RKA security of \(\overline{\textsf {AE}}\) means that a PPT adversary cannot forge a fresh forgery \((f^*, \overline{\textsf {ae}}.\textsf {ct}^*)\) such that \(\overline{\textsf {AE}}\textsf {.Dec}_{f^*(\textsf {k})}(\overline{\textsf {ae}}.\textsf {ct}^*)\ne \bot \), even if the adversary observes multiple outputs of \(\overline{\textsf {AE}}\textsf {.Enc}_{f_j(\textsf {k})}(m_j)\) with his choice of \((f_j, m_j)\). Unfortunately, we found that the INT-\(\mathcal {F}_{\text {aff}}\)-RKA security proof of the specific \(\overline{\textsf {AE}}\) does not go through to the DDH assumption, which in turn affects the KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security proof of the LLJ scheme. Our essential observation is that the DDH adversary is not able to employ the fresh forgery from the adversary of \(\overline{\textsf {AE}}\) to solve the DDH problem, since the DDH adversary does not have any trapdoor to convert the computing power (forgery) to a decision bit.
As for KDM\([\mathcal {F}_{\text {poly}}^d]\)-CCA security, [CCS09]’s paradigm is the unique path to it up to now. Unfortunately, the only efficient KDM\([\mathcal {F}_{\text {poly}}^d]\)-CPA secure scheme [MTY11] does not compose well with Groth-Sahai proofs, so it has to resort to the general NIZK. Other KDM\([\mathcal {F}_{\text {poly}}^d]\)-CPA secure schemes either is highly impractical [BHHI10] or has ciphertext containing \(O(\ell ^{d+1})\) group elements [BGK11], which grows exponentially with the degree d.
Our Contribution. We work on the design of efficient PKE with KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security and KDM\([\mathcal {F}_{\text {poly}}^d]\)-CCA security.
-
We identify the proof flaw in [LLJ15], where an efficient KDM\([\mathcal {F}_{\text {aff}}]\)-CCA secure PKE was claimed. We show that for “Authenticated Encryption” (\(\overline{\textsf {AE}}\)) used in the LLJ scheme, the INT-\(\mathcal {F}_{\text {aff}}\)-RKA security reduction to the DDH assumption does not work. This proof flaw directly affects the KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security proof of the LLJ scheme.
-
We provide the first efficient KDM\([\mathcal {F}_{\text {aff}}]\)-CCA secure PKE w.r.t. affine functions with compact ciphertexts. Our scheme has ciphertexts consisting only of a constant number of group elements and is free of NIZK.
-
We provide the first efficient KDM\([\mathcal {F}_{\text {poly}}^d]\)-CCA secure PKE w.r.t. polynomial functions of bounded degree d with almost compact ciphertexts. Our scheme is free of NIZK. The number of group elements in a ciphertext is polynomial in d, independent of the security parameter \(\ell \).
We summarize known PKEs either achieving KDM-CCA security or against function set \(\mathcal {F}_{\text {poly}}^d\) in Table 1.
Our Approach. The challenge for KDM\([\mathcal {F}]\)-CCA security of PKE lies in the fact that the adversary \(\mathcal {A}\) has multiple access to the encryptions of f(sk) and decryption oracle \(\textsf {Dec}(sk, \cdot )\), with \(f\in \mathcal {F}\) and sk the secret key. Let us consider only one secret key for simplicity. The information of sk might be leaked completely via encryptions of f(sk).
To solve this problem, we follow a KEM+DEM style and construct our PKE with three building blocks: KEM, \(\mathcal {E}\) and \(\mathsf {AIAE}\), as shown in Fig. 1.
-
We propose a new concept “Authenticated Encryption with Auxiliary-Input” (\(\mathsf {AIAE}\)). We define for it new security notions dealing with related-key attacks, namely weak INT- \(\mathcal {F}'\) -RKA security and IND-\(\mathcal {F}'\)-RKA security.
-
We design the other building blocks KEM and \(\mathcal {E}\). \(\textsf {KEM}.\textsf {Enc}\) encapsulates a key \(\textsf {k}\) for \(\mathsf {AIAE}\), and the encapsulation \(\textsf {kem.ct}\) serves as an auxiliary input \(\textsf {aux}\) for \(\mathsf {AIAE}.\textsf {Enc}\). \(\mathcal {E}.\textsf {Enc}\) encrypts \(\textsf {m}\) to get a ciphertext \(\mathcal {E}.\textsf {ct}\), which serves as an input for \(\mathsf {AIAE}.\textsf {Enc}\).
We show how to achieve KDM[\(\mathcal {F}\)]-CCA security with our three building blocks.
-
\(\mathcal {E}.\textsf {Enc}\) can behave like an entropy filter (the concept was named in [LLJ15]) for \(\mathcal {F}\). That is, through some computationally indistinguishable change, some entropy of sk is always reserved even if multiple encryptions of \(f_{{j}}(sk)\) are given to \(\mathcal {A}\). Here \(f_j \in \mathcal {F}\) is chosen by \(\mathcal {A}\).
-
The fresh keys \(\textsf {k}_j\) used by \(\mathsf {AIAE}.\textsf {Enc}\) can be expressed as functions of a base key \(\textsf {k}^*\), i.e., \(\textsf {k}_j = f'_j(\textsf {k}^*)\), where \(f'_j \in \mathcal {F}'\) for some function set \(\mathcal {F}'\). We stress that \(\mathcal {F}'\) might be different from \(\mathcal {F}\).
-
\(\textsf {KEM.Enc}\) is able to use the remaining entropy of sk to protect the base key \(\textsf {k}^*\), via some computationally indistinguishable change.
-
The weak INT-\(\mathcal {F}'\)-RKA security of \(\mathsf {AIAE}\) guarantees: given multiple AIAE ciphertext-auxiliary input pair \((\mathsf {aiae}.\textsf {ct}_j, \textsf {aux}_j)\) encrypted by \(f'_j(\textsf {k}^*)\), it is infeasible for a PPT algorithm to forge a new \((f', \mathsf {aiae}.\textsf {ct}, \textsf {aux})\) satisfying (1) \(\mathsf {AIAE}.\textsf {Dec}_{f'(\textsf {k}^*)}(\mathsf {aiae}.\textsf {ct}, \textsf {aux})\ne \bot \); (2) if \(\textsf {aux}=\textsf {aux}_j\) for some j then \(f'=f'_j\).
-
Decryption oracle can reject all invalid ciphertexts that are not properly generated by the encryption algorithm, via some computationally indistinguishable change. If the invalid ciphertext makes \(\textsf {KEM.Dec}\) decapsulate a key \(f'(\textsf {k}^*)\), \(\mathsf {AIAE}.\textsf {Dec}\) will output \(\bot \), due to its weak INT-\(\mathcal {F}'\)-RKA security. Otherwise, the invalid ciphertext will be rejected by \(\mathcal {E}.\textsf {Dec}\) or \(\textsf {KEM.Dec}\), due to the remaining entropy of sk. As a result, no extra information about sk is leaked.
-
The IND-\(\mathcal {F}'\)-RKA security of \(\mathsf {AIAE}\) ensures: given multiple AIAE ciphertext-auxiliary input pair \((\mathsf {aiae}.\textsf {ct}_j, \textsf {aux}_j)\) with key \(f'_j(\textsf {k}^*)\) encrypting either \(m_0\) or \(m_1\), it is infeasible for a PPT algorithm to distinguish which case it is, even if \(f'_j\in \mathcal {F}'\) is submitted by the algorithm.
-
By the IND-\(\mathcal {F}'\)-RKA security of \(\mathsf {AIAE}\), the encryption of \(\mathcal {E}.\textsf {ct}\) can be replaced with an encryption of all zeros. Then the KDM\([\mathcal {F}]\)-CCA security follows.
With this approach, we can construct PKEs possessing KDM[\(\mathcal {F}_{\text {aff}}\)]-CCA and KDM[\(\mathcal {F}_{\text {poly}}^d\)]-CCA security respectively, by designing specific building blocks.
Our approach of PKE construction. Here KEM and \(\mathcal {E}\) share the same public/secret key pair. \(\mathsf {AIAE}.\textsf {Enc}\) uses \(\textsf {k}\) output by KEM to encrypt \(\mathcal {E}.\textsf {ct}\) with auxiliary input \(\textsf {aux}: = \textsf {kem.ct}\), and outputs ciphertext \(\mathsf {aiae}.\textsf {ct}\).
Comparison with LLJ. We inherit the idea of utilizing RKA security of AE to achieve KDM security from LLJ. However, our approach deviates from LLJ in three aspects.
-
1.
The structure of our scheme is different from LLJ. It is also possible to explain the LLJ scheme with three components KEM, \(\mathcal {E}\) and \(\overline{\textsf {AE}}\). However, their components were composed in a different way. In the LLJ scheme, the output \(\textsf {kem.ct}\) of KEM serves as an additional input for \(\mathcal {E}.\textsf {Enc}\). With their structure, \(\mathcal {E}\) is expected to authenticate \(\textsf {kem.ct}\). In our approach, \(\textsf {kem.ct}\) is the auxiliary input of \(\mathsf {AIAE}\), thus can be authenticated by \(\mathsf {AIAE}\).
-
2.
The syntax and security requirements of our \(\mathsf {AIAE}\) are different from LLJ’s \(\overline{\textsf {AE}}\). Their \(\overline{\textsf {AE}}\) does not support auxiliary input, and the security proof of their \(\overline{\textsf {AE}}\) instantiation has some problem, as shown in Sect. 3.
-
3.
Our KEM and \(\mathcal {E}\) are newly designed building blocks which compose well with our \(\mathsf {AIAE}\). We give two designs of \(\mathcal {E}\) to support KDM[\(\mathcal {F}_{\text {aff}}\)]-CCA and KDM[\(\mathcal {F}_{\text {poly}}^d\)]-CCA security respectively.
2 Preliminaries
Let \(\ell \in \mathbb {N}\) denote the security parameter. For \(i, j \in \mathbb {N}\) with \(i < j\), define \([i, j]:=\{ i, i+1, \cdots ,j \}\) and \([j]:=\{1, 2, \cdots ,j\}\). Denote by  the operation of picking an element s from set \(\mathcal {S}\) uniformly at random. For an algorithm \(\mathcal {A}\), denote by
the operation of picking an element s from set \(\mathcal {S}\) uniformly at random. For an algorithm \(\mathcal {A}\), denote by  , or simply
, or simply  , the operation of running \(\mathcal {A}\) with input x and randomness r and assigning output to y. Let \(\varepsilon \) denote the empty string. For a primitive XX and a security notion YY, we typically denote the advantage of a PPT adversary \(\mathcal {A}\) by \(\mathsf {Adv}_{\text {XX},\mathcal {A}}^{\text {YY}}(\ell )\) and define \(\mathsf {Adv}_{\text {XX}}^{\text {YY}}(\ell ):=\max _{\text {PPT} \mathcal {A}} \mathsf {Adv}_{\text {XX}, \mathcal {A}}^{\text {YY}}(\ell )\). Let \(2^{-\varOmega (\ell )}\) denote the value upper bounded by \(2^{- c \cdot \ell }\) for some constant \(c > 0\).
, the operation of running \(\mathcal {A}\) with input x and randomness r and assigning output to y. Let \(\varepsilon \) denote the empty string. For a primitive XX and a security notion YY, we typically denote the advantage of a PPT adversary \(\mathcal {A}\) by \(\mathsf {Adv}_{\text {XX},\mathcal {A}}^{\text {YY}}(\ell )\) and define \(\mathsf {Adv}_{\text {XX}}^{\text {YY}}(\ell ):=\max _{\text {PPT} \mathcal {A}} \mathsf {Adv}_{\text {XX}, \mathcal {A}}^{\text {YY}}(\ell )\). Let \(2^{-\varOmega (\ell )}\) denote the value upper bounded by \(2^{- c \cdot \ell }\) for some constant \(c > 0\).
Games. Our security proof will be game-based security reductions. A game \(\mathsf {G}\) starts with an Initialize procedure and ends with a Finalize procedure. There are also some optional procedures \(\textsc {Proc}_1, \cdots , \textsc {Proc}_n\) performing as oracles. All procedures are described using pseudo-code, where initially all variables are empty strings \(\varepsilon \) and all sets are empty. An adversary \(\mathcal {A}\) is executed in game \(\mathsf {G}\) if it first calls \(\textsc {Initialize}\), obtaining its output. Then the adversary may make arbitrary oracle-queries to procedures \(\textsc {Proc}_i\) according to their specification, and obtain their outputs. Finally it makes one single call to \(\textsc {Finalize}\). By \(\mathsf {G}^{\mathcal {A}}\Rightarrow b\) we means that \(\mathsf {G}\) outputs b after interacting with \(\mathcal {A}\), and b is in fact the output of \(\textsc {Finalize}\). By \(a \mathop {=}\limits ^{\mathsf {G}} b\) we mean that a equals b or is computed as b in game \(\mathsf {G}\).
2.1 Public-Key Encryption and KDM-CCA Security
A public-key encryption (PKE) scheme is made up of four PPT algorithms \(\textsf {PKE}=(\textsf {Setup}, \textsf {Gen}, \textsf {Enc},\) \(\textsf {Dec})\): \(\textsf {Setup}( 1^{\ell })\) generates a public parameter \(\textsf {prm}\), which implicitly defines a secret key space \(\mathcal {SK}\) and a message space \(\mathcal {M}\); \(\textsf {Gen}( \textsf {prm})\) takes as input the public parameter \(\textsf {prm}\) and generates a public/secret key pair \((\textsf {pk}, \textsf {sk})\); \(\textsf {Enc}(\textsf {pk}, m)\) takes as input the public key \(\textsf {pk}\) and a message m, and outputs a ciphertext \(\textsf {pke}\textsf {.ct}\); \(\textsf {Dec}(\textsf {sk}, \textsf {pke}\textsf {.ct})\) takes as input the secret key \(\textsf {sk}\) and a ciphertext \(\textsf {pke}\textsf {.ct}\) and outputs either a message m or a failure symbol \(\perp \). The correctness of \(\mathsf {PKE}\) requires that, for all  , all
, all  , all \(m \in \mathcal {M}\) and all
, all \(m \in \mathcal {M}\) and all  , it holds that \(\textsf {Dec}(\textsf {sk}, \textsf {pke}\textsf {.ct}) = m\).
, it holds that \(\textsf {Dec}(\textsf {sk}, \textsf {pke}\textsf {.ct}) = m\).
Let \(n \in \mathbb {N}\) and \(\mathcal {F}\) be a family of functions from \(\mathcal {SK}^n\) to \(\mathcal {M}\). We define the n-KDM\([\mathcal {F}]\)-CCA security via the security game in Fig. 2.
Definition 1
(KDM[\(\mathcal {F}\)]-CCA Security for PKE). Scheme \(\mathsf {PKE}\) is n-KDM\([\mathcal {F}]\)-CCA secure if for any PPT adversary \(\mathcal {A}\), \(\mathsf {Adv}_{\mathsf {PKE}, \mathcal {A}}^{kdm\text {-}cca}(\ell ) := | \Pr [ n\text {-}\mathsf {KDM}[\mathcal {F}]\text {-}\mathsf {CCA}^{\mathcal {A}} \Rightarrow 1 ] - 1 / 2 |\) is negligible in \(\ell \), where game n-\(\mathsf {KDM}[\mathcal {F}]\)-\(\mathsf {CCA}\) is specified in Fig. 2.
2.2 Key Encapsulation Mechanism
A key encapsulation mechanism (KEM) consists of three PPT algorithms \(\textsf {KEM}=(\textsf {KEM.Gen}, \textsf {KEM.Enc}, \textsf {KEM.Dec})\): KEM.Gen
\((1^{\ell })\) outputs a public/secret key pair \((\textsf {pk}, \textsf {sk})\); KEM.Enc
\((\textsf {pk})\) uses the public key \(\textsf {pk}\) to compute a key \(\textsf {k}\) and a ciphertext (or encapsulation) \(\textsf {kem.ct}\); KEM.Dec
\((\textsf {sk}, \textsf {kem.ct})\) takes as input the secret key \(\textsf {sk}\) and a ciphertext \(\textsf {kem.ct}\), and outputs either a key \(\textsf {k}\) or a failure symbol \(\perp \). The correctness of KEM requires that, for all  and all
and all  , it holds that KEM.Dec
\((\textsf {sk}, \textsf {kem.ct})=\textsf {k}\).
, it holds that KEM.Dec
\((\textsf {sk}, \textsf {kem.ct})=\textsf {k}\).
2.3 Authenticated Encryption: One-Time Security and Related-Key Attack Security
Definition 2
(Authenticated Encryption). An authenticated encryption (AE) scheme \(\mathsf {AE} = (\mathsf {AE.Setup}, \mathsf {AE.Enc}, \mathsf {AE.Dec})\) consists of three PPT algorithms:
-
\(\mathsf {AE.Setup}(1^{\ell })\) outputs a system parameter \(\mathsf {prm}_{\mathsf {AE}}\), which is an implicit input to \(\mathsf {AE.Enc}\) and \(\mathsf {AE.Dec}\). The parameter \(\mathsf {prm}_{\mathsf {AE}}\) implicitly defines a message space \(\mathcal {M}\) and a key space \({\mathcal {K}_{\mathsf {AE}}}\).
-
\(\mathsf {AE.Enc}(\mathsf {k}, m)\) takes as input a key \(\mathsf {k}\) \(\in {\mathcal {K}_{\mathsf {AE}}}\) and a message \(m \in \mathcal {M}\), and outputs a ciphertext \(\mathsf {ae}\mathsf {.ct}\).
-
\(\mathsf {AE.Dec}(\mathsf {k}, \mathsf {ae}\mathsf {.ct})\) takes as input a key \(\mathsf {k}\) \(\in {\mathcal {K}_{\mathsf {AE}}}\) and a ciphertext \(\mathsf {ae}\mathsf {.ct}\), and outputs a message \(m \in \mathcal {M}\) or a rejection symbol \(\bot \).
Correctness of \(\mathsf {AE}\) requires that, for all  , all \(\mathsf {k} \in {\mathcal {K}_{\mathsf {AE}}}\), all \(m \in \mathcal {M}\) and all
, all \(\mathsf {k} \in {\mathcal {K}_{\mathsf {AE}}}\), all \(m \in \mathcal {M}\) and all  , it holds that \(\mathsf {AE.Dec}(\mathsf {k}, \mathsf {ae}\mathsf {.ct}) = m\).
, it holds that \(\mathsf {AE.Dec}(\mathsf {k}, \mathsf {ae}\mathsf {.ct}) = m\).
The security notions for AE include One-time ciphertext-indistinguishability (IND-OT) and One-time ciphertext-integrity (INT-OT). The IND-OT and INT-OT securities of \(\textsf {AE}\) are formalized via the security games in Fig. 3.
Definition 3
(One-Time Security for AE). Scheme \(\mathsf {AE}\) is one-time secure (OT-secure) if it is IND-OT secure and INT-OT secure, i.e., for any PPT adversary \(\mathcal {A}\), both \(\mathsf {Adv}_{\mathsf {AE}, \mathcal {A}}^{ind\text {-}ot}(\ell ) := | \Pr [ \mathsf {IND}\text {-}\mathsf {OT}^{\mathcal {A}} \Rightarrow 1 ] - 1 / 2 |\) and \(\mathsf {Adv}_{\mathsf {AE}, \mathcal {A}}^{int\text {-}ot}(\ell ) := \Pr [ \mathsf {INT}\text {-}\mathsf {OT}^{\mathcal {A}} \Rightarrow 1 ]\) are negligible in \(\ell \), where games \(\mathsf {IND}\)-\(\mathsf {OT}\) and \(\mathsf {INT}\)-\(\mathsf {OT}\) are specified in Fig. 3.
Let \(\mathcal {F}\) be a family of functions from \(\mathcal {K}_{\mathsf {AE}}\) to \(\mathcal {K}_{\mathsf {AE}}\). The \(\mathcal {F}\)-Related-Key Attack for AE scheme was formalized in [LLJ15], and RKA security notions characterize the ciphertext indistinguishability (IND-\(\mathcal {F}\)-RKA) and integrity (INT-\(\mathcal {F}\)-RKA) even if the adversary has multiple access to the encryption oracle and designates a function \(f\in \mathcal {F}\) each time such that the encryption oracle uses \(f(\textsf {k})\) as the key.
Definition 4
(IND-RKA and INT-RKA Securities for AE). Scheme \(\mathsf {AE}\) is IND-\(\mathcal {F}\)-RKA secure and INT-\(\mathcal {F}\)-RKA secure, if for any PPT adversary \(\mathcal {A}\), both \(\mathsf {Adv}_{\mathsf {AE}, \mathcal {A}}^{ind\text {-}rka}(\ell ) := | \Pr [ \mathsf {IND}\text {-}\mathcal {F}\text {-}\mathsf {RKA}^{\mathcal {A}} \Rightarrow 1 ] - 1 / 2 |\) and \(\mathsf {Adv}_{\mathsf {AE}, \mathcal {A}}^{int\text {-}rka}(\ell ) := \Pr [ \mathsf {INT}\text {-}\mathcal {F}\text {-}\mathsf {RKA}^{\mathcal {A}} \Rightarrow 1 ]\) are negligible in \(\ell \), where games \(\mathsf {IND}\)-\(\mathcal {F}\)-\(\mathsf {RKA}\) and \(\mathsf {INT}\)-\(\mathcal {F}\)-\(\mathsf {RKA}\) are specified in Fig. 4.
2.4 DCR, DDH, DL and IV\(_d\) Assumptions
Let \(\textsf {GenN}(1^\ell )\) be a PPT algorithm outputting (N, p, q), where p, q are safe primes of \(\ell \) bits and \(N=pq\), such that \(\bar{N}=2N+1\) is also a prime. Let \(s\in \mathbb {N}\) and \(T = 1 + N\). Define \(\mathbb {QR}_{N^s}:= \big \{a^2 \text { mod } N^s ~\big |~ a\in \mathbb {Z}_{N^s}^* \big \}\), \(\mathbb {SCR}_{N^s}:= \big \{a^{2N^{s-1}} \text { mod } N^s ~\big |~ a\in \mathbb {Z}_{N^s}^* \big \}\), and \(\mathbb {RU}_{N^s} := \big \{T^r\text { mod } N^s ~\big |~r\in [N^{s-1}] \big \}\). Then \(\mathbb {SCR}_{N^s}\) is a cyclic group of order \(\phi (N)/4\), and \(\mathbb {QR}_{N^s} = \mathbb {SCR}_{N^s} \otimes \mathbb {RU}_{N^s}\), where \(\otimes \) denotes internal direct product. Let \(\mathbb {QR}_{\bar{N}} := \big \{a^2 \text { mod } \bar{N} ~\big |~ a\in \mathbb {Z}_{\bar{N}} \big \}\), then \(\mathbb {QR}_{\bar{N}}\) is a cyclic group of order \(N=pq\).
For \(X \in \mathbb {RU}_{N^s}\), the discrete logarithm \(\text {dlog}_{T}(X) \in [N^{s-1}]\) can be efficiently computed given only N and X [DJ01]. Note that \(\mathbb {Z}_{N^s}^*= \mathbb {Z}_2 \otimes \mathbb {Z}_2' \otimes \mathbb {SCR}_{N^s}\otimes \mathbb {RU}_{N^s}\), hence for any \(u = u(\mathbb {Z}_2) \cdot u(\mathbb {Z}'_2) \cdot u(\mathbb {SCR}_{N^s}) \cdot T^x \in \mathbb {Z}_{N^s}^*\), \(u^{\phi (N)} = T^{x \cdot \phi (N)} \in \mathbb {RU}_{N^s}\) and
The formal definitions of the Decisional Composite Residuosity (DCR) and the Discrete Logarithm (DL) assumptions are in the full version [HLL16]. The DCR assumption implies the Interactive Vector (IV\(_d\)) assumption according to [BG10]. We adopt the version in [LLJ15].
Definition 5
(IV \(_d\) Assumption). The IV\(_d\) Assumption holds w.r.t. \(\mathsf {GenN}\) and group \(\mathbb {QR}_{N^s}\) if for any PPT adversary \(\mathcal {A}\), the following advantage is negligible in \(\ell \):
where  ,
,  , \(b \leftarrow \text {\tiny \textsf {\$}}\{0,1\}\), and the oracle \(\textsc {Chal}_{{IV }_d}^b(\cdot )\) can be queried by \(\mathcal {A}\) adaptively. \(\mathcal {A}\) submits \((\delta _1, \cdots , \delta _d)\) to the oracle. \(\textsc {Chal}_{{IV }_d}^b(\delta _1, \cdots , \delta _d)\) selects random
, \(b \leftarrow \text {\tiny \textsf {\$}}\{0,1\}\), and the oracle \(\textsc {Chal}_{{IV }_d}^b(\cdot )\) can be queried by \(\mathcal {A}\) adaptively. \(\mathcal {A}\) submits \((\delta _1, \cdots , \delta _d)\) to the oracle. \(\textsc {Chal}_{{IV }_d}^b(\delta _1, \cdots , \delta _d)\) selects random  . If \(b = 0\), the oracle returns \((g_1^r, \cdots , g_d^r)\); otherwise it returns \((g_1^r T^{\delta _1}, \cdots , g_d^r T^{\delta _d})\), where \(T = 1+N\).
. If \(b = 0\), the oracle returns \((g_1^r, \cdots , g_d^r)\); otherwise it returns \((g_1^r T^{\delta _1}, \cdots , g_d^r T^{\delta _d})\), where \(T = 1+N\).
Definition 6
(DDH Assumption). The Decisional Diffie-Hellman (DDH) Assumption holds w.r.t. \(\mathsf {GenN}\) and group \(\mathbb {QR}_{\bar{N}}\) if for any PPT adversary \(\mathcal {A}\), the following advantage is negligible in \(\ell \):
where  ,
,  ,
,  .
.
2.5 Collision Resistant Hashing and Universal Hashing
Definition 7
(Collision Resistant Hashing). A family of functions \(\mathcal {H} = \{\mathsf {H}: \mathcal {X} \longrightarrow \mathcal {Y}\}\) is collision-resistant if for any PPT adversary \(\mathcal {A}\), the following advantage is negligible in \(\ell \):

Definition 8
(Universal Hashing). A family of functions \(\mathcal {H} = \{\mathsf {H}: \mathcal {X} \longrightarrow \mathcal {Y}\}\) is universal, if for all distinct \(x, x' \in \mathcal {X}\), it follows that

3 \(\overline{\textsf {AE}}\) of the LLJ Scheme and Its INT-RKA Security
The LLJ scheme [LLJ15] makes use of an important primitive “Authenticated Encryption” \(\overline{\textsf {AE}}\). Its KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security heavily relies on the IND-\(\mathcal {F}_{\text {aff}}\)-RKA security and INT-\(\mathcal {F}_{\text {aff}}\)-RKA security of their \(\overline{\textsf {AE}}\). LLJ claimed INT-\(\mathcal {F}_{\text {aff}}\)-RKA security of their \(\overline{\textsf {AE}}\), however, we point out that their security proof does not go through to the DDH assumption, which in turn affects the KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security proof of the LLJ scheme.
Let us briefly review LLJ’s \(\overline{\textsf {AE}}\) as follows. The public parameter is \(\mathsf {prm}_{\overline{\mathsf {AE}}} = (N, \bar{N}, g)\) where \(N=pq\), \(\bar{N} = 2 N+1\), and g is a generator of group \(\mathbb {QR}_{\bar{N}}\). Let \(\textsf {AE}\) be an IND-OT and INT-OT secure authenticated encryption, and \(\textsf {H}\) be a 4-wise independent hash function. The secret key space is \(\mathbb {Z}_N\).
-
\(\overline{\textsf {AE}}.\textsf {Enc}(k, m)\) computes \(u=g^r\) with
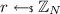 , \(\kappa = \textsf {H}(u^k, u)\) and invokes
, \(\kappa = \textsf {H}(u^k, u)\) and invokes  . It outputs the ciphertext \(\langle u, \chi \rangle \).
. It outputs the ciphertext \(\langle u, \chi \rangle \). -
\(\overline{\textsf {AE}}.\textsf {Dec}(k, \langle u, \chi \rangle )\) computes \(\kappa = \textsf {H}(u^k, u)\) and outputs \(m/\bot \leftarrow {\textsf {AE.Dec}}({\kappa }, \chi )\).
In the LLJ scheme, \(\overline{\textsf {AE}}\) should have RKA security w.r.t. \(\mathcal {F}_{\text {aff}}=\{ {f: k \longmapsto } a k+b ~|~ a\ne 0\}\). Let us check their security proof. See Table 2. The proof idea is to use the DDH assumption to make sure that each \(\kappa _\lambda \), \(\lambda \in [Q_e]\), is random to the adversary. Then the INT-OT of AE guarantees that the adversary cannot make a fresh forgery \(\big (f^*=(a^*,b^*), \langle u^*, \chi ^* \rangle \big )\) such that \(\overline{\textsf {AE}}.\textsf {Dec}({a^* k+b^*}, \langle u^*, \chi ^* \rangle )\ne \bot \).
In [LLJ15], the indistinguishability of Game \(1. (i-1)\) and Game 1.i is reduced to the DDH assumption. A PPT algorithm \(\mathcal {B}\) is constructed to solve the DDH problem by employing an INT-\(\mathcal {F}_{\text {aff}}\)-RKA adversary \(\mathcal {A}\). Given the challenge \((g, g^{r_i}, g^k, Z)\), \(\mathcal {B}\) wants to tell whether \(Z=g^{k r_i}\) or \(Z=g^{z_i}\) for a random \(z_i\). \(\mathcal {B}\) simulates the INT-\(\mathcal {F}_{\text {aff}}\)-RKA game for \(\mathcal {A}\) by computing \(\kappa _i = \textsf {H}(Z^{a_i}g^{r_i b_i}, g^{r_i})\). If \(Z=g^{kr_i}\), \(\mathcal {B}\) simulates Game \(1.(i-1)\) for \(\mathcal {A}\); if \(Z=g^{z_i}\), \(\mathcal {B}\) simulates Game 1.i.
The problem is now that \(\mathcal {B}\) does not know the value of secret key k (it knows \(g^k\)). When \(\mathcal {A}\) submits a fresh forgery \(\big (f^*=(a^*,b^*), \langle u^*, \chi ^* \rangle \big )\), \(\mathcal {B}\) is not able to see whether \(\overline{\textsf {AE}}.\textsf {Dec}({a^* k+b^*}, \langle u^*, \chi ^* \rangle )\ne \bot \) or not without the knowledge of k. More precisely, \(\mathcal {B}\) can not compute \(\kappa ^* = \textsf {H}(u^{*a^*k+b^*}, u^*) = \textsf {H}\big ((u^{*k})^{a^*} \cdot u^{*b^*}, u^* \big )\) from \(g^k\) and \(u^*\), unless it is able to compute the CDH value \(u^{*k}\) from \(g^k\) and \(u^*\). Without \(\kappa ^*\), it is hard for \(\mathcal {B}\) to decide whether \(\textsf {AE}\textsf {.Dec}(\kappa ^*, \chi ^*) \ne \bot \) or not. In other words, \(\mathcal {B}\) cannot find an efficient (PPT) way to transform the computing power (forgery) of \(\mathcal {A}\) into its own decisional power (decision bit) to determine \((g, g^{r_{{i}}}, g^k, Z)\) to be a DDH tuple or a random tuple. The failure of the INT-\(\mathcal {F}_{\text {aff}}\)-RKA security proof results in the failure of the KDM\([\mathcal {F}_{\text {aff}}]\)-CCA proof of the LLJ scheme since INT-\(\mathcal {F}_{\text {aff}}\)-RKA security is used to prevent a KDM\([\mathcal {F}_{\text {aff}}]\)-CCA adversary from learning more information about the secret key by querying some invalid ciphertexts for decryption.
4 Authenticated Encryption with Auxiliary-Input
We do not see any hope of successfully fixing the security proof of the LLJ’s \(\overline{\textsf {AE}}\) in [LLJ15]. Alternatively, we resort to a different building block, namely \(\mathsf {AIAE}\). The intuition is as follows. If LLJ’s \(\overline{\textsf {AE}}\) is regarded as (ElGamal + OT-AE), we can design a new \(\mathsf {AIAE}\) as (Kurosawa-Desmedt [KD04] + OT-AE). But a new problem with our design arises: the secret key of KEM [KD04] consists of several elements, i.e., \(\mathsf {k}=(k_1, k_2, k_3, k_4)\). The affine function of \(\mathsf {k}\) is too complicated to prove the INT-\(\mathcal {F}_{\text {aff}}\)-RKA security. Fortunately, (a weak) INT-RKA security follows w.r.t. a smaller restricted affine function set \(\mathcal {F}_{\text {raff}} = \big \{ f: (k_1, k_2, k_3, k_4) \longmapsto a \cdot (k_1, k_2, k_3, k_4)+(b_1, b_2, b_3, b_4) ~\big |~ a \ne 0 \big \}\).
To make \(\mathsf {AIAE}\) serve KDM-CCA security of our PKE construction in Fig. 1, we have the following requirements.
-
\(\mathsf {AIAE}\) must have auxiliary input aux.
-
A weak INT-\(\mathcal {F}\)-RKA security is defined for \(\mathsf {AIAE}\). Compared to INT-\(\mathcal {F}\)-RKA security, the weak version has an additional special rule for the adversary’s forgery \((\textsf {aux}^*, f^*, \textsf {aiae.ct}^*)\) to be successful: if the adversary has already queried \((m, \textsf {aux}^*, f)\) to the encryption oracle Enc, it must hold that \(f^*=f\).
Next, we introduce the formal definitions of Authenticated Encryption with Auxiliary-Input, its IND- \(\mathcal {F}\) -RKA Security and Weak INT- \(\mathcal {F}\) -RKA Security.
4.1 AIAE and Its Related-Key Attack Security
Definition 9
(AIAE). An auxiliary-input authenticated encryption (AIAE) scheme \(\mathsf {AIAE}= (\mathsf {AIAE}.\mathsf {Setup}, \mathsf {AIAE}.\mathsf {Enc}, \mathsf {AIAE}.\mathsf {Dec})\) consists of three PPT algorithms:
-
\(\mathsf {AIAE}.\mathsf {Setup}(1^{\ell })\) outputs a system parameter \(\mathsf {prm}_{\mathsf {AIAE}}\), which is an implicit input to \(\mathsf {AIAE}.\mathsf {Enc}\) and \(\mathsf {AIAE}.\mathsf {Dec}\). The parameter \(\mathsf {prm}_{\mathsf {AIAE}}\) implicitly defines a message space \(\mathcal {M}\), a key space \({\mathcal {K}_{\mathsf {AIAE}}}\) and an auxiliary-input space \(\mathcal {AUX}\).
-
\(\mathsf {AIAE}.\mathsf {Enc}(\mathsf {k}, m, \mathsf {aux})\) takes as input a key \(\mathsf {k}\) \(\in {\mathcal {K}_{\mathsf {AIAE}}}\), a message \(m \in \mathcal {M}\) and an auxiliary input \(\mathsf {aux} \in \mathcal {AUX}\), and outputs a ciphertext \(\mathsf {aiae}\mathsf {.ct}\).
-
\(\mathsf {AIAE}.\mathsf {Dec}(\mathsf {k}, \mathsf {aiae}\mathsf {.ct}, \mathsf {aux})\) takes as input a key \(\mathsf {k}\) \(\in {\mathcal {K}_{\mathsf {AE}}}\), a ciphertext \(\mathsf {aiae}\mathsf {.ct}\) and an auxiliary input \(\mathsf {aux} \in \mathcal {AUX}\), and outputs a message \(m \in \mathcal {M}\) or a rejection symbol \(\bot \).
Correctness of \(\mathsf {AIAE}\) requires that, for all  , all \(\mathsf {k} \in {\mathcal {K}_{\mathsf {AIAE}}}\), all \(m \in \mathcal {M}\), all \(\mathsf {aux} \in \mathcal {AUX}\) and all
, all \(\mathsf {k} \in {\mathcal {K}_{\mathsf {AIAE}}}\), all \(m \in \mathcal {M}\), all \(\mathsf {aux} \in \mathcal {AUX}\) and all  , we have that \(\mathsf {AIAE}.\mathsf {Dec}(\mathsf {k}, \mathsf {aiae}\mathsf {.ct}, \mathsf {aux}) = m\).
, we have that \(\mathsf {AIAE}.\mathsf {Dec}(\mathsf {k}, \mathsf {aiae}\mathsf {.ct}, \mathsf {aux}) = m\).
If the auxiliary-input space \(\mathcal {AUX} = \emptyset \) for all possible parameters \(\mathsf {prm}_{\mathsf {AIAE}}\), the above definition is reduced to traditional AE.
Let \(\mathcal {F}\) be a family of functions from \(\mathcal {K}_{\mathsf {AIAE}}\) to \(\mathcal {K}_{\mathsf {AIAE}}\). We define the related-key security notions for \(\mathsf {AIAE}\) via Fig. 5.
Games \(\mathsf {IND}\)-\(\mathcal {F}\)-\(\mathsf {RKA}\) (left) and \(\mathsf {weak}\)-\(\mathsf {INT}\)-\(\mathcal {F}\)-\(\mathsf {RKA}\) (right) for defining securities of auxiliary-input authenticated encryption scheme \(\mathsf {AIAE}\). We note that the weak INT-\(\mathcal {F}\)-RKA security needs a special rule to return 0 in Finalize as shown in the shadow.
Definition 10
(IND- \(\mathcal {F}\) -RKA and Weak INT- \(\mathcal {F}\) -RKA Securities for AIAE). Scheme \(\mathsf {AIAE}\) is IND-\(\mathcal {F}\)-RKA secure and weak INT-\(\mathcal {F}\)-RKA secure, if for any PPT adversary \(\mathcal {A}\), both \(\mathsf {Adv}_{\mathsf {AIAE}, \mathcal {A}}^{ind\text {-}rka}(\ell ) := | \Pr [ \mathsf {IND}\text {-}\mathcal {F}\text {-}\mathsf {RKA}^{\mathcal {A}} \Rightarrow 1 ] - 1 / 2 |\) and \(\mathsf {Adv}_{\mathsf {AIAE}, \mathcal {A}}^{weak\text {-}int\text {-}rka}(\ell ) := \Pr [ \mathsf {weak}\text {-}\mathsf {INT}\text {-}\mathcal {F}\text {-}\mathsf {RKA}^{\mathcal {A}} \Rightarrow 1 ]\) are negligible in \(\ell \), where games \(\mathsf {IND}\)-\(\mathcal {F}\)-\(\mathsf {RKA}\) and \(\mathsf {weak}\)-\(\mathsf {INT}\)-\(\mathcal {F}\)-\(\mathsf {RKA}\) are specified in Fig. 5.
4.2 AIAE from OT-secure AE and DDH Assumption
Let \(\textsf {AE} = (\textsf {AE}.\textsf {Setup}, \textsf {AE}.\textsf {Enc}, \textsf {AE}.\textsf {Dec})\) be a traditional (without auxiliary-input) authenticated encryption scheme with key space \(\mathcal {K}_{\textsf {AE}}\) and message space \(\mathcal {M}\). Let \(\mathcal {H}_1 = \{ \textsf {H}_1: \{0, 1\}^* \rightarrow \mathbb {Z}_N \}\) and \(\mathcal {H}_2 = \{ \textsf {H}_2: \mathbb {QR}_{\bar{N}} \rightarrow \mathcal {K}_{\textsf {AE}} \}\) be two families of hash functions with \(|\mathcal {K}_{\textsf {AE}}| / |\mathbb {QR}_{\bar{N}}|\) (\(= |\mathcal {K}_{\textsf {AE}}| / N\)) \(\le 2^{-\varOmega (\ell )}\). The proposed scheme \(\mathsf {AIAE}= (\mathsf {AIAE}\textsf {.Setup}, \mathsf {AIAE}\textsf {.Enc}, \mathsf {AIAE}\textsf {.Dec})\) with key space \(\mathcal {K}_{\mathsf {AIAE}} = (\mathbb {Z}_N)^4\), message space \(\mathcal {M}\) and auxiliary-input space \(\mathcal {AUX} = \{0, 1\}^*\) is defined in Fig. 6.
The correctness of \(\mathsf {AIAE}\) follows from the correctness of \(\textsf {AE}\) directly. Note that the factors p, q of N in \(\mathsf {prm}_{\mathsf {AIAE}}\) are not needed in the encryption and decryption algorithms of \(\mathsf {AIAE}\). Jumping ahead, the factors p, q are necessary when the security of the PKEs presented in Sects. 5 and 6 is reduced to the security of \(\mathsf {AIAE}\). We now show the RKA-security of \(\mathsf {AIAE}\) through the following theorem.
Theorem 1
If the underlying scheme \(\mathsf {AE}\) is OT-secure, the DDH assumption holds w.r.t. \(\mathsf {GenN}\) and \(\mathbb {QR}_{\bar{N}}\), \(\mathcal {H}_1\) is collision resistant and \(\mathcal {H}_2\) is universal, then the resulting scheme \(\mathsf {AIAE}\) in Fig. 6 is IND-\(\mathcal {F}_{\text {raff}}\)-RKA and weak INT-\(\mathcal {F}_{\text {raff}}\)-RKA secure, where the restricted affine function set is defined as \(\mathcal {F}_{\text {raff}}: = \big \{ f_{(a, \mathsf {b})}: (k_1, k_2, k_3, k_4) \in \mathbb {Z}_N^4 \longmapsto (a k_1+b_1, a k_2 + b_2, a k_3 + b_3, a k_4 + b_4) \in \mathbb {Z}_N^4 ~\big |~ a \in \mathbb {Z}_{N}^*, ~\mathsf {b} = (b_1, b_2, b_3, b_4) \in \mathbb {Z}_N^4 \big \}\).
Proof of IND- \(\mathcal {F}_{\text {raff}}\) -RKA security of \(~{{\mathbf {\mathsf{{AIAE}}}}}\) in Theorem 1. The proof proceeds with a sequence of games. Suppose that \(\mathcal {A}\) is a PPT adversary against the IND-\(\mathcal {F}_{\text {raff}}\)-RKA security of \(\mathsf {AIAE}\), who makes at most \(Q_e\) times of \(\textsc {Enc}\) queries. Let \(\Pr _{i}[ \cdot ]\) (resp., \(\Pr _{i'}[ \cdot ]\)) denote the probability of a particular event occurring in game \(\mathsf {G}_i\) (resp., game \(\mathsf {G}_i'\)).
-
Game \(\mathsf {G}_1\): This is the original \(\mathsf {IND}\)-\(\mathcal {F}_{\text {raff}}\)-\(\mathsf {RKA}\) security game. Let \(\mathsf {Win}\) denote the event that \(\beta ' = \beta \). Then by definition, \(\mathsf {Adv}_{\mathsf {AIAE}, \mathcal {A}}^{ind\text {-}rka}(\ell ) = \big | \Pr _1[\mathsf {Win}] -\frac{1}{2} \big |\).
Denote \(\mathsf {prm}_{\mathsf {AIAE}} = (N, p, q, \bar{N}, g_1, g_2, \textsf {H}_1, \textsf {H}_2)\) and \(\mathsf {k}= (k_1, k_2, k_3, k_4)\). To answer the \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((m_{\lambda , 0}, m_{\lambda , 1}, \textsf {aux}_\lambda , f_\lambda )\), where \(f_\lambda = \langle a_\lambda , \textsf {b}_\lambda = (b_{\lambda , 1}, b_{\lambda , 2}, b_{\lambda , 3}, b_{\lambda , 4}) \rangle \in \mathcal {F}_{\text {raff}}\), the challenger proceeds as follows:
-
1.
pick
 and compute \((c_{\lambda , 1}, c_{\lambda , 2}) := (g_1^{w_\lambda }, g_2^{w_\lambda }) \in \mathbb {QR}_{\bar{N}}^2\),
and compute \((c_{\lambda , 1}, c_{\lambda , 2}) := (g_1^{w_\lambda }, g_2^{w_\lambda }) \in \mathbb {QR}_{\bar{N}}^2\), -
2.
compute a tag \(t_\lambda := \textsf {H}_1(c_{\lambda , 1}, c_{\lambda , 2}, \textsf {aux}_\lambda ) \in \mathbb {Z}_N\),
-
3.
compute an encryption key for AE scheme using a related key \(f_\lambda (\mathsf {k})\):
$$\begin{aligned} \kappa _\lambda := \textsf {H}_2\big ( c_{\lambda , 1}^{ (a_\lambda k_1+b_{\lambda , 1}) + (a_\lambda k_3+b_{\lambda , 3}) t_\lambda } \cdot c_{\lambda , 2}^{ (a_\lambda k_2+b_{\lambda , 2}) + (a_\lambda k_4+b_{\lambda , 4}) t_\lambda } \big ) \in \mathcal {K}_{\textsf {AE}}, \end{aligned}$$ -
4.
invoke
 ,
,
and returns the challenge ciphertext \(\langle c_{\lambda , 1}, c_{\lambda , 2}, \chi _\lambda \rangle \) to the adversary \(\mathcal {A}\).
-
1.
-
Game \(\mathsf {G}_{1,i}\), \(i \in [Q_e + 1]\): This game is the same as game \(\mathsf {G}_1\), except that, the challenger does not use secret key \(\mathsf {k}\) to answer the \(\lambda \)-th (\(\lambda \in [i-1]\)) Enc query at all, and instead, it changes steps 1, 3 to steps \(1'\), \(3'\) as follows:
-
\(1'\). pick
 and compute \((c_{\lambda , 1}, c_{\lambda , 2}) := (g_1^{w_{\lambda , 1}}, g_2^{w_{\lambda , 2}})\),
and compute \((c_{\lambda , 1}, c_{\lambda , 2}) := (g_1^{w_{\lambda , 1}}, g_2^{w_{\lambda , 2}})\), -
\(3'\). choose an encryption key
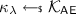 randomly for the AE scheme.
randomly for the AE scheme.
The challenger still answers the \(\lambda \)-th (\(\lambda \in [i, Q_e]\)) Enc query as in \(\mathsf {G}_1\), i.e., using steps 1, 3.
Clearly \(\mathsf {G}_{1,1}\) is identical to \(\mathsf {G}_{1}\), thus
 .
. -
-
Game \(\mathsf {G}_{1,i}'\), \(i \in [Q_e]\): This game is the same as game \(\mathsf {G}_{1,i}\), except that the challenger answers the i-th Enc query using steps \(1'\), 3 (rather than steps 1, 3 in game \(\mathsf {G}_{1,i}\)).
The only difference between \(\mathsf {G}_{1,i}\) and \(\mathsf {G}_{1,i}'\) is the distribution of \((g_1, g_2, c_{i, 1},\) \(c_{i, 2})\). In game \(\mathsf {G}_{1,i}\), \((g_1, g_2, c_{i, 1}, c_{i, 2})\) is a DDH tuple, while in game \(\mathsf {G}_{1,i}'\), it is a random tuple. It is straightforward to construct a PPT adversary to solve the DDH problem w.r.t. GenN and \(\mathbb {QR}_{\bar{N}}\), thus we have that

We analyze the difference between \(\mathsf {G}_{1,i}'\) and \(\mathsf {G}_{1,i+1}\) via the following lemma. Its proof is provided in the full version [HLL16].
Lemma 1
For all \(i \in [Q_e]\),  .
.
-
Game \(\mathsf {G}_{2}\): This game is the same as game \(\mathsf {G}_{1, Q_e+1}\), except that, to answer the \(\lambda \)-th (\(\lambda \in [Q_e ]\)) Enc query, the challenger changes step 4 to step \(4'\):
\(4'\). invoke
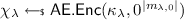 .
.
In game \(\mathsf {G}_{1, Q_e+1}\), the challenger computes the AE encryption of \(m_{\lambda , \beta }\) under encryption key \(\kappa _\lambda \) in \(\textsc {Enc}\), while in game \(\mathsf {G}_{2}\) it computes the AE encryption of \(0^{|m_{\lambda , 0}|}\) in \(\textsc {Enc}\). Both in games \(\mathsf {G}_{1, Q_e+1}\) and \(\mathsf {G}_{2}\), we have that each \(\kappa _\lambda \) is chosen uniformly from \(\mathcal {K}_{\textsf {AE}}\) and independent of other parts of the game. Therefore we can reduce the differences between \(\mathsf {G}_{1, Q_e+1}\) and \(\mathsf {G}_{2}\) to the IND-OT security of \(\textsf {AE}\) by a standard hybrid argument, and have that  .
.
Now in game \(\mathsf {G}_{2}\), since the challenger always encrypts the constant message \(0^{|m_{\lambda , 0}|}\), the challenge bit \(\beta \) is completely hidden. Then  .
.
Taking all things together, the IND-\(\mathcal {F}_{\text {raff}}\)-RKA security of \(\mathsf {AIAE}\) follows. \(\blacksquare \)
Proof of Weak INT- \(\mathcal {F}_{\text {raff}}\) -RKA security of \({{\mathbf {\mathsf{{AIAE}}}}}\) in Theorem 1. Again, we prove it through a sequence of games. These games are defined almost the same as those in the previous proof. Suppose that \(\mathcal {A}\) is a PPT adversary against the weak INT-\(\mathcal {F}_{\text {raff}}\)-RKA security of \(\mathsf {AIAE}\), who makes at most \(Q_e\) times of \(\textsc {Enc}\) queries.
-
Game \(\mathsf {G}_0\): This is the original \(\mathsf {weak}\)-\(\mathsf {INT}\)-\(\mathcal {F}_{\text {raff}}\)-\(\mathsf {RKA}\) security game.
Denote \(\mathsf {prm}_{\mathsf {AIAE}} = (N, p, q, \bar{N}, g_1, g_2, \textsf {H}_1, \textsf {H}_2)\) and \(\mathsf {k}= (k_1, k_2, k_3, k_4)\). To answer the \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((m_{\lambda }, \textsf {aux}_\lambda , f_\lambda )\), the challenger proceeds with steps \(1{\thicksim }4\), similar to the previous proof, and returns the challenge ciphertext \(\langle c_{\lambda , 1}, c_{\lambda , 2}, \chi _\lambda \rangle \) to the adversary \(\mathcal {A}\). Moreover, the challenger will put \(\big ( \textsf {aux}_\lambda , f_\lambda , \langle c_{\lambda , 1}, c_{\lambda , 2}, \chi _\lambda \rangle \big )\) to a set \(\mathcal {Q}_{\mathcal {ENC}}\), put \((\textsf {aux}_\lambda , f_\lambda )\) to a set \(\mathcal {Q}_{\mathcal {AUXF}}\), and put \(( c_{\lambda , 1}, c_{\lambda , 2}, \textsf {aux}_\lambda , t_\lambda )\) to a set \(\mathcal {Q}_{\mathcal {TAG}}\). Finally, the adversary outputs a forgery \(\big (\textsf {aux}^*, f^* = \langle a^*, \textsf {b}^* = (b_1^*, b_2^*, b_3^*, b_4^*) \rangle ,\) \(\langle c_1^*, c_2^*, \chi ^* \rangle \big )\).
Let \(\mathsf {Forge}\) be the event that the following Finalize procedure outputs 1:
-
If \(\big (\textsf {aux}^*, f^*, \langle c_1^*, c_2^*, \chi ^* \rangle \big ) \in \mathcal {Q}_{\mathcal {ENC}}\), Return 0.
-
If there exists \((\textsf {aux}_\lambda , f_\lambda ) \in \mathcal {Q}_{\mathcal {AUXF}}\) such that \(\textsf {aux}_\lambda = \textsf {aux}^*\) but \(f_\lambda \ne f^*\), Return 0.
-
If \((c_1^*, c_2^*) \notin \mathbb {QR}_{\bar{N}}^2 \vee (c_1^*, c_2^*) = (1, 1)\), Return 0.
-
\(t^* := \textsf {H}_1(c_1^*, c_2^*, \textsf {aux}^*)\), \(\kappa ^* := \textsf {H}_2\big ( c_1^{* (a^* k_1 +b_1^*) + (a^* k_3 +b_3^*) t^*} \cdot c_{2}^{* (a^* k_2+b_2^*) + (a^* k_4+b_4^*) t^*} \big )\).
Return \((\textsf {AE.Dec}(\kappa ^*, \chi ^*) \ne \bot )\).
By definition, it follows that, \(\mathsf {Adv}_{\mathsf {AIAE}, \mathcal {A}}^{weak\text {-}int\text {-}rka}(\ell ) = \Pr _0[\mathsf {Forge}]\).
-
-
Game \(\mathsf {G}_{1}\): This game is the same as game \(\mathsf {G}_0\), except that, the challenger adds the following new rule to the Finalize procedure:
-
If there exists \((c_{\lambda , 1}, c_{\lambda , 2}, \textsf {aux}_\lambda , t_\lambda ) \in \mathcal {Q}_{\mathcal {TAG}}\) such that \(t_{\lambda } = t^*\) but \((c_{\lambda , 1}, c_{\lambda , 2},\) \(\textsf {aux}_\lambda ) \ne (c_1^*, c_2^*, \textsf {aux}^*)\), Return 0.
Since \(t_\lambda = \textsf {H}_1(c_{\lambda , 1}, c_{\lambda , 2}, \textsf {aux}_\lambda )\) and \(t^* = \textsf {H}_1(c_1^*, c_2^*, \textsf {aux}^*)\), any difference between \(\mathsf {G}_0\) and \(\mathsf {G}_1\) will imply a collision of \(\textsf {H}_1\). Thus
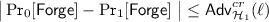 .
. -
-
Game \(\mathsf {G}_{1,i}\), \(i \in [Q_e + 1]\): This game is the same as game \(\mathsf {G}_1\), except that, the challenger does not use secret key \(\mathsf {k}\) to answer the \(\lambda \)-th (\(\lambda \in [i-1 ]\)) Enc query at all, and instead, it changes the steps 1, 3 to the steps \(1'\), \(3'\) respectively, as in the previous proof.
Clearly
 .
. -
Game \(\mathsf {G}_{1,i}'\), \(i \in [Q_e]\): This game is the same as game \(\mathsf {G}_{1,i}\), except that the challenger answers the i-th Enc query using steps \(1'\), 3 (rather than steps 1, 3 in game \(\mathsf {G}_{1,i}\)), as in the previous proof.
The only difference between \(\mathsf {G}_{1,i}\) and \(\mathsf {G}_{1,i}'\) is the distribution of \((g_1, g_2, c_{i, 1},\) \(c_{i, 2})\). In game \(\mathsf {G}_{1,i}\), \((g_1, g_2, c_{i, 1}, c_{i, 2})\) is a DDH tuple, while in game \(\mathsf {G}_{1,i}'\), it is a random tuple. It is straightforward to construct a PPT adversary to solve the DDH problem w.r.t. GenN and \(\mathbb {QR}_{\bar{N}}\). We stress that the PPT adversary (simulator) can detect the occurrence of event \(\mathsf {Forge}\) efficiently since it can choose the secret key \(\mathsf {k}= (k_1, k_2, k_3, k_4)\) itself. Thus we can reduce the difference between \(\mathsf {G}_{1,i}\) and \(\mathsf {G}_{1,i}'\) to the DDH assumption smoothly.
Lemma 2
For all \(i \in [Q_e]\), 
Proof. We construct a PPT adversary \(\mathcal {B}\) to solve the DDH problem. \(\mathcal {B}\) is given (N, p, q, \(g_1, g_2, g_1^{x_1}, g_2^{x_2})\), where  ,
,  , and aims to distinguish whether
, and aims to distinguish whether  or
or  .
.
\(\mathcal {B}\) will simulate game \(\textsf {G}_{1,i}\) or \(\textsf {G}_{1,i}'\) for adversary \(\mathcal {A}\). First, \(\mathcal {B}\) picks  ,
,  randomly, sets \(\mathsf {prm}_{\mathsf {AIAE}} := (N, p, q, \bar{N} = 2N+1, g_1, g_2, \textsf {H}_1, \textsf {H}_2)\) and sends \(\mathsf {prm}_{\mathsf {AIAE}}\) to \(\mathcal {A}\). Then \(\mathcal {B}\) generates the secret key \(\mathsf {k}= (k_1, k_2, k_3, k_4)\) itself.
randomly, sets \(\mathsf {prm}_{\mathsf {AIAE}} := (N, p, q, \bar{N} = 2N+1, g_1, g_2, \textsf {H}_1, \textsf {H}_2)\) and sends \(\mathsf {prm}_{\mathsf {AIAE}}\) to \(\mathcal {A}\). Then \(\mathcal {B}\) generates the secret key \(\mathsf {k}= (k_1, k_2, k_3, k_4)\) itself.
To answer the \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((m_\lambda , \textsf {aux}_\lambda , f_\lambda )\), where \(f_\lambda = \langle a_{\lambda }, \textsf {b}_{\lambda } = (b_{\lambda ,1}, b_{\lambda ,2}, b_{\lambda ,3},\) \(b_{\lambda ,4}) \rangle \in \mathcal {F}_{\text {raff}}\), \(\mathcal {B}\) proceeds as follows:
-
If \(\lambda \in [i-1]\), \(\mathcal {B}\) proceeds the same as in \(\textsf {G}_{1,i}\) and \(\textsf {G}_{1,i}'\). That is, \(\mathcal {B}\) picks
 randomly and sets \((c_{\lambda , 1}, c_{\lambda , 2}) := (g_1^{w_{\lambda , 1}}, g_2^{w_{\lambda , 2}})\). Then \(\mathcal {B}\) chooses
randomly and sets \((c_{\lambda , 1}, c_{\lambda , 2}) := (g_1^{w_{\lambda , 1}}, g_2^{w_{\lambda , 2}})\). Then \(\mathcal {B}\) chooses  and invokes
and invokes 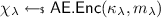 .
. -
If \(\lambda \in [i+1, Q_e]\), \(\mathcal {B}\) proceeds the same as in \(\textsf {G}_{1,i}\) and \(\textsf {G}_{1,i}'\). That is, \(\mathcal {B}\) picks
 randomly and sets \((c_{\lambda , 1}, c_{\lambda , 2}) := (g_1^{w_\lambda }, g_2^{w_\lambda })\). Then \(\mathcal {B}\) computes \(t_\lambda := \textsf {H}_1(c_{\lambda , 1}, c_{\lambda , 2}, \textsf {aux}_\lambda )\), \(\kappa _\lambda := \textsf {H}_2\big ( c_{\lambda , 1}^{ (a_\lambda k_1+b_{\lambda , 1}) + (a_\lambda k_3+b_{\lambda , 3}) t_\lambda } \cdot c_{\lambda , 2}^{ (a_\lambda k_2+b_{\lambda , 2}) + (a_\lambda k_4+b_{\lambda , 4}) t_\lambda } \big )\), and invokes
randomly and sets \((c_{\lambda , 1}, c_{\lambda , 2}) := (g_1^{w_\lambda }, g_2^{w_\lambda })\). Then \(\mathcal {B}\) computes \(t_\lambda := \textsf {H}_1(c_{\lambda , 1}, c_{\lambda , 2}, \textsf {aux}_\lambda )\), \(\kappa _\lambda := \textsf {H}_2\big ( c_{\lambda , 1}^{ (a_\lambda k_1+b_{\lambda , 1}) + (a_\lambda k_3+b_{\lambda , 3}) t_\lambda } \cdot c_{\lambda , 2}^{ (a_\lambda k_2+b_{\lambda , 2}) + (a_\lambda k_4+b_{\lambda , 4}) t_\lambda } \big )\), and invokes  .
. -
If \(\lambda = i\), \(\mathcal {B}\) embedded its DDH challenge to \((c_{i, 1}, c_{i, 2}) := (g_1^{x_1}, g_2^{x_2})\). Then it computes \(t_i := \textsf {H}_1(c_{i, 1}, c_{i, 2}, \textsf {aux}_i)\), \(\kappa _i := \textsf {H}_2\big ( c_{i, 1}^{ (a_i k_1+b_{i, 1}) + (a_i k_3+b_{i, 3}) t_i} \cdot c_{i, 2}^{ (a_i k_2+b_{i, 2}) + (a_i k_4+b_{i, 4}) t_i} \big )\), and invokes
 .
.
\(\mathcal {B}\) returns the challenge ciphertext \(\langle c_{\lambda , 1}, c_{\lambda , 2}, \chi _\lambda \rangle \) to \(\mathcal {A}\), and puts \(\big ( \textsf {aux}_\lambda ,\) \(f_\lambda , \langle c_{\lambda , 1}, c_{\lambda , 2}, \chi _\lambda \rangle \big )\) to \(\mathcal {Q}_{\mathcal {ENC}}\), \(( \textsf {aux}_\lambda , f_\lambda )\) to \(\mathcal {Q}_{\mathcal {AUXF}}\), and \(( c_{\lambda , 1}, c_{\lambda , 2}, \textsf {aux}_\lambda , t_\lambda )\) to \(\mathcal {Q}_{\mathcal {TAG}}\).
In the case of that \((N, p, q, g_1, g_2, g_1^{x_1}, g_2^{x_2})\) is a DDH tuple, i.e.,  , \(\mathcal {B}\) simulates game \(\textsf {G}_{1,i}\) perfectly for \(\mathcal {A}\); in the case of that \((N, p, q, g_1,\) \(g_2, g_1^{x_1}, g_2^{x_2})\) is a random tuple, i.e.,
, \(\mathcal {B}\) simulates game \(\textsf {G}_{1,i}\) perfectly for \(\mathcal {A}\); in the case of that \((N, p, q, g_1,\) \(g_2, g_1^{x_1}, g_2^{x_2})\) is a random tuple, i.e.,  , \(\mathcal {B}\) simulates game \(\textsf {G}_{1,i}'\) perfectly for \(\mathcal {A}\).
, \(\mathcal {B}\) simulates game \(\textsf {G}_{1,i}'\) perfectly for \(\mathcal {A}\).
Finally \(\mathcal {B}\) receives a forgery \(\big (\textsf {aux}^*, f^*, \langle c_1^*, c_2^*, \chi ^* \rangle \big )\) from \(\mathcal {A}\), where \(f^* = \langle a^*, \textsf {b}^* = (b_{1}^*, b_{2}^*, b_{3}^*, b_{4}^*) \rangle \in \mathcal {F}_{\text {raff}}\). \(\mathcal {B}\) determines whether or not the \(\textsc {Finalize}\) procedure outputs 1 using the secret key \(\mathsf {k}= (k_1, k_2, k_3, k_4)\). That is,
-
If \(\big (\textsf {aux}^*, f^*, \langle c_1^*, c_2^*, \chi ^* \rangle \big ) \in \mathcal {Q}_{\mathcal {ENC}}\), \(\mathcal {B}\) outputs 0 (to its DDH challenger).
-
If there exists \((\textsf {aux}_\lambda , f_\lambda ) \in \mathcal {Q}_{\mathcal {AUXF}}\) such that \(\textsf {aux}_\lambda = \textsf {aux}^*\) but \(f_\lambda \ne f^*\), \(\mathcal {B}\) outputs 0.
-
If \((c_1^*, c_2^*) \notin \mathbb {QR}_{\bar{N}}^2 \vee (c_1^*, c_2^*) = (1, 1)\), \(\mathcal {B}\) outputs 0.
-
\(t^* := \textsf {H}_1(c_1^*, c_2^*, \textsf {aux}^*)\), \(\kappa ^* := \textsf {H}_2\big ( c_1^{* (a^* k_1 +b_1^*) + (a^* k_3 +b_3^*) t^*} \cdot c_{2}^{* (a^* k_2+b_2^*) + (a^* k_4+b_4^*) t^*} \big )\).
-
If there exists \((c_{\lambda , 1}, c_{\lambda , 2}, \textsf {aux}_\lambda , t_\lambda ) \in \mathcal {Q}_{\mathcal {TAG}}\) such that \(t_{\lambda } = t^*\) but \((c_{\lambda , 1}, c_{\lambda , 2},\) \(\textsf {aux}_\lambda ) \ne (c_1^*, c_2^*, \textsf {aux}^*)\), \(\mathcal {B}\) outputs 0.
-
Output \((\textsf {AE.Dec}(\kappa ^*, \chi ^*) \ne \bot )\).
With the secret key \(\mathsf {k}= (k_1, k_2, k_3, k_4)\), \(\mathcal {B}\) simulates \(\textsc {Finalize}\) perfectly, the same as in games \(\textsf {G}_{1,i}\) and \(\textsf {G}_{1,i}'\), and \(\mathcal {B}\) outputs 1 to its DDH challenger if and only if \(\textsc {Finalize}\) outputs 1, i.e., the event \(\textsf {Forge}\) occurs.
As a consequence,  . \(\blacksquare \)
. \(\blacksquare \)
We analyze the difference between \(\mathsf {G}_{1,i}'\) and \(\mathsf {G}_{1,i+1}\) via the following lemma, and the proof is in the full version [HLL16] due to the lack of space.
Lemma 3
For all \(i \in [Q_e]\),  .
.
Now in game \(\mathsf {G}_{1,Q_e + 1}\), the challenger does not use the secret key \(\mathsf {k}\) to compute \(\kappa _{\lambda }\) at all, hence \(\mathsf {k}= (k_1, k_2, k_3, k_4)\) is uniformly random to the adversary \(\mathcal {A}\). As a result, in the Finalize procedure defining the event Forge,
where \(w = \text {dlog}_{g_1} g_2 \in \mathbb {Z}_N\) and \((w_{1}^*, w_{2}^*) = (\text {dlog}_{g_1} c_{1}^*, \text {dlog}_{g_2} c_{2}^*) \in \mathbb {Z}_N^2 {\setminus \{(0,0)\}}\). The term \((w_{1}^* k_1 + w_{2}^* w k_2)\) is uniformly distributed over \(\mathbb {Z}_N\). Then as long as \(a^* \in \mathbb {Z}_N^*\), Y will be uniformly distributed over \(\mathbb {QR}_{\bar{N}}\) and independent of \(\textsf {H}_2\). By the Leftover Hash Lemma, \(\kappa ^*= \textsf {H}_2(Y)\) is statistically close to the uniform distribution over \(\mathcal {K}_{\textsf {AE}}\). Thus \(\textsf {AE.Dec}(\kappa ^*, \chi ^*) \ne \bot \) will hold with probability at most \(\mathsf {Adv}_{\textsf {AE}}^{int\text {-}ot}(\ell )\). Then  .
.
Taking all things together, the weak INT-\(\mathcal {F}_{\text {raff}}\)-RKA security of \(\mathsf {AIAE}\) follows. \(\blacksquare \)
Remark. We stress that the problem in the INT-\(\mathcal {F}_{\text {aff}}\)-RKA security proof of LLJ’s \(\overline{\textsf {AE}}\) does not appear here. The weak INT-\(\mathcal {F}_{\text {raff}}\)-RKA security of our \(\mathsf {AIAE}\) can be reduced to the DDH assumption smoothly. More precisely, in the security analysis of games \(\textsf {G}_{1,i}\) and \(\textsf {G}_{1,i}'\) (cf. Lemma 2), the simulator chooses the secret key itself and uses it to detect the occurrence of event \(\textsf {Forge}\) efficiently. Therefore the simulator can always make use of the difference between \(\Pr _{1, i}[\textsf {Forge}]\) and \(\Pr _{1, i'}[\textsf {Forge}]\) to solve the DDH problem.
5 PKE with n-KDM\([\mathcal {F}_{\text {aff}}]\)-CCA Security
Let \(\mathsf {AIAE}= (\mathsf {AIAE}\textsf {.Setup}, \mathsf {AIAE}\textsf {.Enc}, \mathsf {AIAE}\textsf {.Dec})\) be the DDH-based auxiliary-input authenticated encryption scheme constructed from OT-secure AE, with key space \((\mathbb {Z}_N)^4\) and a suitable message space \(\mathcal {M}\) (cf. Fig. 6). Following our approach in Fig. 1, we have to design the other two building blocks.
- \({\textsf {KEM}}\)::
-
With respect to this \(\mathsf {AIAE}\), we design a \(\textsf {KEM}\) which can encapsulate a key tuple \((k_1, k_2, k_3, k_4) \in (\mathbb {Z}_N)^4\).
- \(\mathcal {E}\)::
-
With respect to the affine function \(\mathcal {F}_{\text {aff}}\), we design a public-key encryption \(\mathcal {E}\) such that \(\mathcal {E}.\textsf {Enc}\) can be changed to an entropy filter for affine functions in a computationally indistinguishable way.
The proposed \(\textsf {PKE} = (\textsf {Setup}, \textsf {Gen}, \textsf {Enc}, \textsf {Dec})\) is defined in Fig. 7, where the shadowed parts describe algorithms of building blocks \(\textsf {KEM}\) and \(\mathcal {E}\).
Construction of \(\textsf {PKE}\) from \(\mathsf {AIAE}\). The shadowed parts describe algorithms of building blocks \(\textsf {KEM}\) and \(\mathcal {E}\). Here p, q contained in \(\mathsf {prm}_{\mathsf {AIAE}}\) are not provided in \(\mathsf {prm}_{\mathsf {AIAE}}'\), since they are not necessary in the encryption and decryption algorithms of \(\mathsf {AIAE}\).
The correctness of \(\textsf {PKE}\) follows from the correctness of \(\mathsf {AIAE}\), \(\mathcal {E}\) and \(\textsf {KEM}\) directly. We now show its KDM-CCA-security through the following theorem.
Theorem 2
If the underlying scheme \(\mathsf {AIAE}\) is IND-\(\mathcal {F}_{\text {raff}}\)-RKA and weak INT-\(\mathcal {F}_{\text {raff}}\)-RKA secure, the DCR assumption holds w.r.t. \(\mathsf {GenN}\) and group \(\mathbb {QR}_{N^s}\), and the DL Assumption holds w.r.t. \(\mathsf {GenN}\) and group \(\mathbb {SCR}_{N^s}\), then the resulting scheme \(\mathsf {PKE}\) in Fig. 7 is n-KDM[\(\mathcal {F}_{\text {aff}}\)]-CCA secure.
Proof of Theorem 2. Suppose that \(\mathcal {A}\) is a PPT adversary against the n-KDM[\(\mathcal {F}_{\text {aff}}\)]-CCA security of \(\textsf {PKE}\), who makes at most \(Q_e\) times of \(\textsc {Enc}\) queries and \(Q_d\) times of \(\textsc {Dec}\) queries. We prove the theorem by defining a sequence of games. Before presenting the full detailed proof, we first give a high-level description how n-KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security is achieved.
-
(1)
For the n secret key tuples, each tuple can be divided into two parts: for \(i\in [n]\), \(\textsf {sk}_i=(x_{i,j}, y_{i,j})_{j = 1}^4 = \big ( (x_{i,j}, y_{i,j})_{j = 1}^4 \text { mod } N, (x_{i,j}, y_{i,j})_{j = 1}^4 \text { mod } \phi (N)/4\big )\).
-
(2)
Each secret key tuple can be generated by adding a random shift \((\overline{x}_{i,j}, \overline{y}_{i,j})_{j = 1}^4\) to a fixed base \((x_{j}, y_{j})_{j = 1}^4\), i.e., \(\textsf {sk}_i = (x_{i,j}, y_{i,j})_{j=1}^4 := (x_{j}, y_{j})_{j=1}^4 + (\overline{x}_{i,j}, \overline{y}_{i,j})_{j=1}^4\).
-
(3)
Every public key tuple \( \textsf {pk}_i = (h_{i,1}, \cdots , h_{i,4})\) only reveals information about the (\( \text {mod } \phi (N)/4\)) part of the secret key tuple \(\mathsf {sk}_i\).
-
(4)
For each encryption query from the adversary \((f_\lambda , i_\lambda )\), if the Enc oracle encrypts \(f_\lambda ( \textsf {sk}_1, \cdots , \textsf {sk}_n)\), the ciphertext might reveal information about \(\textsf {sk}_i\) through \(\mathcal {E}\).ct. We have to change this fact such that the leaked information about \(\textsf {sk}_i\) in Enc is bounded.
-
By IV\(_d\) assumption, we can change the generation of \(\mathcal {E}\).ct by oracle Enc such that it does not reveal any information about \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\), i.e., the (\(\text {mod } N\)) part of the base secret key tuple.
-
By IV\(_d\) assumption, we can change the generation of \(\textsf {kem.ct}\)(\(= \textsf {aux}\)) by Enc such that it encapsulates a different key, other than the key used in \(\mathsf {AIAE}.\textsf {Enc}\). If \(\mathsf {AIAE}.\textsf {Enc}\) uses key \((r_{\lambda }{k}^*_j+s_{\lambda ,j})_{j = 1}^4\), then KEM.Enc encapsulates \(\big (r_\lambda (k^*_j - \alpha _j x_j - \alpha _{j+1} y_j) - r_\lambda (\alpha _j \bar{x}_{i_\lambda ,j} + \alpha _{j+1} \bar{y}_{i_\lambda ,j}) + s_{\lambda ,j}\big )_{j = 1}^4 \text { mod } N\). Thus, \((k^*_1, \cdots , k^*_4)\) is now protected by \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\).
-
-
(5)
Oracle Dec might also leak information about \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\). Therefore, we change how oracle Dec works so that decryption does not use \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\) any more. Observe that as long as the ciphertext queried by the adversary satisfies \(\forall {j\in [5]}, u_{j} \in \mathbb {SCR}_{N^2}\) and \(\forall {j\in [8]}, \tilde{u}_{j} \in \mathbb {SCR}_{N^s}\), Dec can use \(\phi (N)\) and the \((\text {mod } \phi (N)/4)\) part of secret key for decryption.
-
If \(\exists j \in [5], u_{j} \notin \mathbb {SCR}_{N^2}\) in the ciphertext queried by the adversary, we expect that \(\mathsf {AIAE}.\textsf {Dec}\) will reject, due to its weak INT-\(\mathcal {F}_{\text {raff}}\)-RKA security.
-
If \(\exists j \in [8], \tilde{u}_{j} \notin \mathbb {SCR}_{N^s}\) in the ciphertext queried by the adversary, we expect decryption will result in \(t\ne g_1^m \text { mod } N\), so \(\mathcal {E}\).Dec will reject.
-
-
(6)
Consequently, both \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\) and \((k^*_1, \cdots , k^*_4)\) are random to the adversary, and \(\mathsf {AIAE}.\textsf {Enc}\) always uses the restricted affine function of \((k^*_1, \cdots , k^*_4)\) for encryption. Then IND-\(\mathcal {F}_{\text {raff}}\)-RKA security of \(\mathsf {AIAE}\) implies the n-KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security.
In the proof, \(\mathsf {G}_{1}\text {-}\mathsf {G}_{2}\) are dedicated to deal with the n-user case; the aim of \(\mathsf {G}_{3}\text {-}\mathsf {G}_{4}\) is to eliminate the use of the (\(\text {mod } N\)) part of \((x_{j}, y_{j})_{j = 1}^4\) in \(\textsc {Enc}\); the aim of \(\mathsf {G}_{5}\text {-}\mathsf {G}_{6}\) is to use \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\) to hide the \(\mathsf {AIAE}\)’s base key \((k^*_1, \cdots , k^*_4)\) in \(\textsc {Enc}\), however, \(\textsc {Dec}\) may still leak the information about \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\); the aim of \(\mathsf {G}_{7}\text {-}\mathsf {G}_{8}\) is to eliminate the use of \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\) in \(\textsc {Dec}\); finally, in \(\mathsf {G}_{9}\text {-}\mathsf {G}_{10}\), the IND-\(\mathcal {F}_{\text {raff}}\)-RKA security of \(\mathsf {AIAE}\) is used to prove the n-KDM\([\mathcal {F}_{\text {aff}}]\)-CCA security of \(\mathsf {PKE}\), since \((k^*_1, \cdots , k^*_4)\) is perfectly hided by \((x_{j}, y_{j})_{j = 1}^4 \text { mod } N\).
-
Game \(\mathsf {G}_0\): This is the original n-\(\mathsf {KDM}\) \([\mathcal {F}_{\text {aff}}]\)-\(\mathsf {CCA}\) game. Let \(\mathsf {Win}\) denote the event that \(\beta ' = \beta \). Then by definition, \(\mathsf {Adv}_{{\textsf {PKE}}, \mathcal {A}}^{kdm\text {-}cca}(\ell ) = \big | \Pr _0[\mathsf {Win}] -\frac{1}{2} \big |\).
Denote by \(\textsf {pk}_i = (h_{i, 1}, \cdots , h_{i, 4})\) and \(\textsf {sk}_i = ( x_{i, 1}, y_{i, 1}, \cdots , x_{i, 4}, y_{i, 4} )\) the public and secret keys of the i-th user respectively, \(i \in [n]\).
-
Game \(\mathsf {G}_{1}\): This game is the same as game \(\mathsf {G}_0\), except that, when answering the \(\textsc {Dec}\) query \((\langle \textsf {aux}, \mathsf {aiae}.\textsf {ct} \rangle ,\,i \in [n])\), the challenger outputs \(\bot \) if \(\langle \textsf {aux}, \mathsf {aiae}.\textsf {ct} \rangle = \langle \textsf {aux}_\lambda , \mathsf {aiae}.\textsf {ct}_\lambda \rangle \) for some \(\lambda \in [Q_e]\), where \(\langle \textsf {aux}_\lambda , \mathsf {aiae}.\textsf {ct}_\lambda \rangle \) is the challenge ciphertext for the \(\lambda \)-th Enc query \((f_\lambda , i_\lambda )\).
- Case 1::
-
\((\langle \textsf {aux}, \mathsf {aiae}.\textsf {ct} \rangle , i) = (\langle \textsf {aux}_\lambda , \mathsf {aiae}.\textsf {ct}_\lambda \rangle , i_\lambda )\).
Dec will output \(\bot \) in game \(\mathsf {G}_0\) since \((\langle \textsf {aux}_\lambda , \mathsf {aiae}.\textsf {ct}_\lambda \rangle , i_\lambda )\) is prohibited.
- Case 2::
-
\(\langle \textsf {aux}, \mathsf {aiae}.\textsf {ct} \rangle = \langle \textsf {aux}_\lambda , \mathsf {aiae}.\textsf {ct}_\lambda \rangle \) but \(i \ne i_\lambda \).
We show that in game \(\mathsf {G}_0\), Dec will output \(\bot \), due to \(e_{\lambda ,1} u_{\lambda ,1}^{x_{i,1}} u_{\lambda ,2}^{y_{i,1}} \notin \mathbb {RU}_{N^2}\), with overwhelming probability. Recall that \(u_{\lambda ,1} = g_1^{r_\lambda }, u_{\lambda ,2} = g_2^{r_\lambda }, e_{\lambda ,1} = h_{i_\lambda , 1}^{r_\lambda } T^{k_{\lambda , 1}}\), so
$$\begin{aligned} e_{\lambda ,1} u_{\lambda ,1}^{x_{i,1}} u_{\lambda ,2}^{y_{i,1}} = h_{i_\lambda , 1}^{r_\lambda } T^{k_{\lambda , 1}} \cdot (g_1^{r_\lambda })^{x_{i,1}} (g_2^{r_\lambda })^{y_{i,1}} = (h_{i_\lambda , 1} h_{i,1}^{-1})^{r_\lambda } T^{k_{\lambda , 1}} \text { mod }N^2, \end{aligned}$$where \(h_{i_\lambda , 1}\) and \(h_{i,1}\) are parts of public key of different users \(i_\lambda \) and i respectively and are uniformly distributed over \(\mathbb {SCR}_{N^s}\). So \(h_{i_\lambda , 1} h_{i,1}^{-1} \ne 1\), hence \(e_{\lambda ,1} u_{\lambda ,1}^{x_{i,1}} u_{\lambda ,2}^{y_{i,1}} \notin \mathbb {RU}_{N^2}\), except with probability \(2^{-\varOmega (\ell )}\).
By a union bound, \(\mathsf {G}_0\) and \(\mathsf {G}_1\) are identical except with probability \(Q_d \cdot 2^{-\varOmega (\ell )}\), therefore
 .
. -
Game \(\mathsf {G}_{2}\): This game is the same as game \(\mathsf {G}_1\), except that, the challenger samples the secret keys \(\textsf {sk}_i = ( x_{i, 1}, y_{i, 1}, \cdots , x_{i, 4}, y_{i, 4} )\), \(i \in [n]\), in a different way. First, it chooses random \((x_1,y_1, \cdots , x_4, y_4)\) and \((\bar{x}_{i,1}, \bar{y}_{i,1}, \cdots , \bar{x}_{i,4}, \bar{y}_{i,4} )\), \(i\in [n]\), from \(\big [ \lfloor {N^2}/{4} \rfloor \big ]\), then it computes \((x_{i,1}, y_{i,1}, \cdots , x_{i,4}, y_{i,4})=(x_{1}, y_{1}, \cdots ,\) \(x_{4}, y_{4}) +(\overline{x}_{i,1}, \overline{y}_{i,1}, \cdots , \overline{x}_{i,4}, \overline{y}_{i,4}) \text { mod } \lfloor {N^2}/{4} \rfloor \) for \(i \in [n]\).
Obviously, the secret keys \(\textsf {sk}_i = ( x_{i, 1}, y_{i, 1}, \cdots , x_{i, 4}, y_{i, 4} )\) are uniformly distributed. Hence \(\mathsf {G}_2\) is identical to \(\mathsf {G}_1\), and
 .
. -
Game \(\mathsf {G}_{3}\): This game is the same as game \(\mathsf {G}_2\), except that, when responding to the adversary’s \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((f_\lambda , i_\lambda )\), instead of using the public keys \(\textsf {pk}_{i_\lambda } = (h_{i_\lambda , 1}, \cdots , h_{i_\lambda , 4})\), the challenger uses the secret keys \(\textsf {sk}_{i_\lambda } = (x_{i_\lambda , 1}, y_{i_\lambda , 1}, \cdots , x_{i_\lambda , 4}, y_{i_\lambda , 4})\) to prepare \((e_{\lambda , 1}, \cdots , e_{\lambda , 4})\) and \(\tilde{e}_{\lambda }\) as follows:
-
\((e_{\lambda ,1}, \cdots , e_{\lambda ,4}) :=( u_{\lambda , 1}^{- x_{i_\lambda ,1}} {u}_{\lambda , 2}^{- y_{i_\lambda ,1}} T^{k_{\lambda ,1}}, \cdots , u_{\lambda ,4}^{- x_{i_\lambda ,4}} {u}_{\lambda ,5}^{- y_{i_\lambda ,4}} T^{k_{\lambda ,4}}) \text { mod } N^2\),
-
\(\tilde{e}_\lambda := \tilde{u}_{\lambda ,1}^{- x_{i_\lambda ,1}} \tilde{u}_{\lambda ,2}^{- y_{i_\lambda ,1}} \tilde{u}_{\lambda ,3}^{- x_{i_\lambda ,2}} \tilde{u}_{\lambda ,4}^{- y_{i_\lambda ,2}} \tilde{u}_{\lambda ,5}^{- x_{i_\lambda ,3}} \tilde{u}_{\lambda ,6}^{- y_{i_\lambda ,3}} \tilde{u}_{\lambda ,7}^{- x_{i_\lambda ,4}} \tilde{u}_{\lambda ,8}^{- y_{i_\lambda ,4}} T^{m_{\beta }} \text { mod } N^s\).
Observe that for \(j\in \{1,2,3,4\}\),
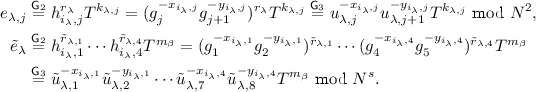
Thus \(\mathsf {G}_3\) is identical to \(\mathsf {G}_2\), and \(\Pr _2[\mathsf {Win}] = \Pr _3[\mathsf {Win}]\).
-
-
Game \(\mathsf {G}_{4}\): This game is the same as game \(\mathsf {G}_3\), except that, in the case of the challenge bit \(\beta = 1\), to answer the \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((f_\lambda , i_\lambda )\), the challenger does not use \((x_1,y_1, \cdots , x_4, y_4) \text { mod } N\) to compute \(\tilde{e}_{\lambda }\) any more, and instead, it computes \((\tilde{u}_{\lambda ,1}, \cdots , \tilde{u}_{\lambda ,8})\) and \(\tilde{e}_{\lambda }\) as follows:
-
\((\tilde{u}_{\lambda ,1}, \cdots , \tilde{u}_{\lambda ,8}) := (g_1^{\tilde{r}_{\lambda ,1}} T^{\sum _{i = 1}^n a_{i, 1}}, g_2^{\tilde{r}_{\lambda ,1}} T^{\sum _{i = 1}^n b_{i, 1}}, g_2^{\tilde{r}_{\lambda ,2}} T^{\sum _{i = 1}^n a_{i, 2}}, g_3^{\tilde{r}_{\lambda ,2}} \) \(~~~~\cdot T^{\sum _{i = 1}^n b_{i, 2}}, g_3^{\tilde{r}_{\lambda ,3}} T^{\sum _{i = 1}^n a_{i, 3}}, g_4^{\tilde{r}_{\lambda ,3}} T^{\sum _{i = 1}^n b_{i, 3}}, g_4^{\tilde{r}_{\lambda ,4}} T^{\sum _{i = 1}^n a_{i, 4}}, g_5^{\tilde{r}_{\lambda ,4}} T^{\sum _{i = 1}^n b_{i, 4}})\),
-
\(\tilde{e}_\lambda := h_{i_\lambda ,1}^{\tilde{r}_{\lambda ,1}} \cdots h_{i_\lambda ,4}^{\tilde{r}_{\lambda ,4}} T^{ \sum _{i = 1}^n \sum _{j = 1}^4 (a_{i,j} (\bar{x}_{i,j} - \bar{x}_{i_\lambda ,j}) + b_{i,j} (\bar{y}_{i,j} - \bar{y}_{i_\lambda ,j})) + c} \text { mod } N^s\),
where \(f_\lambda = ( \{ a_{i,1}, b_{i,1},\) \(\cdots , a_{i,4}, b_{i,4} \}_{i \in [n]}, c ) \in \mathcal {F}_{\text {aff}}\).
Observe that,
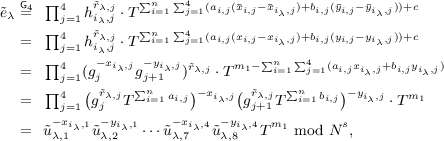
where the third equality follows from \(m_{1} = \sum _{i =1}^n \sum _{j = 1}^4 (a_{i,j} x_{i,j} + b_{i,j} y_{i,j} ) + c\). Therefore, \(\tilde{e}_\lambda \) can be computed from \((\tilde{u}_{\lambda ,1}, \cdots , \tilde{u}_{\lambda ,8})\) in the same way as in \(\mathsf {G}_{3}\) and \(\mathsf {G}_{4}\). Hence the only difference between \(\mathsf {G}_{3}\) and \(\mathsf {G}_{4}\) is the distribution of \((\tilde{u}_{\lambda ,1}, \cdots , \tilde{u}_{\lambda ,8})\) themselves. We analyze the difference via the following lemma, and the proof is presented in the full version [HLL16].
-
Lemma 4
There exists a PPT adversary \(\mathcal {B}_{1}\) against the IV\(_5\) assumption w.r.t. \(\mathsf {GenN}\) and \(\mathbb {QR}_{N^s}\), such that 
-
Game \(\mathsf {G}_{5}\): This game is the same as game \(\mathsf {G}_4\), except that, the challenger chooses random \(r^* \in \big [ \lfloor {N}/{4} \rfloor \big ]\) and \(\alpha _1, \cdots , \alpha _5\in \mathbb {Z}_N\) beforehand (in Initialize). In addition, to respond to the \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((f_\lambda , i_\lambda )\), the challenger computes \((u_{\lambda ,1}, \cdots , u_{\lambda , 5})\) as follows:
-
\((u_{\lambda ,1}, \cdots , u_{\lambda , 5}) := ((g_1^{r^*} T^{\alpha _1})^{r_{\lambda }}, \cdots , (g_5^{r^*} T^{\alpha _5})^{r_{\lambda }}) \text { mod } N^2\).
The only difference between \(\mathsf {G}_{4}\) and \(\mathsf {G}_{5}\) is the distribution of \((u_{\lambda ,1}, \cdots , u_{\lambda , 5})\). In game \(\mathsf {G}_{4}\), it equals \((g_1^{r_{\lambda }}, \cdots , g_5^{r_{\lambda }}) \text { mod } N^2\), while in game \(\mathsf {G}_{5}\), it equals \(((g_1^{r^*} T^{\alpha _1})^{r_{\lambda }}, \cdots , (g_5^{r^*} T^{\alpha _5})^{r_{\lambda }}) \text { mod } N^2\). Similar to the previous lemma, it is straightforward to construct a PPT adversary to solve IV\(_5\) problem by employing the power of adversary \(\mathcal {A}\). Thus
 .
. -
-
Game \(\mathsf {G}_{6}\): This game is the same as game \(\mathsf {G}_5\), except that, the challenger chooses a random tuple \(\mathsf {k}^* = (k_1^*, k_2^*, k_3^*, k_4^*)\) beforehand (in Initialize). In addition, to respond to the \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((f_\lambda , i_\lambda )\), the challenger uses a different way to generate \(\mathsf {k}_{\lambda } = (k_{\lambda ,1}, k_{\lambda ,2}, k_{\lambda ,3}, k_{\lambda ,4})\) and \((e_{\lambda ,1}, \cdots , e_{\lambda ,4})\):
-
pick
 and
and  uniformly, and compute \(\mathsf {k}_{\lambda } = (k_{\lambda ,1}, k_{\lambda ,2}, k_{\lambda ,3}, k_{\lambda ,4}) := (r_\lambda k_1^* + s_{\lambda ,1}, \cdots , r_\lambda k_4^* + s_{\lambda ,4})\).
uniformly, and compute \(\mathsf {k}_{\lambda } = (k_{\lambda ,1}, k_{\lambda ,2}, k_{\lambda ,3}, k_{\lambda ,4}) := (r_\lambda k_1^* + s_{\lambda ,1}, \cdots , r_\lambda k_4^* + s_{\lambda ,4})\). -
\((e_{\lambda ,1}, \cdots , e_{\lambda ,4}) :=\) \(( h_{i_\lambda ,1}^{r^* r_\lambda } T^{r_\lambda (k^*_1 - \alpha _1 x_{i_\lambda ,1} - \alpha _{2} y_{i_\lambda ,1}) + s_{\lambda ,1}}, \cdots , h_{i_\lambda ,4}^{r^* r_\lambda } T^{r_\lambda (k^*_4 - \alpha _4 x_{i_\lambda ,4} - \alpha _{5} y_{i_\lambda ,4}) + s_{\lambda ,4}})\).
Clearly \(\mathsf {k}_{\lambda }\) is uniformly distributed over \(\mathbb {Z}_N^4\), as in game \(\mathsf {G}_{5}\). At the same time, observe that for \(j\in \{1, 2, 3, 4\}\),
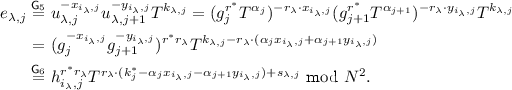
Thus \(\mathsf {G}_6\) is identical to \(\mathsf {G}_5\), and
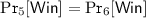 .
. -
-
Game \(\mathsf {G}_{7}\): This game is the same as game \(\mathsf {G}_6\), except for a modification to answering the \(\textsc {Dec}\) queries \((\langle \textsf {aux}, \mathsf {aiae}.\textsf {ct} \rangle , i \in [n])\). The challenger uses the i-th user’s secret key \(\textsf {sk}_{i} = (x_{i, 1}, y_{i, 1}, \cdots , x_{i, 4}, y_{i, 4})\) together with \(\phi (N)\) to compute the decryption of ciphertext \(\langle \textsf {aux}, \mathsf {aiae}.\textsf {ct} \rangle \), where \(\textsf {aux} = (u_1, \cdots , u_5, e_1,\) \(\cdots , e_4)\). More precisely, it computes \(\mathsf {k}= (k_1, \cdots , k_4)\) and m as follows:
-
\((\alpha _1', \cdots , \alpha _5') := \big (\text {dlog}_{T} (u_1^{\phi (N)}) / \phi (N), \cdots , \text {dlog}_{T} (u_5^{\phi (N)}) / \phi (N)\big ) \text { mod } N\), \((\gamma _1', \cdots , \gamma _4') := \big (\text {dlog}_{T} (e_1^{\phi (N)}) / \phi (N), \cdots , \text {dlog}_{T} (e_4^{\phi (N)}) / \phi (N)\big ) \text { mod } N\), \(\mathsf {k}= (k_1, \cdots , k_4) := (\alpha _1' x_{i,1} + \alpha _2' y_{i,1} + \gamma _1', \cdots , \alpha _4' x_{i,4} + \alpha _5' y_{i,4} + \gamma _4') \text { mod } N\),
-
\({{\mathcal {E}}\textsf {.ct}} = (\tilde{u}_1, \cdots , \tilde{u}_8, \tilde{e}, t) / \bot \leftarrow \mathsf {AIAE}\textsf {.Dec}\big ( \mathsf {k}, \mathsf {aiae}\textsf {.ct}, \textsf {aux} \big )\),
-
\((\tilde{\alpha }_1, \cdots , \tilde{\alpha }_8) := \big (\text {dlog}_{T} (\tilde{u}_1^{\phi (N)}) / \phi (N), \cdots , \text {dlog}_{T} (\tilde{u}_8^{\phi (N)}) / \phi (N)\big ) \text { mod } N^{s-1}\), \(\tilde{\gamma } := \text {dlog}_{T} (\tilde{e}^{\phi (N)}) / \phi (N) \text { mod } N^{s-1}\), and \(m := \tilde{\alpha }_1 x_{i,1} + \tilde{\alpha }_2 y_{i,1} + \tilde{\alpha }_3 x_{i,2} + \tilde{\alpha }_4 y_{i,2} + \tilde{\alpha }_5 x_{i,3} + \tilde{\alpha }_6 y_{i,3} + \tilde{\alpha }_7 x_{i,4} + \tilde{\alpha }_8 y_{i,4} + \tilde{\gamma }\text { mod } N^{s-1}\).
According to Eq. (1), for \(j \in \{1, 2, 3, 4\}\), we have that
These changes are conceptual. So \(\mathsf {G}_7\) is identical to \(\mathsf {G}_6\),
 .
. -
-
Game \(\mathsf {G}_{8}\): This game is the same as game \(\mathsf {G}_7\), except that, the challenger adds an additional rejection rule when answering Dec queries as follows:
-
if \(\alpha '_1 \ne 0 \vee \cdots \vee \alpha '_5 \ne 0 ~ \vee ~ \tilde{\alpha }_1 \ne 0 \vee \cdots \vee \tilde{\alpha }_8 \ne 0\), return \(\bot \).
That is, the challenger will not output m in Dec unless \(\alpha _1' = \cdots = \alpha _5' = 0\) and \(\tilde{\alpha }_1 = \cdots = \tilde{\alpha }_8 = 0\) holds. Thus the values of \((x_{i,j}, y_{i,j})_{j = 1}^{4} \text { mod } N\), in particular \((x_{j}, y_{j})_{j = 1}^{4} \text { mod } N\), are not used any more in Dec.
Let \(\mathsf {Bad}\) denote the event that \(\mathcal {A}\) makes a Dec query \(\big (\langle \textsf {aux}, \mathsf {aiae}\textsf {.ct} \rangle , i \in [n]\big )\), such that
$$\begin{aligned}&e_1 u_1^{x_{i,1}} u_2^{y_{i,1}}, \cdots , e_4 u_4^{x_{i,4}} u_5^{y_{i,4}} \in \mathbb {RU}_{N^2} ~ \wedge ~ \mathsf {AIAE}\textsf {.Dec}\big ( \mathsf {k}, \mathsf {aiae}\textsf {.ct}, \textsf {aux} \big ) \ne \bot \end{aligned}$$(2)$$\begin{aligned}&\wedge ~ \tilde{e} \tilde{u}_1^{x_{i,1}} \tilde{u}_2^{y_{i,1}} \tilde{u}_3^{x_{i,2}} \tilde{u}_4^{y_{i,2}} \tilde{u}_5^{x_{i,3}} \tilde{u}_6^{y_{i,3}} \tilde{u}_7^{x_{i,4}} \tilde{u}_8^{y_{i,4}} \in \mathbb {RU}_{N^s} ~\wedge ~ t = g_1^m \text { mod } N \\ \nonumber&\qquad \wedge ~ \big (\alpha '_1 \ne 0 \vee \cdots \vee \alpha '_5 \ne 0 ~ \vee ~ \tilde{\alpha }_1 \ne 0 \vee \cdots \vee \tilde{\alpha }_8 \ne 0 \big ). \end{aligned}$$(3)Clearly, games \(\mathsf {G}_7\) and \(\mathsf {G}_8\) are the same until \({\mathsf {Bad}}\) happens. Therefore, we have that
 To prove that \(\mathsf {G}_7\) and \(\mathsf {G}_8\) are indistinguishable, we have to show that
To prove that \(\mathsf {G}_7\) and \(\mathsf {G}_8\) are indistinguishable, we have to show that  is negligible. This is not an easy task, and we further divide \(\mathsf {Bad}\) to two disjoint sub-events:
is negligible. This is not an easy task, and we further divide \(\mathsf {Bad}\) to two disjoint sub-events:-
\(*\) \(\mathsf {Bad}'\) denotes the event that \(\mathcal {A}\) makes a Dec query such that
$$\begin{aligned} \begin{aligned} \text {Conditions (2), (3) hold} ~\wedge ~ \big (\alpha '_1 \ne 0 \vee \cdots \vee \alpha '_5 \ne 0 \big ). \end{aligned} \end{aligned}$$ -
\(*\) \(\widetilde{\mathsf {Bad}}\) denotes the event that \(\mathcal {A}\) makes a Dec query such that
$$\begin{aligned} \begin{aligned} \text {Conditions (2), (3) hold} ~\wedge ~ \big (\alpha _1' = \cdots = \alpha _5' = 0 \big ) ~ \wedge ~ \big (\tilde{\alpha }_1 \ne 0 \vee \cdots \vee \tilde{\alpha }_8 \ne 0 \big ). \end{aligned} \end{aligned}$$
Then
 We give an upper bound for
We give an upper bound for  via the following lemma. See the full version [HLL16] for the proof. The analysis of
via the following lemma. See the full version [HLL16] for the proof. The analysis of  is deferred to subsequent games.
is deferred to subsequent games. -
Lemma 5
 .
.
-
Game \(\mathsf {G}_{9}\): This game is the same as game \(\mathsf {G}_8\), except that, the challenger chooses another random tuple \(\overline{\mathsf {k}}^* = (\bar{k}^*_1, \bar{k}^*_2, \bar{k}^*_3, \bar{k}^*_4)\) besides \(\mathsf {k}^* = ({k}^*_1, {k}^*_2, {k}^*_3, {k}^*_4)\) in Initialize. In addition, to answer the \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((f_\lambda , i_\lambda )\), the challenger uses a different key for \(\mathsf {AIAE}\) to compute \({\mathsf {aiae}\textsf {.ct}}_{\lambda }\):
-
set \(\overline{\mathsf {k}}_{\lambda } = (\bar{k}_{\lambda ,1}, \bar{k}_{\lambda ,2}, \bar{k}_{\lambda ,3}, \bar{k}_{\lambda ,4}) := (r_\lambda \bar{k}_1^* + s_{\lambda ,1}, \cdots , r_\lambda \bar{k}_4^* + s_{\lambda ,4})\);
-
invoke
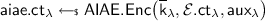 .
.
But the challenger still uses \(\mathsf {k}^*=({k}^*_1, {k}^*_2, {k}^*_3, {k}^*_4)\) to compute \((e_{\lambda ,1}, \cdots , e_{\lambda ,4})\).
In game \(\mathsf {G}_8\), the only place that needs the value of \((x_{1}, y_1, \cdots , x_4, y_4) \text { mod } N\) is the computation of \((e_{\lambda , 1},\) \(\cdots , e_{\lambda , 4})\) in Enc. More precisely, for \(j \in \{1, 2, 3, 4\}\),
$$\begin{aligned} e_{\lambda , j}= & {} h_{i_\lambda ,j}^{r^* r_\lambda } T^{r_\lambda \cdot (k^*_j - \alpha _j x_{i_\lambda ,j} - \alpha _{j+1} y_{i_\lambda ,j}) + s_{\lambda ,j}} \text { mod } N^2 \\= & {} h_{i_\lambda ,j}^{r^* r_\lambda } T^{r_\lambda \cdot (k^*_j - \alpha _j x_j - \alpha _{j+1} y_j - \alpha _j \bar{x}_{i_\lambda ,j} - \alpha _{j+1} \bar{y}_{i_\lambda ,j}) + s_{\lambda ,j}} \text { mod } N^2. \end{aligned}$$We stress that the computation of \(t_\lambda = g_1^{m_\beta } \text { mod }N\) in Enc only uses the values of \((x_{1}, y_1, \cdots , x_4,\) \(y_4) \text { mod } \phi (N)/4\), since the order of \(g_1 \in \mathbb {SCR}_{N^s}\) is \(\phi (N)/4\). We also note that neither \(\mathsf {k}^* = (k_1^*, k_2^*, k_3^*, k_4^*)\) nor \((x_j, y_j)_{j=1}^{4} \text { mod } N\) is involved in Dec since \(\textsc {Dec}\) rejects the ciphertext unless \(\alpha _1' = \cdots = \alpha _5' = 0\) and \(\tilde{\alpha }_1 = \cdots = \tilde{\alpha }_8 = 0\). As a result, \(\mathsf {k}^* = (k_1^*, k_2^*, k_3^*, k_4^*)\) is totally hidden by the entropy of \((x_{1}, y_1, \cdots , x_4, y_4) \text { mod } N\) and is uniformly random to \(\mathcal {A}\).
Thus the challenger can use an independent \(\overline{\mathsf {k}}^* = (\bar{k}_1^*, \cdots , \bar{k}_4^*)\) to compute \(\overline{\mathsf {k}}_{\lambda }\), and use \(\overline{\mathsf {k}}_{\lambda }\) to do the encryption of the \(\mathsf {AIAE}\) scheme in Enc, as in \(\mathsf {G}_9\).
Then games \(\mathsf {G}_8\) and \(\mathsf {G}_9\) are identically distributed from the point of view of \(\mathcal {A}\), thus we have
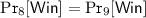 and
and  .
. -
-
Game \(\mathsf {G}_{10}\): This game is the same as game \(\mathsf {G}_9\), except that, to answer the \(\lambda \)-th (\(\lambda \in [Q_e]\)) Enc query \((f_\lambda , i_\lambda )\), the challenger computes \({\mathsf {aiae}\textsf {.ct}}_{\lambda }\) as follows:
-
invoke
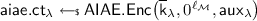 .
.
That is, the challenger computes the \(\mathsf {AIAE}\) encryption of a constant \(0^{\ell _{\mathcal {M}}}\) instead of \( \mathcal {E}\textsf {.ct}_{\lambda }\) in \(\textsc {Enc}\). Note that in games \(\mathsf {G}_9\) and \(\mathsf {G}_{10}\), the key \(\overline{\mathsf {k}}^* = (\bar{k}^*_1, \bar{k}^*_2, \bar{k}^*_3, \bar{k}^*_4)\) is used only in the computation of the \(\mathsf {AIAE}\) encryption, where it uses \(\overline{\mathsf {k}}_{\lambda } = r_{\lambda } \cdot \overline{\mathsf {k}}^* + \textsf {s}_{\lambda }\), \(\textsf {s}_{\lambda } = (s_{\lambda ,1}, \cdots , s_{\lambda , 4})\), as the encryption key. The difference between \(\mathsf {G}_9\) and \(\mathsf {G}_{10}\) can be reduced to the IND-\(\mathcal {F}_{\text {raff}}\)-RKA security of the \(\mathsf {AIAE}\) scheme directly. Thus we have that both
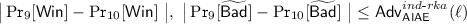 .
.Now in \(\mathsf {G}_{10}\), the challenger computes the \(\mathsf {AIAE}\) encryption of a constant \(0^{\ell _{\mathcal {M}}}\) in \(\textsc {Enc}\), thus the challenge bit \(\beta \) is completely hidden. Then
 .
.We give an upper bound for
 via the following lemma, and present its proof in the full version [HLL16].
via the following lemma, and present its proof in the full version [HLL16]. -
Lemma 6
 .
.
Taking all things together, the n-KDM[\(\mathcal {F}_{\text {aff}}\)]-CCA security of \({\textsf {PKE}}\) follows. \(\blacksquare \)
6 PKE with n-KDM[\(\mathcal {F}_{\text {poly}}^d\)]-CCA Security
6.1 The Basic Idea
We consider how to construct a PKE which is n-KDM-CCA secure w.r.t. the set of polynomial functions of bounded degree d, denoted by \(\mathcal {F}_{\text {poly}}^{d}\), where d can be polynomial in security parameter \(\ell \). We will consider adversaries submitting f in the format of Modular Arithmetic Circuit (MAC) [MTY11], i.e., a polynomial-size circuit which computes f. In particular, we do not require a prior bound on the size of circuits, but only require a prior bound d on the degree of the polynomials. Our construction still follows the approach in Fig. 1. In fact, our n-KDM[\(\mathcal {F}_{\text {poly}}^d\)]-CCA secure PKE shares the same building blocks \(\textsf {KEM}\) and \(\mathsf {AIAE}\) with the previous PKE in Fig. 7 which has n-KDM[\(\mathcal {F}_{\text {aff}}\)]-CCA security. What we should do is to design a new building block \(\mathcal {E}\), which can function as an entropy filter for polynomial functions. Our new \(\mathcal {E}\) still share the same secret/public key pair with \(\textsf {KEM}\). Hence for \(i\in [n]\), we have \(\textsf {sk}_i=(x_{i,1}, y_{i,1}, \cdots ,x_{i,4}, y_{i,4})\) and \(\textsf {pk}_i=(h_{i,1}, \cdots , h_{i,4})\) with \(h_{i,1}=g_1^{{-}x_{i,1}}g_2^{{-} y_{i,1}}\), \(\cdots \), \(h_{i,4}=g_4^{{-} x_{i,4}}g_5^{{-} y_{i,4}} \text { mod }N^s\).
6.2 Reducing Polynomials of 8n Variables to Polynomials of 8 Variables
How to Reduce 8n -Variable Polynomial \(f_\lambda \) in \(\textsc {Enc}\) \((f_\lambda , i_{\lambda }\in [n])\). In the n-\(\mathsf {KDM}\)[\(\mathcal {F}_{\text {poly}}^d\)]-\(\mathsf {CCA}\) game, the adversary will submit \((f_\lambda , i_{\lambda }\in [n])\) to \(\textsc {Enc}\) as its \(\lambda \)-th KDM encryption query. Here \(f_\lambda \) is a degree-d polynomial \(f_\lambda \big ( (x_{i,j},y_{i,j})_{i\in [n], j\in [4]} \big )\) of the n secret keys, which has 8n variables. Note that \(f_\lambda \) will contain at most \(\left( {\begin{array}{c}8n+d\\ 8n\end{array}}\right) \) \(= \varTheta (d^{8n})\) monomials, which is exponentially large.
To reduce the number of monomials, we can always change the polynomial \(f_\lambda \big ( (x_{i,j},y_{i,j})_{i\in [n], j\in [4]} \big )\) of 8n variables to a polynomial \(f_\lambda '\big ( (x_{i_\lambda ,j},y_{i_\lambda ,j})_{j\in [4]} \big )\) of 8 variables as follows. Then \(f_\lambda '\) will contain at most \(\left( {\begin{array}{c}8+d\\ 8\end{array}}\right) =\varTheta (d^8)\) monomials, which is polynomial in \(\ell \).
In Initialize, the secret keys can be generated with \({x}_{i,j} := x_j + \bar{x}_{i,j}\) and \({y}_{i,j} := y_j + \bar{y}_{i,j} \text { mod } \lfloor {N^2}/{4} \rfloor \) for \(i \in [n]\) and \(j \in [4]\). Then with the values of \((\bar{x}_{i,j},\bar{y}_{i,j})_{i\in [n],\,j\in [4]}\), we can represent \(({x}_{i,j}, {y}_{i,j})_{i\in [n],\,j\in [4]}\) as shifts of \((x_{i_\lambda ,j},y_{i_\lambda ,j})_{j\in [4]}\):
and reduce the polynomial \(f_\lambda \) in 8n variables \(({x}_{i,j}, {y}_{i,j})_{i\in [n],\,j\in [4]}\) to a polynomial \(f'_\lambda \) in 8 variables \((x_{i_\lambda ,j},y_{i_\lambda ,j})_{j\in [4]}\):
The resulting polynomial \(f'_\lambda \) is also of degree at most d, and the coefficients \(a_{(c_1,\cdots ,c_8)}\) are determined by \((\bar{x}_{i,j},\bar{y}_{i,j})_{i\in [n],j\in [4]}\) completely.
How to Determine Coefficients \(a_{(c_1,\cdots ,c_8)}\) for \(f'_\lambda \) Efficiently with Only \((\bar{x}_{i,j},\bar{y}_{i,j})_{i\in [n],\,j\in [4]}\). Repeat choosing values of \((x_{i_{\lambda },j}, y_{i_{\lambda },j})_{j\in [4]}\) randomly, feeding MAC (which functions as \(f_\lambda \)) with input of \((x_{i_\lambda ,j} + \bar{x}_{i,j} - \bar{x}_{i_\lambda ,j}, y_{i_\lambda ,j} + \bar{y}_{i,j} - \bar{y}_{i_\lambda ,j})_{i\in [n],\, j\in [4]}\), where \((\bar{x}_{i,j},\bar{y}_{i,j})_{i\in [n],j\in [4]}\) always takes the values chosen in Initialize, and recording the output of MAC. After about \(\left( {\begin{array}{c}8+d\\ 8\end{array}}\right) =\varTheta (d^8)\) times, we can extract all \(a_{(c_1,\cdots ,c_8)}\) by simply solving a system of linear equations (with \(a_{(c_1,\cdots ,c_8)}\) unknowns):
This can be done in time polynomial in \(\ell \).
6.3 How to Design \(\mathcal {E}\): A Warmup
Let us first consider a simple case: design \(\mathcal {E}\) w.r.t. a specific type of monomials
We describe the encryption and decryption algorithms \(\mathcal {E}.\textsf {Enc}\), \(\mathcal {E}.\textsf {Dec}\) in Fig. 8.
Security proof. We can prove KDM-CCA security w.r.t. the specific type of monomials, i.e., \(a \cdot x_{i_{\lambda },1} y_{i_{\lambda },1}\) \(x_{i_{\lambda },2} y_{i_{\lambda },2} x_{i_{\lambda },3} y_{i_{\lambda },3} x_{i_{\lambda },4} y_{i_{\lambda },4}\), in a similar way as the proof of Theorem 2. The only difference lies in games \(\textsf {G}_3\)-\(\textsf {G}_4\), which are related to \(\mathcal {E}\). We replace \(\textsf {G}_3\)-\(\textsf {G}_4\) with the following three steps (Step 1–Step 3). More precisely, we change the \(\mathcal {E}.\textsf {Enc}\) part of \(\textsc {Enc}\) so that it can reserve the entropy of \((x_1, y_1, \cdots , x_4, y_4) \text { mod } N\), behaving like an entropy filter w.r.t. this specific kind of monomials.
Suppose that the adversary submits \((f_\lambda , i_{\lambda }\in [n])\) to Enc. Our aim is to reserve the entropy of \((x_j, y_j)_{j = 1}^{4} \text { mod } N\) from \(\mathcal {E}.\textsf {Enc}\big ( \textsf {pk}_{i_{\lambda }}, f_\lambda \big ( (x_{i,j},y_{i,j})_{i\in [n],\, j\in [4]} \big ) \big )\).
-
Step 0: In Initialize, the secret keys are generated with \({x}_{i,j} := x_j + \bar{x}_{i,j}\) and \({y}_{i,j} := y_j + \bar{y}_{i,j} \text { mod } \lfloor {N^2}/{4} \rfloor \) for \(i \in [n]\), \(j \in [4]\). This is the same as \(\textsf {G}_2\) in the proof of Theorem 2.
-
Step 1: Use \((\bar{x}_{i,j},\bar{y}_{i,j})_{i\in [n],j\in [4]}\) to re-explain \((f_\lambda , i_{\lambda }\in [n])\) as \((f'_\lambda , i_{\lambda }\in [n])\), and determine the coefficient a of the monomial
$$\begin{aligned} f'_\lambda \big ( (x_{i_\lambda ,j},y_{i_\lambda ,j})_{j \in [4]} \big )=a \cdot x_{i_{\lambda },1} y_{i_{\lambda },1} x_{i_{\lambda },2} y_{i_{\lambda },2} x_{i_{\lambda },3} y_{i_{\lambda },3} x_{i_{\lambda },4} y_{i_{\lambda },4}. \end{aligned}$$ -
Step 2: Use secret key \(\mathsf {sk}_{i_\lambda } = (x_{i_\lambda ,j},y_{i_\lambda ,j})_{j \in [4]}\) (together with public key \(\mathsf {pk}_{i_\lambda } = (h_{i_\lambda ,j})_{j \in [4]}\)) to implement \(\mathcal {E}.\textsf {Enc}\) (This corresponds to \(\textsf {G}_3\) in the proof of Theorem 2).
-
– Setup table, just like \(\mathcal {E}.\textsf {Enc}\).
-
– Compute \(\hat{v}_0, \cdots , \hat{v}_8\) from table, just like \(\mathcal {E}.\textsf {Dec}\).
-
– Use \(\hat{v}_8\) instead of \(\tilde{v}_8\) to compute \(\tilde{e}\) with \(\tilde{e} := \hat{v}_{8}\cdot T^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )} \text { mod }N^s\), and \(t := g_1^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )} \text { mod } N\).
It is easy to check that \(\hat{v}_0, \cdots , \hat{v}_8\) computed from table (via \(\mathcal {E}.\textsf {Dec}\)) are identical to \(\tilde{v}_0, \cdots , \tilde{v}_8\) that are used to generate table (via \(\mathcal {E}.\textsf {Enc}\)). Thus this change is conceptual.
-
-
Step 3: This corresponds to \(\textsf {G}_4\) in the proof of Theorem 2.
-
– \({\textsf {table}}\) is set up in a similar way as in \(\mathcal {E}.\textsf {Enc}\), but with the following difference. The item of row 1 and column 1 in table now is computed as \(\hat{u}_{1,1}=(\tilde{u}_{1,1} T^{a})\cdot \tilde{v}_{0}\) instead of \(\hat{u}_{1,1} =\tilde{u}_{1,1}\cdot \tilde{v}_{0}\). This change is computationally indistinguishable, due to the IV\(_5\) assumption. (We refer to a detailed analysis in the full version [HLL16].)
-
– Compute \(\hat{v}_0, \cdots , \hat{v}_8\) from table, just like \(\mathcal {E}.\textsf {Dec}\).
-
– \(\tilde{e} := \hat{v}_{8}\cdot T^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )} \text { mod }N^s\), and \(t := g_1^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )} \text { mod } N\).
It is easy to check that \(\hat{v}_0 = \tilde{v}_0, \hat{v}_1 = \tilde{v}_1 \cdot T^{- a x_{i_\lambda , 1}}, \hat{v}_2 = \tilde{v}_2 \cdot T^{- a x_{i_\lambda , 1} y_{i_\lambda , 1}}\), \(\cdots \), \(\hat{v}_8 = \tilde{v}_8 \cdot T^{- a x_{i_\lambda , 1} y_{i_\lambda , 1} \cdots x_{i_\lambda , 4} y_{i_\lambda , 4}}\) \(= \tilde{v}_8 \cdot T^{- f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )}\), thus \(\tilde{e} = \hat{v}_{8}\cdot T^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )} = \tilde{v}_8\). Therefore we can also implement Step 3 equivalently as follows.
-
-
Step 3 (Equivalent Form):
-
– \({\textsf {table}}\) is set up in a similar way as in \(\mathcal {E}.\textsf {Enc}\), but with the following difference. The item of row 1 and column 1 in table is computed as \(\hat{u}_{1,1}=(\tilde{u}_{1,1} T^{a})\cdot \tilde{v}_{0}\) instead of \(\hat{u}_{1,1} =\tilde{u}_{1,1}\cdot \tilde{v}_{0}\).
-
– \(\tilde{e} := \tilde{v}_8 \text { mod }N^s\), and \(t := g_1^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} ) \text { mod } \phi (N)/4} \text { mod } N\).
In this step, \(\mathcal {E}.\) Enc does not use \((x_1, y_1, \cdots , x_4, y_4) \text { mod } N\) at all (only uses \((\bar{x}_{i,j},\bar{y}_{i,j})_{i\in [n],j\in [4]}\) and \((x_1, y_1, \cdots ,\) \(x_4, y_4) \text { mod } \phi (N)/4\)).
-
Consequently, through the computationally indistinguishable change, the entropy of \((x_1, y_1, \cdots , x_4,\) \(y_4) \text { mod } N\) is reserved by the \(\mathcal {E}.\textsf {Enc}\) part of \(\textsc {Enc}\).
Similarly, Dec can be changed to do decryptions without \((x_j, y_j)_{j = 1}^{4} \text { mod } N\). This can be done with \(\phi (N)\) and the \((\text {mod } \phi (N)/4)\) part of secret key. (This corresponds to \(\textsf {G}_7\)-\(\textsf {G}_8\) in the proof of Theorem 2). Use \(\phi (N)\) to make sure that all items in table of \(\mathcal {E}.\textsf {ct}\) belong to \(\mathbb {SCR}_{N^s}\). If not, reject immediately. As a result, Dec does not leak any information of \((x_1, y_1, \cdots , x_4, y_4) \text { mod } N\). This change is computationally indistinguishable, just like the analysis of \(\Pr [{{\mathsf {Bad}}}]\) as in the proof of Theorem 2.
6.4 The General \(\mathcal {E}\) Designed for \(\mathcal {F}_{\text {poly}}^d\)
The previous subsection showed how to design \(\mathcal {E}\) for a specific type of monomials. A general \(f'_\lambda \) of degree d contains at most \(\left( {\begin{array}{c}8+d\\ 8\end{array}}\right) =\varTheta (d^8)\) monomials. To design a general \(\mathcal {E}\) for \(\mathcal {F}_{\text {poly}}^d\), we have to consider all possible types of monomials. For each type of non-constant monomial, we create a table and each table is associated with a \(\tilde{v}\), which is called a title, and those \(\tilde{v}\)’s are used to hide message in \(\tilde{e}\). We describe \(\mathcal {E}.\textsf {Enc}\) and \(\mathcal {E}.\textsf {Dec}\) in Fig. 9.
Top: \(\mathcal {E}\) .Enc (left) and \(\mathcal {E}\) .Dec (right) of \(\mathcal {E}\) designed for \(\mathcal {F}_{\text {poly}}^d\); Middle: \(\textsf {TableGen}\), which generates \(\textsf {table}^{(\textsf {c})}\) together with a title \(\tilde{v}^{(\textsf {c})}\); Bottom: \(\textsf {CalculateV}\), which calculates a title \(\hat{v}^{(\textsf {c})}\) from \(\textsf {table}^{(\textsf {c})}\) using secret key.
There are totally \(\left( {\begin{array}{c}8+d\\ 8\end{array}}\right) -1\) types of non-constant monomials of degree at most d if we neglect the coefficients. Each type of non-constant monomial \(x_{i_{\lambda },1}^{c_1} y_{i_{\lambda },1}^{c_2} x_{i_{\lambda },2}^{c_3}\) \(y_{i_{\lambda },2}^{c_4} x_{i_{\lambda },3}^{c_5} y_{i_{\lambda },3}^{c_6} x_{i_{\lambda },4}^{c_7} y_{i_{\lambda },4}^{c_8}\) is associated with a tuple \(\textsf {c} = (c_1, \cdots c_8)\), which determines degrees of each variable. Denote by \(\mathcal {S}\) the set containing all such tuples, i.e., \(\mathcal {S} := \big \{ \textsf {c} = (c_1, \cdots c_8)~\big |~ 1\le c_1 + \cdots + c_8 \le d \big \}\).
For each \(\textsf {c} = (c_1, \cdots c_8) \in \mathcal {S}\), we generate \(\textsf {table}^{(\textsf {c})}\) and its title \(\tilde{v}^{(\textsf {c})}\) for monomial \(x_{i_{\lambda },1}^{c_1} y_{i_{\lambda },1}^{c_2} x_{i_{\lambda },2}^{c_3} y_{i_{\lambda },2}^{c_4}\) \(x_{i_{\lambda },3}^{c_5} y_{i_{\lambda },3}^{c_6} x_{i_{\lambda },4}^{c_7} y_{i_{\lambda },4}^{c_8}\) via the algorithm \(\textsf {TableGen}\) illustrated in Fig. 9. Intuitively, TableGen generates \(\textsf {table}^{(\textsf {c})}\) of \(1 + c_1 + \cdots +c_8\) rows. The 0-th row of \(\textsf {table}^{(\textsf {c})}\) is \(\tilde{u}_{0,1}, \cdots , \tilde{u}_{0,8}\). The form of other rows are similar to row 0 with a small difference: the next \(c_1\) rows in the 1-st column are multiplied with \(\tilde{v}_0\), \(\tilde{v}_1\), \(\cdots , \tilde{v}_{c_1-1}\) respectively; the next \(c_2\) rows in the 2-nd column are multiplied with \(\tilde{v}_{c_1}\), \(\tilde{v}_{c_1+1}\), \(\cdots , \tilde{v}_{c_1+c_2-1}\) respectively, and so forth. TableGen also generates a title \(\tilde{v}^{(\textsf {c})}\) for \(\textsf {table}^{(\textsf {c})}\). The product of all the titles, i.e., \(\prod _{\textsf {c} \in \mathcal {S}}\tilde{v}^{(\textsf {c})}\), is used to hide \(T^m\) in \(\tilde{e}\).
On the other hand, the title \(\hat{v}^{(\textsf {c})} = \tilde{v}^{(\textsf {c})}\) can be recovered from \(\textsf {table}^{(\textsf {c})}\) with secret key \(\textsf {sk} = (x_1, y_1, \cdots , x_4, y_4)\) via the CalculateV algorithm in Fig. 9. Therefore, one can always use the secret key to extract the titles \((\tilde{v}^{(\textsf {c})})_{\textsf {c} \in \mathcal {S}}\) from tables \(\big (\textsf {table}^{(\textsf {c})}\big )_{\textsf {c} \in \mathcal {S}}\) one by one with CalculateV and then recover m correctly.
Security proof. The proof of KDM\([\mathcal {F}_{\text {poly}}^d]\)-CCA security is similar to that of Theorem 2. But games \(\textsf {G}_3\)-\(\textsf {G}_4\) should be replaced with the following three steps (Step 1–Step 3), so that the \(\mathcal {E}.\textsf {Enc}\) part of \(\textsc {Enc}\) can be changed to work as an entropy filter, i.e., reserving the entropy of \((x_1, y_1, \cdots , x_4, y_4) \text { mod } N\), w.r.t. any polynomial of degree at most d.
Suppose that the adversary submits \((f_\lambda ,i_{\lambda }\in [n])\) to Enc. Our aim is to reserve the entropy of \((x_j, y_j)_{j = 1}^{4} \text { mod } N\) from \(\mathcal {E}.\textsf {Enc}\big ( \textsf {pk}_{i_{\lambda }}, f_\lambda \big ( (x_{i,j},y_{i,j})_{i\in [n], j\in [4]} \big ) \big )\).
-
Step 0: In Initialize, the secret keys are generated with \({x}_{i,j} := x_j + \bar{x}_{i,j}\) and \({y}_{i,j} := y_j + \bar{y}_{i,j} \text { mod } \lfloor {N^2}/{4} \rfloor \) for \(i \in [n]\), \(j \in [4]\). This is the same as \(\textsf {G}_2\) in the proof of Theorem 2.
-
Step 1: Use \((\bar{x}_{i,j},\bar{y}_{i,j})_{i\in [n],j\in [4]}\) to re-explain \((f_\lambda , i_{\lambda }\in [n])\) as \((f'_\lambda , i_{\lambda }\in [n])\), and determine the coefficients \(a_{(c_1,\cdots ,c_8)}\) of each monomial of \(f'_\lambda \), as discussed in Subsect. 6.2. Note that \(a_{(c_1,\cdots ,c_8)} = 0\) if the associated monomial does not appear in \(f'_\lambda \). Then
$$\begin{aligned} f'_\lambda \big ((x_{i_\lambda ,j},y_{i_\lambda ,j})_{j \in [4]}\big ) = \textstyle \sum \limits _{(c_1, \cdots , c_8) \in \mathcal {S}}a_{(c_1, \cdots , c_8)}\cdot x_{i_{\lambda },1}^{c_1} y_{i_{\lambda },1}^{c_2} x_{i_{\lambda },2}^{c_3} y_{i_{\lambda },2}^{c_4} x_{i_{\lambda },3}^{c_5} y_{i_{\lambda },3}^{c_6} x_{i_{\lambda },4}^{c_7} y_{i_{\lambda },4}^{c_8} + \delta , \end{aligned}$$where \(\delta \) \(= a_{(0,\cdots ,0)}\) denotes the constant term of \(f'_\lambda \).
-
Step 2: Use secret key \(\mathsf {sk}_{i_\lambda } = (x_{i_\lambda ,j},y_{i_\lambda ,j})_{j \in [4]}\) (together with public key \(\mathsf {pk}_{i_\lambda } = (h_{i_\lambda ,j})_{j \in [4]}\)) to implement \(\mathcal {E}.\textsf {Enc}\) (This corresponds to \(\textsf {G}_3\) in the proof of Theorem 2).
-
– For each \(\textsf {c} = (c_1, \cdots , c_8) \in \mathcal {S}\)
(1)
 ,
,(2) \(\hat{v}^{(\textsf {c})} \leftarrow \textsf {CalculateV}(\textsf {sk}_{i_\lambda }, \textsf {table}^{(\textsf {c})}, \textsf {c} )\).
-
– Use \(\big ( \hat{v}^{(\textsf {c})} \big )_{\textsf {c} \in \mathcal {S}}\) instead of \(\big ( \tilde{v}^{(\textsf {c})} \big )_{\textsf {c} \in \mathcal {S}}\) to compute \(\tilde{e}\) with \(\tilde{e} := \prod _{\textsf {c} \in \mathcal {S}}\hat{v}^{(\textsf {c})} \cdot T^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )} \text { mod }N^s\), and \(t := g_1^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )} \text { mod } N\).
It is easy to check that for each \(\textsf {c} = (c_1, \cdots , c_8) \in \mathcal {S}\), \(\hat{v}^{(\textsf {c})}\) computed from \(\textsf {table}^{(\textsf {c})}\) via CalculateV is identical to \(\tilde{v}^{(\textsf {c})}\) associated with \(\textsf {table}^{(\textsf {c})}\) via TableGen. Thus this change is conceptual.
-
-
Step 3: This corresponds to \(\textsf {G}_4\) in the proof of Theorem 2.
-
– For each \(\textsf {c} = (c_1, \cdots , c_8) \in \mathcal {S}\)
-
(1)
Compute \(\textsf {table}^{(\textsf {c})}\) via
 , but with one difference. The item of row 1 and column \(j := \min \{ i~|~ 1 \le i \le 8, c_i \ne 0 \}\) in \(\textsf {table}^{(\textsf {c})}\) now is computed as \(\hat{u}_{1,j}=(\tilde{u}_{1,j} T^{a_{(c_1, \cdots , c_8)}})\cdot \tilde{v}_{0}\) instead of \(\hat{u}_{1,j} =\tilde{u}_{1,j}\cdot \tilde{v}_{0}\). This change is computationally indistinguishable, due to the IV\(_5\) assumption.
, but with one difference. The item of row 1 and column \(j := \min \{ i~|~ 1 \le i \le 8, c_i \ne 0 \}\) in \(\textsf {table}^{(\textsf {c})}\) now is computed as \(\hat{u}_{1,j}=(\tilde{u}_{1,j} T^{a_{(c_1, \cdots , c_8)}})\cdot \tilde{v}_{0}\) instead of \(\hat{u}_{1,j} =\tilde{u}_{1,j}\cdot \tilde{v}_{0}\). This change is computationally indistinguishable, due to the IV\(_5\) assumption. -
(2)
Invoke \(\hat{v}^{(\textsf {c})} \leftarrow \textsf {CalculateV}(\textsf {sk}_{i_\lambda }, \textsf {table}^{(\textsf {c})}, \textsf {c} )\) to extract a title \(\hat{v}^{(\textsf {c})}\) from the modified \(\textsf {table}^{(\textsf {c})}\).
-
(1)
-
– \(\tilde{e} := \prod _{\textsf {c} \in \mathcal {S}}\hat{v}^{(\textsf {c})} \cdot T^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )}\), and \(t := g_1^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )} \text { mod } N\).
Observe that for each \(\textsf {c} = (c_1, \cdots , c_8) \in \mathcal {S}\),
$$\begin{aligned} \hat{v}^{(\textsf {c})} =\tilde{v}^{(\textsf {c})} \cdot T^{-a_{(c_1, \cdots , c_8)}x_{i_{\lambda },1}^{c_{1}}y_{i_{\lambda },1}^{c_{2}}x_{i_{\lambda },2}^{c_{3}} y_{i_{\lambda },2}^{c_{4}}x_{i_{\lambda },3}^{c_{5}}y_{i_{\lambda },3}^{c_{6}}x_{i_{\lambda },4}^{c_{7}} y_{i_{\lambda },4}^{c_{8}}}. \end{aligned}$$Then \(\tilde{e}= \prod _{\textsf {c} \in \mathcal {S}}\hat{v}^{(\textsf {c})} \cdot T^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} )}\)
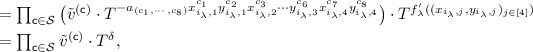
where \(\delta \) is the constant term of \(f'_\lambda \). Therefore we can implement Step 3 equivalently as follows.
-
-
Step 3 (Equivalent Form):
-
– For each \(\textsf {c} = (c_1, \cdots , c_8) \in \mathcal {S}\)
-
Compute \(\textsf {table}^{(\textsf {c})}\) via
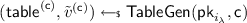 , but with one difference. The item of row 1 and column \(j := \min \{ i~|~ 1 \le i \le 8, c_i \ne 0 \}\) in \(\textsf {table}^{(\textsf {c})}\) now is computed as \(\hat{u}_{1,j}=(\tilde{u}_{1,j} T^{a_{(c_1, \cdots , c_8)}})\cdot \tilde{v}_{0}\) instead of \(\hat{u}_{1,j} =\tilde{u}_{1,j}\cdot \tilde{v}_{0}\).
, but with one difference. The item of row 1 and column \(j := \min \{ i~|~ 1 \le i \le 8, c_i \ne 0 \}\) in \(\textsf {table}^{(\textsf {c})}\) now is computed as \(\hat{u}_{1,j}=(\tilde{u}_{1,j} T^{a_{(c_1, \cdots , c_8)}})\cdot \tilde{v}_{0}\) instead of \(\hat{u}_{1,j} =\tilde{u}_{1,j}\cdot \tilde{v}_{0}\).
-
-
– \(\tilde{e} := \prod _{\textsf {c} \in \mathcal {S}} \tilde{v}^{(\textsf {c})} \cdot T^{\delta }\), and \(t := g_1^{f'_\lambda ( (x_{i_{\lambda },j},y_{i_{\lambda },j})_{j\in [4]} ) \text { mod } \phi (N)/4} \text { mod } N\).
In this step, \(\mathcal {E}.\) Enc does not use \((x_1, y_1, \cdots , x_4, y_4) \text { mod } N\) at all (only uses \((\bar{x}_{i,j},\bar{y}_{i,j})_{i\in [n],j\in [4]}\) and \((x_1, y_1, \cdots ,\) \(x_4, y_4) \text { mod } \phi (N)/4\)).
-
As a result, through the computationally indistinguishable change, the entropy of \((x_1, y_1, \cdots , x_4,\) \(y_4) \text { mod } N\) is reserved by the \(\mathcal {E}.\textsf {Enc}\) part of \(\textsc {Enc}\).
Similarly, Dec can be changed to do decryptions without \((x_j, y_j)_{j = 1}^{4} \text { mod } N\), the same argument as in Subsect. 6.3.
References
Applebaum, B., Cash, D., Peikert, C., Sahai, A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 595–618. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_35
Brakerski, Z., Goldwasser, S.: Circular and leakage resilient public-key encryption under subgroup indistinguishability. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 1–20. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_1
Brakerski, Z., Goldwasser, S., Kalai, Y.T.: Black-box circular-secure encryption beyond affine functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 201–218. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_13
Barak, B., Haitner, I., Hofheinz, D., Ishai, Y.: Bounded key-dependent message security. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 423–444. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_22
Boneh, D., Halevi, S., Hamburg, M., Ostrovsky, R.: Circular-secure encryption from decision Diffie-Hellman. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 108–125. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_7
Black, J., Rogaway, P., Shrimpton, T.: Encryption-scheme security in the presence of key-dependent messages. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 62–75. Springer, Heidelberg (2003). doi:10.1007/3-540-36492-7_6
Camenisch, J., Chandran, N., Shoup, V.: A public key encryption scheme secure against key dependent chosen plaintext and adaptive chosen ciphertext attacks. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 351–368. Springer, Heidelberg (2009). doi:10.1007/978-3-642-01001-9_20
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 93–118. Springer, Heidelberg (2001). doi:10.1007/3-540-44987-6_7
Damgård, I., Jurik, M.: A generalisation, a simplification and some applications of Paillier’s probabilistic public-key system. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 119–136. Springer, Heidelberg (2001). doi:10.1007/3-540-44586-2_9
Galindo, D., Herranz, J., Villar, J.: Identity-based encryption with master key-dependent message security and leakage-resilience. In: Foresti, S., Yung, M., Martinelli, F. (eds.) ESORICS 2012. LNCS, vol. 7459, pp. 627–642. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33167-1_36
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Sci. 28(2), 270–299 (1984)
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_24
Han, S., Liu, S., Lyu, L.: Efficient KDM-CCA secure public-key encryption for polynomial functions. IACR Cryptology ePrint Archive, Report 2016/829 (2016)
Hofheinz, D.: Circular chosen-ciphertext security with compact ciphertexts. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 520–536. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_31
Kurosawa, K., Desmedt, Y.: A new paradigm of hybrid encryption scheme. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 426–442. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_26
Lu, X., Li, B., Jia, D.: KDM-CCA security from RKA secure authenticated encryption. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 559–583. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46800-5_22
Malkin, T., Teranishi, I., Yung, M.: Efficient circuit-size independent public key encryption with KDM security. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 507–526. Springer, Heidelberg (2011). doi:10.1007/978-3-642-20465-4_28
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) STOC 2005, pp. 84–93. ACM (2005)
Acknowledgments
The authors are supported by the National Natural Science Foundation of China Grant (Nos. 61672346, 61373153 and 61133014). We thank the anonymous reviewers for their comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Han, S., Liu, S., Lyu, L. (2016). Efficient KDM-CCA Secure Public-Key Encryption for Polynomial Functions. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10032. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53890-6_11
Download citation
DOI: https://doi.org/10.1007/978-3-662-53890-6_11
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53889-0
Online ISBN: 978-3-662-53890-6
eBook Packages: Computer ScienceComputer Science (R0)









 ,
,  . It outputs the ciphertext
. It outputs the ciphertext 

 and compute
and compute  ,
, and compute
and compute 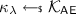 randomly for the
randomly for the  .
.
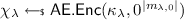 .
.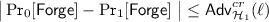 .
. .
. randomly and sets
randomly and sets  and invokes
and invokes 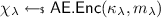 .
. randomly and sets
randomly and sets  .
. .
.
 .
. .
.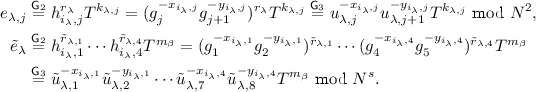
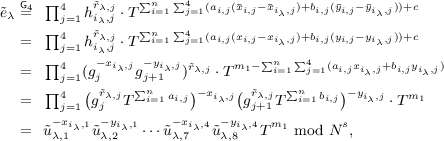
 .
. and
and  uniformly, and compute
uniformly, and compute 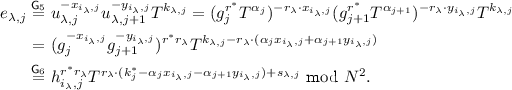
 .
.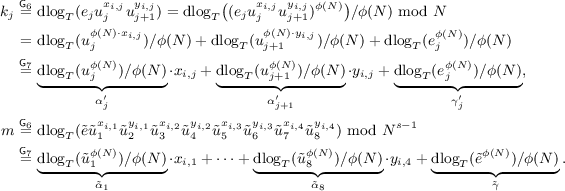
 .
. To prove that
To prove that 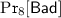 is negligible. This is not an easy task, and we further divide
is negligible. This is not an easy task, and we further divide  We give an upper bound for
We give an upper bound for  via the following lemma. See the full version [
via the following lemma. See the full version [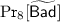 is deferred to subsequent games.
is deferred to subsequent games.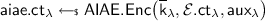 .
.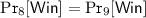 and
and  .
.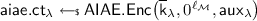 .
.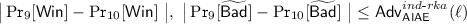 .
. .
. via the following lemma, and present its proof in the full version [
via the following lemma, and present its proof in the full version [

 ,
, , but with one difference. The item of row 1 and column
, but with one difference. The item of row 1 and column 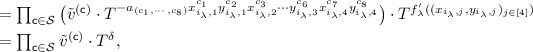
 , but with one difference. The item of row 1 and column
, but with one difference. The item of row 1 and column 