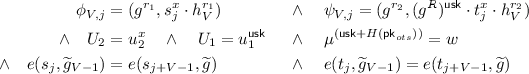Cut Down the Tree to Achieve Constant Complexity in Divisible E-cash

Abstract

Divisible e-cash, proposed in 1991 by Okamoto and Ohta, addresses a practical concern of electronic money, the problem of paying the exact amount. Users of such systems can indeed withdraw coins of a large value N and then divide it into many pieces of any desired values $V\le N$. Such a primitive therefore allows to avoid the use of several denominations or change issues. Since its introduction, many constructions have been proposed but all of them make use of the same framework: they associate each coin with a binary tree, which implies, at least, a logarithmic complexity for the spendings.

In this paper, we propose the first divisible e-cash system without such a tree structure, and so without its inherent downsides. Our construction is the first one to achieve constant-time spendings while offering a quite easy management of the coins. It compares favorably with the state-of-the-art, while being provably secure in the standard model.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Electronic payment systems have a strong impact on individual’s privacy, and this is often underestimated by the users. Transaction informations, such as payee’s identity, date and location, allow a third party (usually, the financial institution) to learn a lot of things about the users: individuals’ whereabouts, religious beliefs, health status, etc., which can eventually be quite sensitive.

However, secure e-payment and strong privacy are not incompatible, as shown by Chaum in 1982 [12]: he introduced the concept of electronic cash (e-cash), the digital analogue of regular cash, and in particular with its anonymity property. Typically, e-cash systems consider three kinds of parties, the bank, users and merchants. The bank issues coins, which can be withdrawn by users, and then be spent to merchants. Eventually, the merchants deposit the money on their account at the bank. It is better when the spending process does not involve the bank, in which case the e-cash system is said offline. Ideally, users and merchants should form a single set, which means that anyone receiving a coin should be able to spend it again without depositing it to the bank. Unfortunately, such a solution, called transferable e-cash implies [13] coins of growing size which quickly becomes cumbersome.

Although most of the features of regular cash, such as anonymity, can be reproduced by e-cash, there is one fundamental difference between these two systems: the latter can easily by duplicated, as any digital information. This property is a major issue for money, since dishonest users could spend several times the same coin to different merchants. To deter this bad behavior, e-cash systems must enable (1) detection of double-spending (i.e. the reuse of a spent coin), or alternatively over-spending (i.e. spending more money than withdrawn) and (2) identification of defrauders.

Unfortunately, achieving such properties becomes tricky when anonymity of transactions is required. Indeed, the bank can no longer trace the users’ payments and check that, for each of them, the global amount spent remains lower than the amount he withdrew. To enable detection of double-spending/over-spending, most of the e-cash systems then make use of serial numbers: every coin is associated with a unique number, only known to its owner until he spends the coin. The serial number is indeed revealed during the transaction and stored by the bank in a database. The bank can thus detect any reuse of serial numbers and so any double-spending.

1.1 Divisible E-cash

In 1991, Okamoto and Ohta [21] showed that e-cash can do more than simply emulate regular cash. They introduced the notion of divisible e-cash, where users withdraw coins of value N and have the ability of dividing it into many pieces of any desired values $V_i\le N$ such that $\sum _i V_i = N$. Such a property enables the user to pay the exact amount whatever the amount of the initially withdrawn coin was, which was a problem for traditional e-cash (and regular cash) systems. The authors proposed a framework representing each coin of value $N=2^n$ by a binary tree where each leaf is associated with a serial number, and so with a value 1. When a user wants to spend a value $2^\ell \le N$, he reveals an information related to a node s of depth $n-\ell$, allowing the bank to recover the $2^\ell$ serial numbers associated with the leaves descending from s. The benefit of this tree structure is to provide a partial control on the amount of serial numbers the user reveals. The latter can indeed send them by batches of $2^\ell$, for any $0\le \ell \le n$, which is much more efficient than sending them one by one, while ensuring that no information on serial numbers which do not descend from the spent nodes will leak.

Following this seminal work, a large number of constructions (including for example the following papers [2, 8,9,10,11, 20]) have been proposed, all of them making use of this framework, with a binary tree. In 2007, Canard and Gouget [8] proposed the first anonymous construction in the random oracle model, and recently, Canard et al. [10] showed that both anonymity and efficiency can be achieved in the standard model.

However, this binary tree structure has a major downside: it is tailored to spend powers of 2. Unfortunately, such an event is unlikely in real life. In practice, to pay a value V, the users must write $V=\sum _i b_i\cdot 2^i$, for $b_i\in \{0,1\}$ and then repeat the ${\texttt {Spend}}$ protocol v times, where $v=\sum _i b_i$. Therefore, the constant-time property claimed by several constructions is somewhat misleading: spendings can be performed in constant-time as long as V is a power of 2 but not in the general case, and in the worst case the complexity is logarithmic.

Moreover, this structure makes the coin management slightly more difficult. Indeed, let us consider the case illustrated by the Fig. 1, where a user has already spent a value $V_1 = 3$ and so revealed the first three serial numbers ${\mathtt {SN}}_1, {\mathtt {SN}}_2$ and ${\mathtt {SN}}_3$. Now assume that the user wants to spend a value $V_2=2$. He cannot use the node $s_{01}$, since ${\mathtt {SN}}_3$ has already been revealed and so must use $s_{10}$ or $s_{11}$. This means that the serial number ${\mathtt {SN}}_4$ will remain isolated, and the user will have to spend it later as a unit. It is then necessary to maintain a list of unspent serial numbers and try to avoid the presence of several “holes” in the tree, which thereafter restricts a lot the value that can be spent at once.

Fig. 1.

Tree-based divisible coin

1.2 Our Contribution

In this work, we aim at a greater simplicity and a better efficiency, and propose the first divisible e-cash system which truly achieves constant-time spendings. The main novelty of our construction it that we get rid of the tree structure and so of its inherent downsides that we have described above. Our scheme enables users to reveal, by sending a constant number of elements, the sequence of V serial numbers ${\mathtt {SN}}_j,\ldots ,{\mathtt {SN}}_{j+V-1}$, for any j and V of their choice (provided that $j+V-1\le N$), even if V is not a power of 2. If we reconsider the previous example, this means that the user can now reveal, with a constant complexity, ${\mathtt {SN}}_4,\ldots , {\mathtt {SN}}_{4+V_2-1}$, for any value $V_2$.

We start from [10], which introduced the idea of a unique coin’s structure, but make several changes to achieve constant-time spendings. The most important one is that we generate the public parameters in such a way that a same element can be used for spendings of any possible amount. This stands in sharp contrast with previous constructions where each element was associated with a node of the tree and so with a unique amount. More specifically, we use bilinear groups (i.e. a set of three cyclic groups ${\mathbb {G}}_1$, ${\mathbb {G}}_2$ and ${\mathbb {G}}_T$ of prime order p, along with a bilinear map $e:{\mathbb {G}}_1\times {\mathbb {G}}_2\rightarrow {\mathbb {G}}_T$) and set the N serial numbers of a coin as ${\mathtt {SN}}_j= e(s,{\widetilde{g}})^{x\cdot y^j}$, for $j=1,\ldots ,N$, where x is the coin’s secret and $(y,s,{\widetilde{g}})\in {\mathbb {Z}}_p\times {\mathbb {G}}_1\times {\mathbb {G}}_2$ are global parameters of the system (not all public). These parameters additionally contain the elements $s_j = s^{y^j}\in {\mathbb {G}}_1$, for $j=1,\ldots ,N$ and ${\widetilde{g}}_j = {\widetilde{g}}^{y^j}\in {\mathbb {G}}_2$, for $j=1,\ldots ,N-1$. The relations between all these elements (namely the fact that they all depend on y) are at the heart of the efficiency of our construction but have a strong impact on anonymity. Indeed, (1) they could be used by an adversary to link transactions together and (2) they make the anonymity property much more difficult to prove.

Regarding (2), the problem comes from the fact that the reduction in the anonymity proof must take all these relations into account while being able to reveal the non-critical serial numbers $\{e(s,{\widetilde{g}})^{x\cdot y^j}\}_{j=1}^{j^*-1}\cup \{e(s,{\widetilde{g}})^{x\cdot y^j}\}_{j=j^*+V^*}^{N}$ and to insert the challenge serial numbers in $\{e(s,{\widetilde{g}})^{x\cdot y^j}\}_{j=j^*}^{j^*+V^*-1}$, for any $j^*,V^*\in [1,N]$. Nonetheless, we manage to prove the anonymity of our construction under an assumption which, albeit new and rather complex, does not depend on either $j^*$ and $V^*$. We stress that the latter point was far from obvious. We also investigate in the full version [22] another way of generating the public parameters which allows to rely on a more classical assumption but at the cost of significant increase of the complexity (which nevertheless remains constant).

Regarding (1), we must pay attention to the way the serial numbers ${\mathtt {SN}}_i$, for $i=j,\ldots ,j+V-1$, are revealed during a spending of value V. For example, we show in Sect. 4.1 that the solution from [10] (namely sending $s_j^x$) would trivially be insecure in our setting. The user will then rather send $s_j^x$ encrypted in a way that prevents anyone from testing relations between spendings while ensuring that only a specific amount of serial numbers can be recovered from it.

Our ${\texttt {Spend}}$ protocol is then quite efficient: it mostly consists in sending an encryption of $s_j^x$ along with a proof of well-formedness. As illustrated on Fig. 3 of Sect. 5.2, it outperforms the state-of-the-art [11, 20], whose complexity logarithmically depends on the spent value V. Since spending is the operation subject to the strongest time constraints (for example, it should be performed in less than 300 ms in a public transport system [19]) we argue that our construction makes all the features of e-cash systems much more accessible.

1.3 Organization

In Sect. 2, we recall some definitions and present the computational assumptions underlying the security of our scheme. Section 3 reviews the syntax of a divisible E-cash system along with security properties definitions. We provide in Sect. 4 a high level description of our construction and a more detailed presentation in Sect. 5. The latter additionally contains a comparison with state-of-the-art. Eventually, the security analysis is performed in Sect. 6.

Due to space limitations, the description of an alternative scheme which is less efficient, but whose anonymity relies on a quite classical assumption, is postponed to the full version [22]. The latter also presents an instantiation of our divisible e-cash system and contains a proof of hardness of our new assumption in the generic bilinear group model.

2 Preliminaries

2.1 Bilinear Groups

Bilinear groups are a set of three cyclic groups ${\mathbb {G}}_1$, ${\mathbb {G}}_2$, and ${\mathbb {G}}_{T}$ of prime order p, along with a bilinear map $e: {\mathbb {G}}_1 \times {\mathbb {G}}_2 \rightarrow {\mathbb {G}}_T$ with the following properties:

• 1. for all $g\in {\mathbb {G}}_1, {\widetilde{g}}\in {\mathbb {G}}_2$ and $a,b \in {\mathbb {Z}}_p$, $e(g^a,{\widetilde{g}}^b)=e(g,{\widetilde{g}})^{a\cdot b}$;

• 2. for $g \ne 1_{{\mathbb {G}}_1}$ and ${\widetilde{g}}\ne 1_{{\mathbb {G}}_2}$, $e(g,{\widetilde{g}}) \ne 1_{{\mathbb {G}}_T}$;

• 3. the map e is efficiently computable.

Galbraith et al. [16] defined three types of pairings: in Type-1, ${\mathbb {G}}_1={\mathbb {G}}_2$; in Type-2, ${\mathbb {G}}_1\ne {\mathbb {G}}_2$ but there exists an efficient homomorphism $\phi : {\mathbb {G}}_2\rightarrow {\mathbb {G}}_1$, while no efficient one exists in the other direction; in Type-3, ${\mathbb {G}}_1\ne {\mathbb {G}}_2$ and no efficiently computable homomorphism exists between ${\mathbb {G}}_1$ and ${\mathbb {G}}_2$, in either direction.

Although Type-1 pairings were mostly used in the early-age of pairing-based cryptography, they have been gradually discarded in favour of Type-3 pairings. Indeed, the latter offer a better efficiency and are compatible with several computational assumptions, such as the ${\mathsf {SXDH}}$ and the $N-\mathsf {MXDH}'$ ones we present below, which do not hold in the former.

2.2 Computational Assumptions

Our security analysis makes use of the ${\mathsf {SXDH}}$, $q-{\mathsf {SDH}}$ [6] and $N-{\mathsf {BDHI}}$ [5] assumptions which have been considered reasonable for Type-3 pairings.

Definition 1

( ${\mathsf {SXDH}}$ assumption). For $k\in \{1,2\}$, the ${\mathsf {DDH}}$ assumption is hard in ${\mathbb {G}}_k$ if, given $(g,g^x,g^y,g^z)\in {\mathbb {G}}_k^4$, it is hard to distinguish whether $z=x\cdot y$ or z is random. The ${\mathsf {SXDH}}$ assumption holds if ${\mathsf {DDH}}$ is hard in both ${\mathbb {G}}_1$ and ${\mathbb {G}}_2$

Definition 2

( $q-{\mathsf {SDH}}$ assumption). Given $(g,g^x,g^{x^2},...,g^{x^q})\in {\mathbb {G}}_1$, it is hard to output a pair $(m,g^{\frac{1}{x+m}})\in {\mathbb {Z}}_p\times {\mathbb {G}}_1$.

Definition 3

( $N-{\mathsf {BDHI}}$ assumption). Given $(\{g^{y^i}\}_{i=0}^N,\{{\widetilde{g}}^{y^i}\}_{i=0}^N)\in {\mathbb {G}}_1^{N+1}\times {\mathbb {G}}_2^{N+1}$, it is hard to compute $G=e(g,{\widetilde{g}})^{1/y}\in {\mathbb {G}}_T$.

However, the anonymity of our construction relies on a new assumption, that we call $N-\mathsf {MXDH}'$. To provide more confidence in the latter, we first introduced a weaker variant, called $N-\mathsf {MXDH}$, that holds (as we prove it in the full version [22]) in the generic bilinear group model for Type-3 pairings and next prove that both variants are actually related as stated in Theorem 6.

Definition 4

$\forall N\in \mathbb {N}^*$, we define $C= N^3-N^2$, $S=C+1$, $E=N^2-N$, $D=S+E$ and $P=D+C$, along with the following assumptions.

• ${\varvec{(}}N-\mathsf {MXDH}$ $\mathbf{{assumption}}{\varvec{).}}$ Given $\{(g^{\gamma ^k})_{k=0}^P, ( g^{\alpha \cdot \delta \cdot \gamma ^{-k}})_{k=0}^E,(g^{\chi \cdot \gamma ^k})_{k=D+1}^{P},(g^{\alpha \cdot \gamma ^{-k}}, g^{\chi \cdot \gamma ^k/\alpha })_{k=0}^{C}\}\in {\mathbb {G}}_1^{P+E+3S+1}$, as well as $({\widetilde{g}}^{\gamma ^k}, {\widetilde{g}}^{\alpha \cdot \gamma ^{-k}})_{k=0}^C\in {\mathbb {G}}_2^{2S}$ and an element $g^{z}\in {\mathbb {G}}_1$, it is hard to decide whether $z = \delta + \chi \gamma ^D/\alpha$ or z is random.

• ${\varvec{(}}N-\mathsf {MXDH}'$ $\mathbf{{assumption}}{\varvec{).}}$ Given $\{(g^{\gamma ^k},h^{\gamma ^k})_{k=0}^P, (g^{\alpha \cdot \delta \cdot \gamma ^{-k}}, h^{\alpha \cdot \delta \cdot \gamma ^{-k}})_{k=0}^E, (g^{\chi \cdot \gamma ^k}, h^{\chi \cdot \gamma ^k})_{k=D+1}^{P}, (g^{\alpha \cdot \gamma ^{-k}},g^{\chi \cdot \gamma ^k/\alpha }, h^{\chi \cdot \gamma ^k/\alpha })_{k=0}^{C} \}\in {\mathbb {G}}_1^{2P+5S+2E+2}$, as well as $({\widetilde{g}}^{\gamma ^k}, {\widetilde{g}}^{\alpha \cdot \gamma ^{-k}})_{k=0}^C\in {\mathbb {G}}_2^{2S}$ and a pair $(g^{z_1},h^{z_2})\in {\mathbb {G}}_1^2$, it is hard to decide whether $z_1=z_2 = \delta + \chi \gamma ^D/\alpha$ or $(z_1,z_2)$ is random.

In the full version [22], we present another divisible e-cash protocol whose proof relies on a more classical assumption, but at the cost of larger public parameters and more complex (but still constant-size) protocols.

Regarding the $N-\mathsf {MXDH}$ assumption, the core idea is that the elements provided in an instance allow to compute the sets $\mathcal {S}_1=\{e(g,{\widetilde{g}})^{\chi \cdot \gamma ^k}\}_{k= 0}^{S-1}$ and $\mathcal {S}_2=\{e(g,{\widetilde{g}})^{\chi \cdot \gamma ^k}\}_{k= D+1}^{P+C}$ but no element of ${\mathcal {S}}_3=\{e(g,{\widetilde{g}})^{\chi \cdot \gamma ^k}\}_{k=S}^D$. In the security proof, we will manage to force the $V^*$ “challenge” serial numbers ${\mathtt {SN}}_{j^*},\ldots ,{\mathtt {SN}}_{j^*+V^*-1}$ (where $V^*$ is the amount of the challenge transaction, i.e the one where the adversary tries to identify the spender) to belong to ${\mathcal {S}}_3$ while ensuring that the other ones belong to ${\mathcal {S}}_1\cup {\mathcal {S}}_2$ and so can be simulated. This requires a great flexibility from the assumption, since the number $V^*$ and the index $j^*$ are adaptively chosen by the adversary. If N is the amount of the divisible coin, this means that it must be possible, for any $(j^*,V^*)\in [1,N]^2$, to insert $j^*-1$ serial numbers in ${\mathcal {S}}_1$, $V^*$ in ${\mathcal {S}}_3$ and $N+1-(j^*+V^*)$ in ${\mathcal {S}}_2$, all of these sets being constant. We show in Sect. 6.3 that this is the case when the integers C, S, E, D and P are chosen as in the above definition.

Theorem 5

The $N-\mathsf {MXDH}$ assumption holds in the generic bilinear group model: after $q_G$ group and pairing oracle queries, no adversary can solve the $N-\mathsf {MXDH}$ problem with probability greater than $2N^3\cdot (7N^3+q_G)^2/p$.

The proof, that is quite classical, can be found in the full version [22]. It is worthy to note that the integer N will represent the amount of a divisible coin and so will remain negligible compared to p. For example, a typical value for N is 1000 which allows users to withdraw coins of value $10 \$$, if the basic unit is the cent.

Theorem 6

The $N-\mathsf {MXDH}'$ assumption holds if both the ${\mathsf {DDH}}$ assumption in ${\mathbb {G}}_1$ and the $N-\mathsf {MXDH}$ assumption hold.

Proof

Let ${\mathcal {A}}$ be an adversary against the $N-\mathsf {MXDH}'$ assumption with a non-negligible advantage

$$\mathtt {Adv}({\mathcal {A}})=|\Pr [{\mathcal {A}}({\mathcal {S}},g^{z},h^{z})|z=\delta + \chi \cdot \gamma ^D/\alpha ] -\Pr [{\mathcal {A}}({\mathcal {S}},g^{z_1},h^{z_2})| z_1,z_2\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p]|,$$

where ${\mathcal {S}}$ refers to the set of all elements, except $g^{z_1}$ and $h^{z_2}$, provided in an $N-\mathsf {MXDH}'$ challenge. We define hybrid distributions:

$$\begin{aligned} \mathtt {Adv}_1({\mathcal {A}})&= |\Pr [{\mathcal {A}}({\mathcal {S}},g^{z},h^{z})|z=\delta + \chi \cdot \gamma ^D/\alpha ] -\Pr [{\mathcal {A}}({\mathcal {S}},g^{z},h^{z})|z\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p]| \\ \mathtt {Adv}_2({\mathcal {A}})&= |\Pr [{\mathcal {A}}({\mathcal {S}},g^{z},h^{z})|z\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p] -\Pr [{\mathcal {A}}({\mathcal {S}},g^{z_1},h^{z_2})| z_1,z_2\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p]|, \end{aligned}$$

we then have: $\mathtt {Adv}({\mathcal {A}}) \le \mathtt {Adv}_1({\mathcal {A}}) + \mathtt {Adv}_2({\mathcal {A}})$.

Since $\mathtt {Adv}({\mathcal {A}})$ is non-negligible, at least $\mathtt {Adv}_1({\mathcal {A}})$ or $\mathtt {Adv}_2({\mathcal {A}})$ is non-negligible.

In the former case, ${\mathcal {A}}$ can be used to break the $N-\mathsf {MXDH}$ assumption: from an $N-\mathsf {MXDH}$ instance, one can generate an $N-\mathsf {MXDH}'$ instance with a random scalar c and setting $h= g^c$. By running ${\mathcal {A}}$ on this instance, it gives a valid guess for it if and only if this would be a valid guess for the $N-\mathsf {MXDH}$ instance. The advantage is thus the same.

In the latter case, ${\mathcal {A}}$ can be used to break the ${\mathsf {DDH}}$ assumption in ${\mathbb {G}}_1$. Indeed, let $(g,g^{z_1},h,h^{z_2})$ be a ${\mathsf {DDH}}$ challenge. One can compute a valid set ${\mathcal {S}}$ from g and h by using random (known) scalars $\alpha ,\gamma$ and $\delta$, and then run ${\mathcal {A}}$ on $({\mathcal {S}},g^{z_1},h^{z_2})$.   $\square$

One can note that the $N-\mathsf {MXDH}$ and $N-{\mathsf {MXDH}}'$ assumptions would actually be equivalent if the former implied the ${\mathsf {DDH}}$ assumption in ${\mathbb {G}}_1$ (which does not seem to be true). Nevertheless, this theorem shows that the $N-\mathsf {MXDH}'$ assumption is not much stronger than the $N-\mathsf {MXDH}$ one, since the ${\mathsf {DDH}}$ assumption can be considered reasonable.

2.3 Digital Signature Scheme

A digital signature scheme $\varSigma$ is defined by three algorithms:

• the key generation algorithm $\varSigma .{\texttt {Keygen}}$ which outputs a pair of signing and verification keys $({\mathsf {sk}},{\mathsf {pk}})$ – we assume that ${\mathsf {sk}}$ always contains ${\mathsf {pk}}$;

• the signing algorithm $\varSigma .{\texttt {Sign}}$ which, on input the signing key ${\mathsf {sk}}$ and a message m, outputs a signature $\sigma$;

• and the verification algorithm $\varSigma .{\texttt {Verify}}$ which, on input m, $\sigma$ and ${\mathsf {pk}}$, outputs 1 if $\sigma$ is a valid signature on m under ${\mathsf {pk}}$, and 0 otherwise.

The standard security notion for a signature scheme is existential unforgeability under chosen-message attacks (EUF-CMA) [17] which means that it is hard, even given access to a signing oracle, to output a valid pair $(m,\sigma )$ for a message m never asked to the oracle. In this paper we will also use variants, first with selective chosen-message attacks (SCMA) which restricts means for the adversary by limiting the oracle queries to be asked before having seen the key ${\mathsf {pk}}$; or with one-time signature (OTS), which limits the adversary to ask one query only to the signing oracle; and with strong unforgeability (SUF) which relaxes the goal of the adversary which must now output a valid pair $(m,\sigma )$ that was not returned by the signing oracle (a new signature for an already signed message is a valid forgery).

2.4 Groth-Sahai Proof Systems

In [18], Groth and Sahai proposed a non-interactive proof system, in the common reference string (CRS) model, which captures most of the relations for bilinear groups. There are two types of setup for the CRS that yield either perfect soundness or perfect witness indistinguishability, while being computationally indistinguishable (under the ${\mathsf {SXDH}}$ assumption, in our setting).

To prove that some variables satisfy a set of relations, the prover first commits to them (by using the elements from the CRS) and then computes one proof element per relation. Efficient non-interactive witness undistinguishable proofs are available for

• pairing-product equations, for variables $\{X_i\}_{i=1}^n\in {\mathbb {G}}_1$, $\{{\widetilde{X}}_i\}_{i=1}^n\in {\mathbb {G}}_2$ and constant $t_T\in {\mathbb {G}}_T$, $\{A_i\}_{i=1}^n\in {\mathbb {G}}_1$, $\{\widetilde{B}_i\}_{i=1}^n\in {\mathbb {G}}_2$, $\{a_{i,j}\}_{i,j=1}^n\in {\mathbb {Z}}_p$:

  $$\prod \limits _{i=1}^n e(A_i,{\widetilde{X}}_i) \prod \limits _{i=1}^n e(X_i,\widetilde{B}_i) \prod \limits _{i=1}^n \prod \limits _{j=1}^n e(X_i,{\widetilde{X}}_j)^{a_{i,j}}=t_T;$$

• or multi-exponentiation equations, for variables $\{X_i\}_{i=1}^n\in {\mathbb {G}}_k$, $\{y_i\}_{i=1}^n\in {\mathbb {Z}}_p$ and constant $T\in {\mathbb {G}}_k$, $\{A_i\}_{i=1}^n\in {\mathbb {G}}_k$, $\{b_i\}_{i=1}^n\in {\mathbb {Z}}_p$, $\{a_{i,j}\}_{i,j=1}^n\in {\mathbb {Z}}_p$ for $k\in \{1,2\}$:

  $$\prod \limits _{i=1}^n A_i^{y_i} \prod \limits _{j=1}^n X_j^{b_j}\prod \limits _{i=1}^n \prod \limits _{j=1}^n X_j^{y_i\cdot a_{i,j}}=T.$$

Multi-exponentiation equations and pairing-product equations such that $t_T=1_{{\mathbb {G}}_T}$ also admit non-interactive zero-knowledge (${\mathsf {NIZK}}$) proofs at no additional cost.

3 Divisible E-cash System

We recall in this section the syntax and the security model of a divisible e-cash system, as described in [10].

3.1 Syntax

A divisible e-cash system is defined by the following algorithms, that involve three types of entities, the bank ${\mathcal {B}}$, a user ${\mathcal {U}}$ and a merchant ${\mathcal {M}}$.

• ${\texttt {Setup}}(1^k,N)$: On input a security parameter k and an integer N, this probabilistic algorithm outputs the public parameters ${ pp }$ for divisible coins of global value N. We assume that ${ pp }$ are implicit to the other algorithms, and that they include k and N. They are also an implicit input to the adversary, we will then omit them.

• ${\texttt {BKeygen}}()$: This probabilistic algorithm executed by the bank ${\mathcal {B}}$ outputs a key pair $({\mathsf {bsk}},{\mathsf {bpk}})$. It also sets L as an empty list, that will store all deposited coins. We assume that ${\mathsf {bsk}}$ contains ${\mathsf {bpk}}$.

• ${\texttt {Keygen}}()$: This probabilistic algorithm executed by a user ${\mathcal {U}}$ (resp. a merchant ${\mathcal {M}}$) outputs a key pair $({\mathsf {usk}},{\mathsf {upk}})$ (resp. $({\mathsf {msk}},\mathsf {mpk})$). We assume that ${\mathsf {usk}}$ (resp. ${\mathsf {msk}}$) contains ${\mathsf {upk}}$ (resp. $\mathsf {mpk}$).

• ${\texttt {Withdraw}}({\mathcal {B}}({\mathsf {bsk}},{\mathsf {upk}}),{\mathcal {U}}({\mathsf {usk}},{\mathsf {bpk}}))$: This is an interactive protocol between the bank ${\mathcal {B}}$ and a user ${\mathcal {U}}$. At the end of this protocol, the user gets a divisible coin $C$ of value N or outputs $\perp$ (in case of failure) while the bank stores the transcript ${\texttt {Tr}}$ of the protocol execution or outputs $\perp$.

• ${\texttt {Spend}}({\mathcal {U}}({\mathsf {usk}},C,{\mathsf {bpk}},\mathsf {mpk},V),{\mathcal {M}}({\mathsf {msk}},{\mathsf {bpk}},V))$: This is an interactive protocol between a user ${\mathcal {U}}$ and a merchant ${\mathcal {M}}$. At the end of the protocol the merchant gets a master serial number Z of value V (the amount of the transaction they previously agreed on) along with a proof of validity $\varPi$ or outputs $\perp$. ${\mathcal {U}}$ either updates $C$ or outputs $\perp$.

• ${\texttt {Deposit}}({\mathcal {M}}({\mathsf {msk}},{\mathsf {bpk}},(V,Z,\varPi )),{\mathcal {B}}({\mathsf {bsk}},L,\mathsf {mpk}))$: This is an interactive protocol between a merchant ${\mathcal {M}}$ and the bank ${\mathcal {B}}$. ${\mathcal {B}}$ first checks the validity of the transcript $(V,Z,\varPi )$ and that it has not already been deposited. If one of these conditions is not fulfilled, then ${\mathcal {B}}$ aborts and outputs $\perp$. At the end of the protocol ${\mathcal {B}}$ stores the V serial numbers ${\mathtt {SN}}_1,\ldots ,{\mathtt {SN}}_V$ derived from Z in L or returns a transcript $(V',Z',\varPi ')$ such that ${\mathtt {SN}}_i$ is also a serial number derived from $Z'$, for some $i\in [1,V]$.

• ${\texttt {Identify}}((v_1,Z_1,\varPi _1),(v_2,Z_2,\varPi _2),{\mathsf {bpk}})$: On inputs two different valid transcripts $(v_1,Z_1,\varPi _1)$ and $(v_2,Z_2,\varPi _2)$, this deterministic algorithm outputs a user’s public key ${\mathsf {upk}}$ if there is a collision between the serial numbers derived from $Z_1$ and from $Z_2$, and $\perp$ otherwise.

3.2 Security Model

Informally, to reconcile the interests of all parties, a divisible e-cash system should (1) ensure detection of double-spending/over-spending and identification of the defrauders, (2) preserve privacy of its users, (3) ensure that none of them can be falsely accused of fraud. Regarding the first point, we recall that reuse of money cannot be prevented (since digital coin can always be duplicated) but the guarantee of being identified should constitute a strong incentive not to cheat. The third point implicitly ensures that a coin can only be spent by its owner.

These security properties were formally defined as traceability, anonymity and exculpability by the authors of [10]. For consistency, we recall the associated security games, in Fig. 2, which make use of the following oracles:

Fig. 2.

Security games for anonymous divisible E-cash

• ${\mathcal {O}}{\texttt {Add}}()$ is an oracle used by the adversary ${\mathcal {A}}$ to register a new honest user (resp. merchant). The oracle runs the ${\texttt {Keygen}}$ algorithm, stores ${\mathsf {usk}}$ (resp. ${\mathsf {msk}}$) and returns ${\mathsf {upk}}$ (resp. $\mathsf {mpk}$) to ${\mathcal {A}}$. In this case, ${\mathsf {upk}}$ (resp. $\mathsf {mpk}$) is said honest.

• ${\mathcal {O}}{\texttt {Corrupt}}({\mathsf {upk}}/\mathsf {mpk})$ is an oracle used by ${\mathcal {A}}$ to corrupt an honest user (resp. merchant) whose public key is ${\mathsf {upk}}$ (resp. $\mathsf {mpk}$). The oracle then returns the corresponding secret key ${\mathsf {usk}}$ (resp. ${\mathsf {msk}}$) to ${\mathcal {A}}$ along with the secret values of every coin withdrawn by this user. From now on, ${\mathsf {upk}}$ (resp. $\mathsf {mpk}$) is said corrupted.

• ${\mathcal {O}}{{\texttt {AddCorrupt}}}({\mathsf {upk}}/\mathsf {mpk})$ is an oracle used by ${\mathcal {A}}$ to register a new corrupted user (resp. merchant) whose public key is ${\mathsf {upk}}$ (resp. $\mathsf {mpk}$). In this case, ${\mathsf {upk}}$ (resp. $\mathsf {mpk}$) is said corrupted. The adversary could use this oracle on a public key already registered (during a previous ${\mathcal {O}}{\texttt {Add}}$ query) but for simplicity, we do not consider such case as it will gain nothing more than using the ${\mathcal {O}}{\texttt {Corrupt}}$ oracle on the same public key.

• ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}({\mathsf {upk}})$ is an oracle that executes the user’s side of the ${\texttt {Withdraw}}$ protocol. This oracle will be used by ${\mathcal {A}}$ playing the role of the bank against the user with public key ${\mathsf {upk}}$.

• ${\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {B}}}}({\mathsf {upk}})$ is an oracle that executes the bank’s side of the ${\texttt {Withdraw}}$ protocol. This oracle will be used by ${\mathcal {A}}$ playing the role of a user whose public key is ${\mathsf {upk}}$ against the bank.

• ${\mathcal {O}}{{\texttt {Spend}}}({\mathsf {upk}},V)$ is an oracle that executes the user’s side of the ${\texttt {Spend}}$ protocol for a value V. This oracle will be used by ${\mathcal {A}}$ playing the role of the merchant ${\mathcal {M}}$.

In the experiments, users are denoted by their public keys ${\mathsf {upk}}$, $c_{{\mathsf {upk}}}$ denotes the amount already spent by user ${\mathsf {upk}}$ during ${\mathcal {O}}{{\texttt {Spend}}}$ queries and $m_{{\mathsf {upk}}}$ the number of divisible coins that he has withdrawn. This means that the total amount available by a user ${\mathsf {upk}}$ is $m_{\mathsf {upk}}\cdot N$. The number of coins withdrawn by all users during an experiment is denoted by m.

In the anonymity security game, we differ a little bit from [10]: while $c_{{\mathsf {upk}}_b}$ is increased by V at step 6 during the ${\texttt {Spend}}$ protocol, $c_{{\mathsf {upk}}_{1-b}}$ is also increased by V at step 7 to avoid ${\mathcal {A}}$ trivially wins by trying to make one of the two players to overspend money.

Let ${\mathcal {A}}$ be a probabilistic polynomial adversary. A divisible E-cash system is:

• traceable if ${\texttt {Succ}}^{{\textit{tra}}}({\mathcal {A}}) = \Pr [{\texttt {Exp}}_{\mathcal {A}}^{{\textit{tra}}}(1^k,V)=1]$ is negligible for any ${\mathcal {A}}$;

• exculpable if ${\texttt {Succ}}^{{\textit{excu}}}({\mathcal {A}}) = \Pr [{\texttt {Exp}}_{\mathcal {A}}^{{\textit{excu}}}(1^k,V)=1]$ is negligible for any ${\mathcal {A}}$;

• anonymous if ${\texttt {Adv}}^{{\textit{anon}}}({\mathcal {A}}) = |\Pr [{\texttt {Exp}}_{\mathcal {A}}^{{\textit{anon}}-1}(1^k,V)]$ - Pr$[{\texttt {Exp}}_{\mathcal {A}}^{{\textit{anon}}-0}(1^k,V)]|$ is negligible for any ${\mathcal {A}}$.

4 Our Construction

4.1 High Level Description

Our Approach. We start from [10, 11], in order to keep the quite easy and efficient withdrawal procedure (which mostly consists in certifying secret scalars). But we would like to improve on the spending procedure, and namely to get everything really constant (both in time and in size). Indeed, the user should be able to send only one information revealing the serial numbers, corresponding to the amount to be spent. But he should also be able to choose the sequence he discloses. For example, if he wants to pay a value V with a coin whose $(j-1)$ first serial numbers have already been used, then he should be able to send an element $\phi _{V,j}$ revealing the V serial numbers ${\mathtt {SN}}_j,\ldots ,{\mathtt {SN}}_{j+V-1}$.

Description. All the serial numbers have the same structure, and are just customized by a random secret scalar x which constitutes the secret of the coin (our withdrawals are thus similar to the ones of [10, 11]). More specifically, the public parameters contain the N values $s_j=s^{y^j}$ (for $j=1,\ldots ,N$), with a public group element $s\in {\mathbb {G}}_1$, and some secret scalar $y\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p$: for any coin’s secret x, this defines the serial numbers ${\mathtt {SN}}_j = e(s,{\widetilde{g}})^{x\cdot y^{j}}$.

The critical point is to find a way to construct the unique $\phi _{V,j}$ and to decide which elements should be provided in the public parameters ${ pp }$ to enable the bank to compute the serial numbers (all the expected ones, but not more).

First Attempt. One could define $\phi _{V,j}$ as $s_j^x$, in which case ${ pp }$ should contain the set ${\mathcal {S}}=\{{\widetilde{g}}_k = {\widetilde{g}}^{y^k}\}_{k=0}^{N-1}$. Indeed, a user with a fresh coin (i.e. never involved in a spending) must be able to spend a value N by revealing $s_1^x$ and so the bank needs to know ${\mathcal {S}}$ to recover ${\mathtt {SN}}_i\leftarrow e(s_1^x,{\widetilde{g}}_{i-1})$, for $i=1,\ldots ,N$. One can note that ${\mathcal {S}}$ is actually enough for any spending, since, for any $j\in [1,N]$, recovering ${\mathtt {SN}}_{j},\ldots ,{\mathtt {SN}}_{j+V-1}$ from $\phi _{V,j}$ still requires elements from $\{{\widetilde{g}}_k\}_{k=0}^{V-1}$.

However, there is an obvious problem with this solution. Once ${\mathcal {S}}$ is published, nothing prevents the bank from computing more serial numbers than the amount V of the transaction. For example, if a user with a fresh coin spends a value 1, then the bank is still able to recover all the serial numbers from $\phi _{1,1}=s_1^x$.

Our Solution. It is therefore necessary to provide a way, for the user, to control the amount of serial numbers which can be recovered from the element $s_j^x$. To this end, we define N (one for each possible value $V\in [1,N]$) ElGamal [14] public keys $h_V=g^{a_V}$ and add the sets ${\mathcal {S}}_V=\{{\widetilde{g}}_k^{-a_V}\}_{k=0}^{V-1}$, for $V=1,\ldots ,N$, to ${ pp }$. To reveal V serial numbers from $s_j^x$, the user now encrypts it under $h_V$, which defines $\phi _{V,j}$ as $(c_0 = g^r,c_1=s_j^x\cdot h_V^r)$, for some $r\in {\mathbb {Z}}_p$. By using the elements from ${\mathcal {S}}_V$, the bank is still able to compute the V serial numbers since:

$$\begin{aligned} e(c_1,{\widetilde{g}}_k) \cdot e(c_0, {\widetilde{g}}_k^{-a_V})&= e(s_j^x \cdot h_V^r,{\widetilde{g}}_k) \cdot e(g^r,{\widetilde{g}}_k^{-a_V}) \\&= e(s_j^x,{\widetilde{g}}_k) \cdot e(h_V^r,{\widetilde{g}}_k) \cdot e(g^r,{\widetilde{g}}_k^{-a_V}) \\&= e(s^{y^j \cdot x},{\widetilde{g}}^{y^k}) \cdot e(g^{a_V \cdot r},{\widetilde{g}}_k) \cdot e(g^{-a_V \cdot r},{\widetilde{g}}_k) \\&= e(s,{\widetilde{g}})^{x\cdot y^{j+k}}={\mathtt {SN}}_{j+k}, \end{aligned}$$

for $k=0,\ldots ,V-1$. But now, it can no longer derive additional serial numbers because ${\mathcal {S}}_V$ only contains V elements. Moreover, the elements of the other sets ${\mathcal {S}}_{V'}$, for $V'\ne V$, are useless since they correspond to other public keys.

One can note that ElGamal encryption was also used in [11] but to prevent an adversary from testing relations across the different levels of the tree. We here use it to enable a total control on the amount of revealed serial numbers. A same element $s_j^x$ can thus be involved in spendings of different values, which is the basis of the efficiency and the flexibility of our scheme.

Security Analysis. An interesting feature of our solution is that the bank does not need to know the index j to compute the serial numbers. This is due to the fact that ${\mathtt {SN}}_{j+1} = {\mathtt {SN}}_j^y$, for all $j\in [1,N-1]$ and so that the computation of a serial number is independent from j. Therefore, a spending does not reveal any additional information about the coin (such as the spent part) and so achieves the strongest notion of anonymity.

However, this has implications on the security analysis, since one must take into account the relations between the different serial numbers. Anonymity will then rely on a new assumption, called $N-\mathsf {MXDH}'$, which seems reasonable for Type-3 pairings, as we explain in Sect. 2.2.

Validity of a Transaction. Serial numbers are central to the detection of double-spending and so to ensure the traceability of the scheme. It is therefore necessary, during a spending of value V, to force the user to send a valid element $\phi _{V,j}$, by requesting a proof that the latter is well-formed. The user must then prove that (1) $\phi _{V,j}$ is an ElGamal encryption of some $s_j^x$ under $h_V$ (which is known since it corresponds to the spent amount), where (2) x has been certified, and (3) $s_j$ is a valid parameter for a transaction of value V. The first two statements can easily be handled using the Groth-Sahai [18] methodology, but this is not the case for the third one. Indeed, as we explained, $s_j$ (and so the index j) cannot be revealed unless breaking the anonymity of the scheme which would only achieve a weaker unlinkability property (as defined in [10]).

We could use the solution from [10] which consists in certifying each $s_j$ under the public keys ${\mathsf {pk}}^{1},\ldots ,{\mathsf {pk}}^{N-j+1}$ and to prove that the $s_j$ to be used is certified under the public key ${\mathsf {pk}}^V$. However, such a solution is quite efficient for tree-based schemes where each $s_j$ is associated with a unique node and so with a single amount, but not for our scheme where $s_j$ can be involved in any transaction of value V such that $V\in [1,N-j+1]$. This would dramatically increase the bank’s public key since it would contain about $N^2/2$ certificates.

While our public parameters will be of quadratic size, because of the sets ${\mathcal {S}}_V$, we hope the part necessary to the user to be at most linear in N. We will then use another solution which exploits the relation $e(s_j,{\widetilde{g}}_{V-1})=e(s_{j+V-1},{\widetilde{g}})$. To prove that $j\le N-V+1$, the user will thus simply prove that there is some $s_k$, for $k\in [1,N]$, such that $e(s_j,{\widetilde{g}}_{V-1})=e(s_k,{\widetilde{g}})$. This can be done efficiently if a certificate on each $s_k$ is provided by the bank. One may note that this proof only ensures that $j\le N-V+1$ and not that $j\ge 1$. However, we will show, in the security analysis, that a user is unlikely to produce a proof for an element $s_j\notin \{s_1,\ldots ,s_N\}$.

Security Tags. Detection of double-spending may not be sufficient to deter users from cheating. To prevent frauds it is also necessary to provide a way to identify dishonest users. Since we aim at achieving the anonymity property, such an identification cannot rely on some trusted entity with the power of tracing any user of the system. We will then use the standard technique of security tags which allows to recover the spender’s identity from any pair of transactions detected as a double-spending. Similarly to the constructions of [10, 11], we will add to the public parameters the elements $t_j$ such that, $\forall j\in [1,N]$, $t_j=s_j^c$ for some $c\in {\mathbb {Z}}_p$ and define, for a transaction involving $\phi _{V,j}$, the security tag as $\psi _{V,j}=(g^{r'},{\mathsf {upk}}^R\cdot t_j^x \cdot h_V^{r'})$ where ${\mathsf {upk}}$ is the user’s public key and R is some public information related to the transaction. As we prove below, such a tag hides the identity of a spender as long as he does not double-spend its coin.

Remark 7

Divisible e-cash systems do not usually specify the way the coin should be spent. As explained above, our construction is the first one to allow sequential spendings, contrarily to tree-based construction where the coins may contain several holes (see Sect. 1.1). Therefore, for sake of simplicity, we assume in the following that the user sequentially reveals the serial numbers and so we associate each coin to an index j. The latter means that ${\mathtt {SN}}_1,\ldots ,{\mathtt {SN}}_{j-1}$ have already been revealed and that the next spending of value V will reveal ${\mathtt {SN}}_j,\ldots ,{\mathtt {SN}}_{j+V-1}$.

However, we stress that the user is free to spend the coin as he wants. The only constraint is that two spendings must not reveal the same serial numbers, otherwise the user will be accused of double-spending.

4.2 Setup

Public Parameters. Let $(p,{\mathbb {G}}_1,{\mathbb {G}}_2,{\mathbb {G}}_T,e)$ be the description of bilinear groups of prime order p, elements $g,h,u_1,u_2,w$ be generators of ${\mathbb {G}}_1$, ${\widetilde{g}}$ be a generator of ${\mathbb {G}}_2$, and H be collision-resistant hash function onto ${\mathbb {Z}}_p$. A trusted authority generates $(z,y)\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p^2$ and, for $i=1,\ldots ,N$ (where N is the value of the coin), $a_i\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p$. It then computes the public parameters as follows:

• $(s,t)\leftarrow (g^z,h^z)$;

• $(s_j,t_j)\leftarrow (s^{y^j},t^{y^j})$, for $j=1,\ldots ,N$;

• ${\widetilde{g}}_k\leftarrow {\widetilde{g}}^{y^k}$, for $k=0,\ldots ,N-1$;

• $h_i\leftarrow g^{a_i}$, for $i=1,\ldots ,N$;

• ${\widetilde{h}}_{i,k} \leftarrow {\widetilde{g}}^{-a_i\cdot y^k}$, for $i=1,\ldots ,N$ and $k=0,\ldots ,i-1$.

These parameters can also be cooperatively generated by a set of users and the bank, in a way similar to the one described in [10]. The point is that none of these entities should know the scalars $(a_i)_i$, y or z.

We divide the public parameters ${ pp }$ into two parts, ${ pp }_{{\mathcal {U}}} \leftarrow \{g,h,u_1,u_2,w, H,$ $\{h_i\}_{i=1}^N,\{(s_j,t_j)\}_{j=1}^N\}$ and ${ pp }_{{\mathcal {B}}} \leftarrow \{\{{\widetilde{g}}_k\}_{k=0}^{N-1},\{({\widetilde{h}}_{i,k})_{k=0}^{i-1}\}_{i=1}^N\}$. The former contains the elements necessary to all the entities of the system whereas the latter contains the elements only useful to the bank during the ${\texttt {Deposit}}$ protocol. We therefore assume that the users and the merchants only store ${ pp }_{{\mathcal {U}}}$ and discard ${ pp }_{{\mathcal {B}}}$. Note that the former is linear in N, while the latter is quadratic.

Our protocols make use of ${\mathsf {NIZK}}$ and NIWI proofs for multi-exponentiations and pairing-product equations which are covered by the Groth-Sahai proof system [18]. We then add to ${ pp }_{{\mathcal {U}}}$ the description of a CRS for the perfect soundness setting and of a one-time signature scheme $\varSigma _{ots}$ (e.g. the one from [6]).

5 Our Divisible E-cash System

In this section, we provide an extended description of our new protocol and then discuss its efficiency. We describe a concrete instantiation in the full version [22].

5.1 The Protocol

• ${\texttt {Keygen}}()$: Each user (resp. merchant) selects a random ${\mathsf {usk}}\leftarrow {\mathbb {Z}}_p$ (resp. ${\mathsf {msk}}$) and gets ${\mathsf {upk}}\leftarrow g^{{\mathsf {usk}}}$ (resp. $\mathsf {mpk}\leftarrow g^{{\mathsf {msk}}}$). In the following, we assume that ${\mathsf {upk}}$ (resp. $\mathsf {mpk}$) is public, meaning that anyone can get an authentic copy of it.

• ${\texttt {BKeygen}}()$: The bank has two important roles to play. It must (1) deliver new coins to users during withdrawals and (2) control the transactions to detect double-spendings and identify the defrauders.

  The first point will require a signature scheme $\varSigma _1$ whose message space is ${\mathbb {G}}_1^2$ to certify the secret values associated with the withdrawn coins. We can therefore use the construction from [1] which is optimal in type-3 bilinear groups.

  The second point relies on the proof of validity of the elements $\phi _{V,j}$ sent during a transaction. As explained above, such a proof requires that the elements $s_k$ are certified, for $k=1,\ldots ,N$. For the same reasons, their dual elements $t_k$ must be certified too. It is therefore necessary to select a structure-preserving signature scheme $\varSigma _0$ whose message space is ${\mathbb {G}}_1^2$. We can then still choose the one from [1] but our security analysis shows that a scheme achieving a weaker security notion would be enough.

  Once the schemes $\varSigma _0$ and $\varSigma _1$ are selected, the bank generates $({\mathsf {sk}}_0,{\mathsf {pk}}_0)\leftarrow \varSigma _0.{\texttt {Keygen}}({ pp })$ and $({\mathsf {sk}}_1,{\mathsf {pk}}_1)\leftarrow \varSigma _1.{\texttt {Keygen}}({ pp })$. It then computes $\tau _j\leftarrow \varSigma _{0}.{\texttt {Sign}}({\mathsf {sk}}_0,(s_j,t_j))$ for all $j\in 1,\ldots ,N$ and sets ${\mathsf {bsk}}\leftarrow {\mathsf {sk}}_1$ and ${\mathsf {bpk}}\leftarrow \{{\mathsf {pk}}_0,{\mathsf {pk}}_1,\tau _1,\ldots ,\tau _N\}$.

• ${\texttt {Withdraw}}({\mathcal {B}}({\mathsf {bsk}},{\mathsf {upk}}),{\mathcal {U}}({\mathsf {usk}},{\mathsf {bpk}}))$: As explained in the previous section, each coin is associated with a random scalar x, which implicitly defines its serial numbers as ${\mathtt {SN}}_k = e(s_j^x,{\widetilde{g}}) = e(s,{\widetilde{g}})^{x\cdot y^k}$, for $k=1,\ldots ,N$. Delivering a new coin thus essentially consists in certifying this scalar x. However, for security reasons, it is necessary to bind the latter with the identity of its owner. Indeed, if this coin is double-spent, it must be possible to identify the user who has withdrawn it. This could be done by certifying the pair $(x,{\mathsf {usk}})\in {\mathbb {Z}}_p^2$ (without revealing them), using for example the scheme from [7], but, in the standard model, the bank will rather certify the pair $(u_1^{{\mathsf {usk}}},u_2^x)\in {\mathbb {G}}_1^2$. This is due to the fact that scalars cannot be efficiently extracted from Groth-Sahai proofs, contrarily to group elements in ${\mathbb {G}}_1$.

  In practice, the user computes $u_1^{\mathsf {usk}}$ and $u_2^{x_1}$ for some random $x_1\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p$ and sends them to the bank along with ${\mathsf {upk}}$. He then proves knowledge of $x_1$ and ${\mathsf {usk}}$ in a zero-knowledge way (using, for example, the Schnorr’s interactive protocol [23]). If the bank accepts the proof, it generates a random $x_2\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p$, computes $u\mathop {\leftarrow }\limits ^{{}_{\$}}u_2^{x_1}\cdot u_2^{x_2}$ and $\sigma \leftarrow \varSigma _1.{\texttt {Sign}}({\mathsf {sk}}_1,(u_1^{{\mathsf {usk}}},u))$ (unless u was used in a previous withdrawal) and returns $\sigma$ and $x_2$ to the user. The latter then sets the coin’s secret $x\leftarrow x_1+x_2$ and coin state $C\leftarrow (x,\sigma ,1)$: the last element of C is the index of the next serial number to be used. Hence the remaining amount on the coin is $N+1$ minus this index.

  Informally, the cooperative generation of the scalar x allows us to exclude (with overwhelming probability) false positives, i.e. a collision in the list L of serial numbers maintained by the bank which would not be due to an actual double-spending. We refer to Remark 8 for more details.

• ${\texttt {Spend}}({\mathcal {U}}({\mathsf {usk}},C,{\mathsf {bpk}},\mathsf {mpk},V),{\mathcal {M}}({\mathsf {msk}},{\mathsf {bpk}},V))$: Let $C=(x,\sigma ,j)$ be the coin the user wishes to spend. The latter selects two random scalars $(r_1,r_2)\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p^2$ and computes $R\leftarrow H({\textit{info}})$, $\phi _{V,j}\leftarrow (g^{r_1},s_j^x\cdot h_V^{r_1})$ and $\psi _{V,j}\leftarrow (g^{r_2},{\mathsf {upk}}^R\cdot t_j^x\cdot h_V^{r_2})$, where ${\textit{info}}$ is some information related to the transaction (such as the date, the amount, the merchant’s public key,...).

  Now, he must prove that (1) his coin $C$ is valid and (2) that the elements $\phi _{V,j}$ and $\psi _{V,j}$ are well-formed. The first point consists in proving knowledge of a valid signature $\sigma$ on $(u_1^{\mathsf {usk}},u_2^x)$, whereas the second point requires to prove knowledge of $\tau _{j+V-1}$ on $(s_{j+V-1},t_{j+V-1})$. This can be efficiently done in the standard model by using the Groth-Sahai methodology [18].

  Unfortunately, the resulting proofs can be re-randomized which enables a dishonest merchant to deposit several versions of the same transcript. To prevent such a randomization, the user generates a one-time signature key pair (${\mathsf {sk}}_{ots},{\mathsf {pk}}_{ots}$) which will be used to sign the whole transcript. To ensure that only the spender can produce this signature, the public key ${\mathsf {pk}}_{ots}$ will be certified into $\mu \leftarrow w^\frac{1}{{\mathsf {usk}}+H({\mathsf {pk}}_{ots})}$. One may note that these problems do not arise in the ROM since the proofs would be simply converted into a (non-randomizable) signature of knowledge by using the Fiat-Shamir heuristic [15].

  More formally, once the user has computed $\phi _{V,j}$, $\psi _{V,j}$ and $\mu$, he computes Groth-Sahai commitments to ${\mathsf {usk}},x,r_1,r_2,s_j,t_j,s_{j+V-1},t_{j+V-1},\tau _{j+V-1},\sigma ,\mu ,$ $U_1=u_1^{\mathsf {usk}}$ and $U_2=u_2^x$. He next provides:

  • 1. a ${\mathsf {NIZK}}$ proof $\pi$ that the committed values satisfy:

    

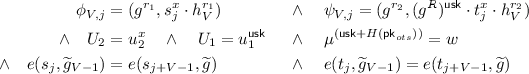
  • 2. a NIWI proof $\pi '$ that the committed values satisfy:

    $$\begin{aligned} 1&=\varSigma _0.{\texttt {Verify}}({\mathsf {pk}}_0,(s_{j+V-1},t_{j+V-1}),\tau _{j+V-1}) \\ \wedge \quad 1&=\varSigma _1.{\texttt {Verify}}({\mathsf {pk}}_1,(U_1,U_2),\sigma ). \end{aligned}$$

  Finally, he computes $\eta \leftarrow \varSigma _{ots}.{\texttt {Sign}}({\mathsf {sk}}_{ots},H(R||\phi _{V,j}||\psi _{V,j}||\pi ||\pi '))$ and sends it to ${\mathcal {M}}$ along with ${\mathsf {pk}}_{ots},\phi _{V,j},\psi _{V,j},\pi$ and $\pi '$.

  The merchant accepts if the proofs and the signatures are correct in which case he stores $(V,Z,\varPi )\leftarrow (V,(\phi _{V,j},\psi _{V,j}),(\pi ,\pi ',{\mathsf {pk}}_{ots},\eta ))$ while the user updates its coin $C\leftarrow (x,\sigma ,j+V)$.

• ${\texttt {Deposit}}({\mathcal {M}}({\mathsf {msk}},{\mathsf {bpk}},(V,Z,\varPi )),{\mathcal {B}}({\mathsf {bsk}},L,\mathsf {mpk}))$: When a transcript is deposited by a merchant, the bank parses it as $(V,(\phi _{V,j},\psi _{V,j}),(\pi ,\pi ',{\mathsf {pk}}_{ots},\eta ))$ and checks its validity (in the same way as the merchant did during the ${\texttt {Spend}}$ protocol). ${\mathcal {B}}$ also verifies that it does not already exist in its database. If everything is correct, ${\mathcal {B}}$ derives the serial numbers from $\phi _{V,j}=(\phi _{V,j}[1],$ $\phi _{V,j}[2])$ by computing ${\mathtt {SN}}_k\leftarrow e(\phi _{V,j}[2],{\widetilde{g}}_k)\cdot e(\phi _{V,j}[1],{\widetilde{h}}_{V,k})$, for $k=0,\ldots ,V-1$. If none of these serial numbers is in L, the bank adds them to this list and stores the associated transcript. Else, there is at least one ${\mathtt {SN}}'\in L$ (associated with a transcript $(V',Z',\varPi ')$) and one $k^*\in [0,V-1]$ such that ${\mathtt {SN}}'={\mathtt {SN}}_{k^*}$. The bank then outputs the two transcripts $(V,Z,\varPi )$ and $(V',Z',\varPi ')$ as a proof of a double-spending.

• ${\texttt {Identify}}((V_1,Z_1,\varPi _1),(V_2,Z_2,\varPi _2),{\mathsf {bpk}})$: The first step before identifying a double-spender is to check the validity of both transcripts and that there is a collision between their serial numbers, i.e. there are $k_1\in [0,V_1-1]$ and $k_2\in [0,V_2-1]$ such that:

  $$\begin{aligned} {\mathtt {SN}}_{k_1}&= e(\phi _{V_1,j_1}[2],{\widetilde{g}}_{k_1})\cdot e(\phi _{V_1,j_1}[1],{\widetilde{h}}_{V_1,k_1})\\&= e(\phi _{V_2,j_2}[2],{\widetilde{g}}_{k_2})\cdot e(\phi _{V_2,j_2}[1],{\widetilde{h}}_{V_2,k_2}) = {\mathtt {SN}}_{k_2} \end{aligned}$$

  Let $T_b$ be $e(\psi _{V_b,j_b}[2],{\widetilde{g}}_{k_b})\cdot e(\psi _{V_b,j_b}[1],{\widetilde{h}}_{V_b,k_b})$, for $b\in \{1,2\}$. The algorithm checks, for each registered public key ${\mathsf {upk}}_i$, whether $T_1\cdot T_2^{-1}=e({\mathsf {upk}}_i,{\widetilde{g}}_{k_1}^{R_1}\cdot {\widetilde{g}}_{k_2}^{-R_2})$ until it gets a match. It then returns the corresponding key ${\mathsf {upk}}^*$ (or $\perp$ if the previous equality does not hold for any ${\mathsf {upk}}_i$), allowing anyone to verify, without the linear cost in the number of users, that the identification is correct.

Remark 8

A collision in the list L means that two transcripts $(V_1,Z_1,\varPi _1) \not =(V_2,Z_2,\varPi _2)$ lead to a same serial number ${\mathtt {SN}}$. Let $Z_b=(\phi _{V_b,j_b},\psi _{V_b,j_b})$, for $b\in \{1,2\}$, the soundness of the ${\mathsf {NIZK}}$ proofs produced by the users during the spendings implies that:

$$\begin{aligned} e(\phi _{V_1,j_1}[2],{\widetilde{g}}_{k_1})\cdot e(\phi _{V_1,j_1}[1],{\widetilde{h}}_{V_1,k_1})&= e(\mathsf {s_1},{\widetilde{g}}_{k_1})^{x_1} = {\mathtt {SN}}\\&= e(\mathsf {s_2},{\widetilde{g}}_{k_2})^{x_2} = e(\phi _{V_2,j_2}[2],{\widetilde{g}}_{k_2})\cdot e(\phi _{V_2,j_2}[1],{\widetilde{h}}_{V_2,k_2}) \end{aligned}$$

for some $k_1\in [0,V_1-1]$, $k_2\in [0,V_2-1]$ and certified scalars $x_1$ and $x_2$, where the elements $\mathsf {s_1}$ and $\mathsf {s_2}$ verify, with $\ell _1,\ell _2\in [1,N]$:

$$e(\mathsf {s_1},{\widetilde{g}}_{V_1-1})=e(s_{\ell _1},{\widetilde{g}})\text { and } e(\mathsf {s_2},{\widetilde{g}}_{V_2-1})=e(s_{\ell _2},{\widetilde{g}}).$$

Therefore, we have, for $b\in \{1,2\}$, $e(\mathsf {s_b},{\widetilde{g}})=e(s,{\widetilde{g}})^{y^{\ell _b-V_b+1}}$, and so

$${\mathtt {SN}}=e(s,{\widetilde{g}})^{x_1\cdot y^{\ell _1-V_1+1+k_1}}=e(s,{\widetilde{g}})^{x_2\cdot y^{\ell _2-V_2+1+k_2}}$$

A collision thus implies that $x_1\cdot x_2^{-1}=y^{\ell _2-\ell _1+V_1-V_2+k_2-k_1}$. Since $x_1$ and $x_2$ are randomly (and cooperatively) chosen, without knowledge of y, a collision for $x_1\ne x_2$ will only occur with negligible probability. We can then assume that these scalars are equal and so that the collision in L is due to a double-spending.

Remark 9

The soundness of the proofs implies that the ${\texttt {Identify}}$ algorithm will output, with overwhelming probability, an identity ${\mathsf {upk}}$ each time a collision is found in L. Indeed, let $(V_1,Z_1,\varPi _1),(V_2,Z_2,\varPi _2)$ be the two involved transcripts, and $k_1,k_2$ such that:

$$\begin{aligned} {\mathtt {SN}}_{k_1}&=e(\phi _{V_1,j_1}[2],{\widetilde{g}}_{k_1})\cdot e(\phi _{V_1,j_1}[1],{\widetilde{h}}_{V_1,k_1})\\&=e(\phi _{V_2,j_2}[2],{\widetilde{g}}_{k_2})\cdot e(\phi _{V_2,j_2}[1],{\widetilde{h}}_{V_2,k_2})={\mathtt {SN}}_{k_2} \end{aligned}$$

For $b\in \{1,2\}$, if $\varPi _b$ is sound, then $(\phi _{V_b,j_b}[1],\phi _{V_b,j_b}[2])=(g^{r_b},s_{j_b}^{x_b}\cdot h_{V_b}^{r_b})$ for some $r_b\in {\mathbb {Z}}_p$ and so:

$$\begin{aligned} {\mathtt {SN}}_{k_1} =e(s_{j_1}^{x_1},{\widetilde{g}}_{k_1}) =e(s_{j_2}^{x_2},{\widetilde{g}}_{k_2})={\mathtt {SN}}_{k_2} \end{aligned}$$

(1)

For the same reasons, $T_b=e(\psi _{V_b,j_b}[2],{\widetilde{g}}_{k_b})\cdot e(\psi _{V_b,j_b}[1],{\widetilde{h}}_{V_b,k_b})=e({\mathsf {upk}}_b^{R_b}\cdot t_{j_b}^{x_b},{\widetilde{g}}_{k_b})$, for $b\in \{1,2\}$.

As explained in the previous remark, the equality (1) is unlikely to hold for different scalars $x_1$ and $x_2$. We may then assume that $x_1=x_2=x$ and so that ${\mathsf {upk}}_1={\mathsf {upk}}_2={\mathsf {upk}}$ since the bank verifies, during a withdrawal, that the same scalar x (or equivalently the same public value $u = u_2^x$) is not used by two different users.

The relation (1) also implies that $e(t_{j_1}^{x},{\widetilde{g}}_{k_1}) =e(t_{j_2}^{x},{\widetilde{g}}_{k_2})$ and so that:

$$T_1\cdot T_2^{-1}=e({\mathsf {upk}}^{R_1},{\widetilde{g}}_{k_1})\cdot e({\mathsf {upk}}^{R_2},{\widetilde{g}}_{k_2})^{-1}=e({\mathsf {upk}},{\widetilde{g}}_{k_1}^{R_1}\cdot {\widetilde{g}}_{k_2}^{-R_2}).$$

The defrauder’s identity ${\mathsf {upk}}$ will then be returned by the algorithm ${\texttt {Identify}}$, unless ${\widetilde{g}}_{k_1}^{R_1}\cdot {\widetilde{g}}_{k_2}^{-R_2}= 1_{{\mathbb {G}}_2}$. However, such an equality is very unlikely for distinct $k_1$ and $k_2$ (for the same reasons as the ones given in Remark 8) but also for $k_1=k_2$ since it would imply that $R_1=R_2$ and so a collision on the hash function H.

The security of our divisible E-Cash system is stated by the following theorems, whose proofs can be found in the next section.

Theorem 10

In the standard model, our divisible E-Cash system is traceable under the $N-{\mathsf {BDHI}}$ assumption if $\varSigma _0$ is an EUF-SCMA signature scheme, $\varSigma _1$ is an EUF-CMA signature scheme, and H is a collision-resistant hash function.

Theorem 11

Let q be a bound on the number of ${\mathcal {O}}{{\texttt {Spend}}}$ queries made by the adversary. In the standard model, our divisible E-Cash system achieves the exculpability property under the $q-{\mathsf {SDH}}$ assumption if $\varSigma _{ots}$ is a SUF-OTS signature scheme, and H is a collision-resistant hash function.

Theorem 12

In the standard model, our divisible E-Cash system is anonymous under the ${\mathsf {SXDH}}$ and the $N-\mathsf {MXDH}'$ assumptions.

Remark 13

A downside of our construction is that its anonymity relies on a quite complex assumption. This is due to the fact that most elements of the public parameters are related, which must be taken into account by the assumption. As we explain in the full version [22], we can rely on a more conventional assumption (while keeping the constant size property) by generating these parameters independently. Unfortunately, this has a strong impact on the efficiency of the protocol. Such a solution must then be considered as a tradeoff between efficiency and security assumption.

5.2 Efficiency

We compare in Fig. 3, the efficiency of our construction with the state-of-the-art, and namely Martens [20] (which improves the construction of [9]) and Canard et al. [11]. One can note that our table differs from those provided in these papers. This is mostly due to the fact that they only describe the most favorable case, where the spent value V is a power of 2. However, in real life, such an event is quite unlikely. Most of the time, the users of such systems will then have to write $V= \sum b_i \cdot 2^i$, for $b_i\in \{0,1\}$ and repeat the ${\texttt {Spend}}$ protocol for each $b_i=1$. Our description therefore considers the Hamming weight v of V (i.e. the number of $b_i$ such that $b_i=1$) but, for a proper comparison, also takes into account the possible optimisations of batch spendings (for example proving that the user’s secret is certified can be done only once).

Fig. 3.

Efficiency comparison between related works and our construction for coins of value N and ${\texttt {Spend}}$ and ${\texttt {Deposit}}$ of value V ($V\le N$). The computation and communication complexities are given from the user’s point of view. (n denotes the smallest integer such that $N\le 2^n$ and v the Hamming weight of V. ${\mathsf {E}}_{{\mathbb {G}}_{}}$ refers to an exponentiation in ${\mathbb {G}}$, ${\mathsf {ME}}_{{\mathbb {G}}_{}} (m)$ to a multi-exponentiation with m different bases in ${\mathbb {G}}$, $\mathsf {P}$ to a pairing computation, and ${\mathsf {Sign}}$ to the cost of the signing protocol whose public key is ${\mathsf {pk}}$. ${\mathsf {NIZK}} \{{\mathsf {E}}_{{\mathbb {G}}_{}} \}$ denotes the cost of a ${\mathsf {NIZK}}$ proof of a multi-exponentiation equation in ${\mathbb {G}}$, ${\mathsf {NIZK}} \{\mathsf {P} \}$ the one of a pairing-product equation, and ${\mathsf {NIZK}} \{{\mathsf {Sign}} \}$ the one of a valid signature. Finally, ${\mathtt {SN}}$ refers to the size of a serial number and $|{\texttt {Spend}}|$ to the size of the transcript of the ${\texttt {Spend}}$ protocol.)

Another difference with [20] comes from the fact that the author considered that “a multi-base exponentiation takes a similar time as a single-base exponentiation”. Although some works (e.g. [4]) have shown that an N-base exponentiation can be done more efficiently that N single-base exponentiations, considering that the cost of the former is equivalent to the one of a single exponentiation is a strong assumption, in particular when N can be greater than 1000 (if the coin’s value is greater than $10\$$). Our table therefore distinguishes multi-base exponentiations from single ones.

An important feature for an electronic payment system is the efficiency of its ${\texttt {Spend}}$ protocol. This is indeed the one subject to the strongest time constraints. For example, public transport services require that payments should be performed in less than 300ms [19], to avoid congestion in front of turnstiles. From this perspective, our scheme is the most effective one and, above all, is the first one to achieve constant time (and size) spendings, no matter which value is spent. Moreover, our divisible E-Cash system offers the same efficiency as the withdrawals of [11], while keeping a reasonable size for the parameters ${ pp }_{{\mathcal {U}}}$. Indeed, in our protocol, ${ pp }_{{\mathcal {U}}}$ just requires 230 KBytes of storage space for $N=1024$ (defining the coin’s value as $10.24 \$$) if Barreto-Naehrig curves [3] are used to instantiate the bilinear groups. For the same settings, ${ pp } _U$ amounts to 263 KBytes for [11] and 98 KBytes for [20].

From the bank’s point of view, the downside of our scheme is the additional parameters ${ pp } _B$ that the bank must store, and they amount to 33 MBytes, but it should not be a problem for this entity. As for the other schemes, each deposit of a value V requires to store V serial numbers whose size can be adjusted by using an appropriate hash function (see Remark 14 below).

Remark 14

As explained in [10], the bank does not need to store the serial numbers but only their smaller hash values, as fingerprints. Therefore, the size of the V elements ${\mathtt {SN}}$ computed during a deposit of value V is the same for all the schemes. The ${\texttt {Deposit}}$ size then mostly depends on the size of the ${\texttt {Spend}}$ transcripts. By achieving smaller, constant-size spendings, we thus alleviate the storage burden of the bank and so improve the scalability of our divisible E-Cash system.

Remark 15

Public identification of defrauders has an impact on the complexity of the system. This roughly doubles the size of the parameters and requires several additional computations during a spending. Such a property also has consequences on the security analysis which must rely on a stronger assumption (namely the $N-\mathsf {MXDH}'$ one instead of its weaker variant) involving more challenge elements.

However, in some situations, it can be possible to consider an authority which would be trusted to revoke user’s anonymity only in case of fraud. The resulting e-cash system, called fair, obviously weakens anonymity but may be a reasonable tradeoff between user’s privacy and legal constraints.

Our scheme can be modified to add such an entity. One way would be to entrust it with the extraction key of the Groth-Sahai proof system. It could then extract the element $U_1=u_1^{{\mathsf {usk}}}$ from any transaction and so identify the spender. The elements $t_j$ would then become unnecessary and could be discarded from the public parameters. Moreover, the elements $\psi _{V,j}$, along with the associated proofs, would also become useless during the ${\texttt {Spend}}$ protocol. The complexity of the scheme would then be significantly improved. The consequences of these changes on the security analysis are discussed in Remark 21 of the next section.

6 Security Analysis

6.1 Proof of Theorem 10: Traceability

Let us consider a successful adversary ${\mathcal {A}}$ which manages to spend more than he has withdrawn without being traced. This formally means that it is able to produce, after $q_w$ withdrawals, u valid transcripts $\{(V_i,Z_i,\varPi _i)\}_{i=1}^u$ representing an amount of $\sum _{i=1}^u V_i > N\cdot q_w$, but such that ${\texttt {Identify}}((V_i,Z_i,\varPi _i),(V_j,Z_j,\varPi _j))=\;\perp$, for all $i\ne j$. We can have the three following cases:

• Type-1 Forgeries: $\exists i$ such that $\varPi _i$ contains commitments to a pair $(s_{\ell _i},t_{\ell _i})$ which was not signed in a $\tau _\ell$ by the bank, during the key generation phase;

• Type-2 Forgeries: $\exists i$ such that $\varPi _i$ contains commitments to a pair $(u_1^{{\mathsf {usk}}},u_2^{x})$ which was never signed by the bank, during a ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}$ query;

• Type-3 Forgeries: $\forall 1\le i \le u$, $\exists \tau _{\ell _i}$ in ${\mathsf {bpk}}$ which is a valid signature on the pair $(s_{\ell _i},t_{\ell _i})$ committed in $\varPi _i$ and the pairs $(u_1^{{\mathsf {usk}}},u_2^{x})$ involved in this transcript were signed by the bank during a ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}$ query, but identification fails.

Intuitively, the first two cases imply an attack against the signatures schemes $\varSigma _0$ or $\varSigma _1$, respectively. This is formally stated by the two following lemmas:

Lemma 16

Any Type-1 forger ${\mathcal {A}}$ with success probability $\varepsilon$ can be converted into an adversary against the EUF-SCMA security of $\varSigma _0$ with the same success probability.

Proof

The reduction ${\mathcal {R}}$ generates the public parameters (the group elements), and sends $\{(s_j,t_j)\}_{j=1}^N$ to the signing oracle of the EUF-SCMA security experiment which returns the signatures $\{\tau _j\}_{j=1}^N$ along with the challenge public key ${\mathsf {pk}}$. It can run $\varSigma _1.{\texttt {Keygen}}$ to get the key pair $({\mathsf {sk}}_1,{\mathsf {pk}}_1)$ and set ${\mathsf {bpk}}$ as $({\mathsf {pk}}_0={\mathsf {pk}},{\mathsf {pk}}_1,\tau _1,\ldots ,\tau _N)$. One may note that ${\mathcal {R}}$ is able to answer any query from ${\mathcal {A}}$ since it knows ${\mathsf {bsk}}={\mathsf {sk}}_1$.

At the end of the game, ${\mathcal {R}}$ extracts (it has generated the CRS of the Groth-Sahai proofs system and so knows the related extraction keys) from $\varPi _i$, for $i\in [1,u]$, a valid signature $\tau _{\ell _i}$ on some pair $(s_{\ell _i},t_{\ell _i})$ under the public key ${\mathsf {pk}}$. Since ${\mathcal {A}}$ is a Type-1 forger with success probability $\varepsilon$, at least one of these pairs does not belong to the set $\{(s_j,t_j)\}_{j=1}^N$ and so is valid forgery which can be used to break the EUF-SCMA security of $\varSigma _0$, with probability $\varepsilon$.   $\square$

Lemma 17

Any Type-2 forger ${\mathcal {A}}$ with success probability $\varepsilon$ can be converted into an adversary against the EUF-CMA security of $\varSigma _1$ with the same success probability.

Proof

The reduction ${\mathcal {R}}$ generates the public parameters (the group elements) and its public key as usual except that it sets ${\mathsf {pk}}_1$ as ${\mathsf {pk}}$, the challenge public key in the EUF-CMA security experiment. ${\mathcal {R}}$ can then directly answer all the queries except the ${\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {B}}}}$ ones for which it will forward the pairs $(u_1^{{\mathsf {usk}}},u_2^{x})$ to the signing oracle and forward the resulting signature $\sigma$ to ${\mathcal {A}}$.

The game ends when ${\mathcal {A}}$ outputs u transcripts such that one of them, $(2^\ell ,Z,\varPi )$, contains a commitment to a pair $(u_1^{{\mathsf {usk}}},u_2^{x})$ which was never signed by the bank during a ${\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {B}}}}$ query. The soundness of the proof implies that it also contains a commitment to an element $\sigma$ such that $\varSigma _1.{\texttt {Verify}}((u_1^{{\mathsf {usk}}},u_2^{x}),\sigma ,{\mathsf {pk}})=1$. Such a forgery can then be used to break the EUF-CMA security of $\varSigma _1$.   $\square$

Now, it remains to evaluate the success probability of a Type-3 forger. The following lemma shows that it is negligible under $N-{\mathsf {BDHI}}$ assumption.

Lemma 18

Any Type-3 forger ${\mathcal {A}}$ with success probability $\varepsilon$ can be converted into an adversary against the $N-{\mathsf {BDHI}}$ assumption with the same success probability.

Proof

Let $(\{g^{y^i}\}_{i=0}^N,\{{\widetilde{g}}^{y^i}\}_{i=0}^N)\in {\mathbb {G}}_1^{N+1}\times {\mathbb {G}}_2^{N+1}$ be a $N-{\mathsf {BDHI}}$ challenge. The reduction ${\mathcal {R}}$ generates random scalars $c, z'\leftarrow {\mathbb {Z}}_p$ and $a_i\leftarrow {\mathbb {Z}}_p$, for $i=1,\ldots ,N$, and sets the public parameters as follows:

• $(s_j,t_j) \leftarrow ((g^{y^{j-1}})^{z'}, (g^{y^{j-1}})^{c\cdot z'})$, for $j=1,\ldots ,N$;

• ${\widetilde{g}}_k \leftarrow {\widetilde{g}}^{y^k}$, for $k=0,\ldots ,N-1$;

• $h_i \leftarrow g^{a_i}$, for $i=1,\ldots ,N$;

• ${\widetilde{h}}_{i,k} \leftarrow ({\widetilde{g}}^{y^k})^{-a_i}$, for $i=1,\ldots ,N$ and $k=0,\ldots ,i-1$.

By setting $(s,t) = (g^{z'\cdot y^{-1}}, g^{c\cdot z'\cdot y^{-1}})$—recall that this pair is not published in ${ pp }$—, one can easily check that the simulation is correct: $s_j = s^{y^j}$ and $t_j = t^{y^j}$. ${\mathcal {R}}$ then generates the CRS for the perfect soundness setting and stores the extraction keys. Finally, it computes the bank’s key pair $({\mathsf {bsk}},{\mathsf {bpk}})$ as usual and so is able to answer every oracle queries.

At the end of the game, ${\mathcal {R}}$ extracts the elements $s^{(i)}$ committed in $\varPi _i$, for $i=1,\ldots ,u$. Each of these proofs also contains a commitment to signature $\tau _{\ell _i}$ on the pair $(s_{\ell _i},t_{\ell _i})$ such that: $e(s^{(i)},{\widetilde{g}}_{V_i-1})=e(s_{\ell _i},{\widetilde{g}})$. Since we here consider Type-3 forgeries, $\ell _i\in [1,N]$ (otherwise $\tau _{\ell _i}\notin {\mathsf {bpk}}$) and so $s_{\ell _i}= s^{y^{\ell _i}}$. Therefore, we have $s^{(i)}=s^{y^{\ell _i-V_i +1}}$, where $\ell _i-V_i +1\le N - V_i+1$. We then distinguish the two following cases.

• Case 1: $\forall i\in [1,u]$, $\ell _i-V_i +1\ge 1$;

• Case 2: $\exists i\in [1,u]$ such that $\ell _i-V_i +1< 1$.

The first case means that ${\mathcal {A}}$ only used valid elements $s^{(i)}$ (i.e. $s^{(i)} = s_{j_i}$ such that $j_i\in [1,N-V_i+1]$) to construct the proofs $\varPi _i$. So all the $(\sum _{i=1}^u V_i)$ serial numbers derived from the u transcripts returned by ${\mathcal {A}}$ belong to the set ${\mathcal {S}}=\{\cup _{k=1}^{q_w} \{e(s,{\widetilde{g}})^{x_k\cdot y^\ell }\}_{\ell =1}^{N}\}$, where $\{x_k\}_{k=1}^{q_w}$ is the list of the scalars certified by the bank during the ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}$ queries. An over-spending means that $\sum _{i=1}^u V_i > N\cdot q_w = |{\mathcal {S}}|$, so there is at least one collision in the list of the serial numbers. However, a collision without identification of a defrauder is unlikely, as we explained in Remark 9. Hence, case 1 can only occur with negligible probability.

Now, let us consider the second case: when such a case occurs, ${\mathcal {R}}$ is able to extract the element $s^{y^{\ell _i-V_i +1}}$ such that $\ell _i-V_i +1\le 0$, and compute $\mathsf {g} \leftarrow (s^{y^{\ell _i-V_i +1}})^{1/z'} = g^{y^{\ell _i-V_i}}$ with $1-N\le \ell _i-V_i\le -1$. Let $k_i$ be the integer such that $\ell _i-V_i+k_i=-1$. The previous inequalities imply that $k_i\in [0,N-2]$ and so ${\mathcal {R}}$ can break the $N-{\mathsf {BDHI}}$ assumption by returning $e(g,{\widetilde{g}})^{y^{-1}}= e(\mathsf {g},{\widetilde{g}}_{k_i})$.   $\square$

6.2 Proof of Theorem 11: Exculpability

The goal of the adversary ${\mathcal {A}}$ is to make the identify procedure to claim an honest user ${\mathsf {upk}}$ guilty of double-spending: it publishes two valid transcripts $(V_1,Z_1,\varPi _1)$ and $(V_2,Z_2,\varPi _2)$ such that ${\mathsf {upk}}={\texttt {Identify}}((V_1,Z_1,\varPi _1),(V_2,Z_2,\varPi _2))$, while this user did not perform the two transactions (maybe one). We can obviously assume that one of these transcripts has been forged by ${\mathcal {A}}$.

Let us consider a successful adversary. We distinguish the two following cases:

• Type-1 forgeries: the public key ${\mathsf {pk}}_{ots}$ of the one-time signature scheme used in this forged transcript is one of those used by the honest user to answer ${\mathcal {O}}{{\texttt {Spend}}}$ queries.

• Type-2 forgeries: ${\mathsf {pk}}_{ots}$ was never used by this honest user.

Lemma 19

Let $q_s$ be a bound on the number of ${\mathcal {O}}{{\texttt {Spend}}}$ queries. Any Type-1 forger ${\mathcal {A}}$ with success probability $\varepsilon$ can be converted into an adversary against the SUF-OTS security of the one-time signature scheme $\varSigma _{ots}$ with success probability greater than $\varepsilon /q_s$.

Proof

The reduction ${\mathcal {R}}$ generates the public parameters along with the bank’s key pair and selects an integer $i^*\in [1,q_s]$. Upon receiving the $i^{th}$ ${\mathcal {O}}{{\texttt {Spend}}}$ query, it acts normally if $i\ne i^*$, but uses the public key ${\mathsf {pk}}_{ots}^*$ and the signing oracle of the SUF-OTS security experiment if $i=i^*$.

Let ${\mathsf {pk}}_{ots}$ be the public key involved in the forged transcript. ${\mathcal {R}}$ aborts if ${\mathsf {pk}}_{ots}\ne {\mathsf {pk}}_{ots}^*$, which occurs with probability $1-1/q_s$. Else, the forged transcript contains a new one-time signature $\eta$ under ${\mathsf {pk}}_{ots}^*$ which can be used against the security of $\varSigma _{ots}$.   $\square$

Lemma 20

Let $q_s$ (resp. $q_a$) be a bound on the number of ${\mathcal {O}}{{\texttt {Spend}}}$ queries (resp. ${\mathcal {O}}{\texttt {Add}}$ queries). Any Type-2 forger ${\mathcal {A}}$ with success probability $\varepsilon$ can be converted into an adversary against the $q_s-{\mathsf {SDH}}$ assumption with success probability $\varepsilon /q_a$.

Proof

Let $(g,g^\alpha ,\ldots ,g^{\alpha _{q_s}})$ be a $q_s-{\mathsf {SDH}}$ challenge, the reduction ${\mathcal {R}}$ will make a guess on the user ${\mathsf {upk}}^*$ framed by ${\mathcal {A}}$ and will act as if its secret key was $\alpha$. Therefore, it selects $1\le i^* \le q_a$ and generates the public parameters as in the ${\texttt {Setup}}$ algorithm except that it sets $u_1$ as $g^z$ for some random $z\in {\mathbb {Z}}_p$. Next, it computes $q_s$ key pairs $({\mathsf {sk}}_{ots}^{(i)},{\mathsf {pk}}_{ots}^{(i)})\leftarrow \varSigma _{ots}.{\texttt {Keygen}}(1^k)$ and sets w as $g^{\prod _{i=1}^{q_s}(\alpha +H({\mathsf {pk}}_{ots}^{(i)}))}$ (which is possible using the $q_s-{\mathsf {SDH}}$ challenge [6], since the exponent is a polynomial in $\alpha$ of degree $q_s$). The reduction will answer the oracle queries as follows.

• ${\mathcal {O}}{\texttt {Add}}()$ queries: When the adversary makes the $i^{th}$ ${\mathcal {O}}{\texttt {Add}}$ query to register a user, ${\mathcal {R}}$ runs the ${\texttt {Keygen}}$ algorithm if $i\ne i^*$ and sets ${\mathsf {upk}}^*\leftarrow g^\alpha$ otherwise.

• ${\mathcal {O}}{\texttt {Corrupt}}({\mathsf {upk}}/\mathsf {mpk})$ queries: ${\mathcal {R}}$ returns the secret key if ${\mathsf {upk}}\ne {\mathsf {upk}}^*$ and aborts otherwise.

• ${\mathcal {O}}{{\texttt {AddCorrupt}}}({\mathsf {upk}}/\mathsf {mpk})$ queries: ${\mathcal {R}}$ stores the public key which is now considered as registered.

• ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}({\mathsf {bsk}},{\mathsf {upk}})$ queries: ${\mathcal {R}}$ acts normally if ${\mathsf {upk}}\ne {\mathsf {upk}}^*$ and simulates the interactive proof of knowledge of $\alpha$ otherwise.

• ${\mathcal {O}}{{\texttt {Spend}}}({\mathsf {upk}},V)$ queries: ${\mathcal {R}}$ acts normally if ${\mathsf {upk}}\ne {\mathsf {upk}}^*$. Else, to answer the $j^{th}$ query on ${\mathsf {upk}}^*$, it computes $\mu \leftarrow g^{\prod _{i=1,i\ne j}^{q_s}(\alpha +H({\mathsf {pk}}_{ots}^{(i)}))}$ which satisfies $\mu =w^{1/(\alpha +H({\mathsf {pk}}_{ots}^{(j)}))}$, and uses ${\mathsf {sk}}_{ots}^{(j)}$ as in the ${\texttt {Spend}}$ protocol.

The adversary then outputs two valid transcripts $(V_1,Z_1,\varPi _1)$ and $(V_2,Z_2,\varPi _2)$ which accuse ${\mathsf {upk}}$ of double-spending. If ${\mathsf {upk}}\ne {\mathsf {upk}}^*$ then ${\mathcal {R}}$ aborts which will occur with probability $1-1/q_a$. Else, the soundness of the proof implies that the forged transcript was signed under ${\mathsf {pk}}_{ots}$ and so that the proof involves an element $\mu =w^{\frac{1}{\alpha +H({\mathsf {pk}}_{ots})}}$. Since here we consider Type-2 attacks, ${\mathsf {pk}}_{ots}\notin \{{\mathsf {pk}}_{ots}^{(i)}\}_i$. Therefore, $H({\mathsf {pk}}_{ots})\notin \{H({\mathsf {pk}}_{ots}^{(i)})\}_i$ with overwhelming probability, due to the collision-resistance of the hash function H. The element $\mu$ can then be used to break the $q_s-{\mathsf {SDH}}$ assumption in ${\mathbb {G}}_1$ (as in [6]).   $\square$

6.3 Proof of Theorem 12: Anonymity

In this proof, we assume that the coins are spent in a sequential way: the index j in $C=(x,\sigma ,j)$ is increased by V after each spending of an amount V, and the new j is used in the next spending. A next coin is used when the previous coin is finished. But the proof would also apply if the user could adaptively choose the coin $(x,\sigma )$, as well as (j, V) for every spending.

We can make the proof with a sequence of games, starting from the initial game for anonymity, with a random bit b (see Fig. 2), where the simulator emulates the challenger but correctly generating all the secret values. The advantage is $\varepsilon$, and we want to show it is negligible.

In a next game, the simulator makes a guess on the amount $V^*\in [1,N]$ chosen by the adversary during the step 3 of the anonymity experiment (see Fig. 2) and also makes a guess $j^*\in [1,N-V^*+1]$ for the actual index of the coin of the user ${\mathsf {upk}}_b$ at the challenge time (but this challenge value could be chosen by the adversary, as said above). In addition, we denote $q_w$ the bound on the number of ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}$ queries, and the simulator selects a random integer $\ell ^*\in [1,q_w]$, for the expected index of the ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}$ query that generates the coin that will be used in the challenge. If during the simulation it appears they are not correct, one stops the simulation. This guess does not affect the success probability of the adversary, when the guess is correct, but just reduces the advantage from $\varepsilon$ to $2\varepsilon /(q_w N^2)$.

Next, the simulator generates the CRS for the Groth-Sahai proofs in the perfect witness indistinguishability setting, so that it can later simulate the proofs. This is indistinguishable from the previous game under the ${\mathsf {SXDH}}$ assumption.

Now, the simulator will simulate the public parameters from an $N-\mathsf {MXDH}'$ challenge:

• $(g^{\gamma ^k},h^{\gamma ^k})_{k=0}^P\in {\mathbb {G}}_1^{2P+2}$,

• $(g^{\alpha \cdot \delta \cdot \gamma ^{-k}}, h^{\alpha \cdot \delta \cdot \gamma ^{-k}})_{k=0}^E\in {\mathbb {G}}_1^{2E+2}$,

• $(g^{\chi \cdot \gamma ^k}, h^{\chi \cdot \gamma ^k})_{k=D+1}^{P}\in {\mathbb {G}}_1^{2C}$,

• and $((g^{\alpha \cdot \gamma ^{-k}})_{k=0}^C, (g^{\chi \cdot \gamma ^k/\alpha }, h^{\chi \cdot \gamma ^k/\alpha })_{k=0}^{C}, )\in {\mathbb {G}}_1^{3S}$,

• as well as $({\widetilde{g}}^{\gamma ^k}, {\widetilde{g}}^{\alpha \cdot \gamma ^{-k}})_{k=0}^C\in {\mathbb {G}}_2^{2S}$,

• and a pair $(g^{z_1},h^{z_2})\in {\mathbb {G}}_1^2$ be an $N-\mathsf {MXDH}'$ challenge.

We recall that $C= N^3-N^2$, $S=C+1$, $E=N^2-N$, $D=S+E=N^3-N+1$ and $P=D+C=2N^3-N^2-N+1$. Let d be the quotient of the division of $N^2$ by $V^*$ (i.e. $N^2=d\cdot V^* + r_d$ with $0\le r_d<V^*$), then the simulator constructs the public parameters as follows.

• g and h are defined from $g^{\gamma ^k}$ and $h^{\gamma ^k}$ respectively, with $k=0$;

• $u_1\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {G}}_1$ and $u_2\leftarrow g^{w_\cdot \gamma ^P}$, for a random $w\in {\mathbb {Z}}_p$;

• ${\widetilde{g}}$ is defined from ${\widetilde{g}}^{\gamma ^k}$, with $k=0$;

• $(s_j,t_j)\leftarrow (g^{\gamma ^{D+d(1-V^*+j-j^*)}},h^{\gamma ^{D+d(1-V^*+j-j^*)}})$, for $j=1,\ldots ,N$;

• ${\widetilde{g}}_k\leftarrow {\widetilde{g}}^{\gamma ^{d\cdot k}}$, for $k=0,\ldots ,N-1$;

• $h_i\leftarrow g^{w_i\cdot \alpha \cdot \gamma ^{d(-i+1)}}$, for $i\in [1,\ldots ,N]$, with $w_i$ a random scalar;

• ${\widetilde{h}}_{i,k}\leftarrow {\widetilde{g}}^{-w_i\cdot \alpha \cdot \gamma ^{d(k-i+1)}}$, for $i\in [1,\ldots ,N]$ and $k=0,\ldots ,i-1$.

We must check that

• (1) the simulation of the parameters is correct: let us define $y = \gamma ^d$, $(s,t)=(g^{\gamma ^{D+d(1-V^*-j^*)}}, h^{\gamma ^{D+d(1-V^*-j^*)}})$, and $a_i=\alpha \cdot w_i \cdot \gamma ^{d(-i+1)}$ for $i\in [1,\ldots ,N]$. We then have:

  • $(s_j,t_j)= ((g^{\gamma ^{D+d(1-V^*-j^*)}})^{\gamma ^{d\cdot j}},(h^{\gamma ^{D+d(1-V^*-j^*)}})^{\gamma ^{d\cdot j}})=(s^{y^j},t^{y^j})$;

  • ${\widetilde{g}}_k= {\widetilde{g}}^{y^k}$, for $k=0,\ldots ,N-1$;

  • $h_i = g^{a_i}$, for $i=1,\ldots ,N$;

  • ${\widetilde{h}}_{i,k}= {\widetilde{g}}^{-a_i\cdot y^k}$, for $i=1,\ldots ,N$ and $k=0,\ldots ,i-1$.

  The simulation is therefore correct;

• (2) all of these elements can be provided from the $N-\mathsf {MXDH}'$ challenge: First, recall that $N^2 = d\cdot V^* + r_d$ with $0\le r_d < V^* \le N$. Then $2 \le V^*+j^*\le N+1$ and $N \le d \le N^2$.

  Let us consider the pairs $(s_j,t_j)=(g^{\gamma ^{D+d(1-V^*+j-j^*)}},h^{\gamma ^{D+d(1-V^*+j-j^*)}})$, for $j=1,\ldots ,N$: $1+j - (V^*+j^*) \ge 2 - (N+1) \ge -N+1$, therefore, $d(1-V^*+j-j^*) \ge -d (N-1) \ge -N^2 (N-1) \ge -C$. Moreover, $d(1-V^*+j-j^*)\le d(N-1)\le N^2(N-1) \le C$. Hence $D-C \le D+d(1-V^*+j-j^*) \le D+C = P$. Since $D = S+E = C+1+E$, $D-C = E+1 = N^2-N+1 \ge 0$. Hence, the pairs $(s_j,t_j)$ can be defined from the tuple $(g^{\gamma ^k},h^{\gamma ^k})_{k=0}^P$ of the $N-\mathsf {MXDH}'$ instance.

  About the elements ${\widetilde{g}}_k = {\widetilde{g}}^{\gamma ^{d\cdot k}}$, since we have $0\le d\cdot k \le N^2(N-1)=C$, for $k=0,\ldots ,N-1$, they all are in the tuple $({\widetilde{g}}^{\gamma ^k})_{k=0}^C$.

  Eventually, let us consider the elements $h_i = g^{w_i\cdot \alpha \cdot \gamma ^{d(-i+1)}}$ and ${\widetilde{h}}_{i,k}={\widetilde{g}}^{-w_i\cdot \alpha \cdot \gamma ^{d(k-i+1)}}$, for $i\in [1,N]$ and $k\in [0,i-1]$. Since $-C\le -d (N-1)\le d (-i+1) \le 0$ and $-C\le d(k-i+1) \le 0$, they all can be computed from the tuples $(g^{\alpha \cdot \gamma ^{-k}})_{k=0}^C$ and $({\widetilde{g}}^{\alpha \cdot \gamma ^{-k}})_{k=0}^C$, just using the additional random scalar $w_i$.

  The reduction ${\mathcal {R}}$ is thus able to generate the public parameters from the $N-\mathsf {MXDH}'$ instance.

The simulator now has to answer all the oracle queries, with all the secret keys.

• ${\mathcal {O}}{\texttt {Add}}()$ queries: run the ${\texttt {Keygen}}$ algorithm and return ${\mathsf {upk}}$ (or $\mathsf {mpk}$);

• ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}({\mathsf {bsk}},{\mathsf {upk}})$ queries: for the $\ell ^{th}$ ${{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}$ query, the simulator plays normally if $\ell \ne \ell ^*$, but sending the pair $(u_1^{{\mathsf {usk}}},(g^{\chi \cdot \gamma ^P})^w = u_2^\chi )$ otherwise (using the $N-\mathsf {MXDH}'$ instance). It can then simulate the proof of knowledge and receives a scalar $x'$ along with a signature $\sigma$ on $(u_1^{{\mathsf {usk}}},u_2^{x^*})$, where $x^*=\chi +x'$. The coin is then implicitly defined as $C^*=(x^*,\sigma ,1)$ and we will now denote its owner by ${\mathsf {upk}}^*$;

• ${\mathcal {O}}{\texttt {Corrupt}}({\mathsf {upk}}/\mathsf {mpk})$ queries: the simulator plays normally (if the guesses are correct, ${\mathsf {upk}}^*$ cannot be asked to be corrupted);

• ${\mathcal {O}}{{\texttt {AddCorrupt}}}({\mathsf {upk}}/\mathsf {mpk})$: the simulator stores the public key which is now considered as registered;

• ${\mathcal {O}}{{\texttt {Spend}}}({\mathsf {upk}},V)$ queries: if the coin to be used for the spending has not been withdrawn during the $\ell ^*-{{\mathcal {O}}{\texttt {Withdraw}_{{\mathcal {U}}}}}$-query, then the simulator knows all the secret keys, and so it can play normally. Else, it proceeds as follows. One can first remark that if the guesses are correct, $j\not \in [j^*-V+1,j^*+V^*-1]$. Otherwise this spending and the challenge spending would lead to a double-spending.

  • If $j\ge j^*+V^*$, then $D+d(1-V^*+j-j^*)\ge D+d \ge D+1$, so $s_j^{x^*}$ and $t_j^{x^*}$ can be computed from the tuple $(g^{\chi \cdot \gamma ^k}, h^{\chi \cdot \gamma ^k})_{k=D+1}^{P}$. Indeed,

    $$\begin{aligned}&s_j^{x^*}= (g^{\gamma ^{D+d(1-V^*+j-j^*)}})^{x^*} = g^{\chi \cdot \gamma ^{D+d(1-V^*+j-j^*)}} \cdot (g^{\gamma ^{D+d(1-V^*+j-j^*)}})^{x'} \\&t_j^{x^*}= (h^{\gamma ^{D+d(1-V^*+j-j^*)}})^{x^*} =h^{\chi \cdot \gamma ^{D+d(1-V^*+j-j^*)}} \cdot (h^{\gamma ^{D+d(1-V^*+j-j^*)}})^{x'}. \end{aligned}$$

    The simulator can then send ElGamal encryptions of $s_j^{x^*}$ and $t_j^{x^*}\cdot g^{R\cdot {\mathsf {usk}}^*}$ under $h_V$ (which yields valid $\phi _{V^*,j^*}$ and $\psi _{V^*,j^*}$) along with simulated proofs.

  • If $j\le j^*-V$, then we proceed as follows.

    Let $r\leftarrow -\chi \cdot \gamma ^{D+d(-V^*+1+j-j^*)+d(V-1)}/\alpha$ and $(r'_1,r'_2)\mathop {\leftarrow }\limits ^{{}_{\$}}{\mathbb {Z}}_p^2$. Then, $(g^{r/w_V+r'_1},s_{j}^{x'} \cdot h_V^{r'_1})$ and $(h^{r/w_V} \cdot g^{r'_2},t_{j}^{x'}\cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_V^{r'_2})$ are valid pairs $\phi _{V,j}$ and $\psi _{V,j}$ which can be computed from the tuple $(g^{\chi \cdot \gamma ^k/\alpha }, h^{\chi \cdot \gamma ^k/\alpha })_{k=0}^{C}$ of the $N-\mathsf {MXDH}'$ instance: Since $d\cdot V^* = N^2 - r_d > N^2-N$,

    $$\begin{aligned}&D+d(-V^*+1+j-j^*)+d(V-1) = D+d(V-V^*+j-j^*) \\&\le D-d\cdot V^*< D - N^2+N < D - E = S = C+1 \end{aligned}$$

    This is thus less or equal to C, as the indices of the tuple.

    It then remains to prove that $(g^{r/w_V+r'_1},s_{j}^{x'} \cdot h_V^{r'_1})$ and $(h^{r/w_V} \cdot g^{r'_2},t_{j}^{x'}\cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_V^{r'_2})$ are valid ElGamal encryptions of $s_j^{x^*}$ and $t_j^{x^*}\cdot g^{R\cdot {\mathsf {usk}}^*}$ under $h_V$. Let c be the secret scalar such that $h=g^c$, $r_1=r/w_V+r'_1$ and $r_2=c\cdot r/w_V+r'_2$, we then have: $g^{r_1} = g^{r/w_V+r'_1}$ and

    $$\begin{aligned} s_{j}^{x^*} \cdot h_V^{r_1}&= s_j^{\chi } \cdot s_{j}^{x'}\cdot h_V^{r/w_V+r'_1} \\&= g^{\chi \cdot \gamma ^{D+d(1-V^*+j-j^*)}} \cdot (g^{w_V\cdot \alpha \cdot \gamma ^{d(-V+1)}})^{r/w_V} \cdot s_{j}^{x'} \cdot h_V^{r'_1}\\&= g^{\chi \cdot \gamma ^{D+d(1-V^*+j-j^*)}} \cdot g^{-\chi \cdot \gamma ^{D+d(1-V^*+j-j^*)}} \cdot s_{j}^{x'} \cdot h_V^{r'_1})\\&= s_{j}^{x'} \cdot h_V^{r'_1} \end{aligned}$$

    Similarly, $g^{r_2} = h^{r/w_W}\cdot g^{r'_2}$ and as just above

    $$\begin{aligned} t_j^{x^*} \cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_V^{r_2}&= t_j^{x'} \cdot t_j^{\chi } \cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_V^{c\cdot r/w_V} \cdot h_V^{r'_2}\\&= t_j^{x'} \cdot h^{\chi \cdot \gamma ^{D+d(1-V^*+j-j^*)}} \cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h^{-\chi \cdot \gamma ^{D+d(1-V^*+j-j^*)}} \cdot h_V^{r'_2}\\&= t_j^{x'} \cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_V^{r'_2} \end{aligned}$$

    The spending is thus correctly simulated since $r'_1$ and $r'_2$ are random scalars.

  During the challenge phase (i.e. the step 3 of the anonymity experiment), ${\mathcal {A}}$ outputs two public keys ${\mathsf {upk}}_0$ and ${\mathsf {upk}}_1$ along a value V. If the guesses were correct, $V=V^*$, ${\mathsf {upk}}^* = {\mathsf {upk}}_b$ and the coin involving $x^*$ is spent, at index $j=j^*$. The simulator selects random $r'_1$ and $r'_2$, computes $R\leftarrow H({\textit{info}})$, and returns, along with the simulated proofs, the pairs

  $$\begin{aligned} \phi _{V^*,j^*}&= ((g^{z_1})^{-1/w_{V^*}} \cdot g^{r'_1}, s_j^{x'} \cdot g^{-\delta \cdot \alpha \cdot \gamma ^{-d(V^*-1)}}\cdot h_{V^*}^{r'_1} ) \\ \psi _{V^*,j^*}&= ((h^{z_2})^{-1/w_{V^*}} \cdot g^{r'_2}, t_j^{x'}\cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h^{-\delta \cdot \alpha \cdot \gamma ^{-d(V^*-1)}}\cdot h_{V^*}^{r'_2} ). \end{aligned}$$

  One can note that $-d(V^*-1)\ge -N^2+N =- E$ and so that the pair $(g^{\delta \cdot \alpha \cdot \gamma ^{-d(V^*-1)}}, h^{\delta \cdot \alpha \cdot \gamma ^{-d(V^*-1)}})$ belongs to the tuple $(g^{\alpha \cdot \delta \cdot \gamma ^{-k}}, h^{\alpha \cdot \delta \cdot \gamma ^{-k}})_{k=0}^E$. Let $r_1 = -z_1/w_{V^*} +r'_1$ and $r_2 = -(c\cdot z_2)/w_{V^*} +r'_2$. If $z_1=z_2=\delta + \chi \cdot \gamma ^D/\alpha$, then

  $$\begin{aligned} (g^{r_1},s_{j^*}^{x^*}\cdot h_{V^*}^{r_1})&= (g^{r_1},s_{j^*}^{\chi }\cdot s_{j^*}^{x'} \cdot h_{V^*}^{-z_1/w_{V^*}} \cdot h_{V^*}^{r'_1})\\&= (g^{r_1},s_{j^*}^{\chi }\cdot s_{j^*}^{x'} \cdot g^{-\chi \cdot \gamma ^{D+d(1-V^*)}} \cdot g^{-\delta \cdot \alpha \gamma ^{d(1-V^*)}} \cdot h_{V^*}^{r'_1})\\&= (g^{-z_1/w_{V^*}+r'_1},s_{j^*}^{x'}\cdot g^{-\delta \cdot \alpha \gamma ^{d(1-V^*)}} \cdot h_{V^*}^{r'_1}) =\phi _{V^*,j^*} \end{aligned}$$

  and

  $$\begin{aligned} (g^{r_2},t_{j^*}^{x^*}\cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_{V^*}^{r_2})&= (g^{r_2},t_{j^*}^{\chi }\cdot t_{j^*}^{x'} \cdot h_{V^*}^{-(c\cdot z_2)/w_{V^*}} \cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_{V^*}^{r'_2})\\&= (g^{r_2},t_{j^*}^{\chi }\cdot t_{j^*}^{x'} \cdot h^{-\chi \cdot \gamma ^{D+d(1-V^*)}} \cdot h^{-\delta \cdot \alpha \gamma ^{d(1-V^*)}}\cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_{V^*}^{r'_2})\\&= (h^{-z_2/w_{V^*}}\cdot g^{r'_2},t_{j^*}^{x'}\cdot h^{-\delta \cdot \alpha \gamma ^{d(1-V^*)}}\cdot g^{R\cdot {\mathsf {usk}}^*} \cdot h_{V^*}^{r'_2}) =\psi _{V^*,j^*} \end{aligned}$$

  The challenge spending is thus correctly simulated too.

In the next game, we replace the $N-\mathsf {MXDH}'$ instance by a random instance, with random $z_1$ and $z_2$. From the simulation of $\phi _{V^*,j^*}$ and $\psi _{V^*,j^*}$, we see that they perfectly hide ${\mathsf {upk}}^*$. Hence, the advantage of the adversary in this last game is exactly zero.

Remark 21

One can note that the h-based elements $h^{z_2}, \{h^{\gamma ^k}\}_{k=0}^{P}, \{h^{\alpha \cdot \delta \cdot \gamma ^{-k}}\}_{k=0}^E,\{h^{\chi \cdot \gamma ^k}\}_{k=D+1}^P$ and $\{h^{\chi \cdot \gamma ^k/\alpha }\}_{k=0}^{C}$ provided in the $N-\mathsf {MXDH}'$ challenge are only useful to simulate the security tags $\psi _{V,j}$ and $\psi _{V^*,j^*}$. In the case of fair divisible E-Cash system, they would no longer be necessary (see Remark 15) and so the security of the resulting scheme could simply rely on the weaker $N-\mathsf {MXDH}$ assumption.

7 Conclusion

We have proposed the first divisible e-cash system which achieves constant-time spendings, regardless of the spent value. Moreover, our solution keeps the best features of state-of-the-art, such as the efficiency of the withdrawals from [10] and the scalability of [11]. We argue that this is a major step towards the practical use of an e-cash system.

This also shows that the binary-tree structure, used by previous constructions, can be avoided. It may therefore open up new possibilities and incite new work in this area. We provide another construction in the full version [22] whose security proof relies on a more classical assumption, still avoiding the tree structure, but with larger public parameters.