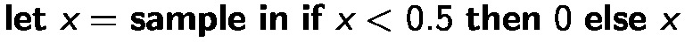Contextual Equivalence for Probabilistic Programs with Continuous Random Variables and Scoring

Abstract

We present a logical relation for proving contextual equivalence in a probabilistic programming language (PPL) with continuous random variables and with a scoring operation for expressing observations and soft constraints.

Our PPL model is based on a big-step operational semantics that represents an idealized sampler with likelihood weighting. The semantics treats probabilistic non-determinism as a deterministic process guided by a source of entropy. We derive a measure on result values by aggregating (that is, integrating) the behavior of the operational semantics over the entropy space. Contextual equivalence is defined in terms of these measures, taking real events as observable behavior.

We define a logical relation and prove it sound with respect to contextual equivalence. We demonstrate the utility of the logical relation by using it to prove several useful examples of equivalences, including the equivalence of a $\beta _v$-redex and its contractum and a general form of expression re-ordering. The latter equivalence is sound for the sampling and scoring effects of probabilistic programming but not for effects like mutation or control.

This material is based upon work sponsored by the Air Force Research Laboratory (AFRL) and the Defense Advanced Research Projects Agency (DARPA) under Contract No. FA8750-14-C-0002. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense or the U.S. Government.

1 Introduction

A universal probabilistic programming language (PPL) consists of a general-purpose language extended with two probabilistic features: the ability to make non-deterministic (probabilistic) choices and the ability to adjust the likelihood of the current execution, usually used to model conditioning. Programs that use these features in a principled way express probabilistic models, and the execution of such programs corresponds to Bayesian inference.

Universal PPLs include Church [8] and its descendants [13, 22] as well as other systems and models [2, 3, 10, 16, 18, 20]. In contrast, other PPLs [4, 12, 14, 17] limit programs to more constrained structures that can be translated to intermediate representations such as Bayes nets or factor graphs.

PPLs can also be divided into those that support continuous random choices and those that support only discrete choices. Most probabilistic programming systems designed for actual use support continuous random variables, and some implement inference algorithms specialized for continuous random variables [4, 21]. On the other hand, much of the literature on the semantics of PPLs has focused on discrete choice—particularly the literature on techniques for proving program equivalence such as logical relations [1] and bisimulation [19]. The semantics that do address continuous random variables and scoring [3, 20] do not focus on contextual equivalence.

This paper addresses the issue of contextual equivalence in a PPL with real arithmetic, continuous random variables, and an explicit scoring operation for expressing observations and soft constraints. We present a model of such a PPL with a big-step operational semantics based on an idealized sampler with likelihood weighting; the program’s evaluation is guided by a supply of random numbers from an “entropy space.” Based on the operational semantics we construct a measure on the possible results of the program, and we define contextual equivalence in terms of these measures. Finally, we construct a binary logical relation, prove it sound with respect to contextual equivalence, and demonstrate proofs that conversions such as $\beta _v$ and expression reordering respect contextual equivalence.

Our language and semantics are similar to that of Borgström et al. [3], except our language is simply typed and our treatment of entropy involves splitting rather than concatenating variable-length sequences. Our entropy structure reflects the independence of subexpression evaluations and simplifies the decomposition of value measures into nested integrals.

Compared with semantics for traditional languages, our model of probabilistic programming is further from the world of computable programming languages so that it can be closer to the world of measures and integration, the foundations of probability theory. It is “syntactic” rather than “denotational” in the sense that the notion of “value” includes $\lambda$-expressions rather than mathematical functions, but on the other hand these syntactic values can contain arbitrary real numbers in their bodies, and our semantics defines and manipulates measures over spaces of such values. We do not address computability in this paper, but we hope our efforts can be reconciled with previous work on incorporating the real numbers into programming languages [6, 7, 9].

We have formalized the language and logical relation in Coq, based on a high-level axiomatization of measures, integration, and entropy. We have formally proven the soundness of the logical relation as well as some of its applications, including $\beta _v$ and restricted forms of expression reordering. The formalization can be found at

https://github.com/cobbal/ppl-ctx-equiv-coq/tree/esop-2017.

The rest of this paper is organized as follows: Sect. 2 introduces probabilistic programming with some example models expressed in our core PPL. Section 3 reviews some relevant definitions and facts from measure theory. Section 4 presents our PPL model, including its syntax, operational semantics, measure semantics, and notion of contextual equivalence. In Sect. 5 we develop a logical relation and show that it is sound with respect to contextual equivalence. Section 6 proves several useful equivalences using using the machinery provided by the logical relation.

2 Probabilistic Programming

In a probabilistic program, random variables are created implicitly as the result of stochastic effects, and dependence between random variables is determined by the flow of values from one random variable to another. Random variables need not correspond to program variables. For example, the following two programs both represent the sum of two random variables distributed uniformly on the unit interval:

We write $\varvec{\mathsf {sample}}$ for the effectful expression that creates a new independent random variable distributed uniformly on the unit interval [0, 1].

Values distributed according to other real-valued distributions can be obtained from a standard uniform by applying the inverse of the distribution’s cumulative distribution function (CDF). For example, $\mathsf{normalinvcdf}(\varvec{\mathsf {sample}})$ produces a value from the standard normal distribution, with mean 0 and standard deviation 1. The familiar parameterized normal can then be defined by scaling and shifting as follows:

The parameters of a normal random variable can of course depend on other random variables. For example,

defines as a function that returns random points—a fresh one each time it is called. The points are concentrated narrowly around some common point, randomly chosen once and shared. (We write to emphasize that ignores its argument.)

The other feature offered by PPLs is some way of expressing conditioning on observed evidence. We introduce conditioning via a hypothetical $\varvec{\mathsf {observe}}$ form. Consider from the program above. Our prior belief about is that it is somewhere in a wide vicinity of 0. Suppose we amend the program by adding the following observations, however:

Given those observations, you might suspect that is in a fairly narrow region around 9. Bayes’ Law quantifies that belief as the posterior distribution on , defined in terms of the prior and the observed evidence.

$$ p(m| data ) \propto p(m) \cdot p( data |m) $$

That is the essence of Bayesian inference: calculating updated distributions on “causes” given observed “effects” and a probabilistic model that relates them.

Some PPLs [5, 13, 15] provide an $\varvec{\mathsf {observe}}$-like form to handle conditioning; they vary in what kinds of expressions can occur in the right-hand side of the observation. Other PPLs provide a more primitive facility, called $\varvec{\mathsf {factor}}$ or $\varvec{\mathsf {score}}$, which takes a real number and uses it to scale the likelihood of the current values of all random variables. To represent an observation, one simply calls $\varvec{\mathsf {factor}}$ with $p( data |x)$; of course, if one is observing the result of a computation, one has to compute the correct probability density. For example, the first observation above would be translated as

The normalpdf operation computes the probability density function density of a standard normal, so to calculate the density for a scaled and shifted normal, we must invert the translation by subtracting the mean and dividing by the scale (). Then, since probability densities are derivatives, to get the correct density of we must divide by the (absolute value of) the derivative of the translation function from the standard normal—that accounts for the second division by .

3 Measures and Integration

This section reviews some basic definitions, theorems, and notations from measure theory. We assume that the reader is familiar with the basic notions of measure theory, including measurable spaces, $\sigma$-algebras, measures, and Lebesgue integration—that is, the notion of integrating a function with respect to a measure, not necessarily the Lebesgue measure on $\mathbb {R}$.

We write $\mathbb {R}^{\ge 0}$ for the non-negative reals—that is, $[0, \infty )$—and $\mathbb {R}^+$ for the non-negative reals extended with infinity—that is, $[0, \infty ]$.

A measure $\mu : \varSigma _X \rightarrow \mathbb {R}^+$ on the measurable space $(X, \varSigma _X)$ is finite if $\mu (X)$ is finite. It is $\sigma$-finite if X is the union of countably many $X_i$ and $\mu (X_i)$ is finite for each $X_i$.

We write $\int _{A} f(x) ~ \mu (dx)$ for the integral of the measurable function $f : X \rightarrow \mathbb {R}$ on the region $A \subseteq X$ with respect to the measure $\mu : \varSigma _X \rightarrow \mathbb {R}^+$ . We occasionally abbreviate this to $\int _{A} f ~ d\mu$ if omitting the variable of integration is convenient. We omit the region of integration A when it is the whole space X.

We rely on the following lemmas concerning the equality of integrals. Tonelli’s theorem allows changing the order of integration of non-negative functions. Since all of our integrands are non-negative, it suits our needs better than Fubini’s theorem. In particular, Tonelli’s theorem holds even when the functions can attain infinite values as well as when the integrals are infinite.

Lemma 1

(Tonelli). If $(X, \varSigma _X)$ and $(Y, \varSigma _Y)$ are measurable spaces and $\mu _X$ and $\mu _Y$ are $\sigma$-finite measures on X and Y, respectively, and $f : X \times Y \rightarrow \mathbb {R}^+$ is measurable, then

$$\begin{aligned} \int _{X} \left( \int _{Y} f(x, y) ~ \mu _Y(dy) \right) ~ \mu _X(dx) = \int _{Y} \left( \int _{X} f(x, y) ~ \mu _X(dx) \right) ~ \mu _Y(dy) \end{aligned}$$

The other main lemma we rely on equates two integrals when the functions and measures may not be the same but are nonetheless related. In particular, there must be a relation such that the measures agree on related sets and the functions have related pre-images—that is, the relation specifies a “coarser” structure on which the measures and functions agree. This lemma is essential for showing the observable equivalence of measures derived from syntactically different expressions.

Lemma 2

(Coarsening). Let $(X, \varSigma _X)$ be a measurable space, $M \subseteq (\varSigma _X \times \varSigma _X)$ be a binary relation on measurable sets, $\mu _1, \mu _2 : \varSigma _X \rightarrow \mathbb {R}^+$ be measures on X, and $f_1, f_2 : X \rightarrow \mathbb {R}^+$ be measurable functions on X. If the measures agree on M-related sets and if the functions have M-related pre-images—that is,

• $\forall (A_1,A_2) \in M,~ \mu _1(A_1) = \mu _2(A_2)$

• $\forall B \in \varSigma _{\mathbb {R}},~ (f_1^{-1}(B), f_2^{-1}(B)) \in M$

then their corresponding integrals are equal:

$$ \int f_1 ~ d\mu _1 = \int f_2 ~ d\mu _2 $$

Proof

Together the two conditions imply that

$$ \forall B \in \varSigma _\mathbb {R},~ \mu _1(f_1^{-1}(B)) = \mu _2(f_2^{-1}(B)) $$

We apply this equality after rewriting the integrals using the “layer cake” perspective to make the pre-images explicit [11].

$$\begin{aligned} \int f_1 ~ d\mu _1 =&\int _0^\infty \mu _1(f_1^{-1}(\,[t, \infty ]\,))~dt \\ =&\int _0^\infty \mu _2(f_2^{-1}(\,[t, \infty ]\,))~dt \\ =&\int f_2 ~ d\mu _2 \end{aligned}$$

   $\square$

Even though in the proof we immediately dispense with the intermediate relation M, we find it useful in the applications of the lemma to identify the relationship that justifies the agreement of the functions and measures.

A useful special case of Lemma 2 is when the measures are the same and the relation is equality of measure.

Lemma 3

Let $f,g : X \rightarrow \mathbb {R}^+$ and let $\mu _X$ be a measure on X. If $\forall B \in \varSigma _{\mathbb {R}},~ \mu _X(f^{-1}(B)) = \mu _X(g^{-1}(B))$, then $\int f ~ d\mu = \int g ~ d\mu$.

Proof

Special case of Lemma 2.    $\square$

Fig. 1.

Syntax

Fig. 2.

Type rules

4 Syntax and Semantics

This section presents the syntax and semantics of a language for probabilistic programming, based on a functional core extended with real arithmetic and stochastic effects.

We define the semantics of this language in two stages. We first define a big-step evaluation relation based on an idealized sampler with likelihood weighting; the evaluation rules consult an “entropy source” which determines the random behavior of a program. From this sampling semantics we then construct an aggregate view of the program as a measure on syntactic values. Contextual equivalence is defined in terms of these value measures.

4.1 Syntax

Figure 1 presents the syntax of our core probabilistic programming language. The language consists of a simply-typed lambda calculus extended with real arithmetic and two effects: a $\varvec{\mathsf {sample}}$ form for random behavior and a $\varvec{\mathsf {factor}}$ form for expressing observations and soft constraints. Figure 2 gives the type rules for the language.

The $\varvec{\mathsf {sample}}$ form returns a real number uniformly distributed between 0 and 1. We assume inverse-CDF and PDF operations—used to produce samples and score observations, respectively—for every primitive real-valued distribution of interest. Recall from Sect. 2 that sampling a normal random variable is accomplished as follows:

and observing a normal random variable is expressed thus:

A Note on Notation: We drop the type annotations on bound variables when they are obvious from the context, and we use syntactic sugar for local bindings and sequencing; for example, we write

instead of

4.2 Evaluation Relation

If we interpret evaluation as idealized importance sampling, the evaluation relation tells us how to produce a single sample given the initial state of the random number generator. Evaluation is defined via the judgment

$$ \sigma \vdash e \Downarrow v, w $$

where $\sigma \in \mathbb {S}$ is an entropy source, e is the expression to evaluate, v is the resulting value, and $w \in \mathbb {R}^{\ge 0}$ is the likelihood weight (Fig. 3).

The $\sigma$ argument acts as the source of randomness—evaluation is a deterministic function of e and $\sigma$. Rather than threading $\sigma$ through evaluation like a store, rules with multiple sub-derivations split the entropy. The indexed family of functions ${\pi }_{i} : \mathbb {S}\rightarrow \mathbb {S}$ splits the entropy source into independent pieces and $\pi _U:\mathbb {S}\rightarrow [0, 1]$ extracts a real number on the unit interval. We discuss the structure of the entropy space further in Sect. 4.3.

Fig. 3.

Evaluation rules

The result of evaluation is a closed value: either a real number or a closed $\lambda$-expression. Let $[\![\tau ]\!]$ be the set of all closed values of type $\tau$. We consider $[\![\tau ]\!]$ a measurable space with a $\sigma$-algebra $\varSigma _{[\![\tau ]\!]}$. See the comments on measurability at the end of this section. Note that the $\sigma$-algebras for function types are defined on syntactic values, not for mathematical functions, so we avoid the issues concerning measurable function spaces [20].

The evaluation rules for the language’s functional fragment are unsurprising. For simple expressions, the entropy is ignored and the likelihood weight is 1. For compound expressions, the entropy is split and sent to sub-expression evaluations, and the resulting weights are multiplied together. We assume a partial function $\delta$ that interprets the primitive operations.¹ For example, $\delta (+, 1, 2) = 3$ and $\delta (\div , 4, 0)$ is undefined.

The rule for $\varvec{\mathsf {sample}}$ extracts a real number uniformly distributed on the unit interval [0, 1]. The $\varvec{\mathsf {factor}}$ form evaluates its subexpression and interprets it as a likelihood weight to be factored into the weight of the current execution—but only if it is positive.

There are two ways evaluation can fail:

• the argument to $\varvec{\mathsf {factor}}$ is zero or negative

• the $\delta$ function is undefined for an operation with a particular set of arguments, such as for $\mathsf{1} \div \mathsf{0}$ or $\mathsf{log(-5)}$

The semantics does not distinguish these situations; in both cases, no evaluation derivation tree exists for that particular combination of $\sigma$ and e.

4.3 Entropy Space

The evaluation relation of Sect. 4.2 represents evaluation of a probabilistic program as a deterministic partial function of points in an entropy space $\mathbb {S}$. To capture the meaning of a program, we must consider the aggregate behavior over the entire entropy space. That requires integration, which in turn requires a measurable space ($\varSigma _\mathbb {S}$) and a base measure on entropy ($\mu _\mathbb {S}: \varSigma _\mathbb {S}\rightarrow \mathbb {R}^+$).

The entropy space must support our formulation of evaluation, which roughly corresponds to the following transformation:

$$ \begin{array}{rcl} &{}~&{} \\ x_1 &{}\sim &{} D_1 \\ &{}\vdots &{} \\ x_n &{}\sim &{} D_n \end{array} \qquad \Rightarrow \qquad \begin{array}{rcl} \sigma &{}\sim &{} \mu _\mathbb {S}\\ x_1 &{}=&{} \mathrm {invcdf}_{D_1}({\pi }_{1}(\sigma )) \\ &{}\vdots &{} \\ x_n &{}=&{} \mathrm {invcdf}_{D_n}({\pi }_{n}(\sigma )) \end{array} $$

The entropy space and its associated functions are ours to choose, provided they satisfy the following criteria:

• It must be a probability space. That is, $\mu _\mathbb {S}(\mathbb {S}) = 1$.

• It must be able to represent common real-valued random variables. It is sufficient to support a standard uniform—that is, a random variable uniformly distributed on the interval [0, 1]. Other distributions can be represented via the inverse-CDF transformation.

• It must support multiple independent random variables. That is, the entropy space must be isomorphic—in a measure-preserving way—to products of itself: $\mathbb {S}\cong \mathbb {S}^2 \cong \mathbb {S}^n\quad (n\ge 1)$.

The following specification formalizes these criteria.

Definition 4

(Entropy). $(\mathbb {S}, \varSigma _\mathbb {S})$ is a measurable space with measure $\mu _\mathbb {S}: \varSigma _\mathbb {S}\rightarrow \mathbb {R}^+$ and functions

$$\begin{aligned} \pi _U&: \mathbb {S}\rightarrow [0,1] \\ {\pi }_{\mathrm {L}}, {\pi }_{\mathrm {R}}&: \mathbb {S}\rightarrow \mathbb {S}\end{aligned}$$

such that the following integral equations hold:

• $\mu _\mathbb {S}(\mathbb {S}) = 1$, and thus for all $k \in \mathbb {R}^+$, $\int k ~ \mu _\mathbb {S}(d\sigma ) = k$,

• for all measurable functions $f : [0,1] \rightarrow \mathbb {R}^+$,

  $$ \int f(\pi _U(\sigma )) ~ \mu _\mathbb {S}(d\sigma ) = \int _{[0,1]} f(x) ~ \lambda (dx) $$

  where $\lambda$ is the Lebesgue measure, and

• for all measurable functions $g : \mathbb {S}\times \mathbb {S}\rightarrow \mathbb {R}^+$,

  $$ \int g({\pi }_{\mathrm {L}}(\sigma ), {\pi }_{\mathrm {R}}(\sigma )) ~ \mu _\mathbb {S}(d\sigma ) = \iint g(\sigma _1, \sigma _2) ~ \mu _\mathbb {S}(d\sigma _1)~\mu _\mathbb {S}(d\sigma _2) $$

That is, $\pi _U$ interprets the entropy as a standard uniform random variable, and ${\pi }_{\mathrm {L}}$ and ${\pi }_{\mathrm {R}}$ split the entropy into a pair of independent parts and return the first or second part, respectively. We generalize from two-way splits to indexed splits via the following family of functions:

Definition 5

(${\pi }_{i}$). Let ${\pi }_{i} : \mathbb {S}\rightarrow \mathbb {S}$ be the family of functions defined thus:

$$\begin{aligned} {\pi }_{1}(\sigma )&= {\pi }_{\mathrm {L}}(\sigma ) \\ {\pi }_{n+1}(\sigma )&= {\pi }_{n}({\pi }_{\mathrm {R}}(\sigma )) \end{aligned}$$

Definition 5 is “wasteful”—for any $n \in \mathbb {N}$, using only ${\pi }_{1}(\sigma )$ through ${\pi }_{n}(\sigma )$ discards part of the entropy—but that does not cause problems, because the wasted entropy is independent and thus integrates away. Thus the a generalized entropy-splitting identity holds for measurable $f : \mathbb {S}^n \rightarrow \mathbb {R}^+$:

$$ \int f({\pi }_{1}(\sigma ), \cdots , {\pi }_{n}(\sigma )) ~ \mu _\mathbb {S}(d\sigma ) = \int \cdots \int f(\sigma _1, \cdots , \sigma _n) ~ \mu _\mathbb {S}(d\sigma _1) \cdots \mu _\mathbb {S}(d\sigma _n) $$

Our preferred concrete representation of $\mathbb {S}$ is the countable product of unit intervals, $[0,1]^\omega$, sometimes called the Hilbert cube. The ${\pi }_{\mathrm {L}}$, ${\pi }_{\mathrm {R}}$, and $\pi _U$ functions are defined as follows:

The $\sigma$-algebra $\varSigma _\mathbb {S}$ is the Borel algebra of the product topology (cf Tychonoff’s Theorem). The basis of the product topology is the set of products of intervals, only finitely many of which are not the whole unit interval $U = [0,1]$:

$$ \left\{ \left( \prod _{i = 1}^k (a_i, b_i)\right) \times U^\omega \quad |\quad 0 \le a_i \le b_i \le 1, k \in \mathbb {N} \right\} $$

We define the measure $\mu _\mathbb {S}$ on a basis element as follows:

$$ \mu _\mathbb {S}\left( \left( \prod _{i=1}^k (a_i, b_i)\right) \times U^\omega \right) = \prod _{i=1}^k (b_i - a_i) $$

That uniquely determines the measure $\mu _\mathbb {S}: \varSigma _\mathbb {S}\rightarrow \mathbb {R}^+$ by the Carathéodory extension theorem.

Another representation of entropy is the Borel space on [0, 1] with (restricted) Lebesgue measure and bit-splitting ${\pi }_{\mathrm {L}}$ and ${\pi }_{\mathrm {R}}$. In fact, both of these representations are examples of standard atomless probability spaces, and all such spaces are isomorphic (modulo null sets). In the rest of the paper, we rely only on the guarantees of Definition 4, not on the precise representation of $\mathbb {S}$.

4.4 Measure Semantics

We represent the aggregate behavior of a closed expression as a measure, obtained by integrating the behavior of the evaluation relation over the entropy space. If $\vdash e : \tau$ then $\mu _{e} : \varSigma _{[\![\tau ]\!]} \rightarrow \mathbb {R}^+$ is the value measure of e, defined as follows:

Definition 6

(Value Measure)

The evaluation relation $\sigma \vdash e \Downarrow v, w$ is a partial function of $(\sigma , e)$—non-deterministic behavior is represented as deterministic dependence on the entropy $\sigma$. From this partial function we define a total evaluation function $\mathrm {ev}(e, \sigma )$ and a total weighting function $\mathrm {ew}(e, \sigma )$. The $\mathrm {evalin}(e, V, \sigma )$ function takes a measurable outcome set of interest and checks whether the result of evaluation falls within that set. If so, it produces the weight of the evaluation; otherwise, it produces 0. We write $\mathbb {I}_{X}$ for the indicator function for X, which returns 1 if its argument is in X and 0 otherwise.

Integrating $\mathrm {evalin}(e, V, \sigma )$ over the entire entropy space yields the value measure $\mu _{e}$. Strictly speaking, the definition above defines $\mu _{e}$ as a measure on $[\![\tau ]\!]_\bot$, but since $\mathrm {ev}(e, \sigma ) = \bot$ only when $\mathrm {ew}(e, \sigma ) = 0$, $\mu _{e}$ never assigns any weight to $\bot$ and thus we can consider it a measure on $[\![\tau ]\!]$.

The following theorem shows that the value measure is an adequate representation of the behavior of a program.

Theorem 7

Let $f : [\![\tau ]\!] \rightarrow \mathbb {R}^+$ be measurable, and let $\vdash e : \tau$. Then

$$ \int f(v) ~ \mu _{e}(dv) = \int f(\mathrm {ev}(e, \sigma )) \cdot \mathrm {ew}(e, \sigma ) ~ \mu _\mathbb {S}(d\sigma ) $$

Proof

First consider the case where f is an indicator function $\mathbb {I}_{X}$:

The equality extends to simple functions—linear combinations of characteristic functions—by the linearity of integration and to measurable functions as the suprema of sets of simple functions.    $\square$

Measurability. For the integral defining $\mu _{e}(V)$ to be well-defined, $\mathrm {evalin}(e, V, \sigma )$ must be measurable when considered as a function of $\sigma$. Furthermore, in later proofs we will need the $\mathrm {ev}(\cdot , \cdot )$ and $\mathrm {ew}(\cdot , \cdot )$ functions to be measurable with respect to the product space on their arguments. More precisely, if we consider a type-indexed family of functions

$$ \mathrm {ev}_\tau : \mathrm {Expr}[\![\tau ]\!] \times \mathbb {S}\rightarrow [\![\tau ]\!] $$

then we need each $\mathrm {ev}_\tau$ to be measurable in $\varSigma _{[\![\tau ]\!]}$ with respect to the product measurable space $\varSigma _{\mathrm {Expr}[\![\tau ]\!]} \times \varSigma _\mathbb {S}$, and likewise for $\mathrm {ew}_\tau$. Note that the space of values $[\![\tau ]\!]$ is a subset of the expressions $\mathrm {Expr}[\![\tau ]\!]$, so we can take $\varSigma _{[\![\tau ]\!]}$ to be $\varSigma _{\mathrm {Expr}[\![\tau ]\!]}$ restricted to the values. But we must still define $\varSigma _{\mathrm {Expr}[\![\tau ]\!]}$ and show the functions are measurable.

We do not present a direct proof of measurability in this paper. Instead, we rely again on Borgström et al. [3]: we treat their language, for which they have proven measurability, as a meta-language. Interpreters for the $\mathrm {ev}$ and $\mathrm {ew}$ functions of our language can be written as terms in this meta-language, and thus their measurability result can be carried over to our language. We take $\mathbb {S}= [0, 1]$ and extend the meta-language with the measurable functions ${\pi }_{\mathrm {L}}$, ${\pi }_{\mathrm {R}}$, and $\pi _U$. The definition of $\varSigma _{\mathrm {Expr}[\![\tau ]\!]}$ is induced by the encoding function that represents our object terms as values in their meta-language and the structure of their measurable space of expressions.

4.5 Digression: Interpretation of Probabilistic Programs

In general, the goal of a probabilistic programming language is to interpret programs as probability distributions.

If a program’s value measure is finite and non-zero, then it can be normalized to yield a probability distribution. The following examples explore different classes of such programs:

• Continuous measures: $\varvec{\mathsf {sample}}$, $\mathsf{normalinvcdf}(\varvec{\mathsf {sample}})$, etc.

• Discrete measures:

• Sub-probability measures:

  

• Mixtures of discrete and continuous: for example,

  

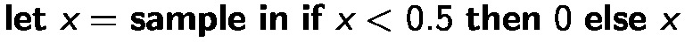
  has a point mass at 0 and is continuous on (0.5, 1).

Our language, however, includes programs that have no interpretation as distributions:

• Zero measure:

• Infinite (but $\sigma$-finite) measures. For example,

  

  has infinite measure because $\int _0^1 \frac{1}{x}~dx$ is infinite. But the measure is $\sigma$-finite because each interval $[\frac{1}{n}, 1]$ has finite measure and the union of all such intervals covers (0, 1], the support of the measure.

• Non-$\sigma$-finite measures. For example,

  

  has $\mu (0) = \infty$. (We conjecture that all value measures definable in this language are either $\sigma$-finite or have a point with infinite weight.)

Zero measures indicate unsatisfiable constraints; more precisely, the set of successful evaluations may not be empty, merely measure zero.

Fig. 4.

Contexts

Infinite value measures arise only from the use of ; the value measure of a program that does not contain is always a sub-probability measure. It may not be a probability measure—recall that $\mathsf{1} \div \mathsf{0}$ and both cause execution to fail. We could eliminate infinite-measure programs by sacrificing expressiveness. For example, if the valid arguments to were restricted to the range (0, 1], as in Börgstrom et al. [3], only sub-probability measures would be expressible. But there are good reasons to allow with numbers greater than 1, such as representing the observation of a normal random variable with a small variance—perhaps a variance computed from another random variable. There is no simple syntactic rule that excludes the infinite-measure programs above without also excluding some useful applications of .

Note that the theorems in this paper apply to all programs, regardless of whether they can be interpreted as probability distributions. In particular, we apply Lemma 1 (Tonelli) only to integrals over $\mu _\mathbb {S}$, which is finite.

4.6 Contextual Equivalence

Two expressions are contextually equivalent ($=_{\mathrm {ctx}}$) if for all closing program contexts C their observable aggregate behavior is the same. We take programs to be real-valued closed expressions; their observable behavior consists of their value measures ($\varSigma _\mathbb {R}\rightarrow \mathbb {R}^+$).

Figure 4 defines contexts and their relationship with type environments. The relation $C : \varGamma$ means that C provides bindings satisfying $\varGamma$ to the expression placed in its hole.

Definition 8

(Contextual equivalence) If $\varGamma \vdash e_1 : \tau$ and $\varGamma \vdash e_2 : \tau$, then $e_1$ and $e_2$ are contextually equivalent ($e_1 =_{\mathrm {ctx}}^\varGamma e_2$) if and only if for all contexts C such that $C : \varGamma$ and $\vdash C[e_1] : \mathbb {R}$ and $\vdash C[e_2] : \mathbb {R}$ and for all measurable sets $A \in \varSigma _\mathbb {R}$,

$$ \mu _{C[e_1]}(A) = \mu _{C[e_2]}(A) $$

Instances of contextual equivalence are difficult to prove directly because of the quantification over all syntactic contexts.

Fig. 5.

Logical relation and auxiliary relations

5 A Logical Relation for Contextual Equivalence

In this section we develop a logical relation for proving expressions contextually equivalent. Membership in the logical relation implies contextual equivalence but is easier to prove directly. We prove soundness via compatibility lemmas, one for each kind of compound expression. The fundamental property (a form of reflexivity) enables simplifications to the logical relation that we take advantage of in Sect. 6 when applying the relation to particular equivalences.

Figure 5 defines the relation

$$\begin{aligned} \varGamma \vdash e_1 \approx e_2 : \tau \end{aligned}$$

and its auxiliary relations (Definition 9). In a deterministic language, we would construct the relation so that two expressions are related if they produce related values when evaluated with related substitutions. In our probabilistic language, two expressions are related if they have related value measures when evaluated with related substitutions. (The notation $e \cdot \gamma$ indicates the substitution $\gamma$ applied to the expression e.)

The $\approx$ relation depends on the following auxiliary relations:

• $\mathcal {V}[\![\tau ]\!]$ relates closed values of type $\tau$. Real values are related if they are identical, and functions are related if they take related inputs to related evaluation configurations ($\mathcal {E}[\![\tau ]\!]$).

• $\mathcal {G}[\![\varGamma ]\!]$ relates substitutions. Variables are mapped to related values.

• $\mathcal {E}[\![\tau ]\!]$ relates closed expressions. Expressions are related if their value measures agree on measurable sets related by $\mathcal {A}[\![\tau ]\!]$.

• $\mathcal {A}[\![\tau ]\!]$ relates measurable sets of values.

When comparing value measures, we must not demand complete equality of the measures; instead, we only require that they agree on $\mathcal {V}[\![\tau ]\!]$-closed measurable value sets. To see why, consider the expressions $\lambda x.\,x+2$ and $\lambda x.\,x+1+1$. As values, they are related by $\mathcal {V}[\![\mathbb {R}\rightarrow \mathbb {R}]\!]$. As expressions, we want them to be related by $\mathcal {E}[\![\mathbb {R}\rightarrow \mathbb {R}]\!]$, but their value measures are not identical; they are Dirac measures on different—but related—syntactic values. In particular:

• $\mu _{ \lambda x.\,x+2 }(\{ \lambda x.\,x+2 \}) = 1$, but

• $\mu _{ \lambda x.\,x+1+1 }(\{ \lambda x.\,x+2 \}) = 0$

The solution is to compare measures only on related measurable sets. For every value in the set given to the first measure, we must include every related value in the set given to the second measure (and vice versa). This relaxation on measure equivalence preserves the spirit of “related computations produce related results.”

Lemma 10

(Symmetry and transitivity). $\mathcal {V}[\![\tau ]\!]$, $\mathcal {G}[\![\varGamma ]\!]$, $\mathcal {E}[\![\tau ]\!]$, $\mathcal {A}[\![\tau ]\!]$, and $\approx$ are symmetric and transitive.

Proof

The symmetry and transitivity of $\approx$ and $\mathcal {G}$ follow from that of $\mathcal {E}$ and $\mathcal {V}$.

We prove symmetry and transitivity of $\mathcal {V}[\![\tau ]\!]$, $\mathcal {E}[\![\tau ]\!]$, and $\mathcal {A}[\![\tau ]\!]$ simultaneously by induction on $\tau$. For a given $\tau$, the properties of $\mathcal {E}[\![\tau ]\!]$ and $\mathcal {A}[\![\tau ]\!]$ follow from $\mathcal {V}[\![\tau ]\!]$. The $\mathbb {R}$ case is trivial. Transitivity for $\mathcal {V}[\![\tau '\rightarrow \tau ]\!]$ is subtle; given $(v_1, v_3) \in \mathcal {V}[\![\tau ']\!]$, we must find a $v_2$ such that $(v_1, v_2) \in \mathcal {V}[\![\tau ']\!]$ and $(v_2, v_3) \in \mathcal {V}[\![\tau ']\!]$ in order to use transitivity of $\mathcal {E}[\![\tau ]\!]$ (induction hypothesis). But we can use symmetry and transitivity of $\mathcal {V}[\![\tau ']\!]$ (also induction hypotheses) to show $(v_1, v_1) \in \mathcal {V}[\![\tau ']\!]$, so $v_1$ is a suitable value for $v_2$.    $\square$

The reflexivity of $\mathcal {V}$, $\mathcal {E}$, $\mathcal {G}$, and $\approx$ is harder to prove. In fact, it is a corollary of the fundamental property of the logical relation (Theorem 15).

5.1 Compatibility Lemmas

The compatibility lemmas show that expression pairs built from related components are themselves related. Equivalently, they allow the substitution of related expressions in single-frame contexts. Given the compatibility lemmas, soundness with respect to contextual equivalence with arbitrary contexts is a short inductive hop away.

Lemma 11

(Lambda Compatibility).

Proof

Let $(\gamma _1, \gamma _2) \in \mathcal {G}[\![\varGamma ]\!]$. We must prove that $\lambda x.\,e_i \cdot \gamma _i$ are in $\mathcal {E}[\![\tau '\rightarrow \tau ]\!]$—that is, the corresponding value measures $\mu _{\lambda x.\,e_i \cdot \gamma _i}$ agree on all $(A_1, A_2) \in \mathcal {A}[\![\tau '\rightarrow \tau ]\!]$.

The value measure $\mu _{\lambda x.\,e_i \cdot \gamma _i}$ is concentrated at $\lambda x.\,e_i \cdot \gamma _i$ with weight 1, so the measures are related if those closures are related in $\mathcal {V}[\![\tau '\rightarrow \tau ]\!]$. That in turn requires that $(e_i \cdot \gamma _i) \left[ x \mapsto v_i \right]$ be related in $\mathcal {E}[\![\tau ]\!]$ for $(v_1, v_2) \in \mathcal {V}[\![\tau ']\!]$. That follows from $\varGamma , x:\tau ' \vdash e_1 \approx e_2 : \tau$, instantiated at $\left[ \gamma _i, x \mapsto v_i \right]$.    $\square$

Lemma 12

(App Compatibility).

Proof

By the premises, the $\mu _{e_i \cdot \gamma _i}$ measures agree on $\mathcal {A}[\![\tau '\rightarrow \tau ]\!]$, and the $\mu _{e_i' \cdot \gamma _i}$ measures agree on $\mathcal {A}[\![\tau ']\!]$. Our strategy is to use Lemma 2 (Coarsening) to rewrite the integrals after unpacking the definition of the value measures and the App rule. The $\mathrm {applyin}$ function defined as follows

$$ \mathrm {applyin}(\lambda x.\,e, v', A, \sigma ) = \mathrm {evalin}(e \left[ x \mapsto v' \right] , A, \sigma ) $$

is useful for expressing the unfolding of the App rule.

Let $(\gamma _1, \gamma _2) \in \mathcal {G}[\![\varGamma ]\!]$. We must prove the expressions $(e_i~e_i') \cdot \gamma _i$ are in $\mathcal {E}[\![\tau ]\!]$.

After unfolding $\mathcal {E}$ and introducing $(A_1, A_2) \in \mathcal {A}[\![\tau ]\!]$, we must show the corresponding value measures agree:

$$ \mu _{(e_1~e_1') \cdot \gamma _1}(A_1) = \mu _{(e_2~e_2') \cdot \gamma _2}(A_2) $$

We rewrite each side as follows:

After rewriting both sides, we have the goal

$$\begin{aligned}&\iiint \mathrm {applyin}(v, v', A_1, \sigma ) ~ \mu _\mathbb {S}(d\sigma )~\mu _{e_1' \cdot \gamma _1}(dv')~\mu _{e_1 \cdot \gamma _1}(dv) \\ =&\iiint \mathrm {applyin}(v, v', A_2, \sigma ) ~ \mu _\mathbb {S}(d\sigma )~\mu _{e_2' \cdot \gamma _2}(dv')~\mu _{e_2 \cdot \gamma _2}(dv) \end{aligned}$$

We show this equality via Lemma 2 (Coarsening) using the binary relation $\mathcal {A}[\![\tau '\rightarrow \tau ]\!]$. By the induction hypothesis we have that $\mu _{e_1 \cdot \gamma _1}, \mu _{e_2 \cdot \gamma _2}$ agree on sets in $\mathcal {A}[\![\tau '\rightarrow \tau ]\!]$. That leaves one other premise to discharge: the functions must have related pre-images. Let $B \in \varSigma _\mathbb {R}$. We must show the pre-images are related by $\mathcal {A}[\![\tau '\rightarrow \tau ]\!]$, where each pre-image is

$$ \left( v \mapsto \iint \mathrm {applyin}(v, v', A_i, \sigma ) ~ \mu _\mathbb {S}(d\sigma )~\mu _{e_i' \cdot \gamma _i}(dv') \right) ^{-1}(B) $$

To show that the function pre-images are in $\mathcal {A}[\![\tau '\rightarrow \tau ]\!]$, we show something stronger: for related values the function values are the same.

Let $(v_1, v_2) \in \mathcal {V}[\![\tau '\rightarrow \tau ]\!]$. We will show that

$$\begin{aligned}&\iint \mathrm {applyin}(v_1, v', A_1, \sigma ) ~ \mu _\mathbb {S}(d\sigma )~\mu _{e_1' \cdot \gamma _i}(dv') \\ =&\iint \mathrm {applyin}(v_2, v', A_2, \sigma ) ~ \mu _\mathbb {S}(d\sigma )~\mu _{e_2' \cdot \gamma _i}(dv') \end{aligned}$$

We show this by again applying Lemma 2 (Coarsening), this time with the relation $\mathcal {A}[\![\tau ']\!]$. Again, the induction hypothesis tells us that the measures $\mu _{e_i' \cdot \gamma _i}$ agree on sets in $\mathcal {A}[\![\tau ']\!]$. We follow the same strategy for showing the function pre-images related. Let $(v_1', v_2') \in \mathcal {V}[\![\tau ']\!]$. We must show

$$ \int \mathrm {applyin}(v_1, v_1', A_1, \sigma ) ~ \mu _\mathbb {S}(d\sigma ) = \int \mathrm {applyin}(v_2, v_2', A_2, \sigma ) ~ \mu _\mathbb {S}(d\sigma ) $$

Since $v_1, v_2 : \tau '\rightarrow \tau$, they must be abstractions. Let $v_1 = \lambda x:\tau '.\,e_1''$ and likewise for $v_2$. Then the goal reduces to

$$ \int \mathrm {evalin}(e_1'' \left[ x \mapsto v_1' \right] , A_1, \sigma ) ~ \mu _\mathbb {S}(d\sigma ) = \int \mathrm {evalin}(e_2'' \left[ x \mapsto v_2' \right] , A_2, \sigma ) ~ \mu _\mathbb {S}(d\sigma ) $$

That is, by the definition of value measure, the following:

$$ \mu _{e_1'' \left[ x \mapsto v_1' \right] }(A_1) = \mu _{e_2'' \left[ x \mapsto v_2' \right] }(A_2) $$

That follows from $(v_1, v_2) \in \mathcal {V}[\![\tau '\rightarrow \tau ]\!]$ and the definitions of $\mathcal {V}$ and $\mathcal {E}$.    $\square$

Lemma 13

(Op Compatibility).

Proof

Similar to but simpler than Lemma 12. Since all operations take real-valued arguments, this proof does not rely on Lemma 2. We rely on the fact that $\delta$, the function that interprets primitive operations, takes related arguments to related results, which holds trivially because reals are related only when they are identical.    $\square$

Lemma 14

(Factor Compatibility).

Proof

Similar to Lemma 13.    $\square$

5.2 Fundamental Property

Theorem 15

(Fundamental Property). If $\varGamma \vdash e : \tau$ then $\varGamma \vdash e \approx e : \tau$.

Proof

By induction on $\varGamma \vdash e : \tau$.

• Case x. Let $(\gamma _1, \gamma _2) \in \mathcal {G}[\![\varGamma ]\!]$. We must prove the value measures $\mu _{x \cdot \gamma _i}$ agree on related $(A_1, A_2) \in \mathcal {A}[\![\tau ]\!]$. The measures are concentrated on $\gamma _i(x)$ with weight 1, so they agree if those values are related by $\mathcal {V}[\![\tau ]\!]$, which they do because the substitutions are related by $\mathcal {G}[\![\varGamma ]\!]$.

• Case r. The value measures are identical Dirac measures concentrated at r.

• Case $\mathbf {sample}$. The value measures are identical.

• Case $\lambda x:\tau _1.\,e_2$. By Lemma 11.

• Case $e~e'$. By Lemma 12.

• Case $op^n (e_1, \cdots , e_n)$. By Lemma 13.

• Case $\mathbf {factor}~e$. By Lemma 14.

   $\square$

Corollary 16

(Reflexivity). $\mathcal {V}[\![\tau ]\!]$, $\mathcal {G}[\![\varGamma ]\!]$, and $\mathcal {E}[\![\tau ]\!]$ are reflexive.

One consequence of the fundamental property is that the $\mathcal {A}[\![\tau ]\!]$, a binary relation on measurable sets, is the least reflexive relation on measurable sets closed under the $\mathcal {V}[\![\tau ]\!]$ relation. We define $\mathcal {A}'[\![\tau ]\!]$ as the collection of $\mathcal {V}[\![\tau ]\!]$-closed measurable sets. To show two expressions related by $\mathcal {E}[\![\tau ]\!]$ it is sufficient to compare their corresponding measures applied to sets in $\mathcal {A}'[\![\tau ]\!]$.

Definition 23

$$ A \in \mathcal {A}'[\![\tau ]\!] \iff A \in \varSigma _{[\![\tau ]\!]} ~\wedge ~ \forall (v_1, v_2) \in \mathcal {V}[\![\tau ]\!],~ (v_1 \in A \iff v_2 \in A) $$

Lemma 18

If $(A_1, A_2) \in \mathcal {A}[\![\tau ]\!]$ then $A_1 = A_2$, and if $A \in \mathcal {A}'[\![\tau ]\!]$ then $(A, A) \in \mathcal {A}[\![\tau ]\!]$.

Proof

By reflexivity of $\mathcal {V}$.    $\square$

Corollary 19

$$ (e_1, e_2) \in \mathcal {E}[\![\tau ]\!] \iff \forall A \in \mathcal {A}'[\![\tau ]\!] ,~ \mu _{e_1}(A) = \mu _{e_2}(A) $$

Another consequence of the fundamental property is that to prove two expressions related by $\approx$ it suffices to show that they are $\mathcal {E}[\![\tau ]\!]$-related when paired with the same arbitrary substitution.

Lemma 20

(Same Substitution Suffices). If $\varGamma \vdash e_1 : \tau$ and $\varGamma \vdash e_2 : \tau$, and if $(e_1 \cdot \gamma , e_2 \cdot \gamma ) \in \mathcal {E}[\![\tau ]\!]$ for all $\gamma \models \varGamma$, then $\varGamma \vdash e_1 \approx e_2 : \tau$.

Proof

Let $(\gamma _1, \gamma _2) \in \mathcal {G}[\![\varGamma ]\!]$; we must show $(e_1 \cdot \gamma _1, e_2 \cdot \gamma _2) \in \mathcal {E}[\![\tau ]\!]$. The premise gives us $(e_1 \cdot \gamma _1, e_2 \cdot \gamma _1) \in \mathcal {E}[\![\tau ]\!]$, and we have $(e_2 \cdot \gamma _1, e_2 \cdot \gamma _2) \in \mathcal {E}[\![\tau ]\!]$ from the fundamental property (Theorem 15) for $e_2$. Finally, transitivity (Lemma 10) yields $(e_1 \cdot \gamma _1, e_2 \cdot \gamma _2) \in \mathcal {E}[\![\tau ]\!]$.    $\square$

Together, Lemmas 19 and 20 simplify the task of proving instances of $\approx$ via arguments about the shape of big-step evaluations and entropy pre-images, as we will see in Sect. 6.

5.3 Soundness

The logical relation is sound with respect to contextual equivalence.

Theorem 21

(Soundness). If $\varGamma \vdash e_1 \approx e_2 : \tau$, then $e_1 =_{\mathrm {ctx}}^\varGamma e_2$.

Proof

First show $\vdash C[e_1] \approx C[e_2] : \mathbb {R}$ by induction on C, using the compatibility Lemmas (11–14). Then unfold the definitions of $\approx$ and $\mathcal {E}[\![\mathbb {R}]\!]$ to get the equivalence of the measures.    $\square$

In the next section, we demonstrate the utility of the logical relation by proving a few example equivalences.

6 Proving Equivalences

Having shown that $\approx$ is sound with respect to $=_{\mathrm {ctx}}$, we can now prove instances of contextual equivalence by proving instances of the $\approx$ relation in lieu of thinking about arbitrary real-typed syntactic contexts.

Specific equivalence proofs fall into two classes, which we characterize as structural and deep based on the kind of reasoning involved. Structural equivalences include $\beta _v$ and commutativity of expressions. In a structural equivalence, the same evaluations happen, just in different regions of the entropy space because the access patterns have been shuffled around. Deep equivalences include conjugacy relationships and other facts about probability distributions; they involve interactions between intermediate measures and mathematical operations. Deep equivalences are a lightweight form of denotational reasoning restricted to the ground type $\mathbb {R}$.

6.1 Structural Equivalences

The first equivalence we prove is $\beta _v$, the workhorse of call-by-value functional programming. Unrestricted $\beta$ conversions (call-by-name) do not preserve equivalence in this language, of course, because they can duplicate (or eliminate) effects. But there is another subset of $\beta$ conversions, which we call $\beta _S$, that moves arbitrary effectful expressions around while avoiding duplication. In particular, $\beta _S$ permits the reordering of expressions in a way that is unsound for languages with mutation and many other effects but sound for probabilistic programming.

Theorem 22

($\beta _v$). If $\varGamma \vdash (\lambda x.\,e)~v : \tau$, then $\varGamma \vdash (\lambda x.\,e)~v \approx e[x \mapsto v] : \tau$.

We present two proofs of this theorem. The first proof shows a correspondence between evaluation derivations for the redex and contractum.

Proof

(by derivation correspondence). For simplicity we assume that the bound variables of $\lambda x.\,e$ are unique and distinct from the domain of $\varGamma$; thus the substitution $e \left[ x \mapsto v \right]$ does not need to rename variables to avoid capturing free references in v.

Let $\gamma \models \varGamma$ and let $A \in \mathcal {A}'[\![\tau ]\!]$. By Lemmas 19 and 20, it is sufficient to show that

$$ \mu _{((\lambda x.\,e)~v) \cdot \gamma }(A) = \mu _{(e \left[ x \mapsto v \right] ) \cdot \gamma }(A) $$

that is,

$$\begin{aligned} \int \mathrm {evalin}(((\lambda x.\,e)~v) \cdot \gamma , A, \sigma ) ~ \mu _\mathbb {S}(d\sigma )&= \int \mathrm {evalin}((e \left[ x \mapsto v \right] ) \cdot \gamma , A, \sigma ) ~ \mu _\mathbb {S}(d\sigma ) \end{aligned}$$

By Lemma 3, it suffices to show that for all $W \in \varSigma _\mathbb {R}$, the entropy pre-images have the same measure. That is,

$$\begin{aligned} \mu _\mathbb {S}(\mathrm {evalin}(((\lambda x.\,e)~v) \cdot \gamma , A, \cdot )^{-1}(W))&= \mu _\mathbb {S}(\mathrm {evalin}((e \left[ x \mapsto v \right] ) \cdot \gamma , A, \cdot )^{-1}(W)) \end{aligned}$$

Every evaluation of $((\lambda x.\,e)~v) \cdot \gamma$ has the following form:

The application of the $\lambda$-expression and the syntactic value argument are both trivial. The evaluation of the body expression depends on e; it contains zero or more leaf evaluations of x yielding $v \cdot \gamma$. These leaf evaluations ignore their entropy argument and have weight 1. We refer to the structure of the e evaluation as $\varDelta _1$.

Likewise, every evaluation derivation of $(e \left[ x \mapsto v \right] ) \cdot \gamma$ has the following form:

$\varDelta _2$ has exactly the same structure as $\varDelta _1$. Consequently, the two expressions evaluate the same if $\varDelta _1$ and $\varDelta _2$ receive the same entropy. In short:

$$ \sigma \vdash ((\lambda x.\,e)~v) \cdot \gamma \Downarrow v_r, w ~\iff ~ {\pi }_{3}(\sigma ) \vdash (e \left[ x \mapsto v \right] ) \cdot \gamma \Downarrow v_r, w $$

Let $S_1, S_2 \subseteq \mathbb {S}$ be the entropy pre-images of the two expressions:

$$\begin{aligned} S_1&= \mathrm {evalin}(((\lambda x.\,e)~v) \cdot \gamma , A, \cdot )^{-1}(W) \\ S_2&= \mathrm {evalin}((e \left[ x \mapsto v \right] ) \cdot \gamma , A, \cdot )^{-1}(W) \end{aligned}$$

We conclude that $S_1 = {\pi }_{3}^{-1}(S_2)$ and thus the pre-images have the same measure.    $\square$

The second proof rewrites the measure of the redex into that of the contractum using integral identities.

Proof

(by integral rewriting). As in the first proof, let $\gamma \models \varGamma$ and $A \in \mathcal {A}'[\![\tau ]\!]$. It will be sufficient to show that

$$ \mu _{((\lambda x.\,e)~v) \cdot \gamma }(A) = \mu _{(e \left[ x \mapsto v \right] ) \cdot \gamma }(A) $$

Using the same steps as in Lemma 12, we can express the value measure of an application as an integral by the value measures of its subexpressions.

$$\begin{aligned} \mu _{((\lambda x.\,e)~v) \cdot \gamma }(A) =&\iiint \mathrm {applyin}(v', v'', A, \sigma ) ~ \mu _\mathbb {S}(d\sigma ) ~\mu _{v \cdot \gamma }(dv'') ~\mu _{\lambda x.\,e \cdot \gamma }(dv') \end{aligned}$$

Both the subexpressions $\lambda x.\,e \cdot \gamma$ and $v \cdot \gamma$ are values, so their value measures are Dirac. We complete the proof using the fact that integration by a Dirac measure is equivalent to substitution.

   $\square$

The second equivalence concerns reordering expression evaluations. In probabilistic programming, and effects can be reordered, as long as they are not duplicated or eliminated. We define simple contexts, a generalization of evaluation contexts, as a class of contexts that an expression may be moved through without changing the number of times it is evaluated.

Definition 23 (Simple Contexts).

$$ \begin{array}{rcl} S&\,{:}{:=}\,&{[~]} ~\vert ~S~e ~\vert ~e~S ~\vert ~(\lambda x.\,S)~e ~\vert ~ op (e, \cdots , S, e, \cdots ) ~\vert ~\mathbf {factor}~S \end{array} $$

Note that $(\lambda x.\,S)~e$ can also be written $\mathbf {let}~x = e~\mathbf {in}~S$.

Theorem 24

(Substitution into Simple Context). If $\varGamma \vdash (\lambda x.\,S[x])~e : \tau$ and x does not occur free in S, then $\varGamma \vdash (\lambda x.\,S[x])~e \approx S[e] : \tau$.

Proof

We can prove the following equivalence for a context $S^1$ consisting of a single frame, such as $([~]~e)$. For all $\lambda$-values f where $\varGamma \vdash S^1[f~e] : \tau$,

$$\begin{aligned} \varGamma \vdash (\lambda x.\,S^1[f~x])~e \approx S^1[f~e] : {\tau } \end{aligned}$$

The proof is similar to that of Theorem 22, but see also below.

The proof for arbitrary S contexts proceeds by induction on S. The base case, $\varGamma \vdash (\lambda x.\,x)~e \approx e : \tau$, is easily proven directly. For the inductive case:

   $\square$

The $\beta _S$ and $\beta _v$ theorems together show that the following terms are equivalent:

First is lifted to the outside with $\beta _S$ to get . Then is replaced with in using $\beta _v$. Finally, the outer is renamed back to .

This reordering can also be shown directly, and the proof is similar to the $S^1 = (\lambda x.\,[~])~e$ case above but simpler to present. It involves a generalization of Lemma 1 (Tonelli).

We first apply the technique from the the second proof of Theorem 22 to express substitution as integration by value measures.

$$\begin{aligned} \mu _{(\lambda x.\,(\lambda y.\,e_3)~e_2)~e_1}(A)&=\int \mu _{((\lambda y.\,e_3)~e_2) \left[ x \mapsto v_1 \right] }(A) ~ \mu _{e_1}(dv_1) \\&=\iint \mu _{e_3 \left[ x \mapsto v_1, y \mapsto v_2 \right] }(A) ~ \mu _{e_2}(dv_2)~\mu _{e_1}(dv_1) \end{aligned}$$

Doing the same to the other side, we now need to show that the order of integration is interchangable:

$$ \iint \mu _{e_3[x \mapsto v_1, y \mapsto v_2]}(A) ~ \mu _{e_2}(dv_2)~\mu _{e_1}(dv_1) = \iint \mu _{e_3[y \mapsto v_2, x \mapsto v_1]}(A) ~ \mu _{e_1}(dv_1)~\mu _{e_2}(dv_2) $$

Since $\mu _{e_1}$ and $\mu _{e_2}$ may not be $\sigma$-finite we cannot immediately apply Lemma 1. Lemma 25 shows exchangability for value measures and completes the proof.

Lemma 25

($\mu _{e}$ interchangable). If $\vdash e_1 : \tau _1$ and $\vdash e_2 : \tau _2$ then for all measurable $f : [\![\tau _1]\!] \times [\![\tau _2]\!] \rightarrow \mathbb {R}^+$,

$$ \iint f(v_1, v_2) ~ \mu _{e_2}(dv_2)~\mu _{e_1}(dv_1) = \iint f(v_1, v_2) ~ \mu _{e_1}(dv_1)~\mu _{e_2}(dv_2) $$

Proof

Since integrals about $\mu _{e}$ can be expressed in terms of the $\sigma$-finite $\mu _\mathbb {S}$, we can apply Lemma 1 (Tonelli) once we have exposed the underlying measures.

   $\square$

6.2 Deep Equivalences

In contrast to structural equivalences such as $\beta _v$, deep equivalences rely on the specific computations being performed and mathematical relationships between them. They generally concern only expressions of ground type ($\mathbb {R}$). Proving them requires “locally denotational” reasoning about expressions and the real-valued measures (or measure kernels, when free variables are present) they represent.

For example, the following theorem encodes the fact that the sum of two normally-distributed random variables is normally distributed.

Theorem 26

(Sum of normals with variable parameters). Let

$$\begin{aligned} e_1&= {\mathbf {normal}~x_{m_1}~ x_{s_1} + \mathbf {normal}~x_{m_2}~ x_{s_2}} \\ e_2&= {\mathbf {normal}~(x_{m_1}+x_{m_2})~ \sqrt{x_{s_1}^2 + x_{s_2}^2}} \end{aligned}$$

and let $\varGamma (x_{m_1}) = \varGamma (x_{m_2}) = \varGamma (x_{s_1}) = \varGamma (x_{s_2}) = \mathbb {R}$. Then $\varGamma \vdash e_1 \approx e_2 : \mathbb {R}$.

Proof

Let $(\gamma _1, \gamma _2) \in \mathcal {G}[\![\varGamma ]\!]$. Since $x_{m_1}, x_{m_2}, x_s$ have ground type, the substitutions agree on their values: let $m_1 = \gamma _1(x_{m_1}) = \gamma _2(x_{m_1})$ and likewise for $m_2$, $s_1$, and $s_2$.

We must show $(e_1 \cdot \gamma _1, e_2 \cdot \gamma _2) \in \mathcal {E}[\![\mathbb {R}]\!]$; that is, $\mu _{e_1 \cdot \gamma _1}(A) = \mu _{e_2 \cdot \gamma _2}(A)$ for all $A \in \varSigma _\mathbb {R}$. The value measures of the $\varvec{\mathsf {normal}}$ expressions are actually the measures of normally-distributed random variables. This reasoning relies on the meaning assigned to the ${\textsf {normalinvcdf}}$ operation as well as $+$ and $*$; recall that

Then we apply the fact from probability that the sum of two normal random variables is a normal random variable.    $\square$

6.3 Combining Equivalences

The transitivity of the logical relation permits equivalence proofs to be decomposed into smaller, simpler steps, using the compatibility lemmas to focus in and rewrite subexpressions of the main expression of interest.

Theorem 27

(Sum of normals). Let

$$\begin{aligned} e_1&= {\mathbf {normal}~e_{m_1}~ e_{s_1} + \mathbf {normal}~x_{m_2}~ e_{s_1}} \\ e_2&= {\mathbf {normal}~(e_{m_1}+e_{m_2})~ \sqrt{e_{s_1}^2 + e_{s_2}^2}} \end{aligned}$$

and let $\varGamma \vdash e_1 : \mathbb {R}$ and $\varGamma \vdash e_2 : \mathbb {R}$. Then $\varGamma \vdash e_1 \approx e_2 : \mathbb {R}$.

Proof

This theorem is just like Theorem 26 except with expressions instead of variables for the parameters to the normal distributions. We use $\beta _S$ (Theorem 24) “in reverse” to move the expressions out and replace them with variables, then we apply the variable case (Theorem 26), then we use $\beta _S$ again to move the parameter expressions back in.    $\square$

7 Conclusion

We have defined a logical relation to help prove expressions contextually equivalent in a probabilistic programming language with continuous random variables and a scoring operation. We have proven it sound and demonstrated its usefulness with a number of applications to both structural equivalences like $\beta _v$ and deep equivalences like the sum of normals.