Abstract
Characteristic Formulae (CF) offer a productive, principled approach to generating verification conditions for higher-order imperative programs, but so far the soundness of CF has only been considered with respect to an informal specification of a programming language (OCaml). This leaves a gap between what is established by the verification framework and the program that actually runs. We present a fully-fledged CF framework for the formally specified CakeML programming language. Our framework extends the existing CF approach to support exceptions and I/O, thereby covering the full feature set of CakeML, and comes with a formally verified soundness theorem. Furthermore, it integrates with existing proof techniques for verifying CakeML programs. This validates the CF approach, and allows users to prove end-to-end theorems for higher-order imperative programs, from specification to language semantics, within a single theorem prover.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In previous work, Charguéraud introduced a framework for the verification of imperative higher-order programs, based on characteristic formulae (CF). Given a source-level program, the approach allows the user to state a specification for it, in the style of Separation Logic [22], and prove the specification using the full power of a proof assistant. It has proved successful in verifying robust and modular specifications for non-trivial programs [6], and even establishing complexity results [7].
The key component of such a framework is a function that produces, from a source-level program  , its characteristic formula
, its characteristic formula  . Applying the logical predicate
. Applying the logical predicate  to an environment
to an environment  , a pre-condition
, a pre-condition  and a post-condition
and a post-condition  yields the proposition
yields the proposition  , which implies program
, which implies program  admits
admits  as a pre-condition and
as a pre-condition and  as a post-condition, in environment
as a post-condition, in environment  . The user is left with the task of proving the goal
. The user is left with the task of proving the goal  using specialised CF tactics alongside general-purpose tactics in an interactive theorem prover.
using specialised CF tactics alongside general-purpose tactics in an interactive theorem prover.
Charguéraud’s work is realised in a tool named CFML, where (a subset of) OCaml is the language of the certified programs, and Coq is the proof assistant that hosts the characteristic formulae. Only part of the soundness theorem for CFML has been proved in Charguéraud’s Coq formalisation.
In this paper, we describe how a CF framework has been constructed and proved sound for the entire CakeML language [26], including its exception mechanism and I/O features. CakeML is a substantial subset of Standard ML, with the notable feature that its compiler has been verified (in the HOL4 proof assistant). In addition to capturing language features not modeled in CFML, we give this framework a fully verified soundness theorem. The entire development is formalised in HOL4, which also plays the role of the proof assistant hosting the characteristic formulae. Though tactic details are not the main topic of this paper, we also provide HOL4 tactic support for our CF framework, just as CFML provides Coq tactics to support the proof of  theorems.
theorems.
This paper’s material goes beyond previous work on characteristic formulae and CFML in the following ways:
-
We give a mechanised proof of soundness of characteristic formulae with respect to CakeML’s formal semantics (Sect. 2). By way of contrast, CFML’s soundness proof is mostly performed outside of Coq.
-
We support additional language features, such as I/O (Sect. 3) and exceptions (Sect. 3.2). This makes our framework go beyond CFML, and thus able to handle all features of the CakeML programming language.
-
We implement technology to make proofs using characteristic formulae interoperate with the existing synthesis tool for CakeML, namely the proof-producing translator from HOL functions to CakeML (Sect. 4).
Code implementing concatenation of files to standard out. The CharIO module is our verified implementation of an FFI interface to a rudimentary file-system model (see Sect. 5 for more details).
As an appetiser, in Fig. 1 we show the code for a simple implementation of the Unix cat program, that we are able to verify using our framework. The specification for cat, proven correct in our framework, and thus a HOL4 theorem, is given in Fig. 2. The main steps of the cat proof are described in Sect. 5.
A CF specification of the cat function from Fig. 1. The  predicate underlies the
predicate underlies the  notation, giving a CF Hoare triple for a function, indicating that if
notation, giving a CF Hoare triple for a function, indicating that if  is applied to
is applied to  in a state satisfying
in a state satisfying  , the result satisfies
, the result satisfies  . The
. The  operator (defined on page 14) corresponds to the separating conjunction of separation logic. Parts of specifications occurring within angle brackets (here, only in the post-condition) are conditions that do not depend on the state of the heap. Above, the implication’s assumptions require that no file name contains a null byte or has 256 characters or more (enforced by the
operator (defined on page 14) corresponds to the separating conjunction of separation logic. Parts of specifications occurring within angle brackets (here, only in the post-condition) are conditions that do not depend on the state of the heap. Above, the implication’s assumptions require that no file name contains a null byte or has 256 characters or more (enforced by the  predicate), that every file name corresponds to a real file in the system, and that fewer than 255 files are open. These various requirements naturally fall out of the way the interactions with the file-system are mediated by the FFI interface. The post-condition states that cat returns a unit value, that the
predicate), that every file name corresponds to a real file in the system, and that fewer than 255 files are open. These various requirements naturally fall out of the way the interactions with the file-system are mediated by the FFI interface. The post-condition states that cat returns a unit value, that the  component (the “cat file-system”) of the state is unchanged, and that the standard output stream has been extended with the contents of all the files.
component (the “cat file-system”) of the state is unchanged, and that the standard output stream has been extended with the contents of all the files.
1.1 Background on CF
This subsection and the next one provide background on CF and CakeML. Readers familiar with these topics can skip ahead to Sect. 1.3.
Characteristic formulae, as introduced in Charguéraud’s PhD thesis [4], are essentially total correctness Hoare triples for ML-style functional programs. The key component of any CF framework is a function  that produces, from a source-level expression
that produces, from a source-level expression  , the expression’s characteristic formula
, the expression’s characteristic formula  . Applying
. Applying  to an environment
to an environment  , pre-condition
, pre-condition  and post-condition
and post-condition  yields a proposition
yields a proposition  , which implies program expression
, which implies program expression  can have
can have  as a pre-condition and
as a pre-condition and  as a post-condition, in environment
as a post-condition, in environment 
While the  function is the main workhorse behind any CF framework, most user-proved specifications are stated in terms of a Hoare-triple-like judgement for functional applications,
function is the main workhorse behind any CF framework, most user-proved specifications are stated in terms of a Hoare-triple-like judgement for functional applications,  , written with Hoare-triple notation. The intuition is that
, written with Hoare-triple notation. The intuition is that  is true if the application of function-value
is true if the application of function-value  to curried arguments
to curried arguments  admits
admits  as a pre-condition and
as a pre-condition and  as a post-condition. An example of a specification stated in terms of
as a post-condition. An example of a specification stated in terms of  is shown in Fig. 2.
is shown in Fig. 2.
Charguéraud’s initial version of CF [5] only applied to pure ML programs. Charguéraud has since extended his approach to support reasoning about imperative stateful ML programs in a style inspired by separation logic and its frame rule [6]. More recently, Charguéraud and Pottier have verified amortized complexity results using CFML [7]. The version we have ported to CakeML is based on Charguéraud’s framework for imperative stateful ML programs, but without support for proofs about complexity results.
In Charguéraud’s implementation of CF, called CFML, the mechanism for generating characteristic formulae from OCaml programs, i.e., the  function, is external to the proof assistant (Coq), and the translation from OCaml to Coq is not completely transparent, e.g., it translates the OCaml’s fixed-size int type to the mathematical integers in Coq. The soundness theorem for CFML has been proved on paper using an idealised semantics for a subset of OCaml. In contrast, our CakeML formalisation of CF models all formal entities in the logic of the proof assistant (HOL4 in our case) and the key theorem, i.e., soundness, is proved as a theorem inside the proof assistant.
function, is external to the proof assistant (Coq), and the translation from OCaml to Coq is not completely transparent, e.g., it translates the OCaml’s fixed-size int type to the mathematical integers in Coq. The soundness theorem for CFML has been proved on paper using an idealised semantics for a subset of OCaml. In contrast, our CakeML formalisation of CF models all formal entities in the logic of the proof assistant (HOL4 in our case) and the key theorem, i.e., soundness, is proved as a theorem inside the proof assistant.
1.2 Background on CakeML
The original goal of the CakeML project, as outlined in the first CakeML paper [18], was to provide a fully proof-producing code generation tool (code extraction tool) that given ML-like functions in higher-order logic (HOL) automatically produces equivalent executable machine code. The CakeML translator [18] is a proof-producing tool which generates CakeML code from functions in HOL. The output of the translator can then be input into a verified compiler [15, 26] that transforms CakeML programs to observationally compatible machine code. The verified CakeML compiler function was bootstrapped in logic using the fully proof-producing work-flow mentioned above [15].
As the compiler is maturing, the focus of CakeML project is shifting to the task of developing a general ecosystem of tools around the CakeML language. This is where CF technology comes into the picture. Our CF formalisation provides a verification framework that enables users to prove correctness theorems for imperative CakeML programs that use any of CakeML’s language features, e.g., references, arrays, exceptions and I/O. One can, of course, prove correctness theorems directly over the CakeML semantics. However, such direct proofs would be incredibly tedious for anything but very simple programs.
The formal semantics of the CakeML language is central to its CF framework and the CF framework’s soundness proof. Figures 3 and 5 provide some detail of CakeML’s operational semantics, which we write in the functional big-step style [20]. Figure 5 shows the definitions of the datatype for the deeply embedded CakeML values that the semantics operates over. Figure 3 shows a few cases of the expression evaluation function  . The figure includes the case of function application
. The figure includes the case of function application  , i.e., application of expression
, i.e., application of expression  to expression
to expression  , and shows the semantics, using the helper function
, and shows the semantics, using the helper function  , of applying a non-recursive
, of applying a non-recursive  value to an argument. For this application, the environment
value to an argument. For this application, the environment  from the
from the  value is extended to map the variable
value is extended to map the variable  to value
to value  . Before evaluation enters the expression from the
. Before evaluation enters the expression from the  a clock is checked and decremented, following the style of functional big-step semantics [20]. In the semantics, each function is only applied to one argument at a time.
a clock is checked and decremented, following the style of functional big-step semantics [20]. In the semantics, each function is only applied to one argument at a time.
1.3 A Tour of the Material
The remainder of this section provides a brief tour of the contributions of this paper: the soundness theorem, our extensions for I/O and exceptions, and our integration of the CakeML CF technology with our existing CakeML proof tools.
We formalise the theorem of soundness of CF with respect to the CakeML semantics. In CFML, the soundness proof is only captured on paper, using idealised semantics for a subset of ML, and the Coq library uses axioms in the places where it would relate to the language semantics. In contrast, we were able to implement an axiom-free CF library for the whole CakeML language, and perform a mechanical proof of soundness, using CakeML’s pre-existing semantics.
This not only validates the CF approach introduced by Charguéraud, but also shows that it is flexible as well as extensible. Although CakeML’s semantics were not designed with CF in mind, we could directly reuse the CakeML language without any modification, and we were able to carry out the proofs without any particular issue (although some technical details differ from the paper proof). Moreover, as detailed in Sect. 3, we could extend the approach to handle new language features that are not supported by CFML.
The soundness theorem, which justifies proving properties about a characteristic formula to give equivalent properties about the program itself, is stated as follows. If the characteristic formula for the deeply embedded expression  (and environment
(and environment  ) holds for some shallowly embedded pre-condition
) holds for some shallowly embedded pre-condition  and shallowly embedded post-condition
and shallowly embedded post-condition  , i.e.,
, i.e.,  , then, starting from a state satisfying
, then, starting from a state satisfying  is guaranteed to successfully evaluate in CakeML’s functional big-step semantics [20], and reach a new state
is guaranteed to successfully evaluate in CakeML’s functional big-step semantics [20], and reach a new state  and value
and value  satisfying
satisfying  . Here
. Here  converts a CakeML state into a representation to which one can apply separation logic connectives, and
converts a CakeML state into a representation to which one can apply separation logic connectives, and  asserts disjoint union:
asserts disjoint union:  .
.

This mechanised proof eliminates the last bits of paper proof that need to be trusted in CFML. Section 2 details the main steps leading to the proof.
We extend the CF framework introduced in CFML to handle two new language features: exceptions, and I/O through CakeML’s foreign-function interface (FFI). These extensions are proved sound with respect to the CakeML semantics, and neatly make our framework able to handle all features of the CakeML programming language.Footnote 1
The extension which adds support for I/O is implemented by carefully modifying the  function, shown in the soundness theorem above. We modified the
function, shown in the soundness theorem above. We modified the  function so that it makes visible the state of the FFI in the pre- and post-conditions. There were numerous tricky details to get right in the definition of
function so that it makes visible the state of the FFI in the pre- and post-conditions. There were numerous tricky details to get right in the definition of  because the design goal was to make I/O reasoning local in the style of separation logic. Our support for I/O is local in that the proof for a piece of code which only uses, say, the print-to-stdout FFI ports does not impose any assumptions on the behaviour, state, or even existence of other FFI ports, e.g., ports for reading-from-stdin. In the spirit of separation logic, our framework allows combining different assertions about the FFI using CF’s equivalent to the separation logic frame rule. Section 3 provides details on how we modified
because the design goal was to make I/O reasoning local in the style of separation logic. Our support for I/O is local in that the proof for a piece of code which only uses, say, the print-to-stdout FFI ports does not impose any assumptions on the behaviour, state, or even existence of other FFI ports, e.g., ports for reading-from-stdin. In the spirit of separation logic, our framework allows combining different assertions about the FFI using CF’s equivalent to the separation logic frame rule. Section 3 provides details on how we modified  to make the FFI available in CF proofs.
to make the FFI available in CF proofs.
Support for exceptions is implemented by making the post-conditions differentiate whether the result is a normal return with a value or a value raised as an exception. The new framework is able to reason about exception handling code. Section 3.2 explains how exceptions are supported and the effect their introduction had on the proofs.
With these extensions our framework covers all of CakeML’s language features and makes it possible to develop a verified standard library for CakeML with complete specifications for library functions that perform I/O or must raise exceptions in certain circumstances. For example, our cat implementation has a routine for opening files, called openIn (whose specification is shown in Fig. 4). A call to the CakeML function for openIn raises an exception if the file could not be opened, e.g., if there is no file at the given path. More precisely,  describes whether a file exists in
describes whether a file exists in  with name
with name  , and the BadFileName exception is raised when no file could be found.
, and the BadFileName exception is raised when no file could be found.
In compiled CakeML code, the actual system call for opening a file is handled by a short stub of C code that is attached to the external side of CakeML’s FFI. If an error occurs, the C code signals failure via the return value for the FFI call and, on the CakeML side, the library routine raises the relevant exception on receiving the error code from the C stub. At present, the external C code is unverified and we just make assumptions about its effect on the rest of the world. In the future, we aim to provide verified external assembly stubs that can replace the current unverified C code.
We integrate the CF framework into the CakeML ecosystem by making it interoperate with an existing synthesis tool, namely the automatic translation from HOL functions into CakeML. This tool [18] essentially implements a proof-producing extraction mechanism: given a function in higher-order logic (HOL), the tool generates CakeML code along with a proof that the produced code correctly implements the HOL function with respect to CakeML’s semantics. As HOL functions are pure, the translator is essentially limited to producing purely functional CakeML code.Footnote 2
At present, the most important use of this translation tool is in bootstrapping the verified CakeML compiler, where we now benefit from CF. The translation tool is used to generate CakeML code for the CakeML compiler’s implementation. The compiler is defined as functions in HOL, so before we can run the compiler on itself, we need to transform the compiler definition into the source language of the compiler, i.e., CakeML abstract syntax. CF comes into the picture because the translation tool can only produce pure functions. Previously we had to manually verify low-level I/O code that reads the input and passes it to the compiler function, and separate code that prints the result of running the CakeML’s compile function. By making the CF and translation tools able to build on each other’s results, we have replaced the difficult manual I/O code proofs by understandable CF proofs about I/O.
The bootstrap has thus far benefited from automatic conversion of translator produced results to CF theorems. The bridge between them also works in the other direction: proved results from CF can be used in the translator. Since the translator essentially only deals in pure functions, the CF-verified programs have to implement a pure interface in order to fit the translator. Such programs are not necessarily pure themselves: they can allocate memory, and use imperative structures and algorithms. We plan to make use of the CF-to-translator direction in the future to provide more efficient drop-in replacements for parts of the bootstrapped compiler. These replacement parts would be verified using CF, and replace the code produced by the translator. The register allocator is a particular example that we believe would benefit from using an imperative-style implementation instead of the current automatically generated pure functional implementation.
Section 4 provides details on how we have connected the translation tool and the CakeML CF framework.
All our developments were carried out in the HOL4 theorem prover, and have been integrated into the main CakeML repository. They are available online at https://cakeml.org and https://code.cakeml.org under the characteristic sub-directory.
2 A Formal Proof of Soundness for Characteristic Formulae
In this section, we explain how CakeML CF differs from CFML, how we avoided axioms in our formalisation, and how we proved soundness of CF for CakeML.
2.1 Adapting CFML to CakeML
A first necessary step towards a proof of soundness was reimplementing the CFML definitions, lemmas and tactics in the CakeML setting. Most of them worked similarly to CFML – in particular the CF definitions and the various tactics (although they are implemented differently). There are however some technical differences worth noting.
CakeML’s semantics uses environments, whereas CMFL assumes substitution semantics. As a consequence, CakeML environments (which map names to semantic values) are threaded through CakeML’s characteristic formulae as a new parameter. Environments are accessed in the generated formulae, e.g., the CF for  , shown below, returns the value for
, shown below, returns the value for  in the given environment. Here \(\rhd \) is the entailment relation on heap predicates, i.e., \(H_1 \rhd H_2\) is true if any heap satisfying \(H_1\) also satisfies \(H_2\), and defined by
in the given environment. Here \(\rhd \) is the entailment relation on heap predicates, i.e., \(H_1 \rhd H_2\) is true if any heap satisfying \(H_1\) also satisfies \(H_2\), and defined by  . The
. The  predicate adds the frame rule of separation logic to the formula.
predicate adds the frame rule of separation logic to the formula.

In practice, environments are never manipulated explicitly by the user. The user states top-level specifications of the form “ ”, specifying the behavior of the application of the function value
”, specifying the behavior of the application of the function value  to some arguments
to some arguments  . The value
. The value  can be fetched given its name as a CakeML function, thanks to a small library that keeps track of top-level definitions.
can be fetched given its name as a CakeML function, thanks to a small library that keeps track of top-level definitions.
As  is in fact a closure, the following lemma applies. This lemma, which is a consequence of the CF soundness theorem, turns the goal into proving the CF of the body of
is in fact a closure, the following lemma applies. This lemma, which is a consequence of the CF soundness theorem, turns the goal into proving the CF of the body of  , for the environment that was packed in the closure. Here
, for the environment that was packed in the closure. Here  creates a
creates a  value that takes several curried arguments.
value that takes several curried arguments.

A custom pretty printer hides the contents of environments from the user. Sub-goals of the form “ ” are always automatically proved by unfolding
” are always automatically proved by unfolding  .
.
CF for CakeML uses a deep embedding of CakeML values, while CFML translates ML values to corresponding Coq values. CakeML values are described by the HOL type v (shown in Fig. 5), which is defined as part of the semantics.
To relate CakeML values of type  to logical values (such as
to logical values (such as  ,
,  , ...), we re-use the refinement invariants presented by Myreen and Owens [18] in the context of a proof-producing translation from HOL functions to CakeML programs. These refinement invariants are a collection of composable predicates that relate HOL types and data structures to the same concepts as deeply embedded CakeML values. The
, ...), we re-use the refinement invariants presented by Myreen and Owens [18] in the context of a proof-producing translation from HOL functions to CakeML programs. These refinement invariants are a collection of composable predicates that relate HOL types and data structures to the same concepts as deeply embedded CakeML values. The  and
and  refinement invariants are defined as follows:
refinement invariants are defined as follows:

A specification for the CakeML addition function can then be written as follows. Here the angle brackets turn a pure proposition into a heap predicate for heaps represented as sets:  and
and  is
is  .
.

This is somewhat heavier than CFML specifications, where Coq integers would simply be used in place of semantic values. We believe it is hardly an issue for more involved data structures, for which it is common to define such predicates anyway in CFML in order to keep track of additional invariants.
Normalisation of input programs and CF generation are performed in the logic, whereas in CFML they are performed by an external tool. Before being fed to the  function, programs are normalised in a process similar to A-normalisation. The motivation is that it significantly simplifies formally reasoning about programs, while preserving their semantics. Figure 6 displays an example of the normalisation process. Due to the fact that
function, programs are normalised in a process similar to A-normalisation. The motivation is that it significantly simplifies formally reasoning about programs, while preserving their semantics. Figure 6 displays an example of the normalisation process. Due to the fact that  is implemented as a total function in the logic, assumptions about the program being in normal form are made explicit in characteristic formulae. In CFML, the external CF generator simply fails on unhandled input programs.
is implemented as a total function in the logic, assumptions about the program being in normal form are made explicit in characteristic formulae. In CFML, the external CF generator simply fails on unhandled input programs.
The  function assumes that the input program is in normal form. This assumption is reflected by the use of the
function assumes that the input program is in normal form. This assumption is reflected by the use of the  predicate in characteristic formulae. This predicate, of type
predicate in characteristic formulae. This predicate, of type  , checks whether an expression is in fact a value or a name bound to a value. It is used in characteristic formulae to assert that some expression must be trivial, because of the normalisation pass. For example, the CF for
, checks whether an expression is in fact a value or a name bound to a value. It is used in characteristic formulae to assert that some expression must be trivial, because of the normalisation pass. For example, the CF for  , below, uses
, below, uses  to assert that evaluation of the condition must be dealt with beforehand, by introducing a let-binding, which the normalisation step does. If for some reason the program appears not to be in normal form, the corresponding CF reduces to
to assert that evaluation of the condition must be dealt with beforehand, by introducing a let-binding, which the normalisation step does. If for some reason the program appears not to be in normal form, the corresponding CF reduces to  .
.

The sub-goals related to  in characteristic formulae are always automatically proved by our CF tactics, and are thus kept hidden from the user.
in characteristic formulae are always automatically proved by our CF tactics, and are thus kept hidden from the user.
2.2 Realising CFML Axioms
Using CakeML’s semantics, we are able to give an implementation of the  predicate, which was axiomatised in CFML.
predicate, which was axiomatised in CFML.
Let us first consider the semantics of a Hoare triple for an expression  in environment
in environment  , denoted
, denoted  . We define validity for such a Hoare triple, which we then use to define
. We define validity for such a Hoare triple, which we then use to define  . The Hoare triple
. The Hoare triple  holds if and only if evaluation of the expression
holds if and only if evaluation of the expression  , in a heap that satisfies the heap predicate
, in a heap that satisfies the heap predicate  , terminates and produces a value
, terminates and produces a value  and a heap satisfying
and a heap satisfying  .
.

In this definition,  and
and  are used to split a state represented as a set of state elements into disjoint subsets:
are used to split a state represented as a set of state elements into disjoint subsets:  similarly
similarly  into three disjoint subsets
into three disjoint subsets  . This state splitting is here in order to make the frame rule available, as explained further down.
. This state splitting is here in order to make the frame rule available, as explained further down.
We now define a simple version of  , called
, called  , which characterises the application of a closure to a single argument. When provided a valid function application, where
, which characterises the application of a closure to a single argument. When provided a valid function application, where  can extract the body of the closure and the extended environment,
can extract the body of the closure and the extended environment,  simply asserts the general Hoare triple defined above. When
simply asserts the general Hoare triple defined above. When  fails,
fails,  asserts that the pre-condition
asserts that the pre-condition  cannot hold of any state (because otherwise the function application would need to succeed).
cannot hold of any state (because otherwise the function application would need to succeed).

Finally we define the  predicate, which characterises the application of a closure to multiple arguments, by iterating
predicate, which characterises the application of a closure to multiple arguments, by iterating  .
.

It is worth noting that our Hoare triple validity integrates the frame rule in its definition. The  predicate (respectively
predicate (respectively  ) expresses that some heap can be split into two (resp. three) disjoint parts. Therefore, the function application may involve only some subpart of the heap
) expresses that some heap can be split into two (resp. three) disjoint parts. Therefore, the function application may involve only some subpart of the heap  , while the rest
, while the rest  is preserved. The function is also allowed to produce some garbage
is preserved. The function is also allowed to produce some garbage  , which is left unconstrained. This is necessary for top-level specifications to be modular, as they are formulated in terms of
, which is left unconstrained. This is necessary for top-level specifications to be modular, as they are formulated in terms of  .
.
The built-in frame rule also means that when carrying proofs using the framework, the definition of  is kept abstract and never unfolded. When faced with a “
is kept abstract and never unfolded. When faced with a “ ” goal, a specification for
” goal, a specification for  , also of the form “
, also of the form “ ” will be fetched and used to prove the goal, either directly or using the frame rule.
” will be fetched and used to prove the goal, either directly or using the frame rule.
2.3 Proving CF Soundness
Soundness of characteristic formulae means that, for every expression  , if
, if  holds, then the Hoare triple
holds, then the Hoare triple  is valid. We define soundness for arbitrary formulae as follows.
is valid. We define soundness for arbitrary formulae as follows.

The main result of this section can now be stated. We prove soundness of  as the following HOL theorem:
as the following HOL theorem:
Theorem 1
(CF are sound wrt. CakeML semantics).

Proof
By induction on the size of  .
.
This proof is most tricky for CakeML language constructs for which characteristic formulae differ significantly from the semantics. The reason is typically to abstract away from specifics of the semantics, and have proof-friendly characteristic formulae. Two instances of this are closures and pattern matching.
CakeML semantics has closure values. Functions evaluate to closures, and function application is defined in terms of applying a closure to values. The CF for function declaration introduces an abstract value  , and a specification
, and a specification  for it. Our formulation differs from that in CFML [6] due to CakeML’s use environment semantics instead of CFML’s substitution semantics.
for it. Our formulation differs from that in CFML [6] due to CakeML’s use environment semantics instead of CFML’s substitution semantics.

In the soundness proof,  is instantiated by a function closure, and one has to prove that
is instantiated by a function closure, and one has to prove that  characterises it.
characterises it.
Proving the soundness of CF for pattern-matching also requires some amount of proof engineering. CakeML semantics provides a logical function that implements a pattern-matching algorithm, and returns whether the match succeeded or not. Characteristic formulae for pattern-matching are instead formulated as nested ifs, which test the equality between the matched value and values produced from the successive patterns.
3 Sound Extensions of CF for I/O and Exceptions
This section explains how our CF framework has extended the original CFML framework to enable reasoning about I/O and exceptions.
3.1 Support for I/O
As mentioned earlier, the goal of our extension for I/O was to enable convenient local reasoning about I/O operations without unreasonable restrictions on the kind of I/O one can verify.
We start with a quick explanation of how I/O is supported in the CakeML language, then show how we made CF pre- and post-conditions able to make assertions about parts of the I/O state, what I/O looks like in the  function’s output, and finally how we have used these techniques in the bootstrapping of the latest CakeML compiler.
function’s output, and finally how we have used these techniques in the bootstrapping of the latest CakeML compiler.
The CakeML language supports I/O through a byte-array-based foreign-function interface (FFI). The abstract syntax for CakeML includes an  expression. The semantics of executing an
expression. The semantics of executing an  expression is to update the state of the FFI which is threaded through the operational semantics together with the state of the CakeML references. The intuition is that CakeML’s FFI state component models the state of the outside world and how the outside world will react to any calls made from the CakeML program to the external world.
expression is to update the state of the FFI which is threaded through the operational semantics together with the state of the CakeML references. The intuition is that CakeML’s FFI state component models the state of the outside world and how the outside world will react to any calls made from the CakeML program to the external world.
The formal definition of the FFI state is shown in Fig. 7. When designing the CakeML semantics we wanted to make the FFI state as flexible as possible, so we left the type of the rest of the world as a type variable  , and we only require that the user provide some oracle function
, and we only require that the user provide some oracle function  that describes how the outside world will react to any FFI call. The FFI state has a
that describes how the outside world will react to any FFI call. The FFI state has a  field that indicates whether the outside world has stopped the process (e.g., due to a call to exit). The FFI state also keeps a list of all calls to the FFI
field that indicates whether the outside world has stopped the process (e.g., due to a call to exit). The FFI state also keeps a list of all calls to the FFI  : each event records the name of the FFI portFootnote 3 that was called, and a list of byte pairs, where
: each event records the name of the FFI portFootnote 3 that was called, and a list of byte pairs, where  of that list is the input to the FFI call and
of that list is the input to the FFI call and  of the list is the state of the array on return from the FFI call.
of the list is the state of the array on return from the FFI call.
We enable reasoning about I/O in CF by modifying the  function to expose an image of the FFI state as part of the set representation that the separation logic connectives operate over.
function to expose an image of the FFI state as part of the set representation that the separation logic connectives operate over.
The role of the  function is to split the state into parts that can be separated using separating conjunction
function is to split the state into parts that can be separated using separating conjunction  . For example, a CakeML state
. For example, a CakeML state  with references at locations 0, 1 and 2 becomes the following. Note that
with references at locations 0, 1 and 2 becomes the following. Note that  can only produce one
can only produce one  for each location
for each location  in the store.
in the store.

We can use  to separate between assertions such as the following. Here
to separate between assertions such as the following. Here  is the value of a reference in the CakeML semantics (Fig. 5), and
is the value of a reference in the CakeML semantics (Fig. 5), and  are constructors of the value type for store values.
are constructors of the value type for store values.

With these definitions it follows from  and that updates to reference
and that updates to reference  do not affect
do not affect  .
.
The simplest way to make it possible to reason about FFI using CF would be to just make  produce sets that contain an element that contains the entire current state of the CakeML FFI, i.e.,
produce sets that contain an element that contains the entire current state of the CakeML FFI, i.e.,  . However, such a simplistic approach would mean that there can only be one assertion about the state of the FFI in any pre- or post-condition since the assertion could not be split by separating conjunction
. However, such a simplistic approach would mean that there can only be one assertion about the state of the FFI in any pre- or post-condition since the assertion could not be split by separating conjunction  . We need to make
. We need to make  split the FFI state into multiple elements of the state component sets so that we can use the separating conjunction in reasoning about FFI states.
split the FFI state into multiple elements of the state component sets so that we can use the separating conjunction in reasoning about FFI states.
The splitting of the FFI state is non-trivial since we want to keep the FFI state as abstract as possible in the CakeML semantics. The FFI state is modelled by a type variable  , and thus we know nothing about its structure. Our solution is to parametrise the
, and thus we know nothing about its structure. Our solution is to parametrise the  function with information on how to partition an FFI state. The information is a pair consisting of:
function with information on how to partition an FFI state. The information is a pair consisting of:
-
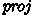 : a projection function of type
: a projection function of type 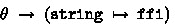 , which given an FFI state of type
, which given an FFI state of type 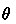 returns a finite map from strings to a new type called
returns a finite map from strings to a new type called 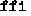 . Here
. Here 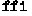 is a datatype that is meant to be convenient for modelling projected FFI states in general.Footnote 4
is a datatype that is meant to be convenient for modelling projected FFI states in general.Footnote 4

-
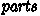 : a list of partitions which are pairs: each pair contains a list of FFI port names (of type
: a list of partitions which are pairs: each pair contains a list of FFI port names (of type 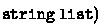 and a behaviour modelling next-state function, i.e., a representation of part of the oracle function in CakeML’s FFI state. The type of the behaviour modelling function is:
and a behaviour modelling next-state function, i.e., a representation of part of the oracle function in CakeML’s FFI state. The type of the behaviour modelling function is: 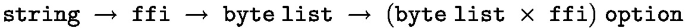
The partitioning information  is considered well-formed and applicable to an FFI state
is considered well-formed and applicable to an FFI state  if:
if:
-
the FFI state
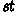 has not hit a stopping state, i.e.,
has not hit a stopping state, i.e., 
-
no partition has names that overlap with other partitions
-
every I/O event has an index that belongs to one of the partitions
-
for each partition,
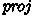 maps all states to the same
maps all states to the same 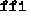 value
value -
the update function
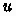 in each partition respects the FFI’s oracle functionFootnote 5
in each partition respects the FFI’s oracle functionFootnote 5
The FFI-enabled definition of  maps CakeML states to the union of the parts of the state that describe the references and the partitioned parts of the FFI state. If the partition for the FFI state is well-defined, then the FFI state is split into a set of
maps CakeML states to the union of the parts of the state that describe the references and the partitioned parts of the FFI state. If the partition for the FFI state is well-defined, then the FFI state is split into a set of  elements, where each such element carries:
elements, where each such element carries:
-
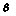 , the projected view of the state of this partition
, the projected view of the state of this partition -
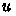 , the update function for the partition
, the update function for the partition -
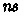 , the FFI port names associated with the partition
, the FFI port names associated with the partition -
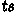 , a list of all previous I/O events for these names.
, a list of all previous I/O events for these names.
We can now make assertions about I/O in CF using  and separation logic connectives. We define a generic
and separation logic connectives. We define a generic  assertion as follows.
assertion as follows.

With these we can make assertions about I/O. For example, the following asserts that the projected FFI state must have a part that is described by  , and a disjoint part that is described by
, and a disjoint part that is described by 

Using such statements in their pre- and post-conditions, the user may express strong specifications concisely.
The following proof obligation is generated every time the  function is applied to the abstract syntax for an FFI expression. This proof obligation can be read as follows: pre-condition
function is applied to the abstract syntax for an FFI expression. This proof obligation can be read as follows: pre-condition  must imply that there is a byte array and I/O partition in the state. The I/O partition must include the
must imply that there is a byte array and I/O partition in the state. The I/O partition must include the  of the called FFI entry point. Furthermore, the result of running the next-state function from the FFI partition, i.e.,
of the called FFI entry point. Furthermore, the result of running the next-state function from the FFI partition, i.e.,  , must successfully return a new state
, must successfully return a new state  and this state and the updated byte array must imply the desired post-condition
and this state and the updated byte array must imply the desired post-condition  . FFI calls return
. FFI calls return 

The proof goal produced by  mentions
mentions  , which from the user’s perspective is the primitive I/O assertion in CakeML CF. Users define their own specialisations of
, which from the user’s perspective is the primitive I/O assertion in CakeML CF. Users define their own specialisations of  for each application, see Sect. 5.
for each application, see Sect. 5.
This support for I/O has, together with the connection between CF and the CakeML translator (Sect. 4), been used to verify the I/O code required for giving input and producing output from the bootstrapped CakeML compiler. The I/O code is a little snippet of code that wraps around the translator-generated pure CakeML code which implements the logical CakeML compile function.
3.2 Support for Exceptions
We implement complete support for specifying CakeML programs that use exceptions. Up to this point, we required expressions to evaluate and reduce to a value: post-conditions were of type  , taking the returned value as an argument. We now allow expressions to raise an exception instead: we define a
, taking the returned value as an argument. We now allow expressions to raise an exception instead: we define a  datatype
datatype  and change the type of post-conditions to be
and change the type of post-conditions to be  We define some wrappers for writing post-conditions, in particular for the cases where the expression never (resp. always) raises an exception.
We define some wrappers for writing post-conditions, in particular for the cases where the expression never (resp. always) raises an exception.  handles both cases by taking one post-condition for each case.
handles both cases by taking one post-condition for each case.

We update the definitions that relate CF to CakeML semantics. For example, the definition of Hoare triple validity we presented earlier contains:

The second component returned by  , of which
, of which  is a constructor, is of type
is a constructor, is of type  where:
where:

This gives us two other cases:  for expressions that raise an exception, and
for expressions that raise an exception, and  for expressions that fail to evaluate. We still rule out the latter, but add support for the former: the definition of Hoare triple validity becomes:
for expressions that fail to evaluate. We still rule out the latter, but add support for the former: the definition of Hoare triple validity becomes:

We update the existing CF definitions as well. We add side-conditions to deal with exceptions; for example the CF for  handles the case where an exception is raised by the first expression.
handles the case where an exception is raised by the first expression.

This uses the entailment relation on post-conditions for the exception case, written  , and defined as
, and defined as  . On exceptions, the post-condition for
. On exceptions, the post-condition for  (\(Q'\)) has to directly entail validity of the post-condition for the whole formula (Q), since
(\(Q'\)) has to directly entail validity of the post-condition for the whole formula (Q), since  does not get executed in case
does not get executed in case  raises an exception.
raises an exception.
Some other side-conditions are not needed for establishing the soundness theorem, but are added to enforce a “no garbage” property on post-conditions. For example, the CF for  becomes as follows, where
becomes as follows, where  is a post-condition false for any value and any heap:
is a post-condition false for any value and any heap:

This requires Q to be false on exceptions, as evaluating a  always produces a value on well scoped code. We believe having such side-conditions make the following proposition true (and plan to prove it as future work): if the CF for e is true for pre-condition H and post-condition Q, then
always produces a value on well scoped code. We believe having such side-conditions make the following proposition true (and plan to prove it as future work): if the CF for e is true for pre-condition H and post-condition Q, then  if and only if e does not raise exceptions.
if and only if e does not raise exceptions.
We update the existing tactics, so that easy side-conditions are automatically proved. We rely on the following lemma:

This is trivially true, as  unfolds to
unfolds to  Thanks to this lemma, carrying out proofs about programs that do not involve exceptions requires no additional effort. The only modification necessary is changing the “
Thanks to this lemma, carrying out proofs about programs that do not involve exceptions requires no additional effort. The only modification necessary is changing the “ ” to “
” to “ ” in post-conditions.
” in post-conditions.
Finally, we handle CakeML’s primitives for exception handling,  and
and  , whose semantics match SML’s. Here
, whose semantics match SML’s. Here 

The entailment relation on post-conditions for the value case, written  is without surprise defined as
is without surprise defined as  . The CFs for
. The CFs for  and
and  resemble the CFs for
resemble the CFs for  and
and  respectively, but with the respectives roles of exceptions and values swapped. The
respectively, but with the respectives roles of exceptions and values swapped. The  auxiliary definition corresponds to the CF for pattern-matching.
auxiliary definition corresponds to the CF for pattern-matching.
Let us present an illustrative example. The cat program presented earlier in Fig. 1 doesn’t do any exception handling, and for simplicity its specification (Fig. 2) requires that all input filenames represent existing files. In this way, our specification above only specifies the non-exceptional behaviour. Nonetheless, the various I/O primitives can be modeled so as to allow the possibility that they might raise various exceptions, and when they are, we can prove more detailed post-conditions capturing those behaviours.
We define a simple cat1exn program that handles invalid filenames. It is implemented as shown in Fig. 8, by calling cat1 and handling the CharIO.BadFileName exception that may be raised.
Figure 9 shows the specification of cat1, and Fig. 10 shows the specification we prove for cat1exn. It relies on the  function, which corresponds to the text displayed by cat1exn, and is defined as:
function, which corresponds to the text displayed by cat1exn, and is defined as:

Proving the specification for cat1exn boils down to proving three subgoals, corresponding to the three conjunctions appearing in the  case of
case of  The first one is trivially solved using the appropriate tactic. The second one requires proving that the post-condition of cat1 entails the post-condition of cat1exn, for the value case. This is true, using a lemma proving that
The first one is trivially solved using the appropriate tactic. The second one requires proving that the post-condition of cat1 entails the post-condition of cat1exn, for the value case. This is true, using a lemma proving that  holds if the file could be found with some content in the file system. The last goal finally requires proving that the file system
holds if the file could be found with some content in the file system. The last goal finally requires proving that the file system  is unchanged in the exception case. Knowing
is unchanged in the exception case. Knowing  this is proved by unfolding
this is proved by unfolding 
4 Interoperating with the CakeML Translator
We prove an equivalence result between the theorems produced by the translator, and a particular shape of CF specifications.
Called on a function  of type
of type  , the translator will produce a CakeML program
, the translator will produce a CakeML program  , and the following theorems. The theorems state that: running the
, and the following theorems. The theorems state that: running the  program results in an environment,
program results in an environment,  in which looking up the variable
in which looking up the variable  yields a value
yields a value  and finally that this value implements the function
and finally that this value implements the function 

We are here mostly interested in the last theorem, expressed using the “arrow” predicate, “ ”, which relates the HOL function
”, which relates the HOL function  to the closure
to the closure  It states that for any argument
It states that for any argument  satisfying
satisfying  evaluating the closure produces a value
evaluating the closure produces a value  satisfying
satisfying  Formally:
Formally:

This is reminiscent of the  predicate used in CF, and indeed we prove that “arrow” is a special case of
predicate used in CF, and indeed we prove that “arrow” is a special case of 
The CF specifications we prove equivalent to “arrow” are of the form  where
where  is some logical predicate of type
is some logical predicate of type  A pure function does not raise exceptions, hence the post-condition is false for exceptions. Both the pre- and post-condition assert emptiness of the heap.
A pure function does not raise exceptions, hence the post-condition is false for exceptions. Both the pre- and post-condition assert emptiness of the heap.
A function  satisfying such a spec can still be called on any heap, thanks to the frame rule built into the CF framework. The specification simply means that the function cannot assume anything about the heap, or access it. Less obviously, this kind of specification allows the function to allocate heap objects (references, arrays, ...) for internal use. This becomes apparent after unfolding the definition of Hoare triple validity that underlies
satisfying such a spec can still be called on any heap, thanks to the frame rule built into the CF framework. The specification simply means that the function cannot assume anything about the heap, or access it. Less obviously, this kind of specification allows the function to allocate heap objects (references, arrays, ...) for internal use. This becomes apparent after unfolding the definition of Hoare triple validity that underlies  (which we recall below).
(which we recall below).

The final heap “ ” is split in three sub-heaps: \(h_f\), \(h_k\) and \(h_g\). The post-condition must be true on \(h_f\), and \(h_k\) was present in the initial heap and is unchanged. There remains \(h_g\), which represents heap objects that may have been allocated by the function and now need to be garbage collected. Consequently, even though such specifications require the function
” is split in three sub-heaps: \(h_f\), \(h_k\) and \(h_g\). The post-condition must be true on \(h_f\), and \(h_k\) was present in the initial heap and is unchanged. There remains \(h_g\), which represents heap objects that may have been allocated by the function and now need to be garbage collected. Consequently, even though such specifications require the function  to offer a pure interface, it is not necessarily pure itself: it can be implemented using imperative structures and algorithms.
to offer a pure interface, it is not necessarily pure itself: it can be implemented using imperative structures and algorithms.
The exact equivalence theorem we prove is as follows:

The arrow-to- direction is the easiest to prove. With the right automation, it allows programs certified using CF to use programs produced by the translator, and automatically retrieve their specification. The
direction is the easiest to prove. With the right automation, it allows programs certified using CF to use programs produced by the translator, and automatically retrieve their specification. The  -to-arrow direction is significantly trickier. It required changing the definition of “arrow” to allow heap allocation (represented by
-to-arrow direction is significantly trickier. It required changing the definition of “arrow” to allow heap allocation (represented by  earlier), and subsequent updating of the translator. Moreover, the proof itself involved careful reasoning about the state of the FFI. This direction makes it possible to provide programs certified using CF as drop-in replacements for translated functions.
earlier), and subsequent updating of the translator. Moreover, the proof itself involved careful reasoning about the state of the FFI. This direction makes it possible to provide programs certified using CF as drop-in replacements for translated functions.
5 Case Study: A Verified cat Implementation
Our case study builds a simple model coupling a read-only file-system with one standard output stream. The type of the read-only file-system is

The files and infds fields are association lists. The files field maps file names to file contents. The infds field maps file descriptors (numbers) to pairs of file names and offsets within that file. File names are of type  ; in CakeML, these map to vectors of characters occupying contiguous blocks of memory. This model supports multiple descriptors reading from a common file at different positions, and is also subject to realistic problems such as the possibility of file descriptors becoming stale.
; in CakeML, these map to vectors of characters occupying contiguous blocks of memory. This model supports multiple descriptors reading from a common file at different positions, and is also subject to realistic problems such as the possibility of file descriptors becoming stale.
The four file-system operations needed for our example are  At this initial stage, we can define the type and its operations in a natural style, concerning ourselves only with the logical model, and not needing to worry about its realisation in the CF framework. (One exception is the use of association lists; it would be more natural to use finite maps, but we must ultimately encode our values into the
At this initial stage, we can define the type and its operations in a natural style, concerning ourselves only with the logical model, and not needing to worry about its realisation in the CF framework. (One exception is the use of association lists; it would be more natural to use finite maps, but we must ultimately encode our values into the  type presented on page 15.)
type presented on page 15.)
Making a model of this sort visible within the CF framework then requires us to cast the operations as messages being sent using single, fixed-size buffers (a mutable array of bytes, to be precise). For example, when accessed from CakeML, the  operation must begin by writing the file descriptor value into such a buffer. The same buffer is then used to store the return value. If the file descriptor passed to
operation must begin by writing the file descriptor value into such a buffer. The same buffer is then used to store the return value. If the file descriptor passed to  is not valid, or if the file descriptor has come to the end of file, the error-condition must be returned using the same buffer.
is not valid, or if the file descriptor has come to the end of file, the error-condition must be returned using the same buffer.
We choose to use a one-byte buffer in the case of  partly because it is simple, but also because it naturally leads to realistic “misfeatures”: bad inputs cause a \(-1\) return code, which must be returned “in-band”. To know whether or not this is genuine, the client has to call the
partly because it is simple, but also because it naturally leads to realistic “misfeatures”: bad inputs cause a \(-1\) return code, which must be returned “in-band”. To know whether or not this is genuine, the client has to call the  test first.
test first.
The final part of the process requires us to write CakeML wrappers that make calls through the FFI. The wrapper code for  using the one-byte buffer onechar, is presented in Fig. 11.
using the one-byte buffer onechar, is presented in Fig. 11.
CakeML code implementing  For the purposes of simplicity this does not catch the error possible when the argument fd is not valid; rather the specification we use imposes “fd-validity” as a pre-condition. By using the
For the purposes of simplicity this does not catch the error possible when the argument fd is not valid; rather the specification we use imposes “fd-validity” as a pre-condition. By using the  function, the code does allow for the successful return of any character, including character 255 (\(-1\)).
function, the code does allow for the successful return of any character, including character 255 (\(-1\)).
We now have a piece of CakeML abstract syntax given the name  as well as a logical function of the same name operating over values of type
as well as a logical function of the same name operating over values of type  We make the logical
We make the logical  values visible to the CF framework by lifting them into the language of assertions over I/O-extended heaps, using the
values visible to the CF framework by lifting them into the language of assertions over I/O-extended heaps, using the  function defined on page 16. The
function defined on page 16. The  predicate is of type
predicate is of type  A proposition
A proposition  asserts that the state of the external file-system is as given by the logical value
asserts that the state of the external file-system is as given by the logical value 
Our specification for  is given in Fig. 12. When this, and the specifications for the other entry-points have been proved, the verification of cat1 and then cat (see Figs. 1 and 2) proceeds quite straightforwardly. In particular, the low-level specifications ensure that the proofs are oblivious to the fact that I/O through the FFI is involved; instead, they proceed just as if the state of the file-system was a part of memory. The proof of cat1 is by induction on the length of the file still to be read; that of cat by induction on the list of arguments.
is given in Fig. 12. When this, and the specifications for the other entry-points have been proved, the verification of cat1 and then cat (see Figs. 1 and 2) proceeds quite straightforwardly. In particular, the low-level specifications ensure that the proofs are oblivious to the fact that I/O through the FFI is involved; instead, they proceed just as if the state of the file-system was a part of memory. The proof of cat1 is by induction on the length of the file still to be read; that of cat by induction on the list of arguments.
The specification of  The
The  value is the closure defined by the abstract-syntax for
value is the closure defined by the abstract-syntax for  The function
The function  returns the current character designated by the given file descriptor, if any; the function
returns the current character designated by the given file descriptor, if any; the function  increments the position of the file descriptor within its file. At the ML level, file descriptors are encoded as bytes, but the underlying model for file-system uses natural numbers. This is why the logic of the specification coerces from one to the other with
increments the position of the file descriptor within its file. At the ML level, file descriptors are encoded as bytes, but the underlying model for file-system uses natural numbers. This is why the logic of the specification coerces from one to the other with  This is also what causes the pre-condition in
This is also what causes the pre-condition in  ’s specification (Fig. 4) requiring that not too many files be open already.
’s specification (Fig. 4) requiring that not too many files be open already.
6 Discussion of Related Work
The CakeML projects aims to build an extensive ecosystem of verification tools around the CakeML programming language. By adapting CF techniques to the setting of CakeML, this paper has extended the toolset and, at the same time, validated some of the pen-and-paper proofs of prior word on CF. Prior work on CF and CakeML is discussed in Sects. 1.1 and 1.2.
In this section we discuss other verification projects that build ecosystems of verification tools around and within theorem provers such as HOL4, Isabelle/HOL, Coq, Nqthm and ACL2.
In the Isabelle/HOL theorem prover, a substantial ecosystem of verification technology has been developed around the Simpl framework by Schirmer [23], which is an extensible framework for Hoare logic over imperative programs. Simpl played a central role in the seL4 micro-kernel verification [14], where the C code was verified using Simpl. Later, a tool called AutoCorres by Greenaway [12] was developed for automatically lifting C programs written in Simpl into more-convenient-to-verify monadic functions in the logic. The AutoCorres tool and Simpl were subsequently used in the recent proof-producing Cogent compiler [19] for its translation validation step. The Cogent compiler compiles a by-design restrictive functional language to C and produces a correctness theorem in Isabelle/HOL for each compiler run.
The Isabelle Refinement Framework by Lammich [16, 17] is a recent set of tools for producing verified code using the Isabelle/HOL prover. In this work, the Sepref tool can synthesise concrete code from high-level descriptions of imperative algorithms and data structures. Lammich’s work takes a top-down path, in contrast to CF and AutoCorres, and the final translation from code in Isabelle/HOL to code running outside the prover is not proved correct w.r.t. any formal semantics of the target programming language.
In the context of Coq, the Bedrock project [9] lead by Chlipala has developed an impressive ecosystem around a separation-logic-inspired Hoare logic for low-level code. Bedrock connects to FIAT [11], which is a set of tools for performing refinement from high-level declarative specifications to concrete implementations. This technology has been applied to complicated examples such as a web server, database applications and even file systems [8].
The Verified Software Toolchain (VST) [2] from Princeton is another substantial verification framework in Coq. VST defines a C-like language, provides a separation logic on top of this C-like language and maps it into the CompCert C compiler, with proof in Coq relating properties proved at the top to the assembly that CompCert produces.
The CertiCoq project [1] also from Princeton aims to build a proof-producing code extraction mechanism for Coq, which will essentially do for Coq what CakeML’s translator and CakeML compiler already does for HOL.
The Nqthm theorem prover hosted a project in this area that was two or three decades ahead of the field: the “CLI stack” project [3] developed a substantial verification toolchain with a verification-friendly programming language supported by a verified compiler, which targetted a machine language for which the project developed a verified hardware implementation. The logic of the Nqthm prover is a pure first-order functional language but the input language of the verified compiler is not functional.
The recent F* project [25] develops a new dependently-typed monadic language with refinement types. One can use F*’s expressive types to verify programs written in F*. Users can have extra confidence in the results since the typechecker for F* has been verified using Coq [24]. Programs developed in F* can be extracted to OCaml for compilation and execution.
There are many other functional languages with type-systems that allow verification using types. Ynot is one that has been re-implemented in Coq [10].
There are numerous verification ecosystem without connections to the above mentioned theorem provers. Most of these other ecosystems only consider imperative programs. HALO is one such system that applies to functional programs [28]. HALO enables verification of contracts for Haskell programs and uses first-order provers in its implementation.
7 Summary
In this paper, we have explained how to build a fully verified CF framework for the entirety of the CakeML language. We have shown how to add support for I/O and exceptions, as well as interoperability with the CakeML tool used for bootstrapping the verified CakeML compiler.
At a higher level, one can read this paper as a validation that Charguéraud’s original work on CF is flexible as well as extensible.
Notes
- 1.
CakeML’s module system is also supported in our CF framework, but supporting modules did not require extending the original ideas of CFML.
- 2.
To be precise: Myreen and Owens [18] show that the tool can also be used for production of stateful CakeML code that maintains a hard-coded invariant over a hard-coded number of references. CF allows for much more flexibility.
- 3.
We have recently switched to using strings for port names, while numbers were used previously [26] for FFI port names. Johannes Åman Pohjola made this improvement.
- 4.
We would have liked to use a type variable instead of
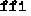 , but a type variable would have been shared between all partitions. Such sharing would need to be done across FFI partitions which goes against the design goal of local specifications and local reasoning. This is a restriction imposed by the HOL type system, which we could have avoided by using a variant of HOL with quantifiers for type variables [13].
, but a type variable would have been shared between all partitions. Such sharing would need to be done across FFI partitions which goes against the design goal of local specifications and local reasoning. This is a restriction imposed by the HOL type system, which we could have avoided by using a variant of HOL with quantifiers for type variables [13]. - 5.
Our use of projection functions and updates at both a concrete and abstract view of the state bears some resemblance to lenses [21]. Note however that lenses must have get and putback functions. Our set up lacks the putback functions, i.e., we only project in one direction. Our initial formalisation had a putback function, but we decided to simplify the definitions and arrived at the current solution with only a get function, which we call
 .
.
References
Anand, A., Appel, A., Morrisett, G., Paraskevopoulou, Z., Pollack, R., Belanger, O.S., Sozeau, M., Weaver, M.: CertiCoq: a verified compiler for Coq. In: The Third International Workshop on Coq for Programming Languages (CoqPL) (2017). http://conf.researchr.org/event/CoqPL-2017/main-certicoq-a-verified-compiler-for-coq
Appel, A.W.: Verified software toolchain. In: Barthe, G. (ed.) ESOP 2011. LNCS, vol. 6602, pp. 1–17. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19718-5_1
Bevier, W.R., Hunt Jr., W.A., Moore, J.S., Young, W.D.: An approach to systems verification. J. Autom. Reason. 5(4), 411–428 (1989). doi:10.1007/BF00243131
Charguéraud, A.: Characteristic formulae for mechanized program verification. Ph.D. thesis, Université Paris-Diderot (2010). http://arthur.chargueraud.org/research/2010/thesis/
Charguéraud, A.: Program verification through characteristic formulae. In: Hudak, P., Weirich, S. (eds.) International Conference on Functional programming (ICFP). ACM (2010)
Charguéraud, A.: Characteristic formulae for the verification of imperative programs. In: Chakravarty, M.M.T., Hu, Z., Danvy, O. (eds.) International Conference on Functional Programming (ICFP). ACM (2011). doi:10.1145/2034773.2034828
Charguéraud, A., Pottier, F.: Machine-checked verification of the correctness and amortized complexity of an efficient union-find implementation. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 137–153. Springer, Heidelberg (2015). doi:10.1007/978-3-319-22102-1_9
Chen, H., Ziegler, D., Chajed, T., Chlipala, A., Kaashoek, M.F., Zeldovich, N.: Using crash hoare logic for certifying the FSCQ file system. In: Gulati, A., Weatherspoon, H. (eds.) USENIX Annual Technical Conference. USENIX Association (2016)
Chlipala, A.: The bedrock structured programming system: combining generative metaprogramming and hoare logic in an extensible program verifier. In: Morrisett, G., Uustalu, T. (eds.) International Conference on Functional Programming (ICFP). ACM (2013). http://doi.acm.org/10.1145/2500365.2500592, doi:10.1145/2500365.2500592
Chlipala, A., Malecha, J.G., Morrisett, G., Shinnar, A., Wisnesky, R.: Effective interactive proofs for higher-order imperative programs. In: Hutton, G., Tolmach, A.P. (eds.) International conference on Functional programming (ICFP). ACM (2009). http://doi.acm.org/10.1145/1596550.1596565, doi:10.1145/1596550.1596565
Delaware, B., Pit-Claudel, C., Gross, J., Chlipala, A.: Fiat: deductive synthesis of abstract data types in a proof assistant. In: Rajamani, S.K., Walker, D., (eds.) Principles of Programming Languages (POPL). ACM (2015). http://doi.acm.org/10.1145/2676726.2677006, doi:10.1145/2676726.2677006
Greenaway, D., Lim, J., Andronick, J., Klein, G.: Don’t sweat the small stuff: formal verification of C code without the pain. In: ACM SIGPLAN Conference on Programming Language Design and Implementation, Edinburgh, UK, pp. 429–439. ACM, June 2014. doi:10.1145/2594291.2594296
Homeier, P.V.: The HOL-omega logic. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 244–259. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_18
Klein, G., Elphinstone, K., Heiser, G., Andronick, J., Cock, D., Derrin, P., Elkaduwe, D., Engelhardt, K., Kolanski, R., Norrish, M., Sewell, T., Tuch, H., Winwood, S.: seL4: formal verification of an OS kernel. In: ACM Symposium on Operating Systems Principles, Big Sky, MT, USA, pp. 207–220. ACM, October 2009
Kumar, R., Myreen, M.O., Norrish, M., Owens, S.: CakeML: a verified implementation of ML. In: Jagannathan, S., Sewell, P. (eds.) Principles of Programming Languages (POPL) (2014). doi:10.1145/2535838.2535841
Lammich, P.: Refinement to imperative/HOL. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 253–269. Springer, Heidelberg (2015). doi:10.1007/978-3-319-22102-1_17
Lammich, P.: Refinement based verification of imperative data structures. In: Avigad, J., Chlipala, A. (eds.) Conference on Certified Programs (CPP). ACM (2016). http://dl.acm.org/citation.cfm?id=2854065, doi:10.1145/2854065.2854067
Myreen, M.O., Owens, S.: Proof-producing translation of higher-order logic into pure and stateful ML. J. Funct. Program. 24(2-3) (2014). doi:10.1017/S0956796813000282
O’Connor, L., Chen, Z., Rizkallah, C., Amani, S., Lim, J., Murray, T.C., Nagashima, Y., Sewell, T., Klein, G.: Refinement through restraint: bringing down the cost of verification. In: Garrigue, J., Keller, G., Sumii, E. (eds.) International Conference on Functional Programming (ICFP). ACM (2016). http://doi.acm.org/10.1145/2951913.2951940, doi:10.1145/2951913.2951940
Owens, S., Myreen, M.O., Kumar, R., Tan, Y.K.: Functional big-step semantics. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 589–615. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49498-1_23
Pierce, B.C.: The weird world of bi-directional programming. ETAPS Invited Talk, March 2006
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: Logic in Computer Science (LICS). IEEE Computer Society (2002)
Schirmer, N.: Verification of sequential imperative programs in Isabelle/HOL. Ph.D. thesis, Technische Universitat Munchen (2006). http://arthur.chargueraud.org/research/2010/thesis/
Strub, P., Swamy, N., Fournet, C., Chen, J.: Self-certification: bootstrapping certified typecheckers in F* with Coq. In: Field, J., Hicks, M. (eds.) Principles of Programming Languages (POPL). ACM (2012). http://doi.acm.org/10.1145/2103656.2103723, doi:10.1145/2103656.2103723
Swamy, N., Hritcu, C., Keller, C., Rastogi, A., Delignat-Lavaud, A., Forest, S., Bhargavan, K., Fournet, C., Strub, P., Kohlweiss, M., Zinzindohoue, J.K., Béguelin, S.Z.: Dependent types and multi-monadic effects in F. In: Bodík, R., Majumdar, R. (eds.) Principles of Programming Languages (POPL). ACM (2016). http://doi.acm.org/10.1145/2837614.2837655, doi:10.1145/2837614.2837655
Tan, Y.K., Myreen, M.O., Kumar, R., Fox, A., Owens, S., Norrish, M.: A new verified compiler backend for CakeML. In: International Conference on Functional Programming (ICFP). ACM Press (2016)
Urban, C., Zhang, X. (eds.): ITP 2015. LNCS, vol. 9236. Springer, Heidelberg (2015)
Vytiniotis, D., Jones, S.L.P., Claessen, K., Rosén, D.: HALO: haskell to logic through denotational semantics. In: Giacobazzi, R., Cousot, R. (eds.) Principles of Programming Languages (POPL). ACM (2013). http://doi.acm.org/10.1145/2429069.2429121, doi:10.1145/2429069.2429121
Acknowledgements
We thank Arthur Charguéraud for advice on characteristic formulae. We thank Mike Gordon and Thomas Sewell for commenting on drafts of this paper. The second author was partially supported by the Swedish Research Council.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Guéneau, A., Myreen, M.O., Kumar, R., Norrish, M. (2017). Verified Characteristic Formulae for CakeML. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_22
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_22
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)












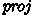 : a projection function of type
: a projection function of type 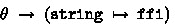 , which given an FFI state of type
, which given an FFI state of type 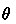 returns a finite map from strings to a new type called
returns a finite map from strings to a new type called  . Here
. Here  is a datatype that is meant to be convenient for modelling projected FFI states in general.
is a datatype that is meant to be convenient for modelling projected FFI states in general.
 : a list of partitions which are pairs: each pair contains a list of FFI port names (of type
: a list of partitions which are pairs: each pair contains a list of FFI port names (of type 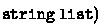 and a behaviour modelling next-state function, i.e., a representation of part of the oracle function in CakeML’s FFI state. The type of the behaviour modelling function is:
and a behaviour modelling next-state function, i.e., a representation of part of the oracle function in CakeML’s FFI state. The type of the behaviour modelling function is: 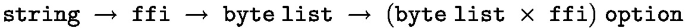
 has not hit a stopping state, i.e.,
has not hit a stopping state, i.e., 
 maps all states to the same
maps all states to the same 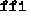 value
value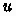 in each partition respects the FFI’s oracle function
in each partition respects the FFI’s oracle function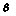 , the projected view of the state of this partition
, the projected view of the state of this partition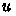 , the update function for the partition
, the update function for the partition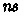 , the FFI port names associated with the partition
, the FFI port names associated with the partition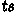 , a list of all previous I/O events for these names.
, a list of all previous I/O events for these names.




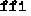 , but a type variable would have been shared between all partitions. Such sharing would need to be done across FFI partitions which goes against the design goal of local specifications and local reasoning. This is a restriction imposed by the HOL type system, which we could have avoided by using a variant of HOL with quantifiers for type variables [
, but a type variable would have been shared between all partitions. Such sharing would need to be done across FFI partitions which goes against the design goal of local specifications and local reasoning. This is a restriction imposed by the HOL type system, which we could have avoided by using a variant of HOL with quantifiers for type variables [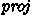 .
.