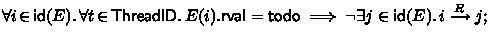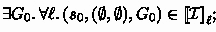Proving Linearizability Using Partial Orders

Abstract

Linearizability is the commonly accepted notion of correctness for concurrent data structures. It requires that any execution of the data structure is justified by a linearization—a linear order on operations satisfying the data structure’s sequential specification. Proving linearizability is often challenging because an operation’s position in the linearization order may depend on future operations. This makes it very difficult to incrementally construct the linearization in a proof.

We propose a new proof method that can handle data structures with such future-dependent linearizations. Our key idea is to incrementally construct not a single linear order of operations, but a partial order that describes multiple linearizations satisfying the sequential specification. This allows decisions about the ordering of operations to be delayed, mirroring the behaviour of data structure implementations. We formalise our method as a program logic based on rely-guarantee reasoning, and demonstrate its effectiveness by verifying several challenging data structures: the Herlihy-Wing queue, the TS queue and the Optimistic set.

1 Introduction

Linearizability is a commonly accepted notion of correctness of concurrent data structures. It matters for programmers using such data structures because it implies contextual refinement: any behaviour of a program using a concurrent data structure can be reproduced if the program uses its sequential implementation where all operations are executed atomically [4]. This allows the programmer to soundly reason about the behaviour of the program assuming a simple sequential specification of the data structure. Linearizability requires that for any execution of operations on the data structure there exists a linear order of these operations, called a linearization, such that: (i) the linearization respects the order of non-overlapping operations (the real-time order); and (ii) the behaviour of operations in the linearization matches the sequential specification of the data structure. To illustrate this, consider an execution in Fig. 1, where three threads are accessing a queue. Linearizability determines which values x the dequeue operation is allowed to return by considering the possible linearizations of this execution. Given (i), we know that in any linearization the enqueues must be ordered before the dequeue, and Enq(1) must be ordered before Enq(3). Given (ii), a linearization must satisfy the sequential specification of a queue, so the dequeue must return the oldest enqueued value. Hence, the execution in Fig. 1 has three possible linearizations: [Enq(1); Enq(2); Enq(3); Deq():1], [Enq(1); Enq(3); Enq(2); Deq():1] and [Enq(2); Enq(1); Enq(3); Deq():2]. This means that the dequeue is allowed to return 1 or 2, but not 3.

Fig. 1.

Example execution.

For a large class of algorithms, linearizability can be proved by incrementally constructing a linearization as the program executes. Effectively, one shows that the program execution and its linearization stay in correspondence under each program step (this is formally known as a forward simulation). The point in the execution of an operation at which it is appended to the linearization is called its linearization point. This must occur somewhere between the start and end of the operation, to ensure that the linearization preserves the real-time order. For example, when applying the linearization point method to the execution in Fig. 1, by point (A) we must have decided if Enq(1) occurs before or after Enq(2) in the linearization. Thus, by this point, we know which of the three possible linearizations matches the execution. This method of establishing linearizability is very popular, to the extent that most papers proposing new concurrent data structures include a placement of linearization points. However, there are algorithms that cannot be proved linerizable using the linearization point method.

In this paper we consider several examples of such algorithms, including the time-stamped (TS) queue [2, 7]—a recent high-performance data structure with an extremely subtle correctness argument. Its key idea is for enqueues to attach timestamps to values, and for these to determine the order in which values are dequeued. As illustrated by the above analysis of Fig. 1, linearizability allows concurrent operations, such as Enq(1) and Enq(2), to take effect in any order. The TS queue exploits this by allowing values from concurrent enqueues to receive incomparable timestamps; only pairs of timestamps for non-overlapping enqueue operations must be ordered. Hence, a dequeue can potentially have a choice of the “earliest” enqueue to take values from. This allows concurrent dequeues to go after different values, thus reducing contention and improving performance.

The linearization point method simply does not apply to the TS queue. In the execution in Fig. 1, values 1 and 2 could receive incomparable timestamps. Thus, at point (A) we do not know which of them will be dequeued first and, hence, in which order their enqueues should go in the linearization: this is only determined by the behaviour of dequeues later in the execution. Similar challenges exist for other queue algorithms such as the baskets queue [12], LCR queue [16] and Herlihy-Wing queue [11]. In all of these algorithms, when an enqueue operation returns, the precise linearization of earlier enqueue operations is not necessarily known. Similar challenges arise in the time-stamped stack [2] algorithm. We conjecture that our proof technique can be applied to prove the time-stamped stack linearizable, and we are currently working on a proof.

In this paper, we propose a new proof method that can handle algorithms where incremental construction of linearizations is not possible. We formalise it as a program logic, based on Rely-Guarantee [13], and apply it to give simple proofs to the TS queue [2], the Herlihy-Wing queue [11] and the Optimistic Set [17]. The key idea of our method is to incrementally construct not a single linearization of an algorithm execution, but an abstract history—a partially ordered history of operations such that it contains the real-time order of the original execution and all its linearizations satisfy the sequential specification. By embracing partiality, we enable decisions about order to be delayed, mirroring the behaviour of the algorithms. At the same time, we maintain the simple inductive style of the standard linearization-point method: the proof of linearizability of an algorithm establishes a simulation between its execution and a growing abstract history. By analogy with linearization points, we call the points in the execution where the abstract history is extended commitment points. The extension can be done in several ways: (1) committing to perform an operation; (2) committing to an order between previously unordered operatons; (3) completing an operation.

Fig. 2.

Abstract histories constructed for prefixes of the execution in Fig. 1: (a) is at point (A); (b) is at the start of the dequeue operation; and (c) is at point (B). We omit the transitive consequences of the edges shown.

Consider again the TS queue execution in Fig. 1. By point (A) we construct the abstract history in Fig. 2(a). The edge in the figure is mandated by the real-time order in the original execution; Enq(1) and Enq(2) are left unordered, and so are Enq(2) and Enq(3). At the start of the execution of the dequeue, we update the history to the one in Fig. 2(b). A dashed ellipse represents an operation that is not yet completed, but we have committed to performing it (case 1 above). When the dequeue successfully removes a value, e.g., 2, we update the history to the one in Fig. 2(c). To this end, we complete the dequeue by recording its result (case 3). We also commit to an order between the Enq(1) and Enq(2) operations (case 2). This is needed to ensure that all linearizations of the resulting history satisfy the sequential queue specification, which requires a dequeue to remove the oldest value in the queue.

We demonstrate the simplicity of our method by giving proofs to challenging algorithms that match the intuition for why they work. Our method is also similar in spirit to the standard linearization point method. Thus, even though in this paper we formulate the method as a program logic, we believe that algorithm designers can also benefit from it in informal reasoning, using abstract histories and commitment points instead of single linearizations and linearization points.

2 Linearizability, Abstract Histories and Commitment Points

Preliminaries. We consider a data structure that can be accessed concurrently via operations $\mathsf{op}\in \mathsf{Op}$ in several threads, identified by $t\in \mathsf{ThreadID}$. Each operation takes one argument and returns one value, both from a set $\mathsf{Val}$; we use a special value $\bot \in \mathsf{Val}$ to model operations that take no argument or return no value. Linearizability relates the observable behaviour of an implementation of such a concurrent data structure to its sequential specification [11]. We formalise both of these by sets of histories, which are partially ordered sets of events, recording operations invoked on the data structure. Formally, an event is of the form $e= [{i}\,{:}\,{(t, \mathsf{op}, a, r)}]$. It includes a unique identifier $i\in \mathsf{EventID}$ and records an operation $\mathsf{op}\in \mathsf{Op}$ called by a thread $t\in \mathsf{ThreadID}$ with an argument $a\in \mathsf{Val}$, which returns a value $r\in \mathsf{Val}\uplus \{ \mathsf{todo}\}$. We use the special return value $\mathsf{todo}$ for events describing operations that have not yet terminated, and call such events uncompleted. We denote the set of all events by $\mathsf{Event}$. Given a set $E\subseteq \mathsf{Event}$, we write $E(i) = (t, \mathsf{op}, a, r)$ if $[{i}\,{:}\,{(t, \mathsf{op}, a, r)}] \in E$ and let $\left\lfloor {E} \right\rfloor$ consist of all completed events from $E$. We let $\mathsf{id}({E})$ denote the set of all identifiers of events from $E$. Given an event identifier $i$, we also use ${E(i)}.\mathsf{tid}$, ${E(i)}.\mathsf{op}$, ${E(i)}.\mathsf{arg}$ and ${E(i)}.\mathsf{rval}$ to refer to the corresponding components of the tuple $E(i)$.

Definition 1

A history¹ is a pair $H= (E, R)$, where $E\subseteq \mathsf{Event}$ is a finite set of events with distinct identifiers and $R\subseteq \mathsf{id}({E}) \times \mathsf{id}({E})$ is a strict partial order (i.e., transitive and irreflexive), called the real-time order. We require that for each $t\in \mathsf{ThreadID}$:

• events in $t$ are totally ordered by $R$:

  

• only maximal events in $R$ can be uncompleted:

  

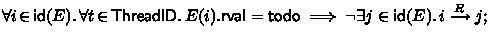
• $R$ is an interval order:

  

We let $\mathsf{History}$ be the set of all histories. A history $(E, R)$ is sequential, written $\mathsf{seq}(E, R)$, if $\mathsf{id}({E}) = \left\lfloor {E} \right\rfloor$ and $R$ is total on $E$.

Informally, ${i} \xrightarrow {R} {j}$ means that the operation recorded by $E(i)$ completed before the one recorded by $E(j)$ started. The real-time order in histories produced by concurrent data structure implementations may be partial, since in this case the execution of operations may overlap in time; in contrast, specifications are defined using sequential histories, where the real-time order is total.

Linearizability. Assume we are given a set of histories that can be produced by a given data structure implementation (we introduce a programming language for implementations and formally define the set of histories an implementation produces in Sect. 5). Linearizability requires all of these histories to be matched by a similar history of the data structure specification (its linearization) that, in particular, preserves the real-time order between events in the following sense: the real-time order of a history $H= (E, R)$ is preserved in a history $H' = (E', R')$, written ${H} \sqsubseteq {H'}$, if $E= E'$ and $R\subseteq R'$.

The full definition of linearizability is slightly more complicated due to the need to handle uncompleted events: since operations they denote have not terminated, we do not know whether they have made a change to the data structure or not. To account for this, the definition makes all events in the implementation history complete by discarding some uncompleted events and completing the remaining ones with an arbitrary return value. Formally, an event $e= [{i}\,{:}\,{(t, \mathsf{op}, a, r)}]$ can be completed to an event $e' = [{i'}\,{:}\,{(t', \mathsf{op}', a', r')}]$, written ${e} \unlhd {e'}$, if $i= i'$, $t= t'$, $\mathsf{op}= \mathsf{op}'$, $a= a'$ and either $r= r' \ne \mathsf{todo}$ or $r' = \mathsf{todo}$. A history $H= (E, R)$ can be completed to a history $H' = (E', R')$, written ${H} \unlhd {H'}$, if $\mathsf{id}({E'}) \subseteq \mathsf{id}({E})$, $\left\lfloor {E} \right\rfloor \subseteq \left\lfloor {E'} \right\rfloor$, $R\cap (\mathsf{id}({E'}) \times \mathsf{id}({E'})) = R'$ and .

Definition 2

A set of histories $\mathcal {H}_1$ (defining the data structure implementation) is linearized by a set of sequential histories $\mathcal {H}_2$ (defining its specification), written $\mathcal {H}_1 \sqsubseteq \mathcal {H}_2$, if $\forall H_1 \in \mathcal {H}_1.\, \exists H_2 \in \mathcal {H}_2.\, \exists H'_1.\, {H_1} \unlhd {H'_1} \wedge {H'_1} \sqsubseteq {H_2}$.

Let $\mathcal {H}_\mathsf{queue}$ be the set of sequential histories defining the behaviour of a queue with $\mathsf{Op}= \{\mathrm{Enq}, \mathrm{Deq}\}$. Due to space constraints, we provide its formal definition in the extended version of this paper [14], but for example, [Enq(2); Enq(1); Enq(3); Deq():2] $\in \mathcal {H}_\mathsf{queue}$ and [Enq(1); Enq(2); Enq(3); Deq():2] $\not \in \mathcal {H}_\mathsf{queue}$.

Proof Method. In general, a history of a data structure ($H_1$ in Definition 2) may have multiple linearizations ($H_2$) satisfying a given specification $\mathcal {H}$. In our proof method, we use this observation and construct a partially ordered history, an abstract history, all linearizations of which belong to $\mathcal {H}$.

Definition 3

A history $H$ is an abstract history of a specification given by the set of sequential histories $\mathcal {H}$ if $\{H' \mid \lfloor H\rfloor \sqsubseteq H' \wedge \mathsf{seq}(H')\} \subseteq \mathcal {H}$, where $\left\lfloor {(E, R)} \right\rfloor = (\left\lfloor {E} \right\rfloor , R\cap (\mathsf{id}({\left\lfloor {E} \right\rfloor }) \times \mathsf{id}({\left\lfloor {E} \right\rfloor })))$. We denote this by $\mathsf{abs}(H, \mathcal {H})$.

We define the construction of an abstract history $H= (E, R)$ by instrumenting the data structure operations with auxiliary code that updates the history at certain commitment points during operation execution. There are three kinds of commitment points:

• 1. When an operation $\mathsf{op}$ with an argument a starts executing in a thread t, we extend E by a fresh event $[i: (t, \mathsf{op}, a, \mathsf{todo})]$, which we order in R after all events in $\left\lfloor {E} \right\rfloor$.

• 2. At any time, we can add more edges to R.

• 3. By the time an operation finishes, we have to assign its return value to its event in E.

Note that, unlike Definitions 2 and 3 uses a particular way of completing an abstract history $H$, which just discards all uncompleted events using $\lfloor - \rfloor$. This does not limit generality because, when constructing an abstract history, we can complete an event (item 3) right after the corresponding operation makes a change to the data structure, without waiting for the operation to finish.

In Sect. 6 we formalise our proof method as a program logic and show that it indeed establishes linearizability. Before this, we demonstrate informally how the obligations of our proof method are discharged on an example.

Fig. 3.

Operations on abstract SP pools $\mathtt{pools}: \mathsf{ThreadID}\rightarrow \mathsf{Pool}$. All operations are atomic.

3 Running Example: The Time-Stamped Queue

We use the TS queue [7] as our running example. Values in the queue are stored in per-thread single-producer (SP) multi-consumer pools, and we begin by describing this auxiliary data structure.

SP Pools. SP pools have well-known linearizable implementations [7], so we simplify our presentation by using abstract pools with the atomic operations given in Fig. 3. This does not limit generality: since linerarizability implies contextual refinement (Sect. 1), properties proved using the abstract pools will stay valid for their linearizable implementations. In the figure and in the following we denote irrelevant expressions by $\_$.

Fig. 4.

The TS queue: enqueue. Shaded portions are auxiliary code used in the proof.

The SP pool of a thread contains a sequence of triples $(p, v, \tau )$, each consisting of a unique identifier $p\in \mathsf{PoolID}$, a value $v \in \mathsf{Val}$ enqueued into the TS queue by the thread and the associated timestamp $\tau \in \mathsf{TS}$. The set of timestamps $\mathsf{TS}$ is partially ordered by $\mathrel {{} <_\mathsf{TS} {}}$, with a distinguished timestamp $\top$ that is greater than all others. We let $\mathtt{pool}$ be the set of states of an abstract SP pool. Initially all pools are empty. The operations on SP pools are as follows:

• insert(t,v) appends a value v to the back of the pool of thread t and associates it with the special timestamp $\top$; it returns an identifier for the added element.

• setTimestamp(t,p,$\tau$) sets to $\tau$ the timestamp of the element identified by p in the pool of thread t.

• getOldest(t) returns the identifier and timestamp of the value from the front of the pool of thread t, or $(\mathrm{NULL}, \mathrm{NULL})$ if the pool is empty.

• remove(t,p) tries to remove a value identified by p from the pool of thread t. Note this can fail if some other thread removes the value first.

Separating insert from setTimestamp and getOldest from remove in the SP pool interface reduces the atomicity granularity, and permits more efficient implementations.

Fig. 5.

The TS queue: dequeue. Shaded portions are auxiliary code used in the proof.

Core TS Queue Algorithm. Figures 4 and 5 give the code for our version of the TS queue. Shaded portions are auxiliary code needed in the linearizability proof to update the abstract history at commitment points; it can be ignored for now. In the overall TS queue, enqueuing means adding a value with a certain timestamp to the pool of the current thread, while dequeuing means searching for the value with the minimal timestamp across per-thread pools and removing it.

In more detail, the $\mathtt{enqueue}(v)$ operation first inserts the value v into the pool of the current thread, defined by myTid (line 3). At this point the value v has the default, maximal timestamp $\top$. The code then generates a new timestamp using newTimestamp and sets the timestamp of the new value to it (lines 6–8). We describe an implementation of newTimestamp later in this section. The key property that it ensures is that out of two non-overlapping calls to this function, the latter returns a higher timestamp than the former; only concurrent calls may generate incomparable timestamps. Hence, timestamps in each pool appear in the ascending order.

The $\mathtt{dequeue}$ operation first generates a timestamp $\mathtt{start\_ts}$ at line 18, which it further uses to determine a consistent snapshot of the data structure. After generating $\mathtt{start\_ts}$, the operation iterates through per-thread pools, searching for a value with a minimal timestamp (lines 22–33). The search starts from a random pool, to make different threads more likely to pick different elements for removal and thus reduce contention. The pool identifier of the current candidate for removal is stored in $\mathtt{cand\_pid}$, its timestamp in $\mathtt{cand\_ts}$ and the thread that inserted it in $\mathtt{cand\_tid}$. On each iteration of the loop, the code fetches the earliest value enqueued by thread $\mathtt{k}$ (line 24) and checks whether its timestamp is smaller than the current candidate’s $\mathtt{cand\_ts}$ (line 27). If the timestamps are incomparable, the algorithm keeps the first one (either would be legitimate). Additionally, the algorithm never chooses a value as a candidate if its timestamp is greater than $\mathtt{start\_ts}$, because such values are not guaranteed to be read in a consistent manner.

If a candidate has been chosen once the iteration has completed, the code tries to remove it (line 35). This may fail if some other thread got there first, in which case the operation restarts. Likewise, the algorithm restarts if no candidate was identified (the full algorithm in [7] includes an emptiness check, which we omit for simplicity).

Timestamp Generation. The TS queue requires that sequential calls to newTimestamp generate ordered timestamps. This ensures that the two sequentially enqueued values cannot be dequeued out of order. However, concurrent calls to newTimestamp may generate incomparable timestamps. This is desirable because it increases flexibility in choosing which value to dequeue, reducing contention.

Fig. 6.

Timestamp generation algorithm.

There are a number of implementations of newTimestamp satisfying the above requirements [2]. For concreteness, we consider the implementation given in Fig. 6. Here a timestamp is either $\top$ or a pair of integers (s, e), representing a time interval. In every timestamp (s, e), $s \le e$. Two timestamps are considered ordered $(s_1, e_1) \mathrel {{} <_\mathsf{TS} {}}(s_2, e_2)$ if $e_1 < s_2$, i.e., if the time intervals do not overlap. Intervals are generated with the help of a shared $\mathtt{counter}$. The algorithm reads the counter as the start of the interval and attempts to atomically increment it with a CAS (lines 40–42), which is a well-known atomic compare-and-swap operation. It atomically reads the counter and, if it still contains the previously read value ts, updates it with the new timestamp $\mathtt{ts}+1$ and returns $\mathsf{true}$; otherwise, it does nothing and returns $\mathsf{false}$. If CAS succeeds, then the algorithm takes the interval start and end values as equal (line 43). If not, some other thread(s) increased the counter. The algorithm reads the counter again and subtracts 1 to give the end of the interval (line 45). Thus, either the current call to newTimestamp increases the counter, or some other thread does so. In either case, subsequent calls will generate timestamps greater than the current one.

This timestamping algorithm allows concurrent enqueue operations in Fig. 1 to get incomparable timestamps. Then the dequeue may remove either 1 or 2 depending on where it starts traversing the pools² (line 22). As we explained in Sect. 1, this makes the standard method of linearization point inapplicable for verifying the TS queue.

4 The TS Queue: Informal Development

In this section we explain how the abstract history is updated at the commitment points of the TS Queue and justify informally why these updates preserve the key property of this history—that all its linearizations satisfy the sequential queue specification. We present the details of the proof of the TS queue in Sect. 7.

Ghost State and Auxiliary Definitions. To aid in constructing the abstract history $(E, R)$, we instrument the code of the algorithm to maintain a piece of ghost state—a partial function $G_\mathsf{ts}: \mathsf{EventID}\rightharpoonup \mathsf{TS}$. Given the identifier $i$ of an event $E(i)$ denoting an $\mathtt{enqueue}$ that has inserted its value into a pool, $G_\mathsf{ts}(i)$ gives the timestamp currently associated with the value. The statements in lines 4 and 9 in Fig. 4 update $G_\mathsf{ts}$ accordingly. These statements use a special command $\mathtt{myEid}()$ that returns the identifier of the event associated with the current operation.

As explained in Sect. 3, the timestamps of values in each pool appear in strictly ascending order. As a consequence, all timestamps assigned by $G_\mathsf{ts}$ to events of a given thread $t$ are distinct, which is formalised by the following property:

Hence, for a given thread $t$ and a timestamp $\tau$, there is at most one enqueue event in $E$ that inserted a value with the timestamp $\tau$ in the pool of a thread $t$. In the following, we denote the identifier of this event by $\mathtt{enqOf}(E, G_\mathsf{ts}, t, \tau )$ and let the set of the identifiers of such events for all values currently in the pools be $\mathsf{inQ}({\mathtt{pools}, E, G_\mathsf{ts}})$:

Commitment Points and History Updates. We further instrument the code with statements that update the abstract history at commitment points, which we now explain. As a running example, we use the execution in Fig. 7, extending that in Fig. 1. As we noted in Sect. 2, when an operations starts, we automatically add a new uncompleted event to E to represent this operation and order it after all completed events in $R$. For example, before the start of Enq(3) in the execution of Fig. 7, the abstract history contains two events Enq(1) and Enq(2) and no edges in the real-time order. At the start of Enq(3) the history gets transformed to that in Fig. 8(a). The commitment point at line 8 in Fig. 4 completes the enqueue by giving it a return value $\bot$, which results in the abstract history in Fig. 8(b).

Fig. 7.

Example execution extending Fig. 1. Dotted lines indicate commitment points at lines 35–43 of the dequeues.

Fig. 8.

Changes to the abstract history of the execution in Fig. 7.

Upon a dequeue’s start, we similarly add an event representing it. Thus, by point (A) in Fig. 7, the abstract history is as shown in Fig. 8(c). At every iteration $\mathtt{k}$ of the loop, the dequeue performs a commitment point at lines 25–26, where we order enqueue events of values currently present in the pool of a thread $\mathtt{k}$ before the current dequeue event. Specifically, we add an edge $(e, \mathtt{myEid}())$ for each identifier e of an enqueue event whose value is in the $\mathtt{k}$’s pool and whose timestamp is not greater than the dequeue’s own timestamp $\mathtt{start\_ts}$. Such ordering ensures that in all linearizations of the abstract history, the values that the current dequeue observes in the pool according to the algorithm are also enqueued in the sequential queue prior to the dequeue. In particular, this also ensures that in all linearizations, the dequeue returns a value that has already been inserted.

The key commitment point in dequeue occurs in lines 35–43, where the abstract history is updated if the dequeue successfully removes a value from a pool. The ghost code at line 31 stores the event identifier for the enqueue that inserted this value in $\mathtt{CAND}$. At the commitment point we first complete the current dequeue event by assigning the value removed from a pool as its return value. This ensures that the dequeue returns the same value in the concrete execution and the abstract history. Finally, we order events in the abstract history to ensure that all linearizations of the abstract history satisfy the sequential queue specification. To this end, we add the following edges to $R$ and then transitively close it:

• 1. $(\mathtt{CAND}, e)$ for each identifier e of an enqueue event whose value is still in the pools. This ensures that the dequeue removes the oldest value in the queue.

• 2. $(\mathtt{myEid}(), d)$ for each identifier d of an uncompleted dequeue event. This ensures that dequeues occur in the same order as they remove values from the queue.

At the commitment point (A) in Fig. 7 the abstract history gets transformed from the one in Fig. 8(c) to the one in Fig. 8(d).

5 Programming Language

To formalise our proof method, we first introduce a programming language for data structure implementations. This defines such implementations by functions $D: \mathsf{Op}\rightarrow \mathsf{Com}$ mapping operations to commands from a set $\mathsf{Com}$. The commands, ranged over by C, are written in a simple while-language, which includes atomic commands $\alpha$ from a set $\mathsf{PCom}$ (assignment, CAS, etc.) and standard control-flow constructs. To conserve space, we describe the precise syntax in the extended version of this paper [14].

Let $\mathsf{Loc}\subseteq \mathsf{Val}$ be the set of all memory locations. We let $\mathsf{State}= \mathsf{Loc}\rightarrow \mathsf{Val}$ be the set of all states of the data structure implementation, ranged over by s. Recall from Sect. 2 that operations of a data structure can be called concurrently in multiple threads from $\mathsf{ThreadID}$. For every thread $t$, we use distinguished locations $\mathtt{arg}[t], \mathtt{res}[t] \in \mathsf{Loc}$ to store an argument, respectively, the return value of an operation called in this thread.

We assume the semantics of each atomic command $\alpha \in \mathsf{PCom}$ given by a non-deterministic state transformers ${[\![}\alpha {]\!]}_t: \mathsf{State}\rightarrow \mathcal {P}({\mathsf{State}}), t\in \mathsf{ThreadID}$. For a state $s$, $[\![{\alpha } ]\!]_{t} ({s})$ is the set of states resulting from thread $t$ executing $\alpha$ atomically in $s$. We then lift this semantics to a sequential small-step operational semantics of arbitrary commands from $\mathsf{Com}$: $\langle {C}, {s} \rangle \mathrel {{\longrightarrow }_{t}} \langle {C'}, {s'} \rangle$. Again, we omit the standard rules of the semantics; see [14].

We now define the set of histories produced by a data structure implementation $D$, which is required by the definition of linearizability (Definition 2, Sect. 2). Informally, these are the histories produced by threads repeatedly invoking data structure operations in any order and with any possible arguments (this can be thought of as running the data structure implementation under its most general client [6]). We define this formally using a concurrent small-step semantics of the data structure D that also constructs corresponding histories: ${\twoheadrightarrow }_{D} \subseteq (\mathsf{Cont}\times \mathsf{State}\times \mathsf{History})^2$, where $\mathsf{Cont}= \mathsf{ThreadID}\rightarrow (\mathsf{Com}\uplus \{\mathsf{idle}\})$. Here a function $c\in \mathsf{Cont}$ characterises the progress of an operation execution in each thread $t$: $c(t)$ gives the continuation of the code of the operation executing in thread $t$, or $\mathsf{idle}$ if no operation is executing. The relation ${\twoheadrightarrow }_{D}$ defines how a step of an operation in some thread transforms the data structure state and the history:

$$ \begin{array}{@{}c@{}} \genfrac{}{}{0.5pt}{}{\displaystyle i\notin \mathsf{id}({E}) \quad a\in \mathsf{Val}\quad E' = E[{i}\,{:}\,{(t, \mathsf{op}, a, \mathsf{todo})}] \quad R' = R\cup \{ (j, i) \mid j\in \left\lfloor {E} \right\rfloor \} }{\displaystyle \langle {c[{t}\,{:}\,{\mathsf{idle}}], s, (E, R)} \rangle \mathrel {{\twoheadrightarrow }_{D}} \langle {c[{t}\,{:}\,{D(\mathsf{op})}], s[{\mathtt{arg}[t]}\,{:}\,{a}], (E', R')} \rangle } \\[10pt] \genfrac{}{}{0.5pt}{}{\displaystyle \langle {C}, {s} \rangle \mathrel {{\longrightarrow }_{t}} \langle {C'}, {s'} \rangle }{\displaystyle \langle {c[{t}\,{:}\,{C}], s, (E, R)} \rangle \mathrel {{\twoheadrightarrow }_{D}} \langle {c[{t}\,{:}\,{C'}], s', (E, R)} \rangle } \\[10pt] \genfrac{}{}{0.5pt}{}{\displaystyle i= \mathsf{last}(t, (E, R)) \quad E(i) = (t, \mathsf{op}, a, \mathsf{todo}) \quad E' = E[{i}\,{:}\,{(t, \mathsf{op}, a, s(\mathtt{res}[t]))}] }{\displaystyle \langle {c[{t}\,{:}\,{\mathsf{skip}}], s, (E, R)} \rangle \mathrel {{\twoheadrightarrow }_{D}} \langle {c[{t}\,{:}\,{\mathsf{idle}}], s, (E', R)} \rangle } \end{array} $$

First, an idle thread $t$ may call any operation $\mathsf{op}\in \mathsf{Op}$ with any argument $a$. This sets the continuation of thread $t$ to $D(\mathsf{op})$, stores $a$ into $\mathtt{arg}[t]$, adds a new event i to the history, ordered after all completed events. Second, a thread $t$ executing an operation may do a transition allowed by the sequential semantics of the operation’s implementation. Finally, when a thread $t$ finishes executing an operation, as denoted by a continuation $\mathsf{skip}$, the corresponding event is completed with the return value in $\mathtt{res}[t]$. The identifier $\mathsf{last}(t, (E, R))$ of this event is determined as the last one in E by thread t according to R: as per Definition 1, events by each thread are totally ordered in a history, ensuring that $\mathsf{last}(t, H)$ is well-defined.

Now given an initial state $s_0 \in \mathsf{State}$, we define the set of histories of a data structure $D$ as . We say that a data structure $(D, s_0)$ is linearizable with respect to a set of sequential histories $\mathcal {H}$ if $\mathcal {H}(D, s_0) \sqsubseteq \mathcal {H}$ (Definition 2).

6 Logic

We now formalise our proof method as a Hoare logic based on rely-guarantee [13]. We make this choice to keep presentation simple; our method is general and can be combined with more advanced methods for reasoning about concurrency [1, 20, 22].

Assertions $P, Q \in \mathsf{Assn}$ in our logic denote sets of configurations $\kappa \in \mathsf{Config}= \mathsf{State}\times \mathsf{History}\times \mathsf{Ghost}$, relating the data structure state, the abstract history and the ghost state from a set $\mathsf{Ghost}$. The latter can be chosen separately for each proof; e.g., in the proof of the TS queue in Sect. 4 we used $\mathsf{Ghost}= \mathsf{EventID}\rightarrow \mathsf{TS}$. We do not prescribe a particular syntax for assertions, but assume that it includes at least the first-order logic, with a set $\mathsf{LVars}$ of special logical variables used in specifications and not in programs. We assume a function ${[\![}{-}{]\!]}_{-} : \mathsf{Assn}\times (\mathsf{LVars}\rightarrow \mathsf{Val}) \rightarrow \mathcal {P}({\mathsf{Config}})$ such that ${[\![}{P}{]\!]}_{\ell }$ gives the denotation of an assertion P with respect to an interpretation $\ell : \mathsf{LVars}\rightarrow \mathsf{Val}$ of logical variables.

Rely-guarantee is a compositional verification method: it allows reasoning about the code executing in each thread separately under some assumption on its environment, specified by a rely. In exchange, the thread has to ensure that its behaviour conforms to a guarantee. Accordingly, judgements of our logic take the form ${\mathcal {R}, \mathcal {G}} \vdash _{t} \left\{ P \right\} \, {C}\,\left\{ Q\right\}$, where $C$ is a command executing in thread t, $P$ and $Q$ are Hoare pre- and post-conditions from $\mathsf{Assn}$, and $\mathcal {R}, \mathcal {G}\subseteq \mathsf{Config}^2$ are relations defining the rely and the guarantee. Informally, the judgement states that $C$ satisfies the Hoare specification $\{P\} \_ \{Q\}$ and changes program configurations according to $\mathcal {G}$, assuming that concurrent threads change program configurations according to $\mathcal {R}$.

Fig. 9.

Proof rule for primitive commands.

Our logic includes the standard Hoare proof rules for reasoning about sequential control-flow constructs, which we defer to [14] due to space constraints. We now explain the rule for atomic commands in Fig. 9, which plays a crucial role in formalising our proof method. The proof rule derives judgements of the form ${\mathcal {R}, \mathcal {G}} \vdash _{t} \left\{ P \right\} \, {\alpha }\,\left\{ Q\right\}$. The rule takes into account possible interference from concurrent threads by requiring the denotations of $P$ and $Q$ to be stable under the rely $\mathcal {R}$, meaning that they are preserved under transitions the latter allows. The rest of the requirements are expressed by the judgement ${\mathcal {G}}\vDash _{t} \left\{ p \right\} \,{\alpha }\, \left\{ q \right\}$. This requires that for any configuration $(s, H, G)$ from the precondition denotation p and any data structure state $s'$ resulting from thread $t$ executing $\alpha$ in $s$, we can find a history $H'$ and a ghost state $G'$ such that the new configuration $(s', H', G')$ belongs to the postcondition denotation q. This allows updating the history and the ghost state (almost) arbitrarily, since these are only part of the proof and not of the actual data structure implementation; the shaded code in Figs. 4 and 5 indicates how we perform these updates in the proof of the TS queue. Updates to the history, performed when $\alpha$ is a commitment point, are constrained by a relation ${\leadsto } \subseteq \mathsf{History}^2$, which only allows adding new edges to the real-time order or completing events with a return value. This corresponds to commitment points of kinds 2 and 3 from Sect. 2. Finally, as is usual in rely-guarantee, the judgement ${\mathcal {G}}\vDash _{t} \left\{ p \right\} \,{\alpha }\, \left\{ q \right\}$ requires that the change to the program configuration be allowed by the guarantee $\mathcal {G}$.

Note that ${\leadsto }$ does not allow adding new events into histories (commitment point of kind 1): this happens automatically when an operation is invoked. In the following, we use a relation ${\dashrightarrow }_t\subseteq \mathsf{Config}^2$ to constrain the change to the program configuration upon an operation invocation in thread t:

Thus, when an operation is invoked in thread $t$, $\mathtt{arg}[t]$ is overwritten by the operation argument and an uncompleted event associated with thread $t$ and a new identifier $i$ is added to the history; this event is ordered after all completed events, as required by our proof method (Sect. 2).

The rule for primitive commands and the standard Hoare logic proof rules allow deriving judgements about the implementations $D(\mathsf{op})$ of every operation $\mathsf{op}$ in a data structure $D$. The following theorem formalises the requirements on these judgements sufficient to conclude the linearizability of $D$ with respect to a given set of sequential histories $\mathcal {H}$. The theorem uses the following auxiliary assertions, describing the event corresponding to the current operation $\mathsf{op}$ in a thread $t$ at the start and end of its execution ($\mathsf{last}$ is defined in Sect. 5):

The assertion $\mathrm{started}_{\mathcal {I}}(t, \mathsf{op})$ is parametrised by a global invariant $\mathcal {I}$ used in the proof. With the help of it, $\mathrm{started}_{\mathcal {I}}(t, \mathsf{op})$ requires that configurations in its denotation be results of adding a new event into histories satisfying $\mathcal {I}$.

Theorem 1

Given a data structure $D$, its initial state $s_0 \in \mathsf{State}$ and a set of sequential histories $\mathcal {H}$, we have $(D, s_0)$ linearizable with respect to $\mathcal {H}$ if there exists an assertion $\mathcal {I}$ and relations $\mathcal {R}_{t}, \mathcal {G}_{t} \subseteq \mathsf{Config}^2$ for each $t\in \mathsf{ThreadID}$ such that:

• 1.

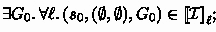
• 2. $\forall t, \ell . \, \mathsf{stable}({[\![}{\mathcal {I}}{]\!]}_{\ell }, \mathcal {R}_t);$

• 3.

• 4. $\forall t, \mathsf{op}.\, ( {\mathcal {R}_t, \mathcal {G}_t} \vdash _{t} \left\{ \begin{array}{@{}c@{}} \mathcal {I} \wedge \mathrm{started}_{\mathcal {I}}(t, \mathsf{op}) \end{array} \right\} \, {D(\mathsf{op})}\,\left\{ \begin{array}{@{}c@{}} \mathcal {I} \wedge \mathrm{ended}(t, \mathsf{op}) \end{array}\right\} )$;

• 5. $\forall t, t'.\, t\ne t' \implies \mathcal {G}_{t} \cup {\dashrightarrow }_{t} \subseteq \mathcal {R}_{t'}$.

Here $\mathcal {I}$ is the invariant used in the proof, which item 1 requires to hold of the initial data structure state $s_0$, the empty history and some some initial ghost state $G_0$. Item 2 then ensures that the invariant holds at all times. Item 3 requires any history satisfying the invariant to be an abstract history of the given specification $\mathcal {H}$ (Definition 3, Sect. 2). Item 4 constraints the judgement about an operation $\mathsf{op}$ executed in a thread t: the operation is executed from a configuration satisfying the invariant and with a corresponding event added to the history; by the end of the operation’s execution, we need to complete the event with the return value matching the one produced by the code. Finally, item 5 formalises a usual requirement in rely-guarantee reasoning: actions allowed by the guarantee of a thread $t$ have to be included into the rely of any other thread $t'$. We also include the relation ${\dashrightarrow }_t$, describing the automatic creation of a new event upon an operation invocation in thread t.

Fig. 10.

The invariant $\mathsf{INV}= \mathsf{INV}_\mathsf{LIN}\wedge \mathsf{INV}_\mathsf{ORD}\wedge \mathsf{INV}_\mathsf{ALG}\wedge \mathsf{INV}_\mathsf{WF}$

7 The TS Queue: Proof Details

In this section, we present some of the details of the proof of the TS Queue. Due to space constraints, we provide the rest of them in the extended version of the paper [14].

Invariant. We satisfy the obligation 1 from Theorem 1 by proving the invariant $\mathsf{INV}$ defined in Fig. 10. The invariant is an assertion consisting of four parts: $\mathsf{INV}_\mathsf{LIN}$, $\mathsf{INV}_\mathsf{ORD}$, $\mathsf{INV}_\mathsf{ALG}$ and $\mathsf{INV}_\mathsf{WF}$. Each of them denotes a set of configurations satisfying the listed constraints for a given interpretation of logical variables $\ell$. The first part of the invariant, $\mathsf{INV}_\mathsf{LIN}$, ensures that every history satisfying the invariant is an abstract history of the queue, which discharges the obligation 1 from Theorem 1. In addition to that, $\mathsf{INV}_\mathsf{LIN}$ requires that a relation $\mathsf{same\_data}$ hold of a configuration $(s, H, G_\mathsf{ts})$ and every linearization $H'$. In this way, we ensure that the pools and the final state of the sequential queue after $H'$ contain values inserted by the same enqueue events (we formalise $\mathsf{same\_data}$ in [14]). The second part, $\mathsf{INV}_\mathsf{ORD}$, asserts ordering properties of events in the partial order that hold by construction. The third part, $\mathsf{INV}_\mathsf{ALG}$, is a collection of properties relating the order on timestamps to the partial order in abstract history. Finally, $\mathsf{INV}_\mathsf{WF}$ is a collection of well-formedness properties of the ghost state.

Loop Invariant. We now present the key verification condition that arises in the dequeue operation: demonstrating that the ordering enforced at the commitment points at lines 25–26 and 35–43 does not invalidate acyclicity of the abstract history. To this end, for the foreach loop (lines 22–33) we build a loop invariant based on distinguishing certain values in the pools as seen by the dequeue operation. With the help of the loop invariant we establish that acyclicity is preserved at the commitment points.

Recall from Sect. 3, that the foreach loop starts iterating from a random pool. In the proof, we assume that the loop uses a thread-local variable $\mathtt{A}$ for storing a set of identifiers of threads that have been iterated over in the loop. We also assume that at the end of each iteration the set $\mathtt{A}$ is extended with the current loop index $\mathtt{k}$.

Note also that for each thread $\mathtt{k}$, the commitment point of a dequeue d at lines 25–26 ensures that enqueue events of values the operation sees in $\mathtt{k}$’s pool precede d in the abstract history. Based on that, during the foreach loop we can we distinguish enqueue events with values in the pools that a dequeue d has seen after looking into pools of threads from $\mathtt{A}$. We define the set of all such enqueue events as follows:

A loop invariant $\mathsf{LI}$ is simply a disjunction of two auxiliary assertions, $\mathrm{isCand}$ and $\mathrm{noCand}$, which are defined in Fig. 11 (given an interpretation of logical variables $\ell$, each of assertions denotes a set of configurations satisfying the listed constraints). The assertion $\mathrm{noCand}$ denotes a set of configurations $\kappa = (s, (E, R), G_\mathsf{ts})$, in which the dequeue operation has not chosen a candidate for removal after having iterated over the pools of threads from $\mathtt{A}$. In this case, $s(\mathtt{cand\_pid}) = \mathrm{NULL}$, and the current dequeue has not seen any enqueue event in the pools of threads from $\mathtt{A}$.

Fig. 11.

Auxiliary assertions for the loop invariant

The assertion $\mathrm{isCand}$ denotes a set of configurations $\kappa = (s, (E, R), G_\mathsf{ts})$, in which an enqueue event $\mathtt{CAND}= \mathtt{enqOf}(E, G_\mathsf{ts}, \mathtt{cand\_tid}, \mathtt{cand\_ts})$ has been chosen as a candidate for removal out of the enqueues seen in the pools of threads from $\mathtt{A}$. As $\mathtt{CAND}$ may be removed by a concurrent dequeue, $\mathrm{isCand}$ requires that $\mathtt{CAND}$ remain in the set $\mathsf{seen}(\kappa , \mathtt{myEid}())$ as long as $\mathtt{CAND}$’s value remains in the pools. Additionally, by requiring $\mathrm{minTS}(\mathtt{CAND})$, $\mathrm{isCand}$ asserts that the timestamp of $\mathtt{CAND}$ is minimal among other enqueues seen by $\mathtt{myEid}()$.

In the following lemma, we prove that the assertion $\mathrm{isCand}$ implies minimality of $\mathtt{CAND}$ in the abstract history among enqueue events with values in the pools of threads from $\mathtt{A}$. The proof is based on the observation that enqueues of values seen in the pools by a dequeue are never preceded by unseen enqueues.

Lemma 1

For every $\ell : \mathsf{LVars}\rightarrow \mathsf{Val}$ and configuration $(s, (E, R), G_\mathsf{ts}) \in {[\![}{\mathrm{isCand}}{]\!]}_{\ell }$, if $\mathtt{CAND}= \mathtt{enqOf}(E, G_\mathsf{ts}, \mathtt{cand\_tid}, \mathtt{cand\_ts})$ and $\mathtt{CAND}\in \mathsf{inQ}({s(\mathtt{pools}), E, G_\mathsf{ts}})$ both hold, then the following is true:

Acyclicity. At the commitment points extending the order of the abstract history, we need to show that the extended order is acyclic as required by Definition 1 of the abstract history. To this end, we argue that the commitment points at lines 25–26 and lines 35–43 preserve acyclicity of the abstract history.

The commitment point at lines 25–26 orders certain completed enqueue events before the current uncompleted dequeue event $\mathtt{myEid}()$. By Definition 1 of the abstract history, the partial order on its events is transitive, and uncompleted events do not precede other events. Since $\mathtt{myEid}()$ does not precede any other event, ordering any completed enqueue event before $\mathtt{myEid}()$ cannot create a cycle in the abstract history.

We now consider the commitment point at lines 35–43 in the current dequeue $\mathtt{myEid}()$. Prior to the commitment point, the loop invariant $\mathsf{LI}$ has been established in all threads, and the check $\mathtt{cand\_pid}\ne \mathrm{NULL}$ at line 34 has ruled out the case when $\mathrm{noCand}$ holds. Thus, the candidate for removal $\mathtt{CAND}$ has the properties described by $\mathrm{isCand}$. If $\mathtt{CAND}$’s value has already been dequeued concurrently, the removal fails, and the abstract history remains intact (and acyclic). When the removal succeeds, we consider separately the two kind of edges added into the abstract history $(E, R)$:

• 1. The case of $(\mathtt{CAND}, e)$ for each $e \in \mathsf{inQ}({\mathtt{pools}, E, G_\mathsf{ts}})$. By Lemma 1, an edge $(e, \mathtt{CAND})$ is not in the partial order $R$ of the abstract history. There is also no sequence of edges ${{e} \xrightarrow {R} {...}} \xrightarrow {R} {\mathtt{CAND}}$, since $R$ is transitive by Definition 1. Hence, cycles do not arise from ordering $\mathtt{CAND}$ before e.

• 2. The case of $(\mathtt{myEid}(), d)$ for each identifier d of an uncompleted dequeue event. By Definition 1 of the abstract history, uncompleted events do not precede other events. Since d is uncompleted event, it does not precede $\mathtt{myEid}()$. Hence, ordering $\mathtt{myEid}()$ in front of all such dequeue events does not create cycles.

Rely and Guarantee Relations. We now explain how we generate rely and guarantee relations for the proof. Instead of constructing the relations with the help of abstracted intermediate assertions of a proof outline for the enqueue and dequeue operations, we use the non-deterministic state transformers of primitive commands together with the ghost code in Figs. 4 and 5. To this end, the semantics of state transformers is extended to account for changes to abstract histories and ghost state. We found that generating rely and guarantee relations in such non-standard way results in cleaner stability proofs for the TS Queue, and makes them similar in style to checking non-interference in the Owicki-Gries method [18].

Let us refer to atomic blocks with corresponding ghost code at line 3, line 8, line 25 and line 35 as atomic steps insert, setTS, scan(k) ($\mathtt{k} \in \mathsf{ThreadID}$) and remove respectively, and let us also refer to the CAS operation at line 42 as genTS. For each thread $t$ and atomic step $\hat{\alpha }$, we assume a non-deterministic configuration transformer ${[\![}\hat{\alpha }{]\!]}_t: \mathsf{Config}\rightarrow \mathcal {P}({\mathsf{Config}})$ that updates state according to the semantics of a corresponding primitive command, and history with ghost state as specified by ghost code.

Given an assertion P, an atomic step $\hat{\alpha }$ and a thread $t$, we associate them with the following relation $\mathcal {G}_{t,\hat{\alpha },P} \subseteq \mathsf{Config}^2$:

Additionally, we assume a relation $\mathcal {G}_{t, \mathtt{local}}$, which describes arbitrary changes to certain program variables and no changes to the abstract history and the ghost state. That is, we say that pools and counter are shared program variables in the algorithm, and all others are thread-local, in the sense that every thread has its own copy of them. We let $\mathcal {G}_{t, \mathtt{local}}$ denote every possible change to thread-local variables of a thread $t$ only.

For each thread $t$, relations $\mathcal {G}_t$ and $\mathcal {R}_t$ are defined as follows:

As required by Theorem 1, the rely relation of a thread $t$ accounts for addition of new events in every other thread $t'$ by including ${\dashrightarrow }_t'$. Also, $\mathcal {R}_{t}$ takes into consideration every atomic step by the other threads. Thus, the rely and guarantee relations satisfy all the requirement 1 of the proof method from Theorem 1. It is easy to see that the requirement 1 is also fulfilled: the global invariant $\mathsf{INV}$ is simply preserved by each atomic step, so it is indeed stable under rely relations of each thread.

The key observation implying stability of the loop invariant in every thread $t$ is presented in the following lemma, which states that environment transitions in the rely relation never extend the set of enqueues seen by a given dequeue.

Lemma 2

If a dequeue event $\mathtt{DEQ}$ generated its timestamp $\mathtt{start\_ts}$, then:

8 The Optimistic Set: Informal Development

The Algorithm. We now present another example, the Optimistic Set [17], which is a variant of a classic algorithm by Heller et al. [8], rewritten to use atomic sections instead of locks. However, this is a highly-concurrent algorithm: every atomic section accesses a small bounded number of memory locations. In this section we only give an informal explanation of the proof and commitment points; the details are provided in [14].

The code in Fig. 12 implements the Optimistic Set as a sorted singly-linked list. Each node in the list has three fields: an integer val storing the key of the node, a pointer next to the subsequent node in the list, and a boolean flag marked that is set true when the node gets removed. The list also has sentinel nodes head and tail that store $-\infty$ and $+\infty$ as keys accordingly. The set defines three operations: insert, remove and contains. Each of them uses an internal operation locate to traverse the list. Given a value v, locate traverses the list nodes and returns a pair of nodes (p, c), out of which c has a key greater or equal to v, and p is the node preceding c.

Fig. 12.

The optimistic set. Shaded portions are auxiliary code used in the proof

The insert (remove) operation spins in a loop locating a place after which a new node should be inserted (after which a candidate for removal should be) and attempting to atomically modify the data structure. The attempt may fail if either p.next = c or !p.marked do not hold: the former condition ensures that concurrent operations have not removed or inserted new nodes immediately after p.next, and the latter checks that p has not been removed from the set. When either check fails, the operation restarts. Both conditions are necessary for preserving integrity of the data structure.

When the elements are removed from the set, their corresponding nodes have the marked flag set and get unlinked from the list. However, the next field of the removed node is not altered, so marked and unmarked nodes of the list form a tree such that each node points towards the root, and only nodes reachable from the head of the list are unmarked. In Fig. 13, we have an example state of the data structure. The insert and remove operations determine the position of a node p in the tree by checking the flag p.marked. In remove, this check prevents removing the same node from the data structure twice. In insert, checking !p.marked ensures that the new node n is not inserted into a branch of removed nodes and is reachable from the head of the list.

In contrast to insert and remove, contains never modifies the shared state and never restarts. This leads to a subtle interaction that may happen due to interference by concurrent events: it may be correct for contains to return $\mathsf{true}$ even though the node may have been removed by the time contains finds it in the list.

Fig. 13.

Example state of the optimistic set. Shaded nodes have their “marked” field set.

Fig. 14.

Example execution of the set. “Ins” and “Rem” denote successful insert and remove operations accordingly, and “Con” denotes contains operations. A–E correspond to commitment points of operations.

Fig. 15.

Changes to the abstract history of the execution in Fig. 14. Edges implied by transitivity are omitted.

In Fig. 13, we illustrate the subtleties with the help of a state of the set, which is a result of executing the trace from Fig. 14, assuming that values 1, 2 and 4 have been initially inserted in sequence by performing “Ins(1)”, “Ins(2)” and “Ins(4)”. We consider the following scenario. First, “Con(2)” and “Con(3)” start traversing through the list and get preempted when they reach the node containing 1, which we denote by $n_1$. Then the operations are finished in the order depicted in Fig. 14. Note that “Con(2)” returns $\mathsf{true}$ even though the node containing 2 is removed from the data structure by the time the contains operation locates it. This surprising behaviour occurs due to the values 1 and 2 being on the same branch of marked nodes in the list, which makes it possible for “Con(2)” to resume traversing from $n_1$ and find 2. On the other hand, “Con(3)” cannot find 3 by traversing the nodes from $n_1$: the contains operation will reach the node $n_2$ and return $\mathsf{false}$, even though 3 has been concurrently inserted into the set by this time. Such behaviour is correct, since it can be justified by a linearization [“Ins(1)”, “Ins(2)”, “Ins(4)”, “Rem(1)”, “Con(2): true”, “Rem(2)”, “Con(3): false”, “Ins(3)”]. Intuitively, such linearization order is possible, because pairs of events (“Con(2): true”, “Rem(2)”) and (“Con(3): false”, “Ins(3)”) overlap in the execution.

Building a correct linearization order by identifying a linearization point of contains is complex, since it depends on presence of concurrent insert and remove operation as well as on current position in the traversal of the data structure. We demonstrate a different approach to the proof of the Optimistic Set based on the following insights. Firstly, we observe that only decisions about a relative order of operations with the same argument need to be committed into the abstract history, since linearizability w.r.t. the sequential specification of a set does not require enforcing any additional order on concurrent operations with different arguments. Secondly, we postpone decisions about ordering contains operations w.r.t. concurrent events till their return values are determined. Thus, in the abstract history for Fig. 14, “Con(2): true” and “Rem(2)” remain unordered until the former encounters the node removed by the latter, and the order between operations becomes clear. Intuitively, we construct a linear order on completed events with the same argument, and let contains operations be inserted in a certain place in that order rather than appended to it.

Preliminaries. We assume that a set $\mathsf{NodeID}$ is a set of pointers to nodes, and that the state of the linked list is represented by a partial map $\mathsf{NodeID}\rightharpoonup \mathsf{NodeID}\times \mathsf{Int} \times \mathsf{Bool}$. To aid in constructing the abstract history $(E, R)$, the code maintains a piece of ghost state—a partial function $G_\mathsf{node}: \mathsf{EventID}\rightharpoonup \mathsf{NodeID}$. Given the identifier $i$ of an event $E(i)$ denoting an $\mathtt{insert}$ that has inserted its value into the set, $G_\mathsf{node}(i)$ returns a node identifier (a pointer) of that value in the data structure. Similarly, for a successful remove event identifier $i$, $G_\mathsf{node}(i)$ returns a node identifier that the corresponding operation removed from the data structure.

Commitment Points. The commitment points in the $\mathtt{insert}$ and $\mathtt{remove}$ operations are denoted by ghost code in Fig. 16. They are similar in structure and update the order of events in the abstract history in the same way described by $\mathtt{OrderInsRem}$. That is, these commitment points maintain a linear order on completed events of operations with the same argument: on the first line of $\mathtt{OrderInsRem}$, the current insert/remove event identified by $\mathtt{myEid}()$ gets ordered after each operation e with the same argument as $\mathtt{myEid}()$. On the second line of $\mathtt{OrderInsRem}$, uncompleted insert and remove events with the same argument are ordered after $\mathtt{myEid}()$. Note that uncompleted contains events remain unordered w.r.t. $\mathtt{myEid}()$, so that later on at the commitment point of contains they could be ordered before the current insert or remove operation (depending on whether they return $\mathsf{false}$ or $\mathsf{true}$ accordingly), if it is necessary.

Fig. 16.

The auxiliary code executed at the commitment points of insert and remove

Fig. 17.

The auxiliary code executed at the commitment point of contains

At the commitment point, the remove operation assigns a return value to the corresponding event. When the removal is successful, the commitment point associates the removed node with the event by updating $G_\mathsf{node}$. Let us illustrate how $\mathtt{commit}_\mathtt{remove}$ changes abstract histories on the example. For the execution in Fig. 14, after starting the operation “Rem(2)” we have the abstract history Fig. 15(a), and then at point (B) “Rem(2)” changes the history to Fig. 15(b). The uncompleted event “Con(2)” remains unordered w.r.t. “Rem(2)” until it determines its return value ($\mathsf{true}$) later on in the execution, at which point it gets ordered before “Rem(2)”.

At the commitment point, the insert operation assigns a return value to the event based on the check $\mathtt{c.val} \ne \mathtt{v}$ determining whether $\mathtt{v}$ is already in the set. In the execution Fig. 14, prior to the start of “Ins(3)” we have the abstract history Fig. 15(c). When the event starts, a new event is added into the history (commitment point of kind 1), which changes it to Fig. 15(d). At point (D) in the execution, $\mathtt{commit}_\mathtt{insert}$ takes place, and the history is updated to Fig. 15(e). Note that “Ins(3)” and “Con(3)” remain unordered until the latter determines its return value ($\mathsf{false}$) and orders itself before “Ins(3)” in the abstract history.

The commitment point at lines 40–42 of the contains operation occurs at the last iteration of the sorted list traversal in the locate method. The last iteration takes place when $\mathtt{curr.val} \ge v$ holds. In Fig. 17, we present the auxiliary code $\mathtt{commit}_\mathtt{contains}$ executed at line 42 in this case. Depending on whether a requested value is found or not, the abstract history is updated differently, so we further explain the two cases separately. In both cases, the contains operation determines which event in the history it should immediately follow in all linearizations.

Case (i). If curr.val = v, the requested value v is found, so the current event $\mathtt{myEid}()$ receives $\mathsf{true}$ as its return value. In this case, $\mathtt{commit}_\mathtt{contains}$ adds two kinds of edges in the abstract history.

• Firstly, $(\mathsf{insOf}(E, \mathtt{curr}), \mathtt{myEid}())$ is added to ensure that $\mathtt{myEid}()$ occurs in all linearizations of the abstract history after the insert event of the node $\mathtt{curr}$.

• Secondly, $(\mathtt{myEid}(), i)$ is added for every other identifier $i$ of an event that does not precede $\mathtt{myEid}()$ and has an argument v. The requirement not to precede $\mathtt{myEid}()$ is explained by the following. Even though at commitment points of insert and remove operations we never order events w.r.t. contains events, there still may be events preceding $\mathtt{myEid}()$ in real-time order. Consequently, it may be impossible to order $\mathtt{myEid}()$ immediately after $\mathsf{insOf}(E, \mathtt{curr})$.

At point (C) in the example from Fig. 14, $\mathtt{commit}_\mathtt{contains}$ in “Con(2)” changes the history from Fig. 15(b) to (c). To this end, “Con(2)” is completed with a return value $\mathsf{true}$ and gets ordered after “Ins(2)” (this edge happened to be already in the abstract history due to the real-time order), and also in front of events following “Ins(2)”, but not preceding “Con(2)”. This does not include “Ins(4)” due to the real-time ordering, but includes “Rem(2)”, so the latter is ordered after the contains event, and all linearizations of the abstract history Fig. 15(c) meet the sequential specification in this example. In general case, we also need to show that successful remove events do not occur between $\mathsf{insOf}(E, \mathtt{curr}), \mathtt{myEid}())$ and $\mathtt{myEid}()$ in the resulting abstract history, which we establish formally in [14]. Intuitively, when $\mathtt{myEid}()$ returns $\mathsf{true}$, all successful removes after $\mathsf{insOf}(E, \mathtt{curr})$ are concurrent with $\mathtt{myEid}()$: if they preceded $\mathtt{myEid}()$ in the real-time order, it would be impossible for the contains operation to reach the removed node by starting from the head of the list in order return $\mathsf{true}$.

Case (ii). Prior to executing $\mathtt{commit}_\mathtt{contains}$, at line 40 we check that $\mathtt{curr.val} \ge \mathtt{v}$. Thus, if curr.val = v does not hold in $\mathtt{commit}_\mathtt{contains}$, the requested value v is not found in the sorted list, and $\mathsf{false}$ becomes the return value of the current event $\mathtt{myEid}()$. In this case, $\mathtt{commit}_\mathtt{contains}$ adds two kinds of edges in the abstract history.

• Firstly, $(\mathsf{lastRemOf}(E, R, \mathtt{v}), \mathtt{myEid}())$ is added, when there are successful remove events of value v (note that they are linearly ordered by construction of the abstract history, so we can choose the last of them). This ensures that $\mathtt{myEid}()$ occurs after a successful remove event in all linearizations of the abstract history.

• Secondly, $(\mathtt{myEid}(), i)$ is added for every other identifier $i$ of an event that does not precede $\mathtt{myEid}()$ and has an argument v, which is analogous to the case (i).

Intuitively, if v has never been removed from the set, $\mathtt{myEid}()$ needs to happen in the beginning of the abstract history and does not need to be ordered after any event.

For example, at point (D) in the execution from Fig. 14, $\mathtt{commit}_\mathtt{contains}$ changes the abstract history from Fig. 15(e) to (f). To this end, “Con(3)” is ordered in front of all events with argument 3 (specifically, “Ins(3)”), since there are no successful removes of 3 in the abstract history. Analogously to the case (i), in general to ensure that all linearizations of the resulting abstract history meet the sequential specification, we need to show that there cannot be any successful insert events of v between $\mathsf{lastRemOf}(E, R, \mathtt{v})$ (or the beginning of the abstract history, if it is undefined) and $\mathtt{myEid}()$. We prove this formally in [14]. Intuitively, when $\mathtt{myEid}()$ returns $\mathsf{false}$, all successful insert events after $\mathsf{lastRemOf}(E, R, \mathtt{v})$ (or the beginning of the history) are concurrent with $\mathtt{myEid}()$: if they preceded $\mathtt{myEid}()$ in the real-time order, the inserted nodes would be possible to reach by starting from the head of the list, in which case the contains operation could not possibly return $\mathsf{false}$.

9 Related Work

There has been a great deal of work on proving algorithms linearizable; see [3] for a broad survey. However, despite a large number of techniques, often supported by novel mathematical theory, it remains the case that all but the simplest algorithms are difficult to verify. Our aim is to verify the most complex kind of linearizable algorithms, those where the linearization of a set of operations cannot be determined solely by examining the prefix of the program execution consisting of these operations. Furthermore, we aim to do this while maintaining a relatively simple proof argument.

Much work on proving linearizability is based on different kinds of simulation proofs. Loosely speaking, in this approach the linearization of an execution is built incrementally by considering either its prefixes or suffixes (respectively known as forward and backward simulations). This supports inductive proofs of linearizability: the proof involves showing that the execution and its linearization stay in correspondence under forward or backward program steps. The linearization point method is an instance of forward simulation: a syntactic point in the code of an operation is used to determine when to add it to the linearization.

As we explained in Sect. 1, forward simulation alone is not sufficient in general to verify linearizability. However, Schellhorn et al. [19] prove that backward simulation alone is always sufficient. They also present a proof technique and use it to verify the Herlihy-Wing queue [11]. However, backwards simulation proofs are difficult to understand intuitively: programs execute forwards in time, and therefore it is much more natural to reason this way.

The queue originally proposed by Herlihy and Wing in their paper on linearizability [11] has proved very difficult to verify. Their proof sketch is based on reasoning about the possible linearizations arising from a given queue configuration. Our method could be seen as being midway between this approach and linearization points. We use partiality in the abstract history to represent sets of possible linearizations, which helps us simplify the proof by omitting irrelevant ordering (Sect. 2).

Another class of approach to proving linearizability is based on special-purpose program logics. These can be seen as a kind of forward simulation: assertions in the proof represent the connection between program execution and its linearization. To get around the incompleteness of forward simulation, several authors have introduced auxiliary notions that support limited reasoning about future behaviour in the execution, and thus allow the proof to decide the order of operations in the linearization [15, 21, 22]. However, these new constructs have subtle semantics, which results in proofs that are difficult to understand intuitively.

Our approach is based on program logic, and therefore is a kind of forward simulation. The difference between us and previous program logics is that we do not explicitly construct a linear order on operations, but only a partial order. This removes the need for special constructs for reasoning about future behaviour, but creates the obligation to show that the partially ordered abstract history can always be linearized.

One related approach to ours is that of Hemed et al. [9], who generalise linearizability to data structures with concurrent specifications (such as barriers) and propose a proof method for establishing it. To this end, they also consider histories where some events are partially ordered—such events are meant to happen concurrently. However, the goal of Hemed et al.’s work is different from ours: their abstract histories are never linearized, to allow concurrent specifications; in contrast, we guarantee the existence of a linearization consistent with a sequential specification. It is likely that the two approaches can be naturally combined.

Aspect proofs [10] are a non-simulation approach that is related to our work. An aspect proof imposes a set of forbidden shapes on the real-time order on methods; if an algorithm avoids these shapes, then it is necessarily linearizable. These shapes are specific to a particular data structure, and indeed the method as proposed in [10] is limited to queues (extended to stacks in [2]). In contrast, our proof method is generic, not tied to a particular kind of data structure. Furthermore, checking the absence of forbidden shapes in the aspect method requires global reasoning about the whole program execution, whereas our approach supports inductive proofs. The original proof of the TS stack used an extended version of the aspect approach [2]. However, without a way of reasoning inductively about programs, the proof of correctness reduced to a large case-split on possible executions. This made the proof involved and difficult. Our proof is based on an inductive argument, which makes it easier.

Another class of algorithms that are challenging to verify are those that use helping, where operations complete each others’ work. In such algorithms, an operation’s position in the linearization order may be fixed by a helper method. Our approach can also naturally reason about this pattern: the helper operation may modify the abstract history to mark the event of the operation being helped as completed.

The Optimistic set was also proven linearizable by O’Hearn et al. in [17]. The essence of the work is a collection of lemmas (including the Hindsight Lemma) proven outside of the logic to justify conclusions about properties of the past of executions based on the current state. Based on our case study of the Optimistic set algorithm, we conjecture that at commitment points we make a constructive decision about extending abstract history where the hindsight proof would use the Hindsight Lemma to non-constructively extend a linearization with the contains operation.

10 Conclusion and Future Work

The popular approach to proving linearizability is to construct a total linearization order by appending new operations as the program executes. This approach is straightforward, but is limited in the range of algorithms it can handle. In this paper, we present a new approach which lifts these limitations, while preserving the appealing incremental proof structure of traditional linearization points. As with linearization points, our fundamental idea can be explained simply: at commitment points, operations impose order between themselves and other operations, and all linearizations of the order must satisfy the sequential specification. Nonetheless, our technique generalises to far more subtle algorithms than traditional linearization points.

We have applied our approach to two algorithms known to present particular problems for linearization points. Although, we have not presented it here, our approach scales naturally to helping, where an operation is completed by another thread. We can support this, by letting any thread complete the operation in an abstract history. In future work, we plan to apply our approach to the Time-Stamped stack [2], which poses verification challenges similar to the TS queue; a flat-combining style algorithm, which depends fundamentally on helping, as well as a range of other challenging algorithms. In this paper we have concentrated on simplifying manual proofs. However, our approach also seems like a promising candidate for automation, as it requires no special meta-theory, just reasoning about partial orders. We are hopeful that we can automate such arguments using off-the-shelf solvers such as Z3, and we plan to experiment with this in future.