Abstract
We give a general description of the transition from qualitative models of programming languages to quantitative ones, as a change of base for enriched categories. This is induced by a monoidal functor from the category of coherence spaces to the category of modules over a complete semiring \({\mathcal {R}}\). Using the properties of this functor, we characterise the requirements for the change of base to preserve the structure of a Lafont category (model of linear type theory with free exponential), and thus to give an adequate semantics of erratic PCF with scalar weights from \({\mathcal {R}}\). Moreover, this model comes with a meaning-preserving functor from the original, qualitative one, which we may use to interpret side-effects such as state. As an example, we show that the game semantics of Idealized Algol bears a natural enrichment over the category of coherence spaces, and thus gives rise by change of base to a \({\mathcal {R}}\)-weighted model, which is fully abstract. We relate this to existing categories of probabilistic games and slot games.
J. Laird—Research Supported by UK EPSRC Grant EP/K037633/1.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Game semantics have been used to successfully describe intensional models of a wide variety of programming language features. With some notable (generally ad-hoc) exceptions, these models are qualitative rather than quantitative in character, possessing an order-theoretic structure which may be characterized as a categorical enrichment over certain categories of domain (such as dI-domains, qualitative domains and prime algebraic lattices). Our aim is to show that this enriched category theory perspective may be used to systematically construct quantitative models (and describe existing ones), using the notion of change of base to vary the enrichment of the model, independently of its intensional structure. Specifically, we describe a monoidal functor from a category of coherence spaces to the category of \({\mathcal {R}}\)-weighted relations, where \({\mathcal {R}}\) is a complete semiring. The change of base induced by this functor allows a semantic translation from a qualitative model, enriched over coherence spaces, to a quantitative one in which program denotations are weighted with values in \({\mathcal {R}}\) corresponding to (e.g.) measures of probability, security, resource usage, etcetera. We illustrate this by example, showing that the well-known games model of Idealized Algol [1] bears a natural enrichment over coherence spaces, and describing the fully abstract semantics of \({\mathcal {R}}\)-weighted Idealized Algol which we obtain from it by change of base.
Related Work. The monoidal categories we use for enrichment are based on existing, extensonal models of computation, and logic — on the qualitative side, coherence spaces or qualitative domains [12]. On the quantitative side, we use the category of weighted relations over a complete semiring \({\mathcal {R}}\) (equivalently, free \({\mathcal {R}}\)-modules and linear functions). This was introduced as a model of linear logic by Lamarche [21] and its computational properties studied in [20] via a semantics of \({\mathcal {R}}\)-weighted PCF.
A more general categorical characterization of these quantitative models, abstracting their key properties, was given in [18]: any model of intuitionistic linear logic with a free exponential and (countably) infinite biproducts yields an adequate model of PCF weighted over its internal semiring. To arrive at such a category using the change of base, we need to show that it preserves the free exponential. However, this is not an enriched functor: instead, we give conditions under which the construction of the cofree commutative comonoid given in [22], as a limit of symmetric tensor powers, is preserved.
Change of base thus provides a simple way to identify further examples of this categorical model, with richer internal structure than sets and weighted relations. This will allow more language features such as side effects to be captured, and also provide a way to attack the full abstraction problem for these models (the weighted relational models for PCF are shown not to be fully abstract in [20]). As an illustrative example we study the games model introduced in [1]. We show that a strictly linear (rather than affine) version of this category of games bears a natural enrichment over coherence spaces — as foreshadowed by in [5] by a projection into a category of (ordered) coherence spaces. Previous quantitative models based on this category of games include Danos and Harmer’s probabilistic games [8], in which strategies are defined by attaching probabilities to positions of the game, and Ghica’s slot games [11], which attach resource weightings to positions in a rather different way — by introducing a class of moves which are persistent when other moves are hidden during composition, allowing the cost of computation to be made explicit. We show that both may be viewed as examples obtained by our change of base construction, and that the corresponding programming languages (Algol weighted with probabilities, and resource costs) may be subsumed into a version of Idealized Algol with weights from a complete semiring, for which we describe a denotational semantics. Full abstraction for this model follows from the result in [1] with very little effort.
1.1 Enriched Categories and Change of Base
Recall that if \({\mathcal {V}}\) is a monoidal category, then a \({\mathcal {V}}\)-category \(\mathcal {C}\) is given by a set of its objects, a \({\mathcal {V}}\)-object \(\mathcal {C}(A,B)\) for each pair of \(\mathcal {C}\)-objects A and B, and \({\mathcal {V}}\)-morphisms \({\mathsf {comp}}_{A,B,C}:{\mathcal {V}}(A,B)\otimes {\mathcal {V}}(B,C) \rightarrow {\mathcal {V}}(A,C)\) and \({\mathsf {id}}_A:I \rightarrow \mathcal {C}(A,A)\) for each A, B, C, satisfying the expected associativity and identity diagrams in \({\mathcal {V}}\).
Intensional semantics such as games models may be represented as \({\mathcal {V}}\)-categories, where \({\mathcal {V}}\) captures some relations or operations on morphisms such as partial orders or algebraic structures. This gives an extensional characterization of the model which can be studied independently of the intensional aspect. An example is the notion of change of base [7], which uses a monoidal functor from \({\mathcal {V}}\) to \({\mathcal {W}}\) to transform any model in a \({\mathcal {V}}\)-category to a model in a \({\mathcal {W}}\)-category satisfying the same equational theory.
More precisely, given monoidal categories \({\mathcal {V}}\) and \({\mathcal {W}}\) any monoidal functor \((F,m):{\mathcal {V}}\rightarrow {\mathcal {W}}\) induces a change of base which takes each \({\mathcal {V}}\)-category \(\mathcal {C}\) to the \({\mathcal {W}}\)-category \(F_*(\mathcal {C})\) over the same objects, with \(F_*(\mathcal {C})(A,B) = F(\mathcal {C}(A,B))\), and composition and identity morphisms \(m_{\mathcal {C}(A,B),\mathcal {C}(B,C)};F({\mathsf {comp}}_{A,B,C})\) and \(m_I;F({\mathsf {id}}_A)\). A simple example is the change of base induced by the monoidal functor \( {\mathcal {V}}(I,\_):{\mathcal {V}}\rightarrow {\mathbf {Set}}\), which sends each \({\mathcal {V}}\)-category \(\mathcal {C}\) to its underlying category \(\mathcal {C}_0\). Note change of base induced by the monoidal functor F comes with an identity-on objects, F-on-morphisms functor \(F_0:\mathcal {C}_0 \rightarrow F_*(\mathcal {C})_0\).
Change of base preserves enriched functors and natural transformations, giving a 2-functor \(F_*\) from the category of \({\mathcal {V}}\)-categories to the category of \({\mathcal {W}}\)-categories. Thus, in particular, it preserves symmetric monoidal structure, and symmetric monoidal closure (the existence of a natural \({\mathcal {V}}\)-isomorphism  . A second example: if \({\mathcal {V}}\) is symmetric monoidal closed, and therefore enriched over itself, then any monoidal functor \(F:{\mathcal {V}}\rightarrow {\mathcal {W}}\) induces a change of base to a \({\mathcal {W}}\)-enriched symmetric monoidal closed category.
. A second example: if \({\mathcal {V}}\) is symmetric monoidal closed, and therefore enriched over itself, then any monoidal functor \(F:{\mathcal {V}}\rightarrow {\mathcal {W}}\) induces a change of base to a \({\mathcal {W}}\)-enriched symmetric monoidal closed category.
2 Coherence Spaces and Weighted Relations
We will describe a monoidal functor from the category of coherence spaces and stable, continuous linear functions to the category of sets and weighted relations (a.k.a. free \({\mathcal {R}}\)-modules). Examples of categories of intensional models which may be enriched over coherence spaces or qualitative domains are common. For instance any symmetric monoidal closed category with a monoidal functor into the category of coherence spaces gives a coherence space enriched category as noted above — examples include categories of hypercoherences [9], event structures [24], concrete data structures [4] and games [5]. (However, the enriched category of games that we describe does not arise in this way.)
A coherence space [12] D is a pair  where |D| is a set of atoms (the web), and
where |D| is a set of atoms (the web), and  is a symmetric and reflexive relation (coherence). A clique X of D is a set of its atoms which is pairwise coherent:
is a symmetric and reflexive relation (coherence). A clique X of D is a set of its atoms which is pairwise coherent:  .
.
The symmetric monoidal (closed) category \({\mathbf {CSpace}}\) has coherence spaces as objects: morphisms from D to E are cliques of the coherence space  , where
, where  and
and  if
if  implies
implies  .
.
In other words, morphisms are certain relations between webs, and are composed accordingly — if \(f:C \rightarrow D\) and \(g:D \rightarrow E\) then \(f;g = \{(c,e)\in |C|\times |E|\ |\ \exists d \in D. (c,d) \in f \wedge (d,e) \in g\}\). Evidently, the identity relation is a clique. The tensor product of coherence spaces is the cartesian product of their webs and coherence relations — i.e. \(|D \otimes E| = |D| \times |E|\), with  if and only if
if and only if  and
and  . The tensor unit is the singleton coherence space \(\{*\}\).
. The tensor unit is the singleton coherence space \(\{*\}\).
The cliques of a coherence space E form an atomistic (Scott) domain, and the morphisms of \({\mathbf {CSpace}}\) correspond to linear, continuous and stable morphisms between the corresponding domains (i.e. preserving suprema of all directed and bounded sets, and infima of finite bounded sets).
Complete Semirings and Weighted Relations. We now recall categories of weighted relations, which will be used to characterise the structure of quantitative models. They are based on monoids with an infinitary “sum” operation.
Definition 1
A complete monoid is a pair \((S,\varSigma )\) of a set S with a sum operation \(\varSigma \) on indexed families of elements of S, satisfying the axioms:
-
Partition Associativity. For any partitioning of the set I into \(\{I_j \ | \ j \in J\}\), \(\varSigma _{i \in I}a_i =\varSigma _{j \in J}\varSigma _{i \in I_j}a_i\).
-
Unary Sum. \(\varSigma _{i \in \{j\}}a_i = a_j\).
We write 0 for the sum of the empty family, which is a neutral element for the sum by the above axioms.
Definition 2
A (commutative) complete semiring \({\mathcal {R}}\) is a tuple \((|{\mathcal {R}}|,\varSigma ,\cdot ,1)\) such that \((|{\mathcal {R}}|,\varSigma )\) is a complete monoid and \((|{\mathcal {R}}|,\cdot ,1)\) is a commutative monoid which distributes over \(\varSigma \) — i.e. \(\varSigma _{i \in I}(a\cdot b_i) = a \cdot \varSigma _{i \in I}b_i\).
A \({\mathcal {R}}\)-module is a monoidal action (“scalar multiplication”) of \((|{\mathcal {R}}|,\cdot ,1)\) on a complete monoid \((S,\varSigma )\), which is distributive on both sides — i.e. \((\varSigma _{i \in I}a_i).v = \varSigma _{i \in I}a_i.v\) and \(a.\varSigma _{i \in I}v_i = \varSigma _{i \in I} a.v_i\).
For any complete semiring the forgetful functor from the category of \({\mathcal {R}}\)-modules and their homomorphisms into the category of sets has a left adjoint, which sends a set X to the “free semimodule” \({\mathcal {R}}^X\), which is the set of functions from X into \({\mathcal {R}}\), with the sum and scalar product defined pointwise. Resolving this adjunction gives a commutative monad \({\mathcal {R}}^\_\) on the category of sets and thus a co-Kleisli category \({\mathbf {Set}}_{{\mathcal {R}}}\) with symmetric monoidal structure (given by the product of sets). Morphisms from X to Y in this category correspond both to \({\mathcal {R}}\)-module homomorphisms from \({\mathcal {R}}^X\) to \({\mathcal {R}}^Y\), and also to \({\mathcal {R}}\)-weighted relations, with which we will henceforth identify them: maps from \(X \times Y\) into \({\mathcal {R}}\), composed by setting \((f;g)(x,z) = \varSigma _{y \in Y}f(x,y)\cdot g(y,z)\). The symmetric monoidal action on weighted relations is \((f \otimes g)((u,v),(x,y)) = f(u,x)\cdot g(v,y)\).
Relations weighted with continuous semirings are discussed in [20], with examples including any complete lattice, the natural or positive real numbers completed with a greatest element \(\infty \), and the so-called exotic semirings. Examples of complete but not continuous semiring weights are considered in [18].
2.1 From Cliques to Weighted Relations
Note that composition of morphisms \(f:C \rightarrow D\) and \(g:D \rightarrow F\) in \({\mathbf {CSpace}}\) has the following property, derived from stability.
Lemma 1
\((c,e) \in f;g\) if and only if there exists a unique \(d \in D\) such that \((c,d) \in f\) and \((d,e) \in g\).
Proof
Existence holds by definition. For uniqueness, suppose \((c,d), (c,d') \in f\) and \((d,e),(d',e) \in g\). Then  and hence \(d = d'\).
and hence \(d = d'\).
We define a functor \(\varPhi ^{\mathcal {R}}:{\mathbf {CSpace}}\rightarrow {\mathbf {Set}}_{\mathcal {R}}\) which sends each object to its underlying set, and each morphism from D to E to its characteristic function — i.e. \(\varPhi ^{\mathcal {R}}(f)(c,d) =1\), if \((c,d) \in f\); \(\varPhi ^{\mathcal {R}}(f)(c,d) =0\), otherwise.
By definition, \(\varPhi ^{\mathcal {R}}({\mathsf {id}}_D)\) is the identity on |D| in \({\mathbf {Set}}_{\mathcal {R}}\). Thus functoriality follows from Lemma 1.
Lemma 2
\(\varPhi ^{\mathcal {R}}(f);\varPhi ^{\mathcal {R}}(g) = \varPhi ^{\mathcal {R}}(f):\varPhi ^{\mathcal {R}}(g)\).
Proof
Suppose \(\varPhi ^{\mathcal {R}}(f;g)(c,e) = 1\) — i.e. \((c,e) \in f;g\). By Lemma 1 there exists a unique \(d \in D\) such that \((c,d) \in f\) and \((d,e) \in g\). Thus \(\varPhi ^{\mathcal {R}}(f)(c,d').\varPhi ^{\mathcal {R}}(f)(c,d') = 1\) if \(d = d'\) and \(\varPhi ^{\mathcal {R}}(f)(c,d').\varPhi ^{\mathcal {R}}(f)(c,d') = 0\) otherwise. Hence \(\varPhi ^{\mathcal {R}}(f);\varPhi ^{\mathcal {R}}(g)(c,e) = \varSigma _{d \in D}\varPhi ^{\mathcal {R}}(f)(c,d).\varPhi ^{\mathcal {R}}(g)(d,e) = 1\).
Otherwise \(\varPhi ^{\mathcal {R}}(f;g)(c,e) = 0\) — i.e. \((c,e) \not \in f;g\), so that for all \(d \in D\), either \((c,d) \not \in f\) or \((d,e) \not \in g\) and so \(\varPhi ^{\mathcal {R}}(f)(c,d).\varPhi ^{\mathcal {R}}(f)(c,d) = 0\). Then \(\varPhi ^{\mathcal {R}}(f);\varPhi ^{\mathcal {R}}(g)(c,e) = \varSigma _{d \in D}\varPhi ^{\mathcal {R}}(f)(c,d).\varPhi ^{\mathcal {R}}(g)(d,e)\).
Evidently, \(\varPhi ^R\) is strict monoidal — \(\varPhi ^R(I) = I\) and \(\varPhi ^{\mathcal {R}}(D \otimes E) = \varPhi ^{\mathcal {R}}(D) \otimes \varPhi ^{\mathcal {R}}(E)\), and faithful. Thus, by change of base, for each ordered complete semiring \({\mathcal {R}}\) we have a 2-functor \(\varPhi ^R_*\) from the category of (symmetric monoidal closed) \({\mathbf {CSpace}}\)-categories to the category of (symmetric monoidal closed) \({\mathbf {Set}}_{\mathcal {R}}\)-categories, with a faithful functor \(\varPhi ^R_0: \mathcal {C}_0 \rightarrow \varPhi ^R_*(\mathcal {C})_0\) for each \({\mathbf {CSpace}}\)-category \(\mathcal {C}\).
Remark 1
If \({\mathcal {R}}\) is idempotent (\(a_i = a\) for all \(i \in I\) (non-empty) implies \(\varSigma _{i \in I}a_i\)) then functoriality no longer depends on Lemma 1 and thus the stability of morphisms. Hence we may define a monoidal functor from the category of sets and relations to the category of \({\mathcal {R}}\)-weighted relations which sends each relation to its characteristic function, yielding a change of base from \({\mathbf {Rel}}\)-enriched to \({\mathbf {Set}}_{{\mathcal {R}}}\) enriched categories whenever \({\mathcal {R}}\) is idempotent.
3 An Example: Games and History-Sensitive Strategies
We illustrate by describing an example of a family of quantitative games models obtained by change of basis applied to a symmetric monoidal category of games and “knowing” strategies enriched over coherence spaces. Its underlying category is essentially the games model of Idealized Algol (IA) introduced by Abramsky and McCusker in [1] and obtained by relaxing the innocence constraint on strategies in the Hyland-Ong games model of PCF [14]. More precisely, we define a different “linear decomposition” of this model into a category in which morphisms are truly linear, rather than affine. We also ignore the requirement of even-prefix-closure on strategies — this does not change the denotation of programs in the model, nor its full abstraction property.
Definition 3
The arena for a game A is a labelled, bipartite directed acyclic graph, given as a tuple \((M_A,M^I_A,\vdash _A,\lambda _A)\) — where \(M_A\) is a set of moves (nodes), \(M_A^I\subseteq M_A\) is a specified set of initial moves (source nodes), \(\vdash _A \subseteq M_A \times (M_A\backslash M^I_A) \) is the enabling (edge) relation and \(\lambda _A:M_A \rightarrow \{O,P\}\times \{Q,A\}\) is a function partitioning the moves between Player or Opponent, and labelling them as either questions or answers, such that initial moves belong to Opponent and each answer is enabled by a question.
A justified sequence s over A is a sequence over \(M_A\), together with a pointer from each non-initial move b in s to some preceding move a in s such that \(a \vdash b\). The set \(L_A\) of legal sequences over A consists of alternating justified sequences s on A which satisfy visibility and well-bracketing as defined in [1]. (Details are omitted as nothing here depends on thiese particular conditions, which may be relaxed or modified in various ways to model different combinations of computational effects.) A game A is a pair \((G_A,P_A)\) of an arena \(G_A\) and a set of justified sequences \(P_A \subseteq L_A\). The key constructions are:
-
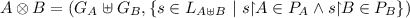 , where \(G_A \uplus G_B\) is the disjoint union of arenas — \((M_A + M_B,M^I_A + M^I_B,\vdash _A + \vdash B_B,[\lambda _A,\lambda _B])\).
, where \(G_A \uplus G_B\) is the disjoint union of arenas — \((M_A + M_B,M^I_A + M^I_B,\vdash _A + \vdash B_B,[\lambda _A,\lambda _B])\). -
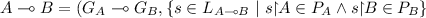 ), where
), where  is the graft of A onto the root nodes of B — \(M_A + M_B, {\mathtt {inr}}(M^I_B), (\vdash _A + \vdash _B) \cup {\mathtt {inr}}(M^I_B)\times {\mathtt {inl}}(M^I_A),[\overline{\lambda _A},\lambda _B]).\)
is the graft of A onto the root nodes of B — \(M_A + M_B, {\mathtt {inr}}(M^I_B), (\vdash _A + \vdash _B) \cup {\mathtt {inr}}(M^I_B)\times {\mathtt {inl}}(M^I_A),[\overline{\lambda _A},\lambda _B]).\)
3.1 Coherence Space Enrichment of Games
We will now define a \({\mathbf {CSpace}}\)-category of games, for which the underlying category is similar to that described in [1] etc. The fact that the inclusion order on strategies provides the latter with an enrichment over the category of cpos and continuous functions was already used in [1], as in other games models, to construct fixed points. Our results amount to showing that strategies form a dI-domain under inclusion, and composition is a bilinear and stable function. Enrichment of a category of games with coherence spaces, or similar categories, is also implicit in earlier work, such as the definition in [5] of a monoidal functor from a similar category of games into a category of ordered coherence spaces. However, this depends on a number of particular features — notably the reconstruction of a strategy on  from its projections on A and B, which is not always possible, so \({\mathbf {CSpace}}\)-enrichment may be seen as a more general property.
from its projections on A and B, which is not always possible, so \({\mathbf {CSpace}}\)-enrichment may be seen as a more general property.
For any game A let \({\mathsf {Coh}}(A)\) be the coherence space  , where \(P^E_A\) is the set of even-length sequences in \(P_A\) and
, where \(P^E_A\) is the set of even-length sequences in \(P_A\) and  if their greatest common prefix \(s \sqcap t\) is even length. A strategy on A is a morphism from I to \({\mathsf {Coh}}(A)\) in \({\mathbf {CSpace}}\), corresponding to a clique of \({\mathsf {Coh}}(A)\) — an even-branching subset of \(P_A^E\). We define a \({\mathbf {CSpace}}\)-category in which objects are games, and the coherence space of morphisms from A to B is
if their greatest common prefix \(s \sqcap t\) is even length. A strategy on A is a morphism from I to \({\mathsf {Coh}}(A)\) in \({\mathbf {CSpace}}\), corresponding to a clique of \({\mathsf {Coh}}(A)\) — an even-branching subset of \(P_A^E\). We define a \({\mathbf {CSpace}}\)-category in which objects are games, and the coherence space of morphisms from A to B is  .
.
Definition 4
For  and
and  , let S|T be the set of sequences u on \(A + B + C\) such that
, let S|T be the set of sequences u on \(A + B + C\) such that  and
and  . Then
. Then  .
.
The identity  is the copycat strategy on A consisting of the sequences on
is the copycat strategy on A consisting of the sequences on  for which each even prefix projects to the same (legal) sequence on both components.
for which each even prefix projects to the same (legal) sequence on both components.
Given strategies  and
and  , let \(\sigma ;\tau \) be the relational composition of \(\sigma \otimes \tau \) with \({\mathsf {comp}}_{A,B,C}\). This corresponds to the parallel composition plus hiding of strategies defined in [1], and so by well-pointedness of \({\mathbf {CSpace}}\), satisfies the diagrams for associativity and identity. So it remains to show that \({\mathsf {comp}}\) is stable, for which we require a further key fact about composition — for any \(t \in \sigma ;\tau \), the “interaction sequence” in \(\sigma |\tau \) which restricts to t is unique. This is essentially a version of the “zipping lemma” of [2].
, let \(\sigma ;\tau \) be the relational composition of \(\sigma \otimes \tau \) with \({\mathsf {comp}}_{A,B,C}\). This corresponds to the parallel composition plus hiding of strategies defined in [1], and so by well-pointedness of \({\mathbf {CSpace}}\), satisfies the diagrams for associativity and identity. So it remains to show that \({\mathsf {comp}}\) is stable, for which we require a further key fact about composition — for any \(t \in \sigma ;\tau \), the “interaction sequence” in \(\sigma |\tau \) which restricts to t is unique. This is essentially a version of the “zipping lemma” of [2].
Lemma 3
\({\mathsf {comp}}_{A,B,C}\) is a clique of  .
.
We define \({\mathbf {CSpace}}\)-enriched symmetric monoidal (closed) structure on \({\mathbf G}\), given by the operation \(\otimes \) with unit I (the game over the empty arena, with \(P_I = \{\varepsilon \}\)) and the morphism  . This corresponds to the action of \(\otimes \) on the underlying category of games defined in [1], giving associator, unitor and twist maps making the relevant diagrams commute. The (natural) isomorphism
. This corresponds to the action of \(\otimes \) on the underlying category of games defined in [1], giving associator, unitor and twist maps making the relevant diagrams commute. The (natural) isomorphism  in \({\mathbf {CSpace}}\) yields symmetric monoidal closure.
in \({\mathbf {CSpace}}\) yields symmetric monoidal closure.
Note that unlike [1] and many similar models, the underlying symetric monoidal category of games is not affine — the unit for the tensor is not a terminal object — there are two morphisms from I to itself, one empty, the other containing the empty sequence. This is a necessary consequence of \({\mathbf {CSpace}}\)-enrichment.
For any complete semiring \({\mathcal {R}}\), change of base yields a symmetric monoidal closed category \({\mathbf G}^{\mathcal {R}}\triangleq \varPhi ^{{\mathcal {R}}}_*({\mathbf G})\) enriched in \({\mathbf {Set}}_{\mathcal {R}}\). Concretely, a morphism \(\phi :A \rightarrow B\) in \({\mathbf G}^{\mathcal {R}}_0\) is a \({\mathcal {R}}\)-weighted strategy — a map from even-length plays on  into \({\mathcal {R}}\). These are composed by setting
into \({\mathcal {R}}\). These are composed by setting

The tensor product of \({\mathcal {R}}\)-weighted strategies \(\phi :A \rightarrow C, \psi :B \rightarrow D\) is  .
.
The faithful, identity-on-objects, monoidal functor \(\varPhi ^{\mathcal {R}}_0:{\mathbf G}_0 \rightarrow {\mathbf G}_0^{\mathcal {R}}\) sends each deterministic strategy \(\sigma :A \rightarrow B\) to the \({\mathcal {R}}\)-weighted strategy \(\sigma _{{\mathcal {R}}}\) with \(\varPhi ^{\mathcal {R}}_0(\sigma )(s) = 1\) if \(s \in \sigma \) and \(\varPhi ^{\mathcal {R}}_0(\sigma )(s) = 0\) otherwise.
By choosing particular semirings we may relate this category to examples in the literature. For instance, if \({\mathcal {R}}\) is the two-element Boolean ring then morphisms in \({\mathbf G}^{\mathcal {R}}_0\) correspond to sets of legal sequences — i.e. non-deterministic strategies, as in the model of may-testing studied in [13, 19].
If \({\mathcal {R}}\) is the probability semiring, \(({\mathbb {R_+^\infty }},\varSigma ,\cdot ,1)\), then \({\mathcal {R}}\)-weighted strategies correspond precisely to the “probabilistic pre-strategies”, introduced by Danos and Harmer [8]. These are refined further by imposing more specfic constraints, although the precursor model is already fully abstract for Probabilistic Algol.
If \({\mathcal {R}}\) is the tropical semiring \(({\mathbb {N}}^\infty ,\bigcup ,+,0)\) then \({\mathbf G}^{\mathcal {R}}_0\) corresponds to a sequential version of Ghica’s category of slot games [10]. This was introduced as a model quantifying resources used in stateful and concurrent computation, in a presentation rather different to weighted strategies, but equivalent to it. Assuming a distinguished token  , which does not occur in the set of moves of any arena, we may define a sequence with costs on the game A to be an interleaving of a sequence \(s \in P_A\) of A with a sequence of
, which does not occur in the set of moves of any arena, we may define a sequence with costs on the game A to be an interleaving of a sequence \(s \in P_A\) of A with a sequence of  moves: a strategy-with-costs on a A is a set of such sequences. Strategies with costs \(\sigma :A \rightarrow B\) and \(\tau :B \rightarrow C\) are composed by parallel composition with hiding of moves in B, so that all slot moves of \(\sigma \) and \(\tau \) propagate to \(\sigma ;\tau \). Taking the weight of a sequence with costs to be the number of slot moves it contains, this is equivalent to the notion of composition for \({\mathbb {T}}\)-weighted strategies — i.e. the category of strategies with costs is isomorphic to the category \({\mathbf G}_{\mathbf {T}}\). The original category of slot games defined in [10] is based on a category (an interleaving model of concurrency, without the alternation condition) which does not, in fact enrich over the category of coherence spaces but does enrich over the category of relations. Thus we may change the base of this model only to free semimodules over an idempotent semiring — of which the tropical semiring is an instance.
moves: a strategy-with-costs on a A is a set of such sequences. Strategies with costs \(\sigma :A \rightarrow B\) and \(\tau :B \rightarrow C\) are composed by parallel composition with hiding of moves in B, so that all slot moves of \(\sigma \) and \(\tau \) propagate to \(\sigma ;\tau \). Taking the weight of a sequence with costs to be the number of slot moves it contains, this is equivalent to the notion of composition for \({\mathbb {T}}\)-weighted strategies — i.e. the category of strategies with costs is isomorphic to the category \({\mathbf G}_{\mathbf {T}}\). The original category of slot games defined in [10] is based on a category (an interleaving model of concurrency, without the alternation condition) which does not, in fact enrich over the category of coherence spaces but does enrich over the category of relations. Thus we may change the base of this model only to free semimodules over an idempotent semiring — of which the tropical semiring is an instance.
4 Additives and Exponentials
We now describe how this change of base can be used to obtain a quantitative semantics of higher-order computation — specifically, an (intuitionistic) Lafont category [16] (a symmetric monoidal closed category \(\mathcal {C}\) with a “free exponential”) with countable biproducts. This notion of categorical model was shown in [18] to yield an adequate model of PCF extended with \({\mathcal {R}}\)-module structure, as described in Sect. 5.
A category \(\mathcal {C}\) has set-indexed biproducts if it has all set-indexed products and coproducts, and these are naturally isomorphic — i.e. for any family J, there is a natural isomorphism (which we may assume to be the identity) between the J-indexed functors \(\varPi _{j \in J}\_\) and \(\coprod _{j \in J}\). Any category with infinite biproducts bears an enrichment over the category of complete monoids and their homomorphisms: Given a family of morphisms \(\{f_j:A \rightarrow B\ |\ j \in J\}\), let \(\varSigma _{j \in J}f_j = \varDelta _A^J;\bigoplus _{j \in J}f_j;\nabla _A^J\), where \(\varDelta ^A_J:A \rightarrow \bigoplus _{j \in J}A\) and \(\nabla ^J_A: \bigoplus _{j \in J}A \rightarrow A\) are the diagonal and co-diagonal. Jf \(\mathcal {C}\) is a symmetric monoidal closed category, then the tensor distributes over biproducts — i.e. \((\bigoplus _{i \in J}A_j) \otimes B = \bigoplus _{j \in J}(A_j \otimes B)\), as they are colimits. The complete monoid enrichment thus extends to the monoidal structure — i.e. the tensor is an enriched functor. Moreover, the endomorphisms on the unit I form a complete, commutative semiring \( {\mathcal {R}}_C = (\mathcal {C}(I,I),\varSigma ,\otimes ,I)\) — the internal semiring of \(\mathcal {C}\).
Conversely, any complete monoid enriched category may be completed with biproducts.
Definition 5
If \(\mathcal {C}\) is complete monoid enriched, let \(\mathcal {C}^\varPi \) be the category in which objects are set-indexed families of objects of \(\mathcal {C}\), and morphisms from \(\{A_i\ |\ i \in I\}\) to \(\{B_j \ |\ j \in J\}\) are \(I \times J\)-indexed sets of morphisms \(\{f_{i,j}:A_i \rightarrow B_j\ |\ \langle i, j\rangle \in I \times J\}\), composed by setting \((f;g)_{ik} = \varSigma _{j \in J}(f_{ij};g_{jk})\).
If \(\mathcal {C}\) is a complete monoid enriched symmetric monoidal category, then we may define the (distributive) tensor product on \(\mathcal {C}^\varPi \): \(\{A_i \ |i \in I\}\otimes \{B_j \ |\ j \in J\} = \{A_i \otimes B_j \ | \langle i,j\rangle \in I \times J\}\), with \((f \otimes g)_{ikjl} = f_{ij}\otimes g_{kl}\).
Note that the biproduct completion of a complete commutative semiring \({\mathcal {R}}\) (regarded as a one-object SMCC) is the category \({\mathbf {Set}}_{{\mathcal {R}}}\).
4.1 The Cofree Commutative Comonoid
A cofree commutative comonoid on an object B in a symmetric monoidal category \(\mathcal {C}\) is an object \((!B,\delta ,\epsilon )\) in \({\mathsf {comon}}(\mathcal {C})\) (the category of commutative commonoids and comonoid morphisms of \(\mathcal {C}\)) with a (natural in A) isomorphism between \(\mathcal {C}(A,B)\) and \({\mathsf {comon}}(\mathcal {C})(A,!B)\) for each commutative comonoid \((A,\delta _A,\epsilon _A)\). Thus \(\mathcal {C}\) has (all) cofree commutative comonoids if and only if the forgetful functor from \({\mathsf {comon}}(\mathcal {C})\) into \(\mathcal {C}\) has a right adjoint. This (monoidal) adjunction resolves a monoidal comonad (the free exponential) \(!:\mathcal {C}\rightarrow \mathcal {C}\).
How can we relate the free exponential to change of base? In general, the category of comonoids of a \({\mathcal {V}}\)-category is not itself \({\mathcal {V}}\)-enriched, so there is no \({\mathcal {V}}\)-adjunction giving rise to a \({\mathcal {V}}\)-enriched free exponential. Moreover, although the categories \({\mathbf {CSpace}}\) and \({\mathbf {Set}}_{{\mathcal {R}}}\) possess cofree commutative comonoids, these are not preserved by \(\varPhi ^{\mathcal {R}}\) (see discussion below). Instead, we describe properties of a \({\mathbf {CSpace}}\)-enriched category which allow the construction of a free exponential on the underlying categories, and their preservation by the functor \(\varPhi ^{\mathcal {R}}_0\). These are based on the existence of symmetric tensor powers:
Definition 6
A family of objects \(\{B^i\ |\ i \in {\mathbb {N}}\}\) in a symmetric monoidal category are symmetric tensor powers of B if:
-
For each n there is a morphism \({\mathsf {eq}}_n:B^n \rightarrow B^{\otimes n}\) such that \((B^n,{\mathsf {eq}}_n)\) is an equalizer for the group G of automorphisms on \(B^{\otimes n}\) derived from the permutations on \(\{1,\ldots ,n\}\).
-
These equalizers are preserved by the tensor product — i.e. \((B^m \otimes B^n,{\mathsf {eq}}_m \otimes {\mathsf {eq}}_n)\) is an equalizer for the products of pairs of permutation automorphisms.
The category of coherence spaces has equalizers for any group G of automorphisms on an object D. Let \({\sim }_G\) be the equivalence relation on |D| induced by G — i.e. \(d {\sim }_G d'\) if there exists \(g \in G\) with \((d,d') \in g\). Then the equalizer for G in \({\mathbf {CSpace}}\) is the coherence space consisting of those equivalence classes of \({\sim }_G\) in which all members are coherent —  — with coherence
— with coherence  if there exists \(d'' \in |D|\) such that \(d {\sim }_G d''\).
if there exists \(d'' \in |D|\) such that \(d {\sim }_G d''\).
The category of sets and weighted relations also has equalizers for automorphism groups — in this case given by the set of all equivalence classes of \({\sim }_G\). Say that an automorphism group \(G:D \Rightarrow D\) in \({\mathbf {CSpace}}\) is coherent whenever  .
.
Proposition 1
\(\varPhi ^{\mathcal {R}}\) preserves the equalizer of G if and only if it is coherent.
Note that unless  , the group of permutations on \(D^{\otimes n}\) in \({\mathbf {CSpace}}\) is not coherent — e.g. if
, the group of permutations on \(D^{\otimes n}\) in \({\mathbf {CSpace}}\) is not coherent — e.g. if  then
then  . So \(\varPhi ^R\) does not preserve symmetric tensor powers (and for essentially the same reason does notin general preserve cofree commutative comonoids).
. So \(\varPhi ^R\) does not preserve symmetric tensor powers (and for essentially the same reason does notin general preserve cofree commutative comonoids).
Given an automorphism group \(G:A \Rightarrow A\) in a \({\mathbf {CSpace}}\)-category, and object B, let \(h^B(G) = \{h^B(g):\mathcal {C}(B,A) \rightarrow \mathcal {C}(B,A)\ |\ g \in G\}\) be the group of automorphisms on \(\mathcal {C}(A,B)\) in \({\mathbf {CSpace}}\) induced by Yoneda embedding. Say that G is coherent if \(h^B(G)\) is coherent for every B.
For instance, in our category of games the group of permutations on \(A^{\otimes n}\) is coherent: an atom of  is a justified sequence over \(M_B \uplus (M_A \times \{1,\ldots ,n\})\), and the equivalence on these sequences induced by the permutation isomorphisms on \(A^{\otimes n}\) is simply that induced by permuting the tags on moves in A. This is coherent because it is Opponent who always plays the first move with any given tag.
is a justified sequence over \(M_B \uplus (M_A \times \{1,\ldots ,n\})\), and the equivalence on these sequences induced by the permutation isomorphisms on \(A^{\otimes n}\) is simply that induced by permuting the tags on moves in A. This is coherent because it is Opponent who always plays the first move with any given tag.
Proposition 2
\(\varPhi ^{\mathcal {R}}_0:\mathcal {C}_0 \rightarrow \mathcal {C}^{\mathcal {R}}_0\) preserves equalizers for coherent groups.
Proof
Suppose \((E,{\mathsf {eq}}:E \rightarrow A)\) is an equalizer for a group \(G:A \Rightarrow A\). Evidently, \(\varPhi _0^{\mathcal {R}}({\mathsf {eq}});\varPhi _0^{\mathcal {R}}(g) = \varPhi _0^{\mathcal {R}}({\mathsf {eq}})\) for all \(g \in G\) so it remains to show the universal property. Let B be any object of \(\mathcal {C}^{\mathcal {R}}_0\) (thus an object of \(\mathcal {C}_0\)). Then \(h^B({\mathsf {eq}});h^B(g) = h^B(g)\) for all \(g \in G\) and for any \(f: I \rightarrow \mathcal {C}(B,A)\) in \({\mathbf {CSpace}}\) such that \(f;h^B(g) = f\) for all \(g \in G\), there exists a unique morphism \(u:I \rightarrow \mathcal {C}(B,E)\) such that \(u;h^B({\mathsf {eq}}) = f\). Observe (by well-pointedness of \({\mathbf {CSpace}}\)) that this implies that \((h^B(E),h^B({\mathsf {eq}}))\) is the equalizer for \(h^B(G)\) in \({\mathbf {CSpace}}\).
Thus \((\varPhi ^{\mathcal {R}}(h^B(E)),\varPhi ^{\mathcal {R}}(h^B({\mathsf {eq}})))\) is an equalizer for \(\varPhi ^{\mathcal {R}}(h^B(G))\) in \({\mathbf {Set}}_{{\mathcal {R}}}\), and so for any \(f:B \rightarrow E\) in \(\varPhi ^{\mathcal {R}}_*(\mathcal {C})\), there exists a unique morphism \(u:B \rightarrow E\) such that \(u;{\mathsf {eq}}= f\) as required.
If our \({\mathbf {Set}}_{{\mathcal {R}}}\)-enriched model possesses symmetric tensor powers and infinite, distributive biproducts, this is sufficient to obtain the free exponential as the biproduct of all symmetric tensor powers of B (the Lafont exponential) — i.e. \(!B = \bigoplus _{n \in {\mathbb {N}}} B^n\), which is equipped with commutative comonoid structure by defining \(\epsilon _{!B}:!B \rightarrow I = \pi _0\) and \(\delta _{!B}:!B \rightarrow !B \otimes !B = \langle \pi _{m+n};\delta _{m,n}\ |\ m,n \in {\mathbb {N}}\rangle \), where \(\delta _{m,n}:B_{m+n} \rightarrow B^m \otimes B^n\) is the unique morphism such that \({\mathsf {eq}}_{m+n} = \delta _{m,n};({\mathsf {eq}}_m \otimes {\mathsf {eq}}_n)\).
Proposition 3
If \(\mathcal {C}\) has symmetric tensor powers, then its biproduct completion \(\mathcal {C}^{\varPi }\) has symmetric tensor powers.
Proof
For \(A = \{A_i \ |\ i \in I\}\), \(A^n = \{A_X\ |\ X \in {\mathcal {M}}_n(I)\}\), where if X has support \(i_1,\ldots , i_k\) then \(A_X = A_{i_1}^{X(1)} \otimes \ldots \otimes A_{i_k}^{X(i_k)}\).
Thus, given any \({\mathbf {CSpace}}\)-enriched category with symmetric tensor powers and consistent permutation groups, we may obtain a Lafont category by changing its base to \({\mathbf {Set}}_{\mathcal {R}}\), and completing with biproducts. In the case of the \({\mathbf {CSpace}}\)-category of games, \({\mathbf G}\), we have already argued that the group of permutations on each tensor power \(A^{\otimes n}\) is consistent, and therefore change of base preserves symmetric tensor powers, if they exist. One way to define them is by decomposing the tensor product in \({\mathbf G}\) using the sequoid [6, 17]. The sequoid  is the game
is the game  — i.e. it is a subgame of \(A \otimes B\) in which the first move (if any) is always in A. Let \(A^n\) be the n-fold sequoid on A — i.e. \(A^0 = I\),
— i.e. it is a subgame of \(A \otimes B\) in which the first move (if any) is always in A. Let \(A^n\) be the n-fold sequoid on A — i.e. \(A^0 = I\),  , so that plays in A consist of n interleaved plays of A, opened in a fixed order.
, so that plays in A consist of n interleaved plays of A, opened in a fixed order.
Proposition 4
\(A^n\) is an n-ary symmetric tensor power.
This is established using the categorical structure underlying the sequoid — it is a monoidal action of \(\mathcal {C}\) upon its subcategory of strict morphisms (strategies on  such that every opening move in A is followed by a move in B) — and the fact that the tensor decomposes into the sequoid (\(A \otimes B\) is the cartesian product of
such that every opening move in A is followed by a move in B) — and the fact that the tensor decomposes into the sequoid (\(A \otimes B\) is the cartesian product of  and
and  ).Footnote 1
).Footnote 1
4.2 Preservation of Cofree Commutative Comonoids
In order to lift the functor between underlying categories which is implicit in the change of base to a functor of CCCs between the co-Kleisli categories of the free exponential (preserving the meaning of types and terms in the \(\lambda \)-calculus) it is necessary for it to preserve cofree commutative comonoids. We give conditions for this to hold based on the construction of the latter described in [22] — i.e. (putting it in a nutshell) as the limit of the diagram:
where \(A_\bullet \) is the product \(A \times I\) (more precisely, the “free pointed object” on A) and \(p_i:(A \times I)^{i+1} \rightarrow (A \times I)^i\) is the unique morphism given by the universal property of the symmetric tensor power such that \(p_i;{\mathsf {eq}}_i:A \bullet ^{i+1} \rightarrow \bullet ^{\otimes i} = {\mathsf {eq}}_{i+1};(A_\bullet ^{\otimes i} \otimes \pi _r)\).
This is a refinement of Lafont’s construction (in categories with biproducts, the above limit is \(\bigoplus _{i \in {\mathbb {N}}}A^i\)). To show that it is preserved by \(\varPhi ^{\mathcal {R}}_*\), we make the further assumption that for each \(p_i\) there is a corresponding morphism \(e_i:A_\bullet ^i \rightarrow A_\bullet ^{i+1}\), forming an embedding projection (e-p) pair \((e_i,p_i):A_i \unlhd B_i\) — i.e. \(e_i;p_i = {\mathsf {id}}_{A_\bullet ^i}\) and \(p_i;e_i \le {\mathsf {id}}_{A^{i+1}}\).
Given an e-p pair from D to E in the category of coherence spaces (which corresponds to a coherence preserving injection from |D| into |E|), define \(p_\bullet \subseteq |E_{\bullet }| \times |D_{\bullet }|\) by \(\{({\mathtt {inl}}(e),{\mathtt {inl}}(d))\ |\ (d,e) \in p\} \cup \{(e,{\mathtt {inr}}(*))\ |\ e = {\mathtt {inr}}(*) \vee \not \exists d\in D.(d,e) \in p\}\).
\({\mathbf {CSpace}}\) has limits for any chain of such pairs \(D_0 \mathop {\unlhd }\limits ^{e_0,p_0} D_1 \mathop {\unlhd }\limits ^{e_1,p_1} \ldots \) \(|\bigsqcup D| = \{x \in \varPi _{i < \omega }|(D_i)_\bullet | \ |\ \exists i.x_i \not = {\mathtt {inr}}(*)\wedge \forall i \in \omega .(x_{i+1},x_{i})\in (p_i)_\bullet \}\), with  if
if  for all i. This is also the limit for \(D_0 \mathop {\unlhd }\limits ^{\varPhi ^{\mathcal {R}}(e_0),\varPhi ^{\mathcal {R}}(p_0)} D_1 \mathop {\unlhd }\limits ^{\varPhi ^{\mathcal {R}}(e_1),\varPhi ^{\mathcal {R}}(p_1)} \ldots \) in \({\mathbf {Set}}_{{\mathcal {R}}}\) — i.e. \(\varPhi ^{\mathcal {R}}\) preserves limits for all e-p chains. As in the case of equalizers, we can use this fact, to show that they are preserved by \(\varPhi ^{\mathcal {R}}_0\).
for all i. This is also the limit for \(D_0 \mathop {\unlhd }\limits ^{\varPhi ^{\mathcal {R}}(e_0),\varPhi ^{\mathcal {R}}(p_0)} D_1 \mathop {\unlhd }\limits ^{\varPhi ^{\mathcal {R}}(e_1),\varPhi ^{\mathcal {R}}(p_1)} \ldots \) in \({\mathbf {Set}}_{{\mathcal {R}}}\) — i.e. \(\varPhi ^{\mathcal {R}}\) preserves limits for all e-p chains. As in the case of equalizers, we can use this fact, to show that they are preserved by \(\varPhi ^{\mathcal {R}}_0\).
Proposition 5
If \(\bigsqcup A\) is a limit for the chain \(A_0 \mathop {\unlhd }\limits ^{e_0,p_0} A_1 \mathop {\unlhd }\limits ^{e_1,p_1} \ldots \) in a \({\mathbf {CSpace}}\)-category \(\mathcal {C}\), then it is a limit in \(\mathcal {C}^{\mathcal {R}}\) for the chain \(A_0 \mathop {\unlhd }\limits ^{\varPhi (e_0,p_0)} A_1 \mathop {\unlhd }\limits ^{\varPhi ^{\mathcal {R}}(e_1,p_1)} \ldots \)
Proof
The universal property is established as in Prop. 2 — for any B, \(\mathcal {C}(B,\bigsqcup A)\) is a limit in \({\mathbf {CSpace}}\) for the e-p chain \(\mathcal {C}(B,A_0) \unlhd \mathcal {C}(B,A) \unlhd \ldots \), and thus \(\varPhi ^{{\mathcal {R}}}(\mathcal {C}(B, \bigsqcup A))\) is a limit for \(\varPhi ^{\mathcal {R}}(\mathcal {C}(B,A_0)) \unlhd \varPhi ^{{\mathcal {R}}}(\mathcal {C}(B,A_2)) \unlhd \ldots \), and hence \(\bigsqcup A\) is a limit for \(A_0 \unlhd A_1 \unlhd \ldots \) in \(\mathcal {C}^{\mathcal {R}}\).
Any cartesian product in \(\mathcal {C}_0\) is a cartesian product in \(\mathcal {C}^{\mathcal {R}}_0\) (since \(\varPhi ^{\mathcal {R}}\) preserves products) and so in particular \(A \times I\) is the free pointed object on A in \(\mathcal {C}^{\mathcal {R}}_0\). Hence, if ! is a limit for \(I \mathop {\leftarrow }\limits ^{p_0} A_\bullet \mathop {\leftarrow }\limits ^{p_1} \ldots A_\bullet ^i \mathop {\leftarrow }\limits ^{p_2} \ldots \) in \(\mathcal {C}_0\) then it is a limit for \(I \mathop {\leftarrow }\limits ^{\varPhi ^{\mathcal {R}}(p_0)} A_\bullet \mathop {\leftarrow }\limits ^{\varPhi ^{\mathcal {R}}(p_1)} \ldots \) in \(\mathcal {C}^{\mathcal {R}}_0\).
As we have observed, our category of games \({\mathbf G}_0\) has all symmetric tensor powers. We also have an embedding-projection pair from \(A^{n}\) to \(A^{n+1}\) for each n — viz \(e_0 = \bot _{I,A}\),  .
.
\({\mathbf G}\) does not have all products, however. In particular, the free pointed object \(A \times I\) does not exist in general — e.g. we may show that there is no object \(I \times I\) such that \({\mathbf G}(I,I \times I) \cong {\mathbf G}(I,I) \times {\mathbf G}(I,I)\). However we may identify a full subcategory of \({\mathbf G}\) (i.e. a collection of objects — the well-opened games) for which products exist. A game A is well-opened if \(P_A\) consists only of sequences containing exactly one initial move. If A and B are well-opened then their product \(A \times B\) consists of the well-opened sequences in \(A \otimes B\). Moreover, if A is well-opened then the free pointed object on A is \((G_A,P_A \cup \varepsilon )\), and the limit !A for the chain \(I \mathop {\leftarrow }\limits ^{p_0} A_\bullet \mathop {\leftarrow }\limits ^{p_1}\ldots \) is the game consisting of all legal interleavings of sequences in \(P_A\). Note also that if B is well opened then  is well-opened. Hence the “co-Kleisli” category \({\mathbf G}_!\) in which objects are well-opened games, and morphisms from A to B are morphisms from !A to B in \({\mathbf G}\) is Cartesian closed. This is equivalent to the cartesian closed category of games constructed in [1], etc. (less the even-prefix-closure condition on strategies). Since \(\varPhi ^{{\mathcal {R}}}_0(!A)\) is the cofree commutative comonoid in \({\mathbf G}^{{\mathcal {R}}}_0\) for each well-opened game, we have a cartesian closed category of well-opened games and \({\mathcal {R}}\)-weighted strategies, \({\mathbf G}^{{\mathcal {R}}}_!\) with a cartesian closed functor \(\varPhi ^{\mathcal {R}}_!:{\mathbf G}_! \rightarrow {\mathbf G}^{{\mathcal {R}}}_!\).
is well-opened. Hence the “co-Kleisli” category \({\mathbf G}_!\) in which objects are well-opened games, and morphisms from A to B are morphisms from !A to B in \({\mathbf G}\) is Cartesian closed. This is equivalent to the cartesian closed category of games constructed in [1], etc. (less the even-prefix-closure condition on strategies). Since \(\varPhi ^{{\mathcal {R}}}_0(!A)\) is the cofree commutative comonoid in \({\mathbf G}^{{\mathcal {R}}}_0\) for each well-opened game, we have a cartesian closed category of well-opened games and \({\mathcal {R}}\)-weighted strategies, \({\mathbf G}^{{\mathcal {R}}}_!\) with a cartesian closed functor \(\varPhi ^{\mathcal {R}}_!:{\mathbf G}_! \rightarrow {\mathbf G}^{{\mathcal {R}}}_!\).
5 \({\mathcal {R}}\)-Weighted Idealized Algol
By the results in [1] we know that \({\mathbf G}_!\) furnishes a semantics of Reynolds’ Idealized Algol — an applied, simply-typed \(\lambda \)-calculus which may be considered as an extension of PCF with integer state (conservative with respect to the operational semantics). So applying the functor \(\varPhi ^{{\mathcal {R}}}_0:{\mathbf G}_0 \rightarrow {\mathbf G}^{\mathcal {R}}_0\) gives us a semantics of Idealized Algol in \({\mathbf G}^{{\mathcal {R}}}_!\). Since the biproduct completion of \({\mathbf G}^{\mathcal {R}}_0\) is an example of the categorical model described in [18] (a Lafont category with biproducts) we also have a semantics of \({\mathcal {R}}\)-weighted PCF in \({\mathbf G}^{{\mathcal {R}}}_!\). This agrees with the semantics of Idealized Algol on their common part (the operations and constants of PCF) and so we may combine both models, to give an interpretation of \({\mathrm {IA}}^{{\mathcal {R}}}\;\)— erratic Idealized Algol with scalar weights from \({\mathcal {R}}\). Moreover — unlike the weighted relational semantics of \({\mathrm {PCF}}^{{\mathcal {R}}}\ \!\)— this model is fully abstract, a property it inherits directly from the qualitative version.
Types of Idealized Algol are formed from ground types \({\mathtt {nat}}\), \({\mathtt {com}}\) (commands) and \({\mathtt {var}}\) (integer references). Terms are formed by extending the \(\lambda \)-calculus with fixed points, with the following constantsFootnote 2:
-
Arithmetic, conditionals: \({\mathtt {0}}:{\mathtt {nat}}\), \({\mathtt {succ}},{\mathtt {pred}}:{\mathtt {nat}}\rightarrow {\mathtt {nat}}\), \({\mathtt {Ifz}}:{\mathtt {nat}}\rightarrow {\mathtt {nat}}\).
-
Imperative programming: \({\mathsf {seq}}:{\mathtt {com}}\rightarrow B \rightarrow B\) (sequential composition) and \({\mathtt {new}}:({\mathtt {var}}\rightarrow B) \rightarrow B\) (new variable declaration) where \(B \in \{{\mathtt {com}},{\mathtt {nat}}\}\), \({\mathtt {assn}}:{\mathtt {nat}}\rightarrow {\mathtt {var}}\rightarrow {\mathtt {com}}\), \({\mathtt {deref}}:{\mathtt {var}}\rightarrow {\mathtt {nat}}\), and \({\mathtt {mkvar}}:{\mathtt {nat}}\rightarrow ({\mathtt {nat}}\rightarrow {\mathtt {com}}) \rightarrow {\mathtt {var}}\) (“bad variable” construction).
-
\({\mathcal {R}}\)-module structure — a nondeterministic choice operator \({\mathtt {or}}:B \rightarrow B \rightarrow B\) and scalar multiplication \({\mathtt {scl(k)}}:B \rightarrow B\) for each \(k \in {\mathcal {R}}\).
The operational semantics for \({\mathrm {IA}}^{{\mathcal {R}}}\;\)extends that given for \({\mathrm {PCF}}^{{\mathcal {R}}}\ \!\)[20], just as Idealized Algol extends PCF. We define a labelled transition system in which states are configurations — pairs \((P,{\mathcal {S}})\) of a (ground-type) program and a store (a sequence \((a_1,n_1),\ldots ,(a_n,n_k)\) of pairs of a location name and integer value). Labels are elements of the monoid \((u,a) \in \{l,r\}^* \times {\mathcal {R}}\) and actions take the form \(E[M],{\mathcal {S}}\mathop {\longrightarrow }\limits ^{u,a} E[M'],{\mathcal {S}}'\), where \(E[\_]\) is an evaluation context, given by the grammar: \(E{:}{:}= [\_]\ |\ E\;M\ |\ {\mathtt {succ}}\;E\ |\ {\mathtt {pred}}\;E\ |\ {\mathtt {Ifz}}\;E\ |\ {\mathsf {seq}}\;E \ |\ {\mathtt {assn}}\;E\ |\ ({\mathtt {assn}}\;{\mathtt {n}})\;E\ |\ {\mathtt {deref}}\;E\) and \(M,{\mathcal {S}}\mathop {\longrightarrow }\limits ^{u,a} M',{\mathcal {S}}'\) is an instance of one of the following rules:

The relation \(\mathop {\longrightarrow }\limits ^{u,a}\) is deterministic, and so we may define the weight in \({\mathcal {R}}\) of each configuration with respect to a sequence \(u \in \{l,r\}^*\) of branching choices: \(w_u(P,{\mathcal {S}}) = a\) if \(P,{\mathcal {S}}\mathop {\longrightarrow }\limits ^{u_1,a_1} \ldots \mathop {\longrightarrow }\limits ^{u_n,a_n} {\mathtt {skip}},{\mathcal {S}}'\), where \((u,a) = (u_1 \cdot \ldots u_n, a_1\cdot \ldots \cdot a_n)\),
\(w_u(P,{\mathcal {S}}') = 0\) if there is no such sequence of reductions.
The total weight of a configuration in \({\mathcal {R}}\) is given by summing the weights over all possible paths: \(w(P,{\mathcal {S}}) \triangleq \varSigma _{u \in \{l,r\}^*}w_u(P,{\mathcal {S}})\), and \(w(P) = w(P,\_)\). From this notion of testing we derive a notion of equivalence: \(P \approx Q\) if for any closing compatible context \(C[\_]:{\mathtt {com}}\), \(w(C[P]) = w(C[Q])\).
As discussed in [20] for PCF, the computational meaning of \({\mathrm {IA}}^{{\mathcal {R}}}\;\)depends on the choice of semiring — it may be regarded as a metalanguage for a family of “resource-sensitive” imperative programming languages and their semantics. The weighted games models discussed previously may be viewed as instances of this. Probabilistic games [8] are used to interpret Idealized Algol extended with a constant \({\mathtt {coin}}:{\mathtt {nat}}\) which reduces to either \({\mathtt {0}}\) or \({\mathtt {1}}\), both with probability 0.5. Thus we may interpret probabilistic Algol inside \({\mathrm {IA}}^{{\mathcal {R}}}\;\)by defining \({\mathtt {coin}} \triangleq {\mathtt {(scl(0.5)\; {\mathtt {0}})\; {\;\mathtt {or}}\; (scl(0.5)\ {\mathtt {1}})}}\).
Slot games are used to give an interpretation of Idealized Concurrent Algol which is sound with respect to an operational semantics which keeps track of the (time, memory, etc.) costs of evaluation as a natural number — each reduction rule is decorated with such a cost, and the worst-case cost is assigned to each program. Setting \({\mathcal {R}}\) to be the tropical semiring, we may define a translation of non-deterministic IA into \({\mathrm {IA}}^{{\mathcal {R}}}\;\)which is sound with respect to this notion of evaluation, by applying a weighting to each operation corresponding to the cost of its evaluation.
5.1 Denotational Semantics
We interpret \({\mathrm {IA}}^{{\mathcal {R}}}\;\)in the category of games and \({\mathcal {R}}\)-weighted strategies by extending the semantics of \({\mathrm {PCF}}^{{\mathcal {R}}}\ \!\)[20] with the image under \(\varPhi ^{\mathcal {R}}_0\) of the semantics of the types and constants of Idealized Algol defined in [1]. (We use the version in which each game consists of only complete sequences, in which every question is answered.) The types \({\mathtt {com}}\), \({\mathtt {nat}}\) and \({\mathtt {var}}\) denote the (well-opened) games \(\varSigma \) (with a single question and answer) N (with a single Opponent question and Player answers for each value \(n \in {\mathbb {N}}\)
Footnote 3) and the product \(N \times \varSigma ^\omega \), respectively. The arrow type \(S \rightarrow T\) denotes the well-opened game  . Terms-in context \(x_1:S_1,\ldots ,x:_n:S_n \vdash M:T\) are interpreted as morphisms from \(\llbracket S_1\rrbracket \times \ldots \times \llbracket S_n\rrbracket \) to \(\llbracket T\rrbracket \) in \({\mathbf G}^{\mathcal {R}}_!\). Each of the constants C : T of Idealized Algol denotes a strategy in \({\mathbf G}_!\), and thus a \({\mathcal {R}}\)-weighted strategy in \({\mathbf G}^{\mathcal {R}}_!\).
. Terms-in context \(x_1:S_1,\ldots ,x:_n:S_n \vdash M:T\) are interpreted as morphisms from \(\llbracket S_1\rrbracket \times \ldots \times \llbracket S_n\rrbracket \) to \(\llbracket T\rrbracket \) in \({\mathbf G}^{\mathcal {R}}_!\). Each of the constants C : T of Idealized Algol denotes a strategy in \({\mathbf G}_!\), and thus a \({\mathcal {R}}\)-weighted strategy in \({\mathbf G}^{\mathcal {R}}_!\).
This leaves the interpretation of the fixed point operator, which takes a term \(\varGamma ,x:T \vdash M:T\) to its fixed point \(\varGamma \vdash \mu x.M:T\). Semantically, this corresponds to a parameterised fixed point operator on our cartesian closed category of games — a map taking each endomorphism \(f \in \mathcal {C}(B \times A,A)\) to a morphism \({\mathsf {fix}}_B(f) \in \mathcal {C}_!(B,A)\) satisfying \({\mathsf {fix}}(f) = \langle B, {\mathsf {fix}}(f) \rangle ;f\). As \({\mathbf G}_!\) is cpo-enriched, this may defined as (parameterised) least fixedpoint. If \({\mathcal {R}}\) is not continuously ordered, then this construction is not available but we may adopt the alternative, described in [18], based on the existence of a bifree algebra for the free exponential in \(({\mathbf G}_0^{\mathcal {R}})^\varPi \) — the object \(\bigoplus _{X \in \mathbb {M}} I\), where \(\mathbb {M}\) is the set of nested finite multisets. This is sufficient (cf. [23]) to define a fixed point operator on the co-Kleisli category \({\mathbf G}_!^{{\mathcal {R}}}\).
The computational adequacy property for our semantics states that the weight for a program of type \({\mathtt {com}}\) computed by the operational semantics is equal to the weight assigned by its denotation to the single well-opened sequence (qa) in \(\llbracket {\mathtt {com}}\rrbracket \). The proof of this follows closely that of [18], defining an equivalent semantics which assigns precise resouce bounds to variables indicating how many times they are called (and in the case of recursively defined variables, a nested finite multiset representing their call-pattern), and proving soundness for this by a nested multiset induction. The only further requirement is a set of equations establishing the soundness of the reduction rules for the constants of Idealized Algol: these were already established in [1] in proving soundness for the semantics in \({\mathbf G}\).
Proposition 6
For every program \(P:{\mathtt {com}}\), \(\llbracket P,{\mathcal {S}}\rrbracket (qa) = w(P,{\mathcal {S}})\).
Although full abstraction fails in the semantics of \({\mathrm {PCF}}^{{\mathcal {R}}}\ \!\)in \({\mathbf {Set}}_{{\mathcal {R}}}\) [18], it holds in our model of \({\mathrm {IA}}^{{\mathcal {R}}}\;\), following readily from the definability property for the game semantics of Idealized Algol in \({\mathbf G}\).
Theorem 1
[1]. For any finite strategy \(\sigma :\llbracket T\rrbracket \) there exists a IA term \(M_\sigma :T\) such that \(\llbracket M_{\sigma }\rrbracket _{{\mathbf G}} = \sigma \).
Thus, in particular, every atomic strategy on \(\llbracket T\rrbracket \) (consisting of a single legal sequence) is definable as a term of Idealized Algol (without fixed points), and so any finitary strategy in \({\mathbf G}_{{\mathcal {R}}}\) (i.e. one for which finitely many sequences have non-zero weight) is definable as a finite weighted sum of Idealized Algol terms.
Corollary 1
(Definability for \({\mathrm {IA}}^{{\mathcal {R}}}\;\) ). For any finitary \({\mathcal {R}}\)-weighted strategy \(\phi :\llbracket T\rrbracket \) there exists a term \(M_\phi :T\) such that \(\llbracket M_{\phi }\rrbracket = \phi \).
Corollary 2
(Full Abstraction for \({\mathrm {IA}}^{{\mathcal {R}}}\;\) ). \(M \approx M'\) if and only if \(\llbracket M\rrbracket = \llbracket M'\rrbracket \)
Proof
This closely follows the proof in the original model — e.g. for completeness suppose \(\llbracket M\rrbracket \not \approx \llbracket M'\rrbracket \), and thus there exists a complete \(s \in P_{\llbracket T\rrbracket }\) such that \(\llbracket M\rrbracket (s) \not = \llbracket M'\rrbracket (s)\). By the definability property, the strategy \(\phi :\llbracket T\rrbracket \rightarrow \llbracket {\mathtt {com}}\rrbracket \) such that \(\phi (t) =1 \) if \(t = qsa\) (and 0 otherwise) denotes a term \(N:T \rightarrow {\mathtt {com}}\) of Idealized Algol and thus \(\llbracket N\;m \rrbracket _{R}(qa) = \llbracket M\rrbracket (s)\) and \(\llbracket N\;M'\rrbracket (qa) = \llbracket M'\rrbracket (s)\). Hence by computational adequacy, \(w(N\;M') \not = w(N\;M')\) and so \(P \not \approx Q\) as required.
This establishes that any inequivalent terms of \({\mathrm {IA}}^{{\mathcal {R}}}\;\)may be separated by a term of Idealized Algol. So, for example, our model is fully abstract for Probabilistic Algol.
6 Conclusions and Further Directions
We have described a general way of moving from qualitative intensional models to quantitative ones, using the notion of change of base of an enriched category. The only really essential properties that this uses from the original model of Idealized Algol are that strategies may be viewed as certain cliques in a coherence space and that composition is a stable, linear function, ruling out interleaving models of concurrency, except in the case of idempotent semirings. For the sake of simplicity, we have sidestepped mention of causal order (e.g. prefix order in games), which gives a finer characterization of strategy behaviour. For example, we may enrich categories over event structures [24, 25] (or dI-domains [3]) — thus a monoidal functor adding weights to event structures may be used to change their base.
Notes
- 1.
This structure may all be be given in enriched form, and is therefore preserved by change of base.
- 2.
We consider the variant of IA with active expressions and bad variables as in [1].
- 3.
In \({\mathbf G}^{\mathcal {R}}\), \(N \cong \bigoplus _{i \in {\mathbb {N}}}\varSigma \).
References
Abramsky, S., McCusker, G.: Linearity, sharing and state: a fully abstract game semantics for Idealized Algol with active expressions. In: O’Hearn, P.W., Tennent, R. (eds.) Algol-like languages. Birkhauser (1997)
Baillot, P., Danos, V., Ehrhard, T., Regnier, L.: AJM games are a model of classical linear logic. In: Proceedings of the Twelfth International Symposium on Logic in Computer Science, LICS 1997 (1997)
Berry, G.: Stable models of typed \(\lambda \)-calculi. In: Ausiello, G., Böhm, C. (eds.) ICALP 1978. LNCS, vol. 62, pp. 72–89. Springer, Heidelberg (1978). doi:10.1007/3-540-08860-1_7
Berry, G., Curien, P.-L.: Sequential algorithms on concrete data structures. Theoret. Comput. Sci. 20, 265–321 (1982)
Calderon, A., McCusker, G.: Understanding game semantics through coherence spaces. Electron. Notes Theoret. Comput. Sci. 265, 231–244 (2010)
Churchill, M., Laird, J., McCusker, G.: Imperative programs as proofs via game semantics. Ann. Pure and Appl. Logic 64, 27–94 (2013)
Cruttwell, G.: Normed Spaces and Change of Base for Enriched Categories. Ph.D. thesis, Dalhousie University (2008)
Danos, V., Harmer, R.: Probabilistic game semantics. ACM Trans. Comput. Logic 3(3), 359–382 (2002)
Ehrhard, T.: Hypercoherence: a strongly stable model of linear logic. In: Girard, J.-Y., Lafont, Y., Regnier, L. (eds.) Advances in Linear Logic. Cambridge University Press, Cambridge (1995)
Ghica, D.: Slot games: a qunatitative model of computation. In: Proceedings of the 32nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 85–97 (2005)
Ghica, D., McCusker, G.: The regular language semantics of second-order Idealised Algol. Theoret. Comput. Sci. 309, 469–502 (2003)
Girard, J.-Y., Taylor, P., Lafont, Y.: Proofs and Types. Cambridge University Press, Cambridge (1990)
Harmer, R., McCusker, G.: A fully abstract games semantics for finite non-determinism. In: Proceedings of the Fourteenth Annual Symposium on Logic in Computer Science, LICS 1999. IEEE Computer Society Press (1998)
Hyland, J.M.E., Ong, C.-H.L.: On full abstraction for PCF: I, II and III. Inf. Comput. 163, 285–408 (2000)
Janelidze, G., Kelly, G.M.: A note on actions of a monoidal category. Theor. Appl. Categories 9(4), 61–91 (2001)
Lafont, Y.: Logiques, catégories et machines. Ph.D thesis, Université Paris 7 (1988)
Laird J.: A categorical semantics of higher-order store. In: Proceedings of CTCS 2002, number 69 in ENTCS. Elsevier (2002)
Laird, J.: Fixed points in quantitative semantics. In: Proceedings of LICS 2016, pp. 347–356. ACM (2016)
Laird, J., Manzonetto, G., McCusker, G.: Constructing differential categories and deconstructing categories of games. Inf. Comput. 222, 247–264 (2013)
Laird, J., Manzonetto, G., McCusker, G., Pagani, M.: Weighted relational models of typed lambda-calculi. In: Proceedings of LICS 2013 (2013)
Lamarche, F.: Quantitative domains and infinitary algebras. Theoret. Comput. Sci. 94, 37–62 (1999)
Melliès, P.-A., Tabareau, N., Tasson, C.: An explicit formula for the free exponential modality of linear logic. In: Albers, S., Marchetti-Spaccamela, A., Matias, Y., Nikoletseas, S., Thomas, W. (eds.) ICALP 2009. LNCS, vol. 5556, pp. 247–260. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02930-1_21
Simpson, A., Plotkin, G.: Complete axioms for categorical fixed-point operators. In: Proceedings of LICS 2000, pp. 30–41. IEEE Press (2000)
Winskel, G.: Event structures. In: Brauer, W., Reisig, W., Rozenberg, G. (eds.) ACPN 1986. LNCS, vol. 255, pp. 325–392. Springer, Heidelberg (1987). doi:10.1007/3-540-17906-2_31
Winskel, G.: Concurrent strategies. In: Proceedings of LICS 2011 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Laird, J. (2017). From Qualitative to Quantitative Semantics. In: Esparza, J., Murawski, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2017. Lecture Notes in Computer Science(), vol 10203. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54458-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-662-54458-7_3
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54457-0
Online ISBN: 978-3-662-54458-7
eBook Packages: Computer ScienceComputer Science (R0)


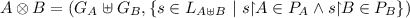 , where
, where 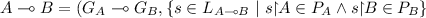 ), where
), where  is the graft of A onto the root nodes of B —
is the graft of A onto the root nodes of B — 