Abstract
Variational systems are ubiquitous in many application areas today. They use features to control presence and absence of system functionality. One challenge in the development of variational systems is their formal analysis and verification. Researchers have addressed this problem by designing aggregate so-called family-based verification algorithms. Family-based model checking allows simultaneous verification of all variants of a system family (variational system) in a single run by exploiting the commonalities between the variants. Yet, the computational cost of family-based model checking still greatly depends on the number of variants. In order to make it computationally cheaper, we can use variability abstractions for deriving abstract family-based model checking, where the variational model of a system family is replaced with an abstract (smaller) version of it which preserves the satisfaction of LTL properties. The variability abstractions can be combined with different partitionings of the set of variants to infer various verification scenarios for the variational model. However, manually finding an optimal verification scenario is hard since it requires a good knowledge of the family and property, while the number of possible scenarios is very large.
In this work, we present an automatic iterative abstraction refinement procedure for family-based model checking. We use Craig interpolation to refine abstract variational models based on the obtained spurious counterexamples (traces). The refinement procedure works until a genuine counterexample is found or the property satisfaction is shown for all variants in the family. We illustrate the practicality of this approach for several variational benchmark models.
Partially supported by The Danish Council for Independent Research under a Sapere Aude project, VARIETE.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Software Product Line Engineering (SPLE) [9] is a popular methodology for building a family of related systems. A large number of related systems (variants) are developed by systematically reusing common parts. Each variant is specified in terms of features (statically configured options) selected for that particular variant. Due to the popularity of SPLs in embedded and critical system domain (e.g. cars, phones, avionics), they require rigourous verification and analysis.
Model checking is a well-known technique for automatic verification of systems against properties expressed in temporal logic [1]. Model checking families of systems is more difficult than model checking single systems, since the number of possible variants is exponential in the number of features. Hence, the simplest enumerative variant-by-variant approach, that applies single-system model checking to each individual variant of a system family, is very inefficient. Indeed, a given execution behaviour is checked as many times as the number of variants that are able to execute it. In order to address this problem, new dedicated family-based model checking algorithms have been introduced [7, 8, 10]. They rely on using compact mathematical structures (so called variational models or featured transition systems) for modelling variational systems, which take the commonality within the family into account, and on which specialized family-based (variability-aware) model checking algorithms can be applied. Each execution behaviour in a variational model is associated with the exact set of variants able to produce it. Therefore, the family-based algorithms check an execution behaviour only once, regardless of how many variants can produce it. In this way, they are able to model check all variants of a family simultaneously in a single step and pinpoint those variants that violate properties. In order to further speed-up family-based model checking, a range of variability abstractions can be introduced [13, 14]. They give rise to abstract family-based model checking. The abstractions are applied at the variability level and aim to reduce the exponential blowup of the number of configurations (variants) to something more tractable by manipulating the configuration space of the family. Abstractions can be combined with partitionings of the set of all variants to generate various verification scenarios. Still, suitable verification scenarios are currently chosen manually from a large set of possible combinations. This often requires a user to have a considerable knowledge of a variational system and property. In order for this approach to be used more widely in industry, automatic techniques are needed for generating verification scenarios.
Abstraction refinement [4, 5, 10] has proved to be one of the most effective techniques for automatic verification of systems with very large state spaces. In this paper, we introduce a purely variability-specific (state-independent) approach to abstraction refinement, which is used for automatic verification of LTL properties over variational models. In general, each variability abstraction computes an over-approximation of the original model, in a such a way that if some property holds for the smaller abstract model then it will hold for the original one. However, if the property does not hold in the abstract model, the found counterexample may be the result of some behaviour in the over-approximation which is not present in the original model. In this case, it is necessary to refine the abstraction so that the behaviour which caused the spurious counterexample is eliminated. The verification procedure starts with the coarsest variability abstraction, and then the obtained abstract model is fed to a model checker. If no counterexample is found, then all variants satisfy the given property. Otherwise, the counterexamples are analysed and classified as either genuine, which correspond to execution behaviours of some variants in the original model, or spurious, which are introduced due to the abstraction. If a genuine counterexample exist, the corresponding variants do not satisfy the given property; otherwise a spurious counterexample is used to refine the abstract models. The procedure is then repeated on the refined abstract variational model only for variants for which no conclusive results have been found. We use Craig interpolation [18, 27] to extract from a spurious counterexample (i.e. the unsatisfiable feature expression associated with it) the relevant information which needs to be known in order to show the unsatisfiability of the associated feature expression. This information is used to compute refined abstract models for the next iteration. The main contribution of this paper is an efficient automatic abstraction refinement procedure for family-based model checking, which uses variability-aware information obtained from spurious counterexamples to guide the verification process. When the employed variability abstractions give rise to abstract models verifiable by a single-system model checker, we obtain a completely automatic alternative to a dedicated family-based model checker. The experiments show that the proposed abstraction refinement procedure combined with the single-system model checker SPIN achieves performance gains compared to the family-based model checker \(\overline{\text {SNIP}}\) when applied to several benchmark variational systems for some interesting properties.
2 Abstract Family-Based Model Checking
We now introduce featured transition systems (FTSs) [8] for modelling variational systems, fLTL temporal formulae [8] for specifying properties of variational systems, and variability abstractions [13, 14] for defining abstract FTSs.
2.1 Featured Transition Systems
Let \(\mathbb {F}= \{A_1, \ldots , A_n\}\) be a finite set of Boolean variables representing the features available in a variational system. A specific subset of features, \(k \subseteq \mathbb {F}\), known as configuration, specifies a variant (valid product) of a variational system. The set of all valid configurations (variants) is defined as: \(\mathbb {K}\subseteq 2^{\mathbb {F}}\). An alternative representation of configurations is based upon propositional formulae. Each configuration \(k \in \mathbb {K}\) can be represented by a formula: \(k(A_1) \wedge \ldots \wedge k(A_n)\), where \(k(A_i) = A_i\) if \(A_i \in k\), and \(k(A_i) = \lnot A_i\) if \(A_i \notin k\) for \(1 \le i \le n\). We will use both representations interchangeably. The set of valid configurations is typically described by a feature model [22], but in this work we disregard syntactic representations of the set \(\mathbb {K}\).
The behaviour of individual variants is given with transition systems.
Definition 1
A transition system (TS) is a tuple \(\mathcal {T}=(S,Act,trans,I,AP,L)\), where S is a set of states; Act is a set of actions; \(trans \subseteq S \times Act \times S\) is a transition relationFootnote 1; \(I \subseteq S\) is a set of initial states; AP is a set of atomic propositions; and \(L : S \rightarrow 2^{AP}\) is a labelling function.
-
An execution (behaviour) of \(\mathcal {T}\) is a nonempty, infinite sequence \(\rho = s_0 \lambda _1 s_1 \lambda _2 \ldots \) with \(s_0 \in I\) such that
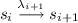 for all \(i \ge 0\). The semantics of the TS \(\mathcal {T}\), denoted as \([\! [\mathcal {T} ]\! ]_{TS}\), is the set of its executions.
for all \(i \ge 0\). The semantics of the TS \(\mathcal {T}\), denoted as \([\! [\mathcal {T} ]\! ]_{TS}\), is the set of its executions.
The combined behaviour of a whole system family is compactly represented with featured transition systems [8]. They are TSs where transitions are also labelled with feature expressions, \(FeatExp(\mathbb {F})\), which represent propositional logic formulae defined over \(\mathbb {F}\) as: \(\psi \, {:}{:=}\,\textit{true}\mid A \in \mathbb {F}\mid \lnot \psi \mid \psi _1 \wedge \psi _2\). The feature expression \(\psi \in FeatExp(\mathbb {F})\) indicates for which variants the corresponding transition is enabled.
Definition 2
An featured transition system (FTS) represents a tuple \(\mathcal {F}=(S,Act,trans,I,AP,L,\mathbb {F},\mathbb {K},\delta )\), where S, Act, trans, I, AP, and L are defined as in TS; \(\mathbb {F}\) is the set of available features; \(\mathbb {K}\) is a set of valid configurations; and \(\delta : trans \rightarrow FeatExp(\mathbb {F})\) is a total function labelling transitions with feature expressions. We write \([\! [\delta (t) ]\! ]\) to denote the set of variants that satisfy \(\delta (t)\), i.e. \(k \in [\! [\delta (t) ]\! ]\) iff \(k\,\models \,\delta (t)\). Moreover:
-
The projection of an FTS \(\mathcal {F}\) to a variant \(k \in \mathbb {K}\), denoted as \(\pi _k(\mathcal {F})\), is the TS \((S,Act,trans',I,AP,L)\), where \(trans'=\{ t \in trans \mid k\,\models \,\delta (t) \}\).
-
The projection of an FTS \(\mathcal {F}\) to a set of variants \(\mathbb {K}' \subseteq \mathbb {K}\), denoted as \(\pi _{\mathbb {K}'}(\mathcal {F})\), is the FTS \((S,Act,trans',I,AP,L,\mathbb {F},\mathbb {K}',\delta )\), where \(trans'=\{ t \in trans \mid \exists k \in \mathbb {K}'. k\,\models \,\delta (t) \}\).
-
The semantics of an FTS \(\mathcal {F}\), denoted as \([\! [\mathcal {F} ]\! ]_{FTS}\), is the union of behaviours of the projections on all variants \(k \in \mathbb {K}\), i.e. \([\! [\mathcal {F} ]\! ]_{FTS} = \cup _{k \in \mathbb {K}} [\! [\pi _k(\mathcal {F}) ]\! ]_{TS}\).
-
The size of an FTS \(\mathcal {F}\) is defined as [8]: \(|\mathcal {F}| = |S| + |trans| + |expr| + |\mathbb {K}|\), where |expr| is the size of all feature expressions bounded by \(O(2^{|\mathbb {F}|} \cdot |trans|)\).
Example 1
Throughout this paper, we will use a beverage vending machine as a running example [8]. The VendingMachine family has five features: VendingMachine (denoted by v) for purchasing a drink which is a mandatory root feature enabled in all products; Tea (denoted by t) for serving tea; Soda (denoted by s) for serving soda; CancelPurchase (denoted by c) for canceling a purchase after a coin is entered; and FreeDrinks (denoted by f) for offering free drinks. The FTS of VendingMachine is shown in Fig. 1a. The feature expression label of a transition is shown next to its label action, separated by a slash. The transitions enabled by the same feature are colored in the same way. For example, the transition  is enabled for variants that contain the feature s. By combining various features, a number of variants of this VendingMachine can be obtained. In Fig. 1b is shown the basic version of VendingMachine that only serves soda, which is described by the configuration: \(\{v,s\}\) (or, as formula \(v \wedge \! s \wedge \! \lnot t \wedge \! \lnot c \wedge \! \lnot f\)). It takes a coin, returns change, serves soda, opens a compartment so that the customer can take the soda, before closing it again. We can obtain the basic vending machine in Fig. 1b by projecting the FTS in Fig. 1a to the configuration \(\{v, s \}\). The set of all valid configurations of VendingMachine can be obtained by combining the above features. For example, we can have \(\mathbb {K}= \{ \{ v, s \}, \{ v, s, t, c, f \}, \{v, s, c\}, \{v, s, c, f \} \}\). \(\square \)
is enabled for variants that contain the feature s. By combining various features, a number of variants of this VendingMachine can be obtained. In Fig. 1b is shown the basic version of VendingMachine that only serves soda, which is described by the configuration: \(\{v,s\}\) (or, as formula \(v \wedge \! s \wedge \! \lnot t \wedge \! \lnot c \wedge \! \lnot f\)). It takes a coin, returns change, serves soda, opens a compartment so that the customer can take the soda, before closing it again. We can obtain the basic vending machine in Fig. 1b by projecting the FTS in Fig. 1a to the configuration \(\{v, s \}\). The set of all valid configurations of VendingMachine can be obtained by combining the above features. For example, we can have \(\mathbb {K}= \{ \{ v, s \}, \{ v, s, t, c, f \}, \{v, s, c\}, \{v, s, c, f \} \}\). \(\square \)
2.2 fLTL Properties
The model checking problem consists of determining whether a model satisfies a given property expressed as LTL (linear time logic) temporal formula [1].
Definition 3
An LTL formula \(\phi \) is defined as: \(\phi \,{:}{:=}\,true \mid a \in AP \mid \lnot \phi \mid \phi _1 \wedge \phi _2 \mid \bigcirc \phi \mid \phi _1 U \phi _2\).
-
Satisfaction of a formula \(\phi \) for an infinite execution \(\rho = s_0 \lambda _1 s_1 \lambda _2 \ldots \) (we write \(\rho _i = s_i \lambda _{i+1} s_{i+1} \ldots \) for the i-th suffix of \(\rho \)) is defined as:
$$\begin{aligned}&\rho \,\models \,true, \qquad \rho \,\models \,a \quad \text {iff} \quad a \in L(s_0), \\&\rho \,\models \,\lnot \phi \quad \text {iff} \quad \rho \not \models \,\phi , \qquad \rho \,\models \,\phi _1 \wedge \phi _2 \quad \text {iff} \quad \rho \,\models \,\phi _1 \text { and } \rho \,\models \,\phi _2, \\&\rho \,\models \,\bigcirc \phi \quad \text {iff} \quad \rho _1\,\models \,\phi \\&\rho \,\models \,\phi _1 U \phi _2 \quad \text {iff} \quad \exists k \ge 0. \, \rho _k\,\models \,\phi _2 \text { and } \forall j \in \{ 0, \ldots , k-1 \}. \, \rho _j\,\models \,\phi _1 \end{aligned}$$ -
A TS \(\mathcal {T}\) satisfies a formula \(\phi \), denoted as \(\mathcal {T}\,\models \,\phi \), iff \(\forall \rho \in [\! [\mathcal {T} ]\! ]_{TS}. \, \rho \,\models \,\phi \).
Note that other temporal operators can be defined as well: \(\Diamond \phi = true \, U \phi \) (eventually) and \(\Box \phi = \lnot \Diamond \lnot \phi \) (always). When we consider variational systems, we sometimes want to define properties with a modality that specifies the set of variants for which they hold.
Definition 4
-
An feature LTL (fLTL) formula is defined as: \([\chi ] \phi \), where \(\phi \) is an LTL formula and \(\chi \in FeatExp(\mathbb {F})\) is a feature expression.
-
An FTS \(\mathcal {F}\) satisfies an fLTL formula \([\chi ] \phi \), denoted as \(\mathcal {F}\,\models \,[\chi ]\phi \), iff \(\forall k \in \mathbb {K}\cap [\! [\chi ]\! ]. \, \pi _k(\mathcal {F})\,\models \,\phi \). An FTS \(\mathcal {F}\) satisfies an LTL formula \(\phi \) iff \(\mathcal {F}\,\models \,[true]\phi \).
Note that \(\mathcal {F}\,\models \,[\chi ]\phi \) iff \(\pi _{[\! [\chi ]\! ]}(\mathcal {F})\,\models \,\phi \). Therefore, for simplicity in the following we focus on verifying only LTL properties \(\phi \).
Example 2
Consider the FTS VendingMachine in Fig. 1a. Suppose that states ⑤ and ⑥are labelled with the proposition \(\texttt {selected}\), and the state ⑧ with the proposition \(\texttt {open}\). An example property \(\phi \) is: \(\Box (\texttt {selected} \implies \Diamond \texttt {open})\), which states that after selecting a beverage, the machine will eventually \(\texttt {open}\) the compartment to allow the customer to take his drink. The basic vending machine satisfies this property: \(\pi _{\{v, s\}}(\textsc {VendingMachine})\,\models \,\phi \), but the entire variational system does not satisfy it: \(\textsc {VendingMachine}\not \,\models \,\phi \). For example, if the feature f (FreeDrinks) is enabled, a counter-example where the state ⑧ is never reached is:  . The set of violating products is \(\{ \{ v, s, t, c, f \}, \{v, s, c, f \} \} \subseteq \mathbb {K}\). However, we have that \(\textsc {VendingMachine}\,\models \,[\lnot f] \phi \). Therefore, we can conclude that the feature f is responsible for violation of the property \(\phi \). \(\square \)
. The set of violating products is \(\{ \{ v, s, t, c, f \}, \{v, s, c, f \} \} \subseteq \mathbb {K}\). However, we have that \(\textsc {VendingMachine}\,\models \,[\lnot f] \phi \). Therefore, we can conclude that the feature f is responsible for violation of the property \(\phi \). \(\square \)
2.3 Variability Abstractions
We now define variability abstractions [13, 14] for decreasing the sizes of FTSs, in particular for reducing the number of features, the configuration space, and the size of feature expressions. The goal of variability abstractions is to weaken feature expressions, in order to make transitions in FTSs available to more variants. We define variability abstractions as Galois connections for reducing the Boolean complete lattice of propositional formulae over \(\mathbb {F}\): \((\textit{FeatExp}(\mathbb {F})_{/\equiv },\,\models ,\vee ,\wedge ,\textit{true},\textit{false})\). Elements of \(\textit{FeatExp}(\mathbb {F})_{/\equiv }\) are equivalence classes of propositional formulae \(\psi \in \textit{FeatExp}(\mathbb {F})\) obtained by quotienting by the semantic equivalence \(\equiv \). The pre-order relation \(\models \) is defined as the satisfaction relation from propositional logic, whereas the least upper bound operator is \(\vee \) and the greatest lower bound operator is \(\wedge \). Furthermore, the least element is false, and the greatest element is \(\textit{true}\). Subsequently, we will lift the definition of variability abstractions to FTSs.
The join abstraction, \(\varvec{\alpha }^{ \text {join} }\), confounds the control-flow of all variants, obtaining a single variant that includes all executions occurring in any variant. The information about which transitions are associated with which variants is lost. Each feature expression \(\psi \) defined over \(\mathbb {F}\) is replaced with true if there exists at least one configuration from \(\mathbb {K}\) that satisfies \(\psi \). The new abstract set of features is empty: \(\varvec{\alpha }^{ \text {join} }(\mathbb {F})=\emptyset \), and the abstract set of valid configurations is a singleton: \(\varvec{\alpha }^{ \text {join} }(\mathbb {K}) = \{ \textit{true}\}\) if \(\mathbb {K}\ne \emptyset \). The abstraction \(\varvec{\alpha }^{ \text {join} }: \textit{FeatExp}(\mathbb {F}) \rightarrow \textit{FeatExp}(\emptyset )\) and concretization functions \(\varvec{\gamma }^{ \text {join} }: \textit{FeatExp}(\emptyset ) \rightarrow \textit{FeatExp}(\mathbb {F})\) are:
The proposed abstraction-concretization pair is a Galois connectionFootnote 2 [13, 14].
The feature ignore abstraction, \(\varvec{\alpha }^{ \text {fignore} }_{A}\), ignores a single feature \(A \in \mathbb {F}\) by confounding the control flow paths that only differ with regard to A, but keeps the precision with respect to control flow paths that do not depend on A. Let \(\psi \) be a formula into negation normal form (NNF). We write \(\psi [l_A \mapsto true]\) to denote the formula \(\psi \) where the literal of A, that is A or \(\lnot A\), is replaced with \(\textit{true}\). The abstract sets of features and configurations are: \(\varvec{\alpha }^{ \text {fignore} }_{A}(\mathbb {F})=\mathbb {F}\!\setminus \!\{A\}\), and \(\varvec{\alpha }^{ \text {fignore} }_{A}(\mathbb {K}) = \{ k[l_A \mapsto true] \mid k\in \mathbb {K}\}\). The abstraction and concretization functions between \(FeatExp(\mathbb {F})\) and \(FeatExp(\varvec{\alpha }^{ \text {fignore} }_{A}(\mathbb {F}))\), which form a Galois connection [13, 14], are defined as:
where \(\psi \) and \(\psi '\) are in NNF.
The sequential composition \(\alpha _2 \circ \alpha _1\) runs two abstractions \(\alpha _1\) and \(\alpha _2\) in sequence (see [13, 14] for precise definition). In the following, we will simply write \((\alpha ,\gamma )\) for any Galois connection  constructed using the operators presented in this section.
constructed using the operators presented in this section.
Given a Galois connection \((\alpha ,\gamma )\) defined on the level of feature expressions, we now induce a notion of abstraction between FTSs.
Definition 5
Let \(\mathcal {F}=(S,Act,trans,I,AP,L,\mathbb {F},\mathbb {K},\delta )\) be an FTS, and \((\alpha ,\gamma )\) be a Galois connection. We define \(\alpha (\mathcal {F})=(S,Act,trans,I,AP,L,\alpha (\mathbb {F}),\alpha (\mathbb {K}),\alpha (\delta ))\), where \(\alpha (\delta ) : trans \rightarrow FeatExp(\alpha (\mathbb {F}))\) is defined as: \(\alpha (\delta ) (t) = \alpha (\delta (t))\).
Example 3
Consider the FTS \(\mathcal {F}\!=\! \textsc {VendingMachine}\) in Fig. 1a with the set of valid configurations \(\mathbb {K}= \{ \{ v, s \}, \{ v, s, t, c, f \}, \{v, s, c\}, \{v, s, c, f \} \}\). We show \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}({\mathcal {F}}))\) and \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}({\mathcal {F}}))\) in Fig. 2. We do not show transitions labelled with the feature expression false and unreachable states. Also note that both \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}({\mathcal {F}}))\) and \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}({\mathcal {F}}))\) are ordinary TSs, since all transitions are labeled with the feature expression \(\textit{true}\).
For \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}(\mathcal {F}))\) in Fig. 2a, note that \(\mathbb {K}\cap [\! [f ]\! ] = \{ \{ v, s, t, c, f \}, \{ v, s, c, f \} \}\). So, transitions annotated with \(\lnot f\) are not present in \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}(\mathcal {F}))\).
For \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}(\mathcal {F}))\) in Fig. 2b, note that \(\mathbb {K}\cap [\! [\lnot f ]\! ] = \{ \{ v, s \}, \{ v, s, c \} \}\), and so transitions annotated with the features t and f (Tea and FreeDrinks) are not present in \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}(\mathcal {F}))\). \(\square \)
Abstract FTSs have interesting preservation properties [13, 14].
Theorem 1
(Soundness). Let \((\alpha ,\gamma )\) be a Galois connection and \(\mathcal {F}\) be an FTS. If \(\alpha (\mathcal {F})\,\models \,\phi \), then \(\mathcal {F}\,\models \,\phi \).
The family-based model checking problem given in Definition 4 can be reduced to a number of smaller problems by partitioning the set of variants.
Proposition 1
Let the subsets \(\mathbb {K}_1, \mathbb {K}_2, \ldots , \mathbb {K}_n\) form a partition of the set \(\mathbb {K}\). Then: \(\mathcal {F}\,\models \,\phi \), if and only if, \(\pi _{\mathbb {K}_1}(\mathcal {F})\,\models \,\phi , \ldots , \pi _{\mathbb {K}_n}(\mathcal {F})\,\models \,\phi \).
Corollary 1
Let \(\mathbb {K}_1, \mathbb {K}_2, \ldots , \mathbb {K}_n\) form a partition of \(\mathbb {K}\), and \((\alpha _1,\!\gamma _1), \ldots , (\alpha _n, \!\gamma _n)\) be Galois connections. If \(\alpha _1(\pi _{\mathbb {K}_1}(\mathcal {F}))\,\models \,\phi , \ldots , \alpha _n(\pi _{\mathbb {K}_n}(\mathcal {F})) \,\models \,\phi \), Then \(\mathcal {F}\,\models \,\phi \).
In other words, correctness of abstract FTSs implies correctness of the concrete FTS. Note that verification of abstract FTSs can be drastically (even exponentially) faster. However, if abstract FTSs invalidate a property then the concrete FTS may still satisfy the property, i.e. the found counterexample in abstract FTSs may be spurious. In this case, we need to refine the abstract FTSs in order to eliminate the spurious counterexample.
Example 4
Recall the formula \(\phi =\Box (\texttt {selected} \implies \Diamond \, \texttt {open})\) from Example 2, and \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}({\scriptstyle \textsc {VendingMachine}}))\) and \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}({\scriptstyle \textsc {VendingMachine}}))\) shown in Fig. 2. First, we can successfully verify that \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}({\scriptstyle \textsc {VendingMachine}}))\,\models \,\phi \), which implies that all valid variants from \(\mathbb {K}\) that do not contain the feature f (those are \(\{v,s\}\) and \(\{v,s,c\}\)) satisfy the property \(\phi \). On the other hand, we have \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}({\scriptstyle \textsc {VendingMachine}})) not\,\models \,\phi \) with the counterexample:  . This counterexample is genuine for the variants from \(\mathbb {K}\) that contain the feature f (those are \(\{v,s,t,c,f\}\) and \(\{v,s,c,f\}\)). In this way, the problem of verifying the FTS \({\scriptstyle \textsc {VendingMach.}}\) against \(\phi \) can be reduced to verifying whether two TSs, \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}({\scriptstyle \textsc {VendingMach.}}))\) and \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}({\scriptstyle \textsc {VendingMach.}}))\), satisfy \(\phi \). \(\square \)
. This counterexample is genuine for the variants from \(\mathbb {K}\) that contain the feature f (those are \(\{v,s,t,c,f\}\) and \(\{v,s,c,f\}\)). In this way, the problem of verifying the FTS \({\scriptstyle \textsc {VendingMach.}}\) against \(\phi \) can be reduced to verifying whether two TSs, \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}({\scriptstyle \textsc {VendingMach.}}))\) and \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}({\scriptstyle \textsc {VendingMach.}}))\), satisfy \(\phi \). \(\square \)
3 Abstraction Refinement
We now describe the abstraction refinement procedure (ARP), which uses spurious counterexamples to iteratively refine abstract variational models until either a genuine counterexample is found or the property satisfaction is shown for each variant in the family. Thus, the ARP determines for each variant whether or not it satisfies a property, and provides a counterexample for each variant that do not satisfy the given property.
The ARP for checking \(\mathcal {F}\,\models \,\phi \), where \(\mathcal {F}\!\!=\!(S,\!\textit{Act},\!\textit{trans},\!I,\!{\textit{AP}},\!L, \mathbb {F}, \mathbb {K}, \delta )\), is illustrated in Fig. 3. We apply an initial abstraction \(\alpha \), thus obtaining an initial abstract variational model \(\alpha (\mathcal {F})\). If the initial abstract model satisfies the given property, then all variants satisfy it and we stop. Otherwise, the model checker returns a counterexample. Let \(\psi \) be the feature expression computed by conjoining feature expressions labelling all transitions that belong to this counterexample in \(\mathcal {F}\). There are two cases to consider.
First, if \(\psi \) is satisfiable and \(\mathbb {K}\cap [\! [\psi ]\! ] \ne \emptyset \), then the found counterexample is genuine for variants in \(\mathbb {K}\cap [\! [\psi ]\! ]\). For the other variants from \(\mathbb {K}\cap [\! [\lnot \psi ]\! ]\), the found counterexample cannot be executed (i.e. the counterexample is spurious for \(\mathbb {K}\cap [\! [\lnot \psi ]\! ]\)). Therefore, we call the ARP again to verify \(\pi _{[\! [\lnot \psi ]\! ]}(\mathcal {F})\) with updated set of valid configurations \(\mathbb {K}\cap [\! [\lnot \psi ]\! ]\).
Second, if \(\psi \wedge (\bigvee _{k \in \mathbb {K}}k)\) is unsatisfiable (i.e. \(\mathbb {K}\cap [\! [\psi ]\! ] = \emptyset \)), then the found counterexample is spurious for all variants in \(\mathbb {K}\) (due to incompatible feature expressions). Now, we describe how a feature expression \(\psi '\) used for constructing refined abstract models is determined by means of Craig interpolation [27] from \(\psi \) and \(\mathbb {K}\). First, we find the minimal unsatisfiable core \(\psi ^c\) of \(\psi \!\wedge \! (\bigvee _{k \in \mathbb {K}}k)\), which contains a subset of conjuncts in \(\psi \!\wedge \! (\bigvee _{k \in \mathbb {K}}k)\), such that \(\psi ^c\) is still unsatisfiable and if we drop any single conjunct in \(\psi ^c\) then the result becomes satisfiable. We group conjuncts in \(\psi ^c\) in two groups X and Y such that \(\psi ^c=X \wedge Y=false\). Then, the interpolant \(\psi '\) is such that: (1) \(X \implies \psi '\), (2) \(\psi ' \wedge Y=false\), (3) \(\psi '\) refers only to common variables of X and Y. Intuitively, we can think of the interpolant \(\psi '\) as a way of filtering out irrelevant information from X. In particular, \(\psi '\) summarizes and translates why X is inconsistent with Y in their shared language. Once the interpolant \(\psi '\) is computed, we call the ARP to check \(\pi _{[\! [\psi ' ]\! ]}(\mathcal {F})\,\models \,\phi \) for variants in \(\mathbb {K}\cap [\! [\psi ' ]\! ]\), and \(\pi _{[\! [\lnot \psi ' ]\! ]}(\mathcal {F})\,\models \,\phi \) for variants in \(\mathbb {K}\cap [\! [\lnot \psi ' ]\! ]\). By construction, we guarantee that the found spurious counterexample does not occur neither in \(\pi _{[\! [\psi ' ]\! ]}(\mathcal {F})\) nor in \(\pi _{[\! [\lnot \psi ' ]\! ]}(\mathcal {F})\).
Note that, in Step 1, the initial abstraction can be chosen arbitrarily. This choice does not affect correctness and termination of the ARP, but it allows experimentation with different heuristics in concrete implementations. For example, if we use the initial abstraction \(\varvec{\alpha }^{ \text {join} }\), then as an abstract model we obtain an ordinary TS where all feature expressions associated with transitions of \(\mathcal {F}\) occurring in some valid variant are replaced with \(\textit{true}\). Therefore, the verification step can be performed using a single-system model checker (e.g. SPIN). Also note that we call the ARP until there are no more counterexamples or the updated set of valid configurations \(\mathbb {K}\) becomes empty.
Example 5
Let \(\mathcal {F}\) be VendingMachine of Fig. 1a with configurations \(\mathbb {K}= \{ \{ v, s \}, \{ v, s, t, c, f \}, \{v, s, c\}, \{v, s, c, f \} \}\). Let \(\varvec{\alpha }^{ \text {join} }\) be the initial abstraction.
We check \(\mathcal {F}\,\models \,\phi \), where \(\phi =\Box (\texttt {selected} \implies \Diamond \, \texttt {open})\) using the ARP. We first check \(\varvec{\alpha }^{ \text {join} }(\mathcal {F})\,\models \,\phi \)? The following spurious counterexample is reported:  . The associated feature expression in \(\mathcal {F}\) is: \((v \wedge \lnot f) \wedge v \wedge t \wedge f\). The minimal unsatisfiable core is: \((v \wedge \lnot f) \wedge f\), and the found interpolant is \(\lnot f\). In this way, we have found that the feature f is responsible for the spuriousness of the given counterexample. Thus, in the next iteration we check \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}(\mathcal {F}))\,\models \,\phi \) and \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}(\mathcal {F}))\,\models \,\phi \), which give conclusive results for all variants from \(\mathbb {K}\) as explained in Example 4.
. The associated feature expression in \(\mathcal {F}\) is: \((v \wedge \lnot f) \wedge v \wedge t \wedge f\). The minimal unsatisfiable core is: \((v \wedge \lnot f) \wedge f\), and the found interpolant is \(\lnot f\). In this way, we have found that the feature f is responsible for the spuriousness of the given counterexample. Thus, in the next iteration we check \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot f ]\! ]}(\mathcal {F}))\,\models \,\phi \) and \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [f ]\! ]}(\mathcal {F}))\,\models \,\phi \), which give conclusive results for all variants from \(\mathbb {K}\) as explained in Example 4.
Consider the property \(\phi ' =\Box \Diamond \, \texttt {open}\). The following counterexample is found in \(\varvec{\alpha }^{ \text {join} }(\mathcal {F})\):  . The associated feature expression in \(\mathcal {F}\) is: \(v \wedge \lnot f \wedge c\), so this is a genuine counterexample for the variant \(\{v,s,c\} \in \mathbb {K}\). In the next iteration, we check \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot (v \wedge \lnot f \wedge c) ]\! ]}(\mathcal {F}))\,\models \,\phi '\) for variants \(\mathbb {K}\backslash \{v,s,c\}\). We obtain the counterexample:
. The associated feature expression in \(\mathcal {F}\) is: \(v \wedge \lnot f \wedge c\), so this is a genuine counterexample for the variant \(\{v,s,c\} \in \mathbb {K}\). In the next iteration, we check \(\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot (v \wedge \lnot f \wedge c) ]\! ]}(\mathcal {F}))\,\models \,\phi '\) for variants \(\mathbb {K}\backslash \{v,s,c\}\). We obtain the counterexample:  , with associated feature expression \(f \wedge c\), realizable for variants \(\{v,s,t,c,f\}\) and \(\{v,s,c,f\}\)). In the final iteration, we check \(\varvec{\alpha }^{ \text {join} }\big (\pi _{[\! [\lnot (f \wedge c) ]\! ]} (\pi _{[\! [\lnot (v \wedge \lnot f \wedge c) ]\! ]}(\mathcal {F}))\big )\,\models \,\phi '\) for the variant \(\{v,s\}\). The property holds, so \(\phi '\) is satisfied by \(\{v,s\}\). \(\square \)
, with associated feature expression \(f \wedge c\), realizable for variants \(\{v,s,t,c,f\}\) and \(\{v,s,c,f\}\)). In the final iteration, we check \(\varvec{\alpha }^{ \text {join} }\big (\pi _{[\! [\lnot (f \wedge c) ]\! ]} (\pi _{[\! [\lnot (v \wedge \lnot f \wedge c) ]\! ]}(\mathcal {F}))\big )\,\models \,\phi '\) for the variant \(\{v,s\}\). The property holds, so \(\phi '\) is satisfied by \(\{v,s\}\). \(\square \)
Theorem 2
The ARP terminates and is correct.
Proof
At the end of an iteration, the ARP either terminates with answer ‘yes’, or finds a genuine counterexample and updates \(\mathbb {K}\) into \(\mathbb {K}'\), or finds a spurious counterexample and updates \(\mathbb {K}\) into \(\mathbb {K}_1\) and \(\mathbb {K}_2\). Given that \(\mathbb {K}' \subset \mathbb {K}\) (the counterexample is genuine for some non-empty subset of \(\mathbb {K}\)), and \(\mathbb {K}_1 \subset \mathbb {K}\), \(\mathbb {K}_2 \subset \mathbb {K}\) (by def. \(\mathbb {K}_1 \ne \emptyset \), \(\mathbb {K}_2 \ne \emptyset \), \(\mathbb {K}_1 \cup \mathbb {K}_2 = \mathbb {K}\)), the number of possible updates and calls to the ARP are finite. Therefore, the number of iterations is also finite.
If the ARP terminates with answer that a property is satisfied (resp., property is not satisfied) by a variant, then the answer is correct by Theorem 1, since any abstraction constructs an over-approximated model for a given set of variants. \(\square \)
4 Evaluation
In this section, we describe our implementation of the ARP, and present the results of experiments carried out on several variational models. We use experiments to evaluate in which cases and to what extent our ARP technique outperforms the family-based model checking algorithms of FTS [7, 8] implemented in \(\overline{\text {SNIP}}\) Footnote 3.
Implementation. It is difficult to use FTSs directly to model large variational systems. Therefore, \(\overline{\text {SNIP}}\) uses the high-level languages \(f{\textsc {Promela}}\) and TVL for modeling variational systems and their configuration sets, respectively. \(f{\textsc {Promela}}\) is an extension of Promela, the language of the SPIN model checker [19], adding feature variables, \(\mathbb {F}\), and a new guarded-by-features statement, “gd”. The “\(\texttt {gd}\)” is a non-deterministic statement similar to Promela’s “\(\texttt {if}\)”, except that only feature expressions can be used as guards. Actually, this is the only place where features may be used. Thus, “gd” plays the same role in \(f{\textsc {Promela}}\) as “\(\texttt {\#ifdef}\)” in the C Preprocessor [24]. TVL [6] is a textual modelling language for describing the set of valid configurations, \(\mathbb {K}\), for an \(f{\textsc {Promela}}\) model along with all available features, \(\mathbb {F}\). It has been shown in [13, 14] that variability abstractions and projections can be implemented as syntactic source-to-source transformations of \(f{\textsc {Promela}}\) and TVL models, which enable an effective computation of abstract models syntactically from high-level modelling languages. More precisely, let M and T be \(f{\textsc {Promela}}\) and TVL models, and let \([\! [M ]\! ]_T\) represent the FTS obtained by their compilation. Since variability abstractions affect only variability-specific aspects of a system, for any abstraction \(\alpha \) we can define \(\alpha (M)\) and \(\alpha (T)\) as syntactic transformations such that \(\alpha ([\! [M ]\! ]_T) = [\! [\alpha (M) ]\! ]_{\alpha (T)}\). That is, the abstract model obtained by applying \(\alpha \) on the FTS \([\! [M ]\! ]_T\) coincides with the FTS obtained by compiling \(\alpha (M)\) and \(\alpha (T)\). The same applies for projections \(\pi _{[\! [\psi ]\! ]}\). The \(f{\textsc {Promela}}\) Reconfigurator tool [13, 14] syntactically calculates the transformations corresponding to abstractions and projections. This is important for two reasons. First, it allows to easily implement our technique based on abstractions and projections. Second, we avoid the need for intermediate storage in memory of the concrete full-blown FTSs. In our implementation of the ARP, we use \(\varvec{\alpha }^{ \text {join} }\) as the initial abstraction. Hence, after applying \(\varvec{\alpha }^{ \text {join} }\) on \(f{\textsc {Promela}}\) and TVL models M and T, we obtain an ordinary Promela model and we call SPIN to check \([\! [\alpha (M) ]\! ]_{\alpha (T)}\,\models \,\phi \)? If a counterexample trace is returned, we inspect the error trace in detail by using SPIN’s simulation mode. We replay the error trace through \(\alpha (M)\) and M simultaneously, and we find the feature expression \(\psi \) that characterizes this trace in M. In order to do this, we use the fact that \(\alpha (M)\) and M have the same control structures (same number of lines and statements), except that “gd” statements in M are replaced with “if” statements in \(\alpha (M)\) by the corresponding transformations that affect only their guards.
Experimental setup. For our experiments, we use: a warm-up example to demonstrate specific characteristics of our ARP, and the MinePump [25] variational system whose \(f{\textsc {Promela}}\) model was created as part of the \(\overline{\text {SNIP}}\) project. We verify a range of properties by using (1) the ARP with \(\varvec{\alpha }^{ \text {join} }\) as the initial abstraction and SPIN as the verification tool (denoted ARP+SPIN), and by using (2) plain family-based model checking with \(\overline{\text {SNIP}}\). The reported performance numbers constitute the average runtime of five independent executions. For each experiment, we measure: Time which is the time to verify in seconds; and Space which is the number of explored states plus the number of re-explored states (this is equivalent to the number of transitions fired). For the ARP, along with the total time the ARP takes to complete we also report in parentheses the time taken by SPIN to perform the actual model checking tasks. The rest of the total time the ARP uses to calculate abstractions, projections, analyze error traces, etc. We only measure the times to generate a process analyser (pan) for \(\text {SPIN}\) and to execute it. We do not count the time for compiling pan, as it is due to a design decision in \(\text {SPIN}\) rather than its verification algorithm. All experiments were executed on a LUbunutuVM 64-bit Intel\(^\circledR \) Core\(^{TM}\) i7-4600U CPU running at 2.10 GHz with 4 GB memory. The implementation, benchmarks, and all results obtained from our experiments are available from: http://www.itu.dk/people/adim/arp.html.
Warm-up example. Consider the \(f{\textsc {Promela}}\) model \(\mathcal {F}\) given in Fig. 4a. After declaring feature variables, \(\texttt {A1} \ldots \texttt {An}\), the process \(\texttt {foo()}\) is defined. The first gd statement specifies that i++ is available for variants that contain the feature A1, and skip for variants with \(\lnot \texttt {A1}\). The following gd statements are similar, except that their guards are the features from A2 to An. We want to check the assertion, \(\texttt {i} \ge k\), where k is a meta-variable that can be replaced with different values: 0, 1, ..., n. The corresponding TVL model specifies that all features are optional and unconstrained, which means that all possible \(2^\texttt {n}\) configurations are valid. We use two approaches to check the above assertions: ARP+SPIN and the family-based model checker \(\overline{\text {SNIP}}\). The initial abstract model \(\varvec{\alpha }^{ \text {join} }(\mathcal {F})\) used in the ARP is shown in Fig. 4b. Since there are valid variants where Aj is enabled and valid variants where Aj is disabled (for any \(j \in \{1, \ldots , \texttt {n} \}\)), we have that both statements i++ and skip become available in \(\varvec{\alpha }^{ \text {join} }(\mathcal {F})\) for all “\(\texttt {gd}\)” statements.
When \(k=0\), the assertion \(\texttt {i} \ge 0\) is satisfied by all variants. The ARP terminates in one iteration with only one call to SPIN, which reports that \(\varvec{\alpha }^{ \text {join} }(\mathcal {F})\) satisfies the assertion. When \(k=1\), the ARP needs two iterations to find a (genuine) counterexample which corresponds to a single configuration where all features are disabled, and to certify that all other variants satisfy the assertion. When \(k=2\), the ARP runs in \(\texttt {n}+1\) iterations producing \(\texttt {n}+1\) erroneous variants: one variant where all features are disabled, and \(\texttt {n}\) variants where exactly one feature is enabled and all others are disabled. When \(k=\texttt {n}\), the ARP will need \(\texttt {n}+1\) iterations to terminate reporting that there is only one variant, where all features are enabled, that satisfies the assertion \(\texttt {i} \ge \texttt {n}\). All other variants are erroneous. This represents the worst case for our ARP, since all possible variants will be generated explicitly and checked by SPIN in a brute-force fashion. In addition, we have the overhead of generating all intermediate projections and abstractions as well as their verification with SPIN, for which spurious counterexamples are obtained. The performance results are shown in Fig. 5. We say that a task is infeasible when it is taking more time than the given timeout threshold, which we set on 1 h. Notice that \(\overline{\text {SNIP}}\) reports the correct results in only one iteration for all cases. Yet, as shown in Fig. 5, for \(\texttt {n} = 25\) (for which \(|\mathbb {K}| = 2^{25} = 33,554,432\) variants) \(\overline{\text {SNIP}}\) timeouts after visiting 150 M states. On the other hand, our ARP based approach is feasible even for very large values of \(\texttt {n}\) when k is smaller (see Fig. 5). In general, the ARP aims to partition the configuration space into subspaces that satisfy and violate the property at hand. When k is higher, that split becomes more irregular and the ARP needs to perform more iterations and calls to SPIN to find it automatically. Therefore, in those cases it takes more time to complete.
MinePump. The MinePump variational system is given by an \(f{\textsc {Promela}}\) model with 200 LOC and a TVL model that contains 7 independent optional features: Start, Stop, MethaneAlarm, MethaneQuery, Low, Normal, and High, thus yielding \(2^7\) = 128 variants. The FTS of MinePump has 21,177 states. It consists of 5 processes: a controller, a pump, a watersensor, a methanesensor, and a user. When activated, the controller should switch on the pump when the water level in the mine is high, but only if there is no methane within it.
For evaluation, we consider five interesting properties of MinePump (taken from [8]). First, we consider three properties, \(\varphi _1\), \(\varphi _2\) and \(\varphi _3\), that are intended to be satisfied by all variants. The property \(\varphi _1\) is the absence of deadlock; the property \(\varphi _2\) is that under a fairness assumption (the system will infinity often read messages of various types) the pump is never indefinitely off when the water level is high and there is no methane; whereas the property \(\varphi _3\) is that if the pump is switched on then the controller state is running. For all three properties, the ARP terminates after one iteration reporting that the properties are satisfied by all variants. Then, we have two properties, \(\varphi _4\) and \(\varphi _5\), which are satisfied by some variants and violated by others, such that there are different counterexamples corresponding to violating variants. The property \(\varphi _4\) (when the water is high and there is no methane, the pump will not be switched on at all eventually) is violated by variants that satisfy Start \(\wedge \) High (32 variants in total). The property \(\varphi _5\) (when the water is low, then the pump will be off) is also violated by variants satisfying Start \(\wedge \) High. For both properties, our ARP runs in seven iterations, producing 12 different counterexamples for \(\varphi _4\) and 13 different counterexamples for \(\varphi _5\). Figure 6 shows the performance results of verifying properties, \(\varphi _1\) to \(\varphi _5\), using our ARP with SPIN approach and the \(\overline{\text {SNIP}}\). The ARP achieves improvements in both Time and Space in most cases, especially for properties \(\varphi _1\) to \(\varphi _3\) satisfied by all variants which are verified in only one iteration. Of course, the performances of the ARP will start to decline for properties for which the ARP needs higher number of iterations and calls to SPIN in order to complete. However, we can see that for both \(\varphi _4\) and \(\varphi _5\) the actual verification time taken by SPIN (given in parentheses) in our ARP is still considerable smaller than the time taken by \(\overline{\text {SNIP}}\). Still, in these cases we obtain very long counterexamples (around thousand steps) so the ARP will need some additional time to process them.
Discussion. In conclusion, the ARP achieves the best results when the property to be checked is either satisfied by all variants or only a few erroneous variants exist. In those cases, the ARP will report conclusive results in few iterations. The worst case is when every variant triggers a different counterexample, so our ARP ends up in verifying all variants one by one in a brute-force fashion (plus the overhead for generating and verifying all intermediate abstract models). Variability abstractions weaken feature expressions used in FTSs, thus increasing the commonality between the behaviours of variants. In the case of \(\varvec{\alpha }^{ \text {join} }\) this enables the use of (single-system) SPIN model checker. SPIN is a highly-optimized industrial-strength tool which is much faster than the \(\overline{\text {SNIP}}\) research prototype. SPIN contains many optimisation algorithms, which are result of more than three decades research on advanced computer aided verification. For example, partial order reduction, data-flow analysis and statement merging are not implemented in \(\overline{\text {SNIP}}\) yet. Note that we can also implement the ARP to work with \(\overline{\text {SNIP}}\) by using \(\varvec{\alpha }^{ \text {fignore} }\) instead of \(\varvec{\alpha }^{ \text {join} }\) as the initial abstraction. The ARP will work correctly for any choice of features to be ignored by \(\varvec{\alpha }^{ \text {fignore} }\). However, in order the ARP to terminate faster and achieve some speedups, the ignored features should be chosen carefully by exploiting the knowledge of the variational system and property at hand.
5 Related Work
Family-based (lifted) analyses and verification techniques have been a topic of considerable research recently (see [30] for a survey). Some successful examples are lifted syntax checking [17, 24], lifted type checking [23], lifted static data-flow analysis [3, 15, 16, 28], lifted verification [20, 21, 29], etc.
In the context of family-based model checking, one of the earliest attempts for modelling variational systems is by using modal transition systems (MTSs) [2, 26]. Following this, Classen et al. present FTSs in [7, 8] and show how specifically designed family-based model checking algorithms (implemented in \(\overline{\text {SNIP}}\)) can be used for verifying FTSs against fLTL properties. An FTS-specific verification procedure based on counterexample guided abstraction refinement has been proposed in [10]. Abstractions on FTSs are introduced by using existential F-abstraction functions (as opposed to Galois connections here), and simulation relation is used to relate different abstraction levels. There are other important differences between the approach in [10] and our ARP. Refinement of feature abstractions in [10] is defined by simply replacing the abstract (weakened) feature expressions occurring in transitions of the spurious counterexample by their concrete feature expressions. In contrast, we use Craig interpolation as well as suitable combinations of variability abstractions and projections to generate refined abstract models. The abstractions in [10] are applied on feature program graphs (an intermediate structure between high-level \(f{\textsc {Promela}}\) models and FTSs) in \(\overline{\text {SNIP}}\). In contrast, we apply variability abstractions as preprocessor transformations directly on high-level \(f{\textsc {Promela}}\) models thus avoiding to generate any intermediate concrete semantic model in the memory. In the case of \(\varvec{\alpha }^{ \text {join} }\), this leads to generating Promela models and using \(\text {SPIN}\) for the ARP. The work [12] presents an approach for family-based software model checking of #ifdef-based second-order program families using symbolic game semantics models [11].
6 Conclusion
In this work we have proposed an automatic abstraction refinement procedure for family-based model checking of variational systems. Automatic refinement gives us an adaptive divide-and-conquer strategy for the configuration space. The obtained tool represents a completely automatic alternative to the family-based model checker \(\overline{\text {SNIP}}\), which is simpler, easier to maintain, and more efficient for some interesting properties than \(\overline{\text {SNIP}}\). It automatically benefits from all optimizations of SPIN. The overall design principle is general and can be applied to lifting of other automatic verification tools to variational systems.
Notes
- 1.
We often write
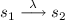 when \((s_1,\lambda ,s_2) \in trans\).
when \((s_1,\lambda ,s_2) \in trans\). - 2.
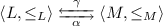 is a Galois connection between complete lattices L and M iff \(\alpha \) and \(\gamma \) are total functions that satisfy: \(\alpha (l) \le _M m \iff l \le _L \gamma (m)\) for all \(l \in L, m \in M\). Here \(\leqslant _L\) and \(\leqslant _M\) are the pre-order relations for L and M, respectively.
is a Galois connection between complete lattices L and M iff \(\alpha \) and \(\gamma \) are total functions that satisfy: \(\alpha (l) \le _M m \iff l \le _L \gamma (m)\) for all \(l \in L, m \in M\). Here \(\leqslant _L\) and \(\leqslant _M\) are the pre-order relations for L and M, respectively. - 3.
The project on development of the \(\overline{\text {SNIP}}\) tool (https://projects.info.unamur.be/fts/) is independent of SPIN. \(\overline{\text {SNIP}}\) has been implemented from scratch. We put a line over \(\overline{\text {SNIP}}\) to make the distinction from SPIN clearer.
References
Baier, C., Katoen, J.: Principles of Model Checking. MIT Press, Cambridge (2008)
ter Beek, M.H., Fantechi, A., Gnesi, S., Mazzanti, F.: Modelling and analysing variability in product families: model checking of modal transition systems with variability constraints. J. Log. Algebr. Meth. Program. 85(2), 287–315 (2016). http://dx.doi.org/10.1016/j.jlamp.2015.09.004
Bodden, E., Tolêdo, T., Ribeiro, M., Brabrand, C., Borba, P., Mezini, M.: SPL\(^\text{LIFT}\): statically analyzing software product lines in minutes instead of years. In: ACM SIGPLAN Conference on PLDI 2013, pp. 355–364 (2013)
Clarke, E., Grumberg, O., Jha, S., Lu, Y., Veith, H.: Counterexample-guided abstraction refinement. In: Emerson, E.A., Sistla, A.P. (eds.) CAV 2000. LNCS, vol. 1855, pp. 154–169. Springer, Heidelberg (2000). doi:10.1007/10722167_15
Clarke, E.M., Kroening, D., Sharygina, N., Yorav, K.: Predicate abstraction of ANSI-C programs using SAT. Formal Meth. Syst. Des. 25(2–3), 105–127 (2004). http://dx.doi.org/10.1023/B:FORM.0000040025.89719.f3
Classen, A., Boucher, Q., Heymans, P.: A text-based approach to feature modelling: syntax and semantics of TVL. Sci. Comput. Program. 76(12), 1130–1143 (2011). http://dx.doi.org/10.1016/j.scico.2010.10.005
Classen, A., Cordy, M., Heymans, P., Legay, A., Schobbens, P.: Model checking software product lines with SNIP. STTT 14(5), 589–612 (2012). http://dx.doi.org/10.1007/s10009-012-0234-1
Classen, A., Cordy, M., Schobbens, P., Heymans, P., Legay, A., Raskin, J.: Featured transition systems: foundations for verifying variability-intensive systems and their application to LTL model checking. IEEE Trans. Softw. Eng. 39(8), 1069–1089 (2013). http://doi.ieeecomputersociety.org/10.1109/TSE.2012.86
Clements, P., Northrop, L.: Software Product Lines: Practices and Patterns. Addison-Wesley, Reading (2001)
Cordy, M., Heymans, P., Legay, A., Schobbens, P., Dawagne, B., Leucker, M.: Counterexample guided abstraction refinement of product-line behavioural models. In: Cheung, S., Orso, A., Storey, M.D. (eds.) Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering (FSE-22), pp. 190–201. ACM (2014). http://doi.acm.org/10.1145/2635868.2635919
Dimovski, A.S.: Program verification using symbolic game semantics. Theor. Comput. Sci. 560, 364–379 (2014). http://dx.doi.org/10.1016/j.tcs.2014.01.016
Dimovski, A.S.: Symbolic game semantics for model checking program families. In: Bošnački, D., Wijs, A. (eds.) SPIN 2016. LNCS, vol. 9641, pp. 19–37. Springer, Heidelberg (2016). doi:10.1007/978-3-319-32582-8_2
Dimovski, A.S., Al-Sibahi, A.S., Brabrand, C., Wąsowski, A.: Family-based model checking without a family-based model checker. In: Fischer, B., Geldenhuys, J. (eds.) SPIN 2015. LNCS, vol. 9232, pp. 282–299. Springer, Heidelberg (2015). doi:10.1007/978-3-319-23404-5_18
Dimovski, A.S., Al-Sibahi, A.S., Brabrand, C., Wasowski, A.: Efficient family-based model checking via variability abstractions. STTT 1–19 (2016). doi:10.1007/s10009-016-0425-2
Dimovski, A.S., Brabrand, C., Wasowski, A.: Variability abstractions: trading precision for speed in family-based analyses. In: 29th European Conference on Object-Oriented Programming, ECOOP 2015. LIPIcs, vol. 37, pp. 247–270. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2015). http://dx.doi.org/10.4230/LIPIcs.ECOOP.2015.247
Dimovski, A.S., Brabrand, C., Wąsowski, A.: Finding suitable variability abstractions for family-based analysis. In: Fitzgerald, J., Heitmeyer, C., Gnesi, S., Philippou, A. (eds.) FM 2016. LNCS, vol. 9995, pp. 217–234. Springer, Heidelberg (2016). doi:10.1007/978-3-319-48989-6_14
Gazzillo, P., Grimm, R.: Superc: parsing all of C by taming the preprocessor. In: Vitek, J., Lin, H., Tip, F. (eds.) ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2012, Beijing, China, 11–16 June 2012, pp. 323–334. ACM (2012). http://doi.acm.org/10.1145/2254064.2254103
Henzinger, T.A., Jhala, R., Majumdar, R., McMillan, K.L.: Abstractions from proofs. In: Proceedings of the 31st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2004, pp. 232–244. ACM (2004). http://doi.acm.org/10.1145/964001.964021
Holzmann, G.J.: The SPIN Model Checker - Primer and Reference Manual. Addison-Wesley, Reading (2004)
Iosif-Lazar, A.F., Al-Sibahi, A.S., Dimovski, A.S., Savolainen, J.E., Sierszecki, K., Wasowski, A.: Experiences from designing and validating a software modernization transformation (E). In: 30th IEEE/ACM International Conference on Automated Software Engineering, ASE 2015, pp. 597–607 (2015). http://dx.doi.org/10.1109/ASE.2015.84
Iosif-Lazar, A.F., Melo, J., Dimovski, A.S., Brabrand, C., Wasowski, A.: Effective analysis of c programs by rewriting variability. In: The Art, Science, and Engineering of Programming, Programming 2017 (2017)
Kang, K.C., Cohen, S.G., Hess, J.A., Novak, W.E., Peterson, A.S.: Feature-oriented domain analysis (FODA) feasibility study. Technical report, Carnegie-Mellon University Software Engineering Institute, November 1990
Kästner, C., Apel, S., Thüm, T., Saake, G.: Type checking annotation-based product lines. ACM Trans. Softw. Eng. Methodol. 21(3), 14 (2012)
Kästner, C., Giarrusso, P.G., Rendel, T., Erdweg, S., Ostermann, K., Berger, T.: Variability-aware parsing in the presence of lexical macros and conditional compilation. In: Proceedings of the 26th Annual ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, OOPSLA 2011, pp. 805–824 (2011). http://doi.acm.org/10.1145/2048066.2048128
Kramer, J., Magee, J., Sloman, M., Lister, A.: Conic: an integrated approach to distributed computer control systems. IEE Proc. 130(1), 1–10 (1983)
Larsen, K.G., Nyman, U., Wąsowski, A.: Modal I/O automata for interface and product line theories. In: Nicola, R. (ed.) ESOP 2007. LNCS, vol. 4421, pp. 64–79. Springer, Heidelberg (2007). doi:10.1007/978-3-540-71316-6_6
McMillan, K.L.: Applications of craig interpolants in model checking. In: Halbwachs, N., Zuck, L.D. (eds.) TACAS 2005. LNCS, vol. 3440, pp. 1–12. Springer, Heidelberg (2005). doi:10.1007/978-3-540-31980-1_1
Midtgaard, J., Dimovski, A.S., Brabrand, C., Wasowski, A.: Systematic derivation of correct variability-aware program analyses. Sci. Comput. Program. 105, 145–170 (2015). http://dx.doi.org/10.1016/j.scico.2015.04.005
von Rhein, A., Thüm, T., Schaefer, I., Liebig, J., Apel, S.: Variability encoding: from compile-time to load-time variability. J. Log. Algebr. Meth. Program. 85(1), 125–145 (2016). http://dx.doi.org/10.1016/j.jlamp.2015.06.007
Thüm, T., Apel, S., Kästner, C., Schaefer, I., Saake, G.: A classification and survey of analysis strategies for software product lines. ACM Comput. Surv. 47(1), 6 (2014). http://doi.acm.org/10.1145/2580950
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Dimovski, A.S., Wąsowski, A. (2017). Variability-Specific Abstraction Refinement for Family-Based Model Checking. In: Huisman, M., Rubin, J. (eds) Fundamental Approaches to Software Engineering. FASE 2017. Lecture Notes in Computer Science(), vol 10202. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54494-5_24
Download citation
DOI: https://doi.org/10.1007/978-3-662-54494-5_24
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54493-8
Online ISBN: 978-3-662-54494-5
eBook Packages: Computer ScienceComputer Science (R0)


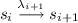 for all
for all 





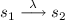 when
when 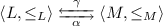 is a Galois connection between complete lattices L and M iff
is a Galois connection between complete lattices L and M iff 