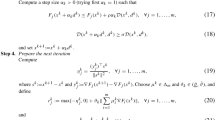Abstract
We discuss methods for solving the unconstrained optimization problem on parallel computers, when the number of variables is sufficiently small that quasi-Newton methods can be used. We concentrate mainly, but not exclusively, on problems where function evaluation is expensive. First we discuss ways to parallelize both the function evaluation costs and the linear algebra calculations in the standard sequential secant method, the BFGS method. Then we discuss new methods that are appropriate when there are enough processors to evaluate the function, gradient, and part but not all of the Hessian at each iteration. We develop new algorithms that utilize this information and analyze their convergence properties. We present computational experiments showing that they are superior to parallelization either the BFGS methods or Newton's method under our assumptions on the number of processors and cost of function evaluation. Finally we discuss ways to effectively utilize the gradient values at unsuccessful trial points that are available in our parallel methods and also in some sequential software packages.
Similar content being viewed by others
References
K.W. Brodlie, A.R. Gourlay and J. Greenstadt, “Rank-one and rank-two corrections to positive definite matrices expressed in product form,”Journal of the Institute of Mathematics and its Applications 11 (1973) 73–82.
R.H. Byrd and J. Nocedal, “A tool for the analysis of quasi-Newton methods with application to unconstrained minimization,” Technical Report ANL/MCS-TM-103, Mathematics and Computer Science Division, Argonne National Laboratory (1987).
R.H. Byrd, R.B. Schnabel and G.A. Shultz, “Using parallel function evaluations to improve Hessian approximations for unconstrained optimization,” Technical Report CU-CS-361–87, Department of Computer Science, University of Colorado at Boulder (1987), to appear inAnnals of Operations Research.
A.R. Conn, N.I.M. Gould and Ph.L. Toint, “Testing a class of methods for solving minimization problems with simple bounds on the variables,” Research Report CS-86–45, Faculty of Mathematics, University of Waterloo, Waterloo, Canada (1986).
W.C. Davidon, “Optimally conditioned optimization algorithms without line searches,”Mathematical Programming 9 (1975) 1–30.
J.E. Dennis Jr. and J.J. Moré, “A characterization of superlinear convergence and its application to quasi-Newton methods,”Mathematics of Computation 28 (1974) 549–560.
J.E. Dennis Jr. and R.B. Schnabel,Numerical Methods for Nonlinear Equations and Unconstrained Optimization (Prentice-Hall, Englewood Cliffs, New Jersey, 1983).
J.E. Dennis Jr. and R.B. Schnabel, “A view of unconstrained optimization,” Technical Report CU-CS-376-87, Department of Computer Science, University of Colorado at Boulder, to appear in: G.L. Nemhauser, A.H.J. Rinnoy Kan and M.J. Todd, eds.,Handbooks in Operations Research and Management Science, Vol. 1,Optimization (North-Holland, Amsterdam, 1987).
L.C.W. Dixon, “The place of parallel computation in numerical optimisation I, the local problem,” Technical Report No. 118, Numerical Optimisation Centre, The Hatfield Polytechnic (1981).
L.C.W. Dixon and K.D. Patel, “The place of parallel computation in numerical optimisation IV, parallel algorithms for nonlinear optimisation,” Technical Report No. 125, Numerical Optimisation Centre, The Hatfield Polytechnic (1982).
R. Fletcher,Practical Method of Optimization, Vol. 1, Unconstrained Optimization (John Wiley and Sons, New York, 1980).
P.E. Gill, G.H. Golub, W. Murray and N.A. Saunders, “Methods for modifying matrix factorizations,”Mathematics of Computation 28 (1974) 505–535.
P.E. Gill, W. Murray and M.H. Wright,Practical Optimization (Academic Press, London, 1981).
D. Goldfarb, “Factorized variable metric methods for unconstrained optimization,”Mathematics of Computation 30 (1976) 796–811.
L. Grandinetti, “Factorization versus nonfactorization in quasi-Newtonian methods for differentiable optimization,” Report N5, Dipartimento di Sistemi, Universita della Calabria (1978).
S.P. Han, “Optimization by updated conjugate subspaces,” in: D.F. Griffiths and G.A. Watson, eds.,Numerical Analysis: Pitman Research Notes in Mathematics Series 140 (Longman Scientific and Technical, Burnt Mill, England, 1986), pp. 82–97.
F.A. Lootsma, “Parallel unconstrained optimization methods,” Report No. 84–30, Department of Mathematics and Informatics, Technische Hogeschool Delft (1984).
J.J. Moré, B.S. Garbow and K.E. Hillstrom, “Testing unconstrained optimization software,”ACM Transactions on Mathematical Software 7 (1981) 17–41.
J.J. Moré and D.C. Sorensen, “Computing a trust region step,”SIAM Journal on Scientific and Statistical Computing 4 (1983) 553–572.
B.A. Murtagh and M.A. Saunders, “MINOS 5.0 User's Guide,” Technical Report SOL 83–20, Department of Operations Research, Stanford University (1983).
K.D. Patel, “Implementation of a parallel (SIMD) modified Newton method on the ICL DAP,” Technical Report No. 131, Numerical Optimisation Centre, The Hatfield Polytechnic (1982).
M.J.D. Powell, “Some global convergence properties of a variable metric method without exact line searches,” in: R. Cottle and C. Lemke, eds.,Nonlinear Programming (AMS, Providence, RI, 1976) pp. 53–72.
M.J.D. Powell, “Updating conjugate directions by the BFGS formula,”Mathematical Programming 38 (1987) 29–46.
R.B. Schnabel, “Quasi-Newton methods using multiple secant equations,” Technical Report CU-CS-247–83, Department of Computer Science, University of Colorado at Boulder (1983).
R.B. Schnabel, “Concurrent function evaluations in local and global optimization,”Computer Methods in Applied Mechanics and Engineering 64 (1987) 537–552.
R.B. Schnabel and P. Frank, “Tensor methods for nonlinear equations,”SIAM Journal on Numerical Analysis 21 (1984) 815–843.
R.B. Schnabel, J.E. Koontz and B.E. Weiss, “A modular system of algorithms of unconstrained minimization,”ACM Transactions on Mathematical Software 11 (1985) 419–440.
D.F. Shanno and K.H. Phua, “Matrix conditions and nonlinear optimization,”Mathematical Programming 14 (1987a) 145–160.
P.J.M. van Laarhoven, “Parallel variable metric methods for unconstrained optimization,”Mathematical Programming 33 (1985) 68–81.
Author information
Authors and Affiliations
Additional information
Research supported by AFOSR grant AFOSR-85-0251, ARO contract DAAG 29-84-K-0140, NSF grants DCR-8403483 and CCR-8702403, and NSF cooperative agreement DCR-8420944.
Rights and permissions
About this article
Cite this article
Byrd, R.H., Schnabel, R.B. & Shultz, G.A. Parallel quasi-Newton methods for unconstrained optimization. Mathematical Programming 42, 273–306 (1988). https://doi.org/10.1007/BF01589407
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01589407