Skip to main content
Springer Nature Link
Log in

Conservative and fourth-order compact difference schemes for the generalized Rosenau–Kawahara–RLW equation

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

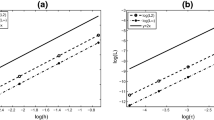
In this article, we present two conservative and fourth-order compact finite-difference schemes for solving the generalized Rosenau–Kawahara–RLW equation. The proposed schemes are energy-conserved, convergent, and unconditionally stable, and the numerical convergence orders in both \(l_{2}\)-norm and \(l_{\infty }\)-norm are of \(O(\tau ^{2}+h^{4})\). Numerical experiments demonstrate that the present schemes are efficient and reliable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Cui Y, Mao D (2007) Numerical method satisfying the first two conservation laws for the Korteweg–de Vries equation. J Comput Phys 227:376–399

    Article  MathSciNet  Google Scholar 

  2. Wang M, Li DF, Zhang CJ, Tang YB (2012) Long time behavior of solutions of gKdV equations. J Math Anal Appl 390:136–150

    Article  MathSciNet  Google Scholar 

  3. Shen JY, Wang XP, Sun ZZ (2020) The conservation and convergence of two finite difference schemes for KdV equations with initial and boundary value conditions. Numer Math Theor Methods Appl 13:253–280

    Article  MathSciNet  Google Scholar 

  4. Shao X, Xue G, Li C (2013) A conservative weighted finite difference scheme for regularized long wave equation. Appl Math Comput 219:9202–9209

    MathSciNet  MATH  Google Scholar 

  5. Cai JX, Gong YZ, Liang H (2017) Novel implicit/explicit local conservative schemes for the regularized long-wave equation and convergence analysis. J Math Anal Appl 447:17–31

    Article  MathSciNet  Google Scholar 

  6. Bayarassou K (2019) Fourth-order accurate difference schemes for solving Benjamin–Bona–Mahony–Burgers (BBMB) equation. Eng Comput. https://doi.org/10.1007/s00366-019-00812-2

    Article  Google Scholar 

  7. Rosenau P (1988) Dynamics of dense discrete systems. Prog Theor Phys 79:1028–1042

    Article  Google Scholar 

  8. Cai W, Sun Y, Wang Y (2015) Variational discretizations for the generalized Rosenau-type equations. Appl Math Comput 271:860–873

    MathSciNet  MATH  Google Scholar 

  9. Pan X, Zhang L (2012) On the convergence of a conservative numerical scheme for the usual Rosenau–RLW equation. Appl Math Model 36:3371–3378

    Article  MathSciNet  Google Scholar 

  10. Atouani N, Omrani K (2013) Galerkin finite element method for the Rosenau–RLW equation. Comput Math Appl 66:289–303

    Article  MathSciNet  Google Scholar 

  11. Polat N, Kaya D, Tutalar H (2006) An analytic and numerical solution to a modified Kawahara equation and a convergence analysis of the method. Appl Math Comput 179:466–472

    MathSciNet  MATH  Google Scholar 

  12. Zuo J (2009) Solitons and periodic solutions for the Rosenau–KdV and Rosenau–Kawahara equations. Appl Math Comput 215:835–840

    MathSciNet  MATH  Google Scholar 

  13. He D (2015) New solitary solutions and a conservative numerical method for the Rosenau–Kawahara equation with power law nonlinearity. Nonlinear Dyn 82:1177–1190

    Article  MathSciNet  Google Scholar 

  14. Karakoc B, Ak T (2016) Numerical simulation of dispersive shallow water waves with Rosenau–KdV equation. Int J Adv Appl Math Mech 3:32–40

    MathSciNet  MATH  Google Scholar 

  15. Wang X, Dai W (2018) A three-level linear implicit conservative scheme for the Rosenau–KdV–RLW equation. J Comput Appl Math 330:295–306

    Article  MathSciNet  Google Scholar 

  16. Xie J, Zhang Z, Liang D (2019) A conservative splitting difference scheme for the fractional-in-space Boussinesq equation. Appl Numer Math 143:61–74

    Article  MathSciNet  Google Scholar 

  17. Wang J, Liang D, Wang Y (2019) Analysis of a conservative high-order compact finite difference scheme for the Klein–Gordon–Schrödinger equation. J Comput Appl Math 358:84–96

    Article  MathSciNet  Google Scholar 

  18. He D, Pan K (2015) A linearly implicit conservative difference scheme for the generalized Rosenau–Kawahara–RLW equation. Appl Math Comput 271:323–336

    MathSciNet  MATH  Google Scholar 

  19. Burde G (2011) Solitary wave solutions of the high-order KdV models for bi-directional water waves. Commun Nonlinear Sci Numer Simul 16:1314–1328

    Article  MathSciNet  Google Scholar 

  20. Wang X, Dai W (2018) A new implicit energy conservative difference scheme with fourth-order accuracy for the generalized Rosenau–Kawahara–RLW equation. Comput Appl Math 37:6560–6581

    Article  MathSciNet  Google Scholar 

  21. Ghiloufi A, Rahmeni M, Omrani K (2019) Convergence of two conservative high-order accurate difference schemes for the generalized Rosenau–Kawahara–RLW equation. Eng Comput. https://doi.org/10.1007/s00366-019-00719-y

    Article  Google Scholar 

  22. Wang B, Sun T, Liang D (2019) The conservative and fourth-order compact finite difference schemes for regularized long wave equation. J Comput Appl Math 356:98–117

    Article  MathSciNet  Google Scholar 

  23. Moghaderi H, Dehghana M (2016) A multigrid compact finite difference method for solving the one-dimensional nonlinear sine-Gordon equation. Math Methods Appl Sci 38:3901–3922

    Article  MathSciNet  Google Scholar 

  24. Ghiloufi A, Omrani K (2018) New conservative difference schemes with fourth-order accuracy for some model equation for nonlinear dispersive waves. Numer Methods Part D E 34:451–500

    Article  MathSciNet  Google Scholar 

  25. Wang X, Dai W (2019) A conservative fourth-order stable finite difference scheme for the generalized Rosenau–KdV equation in both 1D and 2D. J Comput Appl Math 55:310–331

    Article  MathSciNet  Google Scholar 

  26. Hu B, Xu Y, Hu J (2008) Crank–Nicolson finite difference scheme for the Rosenau–Burgers equation. Appl Math Comput 204:311–316

    MathSciNet  MATH  Google Scholar 

  27. Zhou Y (1990) Applications of discrete functional analysis to the finite difference method. International Academic, Beijing

    Google Scholar 

  28. Browder F (1965) Existence and uniqueness theorems for solutions of nonlinear boundary value problems. Proc Symp Appl Math 17:24–49

    Article  MathSciNet  Google Scholar 

  29. Omrani K, Abidi F, Achouri T (2008) A new conservative finite difference scheme for the Rosenau equation. Appl Math Comput 201:35–43

    MathSciNet  MATH  Google Scholar 

  30. Achouri T (2019) Conservative finite difference scheme for the nonlinear fourth-order wave equation. Appl Math Comput 359:121–131

    MathSciNet  MATH  Google Scholar 

  31. Sun Z, Zhu Q (1998) On Tsertsvadze’s difference scheme for the Kuramoto–Tsuzuki equation. J Comput Appl Math 98(2):289–304

    Article  MathSciNet  Google Scholar 

  32. Rouatbi A, Omrani K (2017) Two conservative difference schemes for a model of nonlinear dispersive equations. Chaos Soliton Fract 104:516–530

    Article  MathSciNet  Google Scholar 

  33. Thomee V, Murthy A (1998) A numerical method for the Benjamin–Ono equation. BIT Numer Math 38:597–611

    Article  MathSciNet  Google Scholar 

  34. Ak T, Dhawan S, Inan B (2018) Numerical solutions of the generalized Rosenau–Kawahara–RLW equation arising in fluid mechanics via B-spline collocation method. Int J Mod Phys C. https://doi.org/10.1142/S0129183118501164

    Article  Google Scholar 

Download references

Acknowledgements

The first two authors were supported in part by Fujian Province Science Foundation for Middle-aged and Young Teachers (no. JAT190368). The authors would like to thank the anonymous reviewers for their valuable suggestions which improve the quality of the manuscript.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Minnan Normal University, Zhangzhou, 363000, Fujian, People’s Republic of China

    Xiaofeng Wang & Hong Cheng

  2. Mathematics and Statistics, College of Engineering and Science, Louisiana Tech University, Ruston, LA, 71272, USA

    Weizhong Dai

Authors
  1. Xiaofeng Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hong Cheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Weizhong Dai
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xiaofeng Wang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Cheng, H. & Dai, W. Conservative and fourth-order compact difference schemes for the generalized Rosenau–Kawahara–RLW equation. Engineering with Computers 38, 1491–1514 (2022). https://doi.org/10.1007/s00366-020-01113-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01113-9

Keywords