Threshold dynamics of a non-autonomous SEIRS model with quarantine and isolation

Abstract

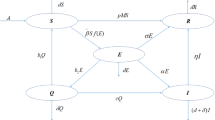
A model for assessing the effect of periodic fluctuations on the transmission dynamics of a communicable disease, subject to quarantine (of asymptomatic cases) and isolation (of individuals with clinical symptoms of the disease), is considered. The model, which is of a form of a non-autonomous system of non-linear differential equations, is analysed qualitatively and numerically. It is shown that the disease-free solution is globally-asymptotically stable whenever the associated basic reproduction ratio of the model is less than unity, and the disease persists in the population when the reproduction ratio exceeds unity. This study shows that adding periodicity to the autonomous quarantine/isolation model developed in Safi and Gumel (Discret Contin Dyn Syst Ser B 14:209–231, 2010) does not alter the threshold dynamics of the autonomous system with respect to the elimination or persistence of the disease in the population.

Appendix

Verification of Assumptions A1–A7 in Wang and Zhao (2008). The purpose here is to check whether the system (4) (or, equivalently, (1)) satisfies Conditions A1–A7 in Wang and Zhao (2008). Since the system (1) is equivalent to (4), the former system will be used in this analysis (for mathematical convenience). Using the notation in Wang and Zhao (2008), system (1) can be re-written as:

$$ \frac{{\hbox{d}}}{{\hbox{d}}t}x(t)={\mathcal{F}}(t,x(t))-{\mathcal{V}}(t,x(t))=f(t,x(t)), $$

(9)

where,

$$ x=\left(\begin{array}{l} S(t) \\ E(t) \\ I(t) \\ Q(t) \\ H(t)\\ R(t) \end{array}\right), \;\;{\mathcal{F}}=\left(\begin{array}{l} 0 \\ \frac{\beta(t)S(t)\left\{\eta_E(t)E(t)+I(t)+\eta(t) [\epsilon_1Q(t)+\epsilon_2H(t)]\right\}}{S(t)+E(t)+I(t)+\epsilon_1Q(t)+\epsilon_2H(t)+R(t) }\\ \kappa(t) E(t) \\ \sigma(t) E(t)\\ \alpha(t) Q(t)\\ 0\end{array}\right),\;\;\; $$

and,

$$ {\mathcal{V}}=\left(\begin{array}{l} -\Uppi-\psi R(t)+\frac{\beta(t)S(t)\left\{\eta_E(t)E(t)+I(t)+\eta(t) [\epsilon_1Q(t)+\epsilon_2H(t)]\right\}} {S(t)+E(t)+I(t)+\epsilon_1Q(t)+\epsilon_2H(t)+R(t)} +\mu S(t) \\ (\kappa(t)+\sigma(t)+\mu)E(t) \\ (\gamma_1+\phi+\mu+\delta_1)I(t)\\ (\alpha(t)+\gamma_2+\mu)Q(t)\\ (\gamma_3+\mu+\delta_2)H(t)\\ -\gamma_1 I(t)-\gamma_2Q(t)-\gamma_3H(t)+(\psi+\mu)R(t) \end{array}\right). $$

Furthermore, let,

$$ {\mathcal{V}}^+=\left(\begin{array}{l} \Uppi+\psi R(t)\\ 0\\ 0\\ 0\\ 0\\ \gamma_1 I(t)+\gamma_2Q(t)+\gamma_3H(t) \end{array}\right), {\mathcal{V}}^-=\left(\begin{array}{l} \frac{\beta(t)S(t)\left\{\eta_E(t)E(t)+I(t)+\eta(t) [\epsilon_1Q(t)+\epsilon_2H(t)]\right\}} {S(t)+E(t)+I(t)+\epsilon_1Q(t)+\epsilon_2H(t)+R(t)}+\mu S(t)\\ (\kappa(t)+\sigma(t)+\mu)E(t) \\ (\gamma_1+\phi+\mu+\delta_1)I(t)\\ (\alpha(t)+\gamma_2(t)+\mu)Q(t)\\ (\gamma_2+\mu+\delta_2)H(t)\\ (\psi+\mu)R(t) \end{array}\right). $$

It is easy to see that $\mathcal{V}=\mathcal{V}^--\mathcal{V}^+.$ The functions $\mathcal{F},\mathcal{V}^+$ and $\mathcal{V}^-$ satisfy the following:

• (A1) For each 1 ≤ i ≤ 6, $\mathcal{F}_i(t,x),\;\;\mathcal{V}^+_{i}(t,x)\;\;\hbox{and}\;\;\mathcal{V}^-_{i}(t,x)$ are non-negative, continuous on ${\mathbb{R}\times \mathbb{R}^6_{+}}$ and continuously differential with respect to x (since each function denotes a direct non-negative transfer of individuals).

• (A2) By assumption (it should be noted that it is assumed that some of the model parameters are ω-periodic functions), there exists a real number ω > 0, such that $\mathcal{F}_i(t,x),\;\;\mathcal{V}^+_{i}(t,x)$ $\hbox{and}\;\;\mathcal{V}^-_{i}(t,x)$ are ω-periodic in t.

• (A3) If x _i  = 0, then $\mathcal{V}^-_{i}=0$ for i = 2, 3, 4, 5.

• (A4) $\mathcal{F}_{i}=0$ for i = 1, 6.

• (A5) Define $X_s=\{ x\ge0:\; x_i=0\; \hbox {for} \;i=2,3,4,5\}.$ It is clear that if x ∈ X _s , then $\mathcal{F}_{i}=\mathcal{V}_i^{+}=0$ for i = 2, 3, 4, 5. System (1) has a disease-free solution, given by x ^* = (${\Uppi}/{\mu}$, 0, 0, 0, 0, 0). Define a 2 × 2 matrix

  $$ M(t)=\left(\frac{\partial f_i(t,x^*)}{\partial x_j}\right)_{i,j=1,6}. $$

  It follows from (9), and the definitions of the matrices ${\mathcal{F}}$ and ${\mathcal{V}},$ that

  $$ M(t)=\left[\begin{array}{ll} -\mu & \psi \\ 0 & -(\mu+\psi)\\ \end{array}\right]. $$

• (A6) Since M(t) is a diagonalizable matrix with negative eigenvalues, then

  $$ \rho(\Upphi_M(\omega))<1. $$

• (A7) Similarly,−${\mathcal{V}}$(t) is a diagonalizable matrix with negative eigenvalues. Hence,

  $$ \rho(\Upphi_{-V}(\omega))<1.$$

  Thus, the system (1) , or (equivalently) (4), satisfies Conditions A1–A7 in Wang and Zhao (2008).