Skip to main content

Advertisement

Springer Nature Link
Log in

An Adaptive Neural Network Algorithm with Quasi Opposition-Based Learning for Numerical Optimization Problems

  • Published:
Cognitive Computation Aims and scope Submit manuscript

Abstract

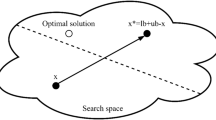
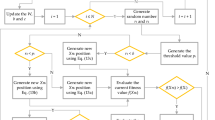
The structure of artificial neural networks and the biological nervous systems serve as the foundation for the creation of the neural network algorithm (NNA). The robust global search capability of NNAs makes it an effective tool for solving a wide range of complex optimization problems. Unfortunately, its limited relevance to many optimization problems is due to its poor exploitation, weak convergence, and tendency to fall into local optima. The paper’s goal is to introduce an enhanced version of the NNA known as the adaptive quasi-opposition-based neural network algorithm (AQOBNNA) in order to overcome these issues. The quasi-opposition-based learning (QOBL) and an adaptive strategy are combined in this suggested algorithm, where the adaptive technique is added to determine whether or not to use QOBL. The QOBL technique replaces a random search individual with the best one throughout the position update phase in order to enhance exploitation and increase exploration capabilities. The performance of the suggested AQOBNNA is assessed using a set of 23 traditional benchmark functions and compared with a number of current methods. It is evident from the experimental data that AQOBNNA performs better overall and outperforms all the algorithms that were examined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Algorithm 1
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data Availability

No data were used to support the study.

References

  1. Abd Elaziz M, Oliva D, Xiong S. An improved opposition-based sine cosine algorithm for global optimization. Expert Syst Appl. 2017;90:484–500.

    MATH  Google Scholar 

  2. Arora S, Singh S. Butterfly optimization algorithm: a novel approach for global optimization. Soft Comput. 2019;23:715–34.

    MATH  Google Scholar 

  3. Ayad J. Survey on neural networks in networking: Applications and advancements. Babylonian Journal of Networking. 2024;2024:135–47.

    MATH  Google Scholar 

  4. Balasubramani K, Natarajan UM. Improving bus passenger flow prediction using Bi-LSTM fusion model and SMO algorithm. Babylonian Journal of Artificial Intelligence. 2024;2024:73–82.

    Google Scholar 

  5. Braik M, Hammouri A, Atwan J, Al-Betar MA, Awadallah MA. White Shark Optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl-Based Syst. 2022;243: 108457.

    Google Scholar 

  6. Chandran V, Mohapatra P. An improved tunicate swarm algorithm with random opposition based learning for global optimization problems. Opsearch. 2024;1–26.https://doi.org/10.1007/s12597-024-00828-3

  7. Chopra N, Ansari MM. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst Appl. 2022;198: 116924.

    Google Scholar 

  8. Civicioglu P, Besdok E. Colony based search algorithm for numerical optimization. Appl Soft Comput. 2024;151: 111162.

    MATH  Google Scholar 

  9. Deb K. Optimal design of a welded beam via genetic algorithms. AIAA J. 1991;29(11):2013–5.

    MATH  Google Scholar 

  10. Derrac J, Garca S, Molina D, Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput. 2011;1(1):3–18.

    MATH  Google Scholar 

  11. Dorigo M, Birattari M, Stutzle T. Ant colony optimization. IEEE Comput Intell Mag. 2006;1(4):28–39.

    MATH  Google Scholar 

  12. Eskandar H, Sadollah A, Bahreininejad A, Hamdi M. Water cycle algorithm-A novel metaheuristic optimization method for solving constrained engineering optimization problems. Computers & Structures. 2012;110:151–66.

    Google Scholar 

  13. Ewees AA, Abd Elaziz M, Houssein EH. Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst Appl. 2018;112:156–72.

    MATH  Google Scholar 

  14. Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst Appl. 2020;152: 113377.

    Google Scholar 

  15. Gupta S, Deep K. A hybrid self-adaptive sine cosine algorithm with opposition based learning. Expert Syst Appl. 2019;119:210–30.

    MATH  Google Scholar 

  16. Gupta S, Deep K. An efficient grey wolf optimizer with opposition-based learning and chaotic local search for integer and mixed-integer optimization problems. Arab J Sci Eng. 2019;44(8):7277–96.

    MATH  Google Scholar 

  17. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H. Harris hawks optimization: Algorithm and applications. Futur Gener Comput Syst. 2019;97:849–72.

    MATH  Google Scholar 

  18. Haeri Boroujeni SP, Pashaei E. A hybird chimp optimization algorithm and generalized normal distribution algorithm with opposition based learninig strategy for solving data clustering problems. Iran Journal of Computer Science. 2024;7(1):65–101.

    Google Scholar 

  19. Ibrahim RA, Abd Elaziz M, Lu S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst Appl. 2018;108:1–27.

    MATH  Google Scholar 

  20. Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm. Applied Soft Computing Journal. 2008;8(1):687–97.

    MATH  Google Scholar 

  21. Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of ICNN’95 - International Conference on Neural Networks. 1995;4:1942–1948.

  22. Kirkpatrick S, Gelatt CD Jr, Vecchi MP. Optimization by simulated annealing science. 1983;220(4598):671–80.

    Google Scholar 

  23. Kouidere A, Damak M. Using neural networks to model complex mathematical functions. Mesopotamian Journal of Big Data. 2022;2022:51–4. https://doi.org/10.58496/MJBD/2022/007

  24. Kouka N, BenSaid F, Fdhila R, Fourati R, Hussain A, Alimi AM. A novel approach of many-objective particle swarm optimization with cooperative agents based on an inverted generational distance indicator. Inf Sci. 2023;623:220–41.

    Google Scholar 

  25. Kundu T, Deepmala, Jain PK. A hybrid salp swarm algorithm based on TLBO for reliability redundancy allocation problems. Appl Intell. 2022;52:12630–67.

  26. Lei D, Cai L, Wu F. Imperialist competition algorithm with quasi-opposition based learniing for function optimization and engineering design problems. Automatika. 2024;65(4):1640–65.

    MATH  Google Scholar 

  27. Li S, Chen H, Wang M, Heidari AA, Mirjalili S. Slime mould algorithm: A new method for stochastic optimization. Futur Gener Comput Syst. 2020;111:300–23.

    MATH  Google Scholar 

  28. Luo R, Peng Z, Hu J, Ghosh BK. Adaptive optimal control of affine nonlinear systems via identifier-critic neural network approximation with relaxed PE conditions. Neural Netw. 2023;167:588–600.

    MATH  Google Scholar 

  29. Mirjalili S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput Appl. 2016;27(4):1053–73.

    MathSciNet  MATH  Google Scholar 

  30. Mirjalili S, Lewis A. The Whale Optimization Algorithm. Adv Eng Softw. 2016;95:51–67.

    MATH  Google Scholar 

  31. Mirjalili S, Mirjalili SM, Lewis A. Grey Wolf Optimizer. Adv Eng Softw. 2014;69:46–61.

    MATH  Google Scholar 

  32. Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl-Based Syst. 2015;89:228–49.

    MATH  Google Scholar 

  33. Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv Eng Softw. 2017;114:163–91.

    MATH  Google Scholar 

  34. Mirjalili S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl-Based Syst. 2016;96:120–33.

    MATH  Google Scholar 

  35. Mohamed AW. A novel differential evolution algorithm for solving constrained engineering optimization problems. J Intell Manuf. 2018;29(3):659–92.

    MATH  Google Scholar 

  36. Qamar R, Zardari BA. Artificial neural networks: An overview. Mesopotamian Journal of Computer Science. 2023;2023:124–33.

    MATH  Google Scholar 

  37. Rahnamayan S, Tizhoosh HR, Salama MM. Quasi-oppositional differential evolution. In: 2007 IEEE congress on evolutionary computation. 2007. (pp. 2229–2236). IEEE.

  38. Rao RV, Savsani VJ, Vakharia DP. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. CAD Computer Aided Design. 2011;43(3):303–15.

    MATH  Google Scholar 

  39. Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a gravitational search algorithm. Inf Sci. 2009;179(13):2232–48.

    MATH  Google Scholar 

  40. Sadollah A, Sayyaadi H, Yadav A. A dynamic metaheuristic optimization model inspired by biological nervous systems: Neural Network Algorithm. Applied Soft Computing Journal. 2018;71:747–82.

    MATH  Google Scholar 

  41. Savsani P, Savsani V. Passing vehicle search (PVS): A novel metaheuristic algorithm. Appl Math Model. 2016;40(5–6):3951–78.

    MATH  Google Scholar 

  42. Simon D. Biogeography-Based Optimization. IEEE Trans Evol Comput. 2008;12(6):702–13.

    MATH  Google Scholar 

  43. Tizhoosh HR. Opposition-based learning: a new scheme for machine intelligence. In: International conference on computational intelligence for modelling, control and automation and international conference on intelligent agents, web technologies and internet commerce (CIMCA-IAWTIC’06). 2005. (Vol. 1, pp. 695–701). IEEE.

  44. Truong KH, Nallagownden P, Baharudin Z, Vo DN. A quasi-oppositional-chaotic symbiotic organisms search algorithm for global optimization problems. Appl Soft Comput. 2019;77:567–83.

    Google Scholar 

  45. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82.

    MATH  Google Scholar 

  46. Xu X, Lin Z, Li X, Shang C, Shen Q. Multi-objective robust optimisation model for MDVRPLS in refined oil distribution. Int J Prod Res. 2022;60(22):6772–92.

    MATH  Google Scholar 

  47. Xu Y, Chen H, Heidari AA, Luo J, Zhang Q, Zhao X, Li C. An efficient chaotic mutative moth-flame-inspired optimizer for global optimization tasks. Expert Syst Appl. 2019;129:135–55.

    MATH  Google Scholar 

  48. Yang XS, Deb S. Cuckoo search via Lévy flights. 2009 World Congress on Nature and Biologically Inspired Computing, NABIC 2009 - Proceedings. 2009. 210–214.

  49. Yang XS, Gandomi AH. BAT algorithm: a novel approach for global engineering optimization. Eng Comput. 2012;29:464–83.

    MATH  Google Scholar 

  50. Yang XS. Flower pollination algorithm for global optimization. International Conference on Unconventional Computing and Natural Computation. 2012. (pp. 240-249). Springer, Berlin, Heidelberg.

  51. Yang J, Yang F, Zhou Y, Wang D, Li R, Wang G, Chen W. A data-driven structural damage detection framework based on parallel convolutional neural network and bidirectional gated recurrent unit. Inf Sci. 2021;566:103–17.

    MATH  Google Scholar 

  52. Zhang Y, Jin Z, Chen Y. Hybrid teaching-learning-based optimization and Neural Network Algorithm for engineering design optimization problems. Knowl-Based Syst. 2020;187: 104836.

    MATH  Google Scholar 

  53. Zhang Y, Jin Z, Chen Y. Hybridizing grey wolf optimization with Neural Network Algorithm for global numerical optimization problems. Neural Comput Appl. 2020;32(14):10451–70.

    MATH  Google Scholar 

  54. Zhang M, Wen G. Duck swarm algorithm: theory, numerical optimization, and applications. Clust Comput. 2024;27:6441–69.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center for Global Health Research, Saveetha Medical College and Hospital, Saveetha Institute of Medical and Technical Sciences, Chennai, 602105, India

    Tanmay Kundu

  2. Department of Mathematics, Sambhu Nath College Labpur, Birbhum, 731303, West Bengal, India

    Tanmay Kundu

  3. Department of Mathematics, Thapar Institute of Engineering & Technology (Deemed University), Patiala, 147004, Punjab, India

    Harish Garg

Authors
  1. Tanmay Kundu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Harish Garg
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Harish Garg.

Ethics declarations

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Conflict of Interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kundu, T., Garg, H. An Adaptive Neural Network Algorithm with Quasi Opposition-Based Learning for Numerical Optimization Problems. Cogn Comput 17, 55 (2025). https://doi.org/10.1007/s12559-025-10415-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12559-025-10415-3

Keywords