Skip to main content

Advertisement

Springer Nature Link
Log in

Fuzzy neural control of uncertain chaotic systems with backlash nonlinearity

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

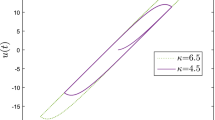
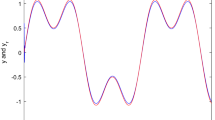
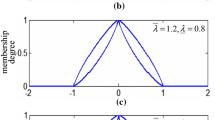
In this paper, a class of uncertain chaotic systems preceded by unknown backlash nonlinearity is investigated. Combining backstepping technique with fuzzy neural network identifying, an adaptive backstepping fuzzy neural controller (ABFNC) for uncertain chaotic systems with unknown backlash is proposed. The proposed ABFNC system is comprised of a fuzzy neural network identifier (FNNI) and a robust controller. The FNNI is the principal controller utilized for online estimation of the unknown nonlinear function. The robust controller is used to attenuate the effects of the approximation error so that the stability and control performance of the closed-loop adaptive system is achieved always. Finally, simulation results show that the ABFNC can achieve favorable tracking performances.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Chen G, Dong X (1993) On feedback control of chaotic continuous-time system. IEEE Trans Circuits Syst I 40:591–601

    Article  MATH  MathSciNet  Google Scholar 

  2. Nijmeijer H, Berghuis H (1995) On Lyapunov control of duffing equation. IEEE Trans Circuits Syst I 42:473–477

    Article  MATH  MathSciNet  Google Scholar 

  3. Hua C, Guan X (2004) Adaptive control for chaotic systems. Chaos, Solitons Fractals 22:55–60

    Article  MATH  MathSciNet  Google Scholar 

  4. Vincent TL, Yu J (1991) Control of a chaotic system. Dyn Control 1:35–52

    Article  MATH  MathSciNet  Google Scholar 

  5. Chen G, Dong X (1998) From chaos to order: methodologies, perspectives, and applications. World Scientific, Singapore

    MATH  Google Scholar 

  6. Zhang HG, Li M, Yang J, Yang DD (2009) Fuzzy model-based robust networked control for a class of nonlinear systems. IEEE Trans Syst Man Cybern Part A Syst Hum 39:437–447

    Article  Google Scholar 

  7. Tong SC, Li YM (2009) Observer-based fuzzy adaptive control for strict-feedback nonlinear systems. Fuzzy Sets Syst 160:1749–1764

    Article  MATH  MathSciNet  Google Scholar 

  8. Tong SC, Li CY, Li YM (2009) Fuzzy adaptive observer backstepping control for MIMO nonlinear systems. Fuzzy Sets Syst 160:2755–2775

    Article  MATH  MathSciNet  Google Scholar 

  9. Liu YJ, Tong SC, Li TS (2011) Observer-based adaptive fuzzy tracking control for a class of uncertain nonlinear MIMO systems. Fuzzy Sets Syst 164:25–44

    Article  MATH  MathSciNet  Google Scholar 

  10. Liu YJ, Chen CLP, Wen GX, Tong SC (2011) Adaptive neural output feedback tracking control for a class of uncertain discrete-time nonlinear systems. IEEE Trans Neural Netw 22:1162–1167

    Article  Google Scholar 

  11. Liu YJ, Tong SC, Wang D, Chen Li TS, LP C (2011) Adaptive neural output feedback controller design with reduced-order observer for a class of uncertain nonlinear SISO systems. IEEE Trans Neural Netw 22:1328–1334

    Article  Google Scholar 

  12. Zhang HG, Lun SX, Liu D (2007) Fuzzy H-infinity filter design for a class of nonlinear discrete-time systems with multiple time delay. IEEE Trans Fuzzy Syst 15:453–469

    Article  Google Scholar 

  13. Zhang HG, Liu XR, Gong QX, Chen B (2010) New sufficient conditions for robust H∞ fuzzy hyperbolic tangent control of uncertain nonlinear systems with time-varying delay. Fuzzy Sets Syst 161:1993–2011

    Article  MATH  MathSciNet  Google Scholar 

  14. Lu Z, Shieh L-S, Chen G, Coleman NP (2006) Adaptive feedback linearization control of chaotic systems via recurrent high-order neural networks. Inf Sci 176:2337–2354

    Article  MATH  MathSciNet  Google Scholar 

  15. Chunmei He (2013) Approximation of polygonal fuzzy neural networks in sense of Choquet integral norms. Int J Mach Learn Cybernet. doi:10.1007/s13042-013-0154-8

  16. Yau H-T (2008) Chaos synchronization of two uncertain chaotic nonlinear gyros using fuzzy sliding mode control. Mech Syst Signal Process 22:408–418

    Article  Google Scholar 

  17. Wang Lijuan (2011) An improved multiple fuzzy NNC system based on mutual information and fuzzy integral. Int J Mach Learn Cybernet 2(1):25–36

    Article  Google Scholar 

  18. Tsang Eric, Wang Xizhao, Yeung Daniel (2000) Improving learning accuracy of fuzzy decision trees by hybrid neural networks. IEEE Trans Fuzzy Syst 8(5):601–614

    Article  Google Scholar 

  19. Lin CT, George Lee CS (1966) Neural fuzzy systems. Prentice-Hall, Englewood Cliffs, NJ

    Google Scholar 

  20. Wang LX (1997) A course in fuzzy systems and control. Prentice-Hall, Englewood Cliffs

    MATH  Google Scholar 

  21. Omidvar O, Elliott DL (1997) Neural systems for control. Academic, New York

    Google Scholar 

  22. Lin D, Wang X (2010) Observer-based decentralized fuzzy neural sliding mode control for interconnected unknown chaotic systems via network structure adaptation. Fuzzy Sets Syst 161:2066–2080

    Article  MATH  Google Scholar 

  23. Chen C-S, Chen H-H (2009) Robust adaptive neural-fuzzy-network control for the synchronization of uncertain chaotic systems. Nonlinear Anal Real World Appl 10:1466–1479

    Article  MATH  MathSciNet  Google Scholar 

  24. Lin D, Wang X, Nian F, Zhang Y (2010) Dynamic fuzzy neural networks modeling and adaptive backstepping tracking control of uncertain chaotic systems. Neurocomputing 73:2873–2881

    Article  Google Scholar 

  25. Su CY, Stepanenko Y, Svoboda J, Leung TP (2000) Robust adaptive control of a class of nonlinear systems with unknown backlash-like hysteresis. IEEE Trans Automat Contr 45:2427–2432

    Article  MATH  MathSciNet  Google Scholar 

  26. Ahmad NJ, Khorrami F (1999) Adaptive control of systems with backlash hysteresis at the input. Proc Am Control Conf 5:3018–3022

    Google Scholar 

  27. Sun X, Zhang W, Jin Y (1992) Stable adaptive control of backlash nonlinear systems with bounded disturbance. Proc IEEE Conf Dec Control 1:274–275

    Google Scholar 

  28. Tao G, Kokotovic PV (1995) Adaptive control of plants with unknown hysteresis. IEEE Trans Automat Contr 40:200–212

    Article  MATH  MathSciNet  Google Scholar 

  29. Zhou J, Wen C (2008) Adaptive backstepping control of uncertain systems. LNCIS 372:97–123

    MathSciNet  Google Scholar 

  30. Lin CT, Cheng WC, Liang SF (2005) An on-line ICA-mixture-mode-based self-constructing fuzzy neural network. IEEE Trans Circuits Syst I(52):207–221

    MathSciNet  Google Scholar 

  31. Chen YC, Teng CC (1995) A model reference control structure using a fuzzy neural network. Fuzzy Sets Syst 73:291–312

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The first author is grateful to the support of the Youth Foundation of Sichuan Provincial Education Department (No. 11ZB097), the Talents Project of Sichuan University of Science and Engineering (No. 2011RC07), the Key project of Artificial Intelligence Key Laboratory of Sichuan Province (No. 2011RZJ02), the Science and Technology Key Project of Zigong (No. 2012D09), the Cultivation Project of Sichuan University of Science and Engineering (No. 2012PY19), and the Innovation Group Build Plan for the Universities in Sichuan (No. 13TD0017). The second author would like to thank the support of National Natural Science Foundation of China (No. 61363082).

Author information

Authors and Affiliations

  1. School of Automatic and Electronic Information, Sichuan University of Science and Engineering, Zigong, 643000, China

    Da Lin & Hong Song

  2. School of Information Engineering, Weifang Vocational College, Weifang, 261041, China

    Hongjun Liu

  3. College of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing, 400067, China

    Fuchen Zhang

Authors
  1. Da Lin
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hongjun Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hong Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Fuchen Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Da Lin.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lin, D., Liu, H., Song, H. et al. Fuzzy neural control of uncertain chaotic systems with backlash nonlinearity. Int. J. Mach. Learn. & Cyber. 5, 721–728 (2014). https://doi.org/10.1007/s13042-013-0218-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-013-0218-9

Keywords