Abstract
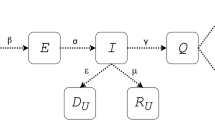
In this work, a new susceptible–exposed–infectious–recovered (SEIR) compartmental model is proposed which has additional media influence for precise quantization of the coronavirus disease 2019 (COVID-19). In the proposed model, first-order ordinary differential equations (ODEs) are used for the formulation of basic reproduction number, whereas genetic algorithm (GA) is used for its estimation. The inclusion of climatic parameters, governmental impact, and human behavioral response toward the disease provides an upper hand in determining the dynamics of its transmissibility, thereby indicating their significance in precising the outcomes. In addition, the future trends for the new normalized confirmed cases of COVID-19 are predicted using the long short-term memory (LSTM) model which helps in evaluating and modifying the current preventive actions taken to improve the situation. The robustness of the proposed model is measured by five different error functions which are tested in five different countries. According to the experimental results, this is observed that the proposed model has a smaller prediction deviation as well and the proposed scheme outperforms state-of-the-art models of COVID-19.








Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data Availability
The datasets analyzed during the current study are available from the corresponding author upon reasonable request.
References
Srivastav AK, Tiwari PK, Srivastava PK, Ghosh M, Kang Y. A mathematical model for the impacts of face mask, hospitalization and quarantine on the dynamics of COVID-19 in India: deterministic vs. stochastic. Math Biosci Eng. 2021;18(1):182–213.
Samsuzzoha MD. A study on numerical solutions of epidemic models. 2012.
Siettos CI, Russo L. Mathematical modeling of infectious disease dynamics. Virulence. 2013;4(4):295–306.
Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond. 1927;115:700–21.
Dixit R, Panda DS, Panda SS. An advanced susceptible–exposed–infectious–recovered model for quantitative analysis of COVID-19. Sādhanā. 2021;46(2):1–10.
Farkas C, Iclanzan D, Olteán-Péter B, Vekov G. Estimation of parameters for a humidity-dependent compartmental model of the COVID-19 outbreak. PeerJ. 2021;9: e10790.
Casagrandi R, Bolzoni L, Levin SA, Andreasen V. The SIRC model and influenza A. Math Biosci. 2006;200(2):152–69.
Feng L. SEIR model combined with LSTM and GRU for the trend analysis of COVID-19. 2021.
Bagal DK, Rath A, Barua A, Patnaik D. Estimating the parameters of susceptible-infected-recovered model of COVID-19 cases in India during lockdown periods. Chaos Solitons Fractals. 2020;140: 110154.
Chowell G, Ammon CE, Hengartner NW, Hyman JM. Estimation of the reproductive number of the Spanish flu epidemic in Geneva, Switzerland. Vaccine. 2006;24(44–46):6747–50.
Ceylan Z. Short-term prediction of COVID-19 spread using grey rolling model optimized by particle swarm optimization. Appl Soft Comput. 2021;109: 107592.
Martinez ME. The calendar of epidemics: seasonal cycles of infectious diseases. PLoS Pathog. 2018;14(11): e1007327.
Fares A. Factors influencing the seasonal patterns of infectious diseases. Int J Prev Med. 2013;4(2):128.
Rai RK, Khajanchi S, Tiwari PK, Venturino E, Misra AK. Impact of social media advertisements on the transmission dynamics of COVID-19 pandemic in India. J Appl Math Comput. 2022;68(1):19–44.
Misra AK, Sharma A, Shukla JB. Modeling and analysis of effects of awareness programs by media on the spread of infectious diseases. Math Comput Model. 2011;53(5–6):1221–8.
Misra AK, Rai RK, Takeuchi Y. Modeling the control of infectious diseases: effects of TV and social media advertisements. Math Biosci Eng. 2018;15(6):1315.
Xiao Y, Tang S, Wu J. Media impact switching surface during an infectious disease outbreak. Sci Rep. 2015;5(1):1–9.
Ljubic B, Roychoudhury S, Cao XH, Pavlovski M, Obradovic S, Nair R, Glass L, Obradovic Z. Influence of medical domain knowledge on deep learning for Alzheimer’s disease prediction. Comput Methods Progr Biomed. 2020;197: 105765.
Santosh T, Ramesh D, Reddy D. LSTM-based prediction of malaria abundances using big data. Comput Biol Med. 2020;124: 103859.
Yudistira N, Sumitro SB, Nahas A, Riama NF. Learning where to look for COVID-19 growth: multivariate analysis of COVID-19 cases over time using explainable convolution-LSTM. Appl Soft Comput. 2021;109: 107469.
Shahid F, Zameer A, Muneeb M. Predictions for COVID-19 with deep learning models of LSTM, GRU and Bi-LSTM. Chaos Solitons Fractals. 2020;140: 110212.
Kumar M, Gupta S, Kumar K, Sachdeva M. Spreading of COVID-19 in India, Italy, Japan, Spain, UK, US: a prediction using ARIMA and LSTM model. Digit Govern Res Pract. 2020;1(4):1–9.
Bedi P, Dhiman S, Gole P, Gupta N, Jindal V. Prediction of COVID-19 trend in India and its four worst-affected states using modified SEIRD and LSTM models. SN Comput Sci. 2021;2(3):1–24.
Kırbaş İ, Sözen A, Tuncer AD, Kazancıoğlu FŞ. Comparative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. Chaos Solitons Fractals. 2020;138: 110015.
Chimmula VKR, Zhang L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals. 2020;135: 109864.
Bai S. Simulations of COVID-19 spread by spatial agent-based model and ordinary differential equations. Int J Simul Process Model. 2020;15(3):268–77.
Tang B, Wang X, Li Q, Bragazzi NL, Tang S, Xiao Y, Wu J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J Clin Med. 2020;9(2):462.
Ralph R, Lew J, Zeng T, Francis M, Xue B, Roux M, Ostadgavahi AT, Rubino S, Dawe NJ, Al-Ahdal MN. 2019-nCoV (Wuhan virus), a novel coronavirus: human-to-human transmission, travel-related cases, and vaccine readiness. J Infect Dev Ctries. 2020;14(1):3–17.
Fisman DN, Greer AL, Tuite AR. Bidirectional impact of imperfect mask use on reproduction number of COVID-19: a next generation matrix approach. Infect Dis Model. 2020;5:405–8.
Zandavi SM, Rashidi TH, Vafaee F. Forecasting the spread of COVID-19 under control scenarios using LSTM and dynamic behavioral models. 2020. arXiv preprint arXiv:2005.12270.
Abadi MQH, Rahmati S, Sharifi A, Ahmadi M. HSSAGA: designation and scheduling of nurses for taking care of COVID-19 patients using novel method of Hybrid Salp Swarm Algorithm and Genetic Algorithm. Appl Soft Comput. 2021;108: 107449.
Rahimi I, Chen F, Gandomi AH. A review on COVID-19 forecasting models. Neural Comput Appl. 2021:1–11.
Demir F. DeepCoroNet: a deep LSTM approach for automated detection of COVID-19 cases from chest X-ray images. Appl Soft Comput. 2021;103: 107160.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
DSP: Conceptualization, Methodology, Data Curation, Writing—Review and Editing. RD: Writing—Review and Editing, Research Supervision. AD: Writing—Original Draft. HD: Research Survey. AS: Research Supervision.
Corresponding author
Ethics declarations
Conflict of interest
All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.
Research involving human and/or animals
Not applicable.
Informed consent
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection “Machine Learning for Pandemic Prediction and Control” guest edited by Anand J Kulkarni, Akash Tayal, Patrick Siarry, Arun Solanki and Ali Husseinzadeh Kashan.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Panda, D.S., Dixit, R., Dixit, A. et al. Mathematical Model and AI Integration for COVID-19: Improving Forecasting and Policy-Making. SN COMPUT. SCI. 5, 246 (2024). https://doi.org/10.1007/s42979-023-02574-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42979-023-02574-7