Abstract
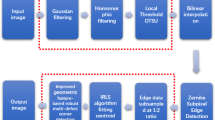
In semiconductor manufacturing, the wafer surface defect detection system is the key role in controlling production quality and efficiency. Recently, computer vision, big data and artificial intelligence contribute to develop the wafer surface defect detection system, efficiently. We suggest optimized operation methods of 2D and 3D scattered data by searching the global minimum of the minimax problem for a set of points in the wafer surface defect detection system. The problem is applied to analyze the wafer surface defect detection system. As a result, mathematically, we obtain the exact solution of circle or sphere from the suggested problems. This is new measurement to analyze the wafer surface defect detection system.


Similar content being viewed by others
Data availability
All data generated or analyzed during this research are included in this paper. This data is available from this paper. If you need to have further information, then email to the corresponding author.
References
Chen S-H, Kang C-H, Perng DB. Detecting and measuring defects in wafer die using GAN and YOLOv3. Appl Sci. 2020;10(8725):1–15.
Kim D. An optimized discrete data classification method in N-dimensional. Comput Math Methods. 2022. https://doi.org/10.1155/2022/8199872.
Kim D. Computational optimized monitoring methodology to avoid crowd crush accidents with scattered data. Appl Math. 2022. https://doi.org/10.3390/appliedmath2040042.
Kim D. Numerical subgrid Bi-cubic methods of partial differential equations in image segmentation, Scientific Reports 14, Article number :8387 (2024). https://doi.org/10.1038/s41598-024-54855-7
Lin J, Keogh E, Lonardi S, Chiu B. A symbolic representation of time series with implications for streaming algorithms. In: Proceedings of 8th ACMSIGMOD workshop research issues data mining knowledge, discovery. 2003. p. 211.
Demjanov VF. Algorithms for some minimax problems. J Comput Syst Sci. 1968;2:342–80.
Drezner Zvi. On location dominance on spherical surfaces. Oper Res. 1981;29(6):1218–9.
Drezner Z, Steiner S, Wesolowsky GO. On the circle closest to a set of points. Comput Oper Res. 2002;29:637–50.
Fekete SP, Mitchell J, Beurer K. On the continuous Fermat Weber problem. Oper Res. 2005;53(1):61–76.
Gugat M, Pfeiffer B. Weber problems with mixed distances and regional demand. Math Methods Oper Res. 2007;66(3):419–49.
Jiang J-L, Yuan X-M. A heuristic algorithm for constrained multi-source Weber problem–the variational inequality approach. Eur J Oper Res. 2008;187(2):357–70.
Morales AK, Erazo FR. A search space reduction methodology for data mining in large databases. Eng Appl Artif Intell. 2009;22:57–65.
Kotyza J. Machacek Z, Koziorek J. Detection of directions in an image as a method for circle detection, IFAC PapersOnline. 2018;51(6):496–501.
Pfeiffer B, Klamroth K. A unified model for Weber problems with continuous and network distances. Comput Oper Res. 2008;35(2):312–26.
Sung C-S, Joo C-M. Locating an obnoxious facility on a Euclidean network to minimize neighborhood damage. Networks. 1994;24(1):1–9.
Shan S. Machine learning models and algorithms for big optimization. Boston: Springer; 2016.
Varuna S, Natesan P. An integration of k-means clustering and naive Bayes classifier for Intrusion detection. In: Proceedings of 3rd international conference on signal processing and communication network. 2015. p. 15.
Weber A. Uber den Standort der Industrien: Erster Teil. Tubingen: Mohr; 1909.
Zhao Q-H, Ha M-H, Peng G-B, Zhang X-K., Support vector machine based on half-suppressed fuzzy c-means clustering. In: Proceedings of international conference on machine learning cybernetics, vol. 2. 2009. pp. 1236–40.
Acknowledgment
The corresponding author is the faculty of Grand Canyon University and Benedictine University.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that I have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kim, D. Optimized Operation Methods of the Wafer Surface Defect Detection. SN COMPUT. SCI. 5, 873 (2024). https://doi.org/10.1007/s42979-024-03076-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42979-024-03076-w