Robust Absolute Stability Criterion for Uncertain Lur’e Differential Inclusion Systems with Time Delay

Abstract

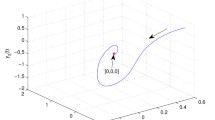
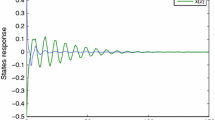
This paper deals with uncertain Lur’e differential inclusion systems with time delay. The set-valued mappings considered are upper semi-continuous, non-empty, closed, convex and bounded. It is proved that original systems can be reduced to their equivalent systems by introducing the dynamic multiplier. Based on the Lyapunov–Krasovskii functional, delay-dependent stability criterion is given to guarantee the robust absolute stability of the systems by LMI method. The result is new to the previous literature. Numerical examples are provided to show the effectiveness of the proposed stability condition.

Appendix: Proof of Lemma 1

Let $S_{[0,T]}(\mathcal{F},x_{0})$ be the set of solutions of differential inclusion $\dot{x}(t)\in \mathcal{F}(t,x(t))$, x(0)=x ₀, and [0,T] be the interval where the solution exists.

Since ϕ(t), t∈[−τ,0] is an absolutely continuous function, the set-valued mapping $\bar{\mathcal{F}}(t,x(t))=\mathcal{F}(x(t),\phi(t-\tau))$ is upper semi-continuous, non-empty, closed, convex and bounded, and for the differential inclusion $\dot{x}(t)\in \bar{\mathcal{F}}(t,x(t))$, x(0)=ϕ(0) there exists a non-empty solution set $S_{[0,T]}(\bar{\mathcal{F}},x_{0})$. Let $\bar{x}(t)\in S_{[0,T]}(\bar{\mathcal{F}},x_{0})$, and define

$$ x_{\tau}(t)=\left \{\begin{array}{l@{\quad }l}\phi(t),&t\in [-\tau,0],\\ \bar{x}(t),&t\in [0,\tau]. \end{array} \right . $$

Then x _τ (t) is a solution of the Cauchy problem of differential inclusion $\dot{x}(t)\in \mathcal{F}(x(t),x(t-\tau))$, t∈[0,τ] with x(t)=ϕ(t), t∈[−τ,0].

Now we estimate the norm of x _τ (t). Because $\dot{x}_{\tau}(t)\in \mathcal{F}(x_{\tau}(t),x_{\tau}(t-\tau))$ and x _τ (0)=x ₀=ϕ(0), it is equivalent to

$$ x_{\tau}(t)\in x_{0}+\int_{0}^{t} \mathcal{F}\bigl(x_{\tau}(s),x_{\tau}(s-\tau)\bigr)\,ds,\quad \forall t \in [0,\tau], $$

(47)

then we have

$$ \begin{aligned}[b] \bigl\Vert x_{\tau}(t)\bigr\Vert &\leq \Vert x_{0}\Vert +\int_{0}^{t} \bigl\Vert \mathcal{F}\bigl(x_{\tau}(s),x_{\tau}(s-\tau)\bigr)\bigr\Vert \,ds \\ &\leq \Vert x_{0}\Vert +\gamma_{3}t+\int _{0}^{t} \gamma_{1} \bigl\Vert x_{\tau}(s)\bigr\Vert \,ds+\int_{0}^{t} \gamma_{2} \bigl\Vert x_{\tau}(s-\tau)\bigr\Vert \,ds \\ &=\Vert x_{0}\Vert +\gamma_{3}t+\int_{0}^{t} \gamma_{1} \bigl\Vert x_{\tau}(s)\bigr\Vert \,ds+\gamma_{2}\int _{-\tau}^{t-\tau}\bigl\Vert x_{\tau}(s)\bigr\Vert \,ds \\ &\leq\Vert x_{0}\Vert +\gamma_{3}t+\int _{0}^{t} \gamma_{1} \bigl\Vert x_{\tau}(s)\bigr\Vert \,ds+\gamma_{2}\int_{-\tau}^{t} \bigl\Vert x_{\tau}(s)\bigr\Vert \,ds \\ &=\Vert x_{0}\Vert +\gamma_{3}t+\int_{0}^{t} (\gamma_{1}+\gamma_{2})\bigl\Vert x_{\tau}(s)\bigr\Vert \,ds+ \gamma_{2}\int_{-\tau}^{0}\bigl\Vert x_{\tau}(s)\bigr\Vert \,ds \\ &=\Vert x_{0}\Vert +\gamma_{3}t+\int_{0}^{t} (\gamma_{1}+\gamma_{2})\bigl\Vert x_{\tau}(s)\bigr\Vert \,ds+ \gamma_{2}\int_{-\tau}^{0}\bigl\Vert \phi(s) \bigr\Vert \,ds. \end{aligned} $$

(48)

Since ϕ(t), t∈[−τ,0] is absolutely continuous, there exists a constant M>0 such that $\gamma_{2}\int_{-\tau}^{0}\Vert \phi(s)\Vert \,ds\leq M$. It follows from (48) that

$$ \bigl\Vert x_{\tau}(t)\bigr\Vert \leq \Vert x_{0}\Vert +M+\gamma_{3}t+\int_{0}^{t} ( \gamma_{1}+\gamma_{2})\bigl\Vert x_{\tau}(s)\bigr\Vert \,ds. $$

(49)

By the Gronwall inequality, we have

$$ \bigl\Vert x_{\tau}(t)\bigr\Vert \leq \bigl(\Vert x_{0}\Vert +M+ \gamma_{3}t\bigr)e^{(\gamma_{1}+\gamma_{2})t}, $$

which means that ∥x _τ (t)∥ is bounded in the interval [0,τ] and independent of the selections of x _τ (t) from the set $S_{[0,\tau]}(\mathcal{F},\phi(t))$. We can continue to consider the Cauchy problem of differential inclusion $\dot{x}(t)\in \mathcal{F}(x(t),x(t-\tau))$, t∈[τ,2τ] with x(t)=x _τ (t), t∈[0,τ] for a fixed x _τ (t). Using a similar procedure, a set of solutions which are defined in the interval of [τ,2τ] can be obtained. Moreover, if the solution is denoted by x _2τ (t), then x _2τ (t) is bounded and independent of the selection x _2τ (t) from the solution set. Thus the solution exists in the interval [0,2τ]. This procedure can be repeated, it means that the solution can be extended to the interval [0,∞). We complete the proof.