Global Adaptive Finite-Time Control for Stochastic Nonlinear Systems via State Feedback

Abstract

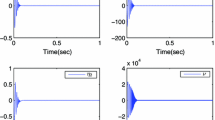
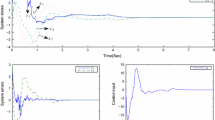
This paper discusses the problem of global adaptive finite-time control for a class of stochastic nonlinear systems with parametric uncertainty. Under the assumption that the drift and diffusion terms satisfy lower-triangular growth conditions, a continuous adaptive controller is designed based on the adding one power integrator technique and parameter separation principle. By constructing an adaptive law to counteract the effects of uncertain parameters, it is proved that system states can be regulated to the origin almost surely in a finite time. Two simulation examples are given to demonstrate the effectiveness of the proposed control procedure.

Appendix

For convenience, some generic functions $\beta _i(\bar{x}_i,\hat{\varTheta })$, $i=1,\ldots ,n$, are used throughout the paper to stand for any nonnegative smooth functions with respect to their variables and may be implicitly changed in different places.

Proof of Proposition 1

The estimate of $|\partial (x_k^{*1/r_k})/\partial x_i|$ can be done by an inductive argument. Note that

$$\begin{aligned} \Big |\frac{\partial x_2^{*\mu /r_2}}{\partial x_1}\Big |=&\Big |\frac{\partial \big (\xi _1\rho _1^{ \mu /r_2}(x_1,\hat{\varTheta })\big )}{\partial x_1}\Big |\le |\xi _1|^{\frac{\mu -r_1}{\mu }}\beta _1(x_1,\hat{\varTheta }). \end{aligned}$$

(40)

Assume that, for $i=1,\ldots ,k-2$,

$$\begin{aligned} \Big |\frac{\partial x_{k-1}^{*\mu /r_{k-1}}}{\partial x_i}\Big |\le \left( \sum _{j=1}^{k-2}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) \beta _{k-2}(\bar{x}_{k-2},\hat{\varTheta }). \end{aligned}$$

(41)

Therefore, it can be verified that

$$\begin{aligned} \Big |\frac{\partial x_{k}^{*\mu /r_{k}}}{\partial x_i}\Big |\le&\Big |\xi _{k-1}\frac{\partial \rho _{k-1}^{\mu /r_k}(\cdot )}{\partial x_i}\Big |+\Big |\rho _{k-1}^{\mu /r_k}(\cdot )\frac{\partial x_{k-1}^{*\mu /r_{k-1}}}{\partial x_i}\Big |\nonumber \\ \le&\,|\xi _{k-1}|^{\frac{\mu -r_i}{\mu }}\beta _{k-1}(\cdot ) +\left( \sum _{j=1}^{k-2}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) \beta _{k-2}(\cdot )\rho _{k-1}^{\mu /r_k}(\cdot )\nonumber \\ \le&\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) \beta _{k-1}(\cdot ),\quad i=1,\ldots ,k-2, \end{aligned}$$

(42)

$$\begin{aligned} \Big |\frac{\partial x_{k}^{*\mu /r_k}}{\partial x_{k-1}}\Big |\le&\Big |\xi _{k-1}\frac{\partial \rho _{k-1}^{\mu /r_k}(\cdot )}{\partial x_{k-1}}\Big |+\Big |\rho _{k-1}^{\mu /r_k}(\cdot )\frac{\mu }{r_{k-1}}x_{k-1}^{\frac{\mu -r_{k-1}}{r_{k-1}}}\Big |\nonumber \\ \le&\,\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_{k-1}}{\mu }}\right) \beta _{k-1}(\cdot ) \end{aligned}$$

(43)

which implies that (41) also holds for the $k$th virtual controller. According to the definition of $\xi _i$, $i=1,\ldots ,k$, and Lemma 4, one gets

$$\begin{aligned} |x_i|\le (|\xi _i|+|\xi _{i-1}\rho _{i-1}^{\mu /r_i}(\cdot )|)^{r_i/\mu } \le |\xi _i| ^{r_i/\mu }+|\xi _{i-1}|^{r_i/\mu }\rho _{i-1}(\cdot ),\quad i=2,\ldots ,k \end{aligned}$$

(44)

which leads to $\forall i=1,\ldots ,k-1$

$$\begin{aligned} \Big |\frac{\partial W_k}{\partial x_i}x_{i+1}\Big |\le&|\xi _k|^3\big (\sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_i}{\mu }}\big ) \big (|\xi _{i+1}|^{r_{i+1}/\mu }+|\xi _{i}|^{r_{i+1}/\mu }\rho _{i}(\cdot )\big )\beta _{k-1}(\cdot )\nonumber \\ \le&\,\frac{1}{3(k-1)}\sum _{j=1}^{k-1}|\xi _j|^{\frac{4\mu +\tau }{\mu }}+|\xi _k|^{\frac{4\mu +\tau }{\mu }}\beta _{k-1}(\cdot ). \end{aligned}$$

(45)

Clearly, Proposition 1 follows from (45). $\square$

Proof of Proposition 2

Under Assumption 1, the drift terms can be estimated as

$$\begin{aligned} |f_i|\le&\left( |\xi _1|^{\frac{r_i+\tau }{\mu }}+\sum _{j=2}^i\left( |\xi _j| ^{\frac{r_i+\tau }{\mu }}+\rho _{j-1}^{\frac{r_i+\tau }{r_j}}(\cdot )|\xi _{j-1}|^{\frac{r_i+\tau }{\mu }}\right) \right) \gamma _{i1}(\bar{x}_i)\varTheta \nonumber \\ \le&\left( |\xi _1|^{\frac{r_i+\tau }{\mu }}+\cdots +|\xi _i|^{\frac{r_i+\tau }{\mu }}\right) \beta _i(\cdot )\varTheta ,\quad i=1,\ldots ,k. \end{aligned}$$

(46)

According to Lemmas 4 and 5, one has $\forall i=1,\ldots ,k$

$$\begin{aligned} \Big |\frac{\partial W_k}{\partial x_i}f_i\Big |\le&|\xi _k|^3\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) \big (|\xi _1|^{r_{i+1}/\mu }+\cdots +|\xi _{i}|^{r_{i+1}/\mu }\big )\beta _{k}(\cdot )\varTheta \nonumber \\ \le&\,\frac{1}{3k}\varTheta \sum _{i=1}^{k-1}|\xi _j|^{\frac{4\mu +\tau }{\mu }} +\varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\beta _k(\cdot ), \end{aligned}$$

(47)

under which Proposition 2 holds naturally. $\square$

Proof of Proposition 3

Based on Assumption 1, one has $\forall i=1,\ldots ,k$

$$\begin{aligned} \Vert g_i\Vert \le&\left( |x_1|^{\frac{2r_i+\tau }{2r_1}}+\cdots +|x_i|^{\frac{2r_i+\tau }{2r_i}}\right) \eta _{i1}(\bar{x}_i)\eta _{i2}(\theta )\nonumber \\ \le&\left( |\xi _1|^{\frac{2r_i+\tau }{2\mu }}+\cdots +|\xi _i|^{\frac{2r_i+\tau }{2\mu }}\right) \beta _i(\cdot )\eta _{i2}(\theta ). \end{aligned}$$

(48)

Similar to the proof in Proposition 1, the estimate of $|\partial ^2(x_k^{*\mu /r_k})/\partial x_i^2|$ can also be done inductively. Specifically, for $i=1,\ldots ,k-1$

$$\begin{aligned} \Big |\frac{\partial ^2 x_{k}^{*\frac{\mu }{r_{k}}}}{\partial x_i^2}\Big |\le \left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -2r_i}{\mu }}\right) \beta _{k-1}(\cdot ). \end{aligned}$$

(49)

Combining (48) and (49), it yields that for $i=1,\ldots ,k-1$,

$$\begin{aligned} \frac{1}{2}\frac{\partial ^2 W_k}{\partial x_i^2}\Vert g_i\Vert ^2 \le&\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -2r_i}{\mu }}\right) |\xi _k|^3\left( \sum _{l=1}^i|\xi _l|^{\frac{2r_i+\tau }{2\mu }}\right) ^2\varTheta \beta _{k-1}(\cdot )\nonumber \\&+\,\left( \sum _{j=1}^{k-1}|\xi _j|^{\frac{\mu -r_i}{\mu }}\right) ^2|\xi _k|^2\left( \sum _{l=1}^i|\xi _l|^{\frac{2r_i+\tau }{2\mu }}\right) ^2\varTheta \beta _{k-1}(\cdot )\nonumber \\ \le&\,\frac{1}{3k}\varTheta \sum _{j=1}^{k-1}|\xi _j|^{\frac{4\mu +\tau }{\mu }}+\varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\bar{h}_{k3}(\cdot ) \end{aligned}$$

(50)

where $\bar{h}_{k3}(\cdot )\ge 0$ is a smooth function of $x_1,\ldots ,x_{k-1},\hat{\varTheta }$. Moreover, for a nonnegative smooth function $\tilde{h}_{k3}(\bar{x}_k,\hat{\varTheta })$

$$\begin{aligned} \frac{1}{2}\frac{\partial ^2 W_k}{\partial x_k^2}\Vert g_k\Vert ^2\le&|\xi _k|^{\frac{3\mu -r_k}{\mu }}\left( |\xi _{k-1}|^{\frac{\mu -r_k}{\mu }}+|\xi _k|^{\frac{\mu -r_k}{\mu }}\right) \left( \sum _{j=1}^k|\xi _j|^{\frac{2r_k+\tau }{2\mu }}\right) ^2\varTheta \beta _k(\cdot )\nonumber \\ \le&\frac{1}{3k}\varTheta \sum _{j=1}^{k-1}|\xi _j|^{\frac{4\mu +\tau }{\mu }}+\varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\tilde{h}_{k3}(\cdot ). \end{aligned}$$

(51)

It is clear that Proposition 3 follows from (50) and (51), by letting $h_{k3}(\cdot )\!=(k\!-1)\bar{h}_{k3}(\cdot )+\tilde{h}_{k3}(\cdot )$. $\square$

Proof of Proposition 4

In a similar way, for $i,j=1,\ldots ,k-1$ and $i\ne j$,

$$\begin{aligned} \Big |\frac{\partial ^2 x_{k}^{*\mu /r_k}}{\partial x_i\partial x_j}\Big |\le \left( \sum _{l=1}^{k-1}|\xi _l|^{\frac{\mu -r_i-r_j}{\mu }}\right) \beta _{k-1}(\cdot ) \end{aligned}$$

(52)

under which

$$\begin{aligned} \frac{\partial ^2 W_k}{\partial x_i\partial x_j}\Vert g_i^T\Vert \Vert g_j\Vert \le&\frac{1}{3(k-1)(k-2)}\varTheta \sum _{l=1}^{k-1}|\xi _l|^{\frac{4\mu +\tau }{\mu }}+ \varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\bar{h}_{k4}(\bar{x}_{k-1},\hat{\varTheta }) \end{aligned}$$

(53)

where $\bar{h}_{k4}(\cdot )$ is a nonnegative smooth function. For $i=k$ and $j\ne k$, there exists a smooth function $\tilde{h}_{k4}(\bar{x}_k,\hat{\varTheta })$ satisfying

$$\begin{aligned} \frac{\partial ^2 W_k}{\partial x_k\partial x_j}\Vert g_k^T\Vert \Vert g_j\Vert \le&\frac{1}{6(k-1)}\varTheta \sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+ \varTheta |\xi _k|^{\frac{4\mu +\tau }{\mu }}\tilde{h}_{k4}(\cdot ). \end{aligned}$$

(54)

which leads to Proposition 4 by combining it with (53). $\square$

Proof of Proposition 5

Using (15) and the definition of $\sigma _k$, one can get

$$\begin{aligned} \frac{\partial W_k}{\partial \hat{\varTheta }}\sigma _k\le&\frac{\partial x_k^{*\mu /r_k}}{\partial \hat{\varTheta }}|\xi _k|^3\left( \sum _{i=1}^k|\xi _i|^{\frac{4\mu +\tau }{\mu }}\right) \beta _k(\cdot )\nonumber \\ \le&\,\frac{1}{3}\sum _{i=1}^{k-1}|\xi _i|^{\frac{4\mu +\tau }{\mu }}+|\xi _k|^{\frac{4\mu +\tau }{\mu }}h_{k5}(\bar{x}_k,\hat{\varTheta }) \end{aligned}$$

(55)

for a nonnegative smooth function $h_{k5}(\cdot )$. In addition, it is easy to obtain that

$$\begin{aligned} \sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _k(\cdot )\xi _k^{\frac{4\mu +\tau }{\mu }}\le \left( 1+\left( \sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _k(\cdot )\right) ^2\right) ^{1/2}\xi _k^{\frac{4\mu +\tau }{\mu }}. \end{aligned}$$

(56)

By choosing $h_{k6}(\bar{x}_k,\hat{\varTheta })=\sqrt{1+(\sum _{i=1}^{k-1}\frac{\partial W_i}{\partial \hat{\varTheta }}\delta _k(\cdot ))^2}$, we complete the proof. $\square$