Skip to main content
SpringerLink
Log in

An Iterative LMI-Based Reduced-Order Observer Design for Fractional-Order Chaos Synchronization

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

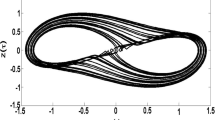
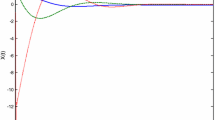
In this paper, attempts are made to design a reduced-order observer for a nonlinear Lipschitz class of fractional-order systems. It is assumed that nonlinear terms not only depend on measurable states but depend on unknown states and inputs as well. The sufficient conditions for stability of the observer based on the Lyapunov technique are derived and converted into linear matrix inequalities (LMIs). To overcome the main drawback of previous research studies which assumed that the sum of terms in infinite series coming from fractional derivative of a Lyapunov function is bounded and its upper bound is predefined, we used an iterative LMI-based algorithm to find out this bound. A four-wing chaotic system is implemented in both PSpice and MATLAB software as a case study. Simulation results are reported to show the effectiveness of the proposed iterative LMI-based reduced-order observer in tracking the unmeasurable state variables of the chaotic fractional system in different initial conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. E.A. Boroujeni, H.R. Momeni, Observer based control of a class of nonlinear fractional order systems using LMI. Int. J. Sci. Eng. Investig. 1, 48–52 (2012)

    Google Scholar 

  2. E.A. Boroujeni, H.R. Momeni, Non-fragile nonlinear fractional order observer design for a class of nonlinear fractional order systems. Signal Process. 92, 2365–2370 (2012)

    Article  Google Scholar 

  3. E.A. Boroujeni, M. Pourgholi, H.R. Momeni, Reduced order linear fractional order observer. in Conference on Control Communication and Computing—ICCC, pp. 1–4 (2013)

  4. S. Boyd, L.E. Ghaoui, E. Feron, V. Balakrishnan, Linear Matrix Inequalities in System and Control Theory (SIAM, Philadelphia, 1994)

    Book  MATH  Google Scholar 

  5. P.L. Butzer, U. Westphal, An Introduction to Fractional Calculus (World Scientific, Singapore, 2000)

    Book  MATH  Google Scholar 

  6. G.E. Carlson, C.A. Halijak, Approximation of fractional capacitors \((1/\text{ s })^{1/n}\) by a regular Newton process. IEEE Trans. Circuit Theory 11, 210–213 (1964)

    Article  Google Scholar 

  7. Y.H. Chang, C.I. Wu, H.C. Chen, C.W. Chang, and H.W. Lin, Fractional-order integral sliding-mode flux observer for sensorless vector-controlled induction motors. in IEEE ACC, pp. 190–195 (2001)

  8. S. Dadras, H.R. Momeni, Fractional sliding mode observer design for a class of uncertain fractional order nonlinear systems. in Conference on Decision and Control and European Control Conference, pp. 6925–30 (2009)

  9. M. Efe, Fractional fuzzy adaptive sliding-mode control of a 2-DOF direct-drive robot arm. IEEE Trans. Syst. Man Cybern. Part B Cybern. 38, 561–570 (2008)

    Google Scholar 

  10. F.W. Fariman, R.D. Gupta, Design of multifunctional reduced order observers. Int. J. Syst. Sci. 11, 1083–1094 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  11. P. Gahinet, A. Nemirovski, A. Laub, M. Chilai, LMI Control Toolbox User’s Guide (The Mathworks, Natick, 1995)

    Google Scholar 

  12. Z.H.W. Gao, The class of all reduced-order state observers. Syst. Anal. Model. Simul. 42, 1309–1317 (2002)

    MathSciNet  MATH  Google Scholar 

  13. R. Hilfer, Application of Fractional Calculus in Physics (World Scientific, New Jersey, 2001)

    Google Scholar 

  14. S.H. Hosseinnia, R. Ghaderi, A. Ranjbar, M. Mahmoudiana, M. Momani, Sliding mode synchronization of an uncertain fractional order chaotic system. Comput. Math. Appl. 59, 1637–1643 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  15. S. Ibrir, On observer design for nonlinear systems. Int. J. Syst. Sci. 37, 1097–1109 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  16. E.M. Jafarov, Robust reduced-order sliding mode observer design. Int. J. Syst. Sci. 42, 567–577 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  17. R.E. Kalman, A new approach to filtering and prediction problems. Trans. ASME J. Basic Eng. 82, 35–45 (1960)

    Article  Google Scholar 

  18. P.P. Khargonekar, I.R. Petersen, K. Zhou, Robust stabilization of uncertain linear systems: quadratic stabilizability and \(\text{ H }\infty \) control theory. IEEE Trans. Autom. Control 35, 356–361 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  19. A. Kiani, F. Fallahi, N. Pariz, A. Leung, A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter. Commun. Nonlinear Sci. Numer. Simulat. 14, 863–879 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations (Elsevier, Amsterdam, Netherlands, 2006)

    MATH  Google Scholar 

  21. Y.H. Lan, Y. Zhou, Non-fragile observer-based robust control for a class of fractional-order nonlinear systems. Syst. Control Lett. 62, 1143–1150 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. Y. Li, Y.Q. Chen, I. Podlubny, Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 59, 1810–1821 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  23. J. Lofberg, YALMIP: a toolbox for modeling and optimization in MATLAB. in IEEE International Symposium on Computer Aided Contol Systems, pp. 284–89 (2004)

  24. D.G. Luenberger, Observing the state of a linear system. IEEE Trans. Military Electron. 8, 74–80 (1964)

    Article  Google Scholar 

  25. D. Matignon, B. Novel, Observer-based controllers for fractional differential systems. in Proceedings of the 36th Conference on Decision and Control, (San Diego, 1997), pp. 4967–4972

  26. I. N’Doye, H. Voos, M. Darouach, Observer-based approach for fractional-order chaotic synchronization and secure communication. IEEE J. Emerg. Select. Topic Circuits Syst. 3, 442–450 (2013)

    Article  Google Scholar 

  27. I. Podlubny, Fractional Differential Equations (Academic Press, New York, 1999)

    MATH  Google Scholar 

  28. D.M. Senejohnny, H. Delavari, Active sliding observer scheme based fractional chaos synchronization. Commun. Nonlinear Sci. Numer. Simulat. 17, 4373–4383 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  29. S.K. Spurgeon, Sliding mode observers: a survey. Int. J. Syst. Sci. 39, 751–764 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. K.E. Starkov, L.N. Coria, L.T. Aguilar, On synchronization of chaotic systems based on the Thau observer design. Commun. Nonlinear Sci. Numer. Simul. 17, 17–25 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  31. V.E. Tarasov, No violation of the Leibniz rule. No fractional derivative. Commun. Nonlinear Sci. Numer. Simulat. 18, 2945–2948 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  32. A. Tornambe, Asymptotic observers for non-linear systems. Int. J. Syst. Sci. 23, 435–442 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  33. M.C. Tripathy, K. Biswas, S. Sen, A design example of a fractional-order Kerwin–Huelsman–Newcomb Biquad filter with two fractional capacitors of different order. Circuits Syst. Signal Process. 32, 1523–1536 (2013)

    Article  MathSciNet  Google Scholar 

  34. D. Valério, Ninteger V. 2.3 Fractional Control Toolbox for Matlab, Fractional Derivatives and Applications (User and programmer manual, Technical University of Lisboa, Lisbon, 2005)

    Google Scholar 

  35. H. Wang, Detecting faults in dynamic and bounded stochastic distributions: an observer based techniques. in IEEE American Control Conference, pp. 482–487 (2001)

  36. G.S. Wang, B. Liang, Z.X. Tang, A parameterized design of reduced-order state observer in linear control systems. Procedia Eng. 15, 974–978 (2011)

    Article  Google Scholar 

  37. H. Wang, X.J. Zhu, S.W. Gao, Z.Y. Chen, Singular observer approach for chaotic synchronization and private communication. Commun. Nonlinear Sci. Numer. Simulat. 16, 1517–1523 (2011)

    Article  Google Scholar 

  38. N. Wiener, Extrapolation, Interpolation and Smoothing of Stationary Time Series (Technology Press and Wiley, New York, 1949)

    MATH  Google Scholar 

  39. L.G. Yuan, Q.G. Yang, Parameter identification and synchronization of fractional-order chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 17, 305–316 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  40. Z. Zhang, H. Shao, Z. Wang, H. Shen, Reduced-order observer design for the synchronization of the generalized Lorenz chaotic systems. Appl. Math. Comput. 218, 7614–7621 (2012)

    MathSciNet  MATH  Google Scholar 

  41. P. Zhou, W. Zhu, Function projective synchronization for fractional order chaotic systems. Nonlinear Anal. Real World Appl. 12, 811–816 (2012)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Electrical Engineering, Shahid Beheshti University, A.C., Tehran, Iran

    Mahdi Pourgholi

  2. Electrical and Computer Engineering Department, Kharazmi University, Tehran, Iran

    Elham Amini Boroujeni

Authors
  1. Mahdi Pourgholi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Elham Amini Boroujeni
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Elham Amini Boroujeni.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pourgholi, M., Boroujeni, E.A. An Iterative LMI-Based Reduced-Order Observer Design for Fractional-Order Chaos Synchronization. Circuits Syst Signal Process 35, 1855–1870 (2016). https://doi.org/10.1007/s00034-016-0253-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-016-0253-3

Keywords

Search

Navigation