SSP-Based UBI Algorithms for Uniform Linear Array

Abstract

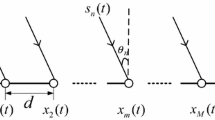
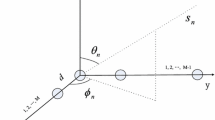
The underdetermined blind identification (UBI) for uniform linear array (ULA) with complex-valued mixing matrix can be processed effectively by the algorithms based on single-source-point (SSP) detection. In this paper, we propose two novel SSP-based methods of UBI in the time–frequency (TF) domain for ULA. One method, called UBI based on linear TF transform (UBI-LT), presents a new SSP detection criterion based on short-time Fourier transform, which modifies IME-RSSP (proposed by Li) by exploiting the phase information of mixture. The other method proposes a new SSP detection criterion based on a cross-term suppression quadratic TF distribution called UBI based on modified quadratic TF distribution (UBI-MQD), which can be seen as an improved version of the SSP-based algorithm proposed by Su. After performing these SSP detection criteria, two methods employ the peak detection and a clustering algorithm to estimate the complex-valued mixing matrix. Two methods have their own advantages and can be chosen by robust systems or high-performance systems. Numerical simulation results show that (1) the proposed methods have better performance than the existing methods with the same means of TF analysis (linear TF transform or quadratic TF distribution), and (2) UBI-LT is more robust than UBI-MQD even on the condition that the source number is large and the signal-to-noise (SNR) is low, while UBI-MQD has higher performance than UBI-LT when the source number is small and the SNR is high.

Appendices

Appendix 1: Proof of Theorem 1

Suppose that the TF point (t, f) is the SSP where only ${s_i}(t)$ is active. Set ${\alpha _i} = - \pi \sin ({\theta _i})$. According to Eqs. (2) and (4), we have

$$\begin{aligned} \mathbf{x}(t,f)= & {} {\mathbf{a}_i}{s_i}(t,f)\nonumber \\= & {} \left( {\begin{array}{*{20}{c}} 1\\ {{e^{j{\alpha _i}}}}\\ \vdots \\ {{e^{j(M - 1){\alpha _i}}}} \end{array}} \right) {s_i}(t,f) \end{aligned}$$

(14)

Then, we can get

$$\begin{aligned} {x_m}(t,f) = {e^{j(m - 1){\alpha _i}}}{s_i}(t,f),\quad m = 1,2, \ldots ,M \end{aligned}$$

(15)

We take advantage of phase and amplitude information and obtain the following equations:

$$\begin{aligned} \left| {\frac{{{x_2}(t,f)}}{{{x_1}(t,f)}}} \right|= & {} \left| {\frac{{{x_3}(t,f)}}{{{x_1}(t,f)}}} \right| = \cdots = \left| {\frac{{{x_M}(t,f)}}{{{x_1}(t,f)}}} \right| = 1\end{aligned}$$

(16)

$$\begin{aligned} \frac{{{x_2}(t,f)}}{{{x_1}(t,f)}}= & {} \frac{{{x_3}(t,f)}}{{{x_2}(t,f)}} = \cdots = \frac{{{x_M}(t,f)}}{{{x_{M - 1}}(t,f)}} \end{aligned}$$

(17)

where Eq. (16) exploits the amplitude information of Eqs. (15) and (17) uses the phase information of Eq. (15). When $M = 2$, SSPs should satisfy Eq. (16) only. If $M > 2$, Eqs. (16) and (17) should be satisfied simultaneously at SSPs. These equations are the necessary conditions for SSPs. If they are strict enough for the false SSPs, they can be seen as a selection criterion for SSPs. In fact, they are rigorous for the false SSPs and we will prove it below.

We assume that $(t',f')$ is a false SSP. According to Eqs. (2) and (3), we can get

$$\begin{aligned} \mathbf{x}(t',f') = \left[ {\begin{array}{*{20}{c}} 1&{}1&{} \cdots &{}1\\ {{e^{j{\alpha _1}}}}&{}{{e^{j{\alpha _2}}}}&{} \cdots &{}{{e^{j{\alpha _N}}}}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {{e^{j(M - 1){\alpha _1}}}}&{}{{e^{j(M - 1){\alpha _2}}}}&{} \cdots &{}{{e^{j(M - 1){\alpha _N}}}} \end{array}} \right] \mathbf{s}(t',f') \end{aligned}$$

(18)

where ${\alpha _i} = - \pi \sin ({\theta _i})\;,i = 1,2, \ldots ,M$. Then, we have

$$\begin{aligned} {x_m}(t',f') = \sum \limits _{i = 1}^N {{e^{j(m - 1){\alpha _i}}}{s_i}(t',f')} \end{aligned}$$

(19)

If $(t',f')$ satisfies Eq. (16), we can obtain

$$\begin{aligned} \left| {\frac{{{x_m}(t',f')}}{{{x_1}(t',f')}}} \right| = \left| {\frac{{\sum _{i = 1}^N {{e^{j(m - 1){\alpha _i}}}{s_i}(t',f')} }}{{\sum _{i = 1}^N {{s_i}(t',f')} }}} \right| = 1,\quad m = 1,2, \ldots ,M \end{aligned}$$

(20)

If Eq. (20) is permanently satisfied for arbitrary ${s_i}(t',f')$, we will get ${\alpha _p} = {\alpha _q},\forall p,q \in \{ 1,\ldots ,N\} ,p \ne q$. Then the DOAs are equal. It is contradictory to the hypothesis ${\theta _i} \ne {\theta _j}(\forall i \ne j)$. So, Eq. (16) is strict for the false SSPs. However, Eq. (20) can be satisfied by some special signals at several false SSPs where ${s_i}(t',f')$ can make Eq. (20) work. In order to avoid that case, we exploit the phase information exhibited by Eq. (17). If the false SSP $(t',f')$ satisfies Eq. (17), we can get

$$\begin{aligned} \frac{{\sum _{i = 1}^N {{e^{j(m - 1){\alpha _i}}}{s_i}(t',f')} }}{{\sum _{i = 1}^N {{e^{j(m - 2){\alpha _i}}}{s_i}(t',f')} }} = \frac{{\sum _{i = 1}^N {{e^{jm{\alpha _i}}}{s_i}(t',f')} }}{{\sum _{i = 1}^N {{e^{j(m - 1){\alpha _i}}}{s_i}(t',f')} }},\quad m = 1,2, \ldots ,M \end{aligned}$$

(21)

Since ${s_i}(t',f')$ can be chosen arbitrarily, we can obtain the paradoxical conclusion ${\alpha _p} = {\alpha _q},\forall p,q \in \{ 1,\ldots ,N\} ,p \ne q$ as well. So, Eq. (17) is also rigorous for the false SSPs. The special signals are hard to satisfy Eqs. (16) and (17) simultaneously.

Thus, the combination of the two equations can be seen as an SSP detection criterion. In practical application, we should modify the two equations with introducing small positive thresholds ${\varepsilon _1}$ and ${\varepsilon _2}$. Then, this criterion can be shown by

$$\begin{aligned}&\sum \limits _{i = 2}^M {\left| {\left| {\frac{{{x_i}(t,f)}}{{{x_1}(t,f)}}} \right| - 1} \right| }< {\varepsilon _1}\\&\sum \limits _{m = 2}^{M - 1} {\left| {\frac{{{x_{m + 1}}(t,f)}}{{{x_m}(t,f)}} - \frac{{{x_m}(t,f)}}{{{x_{m - 1}}(t,f)}}} \right| } < {\varepsilon _2} \end{aligned}$$

When $M = 2$, only first inequality needs to be satisfied. When $M > 2$, two inequalities require to be satisfied simultaneously.

According to Eq. (15), we can obtain the DOA estimation at the SSP (t, f) as follows:

$$\begin{aligned} \theta (t,f) = \arcsin \left( \frac{1}{{ - \pi (i - j)}}\mathrm{angle}\left( \frac{{{x_i}(t,f)}}{{{x_j}(t,f)}}\right) \right) \end{aligned}$$

where $i \ne j$ and $i,j \in \left\{ {1,\ldots ,M} \right\}$.

This completes the proof of Theorem 1. $\square$

Appendix 2: Proof of that When $M=2$, the Detection Criteria in IME-RSSP And UBI-LT Are Equivalent

Suppose that the TF point (t, f) is the SSP where only ${s_i}(t)$ is active. The detection criterion in IME-RSSP can be described by Eq. (5). It comes from a stricter condition below [14].

$$\begin{aligned} \left\| {{\mathbf{Y}^{ - 1}} \cdot \mathbf{Z}} \right\| = 1 \end{aligned}$$

(22)

where $\mathbf{Y} = \left( {\begin{array}{*{20}{c}} {{\hbox {Re}} \left\{ {{x_2}(t,f)} \right\} }&{}{{\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} }\\ {{\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} }&{}{ - {\hbox {Re}} \left\{ {{x_2}(t,f)} \right\} } \end{array}} \right)$ and $\mathbf{Z} = \left( {\begin{array}{*{20}{c}} {{\hbox {Re}} \left\{ {{x_1}(t,f)} \right\} }\\ {{\hbox {Im}} \left\{ {{x_1}(t,f)} \right\} } \end{array}} \right)$. Then we have

$$\begin{aligned} {\mathbf{Y}^{ - 1}} \cdot \mathbf{Z}= & {} {\left( {\begin{array}{*{20}{c}} {{\hbox {Re}} \left\{ {{x_2}(t,f)} \right\} }&{}{{\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} }\\ {{\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} }&{}{ - {\hbox {Re}} \left\{ {{x_2}(t,f)} \right\} } \end{array}} \right) ^{ - 1}}\left( {\begin{array}{*{20}{c}} {{\hbox {Re}} \left\{ {{x_1}(t,f)} \right\} }\\ {{\hbox {Im}} \left\{ {{x_1}(t,f)} \right\} } \end{array}} \right) \\= & {} \frac{1}{{{{\left| {{x_2}(t,f)} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\hbox {Re}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Re}} \left\{ {{x_1}(t,f)} \right\} + {\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Im}} \left\{ {{x_1}(t,f)} \right\} }\\ {{\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Re}} \left\{ {{x_1}(t,f)} \right\} - {\hbox {Re}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Im}} \left\{ {{x_1}(t,f)} \right\} } \end{array}} \right) \end{aligned}$$

According to Eq. (22), we get

$$\begin{aligned}&\left\| {{\mathbf{Y}^{ - 1}} \cdot \mathbf{Z}} \right\| = \left\| {\frac{1}{{{{\left| {{x_2}(t,f)} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\hbox {Re}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Re}} \left\{ {{x_1}(t,f)} \right\} + {\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Im}} \left\{ {{x_1}(t,f)} \right\} }\\ {{\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Re}} \left\{ {{x_1}(t,f)} \right\} - {\hbox {Re}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Im}} \left\{ {{x_1}(t,f)} \right\} } \end{array}} \right) } \right\| \\&\; = \frac{{\sqrt{{{\left( {\hbox {Re} \left\{ {{x_2}(t,f)} \right\} \hbox {Re} \left\{ {{x_1}(t,f)} \right\} + {\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} {\hbox {Im}} \left\{ {{x_1}(t,f)} \right\} } \right) }^2} + {{\left( {{\hbox {Im}} \left\{ {{x_2}(t,f)} \right\} \hbox {Re} \left\{ {{x_1}(t,f)} \right\} - \hbox {Re} \left\{ {{x_2}(t,f)} \right\} \,\,\hbox {Im} \left\{ {{x_1}(t,f)} \right\} } \right) }^2}} }}{{{{\left| {{x_2}(t,f)} \right| }^2}}}\\&\; = 1 \end{aligned}$$

When $M = 2$, the detection criterion in UBI-LT can be only described by Eq. (6). It comes from Eq. (16) and can be rewritten by

$$\begin{aligned}&\left| {\frac{{{x_1}(t,f)}}{{{x_2}(t,f)}}} \right| = \left| {\frac{{{\hbox {Re}} \{ {x_1}(t,f)\} + j{\hbox {Im}} \{ {x_1}(t,f)\} }}{{{\hbox {Re}} \{ {x_2}(t,f)\} + j{\hbox {Im}} \{ {x_2}(t,f)\} }}} \right| \\&\; = \left| {\frac{{\left( {{\hbox {Re}} \{ {x_1}(t,f)\} + j{\hbox {Im}} \{ {x_1}(t,f)\} } \right) \left( {{\hbox {Re}} \{ {x_2}(t,f)\} - j{\hbox {Im}} \{ {x_2}(t,f)\} } \right) }}{{\left( {{\hbox {Re}} \{ {x_2}(t,f)\} + j{\hbox {Im}} \{ {x_2}(t,f)\} } \right) \left( {{\hbox {Re}} \{ {x_2}(t,f)\} - j{\hbox {Im}} \{ {x_2}(t,f)\} } \right) }}} \right| \\&\; = \left| {\frac{{\left( {{\hbox {Re}} \{ {x_1}(t,f)\} {\hbox {Re}} \{ {x_2}(t,f)\} + {\hbox {Im}} \{ {x_1}(t,f)\} {\hbox {Im}} \{ {x_2}(t,f)\} } \right) - j\left( {{\hbox {Im}} \{ {x_2}(t,f)\} {\hbox {Re}} \{ {x_1}(t,f)\} - {\hbox {Re}} \{ {x_2}(t,f)\} {\hbox {Im}} \{ {x_1}(t,f)\} } \right) }}{{\left( {{\hbox {Re}} \{ {x_2}(t,f)\} + j{\hbox {Im}} \{ {x_2}(t,f)\} } \right) \left( {{\hbox {Re}} \{ {x_2}(t,f)\} - j{\hbox {Im}} \{{x_2}(t,f)\} } \right) }}} \right| \\&\; = \frac{{\sqrt{{{\left( {\hbox {Re} \{{x_1}(t,f)\} \,\hbox {Re} \{ {x_2}(t,f)\} + \hbox {Im} \{{x_1}(t,f)\} \,\hbox {Im} \{ {x_2}(t,f)\} } \right) }^2} + {{\left( {\hbox {Im} \{ {x_2}(t,f)\} \,\hbox {Re} \{ {x_1}(t,f)\} - \hbox {Re} \{ {x_2}(t,f)\}\, \hbox {Im} \{ {x_1}(t,f)\} } \right) }^2}} }}{{{{\left| {{x_2}(t,f)} \right| }^2}}}\\&\; = 1 \end{aligned}$$

From the derivation above, we can see that the two different detection criteria are equivalent when $M = 2$.

This completes the proof.

Appendix 3: Proof of Theorem 2

Suppose that the TF point (t, f) is the SSP where only ${s_i}(t)$ is active. Set ${\alpha _i} = - \pi \sin ({\theta _i})$. According to Eqs. (2) and (11), we can get

$$\begin{aligned} {\mathbf{{W}}_\mathbf{{x}}}(t,f)= & {} {\rho _{{s_i}{s_i}}}(t,f){\mathbf{{a}}_i}{} \mathbf{{a}}_i^\mathrm{{H}}\;\nonumber \\= & {} {\rho _{{s_i}{s_i}}}(t,f)\left( {\begin{array}{*{20}{c}} 1\\ {{e^{j{\alpha _i}}}}\\ \vdots \\ {{e^{j(M - 1){\alpha _i}}}} \end{array}} \right) \left( {\begin{array}{*{20}{c}} 1&{{e^{ - j{\alpha _i}}}}&\cdots&{{e^{ - j(M - 1){\alpha _i}}}} \end{array}} \right) \nonumber \\= & {} {\rho _{{s_i}{s_i}}}(t,f)\left( {\begin{array}{*{20}{c}} 1&{}{{e^{ - j{\alpha _i}}}}&{} \cdots &{}{{e^{ - j(M - 1){\alpha _i}}}}\\ {{e^{j{\alpha _i}}}}&{}1&{} \cdots &{}{{e^{ - j(M - 2){\alpha _i}}}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{e^{j(M - 1){\alpha _i}}}}&{}{{e^{j(M - 2){\alpha _i}}}}&{} \cdots &{}1 \end{array}} \right) \end{aligned}$$

(23)

According to the definition of the STFD matrices based on MWVD and STFT in [13], we have

$$\begin{aligned} \mathbf{{W}}_\mathbf{{x}}^\mathrm{MWV}(t,f)= & {} {\mathbf{{W}}_\mathbf{{x}}}(t,f) \odot {\left| {\mathbf{{W}}_\mathbf{{x}}^\mathrm{STFT}(t,f)} \right| ^2}\nonumber \\= & {} \left( {{\rho _{{s_i}{s_i}}}(t,f){\mathbf{{a}}_i}{} \mathbf{{a}}_i^\mathrm{{H}}\;} \right) \odot {\left| {\mathbf{{W}}_\mathbf{{x}}^\mathrm{STFT}(t,f)} \right| ^2}\nonumber \\= & {} {\rho _{{s_i}{s_i}}}(t,f)\left( {\begin{array}{*{20}{c}} {\rho _{{x_1}}^\mathrm{SPEC}(t,f)}&{}0&{} \cdots &{}0\\ 0&{}{\rho _{{x_2}}^\mathrm{SPEC}(t,f)}&{} \cdots &{}0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{} \cdots &{}{\rho _{{x_M}}^\mathrm{SPEC}(t,f)} \end{array}} \right) \nonumber \\= & {} \left( {\begin{array}{*{20}{c}} {\rho _{{x_1}{x_1}}^\mathrm{MWV}(t,f)}&{}0&{} \cdots &{}0\\ 0&{}{\rho _{{x_2}{x_2}}^\mathrm{MWV}(t,f)}&{} \cdots &{}0\\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ 0&{}0&{} \cdots &{}{\rho _{{x_M}{x_M}}^\mathrm{MWV}(t,f)} \end{array}} \right) \end{aligned}$$

(24)

Exploiting the diagonal elements, we get

$$\begin{aligned} \frac{{\rho _{{x_l}{x_l}}^\mathrm{MWV}(t,f)}}{{\rho _{{x_k}{x_k}}^\mathrm{MWV}(t,f)}} = \frac{{\rho _{{x_l}}^\mathrm{SPEC}(t,f)}}{{\rho _{{x_k}}^\mathrm{SPEC}(t,f)}}\;,\forall l \ne k \end{aligned}$$

(25)

This equation is a necessary condition for SSPs. If it is strict enough for the false SSPs, it can be seen as a selection criterion for SSPs. In fact, it is rigorous for the false SSPs and we will prove it below.

We assume that $(t',f')$ is a false SSP. Then we have

$$\begin{aligned} \mathbf{{W}}_\mathbf{{x}}^\mathrm{MWV}(t',f')= & {} {\mathbf{{W}}_\mathbf{{x}}}(t',f') \odot {\left| {\mathbf{{W}}_\mathbf{{x}}^\mathrm{STFT}(t',f')} \right| ^2}\\= & {} \left( {\begin{array}{*{20}{c}} {\rho _{{x_1}{x_1}}^\mathrm{MWV}(t',f')}&{}0&{} \cdots &{}0\\ 0&{}{\rho _{{x_2}{x_2}}^\mathrm{MWV}(t',f')}&{} \cdots &{}0\\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ 0&{}0&{} \cdots &{}{\rho _{{x_M}{x_M}}^\mathrm{MWV}(t',f')} \end{array}} \right) \end{aligned}$$

where $\rho _{{x_i}{x_i}}^\mathrm{MWV}(t',f') = \rho _{{x_i}}^\mathrm{SPEC}(t',f')\sum \nolimits _{q = 1}^N {\sum \nolimits _{p = 1}^N {{e^{j(i - 1)({\alpha _p} - {\alpha _q})}}{\rho _{{s_p}{s_q}}}(t',f')} } , i \in \{ 1, \ldots ,M\}$.

If $(t',f')$ satisfies Eq. (25), we can obtain

$$\begin{aligned} \frac{{\rho _{{x_l}{x_l}}^\mathrm{MWV}(t',f')}}{{\rho _{{x_k}{x_k}}^\mathrm{MWV}(t',f')}}= & {} \frac{{\rho _{{x_l}}^\mathrm{SPEC}(t',f')\sum _{q = 1}^N {\sum _{p = 1}^N {{e^{j(l - 1)({\alpha _p} - {\alpha _q})}}{\rho _{{s_p}{s_q}}}(t',f')} } }}{{\rho _k^\mathrm{SPEC}(t',f')\sum _{q = 1}^N {\sum _{p = 1}^N {{e^{j(k - 1)({\alpha _p} - {\alpha _q})}}{\rho _{{s_p}{s_q}}}(t',f')} } }}\\= & {} \frac{{\rho _{{x_l}}^\mathrm{SPEC}(t',f')}}{{\rho _{{x_k}}^\mathrm{SPEC}(t',f')}}\; \end{aligned}$$

where $l \ne k,l,k \in \{ 1, \ldots ,M\}$. Then, we can get

$$\begin{aligned} \sum \limits _{q = 1}^N {\sum \limits _{p = 1}^N {{e^{j(l - 1)({\alpha _p} - {\alpha _q})}}{\rho _{{s_p}{s_q}}}(t',f')} } = \sum \limits _{q = 1}^N {\sum \limits _{p = 1}^N {{e^{j(k - 1)({\alpha _p} - {\alpha _q})}}{\rho _{{s_p}{s_q}}}(t',f')} } ,\quad \forall l \ne k \end{aligned}$$

Since ${\rho _{{s_p}{s_q}}}(t',f')$ can be chosen arbitrarily, we will get ${\alpha _p} = {\alpha _q},\forall p,q \in \{ 1, \ldots ,N\} ,p \ne q$. It is contradictory to the hypothesis ${\theta _i} \ne {\theta _j}(\forall i \ne j)$. So, this condition is rigorous for the false SSPs.

As a result, Eq. (25) can be seen as an SSP detection criterion. In practical application, we should modify the equation with introducing a small positive threshold ${\varepsilon _5}$. Then, this criterion can be shown by

$$\begin{aligned} \sum \limits _{\begin{array}{*{20}{c}} {i,j = 1},{i \ne j} \end{array}}^M {\left| {\frac{{\rho _{{x_i}{x_i}}^\mathrm{MWV}(t,f)}}{{\rho _{{x_j}{x_j}}^\mathrm{MWV}(t,f)}} - \frac{{\rho _{{x_i}}^\mathrm{SPEC}(t,f)}}{{\rho _{{x_j}}^\mathrm{SPEC}(t,f)}}} \right| } \le {\varepsilon _5} \end{aligned}$$

This completes the proof of Theorem 2.