Skip to main content
SpringerLink
Log in

Scaling Fractal-Chuan Fractance Approximation Circuits of Arbitrary Order

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

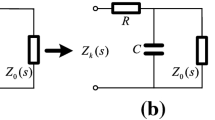
The scaling fractal-chuan fractance approximation circuit (SFCFAC), which can realize the rational approximation of arbitrary-order fractances and has an excellent approximation performance, is presented in this paper. For an original SFCFAC, the progression ratios of resistance and capacitance are limited to the range 0–1. However, it is possible for the values of both progression ratios to be greater than one. The impedance function of an SFCFAC can be represented by an irregular scaling equation. By solving the scaling equation approximately, the operational order of an SFCFAC can be obtained using both progression ratios as \(\mu = -\lg \alpha /\lg (\alpha \beta )\). Therefore, the SFCFAC has fractional operational characteristics, which is explained in theory. Oscillation phenomena are inherent to the SFCFAC. It is necessary to learn about these oscillation characteristics. The approximation performance can be improved by adding a series resistor and a series capacitor to the SFCFAC. The corresponding resistance and capacitance are determined by both progression ratios. The optimization has the advantages of simple operation, evident influence, and good practicality, which will make the SFCFAC competitive in future studies. Moreover, the values of the operational order of SFCFACs are extended from \(-1<\mu <0\) to \(0<|\mu |<2\) without using inductors, which is feasible for practical applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. A. Adhikary, S. Choudhary, S. Sen, Optimal design for realizing a grounded fractional order inductor using GIC. IEEE Trans. Circuits Syst. I Regul. Pap. 65(8), 2411–2421 (2018)

    MathSciNet  Google Scholar 

  2. A. Adhikary, P. Sen, S. Sen, K. Biswas, Design and performance study of dynamic fractors in any of the four quadrants. Circuits Syst. Signal Process. 35(6), 1909–1932 (2016)

    MathSciNet  Google Scholar 

  3. A. Adhikary, S. Sen, K. Biswas, Practical realization of tunable fractional order parallel resonator and fractional order filters. IEEE Trans. Circuits Syst. I Regul. Pap. 63(8), 1142–1151 (2016)

    MathSciNet  Google Scholar 

  4. M.P. Aghababa, Finite-time chaos control and synchronization of fractional-order nonautonomous chaotic (hyperchaotic) systems using fractional nonsingular terminal sliding mode technique. Nonlinear Dyn. 69(1–2), 247–261 (2012)

    MathSciNet  MATH  Google Scholar 

  5. V. Badri, M.S. Tavazoei, Achievable performance region for a fractional-order proportional and derivative motion controller. IEEE Trans. Ind. Electron. 62(11), 7171–7180 (2015)

    Google Scholar 

  6. H.B. Bao, J.D. Cao, Projective synchronization of fractional-order memristor-based neural networks. Neural Netw. 63, 1 (2015)

    MATH  Google Scholar 

  7. N. Bigdeli, H.A. Ziazi, Design of fractional robust adaptive intelligent controller for uncertain fractional-order chaotic systems based on active control technique. Nonlinear Dyn. 87(3), 1703–1719 (2017)

    MathSciNet  MATH  Google Scholar 

  8. K. Biswas, S. Sen, P.K. Dutta, Realization of a constant phase element and its performance study in a differentiator circuit. IEEE Trans. Circuits Syst. II Express Briefs 53(9), 802–806 (2006)

    Google Scholar 

  9. G. Carlson, C. Halijak, Approximation of fractional capacitors \((1/s)^{1/n}\) by a regular newton process. IEEE Trans. Circuit Theory 11(2), 210–213 (1964)

    Google Scholar 

  10. G.E. Carlson, Simulation of the fractional derivative operator \(\sqrt{s}\) and the fractional integral operator \(1/\sqrt{s}\). Carlos A Brebbia (2013), pp. 149–158

  11. A. Charef, Analogue realisation of fractional-order integrator, differentiator and fractional \(PI^{\lambda }D^{\mu }\) controller. IEE Proc. Control Theory Appl. 153(6), 714–720 (2006)

    Google Scholar 

  12. I. Dimeas, I. Petráš, C. Psychalinos, New analog implementation technique for fractional-order controller: a DC motor control. AEÜ Int. J. Electron. Commun. 78, 192–200 (2017)

    Google Scholar 

  13. A.S. Elwakil, Fractional-order circuits and systems: an emerging interdisciplinary research area. IEEE Circuits Syst. Mag. 10(4), 40–50 (2010)

    Google Scholar 

  14. G. Fedele, A fractional-order repetitive controller for periodic disturbance rejection. IEEE Trans. Autom. Control 63(5), 1426–1433 (2018)

    MathSciNet  MATH  Google Scholar 

  15. J.F. Gómez-Aguilar, Fundamental solutions to electrical circuits of non-integer order via fractional derivatives with and without singular kernels. Eur. Phys. J. Plus 133(5), 197 (2018)

    Google Scholar 

  16. J.F. Gómez-Aguilar, A. Atangana, V.F. Morales-Delgado, Electrical circuits RC, LC, and RL described by atangana-baleanu fractional derivatives. Int. J. Circuit Theory Appl. 45(3), 1514–1533 (2017)

    Google Scholar 

  17. J.F. Gómez-Aguilar, V.F. Morales-Delgado, M.A. Taneco-Hernández, D. Baleanu, R.F. Escobar-Jiménez, M.M.A. Qurashi, Analytical solutions of the electrical RLC circuit via Liouville–Caputo operators with local and non-local kernels. Entropy 18(402), 1–12 (2016)

    Google Scholar 

  18. J.F. Gómez-Aguilar, H. Yépez-Martínez, R.F. Escobar-Jiménez, C.M. Astorga-Zaragoza, J. Reyes-Reyes, Analytical and numerical solutions of electrical circuits described by fractional derivatives. Appl. Math. Model. 40(21–22), 9079–9094 (2016)

    MathSciNet  Google Scholar 

  19. T.T. Hartley, C.F. Lorenzo, H. Killory Qammer, Chaos in a fractional order Chua’s system. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 42(8), 485–490 (1995)

    Google Scholar 

  20. Q.Y. He, Scaling Fractal Lattice Fractance (Sichuan University, Chengdu, China, M.S. thesis, 2017)

  21. Q.Y. He, B. Yu, X. Yuan, Carlson iterating rational approximation and performance analysis of fractional operator with arbitrary order. Chin. Phys. B 26(4), 66–74 (2017)

    Google Scholar 

  22. Q.Y. He, X. Yuan, Carlson iteration and rational approximations of arbitrary order fractional calculus operator. Acta Phys. Sin. 65(16), 25–34 (2016)

    Google Scholar 

  23. R.M. Hill, L.A. Dissado, R.R. Nigmatullin, Invariant behaviour classes for the response of simple fractal circuits. J. Phys. Condens. Matter 3(3), 9773 (1991)

    Google Scholar 

  24. R. Hotzel, M. Fliess, On linear systems with a fractional derivation: introductory theory and examples. Math. Comput. Simul. 45(34), 385–395 (1998)

    MathSciNet  MATH  Google Scholar 

  25. T. Kaczorek, Positivity and reachability of fractional electrical circuits. Exp. Mech. 54(9), 1597–1611 (2011)

    Google Scholar 

  26. T.C. Lin, T.Y. Lee, Chaos synchronization of uncertain fractional-order chaotic systems with time delay based on adaptive fuzzy sliding mode control. IEEE Trans. Fuzzy Syst. 19(4), 623–635 (2011)

    Google Scholar 

  27. Y. Luo, Y. Chen, Fractional order [proportional derivative] controller for a class of fractional order systems. Automatica 45(10), 2446–2450 (2009)

    MathSciNet  MATH  Google Scholar 

  28. G.M. Mahmoud, T.M. Abed-Elhameed, M.E. Ahmed, Generalization of combination–combination synchronization of chaotic n-dimensional fractional-order dynamical systems. Nonlinear Dyn. 83(4), 1885–1893 (2016)

    MathSciNet  MATH  Google Scholar 

  29. K. Matsuda, H. Fujii, H\(_{\infty }\) optimized wave-absorbing control: analytical and experimental results. J. Guid. Control Dyn. 16(6), 1146–1153 (1993)

    MATH  Google Scholar 

  30. A.L. Méhautéy, G. Crépy, Introduction to transfer and motion in fractal media: the geometry of kinetics. Solid State Ionics 9(Dec.), 17–30 (1983)

    Google Scholar 

  31. D. Mondal, K. Biswas, Performance study of fractional order integrator using single-component fractional order element. IET Circuits Devices Syst. 5(4), 334–342 (2011)

    Google Scholar 

  32. V.F. Morales-Delgado, J.F. Gómez-Aguilar, M.A. Taneco-Hernandez, Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville–Caputo sense. AEÜ Int. J. Electron. Commun. 85, 108–117 (2018)

    Google Scholar 

  33. K.B. Oldham, Interrelation of current and concentration at electrodes. J. Appl. Electrochem. 21(12), 1068–1072 (1991)

    Google Scholar 

  34. A. Oustaloup, O. Cois, P. Lanusse, P. Melchior, X. Moreau, J. Sabatier, The crone approach: theoretical developments and major applications. IFAC Proc. Vol. 39(11), 324–354 (2006)

    Google Scholar 

  35. A. Oustaloup, F. Levron, B. Mathieu, F.M. Nanot, Frequency-band complex noninteger differentiator: characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 47(1), 25–39 (2000)

    Google Scholar 

  36. I. Petráš, Fractional-order memristor-based Chua’s circuit. IEEE Trans. Circuits Syst. II Express Briefs 57(12), 975–979 (2010)

    Google Scholar 

  37. I. Petráš, D. Bednárová, Fractional order chaotic systems, in IEEE International Conference on Emerging Technologies and Factory Automation (2009), pp. 1031–1038

  38. Y.F. Pu, Analog circuit realization of arbitrary-order fractional Hopfield neural networks: a novel application of fractor to defense against chip cloning attacks. IEEE Access 4(99), 5417–5435 (2016)

    Google Scholar 

  39. Y.F. Pu, Measurement units and physical dimensions of fractance-part I: position of purely ideal fractor in Chuas axiomatic circuit element system and fractional-order reactance of fractor in its natural implementation. IEEE Access 4, 3379–3397 (2016)

    Google Scholar 

  40. Y.F. Pu, Measurement units and physical dimensions of fractance-part II: fractional-order measurement units and physical dimensions of fractance and rules for fractors in series and parallel. IEEE Access 4, 3398–3416 (2016)

    Google Scholar 

  41. Y.F. Pu, Z. Yi, J.L. Zhou, Fractional Hopfield neural networks: fractional dynamic associative recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 28(10), 2319–2333 (2017)

    MathSciNet  Google Scholar 

  42. Y.F. Pu, X. Yuan, B. Yu, Analog circuit implementation of fractional-order memristor: arbitrary-order lattice scaling fracmemristor. IEEE Trans. Circuits Syst. I Regul. Pap. 65(9), 2903–2916 (2018)

    MathSciNet  Google Scholar 

  43. R. Rakkiyappan, J. Cao, G. Velmurugan, Existence and uniform stability analysis of fractional-order complex-valued neural networks with time delays. IEEE Trans. Neural Netw. Learn. Syst. 26(1), 84–97 (2015)

    MathSciNet  MATH  Google Scholar 

  44. B. Ross, A brief history and exposition of the fundamental theory of fractional calculus. Springer Lect. Notes Math. 57, 1–36 (1975)

    Google Scholar 

  45. M.S. Sarafraz, M.S. Tavazoei, Passive realization of fractional-order impedances by a fractional element and RLC components: conditions and procedure. IEEE Trans. Circuits Syst. I Regul. Pap. 64(3), 585–595 (2017)

    Google Scholar 

  46. G. Tsirimokou, A systematic procedure for deriving RC networks of fractional-order elements emulators using MATLAB. AEÜ Int. J. Electron. Commun. 78, 7–14 (2017)

    Google Scholar 

  47. J. Valsa, Fractional-order electrical components, networks and systems, in Radioelektronika (2012), pp. 1–9

  48. J. Valsa, P. Dvorak, M. Friedl, Network model of the CPE. Radioengineering 20(3), 619–626 (2011)

    Google Scholar 

  49. J. Valsa, J. Vlach, RC models of a constant phase element. Int. J. Circuit Theory Appl. 41(1), 59–67 (2013)

    Google Scholar 

  50. G. Velmurugan, R. Rakkiyappan, Hybrid projective synchronization of fractional-order memristor-based neural networks with time delays. Nonlinear Dyn. 11(3), 1–14 (2015)

    MATH  Google Scholar 

  51. G. Velmurugan, R. Rakkiyappan, J. Cao, Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw. 73(1–2), 36 (2015)

    MATH  Google Scholar 

  52. S.L. Wu, M. Al-Khaleel, Parameter optimization in waveform relaxation for fractional-order \(RC\) circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 64(7), 1781–1790 (2017)

    MathSciNet  Google Scholar 

  53. Z.R. Yang, Fractal Physics (Shanghai Science and Technology Eduction Press, Shanghai, 1996)

    Google Scholar 

  54. B. Yu, Q.Y. He, X. Yuan, Scaling fractal-lattice franctance approximation circuits of arbitrary order and irregular lattice type scaling equation. Acta Phys. Sin. 67(7), 070202 (2018)

    Google Scholar 

  55. B. Yu, Q.Y. He, X. Yuan, L.X. Yang, Approximation performance analyses and applications of f characteristics in fractance approximation circuit. J. Sichuan Univ. (Nat. Sci. Ed.) 55(2), 301–306 (2018)

    Google Scholar 

  56. X. Yuan, Mathematical Principles of Fractance Approximation Circuits (Science Press, Beijing, 2015)

    Google Scholar 

  57. Z. Yuan, X. Yuan, On zero-pole distribution of regular RC fractal fractance approximation circuits. Acta Electron. Sin. 45(10), 2511–2520 (2017)

    Google Scholar 

  58. J.Z. Zhang, Fractal (Tsinghua University Press, Beijing, 2011)

    Google Scholar 

  59. H. Zhu, S. Zhou, J. Zhang, Chaos and synchronization of the fractional-order Chuas system. Chaos Solitons Fractals 26(03), 1595–1603 (2016)

    MATH  Google Scholar 

  60. Y.X. Zu, Y.Q. Lv, Network Analysis and Synthesis (China Machine Press, Beijing, 2007)

    Google Scholar 

Download references

Acknowledgements

The work was supported by the National Key Research and Development Program Foundation of China under Grants 2018YFC0830300 and the National Natural Science Foundation of China under Grants 61571312.

Author information

Authors and Affiliations

  1. College of Computer Science, Sichuan University, Chengdu, 610065, China

    Qiu-Yan He & Yi-Fei Pu

  2. College of Physics and Engineering, Chengdu Normal University, Chengdu, 611130, China

    Bo Yu

  3. College of Electronics and Information Engineering, Sichuan University, Chengdu, 610065, China

    Xiao Yuan

Authors
  1. Qiu-Yan He
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi-Fei Pu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bo Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiao Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yi-Fei Pu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

He, QY., Pu, YF., Yu, B. et al. Scaling Fractal-Chuan Fractance Approximation Circuits of Arbitrary Order. Circuits Syst Signal Process 38, 4933–4958 (2019). https://doi.org/10.1007/s00034-019-01117-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-019-01117-x

Keywords

Search

Navigation