Skip to main content
SpringerLink
Log in

Using Derivatives of Second Generating Function for Underdetermined Blind Identification

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

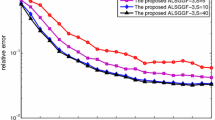
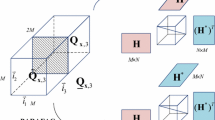
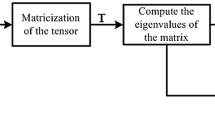
In this paper, we propose a new family of algorithms for underdetermined blind identification based on the second generating function (SGF). For the real case, the proposed algorithm first takes advantage of the partial derivatives of the SGF of the observation signals to construct a tensor and then reconstructs this tensor by grouping the parallel factors. The reconstructed tensor, which expands the length of several dimensions of the original tensor, transforms the underdetermined case into an overdertermined or determined case when \(({M^2} + M)/2 \ge N\), where M is the number of sensors and N is the number of sources. Thus, obtaining the estimation of the mixing matrix by decomposing the reconstructed tensor results in the performance improvement. The analysis of the uniqueness of tensor decomposition and the complex analysis show that the proposed algorithm relaxes the limitation of the maximal number of sources and owns lower computational complexity order compared with the conventional ALESCAF algorithm. We also extend the proposed algorithm to the complex case by complex-to-real transformation. Simulation results verify the effectiveness of the proposed algorithms and show that the proposed algorithms are preferred when the signal-to-noise ratio is higher than 5 dB.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. L. Albera, A. Ferreol, P. Comon et al., Blind identification of overcomplete mixtures of sources (BIOME). Lin. Algebra Appl. 391, 1–30 (2004)

    MathSciNet  MATH  Google Scholar 

  2. P. Bofill, M. Zibulevsky, Underdetermined blind source separation using sparse representations. Signal Process. 81(11), 2353–2362 (2001)

    MATH  Google Scholar 

  3. Y. Cai, D. Liu, Multiuser detection using the Taguchi method for DS-CDMA systems. IEEE Trans. Wirel. Commun. 4(4), 1594–1607 (2005)

    Google Scholar 

  4. J.D. Carroll, J.J. Chang, Analysis of individual differences in multidimensional scaling via n-way generalization of Eckart–Young decomposition. Psychometrika 35(3), 283–319 (1970)

    MATH  Google Scholar 

  5. P. Chevalier, L. Albera, A. Ferréol, P. Comon, On the virtual array concept for higher order array processing. IEEE Trans. Signal Process. 53(4), 1254–1271 (2005)

    MathSciNet  MATH  Google Scholar 

  6. P. Comon, C. Jutten et al., Handbook of Blind Source Separation: Independent Component Analysis and Applications (Academic press, New York, 2010)

    Google Scholar 

  7. P. Comon, X. Luciani, A.L.F. de Almeida, Tensor decompositions, alternating least squares and other tales. J. Chemom. 23, 393–405 (2009)

    Google Scholar 

  8. P. Comon, M. Rajih, Blind identification of under-determined mixtures based on the characteristic function. Signal Process. 86(9), 2271–2281 (2006)

    MATH  Google Scholar 

  9. P. Comon, M. Rajih, Blind identification of complex underdetermined mixtures, in Proceedings of ICA Conference (Granada, 2004), pp. 105–112

  10. A.L.F. de Almeida, X. Luciani, A. Stegeman, P. Comon, CONDFAC decomposition approach to blind identification of underdetermined mixtures based on generating function derivatives. IEEE Trans. Signal Process. 60(11), 5698–5713 (2012)

    MathSciNet  MATH  Google Scholar 

  11. W. Feller, An Introduction to Probability Theory and Its Applications (Wiley, New York, 1973)

    MATH  Google Scholar 

  12. R.A. Harshman, Determination and proof of minimum uniqueness conditions for PARAFAC-1. UCLA Working Papers in Phonet. vol. 22, pp. 111–117 (1972)

  13. R.A. Harshman, Foundations of the Parafac Procedure: Models and Conditions for an Explanatory Multimodal Factor Analysis. UCLA Working Papers in Phonet, vol. 16, pp. 1–84 (1970)

  14. M.M. Hossain, B.E. Levy, D. Thapa, A.L. Oldenburg, C.M. Gallippi, Blind source separation-based motion detector for imaging super-paramagnetic iron oxide (SPIO) particles in magnetomotive ultrasound imaging. IEEE Trans. Med. Imaging 37(10), 2356–2366 (2018)

    Google Scholar 

  15. T. Jiang, N.D. Sidiropoulos, Kruskal’s permutation lemma and the identification of CANDECOMP/PARAFAC and bilinear models with constant modulus constraints. IEEE Trans. Signal Process. 52(9), 2625–2636 (2004)

    MathSciNet  MATH  Google Scholar 

  16. A.M. Kagan, Y.V. Linnika, C.R. Rao, Characterization Problems in Mathematical Statistics (Wiley, New York, 1973)

    Google Scholar 

  17. A. Karfoul, L. Albera, G. Birot, Blind underdetermined mixture identification by joint canonical decomposition of HO cumulants. IEEE Trans. Signal Process. 58(2), 638–649 (2010)

    MathSciNet  MATH  Google Scholar 

  18. A. Karfoul, L. Albera, D.L. Lathauwer, Iterative methods for the canonical decomposition of multi-way arrays: application to blind underdetermined mixture identification. Signal Process. 91(8), 1789–1802 (2011)

    MATH  Google Scholar 

  19. S. Kim, C.D. Yoo, Underdetermined blind source separation based on subspace representation. IEEE Trans. Signal Process. 57(7), 2604–2614 (2009)

    MathSciNet  MATH  Google Scholar 

  20. J.B. Kruskal, Three-way arrays: rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Linear Algebra Appl. 18, 95–138 (1977)

    MathSciNet  MATH  Google Scholar 

  21. M. Küdhne, R. Togneri, S. Nordholm, A new evidence model for missing data speech recognition with applications in reverberant multisource environments. IEEE Trans. Audio Speech Lang. Process. 19(2), 372–384 (2011)

    Google Scholar 

  22. D.L. Lathauwer, J. Castaing, Blind identification of underdetermined mixtures by simultaneous matrix diagonalization. IEEE Trans. Signal Process. 56(3), 1096–1105 (2008)

    MathSciNet  MATH  Google Scholar 

  23. D.L. Lathauwer, J. Castaing, J.F. Cardoso, Fourth-order cumulant based blind identification of underdetermined mixtures. IEEE Trans. Signal Process. 55(6), 2965–2973 (2007)

    MathSciNet  MATH  Google Scholar 

  24. D.L. Lathauwer, B.D. Moor, J. Vandewalle, On the best rank-1 and rank-(\(R_1\), \(R_2\),\(\cdots \), \(R_N\)) approximation of higher-order tensors. SIAM J. Matrix Anal. Appl. 21, 1324–1342 (2000)

    MathSciNet  MATH  Google Scholar 

  25. H. Lin, T. Thaiupathump, S.A. Kassam, Blind separation of complex I/Q independent sources with phase recovery. IEEE Signal Process. Lett. 12(5), 419–422 (2005)

    Google Scholar 

  26. X. Luciani, A.L.F. de Almeida, P. Comon, Blind identification of underdetermined mixtures based on the characteristic function: the complex case. IEEE Trans. Signal Process. 59(2), 540–553 (2011)

    MathSciNet  MATH  Google Scholar 

  27. M. Rajih, P. Comon, Blind identification of under-determined mixtures based on the characteristic function: Influence of the knowledge of source PDF’s, in Proceedings of 1st IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (Puerto Vallarta, 2005), pp. 133–136

  28. M. Rajih, P. Comon, R. Harshman, Enhanced line search: a novel method to accelerate PARAFAC. SIAM J. Matrix Anal. Appl. 30(3), 1148–1171 (2008)

    MathSciNet  MATH  Google Scholar 

  29. N.D. Sidiropoulos, R. Bro, On the uniqueness of multilinear decomposition of N-way arrays. J. Chemom. 14, 229–239 (2000)

    Google Scholar 

  30. Q. Su, Y. Shen, W. Jian et al., Underdetermined blind identification for uniform linear array by a new time-frequency method. Circuits Syst. Signal Process. 36(1), 99–118 (2017)

    MathSciNet  MATH  Google Scholar 

  31. Q. Su, Y. Shen, Y. Wei et al., SSP-based UBI algorithms for uniform linear array. Circuits Syst. Signal Process. 36(10), 4077–4096 (2017)

    MATH  Google Scholar 

  32. P. Tichavský, Z. Koldovský, Weight adjusted tensor method for blind separation of underdetermined mixtures of nonstationary sources. IEEE Trans. Signal Process. 59(3), 1037–1047 (2011)

    Google Scholar 

  33. L. Yang, H. Zhang, Y. Cai, A low-complexity PARAFAC decomposition for underdetermined blind system identification with complex mixtures. Circuits Syst. Signal Process. 37(11), 4842–4860 (2018)

    MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant Nos. 61671472, 61172061, and 61201242 and the Natural Science Foundation of Jiang Su Province in China under Grant Nos. BK20160079, BK20181335, and BK2012057.

Author information

Authors and Affiliations

  1. College of Communications Engineering, Army Engineering University of PLA, Nanjing, 210007, China

    Qiao Su, Yimin Wei, Kui Xu, Hui Li & Yuehong Shen

  2. Graduate School, Army Engineering University of PLA, Nanjing, 210007, China

    Changliang Deng

Authors
  1. Qiao Su
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yimin Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kui Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Changliang Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hui Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Yuehong Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qiao Su.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Proof of that the Limitation of N in (15) is More Relaxed Compared to the ALESCAF Algorithm

Appendix: Proof of that the Limitation of N in (15) is More Relaxed Compared to the ALESCAF Algorithm

The number of sources of the ALESCAF algorithm has the following limitation:

$$\begin{aligned} \left\{ \begin{array}{ll} N \le {((M - 1)q + S)} \big /2 &{}\quad \mathrm{if}\;S < N\\ N \le (M - 1)q&{}\quad \mathrm{if}\;S \ge N. \end{array} \right. \end{aligned}$$
(31)

If \(S < N\), we first compare the right side of the first row in (31) with that in (15) and have

$$\begin{aligned} \begin{array}{l} {{({{(M' - 1)q} \big /{2 + S}})} \big /2} - {{((M - 1)q + S)} \big /2}\\ \quad = {{(M - 2)(M - 1)q} \big /8}. \end{array} \end{aligned}$$
(32)

(32) suggests that when \(M\ge 2\), the upper bound of N in the first row of (15) is more relaxed than that of (31).

As for the case with \(S\ge N\), we compare the right side of the second row in (31) with that in (15) and get

$$\begin{aligned} \begin{array}{l} {{(M' - 1)q} \big /{2 - }}(M - 1)q\\ = {{(M - 2)(M - 1)q} \big /4} \end{array} \end{aligned}$$
(33)

It can be inferred from (33) that the second row in (15) has more relaxed upper bound of N than that in (31). In conclusion, it is true that compared to the ALESCAF algorithm, the limitation on N in (15) is more relaxed.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Su, Q., Wei, Y., Xu, K. et al. Using Derivatives of Second Generating Function for Underdetermined Blind Identification. Circuits Syst Signal Process 39, 4578–4595 (2020). https://doi.org/10.1007/s00034-020-01385-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-020-01385-y

Keywords

Search

Navigation