Skip to main content
SpringerLink
Log in

Design of Nearly-Orthogonal Symmetric Wavelet Filter Banks Based on the Wavelet Orthogonalization Process

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

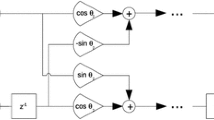
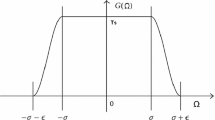
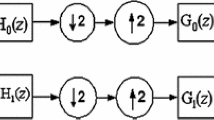
Abstract

This work proposes a new method for nearly-orthogonal wavelet filter banks design based on the wavelet orthogonalization process. A new procedure to extract semi-conjugate filters from non-orthogonal wavelets is used for such purposes. The proposed methodology allows the design of symmetrical odd length nearly-orthogonal wavelet filters according to the frequency domain specifications. Finite impulse response wavelet filters with linear phase are obtained, not implying significant gain distortions and satisfying perfect reconstruction condition as accurately as possible. A signal decomposition example is presented and the wavelet coefficients results are compared with orthogonal and biorthogonal wavelet filter banks. Considering such an example, the best result was obtained by one of the proposed nearly-orthogonal wavelet filter banks. Some nearly-orthogonal wavelet filter banks designed in this work are applied in the context of image compression, involving the reconstruction process. Image compression results from a nearly-orthogonal wavelet filter designed in this work are superior to those from some classical wavelet filters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data Availability

The datasets used during the current study are available in the Public-domain test images for homeworks and projects repository, available at https://homepages.cae.wisc.edu/ece533/images.

Code Availability

Not applicable.

Materials Availability

Not applicable.

Notes

  1. Space of finite energy functions.

  2. Note that \(\omega \) is used as the discrete-time signal frequency parameter, in contrast to the continuous-time signal frequency parameter, where \(\Omega \) is the referent notation.

  3. Space of finite energy discrete signals

References

  1. P.S. Addison, M. Morvidone, J.N. Watson, D. Clifton, Wavelet transform reassignment and the use of low-oscillation complex wavelets. Mech. Syst. Signal Process. 20(6), 1429–1443 (2006)

    Article  Google Scholar 

  2. M. Antonini, M. Barlaud, P. Mathieu, I. Daubechies, Image coding using wavelet transforms. IEEE Trans. Image Process. 1(2), 205–220 (1992)

    Article  Google Scholar 

  3. M. Ayad, D. Chikouche, N. Boukazzoula, M. Rezki, Search of a robust defect signature in gear systems across adaptive Morlet wavelet of vibration signals. IET Signal Proc. 8(9), 918–926 (2014)

    Article  Google Scholar 

  4. G. Battle, A block spin construction of ondelettes. Part I: Lemarié functions. Commun. Math. Phys. 110(4), 601–615 (1987)

    Article  Google Scholar 

  5. C. Chen, X. Chu, Two-dimensional Morlet wavelet transform and its application to wave recognition methodology of automatically extracting two-dimensional wave packets from lidar observations in antarctica. J. Atmos. Solar Terr. Phys. 162, 28–47 (2017)

    Article  Google Scholar 

  6. T. Chen, Y. Wu, Y. Zhao, X. Wang, The analysis and design of one-dimensional nearly-orthogonal symmetric wavelet filter banks. In: IEEE International Conference on Networking and Digital Society (2009), pp. 247–250

  7. T. Chen, Y. Zhao, C. Yu, L. Shen, A new technique for ECG denoising using adaptive wavelet shrinkage. In: IEEE International Colloquium on Computing, Communication, Control and Management (2008), pp. 256–259

  8. A. Cohen, I. Daubechies, J.C. Feauveau, Biorthogonal bases of compactly supported wavelets. Commun. Pure Appl. Math. 45(5), 485–560 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  9. I. Daubechies, Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 41(7), 909–996 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  10. I. Daubechies, Ten Lectures on Wavelets (Society for Industrial and Applied Mathematics, Philadelphia, 1992)

    Book  MATH  Google Scholar 

  11. I. Daubechies, Orthonormal bases of compactly supported wavelets II. Variations on a theme. J. Math. Anal. 24(2), 499–519 (1993)

    MathSciNet  MATH  Google Scholar 

  12. D.L. Donoho, J.M. Johnstone, Ideal spatial adaptation by wavelet shrinkage. Biometrika 81(3), 425–455 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  13. P.J. Edavoor, A.D. Rahulkar, Design and implementation of a novel low complexity symmetric orthogonal wavelet filter-bank. IET Image Proc. 13(5), 785–793 (2019)

    Article  Google Scholar 

  14. D. Grimaldi, Time-of-flight measurement of ultrasonic pulse echoes using wavelet networks. IEEE Trans. Instrum. Meas. 55(1), 5–13 (2006)

    Article  Google Scholar 

  15. A. Grossmann, J. Morlet, Decomposition of hardy functions into square integrable wavelets of constant shape. J. Math. Anal. 15(4), 723–736 (1984)

    MathSciNet  MATH  Google Scholar 

  16. Q. Jin, Z.Q. Luo, K.M. Wong, Optimum filter banks for signal decomposition and its application in adaptive echo cancellation. IEEE Trans. Signal Process. 44(7), 1669–1680 (1996)

    Article  Google Scholar 

  17. S. Lawson, J. Zhu, Image compression using wavelets and jpeg2000: a tutorial. IET Electron. Commun. Eng. J. 14(3), 112–121 (2002)

    Article  Google Scholar 

  18. P.G. Lemarie, Ondelettes á localisation exponentielle. Math. Pures et Appl. 67, 227–236 (1988)

    MathSciNet  MATH  Google Scholar 

  19. J. Lin, L. Qu, Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 234(1), 135–148 (2000)

    Article  Google Scholar 

  20. S. Mallat, Multiresolution approximations and wavelet orthonormal bases of \({L} ^{2}({\mathbb{R}})\). Trans. Am. Math. Soc. 315(1), 69–87 (1989)

    MATH  Google Scholar 

  21. S. Mallat, A theory for multiresolution signal decomposition: the wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 11(7), 674–693 (1989)

    Article  MATH  Google Scholar 

  22. S. Mallat, A Wavelet Tour of Signal Processing (Elsevier, Burlington, 1999)

    MATH  Google Scholar 

  23. S. Murugesan, D.B. Tay, Design of almost symmetric orthogonal wavelet filter bank via direct optimization. IEEE Trans. Image Process. 21(5), 2474–2480 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  24. A.V. Oppenheim, R.W. Schafer, Discrete-Time Signal Processing, 2nd edn. (Prentice Hall, Englewood Cliffs, 1989)

    MATH  Google Scholar 

  25. J.C. Pesquet, H. Krim, H. Carfantan, Time-invariant orthonormal wavelet representations. IEEE Trans. Signal Process. 44(8), 1964–1970 (1996)

    Article  Google Scholar 

  26. F.A.P. Petitcolas, Public-domain test images for homeworks and projects (2018). https://homepages.cae.wisc.edu/ece533/images. Accessed 07 Sep 2018

  27. I.W. Selesnick, J.E. Odegard, C.S. Burrus, Nearly symmetric orthogonal wavelets with non-integer DC group delay. In: IEEE Digital Signal Processing Workshop Proceedings (1996), pp. 431–434

  28. D.B.H. Tay, Z. Lin, Highly localised near orthogonal graph wavelets. IET Electron. Lett. 52(11), 966–968 (2016)

    Article  Google Scholar 

  29. C. Torrence, G.P. Compo, A practical guide to wavelet analysis. Bull. Am. Meteor. Soc. 79(1), 61–78 (1998)

    Article  Google Scholar 

  30. B. Van Wyk, F. Virolleau, The application of optimum quasi bi-orthogonal wavelets to the simulation of room acoustics. In: IEEE South African Symposium on Communications and Signal Processing (1998), pp. 181–186

  31. M. Vetterli, Filter banks allowing perfect reconstruction. Signal Process. 10(3), 219–244 (1986)

    Article  MathSciNet  Google Scholar 

  32. Y. Zhao, M. Swamy, New technique for designing nearly orthogonal wavelet filter banks with linear phase. IET Proc. Vis. Image Signal Process. 147(6), 527–533 (2000)

    Article  Google Scholar 

  33. Y. Zhao, M. Swamy, The analysis and design of two-dimensional nearly-orthogonal symmetric wavelet filter banks. Multidimens. Syst. Signal Process. 24(1), 199–218 (2013)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance code 001.

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, UNESP-São Paulo State University, Brasil Avenue 56, Ilha Solteira, Brazil

    Fabrício Ely Gossler

  2. Department of Mathematics, UEMS-State University of Mato Grosso do Sul, MS 306 Road, KM 06, Cassilândia, Brazil

    Marco Aparecido Queiroz Duarte

  3. Department of Mathematics, UNESP-São Paulo State University, Brasil Avenue 56, Ilha Solteira, Brazil

    Francisco Villarreal

Authors
  1. Fabrício Ely Gossler
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marco Aparecido Queiroz Duarte
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Francisco Villarreal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fabrício Ely Gossler.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gossler, F.E., Duarte, M.A.Q. & Villarreal, F. Design of Nearly-Orthogonal Symmetric Wavelet Filter Banks Based on the Wavelet Orthogonalization Process. Circuits Syst Signal Process 42, 234–254 (2023). https://doi.org/10.1007/s00034-022-02111-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-022-02111-6

Keywords

Search

Navigation