1 Introduction

MISTY [18] is a block cipher designed by Matsui in 1997 and is based on the theory of provable security [20, 21] against the differential attack [4] and the linear attack [16]. MISTY has a recursive structure, and the component function has a unique structure, the so-called MISTY structure [17]. There are two types of MISTY, MISTY1 and MISTY2. MISTY1 adopts the Feistel structure whose F-function is designed by the recursive MISTY structure. MISTY2 does not adopt the Feistel structure and uses only the MISTY structure. Both ciphers achieve provable security against differential and linear attacks. MISTY1 is designed for practical use, and MISTY2 is designed for experimental use.

MISTY1 is a 64-bit block cipher with 128-bit key, and it has a Feistel structure with FL layers. MISTY1 is in the candidate recommended ciphers list of CRYPTREC [7], and it is standardized by ISO/IEC 18033-3 [12]. Moreover, it is a NESSIE-recommended cipher [19] and is described in RFC 2994 [22]. There are many existing attacks against reduced MISTY1, and we summarize these attacks in Table 1. A higher-order differential attack is the most powerful attack against MISTY1 [3]. However, there is no attack against the full MISTY1, i.e., 8-round MISTY1 with 5 FL layers.

Table 1 Summary of single secret key attacks against MISTY1
Full size table

1.1 Integral Attack

The integral attack [14] was first proposed by Daemen et al. to evaluate the security of Square  [8] and was then formalized by Knudsen and Wagner. There are two major techniques to construct an integral characteristic: One uses the propagation characteristic of integral properties [14] and the other estimates the algebraic degree [13, 15]. We often call the second technique a “higher-order differential attack.” A new technique to construct integral characteristics was proposed in EUROCRYPT 2015 [27], and it introduced a new property, the so-called division property, by generalizing the integral property [14]. It showed the propagation characteristic of the division property for any function restricted by an algebraic degree. As a result, several improved results were reported on the structural evaluation of the Feistel network and the Substitution-Permutation network. Moreover, the division property was applied to the generalized Feistel network [29].

1.2 Our Contribution

In [27], S-boxes are randomly chosen depending on round keys, but the algebraic degree is restricted. However, many realistic block ciphers use more efficient structures, e.g., a public S-box and a key addition. In this paper, we show that the division property becomes more useful if an S-box is a public function. Then, we apply our technique to the cryptanalysis of MISTY1. We first evaluate the propagation characteristic of the division property for public S-boxes \(S_7\) and \(S_9\) and show that \(S_7\) has a vulnerable property. We next evaluate the propagation characteristic of the division property for the FI function and then evaluate it for the FO function. Moreover, we evaluate the propagation characteristic for the FL layer. Finally, we devise an algorithm to search for integral characteristics on MISTY1 by assembling these propagation characteristics. As a result, we can construct a new 6-round integral characteristic, where the left 7-bit value of the output is balanced. We recover the round key by using the partial-sum technique [10]. As a result, the secret key of the full MISTY1 can be recovered with \(2^{63.58}\) chosen plaintexts and \(2^{121}\) time complexity. Moreover, if we can use \(2^{63.994}\) chosen plaintexts, the time complexity is reduced to \(2^{108.3}\). Unfortunately, we have to use almost all chosen plaintexts, and recovering the secret key by using fewer chosen plaintexts is left as an open problem.

2 MISTY1

MISTY1 is a Feistel cipher whose F-function has the MISTY structure, and the recommended parameter is 8 rounds with 5 FL layers. Figure 1 shows the structure of MISTY1. Let \(X_i^L\) (resp. \(X_i^R\)) be the left half (resp. the right half) of an i-round input. Moreover, \(X_i^L[j]\) (resp. \(X_i^R[j]\)) denotes the jth bit of \(X_i^L\) (resp. \(X_i^R\)) from the left. MISTY1 is a 64-bit block cipher with 128-bit key, and it has a Feistel structure with FL layers, where the FO function is used in the F-function of the Feistel structure. The component function \(FO_i\) is constructed by using the 3-round MISTY structure, where \(FI_{i,1}\), \(FI_{i,2}\), and \(FI_{i,3}\) are used as the F-function of the MISTY structure, and the four 16-bit round keys \(KO_{i,1}\), \(KO_{i,2}\), \(KO_{i,3}\), and \(KO_{i,4}\) are used. Moreover, the function \(FI_{i,j}\) is constructed by using the 3-round MISTY structure, where a 9-bit S-box \(S_9\) and a 7-bit S-box \(S_7\) are used in the F-function, and a 16-bit round key \(KI_{i,j}\) is used. Here, \(S_9\) and \(S_7\) are defined in “Appendix 1.” The component function \(FL_i\) uses two 16-bit round keys, \(KL_{i,1}\) and \(KL_{i,2}\), where \(\cap \) and \(\cup \) denote a bitwise AND and OR, respectively. These round keys are calculated from the secret key \((K_1, K_2, \ldots , K_8)\) as follows.

Symbol

\(KO_{i,1}\)

\(KO_{i,2}\)

\(KO_{i,3}\)

\(KO_{i,4}\)

\(KI_{i,1}\)

\(KI_{i,2}\)

\(KI_{i,3}\)

\(KL_{i,1}\)

\(KL_{i,2}\)

Key

\(K_i\)

\(K_{i+2}\)

\(K_{i+7}\)

\(K_{i+4}\)

\(K'_{i+5}\)

\(K'_{i+1}\)

\(K'_{i+3}\)

\(K_{\frac{i+1}{2}}\) (odd i)

\(K'_{\frac{i+1}{2}+6}\) (odd i)

\(K'_{\frac{i}{2}+2}\) (even i)

\(K_{\frac{i}{2}+4}\) (even i)

Here, \(K_i\) and \(K_i'\) are identified with \(K_{i-8}\) and \(K_{i-8}'\), respectively, when i exceeds 8. Moreover, \(K'_i\) is defined as the output of \(FI_{i,j}\) where the input is \(K_i\) and the key is \(K_{i+1}\).

Fig. 1
figure 1

Specification of MISTY1

Full size image

3 Integral Characteristic by Division Property

3.1 Notations

We make the distinction between the addition over \(\mathbb {F}_2^n\) and the addition over \(\mathbb {Z}\), and we use \(\oplus \) and \(+\) as the addition over \(\mathbb {F}_2^n\) and the addition over \(\mathbb {Z}\), respectively. For any \(a \in \mathbb {F}_2^n\), the ith element is expressed as a[i], and the Hamming weight w(a) is calculated as \(w(a) = \sum _{i=1}^{n} a[i]\). Moreover, \(a[i_1, i_2, \ldots , i_j]\) denotes a j-bit substring of a as \(a[i_1, i_2, \ldots , i_j] = a[i_1] \Vert a[i_2] \Vert \cdots \Vert a[i_j]\). Let \(1^n \in \mathbb {F}_2^n\) be a value whose all elements are 1. Moreover, let \(0^n \in \mathbb {F}_2^n\) be a value whose all elements are 0. For any set \(\mathbb {K}\), let \(|\mathbb {K}|\) be the number of elements. Moreover, let \(\phi \) be an empty set. For any \({\varvec{a}} \in (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})\), the vectorial Hamming weight is defined as \(W({\varvec{a}})=[w(a_1), w(a_2), \ldots , w(a_m)] \in \mathbb {Z}^m\), where \(a_i\) denotes the ith element of \({\varvec{a}}\). Moreover, for any \(\varvec{k} \in \mathbb {Z}^m\) and \({{\varvec{k}}}' \in \mathbb {Z}^m\), we define \(\varvec{k} \succeq {\varvec{k}}'\) if \(k_i \ge k'_i\) for all \(i\,(1 \le i \le m)\). Otherwise, \({\varvec{k}} \nsucceq {\varvec{k}}'\).

3.1.1 Boolean Function

A Boolean function is a function from \(\mathbb {F}_2^n\) to \(\mathbb {F}_2\). Let \(\mathrm {deg}(f)\) be the algebraic degree of a Boolean function f. Algebraic normal form (ANF) is often used as representation of the Boolean function. Let f be any Boolean function from \(\mathbb {F}_2^n\) to \(\mathbb {F}_2\). Then, it can be represented as

$$\begin{aligned} f( x ) = \bigoplus _{u \in \mathbb {F}_2^n} a_u^f \left( \prod _{i=1}^{n} x[i]^{u[i]} \right) , \end{aligned}$$

where \(a_u^f \in \mathbb {F}_2\) is a constant value depending on f and u. If \(\mathrm {deg}(f)\) is at most d, all \(a_u^f\) satisfying \(d<w(u)\) are 0. An n-bit S-box can be regarded as the collection of n Boolean functions. If the algebraic degrees of its n Boolean functions are at most d, we say the algebraic degree of the S-box is at most d.

3.2 Integral Attack

An integral attack [14] is one of the most powerful cryptanalyses against block ciphers. Attackers prepare N chosen plaintexts and get the corresponding ciphertexts. If the XOR of all corresponding ciphertexts is 0 for all secret keys, we say that the block cipher has an integral characteristic with N chosen plaintexts. In an integral attack, attackers first create an integral characteristic against a reduced-round block cipher. Then, they guess the round keys that are used in the last several rounds and calculate the XOR of the ciphertexts of the reduced-round block cipher. Finally, they evaluate whether or not the XOR is 0. If the XOR is not 0, they can discard the guessed round keys from the candidates of the correct key.

3.3 Division Property

A division property, which was proposed in [27], is used to search for integral characteristics. We first consider a set of plaintexts and evaluate the division property of the set. Then, we propagate the division property and evaluate the division property of the set of texts encrypted over one round. By repeating the propagation, we show the division property of the set of texts encrypted over some rounds. Finally, we can easily determine the existence of the integral characteristic from the propagated division property.

3.3.1 Bit Product Function

We first define two bit product functions \(\pi _u\) and \(\pi _{\varvec{u}}\), which are used to evaluate the division property of a multiset.Footnote 1 Let \(\pi _u {:}\; \mathbb {F}_2^n \rightarrow \mathbb {F}_2\) be a function for any \(u \in \mathbb {F}_2^n\). Let \(x \in \mathbb {F}_2^n\) be the input, and \(\pi _u(x)\) be the AND of x[i] satisfying \(u[i]=1\), i.e., it is defined as

$$\begin{aligned} \pi _u(x) := \prod _{i=1}^{n} x[i]^{u[i]}. \end{aligned}$$

Let \(\pi _{\varvec{u}} {:}\; (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m}) \rightarrow \mathbb {F}_2\) be a function for any \({\varvec{u}} \in (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})\). Let \(\varvec{x} \in (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})\) be the input, and \(\pi _{\varvec{u}}({\varvec{x}})\) be defined as

$$\begin{aligned} \pi _{\varvec{u}}({\varvec{x}}) := \prod _{i=1}^{m} \pi _{u_i}(x_i). \end{aligned}$$

3.3.2 Definition of Division Property

The division property is given against a multiset, and it is calculated by using the bit product function. Let \(\mathbb {X}\) be an input multiset whose elements take a value of \((\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})\). In the division property, we first evaluate a value of \(\bigoplus _{\varvec{x} \in \mathbb {X}} \pi _{\varvec{u}}(\varvec{x})\) for all \(\varvec{u} \in (\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})\). Then, we divide the set of \(\varvec{u}\) into a subset whose sum is 0 and a subset whose sum becomes unknown.Footnote 2 In [27], the focus was on using the Hamming weight of \(\varvec{u}\) to divide the set.

Definition 1

(Division Property) Let \(\mathbb {X}\) be a multiset whose elements take a value of \((\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})\). Let \(\mathbb {K}\) be a set whose elements take an m-dimensional vector whose ith element takes a value between 0 and \(n_i\). When the multiset \(\mathbb {X}\) has the division property \(\mathcal{D}_\mathbb {K}^{{n}_1, {n}_2, \ldots , {n}_{m}}\), it fulfills the following conditions:

$$\begin{aligned} \bigoplus _{\varvec{x} \in \mathbb {X}} \pi _{\varvec{u}}(\varvec{x}) = {\left\{ \begin{array}{ll} \mathrm{unknown} &{}\text{ if } \text{ there } \text{ exist } {\varvec{k}} \in \mathbb {K} \text{ s.t. } W(\varvec{u}) \succeq {\varvec{k}}, \\ 0 &{}\text{ otherwise }. \end{array}\right. } \end{aligned}$$

If there are \({\varvec{k}} \in \mathbb {K}\) and \({\varvec{k}}' \in \mathbb {K}\) satisfying \({\varvec{k}} \succeq {\varvec{k}}'\), \(\varvec{k}\) can be removed from \(\mathbb {K}\) because it is redundant. Assume that the multiset \(\mathbb {X}\) has the division property \(\mathcal{D}_{\mathbb {K}}^{{n}_1, {n}_2, \ldots , {n}_{m}}\). If there is no unit vector \(\varvec{e}_j\) in \(\mathbb {K}\), where \(\varvec{e}_j\) is a vector whose jth element is 1 and the others are 0, \(\bigoplus _{x \in \mathbb {X}} x_j\) is 0. See [27] to better understand the concept in detail.

Example 1

Let \(\mathbb {X}\) be a multiset whose elements take a value of \(\mathbb {F}_2^4\). As an example, we prepare the input multiset \(\mathbb {X}\) as

$$\begin{aligned} \mathbb {X}:= \{\mathtt{0x0,0x3,0x3,0x3,0x5,0x6,0x8,0xB,0xD,0xE}\}. \end{aligned}$$

A following table calculates the summation of \(\pi _u(x)\).

 

0x0

0x3

0x3

0x3

0x5

0x6

0x8

0xB

0xD

0xE

\(\bigoplus \pi _u(x)\)

0000

0011

0011

0011

0101

0110

1000

1011

1101

1110

\(u=0000\)

1

1

1

1

1

1

1

1

1

1

0

\(u=0001\)

0

1

1

1

1

0

0

1

1

0

0

\(u=0010\)

0

1

1

1

0

1

0

1

0

1

0

\(u=0011\)

0

1

1

1

0

0

0

1

0

0

0

\(u=0100\)

0

0

0

0

1

1

0

0

1

1

0

\(u=0101\)

0

0

0

0

1

0

0

0

1

0

0

\(u=0110\)

0

0

0

0

0

1

0

0

0

1

0

\(u=0111\)

0

0

0

0

0

0

0

0

0

0

0

\(u=1000\)

0

0

0

0

0

0

1

1

1

1

0

\(u=1001\)

0

0

0

0

0

0

0

1

1

0

0

\(u=1010\)

0

0

0

0

0

0

0

1

0

1

0

\(u=1011\)

0

0

0

0

0

0

0

1

0

0

1

\(u=1100\)

0

0

0

0

0

0

0

0

1

1

0

\(u=1101\)

0

0

0

0

0

0

0

0

1

0

1

\(u=1110\)

0

0

0

0

0

0

0

0

0

1

1

\(u=1111\)

0

0

0

0

0

0

0

0

0

0

0

For all u satisfying \(w(u) < 3\), \(\bigoplus _{x \in \mathbb {X}} \pi _u(x)\) is 0. Therefore, the multiset has the division property \(\mathcal{D}_3^4\).

Example 2

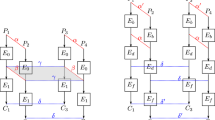
Let \(\mathbb {X}\) be a multiset whose elements take a value of \((\mathbb {F}_2^{8} \times \mathbb {F}_2^{8})\). Assume that the multiset \(\mathbb {X}\) has the division property \(\mathcal{D}_{\{[1,5], [3,3], [4,5], [5,1], [6,0]\}}^{8,8}\). In this case, if \([u_1,u_2]\) is chosen from the gray part in Fig. 2, \(\bigoplus _{[x_1,x_2] \in \mathbb {X}} \pi _{[u_1,u_2]}([x_1,x_2])\) becomes unknown. For example, when \(\varvec{u} = [\mathtt{0x3F, 0xFC}]\) is used, we cannot determine \(\bigoplus _{[x_1,x_2] \in \mathbb {X}} \pi _{[\mathtt{0x3F, 0xFC}]}([x_1,x_2])\) because \(W(\varvec{u})=[6,6]\). On the other hand, if \((u_1,u_2)\) is chosen from the white part in Fig. 2, \(\bigoplus _{[x_1,x_2] \in \mathbb {X}} \pi _{[u_1,u_2]}([x_1,x_2])\) is 0. Note that the division property \(\mathcal{D}_{\{[1,5], [3,3], [5,1], [6,0]\}}^{8,8}\) is the same as \(\mathcal{D}_{\{[1,5], [3,3], [4,5], [5,1], [6,0]\}}^{8,8}\) because the unknown space is invariant.

Fig. 2
figure 2

Division property \(\mathcal{D}_{\{[1,5], [3,3], [5,1], [6,0]\}}^{8,8}\)

Full size image

A similar example is shown in [24] and may help to further understand the division property.

3.3.3 Propagation Rules of Division Property

Some propagation rules for the division property are proven in [27]. We summarize them as follows, and the proof is shown in “Appendix 2.”

  • Rule 1 (Substitution): Let F be a function that consists of m S-boxes, where the bit length and the algebraic degree of the ith S-box is \(n_i\) bits and \(d_i\), respectively. The input and the output take a value of \((\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2} \times \cdots \times \mathbb {F}_2^{n_m})\), and \(\mathbb {X}\) and \(\mathbb {Y}\) denote the input multiset and the output multiset, respectively. Assuming that the multiset \(\mathbb {X}\) has the division property \(\mathcal{D}_{\mathbb {K}}^{{n}_1, {n}_2, \ldots , {n}_{m}}\), the multiset \(\mathbb {Y}\) has the division property \(\mathcal{D}_{\mathbb {K'}}^{{n}_1, {n}_2, \ldots , {n}_{m}}\), where \(\mathbb {K'}\) is calculated as follows: First, \(\mathbb {K'}\) is initialized to \(\phi \). Then, for all \({\varvec{k}}\in \mathbb {K}\),

    $$\begin{aligned} \mathbb {K}' = \mathbb {K'} \cup \Bigg [ \left\lceil \frac{k_1}{d_1} \right\rceil , \left\lceil \frac{k_2}{d_2} \right\rceil , \ldots , \left\lceil \frac{k_m}{d_m} \right\rceil \Bigg ], \end{aligned}$$

    is calculated. Here, when the ith S-box is bijective and \(k_i=n_i\), the ith element of the propagated property becomes \(n_i\) not \(\lceil n_i/d_i \rceil \).

  • Rule 2 (Copy): Let F be a copy function, where the input x takes a value of \(\mathbb {F}_2^{n}\) and the output is calculated as \([y_1,y_2]=[x,x]\). Let \(\mathbb {X}\) and \(\mathbb {Y}\) be the input multiset and the output multiset, respectively. Assuming that the multiset \(\mathbb {X}\) has the division property \(\mathcal{D}_k^n\), the multiset \(\mathbb {Y}\) has the division property \(\mathcal{D}_{\mathbb {K'}}^{n, n}\), where \(\mathbb {K'}\) is calculated as follows: First, \(\mathbb {K'}\) is initialized to \(\phi \). Then, for all \(i~(0 \le i \le k)\),

    $$\begin{aligned} \mathbb {K}' = \mathbb {K'} \cup [k-i, i], \end{aligned}$$

    is calculated.

  • Rule 3 (Compression by XOR): Let F be a function compressed by an XOR, where the input \([x_1,x_2]\) takes a value of \((\mathbb {F}_2^{n} \times \mathbb {F}_2^{n})\) and the output is calculated as \(y=x_1\oplus x_2\). Let \(\mathbb {X}\) and \(\mathbb {Y}\) be the input multiset and the output multiset, respectively. Assuming that the multiset \(\mathbb {X}\) has the division property \(\mathcal{D}_{\mathbb {K}}^{n, n}\), the division property of the multiset \(\mathbb {Y}\) is \(\mathcal{D}_{k'}^{n}\) as

    $$\begin{aligned} k' = \min _{[k_1,k_2] \in \mathbb {K}}\{ k_1 + k_2\}. \end{aligned}$$

    Here, if the minimum value of \(k'\) is larger than n, the propagation characteristic of the division property is aborted. Namely, a value of \(\oplus _{y \in \mathbb {Y}} \pi _v(y)\) is 0 for all \(v \in \mathbb {F}_2^n\).

  • Rule 4 (Split): Let F be a split function, where the input x takes a value of \(\mathbb {F}_2^{n}\) and the output is calculated as \(y_1 \Vert y_2=x\), where \([y_1,y_2]\) takes a value of \((\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n-n_1})\). Let \(\mathbb {X}\) and \(\mathbb {Y}\) be the input multiset and the output multiset, respectively. Assuming that the multiset \(\mathbb {X}\) has the division property \(\mathcal{D}_{k}^{n}\), the multiset \(\mathbb {Y}\) has the division property \(\mathcal{D}_{\mathbb {K'}}^{n_1,n-n_1}\), where \(\mathbb {K'}\) is calculated as follows: First, \(\mathbb {K'}\) is initialized to \(\phi \). Then, for all \(i~(0 \le i \le k)\),

    $$\begin{aligned} \mathbb {K}' = \mathbb {K}' \cup [k-i, i], \end{aligned}$$

    is calculated. Here, \((k-i)\) is less than or equal to \(n_1\), and i is less than or equal to \(n-n_1\).

  • Rule 5 (Concatenation): Let F be a concatenation function, where the input \([x_1,x_2]\) takes a value of \((\mathbb {F}_2^{n_1} \times \mathbb {F}_2^{n_2})\) and the output is calculated as \(y=x_1 \Vert x_2\). Let \(\mathbb {X}\) and \(\mathbb {Y}\) be the input multiset and the output multiset, respectively. Assuming that the multiset \(\mathbb {X}\) has the division property \(\mathcal{D}_{\mathbb {K}}^{n_1,n_2}\), the division property of the multiset \(\mathbb {Y}\) is \(\mathcal{D}_{k'}^{n_1+n_2}\) as

    $$\begin{aligned} k' = \min _{[k_1,k_2] \in \mathbb {K}}\{ k_1 + k_2\}. \end{aligned}$$
Fig. 3
figure 3

Difference between [27] and this paper. The left figure is an assumption used in [27]. The right one is a new assumption used in this paper

Full size image

4 Division Property for Public Function

In an assumption of [27], attackers do not know the specification of an S-box and only know the algebraic degree of the S-box. However, many specific block ciphers usually use a public S-box and an addition of secret subkeys, where an XOR is typically used for the addition. In this paper, we show that the propagation characteristic of the division property can be improved if an S-box is a public function. The difference between [27] and this paper is shown in Fig. 3.

We consider the propagation characteristic of the division property for the function shown in the right figure in Fig. 3. The key XORing is first applied, but it does not affect the division property because it is a linear function. Therefore, when we evaluate the propagation characteristic of the division property, we can remove the key XORing. Next, a public S-box is applied, and we can determine the ANF of the S-box. Assuming that an S-box is a function from n bits to m bits, the ANF is represented as

$$\begin{aligned} y[1]&= f_1(x[1], x[2], \ldots , x[n]), \\ y[2]&= f_2(x[1], x[2], \ldots , x[n]), \\&\vdots \\ y[m]&= f_m(x[1], x[2], \ldots , x[n]), \end{aligned}$$

where \(x[i]\,(1 \le i \le n)\) is an input, \(y[j]\,(1 \le j \le m)\) is an output, and \(f_j\,(1 \le j \le m)\) is a Boolean function. The division property evaluates the input multiset and the output one by using the bit product function \(\pi _{u}\), and we then divide the set of u into a subset whose evaluated value is 0 and a subset whose evaluated value becomes unknown. Namely, we evaluate the equation

$$\begin{aligned} F_u(x[1], x[2], \ldots , x[n]) = \prod _{i=1}^{m} f_i(x[1], x[2], \ldots , x[n])^{u[i]} \end{aligned}$$

and divide the set of u. In [27], a fundamental property of the product of some functions is used, i.e., the algebraic degree of \(F_u\) is at most \(w(u) \times d\) if the algebraic degree of functions \(f_i\) is at most d. However, since we now know the ANF of functions \(f_1, f_2, \ldots , f_m\), we can calculate the accurate algebraic degree of \(F_u\) for all \(u \in \mathbb {F}_2^n\). In this case, if the algebraic degree of \(F_u\) is less than \(w(u) \times d\) for all u for which w(u) is constant, we can improve the propagation characteristic.

4.1 Application to MISTY S-boxes

4.1.1 Evaluation of \(S_7\)

The \(S_7\) of MISTY is a 7-bit S-box with degree 3. We show the ANF of \(S_7\) in “Appendix 1.” We evaluate the property of \((\pi _v \circ S_7)\) to get the propagation characteristic of the division property. The algebraic degree of \((\pi _v \circ S_7)\) increases in accordance with the Hamming weight of v, and it is summarized as follows.

w(v)

0

1

2

3

4

5

6

7

Degree

0

3

5

5

6

6

6

7

One can easily choose a modified S-box \(S'_7\) with algebraic degree 3, such that the algebraic degree of \((\pi _v \circ S_7')\) is at least 6 with \(w(v) \ge 2\). However, for the \(S_7\), the increment of the algebraic degree is bounded by 5 when \(w(v) = 2\) or \(w(v) = 3\) holds.Footnote 3 Then, \(\bigoplus _{x \in \mathbb {X}}(\pi _v \circ S_7)(x)\) is 0 for \(w(v) \le 3\) if \(\mathbb {X}\) has \(\mathcal{D}_6^7\). It means that the necessary condition that \(\bigoplus _{x \in \mathbb {X}}(\pi _v \circ S_7)(x)\) becomes unknown is \(w(v)\ge 4\) and \(\mathcal{D}_4^7\) is propagated from \(\mathcal{D}_6^7\). Thus, the propagation characteristic is represented as the following.

\(\mathcal{D}_k^7\) for input set \(\mathbb {X}\)

\(\mathcal{D}_0^7\)

\(\mathcal{D}_1^7\)

\(\mathcal{D}_2^7\)

\(\mathcal{D}_3^7\)

\(\mathcal{D}_4^7\)

\(\mathcal{D}_5^7\)

\(\mathcal{D}_6^7\)

\(\mathcal{D}_7^7\)

\(\mathcal{D}_k^7\) for output set \(\mathbb {Y}\)

\(\mathcal{D}_0^7\)

\(\mathcal{D}_1^7\)

\(\mathcal{D}_1^7\)

\(\mathcal{D}_1^7\)

\(\mathcal{D}_2^7\)

\(\mathcal{D}_2^7\)

\(\mathcal{D}_4^7\)

\(\mathcal{D}_7^7\)

Note that all propagations except for \(\mathcal{D}_6^7 \rightarrow \mathcal{D}_4^7\) are calculated by following Rule 1. If the modified S-box is applied, the division property \(\mathcal{D}_2^7\) is propagated from the division property \(\mathcal{D}_6^7\) because of Rule 1. Therefore, the deterioration of the division property for the \(S_7\) is smaller than expected for a randomly chosen 7-bit S-box with algebraic degree 3.

4.1.2 Evaluation of \(S_9\)

The \(S_9\) of MISTY is a 9-bit S-box with degree 2. We show the ANF of \(S_9\) in “Appendix 1.” We evaluate the property of \((\pi _v \circ S_9)\) to get the propagation characteristic of the division property. The algebraic degree of \((\pi _v \circ S_9)\) increases in accordance with the Hamming weight of v, and it is summarized as follows.

w(v)

0

1

2

3

4

5

6

7

8

9

Degree

0

2

4

6

8

8

8

8

8

9

Thus, the propagation characteristic is represented as

\(\mathcal{D}_k^9\) for input set \(\mathbb {X}\)

\(\mathcal{D}_0^9\)

\(\mathcal{D}_1^9\)

\(\mathcal{D}_2^9\)

\(\mathcal{D}_3^9\)

\(\mathcal{D}_4^9\)

\(\mathcal{D}_5^9\)

\(\mathcal{D}_6^9\)

\(\mathcal{D}_7^9\)

\(\mathcal{D}_8^9\)

\(\mathcal{D}_9^9\)

\(\mathcal{D}_k^9\) for output set \(\mathbb {Y}\)

\(\mathcal{D}_0^9\)

\(\mathcal{D}_1^9\)

\(\mathcal{D}_1^9\)

\(\mathcal{D}_2^9\)

\(\mathcal{D}_2^9\)

\(\mathcal{D}_3^9\)

\(\mathcal{D}_3^9\)

\(\mathcal{D}_4^9\)

\(\mathcal{D}_4^9\)

\(\mathcal{D}_9^9\)

Unlike the propagation characteristic of the division property for \(S_7\), the one for \(S_9\) is essentially optimal among 9-bit S-boxes with algebraic degree 2.

5 New Integral Characteristic

This section shows how to create integral characteristics for MISTY1 by using the propagation characteristic of the division property. We first evaluate the propagation characteristic for the component functions of MISTY1, i.e., the FI function, the FO function, and the FL layer. Finally, by assembling these characteristics, we devise an algorithm to search for integral characteristics on MISTY1.

5.1 Division Property for FI Function

We evaluate the propagation characteristic of the division property for the FI function by using those for MISTY S-boxes shown in Sect. 4.1. Since there are a zero-extended XOR and a truncated XOR in the FI function, we use a new representation, in which the internal state is expressed as two 7-bit values and one 2-bit value. Figure 4 shows the structure of the FI function with our representation, where we remove the XOR of subkeys because it does not affect the division property.

Fig. 4
figure 4

Structure of FI function

Full size image

Let \(\mathbb {X}_1\) be the input multiset of the FI function. We define every multiset \(\mathbb {X}_2, \mathbb {X}_3, \ldots , \mathbb {X}_{11}\) in Fig. 4. Here, elements of the multiset \(\mathbb {X}_1\), \(\mathbb {X}_5\), \(\mathbb {X}_6\), and \(\mathbb {X}_{11}\) take a value of \((\mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7)\). Elements of the multiset \(\mathbb {X}_2\), \(\mathbb {X}_3\), \(\mathbb {X}_{8}\), and \(\mathbb {X}_{9}\) take a value of \((\mathbb {F}_2^9 \times \mathbb {F}_2^7)\). Elements of the multiset \(\mathbb {X}_4\), \(\mathbb {X}_7\), and \(\mathbb {X}_{10}\) take a value of \((\mathbb {F}_2^2 \times \mathbb {F}_2^7 \times \mathbb {F}_2^7)\). Since elements of \(\mathbb {X}_1\) and \(\mathbb {X}_{11}\) take a value of \((\mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7)\), the propagation for the FI function is calculated on \(\mathcal{D}_{\mathbb {K}}^{7,2,7}\). Here, the propagation is calculated with the following steps.

  • From \(\mathbb {X}_1\) to \(\mathbb {X}_2\): A 9-bit value is created by concatenating the first 7-bit value with the second 2-bit value. The propagation characteristic can be evaluated by using Rule 5.

  • From \(\mathbb {X}_2\) to \(\mathbb {X}_3\): The 9-bit S-box \(S_9\) is applied to the first 9-bit value. The propagation characteristic can be evaluated by using the table shown in Sect. 4.1.

  • From \(\mathbb {X}_3\) to \(\mathbb {X}_4\): The 9-bit output value is split into a 2-bit value and a 7-bit value. The propagation characteristic can be evaluated by using Rule 4.

  • From \(\mathbb {X}_4\) to \(\mathbb {X}_5\): The second 7-bit value is XORed with the last 7-bit value, and then, the order is rotated. The propagation characteristic can be evaluated by using Rule 2 and Rule 3.

  • From \(\mathbb {X}_5\) to \(\mathbb {X}_6\): The 7-bit S-box \(S_7\) is applied to the first 7-bit value. The propagation characteristic can be evaluated by using the table shown in Sect. 4.1.

  • From \(\mathbb {X}_6\) to \(\mathbb {X}_7\): The first 7-bit value is XORed with the last 7-bit value, and then, the order is rotated. The propagation characteristic can be evaluated by using Rule 2 and Rule 3.

  • From \(\mathbb {X}_7\) to \(\mathbb {X}_8\): A 9-bit value is created by concatenating the first 2-bit value with the second 7-bit value. The propagation characteristic can be evaluated by using Rule 5.

  • From \(\mathbb {X}_8\) to \(\mathbb {X}_{11}\): The propagation characteristic is the same as that from \(\mathbb {X}_2\) to \(\mathbb {X}_5\).

As an example, we show the propagation characteristic when \(\mathbb {X}_1\) has the division property \(\mathcal{D}_{\{[4,2,6]\}}^{7,2,7}\) in “Appendix 3.” Algorithm 1 creates the propagation characteristic table for the FI function. It calls \(\mathtt{SizeReduce}(\mathbb {K})\), where redundant vectors are eliminated, i.e., it eliminates \({\varvec{k}}_1 \in \mathbb {K}\) if there exists \({\varvec{k}}_2 \in \mathbb {K}\) satisfying \({\varvec{k}}_1 \succeq \varvec{k}_2\). Algorithm 1 only creates the propagation characteristic table for which the input property is represented by \(\mathcal{D}_{\{{\varvec{k}}\}}^{7,2,7}\). If any input multiset is evaluated, we need to know the propagation characteristic from \(\mathcal{D}_{\mathbb {K}}^{7,2,7}\) with \(|\mathbb {K}| \ge 2\). However, we do not evaluate such propagation in advance because it can be easily evaluated by the table for which the input property is represented by \(\mathcal{D}_{\{{\varvec{k}}\}}^{7,2,7}\). For example, we consider the propagation characteristic from \(\mathcal{D}_{\{{\varvec{k}}, \varvec{k}'\}}^{7,2,7}\) to \(\mathcal{D}_{\mathbb {K}}^{7,2,7}\). We first get \(\mathbb {K}_1\) and \(\mathbb {K}_2\) from the propagation characteristic tables for \(\mathcal{D}_{\{{\varvec{k}}\}}^{7,2,7}\) and \(\mathcal{D}_{\{{\varvec{k}}'\}}^{7,2,7}\), respectively. Then, \(\mathbb {K}\) is calculated as \(\mathbb {K} = \mathbb {K}_1 \cup \mathbb {K}_2\).

figure a

We show all propagation characteristic tables in “Appendix 6.” Here, the propagation table from \({\varvec{k}}\) to \(\mathbb {K}\) is generated, and the number of entries of this table is \(8 \cdot 3 \cdot 8 = 192\). Moreover, we experimentally evaluated the propagation characteristic for the FI function. In our experimental search, for any \(\mathcal{D}_{\{[k_1,k_2,k_3]\}}^{7,2,7}\), we created 100 random input multisets and then evaluated the propagation characteristic. As a result, we confirmed that the experimental propagation characteristics are the same as the theoretical ones shown in “Appendix 6.”

5.2 Division Property for FO Function

figure b

We next evaluate the propagation characteristic of the division property for the FO function by using the propagation characteristic table of the FI function. Here, we remove the XOR of subkeys because it does not affect the division property. The input and output of the FO function take the value of \((\mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7 \times \mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7)\). Therefore, the propagation for the FO function is calculated on \(\mathcal{D}_{\mathbb {K}}^{7,2,7,7,2,7}\).

Table 2 Division property of input is \(\mathcal{D}_{\{[1,1,2,3,1,5]\}}^{7,2,7,7,2,7}\)
Full size table

Similar to the one created for the FI function, we create the propagation characteristic table for the FO function (see Algorithm 2). We create only a table for which the input property is represented by \(\mathcal{D}_{\{{\varvec{k}}\}}^{7,2,7,7,2,7}\) and the output property is represented by \(\mathcal{D}_{\mathbb {K}}^{7,2,7,7,2,7}\). Here, the propagation table from \({\varvec{k}}\) to \(\mathbb {K}\) is generated, and the number of entries of this table is \(8 \cdot 3 \cdot 8 \cdot 8 \cdot 3 \cdot 8 = 36864\). As an example, the propagation characteristic table from \(\mathcal{D}_{\{[1,1,2,3,1,5]\}}^{7,2,7,7,2,7}\) is shown in Table 2.

5.3 Division Property for FL Layer

figure c
figure d

MISTY1 has the FL layer, which consists of two FL functions and is applied once every two rounds. In the FL function, the right half of the input is XORed with the AND between the left half and a subkey \(KL_{i,1}\). Then, the left half of the input is XORed with the OR between the right half and a subkey \(KL_{i,2}\).

Since the input and the output of the FL function take the value of \((\mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7 \times \mathbb {F}_2^7 \times \mathbb {F}_2^2 \times \mathbb {F}_2^7)\), the propagation for the FL function is calculated on \(\mathcal{D}_{\mathbb {K}}^{7,2,7,7,2,7}\). FLEval in Algorithm 3 calculates the propagation characteristic table for the FL function. Here, the propagation table from \(\varvec{k}\) to \(\mathbb {K}\) is generated, and the number of entries of this table is \(8 \cdot 3 \cdot 8 \cdot 8 \cdot 3 \cdot 8 = 36864\). Moreover, the FL layer consists of two FL functions. Therefore, we have to consider the propagation characteristic of the division property \(\mathcal{D}_{\{{\varvec{k}}\}}^{7,2,7,7,2,7,7,2,7,7,2,7}\), where each FL function is applied to the left half and the right one. FLLayerEval in Algorithm 3 calculates the propagation characteristic of the division property for the FL layer.

5.4 New Path Search for Integral Characteristics on MISTY1

We created the propagation characteristic table for the FI and FO functions in Sects. 5.1 and 5.2, respectively. Moreover, we showed the propagation characteristic for the FL layer in Sect. 5.3. By assembling these propagation characteristics, we devise an algorithm to search for integral characteristics on MISTY1. Since the input and the output are represented as eight 7-bit values and four 2-bit values, the propagation is calculated on \(\mathcal{D}_{\mathbb {K}}^{7,2,7,7,2,7,7,2,7,7,2,7}\).

The FL layer is first applied to plaintexts, and it deteriorates the propagation of the division property. Therefore, we first remove only the first FL layer and search for integral characteristics on MISTY1 without the first FL layer. The method for passing through the first FL layer is shown in the next section. Algorithm 4 shows the search algorithm for integral characteristics on MISTY1 without the first FL layer.

As a result, we find 6-round integral characteristics without the first and the last FL layers by using Algorithm 4. Each characteristic uses \(2^{63}\) chosen plaintexts, where any one bit of the first seven bits is constant and the others take all values. Then, such input has the division property \(\mathcal{D}_{\{[6,2,7,7,2,7,7,2,7,7,2,7]\}}^{7,2,7,7,2,7,7,2,7,7,2,7}\). Therefore, we use \({\varvec{k}} = [6,2,7,7,2,7,7,2,7,7,2,7]\) as the input of Algorithm 4.

We perfectly execute SizeReduce every round, and Table 3 shows the propagation of \(\mathbb {K}\), where \(\min _w(\mathbb {K})\) and \(\max _w(\mathbb {K})\) are calculated as

$$\begin{aligned} \mathrm{min}_w(\mathbb {K}) = \min _{{\varvec{k}} \in \mathbb {K}} \left\{ \sum _{i=1}^{12} k_i \right\} , \quad \mathrm{max}_w(\mathbb {K}) = \max _{{\varvec{k}} \in \mathbb {K}} \left\{ \sum _{i=1}^{12} k_i \right\} . \end{aligned}$$

After the 6th round function, we have 131 vectors, which are shown in “Appendix 5.” Since these vectors do not contain (1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0), it means that the first 7 bits are balanced. Our algorithm is written by C++, and the execution time is about 1 day with Core i7-4770 Processor (4 cores) in 16 GB RAM. Figure 5 shows the 6-round integral characteristic, where the bit strings labeled B, i.e., the first 7 bits and last 32 bits, are balanced. Note that the 6-round characteristic becomes a 7-round characteristic if the FL layer after the 6th round function is removed. Compared with the previous 4-round characteristic [11, 28], our characteristic is improved by two rounds.

As shown in Sect. 4, the \(S_7\) of MISTY1 has the vulnerable property that \(\mathcal{D}_4^7\) is provided from \(\mathcal{D}_6^7\). Interestingly, assuming that \(S_7\) does not have this property (changing lines 26–30 in S7Eval), our algorithm cannot construct the 6-round characteristic.

It was already shown in [25] that reduced MISTY1 has a 14th order differential characteristic, and the principle was also discussed in [1, 6]. We also revisit the known characteristic for MISTY1 in “Appendix 4.”

Table 3 Propagation from \(\mathcal{D}_{\{[6,2,7,7,2,7,7,2,7,7,2,7]\}}^{7,2,7,7,2,7,7,2,7,7,2,7}\)
Full size table

5.4.1 Optimized Algorithm

If we execute SizeReduce perfectly, it requires \(O(|\mathbb {K}|^2)\) time complexity, and the execution time of Algorithm 4 is increased. Therefore, we use a more reasonable method.

Let \(\mathcal{D}_{\mathbb {K}}\) be any division property, where \(\mathbb {K}\) contains redundant vectors. Moreover, by executing SizeReduce, we get \(\mathbb {K'}\) from \(\mathbb {K}\). Then, as shown in Sect. 3.3, the unknown set indicated by \(\mathcal{D}_{\mathbb {K}}\) is the same as that by \(\mathcal{D}_{\mathbb {K'}}\). Namely, the result of Algorithm 4 does not change even if we do not perform SizeReduce perfectly. Therefore, we execute a partial SizeReduce which performs faster. The rough SizeReduce first sorts every vector in \(\mathbb {K}\) by using lexicographic order and obtains the following \(|\mathbb {K}|\) vectors,

$$\begin{aligned} {\varvec{k}}^{(1)}, {\varvec{k}}^{(2)}, \ldots , {\varvec{k}}^{(|\mathbb {K}|)}. \end{aligned}$$

Then, there is no \(({\varvec{k}}^{(i)}, {\varvec{k}}^{(j)})\) satisfying \(\varvec{k}^{(i)} \succeq {\varvec{k}}^{(j)}\) such that \(i < j\). We initialize two indices, \(i=1\) and \(j=2\), and evaluate whether or not \({\varvec{k}}^{(j)} \succeq {\varvec{k}}^{(i)}\). If \({\varvec{k}}^{(j)} \succeq {\varvec{k}}^{(i)}\), we remove \({\varvec{k}}^{(j)}\), and increment j. If \({\varvec{k}}^{(j)} \nsucceq {\varvec{k}}^{(i)}\), increment j. Moreover, if we cannot remove \(\varvec{k}^{(j)}\) “th” times consecutively, increment i and set \(j=i+1\). We can choose th freely. If \(th=|\mathbb {K}|\), the above algorithm executes SizeReduce perfectly. From our experiments, \(th=10\) or \(th=100\) are reasonable parameters. We also implemented this efficient algorithm by C++, and the execution time is 12.8 min with Core i7-4770 Processor (4 cores) in 16 GB RAM.

Fig. 5
figure 5

New 6-round integral characteristic

Full size image

6 Key Recovery Using New Integral Characteristic

This section shows the key recovery step of our cryptanalysis, which uses the 6-round integral characteristic shown in Sect. 5. In the characteristic, the left 7-bit value of \(X_7^L\) is balanced. Since the integral characteristic does not cover the first FL layer, we first show how to pass through the first FL layer. Then, we calculate two FL layers and one FO function by guessing round keys from ciphertexts, and we evaluate the balanced seven bits.

Fig. 6
figure 6

\(KL_{1,2}=1\)

Full size image
Fig. 7
figure 7

\(KL_{1,1}=0, KL_{1,2}=0\)

Full size image
Fig. 8
figure 8

\(KL_{1,1}=1, KL_{1,2}=0\)

Full size image

6.1 Passage of First FL Layer

Our new characteristic removes the first FL layer. Therefore, we have to create a set of chosen plaintexts to construct integral characteristics by using guessed round keys \(KL_{1,1}\) and \(KL_{1,2}\). Here, we have to carefully choose the set of chosen plaintexts to avoid the use of the full code book (see Figs. 6, 7, 8). In every figure, \(A_i\) denotes for which we prepare an input set that i bits are active. As an example, we consider an integral characteristic for which the first one bit is constant and the remaining 63 bits are active. Since all bits of the right half are active, we focus only on the left half. We first guess that \(KL_{1,2}[1]=1\), and we then prepare the set of plaintexts as in Fig. 6. We next guess that \((KL_{1,1}[1], KL_{1,2}[1]) = (0,0)\), and we then prepare the set of plaintexts as in Fig. 7. Moreover, we guess that \((KL_{1,1}[1], KL_{1,2}[1]) = (1,0)\), and we then prepare the set of plaintexts as in Fig. 8. These chosen plaintexts construct 6-round integral characteristics if the guessed key bits are correct. Note that we do not use \(2^{62}\) chosen plaintexts of the form \((1A_{15}~1A_{15}~A_{16}~A_{16})\), i.e., we do not use chosen plaintexts satisfying \(P^L[1] = P^L[16] = 1\). Thus, our integral characteristics use \(2^{64}-2^{62} \approx 2^{63.58}\) chosen plaintexts.

Fig. 9
figure 9

Key recovery step

Full size image

6.2 Subkey Recovery Using Partial-Sum Technique

Figure 9 shows the structure of our key recovery step. We guess \(KL_{1,1}[i]\; (= K_1[i])\) and \(KL_{1,2}[i]\; (= K'_7[i])\) and then prepare a set of chosen plaintexts to construct an integral characteristic. In the characteristic, seven bits \(X_7^L[1,\ldots ,7]\) are balanced. Therefore, we evaluate whether or not \(X_7^L[j]\) is balanced for \(j \in \{1,2,\ldots ,7\}\) by using the partial-sum technique [10].

Table 4 Procedure of key recovery step
Full size table

In the first step, we store the frequency of 34 bits \((C^L, C^R[j, 16+j])\) into a voting table for \(j \in \{1,2,\ldots ,7\}\). Then, we partially guess round keys, reduce the size of the voting table, and calculate the XOR of \(X_7^L[j]\). Table 4 summarizes the procedure of the key recovery step, where every value is defined in Fig. 9.

  • Step 1: Prepare the memory that stores how many times each 34-bit value \((C^L, C^R[j, 16+j])\) appears, and pick the values that appear an odd number of times.

  • Step 2: Guess 32-bit \((K_1, K'_7)\), and calculate \(X_9^R\) from \(C^L\). Delete the parity of the number of occurrences of \(C^L\) from the memory, and store that of \(X_9^R\) into the memory. Namely, the memory contains a \(2^{34}\)-bit array that stores the parity of the number of occurrences of the 34-bit string \((X_9^R, C^R[j,16+j])\). The time complexity of Step 2 is \(2^{34} \times 2^{32} = 2^{66}\).

  • Step 3: Additionally guess 32-bit \((K_8, K'_5)\), and calculate \(D_1\) from \(X_9^R\). Delete the parity of the number of occurrences of \(X_9^R[1,\ldots ,16]\) from the memory, and store that of \(D_1\) into the memory. Namely, the memory contains a \(2^{34}\)-bit array that stores the parity of the number of occurrences of the 34-bit string \((D_1, X_9^R[17,\ldots ,32], C^R[j,16+j])\). The time complexity of Step 3 is \(2^{34} \times 2^{64} = 2^{98}\).

  • Step 4: Additionally guess 1-bit \(K'_3[j]\), get \(K_7\) from \((K_7', K_8)\), which is already guessed in Step 2 and Step 3, and calculate \(D_2[j]\) from \(D_1\). Delete the parity of the number of occurrences of \(D_1\) without \(D_1[j]\) from the memory, and store that of \(D_2[j]\) into the memory. Namely, the memory contains a \(2^{20}\)-bit array that stores the parity of the number of occurrences of the 20-bit string \((D_1[j], D_2[j], X_9^R[17,\ldots ,32], C^R[j,16+j])\). The time complexity of Step 4 is \(2^{34} \times 2^{65} = 2^{99}\).

  • Step 5: Additionally guess 32-bit \(K_2\), get \(K_1'[j]\) from \((K_1, K_2)\), which is already guessed in Step 2 and Step 5, and calculate \(D_3[j]\) from \((X_9^R[17,\ldots ,32], D_1[j])\). Delete the parity of the number of occurrences of \((X_9^R[17,\ldots ,32], D_1[j])\) from the memory, and store that of \(D_3[j]\) into the memory. Namely, the memory contains a \(2^{4}\)-bit array that stores the parity of the number of occurrences of the 4-bit string \((D_2[j], D_3[j], C^R[j,16+j])\). The time complexity of Step 5 is \(2^{20} \times 2^{81} = 2^{101}\).

  • Step 6: Additionally guess 2-bit \((K_5[j], K'_2[j])\), get \(K'_3[j]\), which is already guessed in Step 4, and calculate \(X_7^L[j]\) from \((D_2[j], D_3[j], C^R[j,16+j])\). The time complexity of Step 6 is \(2^{4} \times 2^{83} = 2^{87}\).

The total time complexity is

$$\begin{aligned} 2^{66} + 2^{98} + 2^{99} + 2^{101} + 2^{87} \approx 2^{101.5}. \end{aligned}$$

We repeat the above six steps for \(j \in \{1,2,\ldots ,7\}\). Therefore, the time complexity of the key recovery step is \(7 \times 2^{101.5}=2^{104.3}\).

The key recovery step has to guess the 124-bit key

$$\begin{aligned}&K_1, K_2, K_5[1,\ldots ,7], K_7, K_8,\\&K'_1[1,\ldots ,7], K'_2[1,\ldots ,7], K'_3[1,\ldots ,7], K'_5, K'_7. \end{aligned}$$

Here, \(K_7'\) and \(K'_1[1,\ldots ,7]\) are uniquely determined by guessing \(K_7, K_8\) and \(K_1, K_2\), respectively. Thus, the guessed key material is reduced to

$$\begin{aligned}&K_1, K_2, K_5[1,\ldots ,7], K_7, K_8,\\&K'_2[1,\ldots ,7], K'_3[1,\ldots ,7], K'_5, \end{aligned}$$

and its size becomes 101 bits. Moreover, since we already guessed 2 bits, i.e., \(K_1[i]\) and \(K'_7[i]\), to construct integral characteristics, the guessed key bit size is reduced to 99 bits. For wrong keys, the probability that \(X_7^L[1,\ldots ,7]\) is balanced is \(2^{-7}\). Therefore, the number of the candidates of round keys is reduced to \(2^{92}\). Finally, we guess the 27 bits:

$$\begin{aligned} K_5[8,\ldots ,16], K'_2[8,\ldots ,16], K'_3[8,\ldots ,16]. \end{aligned}$$

Note that \(K_3\), \(K_4\), and \(K_6\) are uniquely determined from \((K_2, K'_2)\), \((K_3, K'_3)\), and \((K_5, K'_5)\), respectively. Therefore, the total time complexity is \(2^{92+27}=2^{119}\). We guess the correct key from \(2^{119}\) candidates by using two plaintext–ciphertext pairs, and the time complexity is \(2^{119}+2^{119-64} \approx 2^{119}\). We have to execute the above procedure against \((K_1[i], K'_7[i])=(0,0),(0,1),(1,0),(1,1)\), and the time complexity becomes \(4 \times 2^{119} = 2^{121}\).

6.3 Trade-off Between Time and Data Complexity

In Sect. 6.2, we use only one set of chosen plaintexts, where \((2^{64}-2^{62})\) chosen plaintexts are required. Since the probability that wrong keys are not discarded is \(2^{-7}\), a brute-force search is required with a time complexity of \(2^{128-7}=2^{121}\), and it is larger than the time complexity of the partial-sum technique. Therefore, if we have a higher number of characteristics, the total time complexity can be reduced.

To exploit several characteristics, we choose some constant bits from seven bits (\(i \in \{1,2,\ldots ,7\}\)). If we use a characteristic with \(i=1\), we use chosen plaintexts for which plaintext \(P^L\) takes the following values

$$\begin{aligned} (00A_{14}~~00A_{14}), (00A_{14}~~01A_{14}), (01A_{14}~~00A_{14}), (01A_{14}~~01A_{14}), \\ (00A_{14}~~10A_{14}), (00A_{14}~~11A_{14}), (01A_{14}~~10A_{14}), (01A_{14}~~11A_{14}), \\ (10A_{14}~~00A_{14}), (10A_{14}~~01A_{14}), (11A_{14}~~00A_{14}), (11A_{14}~~01A_{14}), \end{aligned}$$

where \(A_{14}\) denotes that all values appear the same number independently of other bits, e.g., \((00A_{14}~~00A_{14})\) uses \(2^{60}\) chosen plaintexts because \(P^R\) also takes all values. Moreover, if we use a characteristic with \(i=2\), we use chosen plaintexts for which \(P^L\) takes the following values

$$\begin{aligned} (00A_{14}~~00A_{14}), (00A_{14}~~10A_{14}), (10A_{14}~~00A_{14}), (10A_{14}~~10A_{14}), \\ (00A_{14}~~01A_{14}), (00A_{14}~~11A_{14}), (10A_{14}~~01A_{14}), (10A_{14}~~11A_{14}), \\ (01A_{14}~~00A_{14}), (01A_{14}~~10A_{14}), (11A_{14}~~00A_{14}), (11A_{14}~~10A_{14}). \end{aligned}$$

When both characteristics are used, they do not require choosing plaintexts for which \(P^L\) takes \((11A_{14}~~11A_{14})\). Therefore, \((2^{64}-2^{60})\) chosen plaintexts are required, and the probability that wrong keys are not discarded becomes \(2^{-14}\). Similarly, when three characteristics, which require \((2^{64}-2^{58})\) chosen plaintexts, are used, the probability that wrong keys are not discarded becomes \(2^{-21}\).

Table 5 Trade-off between time and data complexity
Full size table

Table 5 summarizes the trade-off between time and data complexity. For the use of each characteristic, we have to execute four key recoveries with the partial-sum technique, i.e., for \((KL_{1,1}[1],KL_{1,2}[1]) \in \{ (0,1), (1,1), (0,0), (1,0) \}\). It shows that the use of four characteristics is optimized from the perspective of time complexity. Namely, when \((2^{64}-2^{56}) \approx 2^{63.994}\) chosen plaintexts are required, the time complexity to recover the secret key is \(2^{108.3}\).

6.4 Follow-Up Results and Open Problem

After a preliminary version [26] was published, Achiya Bar-On improved the key recovery step [2] by using the same integral characteristic shown in this paper. The improved key recovery technique uses the meet-in-the-middle technique [23] under the chosen ciphertext setting. It dramatically reduces the time complexity where the secret key is recovered, and the time complexity is \(2^{69.5}\). On the other hand, it requires the full code book. When we consider the data complexity optimization, our attack, which requires \(2^{121}\) time complexity and \(2^{63.58}\) chosen plaintexts, is still the best attack. We need to construct a more efficient integral characteristic if we want to improve the data complexity, and it is left as an open problem.

7 Conclusions

In this paper, we showed a cryptanalysis of the full MISTY1. MISTY1 was well evaluated and standardized by several projects, such as CRYPTREC, ISO/IEC, and NESSIE. We constructed a new integral characteristic by using the propagation characteristic of the division property. Here, we improved the division property by optimizing the division property for a public S-box. As a result, a new 6-round integral characteristic is constructed, and we can recover the secret key of the full MISTY1 with \(2^{63.58}\) chosen plaintexts and \(2^{121}\) time complexity. If we can use \(2^{63.994}\) chosen plaintexts, our attack can recover the secret key with a time complexity of \(2^{108.3}\).