Tight Security of Cascaded LRW2

Abstract

At CRYPTO ’12, Landecker et al. introduced the cascaded LRW2 (or CLRW2) construction and proved that it is a secure tweakable block cipher up to roughly $2^{2n/3}$ queries. Recently, Mennink has presented a distinguishing attack on CLRW2 in $2n^{1/2}2^{3n/4}$ queries. In the same paper, he discussed some non-trivial bottlenecks in proving tight security bound, i.e., security up to $2^{3n/4}$ queries. Subsequently, he proved security up to $2^{3n/4}$ queries for a variant of CLRW2 using 4-wise independent AXU assumption and the restriction that each tweak value occurs at most $2^{n/4}$ times. Moreover, his proof relies on a version of mirror theory which is yet to be publicly verified. In this paper, we resolve the bottlenecks in Mennink’s approach and prove that the original CLRW2 is indeed a secure tweakable block cipher up to roughly $2^{3n/4}$ queries. To do so, we develop two new tools: First, we give a probabilistic result that provides improved bound on the joint probability of some special collision events, and second, we present a variant of Patarin’s mirror theory in tweakable permutation settings with a self-contained and concrete proof. Both these results are of generic nature and can be of independent interests. To demonstrate the applicability of these tools, we also prove tight security up to roughly $2^{3n/4}$ queries for a variant of DbHtS, called DbHtS-p, that uses two independent universal hash functions.

Appendices

Supplementary Material

Proofs of Propositions 1 and 2

1.1 Proof of Proposition 1

Suppose a compresses to b due to a partition ${\mathcal {P}}$. Then, we call ${\mathcal {P}}$ the compressing partition of a and b. For $s \ge 1$, let p(s) denote the claimed statement. We prove the result by induction on s. We first handle the base case, $s=1$. In this case, we have $b_1=\sum _{i=1}^{r}a_i$. Thus, $a_i \le b_1$ for all $i \in [r]$. Now, a term-by-term comparison gives

$$\begin{aligned} \prod _{i=1}^{r} (2^n)_{a_i} \ge (2^n)_{b_1}, \end{aligned}$$

which shows that the base case p(1) is true. Suppose p(s) is true for all $s = n$, for some $n > 1$. We now show that $p(n+1)$ is true.

Let $a = (a_i)_{i \in [r]}$ and $b = (b_j)_{j \in [s+1]}$ be two sequences over ${{\mathbb {N}}}$, such that $r \ge s+1$ and a compresses to b. Suppose ${\mathcal {P}}$ is a compressing partition of a and b. Consider the sequences $a'=(a_i)_{i\in {\mathcal {P}}_{s+1}}$ and $b'=(b_{s+1})$. We have $|{\mathcal {P}}_{s+1}| \ge 1$ and $b_{s+1} = \sum _{i \in {\mathcal {P}}_{s+1}} a_i$, which means $a'$ compresses to $b'$. Further, $2^n \ge \sum _{i \in {\mathcal {P}}_{s+1}} a_i$. Thus, we can apply p(1) result on $a'$ and $b'$ to get

$$\begin{aligned} \prod _{i \in {\mathcal {P}}_{s+1}}(2^n)_{a_i} \ge (2^n)_{b_{s+1}}. \end{aligned}$$

(27)

For the remaining, let $a{''}=(a_i)_{i\in [r]{\setminus }{\mathcal {P}}_{s+1}}$ and $b{''}=(b_j)_{j \in [s]}$. Again, we have $r-|{\mathcal {P}}_{s+1}| \ge s$, and $b_i = \sum _{j\in {\mathcal {P}}_{i}} a_j$ for all $i \in [s]$. Thus, we can apply the induction hypothesis for p(s) on $a{''}$ and $b{''}$ to get

$$\begin{aligned} \prod _{i \in [r]{\setminus }{\mathcal {P}}_{s+1}}(2^n)_{a_i} \ge \prod _{j\in [s]}(2^n)_{b_{j}}. \end{aligned}$$

(28)

The combination of Eqs. (27) and (28) shows that $p(s+1)$ is true. The result follows by induction. $\square$

1.2 Proof of Proposition 2

For $r \ge 2$, let p(r) denote the claimed statement. We prove the result by induction on r. For now, assume p(2) to be true, as we handle this case later. Suppose the proposition statement, denoted p(r), is true for all $r \ge 2$. We show that the statement $p(r+1)$ is true. Fix some arbitrary $n \in {{\mathbb {N}}}$.

Let $a_1,a_2,b_1,b_2,c_1,\ldots ,c_{r+1},d_1,\ldots ,d_{r+1} \in {{\mathbb {N}}}$, such that $c_i \le a_i$ and $c_i + d_i \le a_i + b_j \le 2^n$, for all $i \in [r+1]$ and $j \in [2]$. Let $i '$ be the smallest index in $[r+1]$, such that $d_{i'} = \min \{d_1,\ldots ,d_{r+1}\}$ (such an element exists by well-ordering principle). Without loss of generality, we assume that $b_1 \ge b_2$. We compare the terms, $(2^n-c_{i'}-j+1)$ and $(2^n-a_{1}-j+1)$, for all $j \in [d_{i'}]$. Since $c_{i'} \le a_{1}$, we must have $(2^n-c_{i'}-j+1) \ge (2^n-a_{1}-j+1)$, for all $j \in [d_{i'}]$. Now, we must have $d_{i'} \le b_1$; otherwise, $d_{i'} > b_1 \ge b_2$ which leads to $\sum _{i \in [r]} d_i > b_1+b_2$. Suppose $d_{i'} < b_1$, then using $(2^n-c_{i'}-j+1)/(2^n-a_{1}-j+1) \ge 1$, we remove all the $(2^n-c_{i'}-j+1)$, $(2^n-a_{1}-j+1)$ terms for all $j \in [d_{i'}]$. This reduces the claimed statement to p(r), which is true by hypothesis. If $d_{i'} = b_1$, then we are left with $\prod _{i \in [r+1]{\setminus }\{i'\}}(2^n-c_i)\cdots (2^n-c_i-d_i+1)$ on the left, where $r \ge 2$, and $(2^n-a_2)\cdots (2^n-a_2-b_2+1)$ on the right. Using a similar line of argument as above, we can again reduce the claimed statement to p(r), which is true by hypothesis. So $p(r+1)$ is true.

Now the base case p(2) can be handled in a similar manner. In this case, we assume without loss of generality that $d_1 \le d_2$ and $b_1 \ge b_2$, where $d_1 + d_2 = b_1 + b_2$. Since $c_1 \le a_{1}$, we must have $(2^n-c_1-j+1) \ge (2^n-a_{1}-j+1)$, for all $j \in [d_1]$. Now, we must have $d_1 \le b_1$; otherwise, $d_1 > b_1 \ge b_2$ which leads to $d_1 + d_2 > b_1+b_2$. If $d_1 = b_1$, then after removing all the terms corresponding to $(c_1,d_1)$ and $(a_1,b_1)$, we have $(2^n-c_2)\cdots (2^n-c_2-d_2+1)$ on the left and $(2^n-a_2)\cdots (2^n-a_2-b_2+1)$, where $c_2 \le a_2$ and $c_2+b_2 \le a_2+b_2$, whence $(2^n-c_2)\cdots (2^n-c_2-d_2+1) \ge (2^n-a_2)\cdots (2^n-a_2-b_2+1)$. If $d_1 < b_1$, then we compare terms from $(2^n-c_2)\cdots (2^n-c_2-d_2+1)$ with $(2^n-a_1-d_1)\cdots (2^n-a_1-b_1+1)(2^n-a_2)\cdots (2^n-a_2-b_2+1)$. First $(2^n-c_2-d_2+j) \ge (2^n-a_2-b_2+j)$ for $j \in [b_2]$, as $c_2+d_2 \le a_2+b_2$. We remove all these terms to get $(2^n-c_2)\cdots (2^n-c_2-d_2+b_2+1)$ on the left and $(2^n-a_1-d_1)\cdots (2^n-a_1-b_1+1)$ on the right, where the number of terms $d_2-b_2=b_1-d_1$. Since $c_2 \le a_1$, $(2^n-c_2-j+1) \ge (2^n-a_1-d_1-j+1)$ for all $j \in [b_1-d_1]$. This shows that p(2) is true. $\square$

Mennink’s Attack on CLRW2

In [29], Mennink gave an $O(n^{1/2}2^{3n/4})$ query attack on CLRW2. The attack is generic in nature as it does not exploit the weaknesses in the underlying block cipher. Rather it assumes that the block cipher instances are independent random permutations. Also the attack works for any hash function, including $\text {AXU}$. We briefly describe the attack and refer the readers to [29] for a more concrete and formal description, analysis and experimental verification of the attack.

Attack Description: Suppose in the transcript generated by a distinguisher, there exist four queries $(t,m_1,c_1)$, $(t',m_2,c_2)$, $(t, m_3,c_3)$ and $(t',m_4,c_4)$, such that the following equations hold:

$$\begin{aligned} m_1 \oplus h_1(t)&= m_2 \oplus h_1(t')\nonumber \\ c_2 \oplus h_2(t')&= c_3 \oplus h_2(t)\nonumber \\ m_3 \oplus h_1(t)&= m_4 \oplus h_1(t'). \end{aligned}$$

(29)

Using notations analogous to Fig. 1, we equivalently have $x_1 = x_2$; $u_2 = u_3$; and $x_3 = x_4$. Since ${x^4}\leftrightsquigarrow {y^4}$ and ${v^4}\leftrightsquigarrow {u^4}$, looking at the equations generated by the corresponding y and v values, we have $v_1 = y_1 \oplus \lambda (t) = y_2 \oplus \lambda (t) = v_2 \oplus \lambda (t') \oplus \lambda (t) = v_3 \oplus \lambda (t) \oplus \lambda (t') = y_3 \oplus \lambda (t') = v_4$. This immediately gives $u_1 = u_4$, i.e.,

$$\begin{aligned} c_4 \oplus h_2(t') = c_1 \oplus h_2(t). \end{aligned}$$

(30)

In other words, Eq. (30) is implied by the existence of Eq. (29), and by combining all four equations, we have

$$\begin{aligned} m_1 \oplus m_2&= m_3 \oplus m_4 = \alpha ,\\ c_1 \oplus c_4&= c_2 \oplus c_3 = \beta , \end{aligned}$$

where $\alpha = h_1(t) \oplus h_1(t')$ and $\beta = h_2(t) \oplus h_2(t')$. While the distinguisher does not know $\alpha$ and $\beta$, it can exploit the relations:

$$\begin{aligned} m_1 \oplus m_2&= m_3 \oplus m_4, \end{aligned}$$

(31)

$$\begin{aligned} c_1 \oplus c_4&= c_2 \oplus c_3. \end{aligned}$$

(32)

If for some value a we have about $2^n$ quadruples satisfying

$$\begin{aligned} m_1 \oplus m_2 = m_3 \oplus m_4 = a, \end{aligned}$$

(33)

then, for CLRW2, the expected number of solutions for Eqs. (31)–(32) is approximately 2 for $a = \alpha$. On the other hand, for ${{\widetilde{\Pi }}}$, the expected number of solutions is always close to 1 for any $a \in \{0,1\}^n$. In [29], it has been shown that approximately $2n^{1/2}2^{3n/4}$ queries are sufficient for the distinguisher to ensure that Eq. (33) has about $2^n$ solutions. Given these many queries, the distinguisher can attack by observing the number of solutions for Eqs. (31)–(32) for each value of a.

Proof of Lemma 4.2

Proof

We follow a similar proof approach as considered in Lemma 4.1. We define a binary random vector ${\textsf {I}} = ({\textsf {I}}_{i,j}: i \ne j)$ where ${\textsf {I}}_{i,j}$ takes value 1 if $\texttt {E}_{i,j}$ holds, otherwise zero. The sample space of the random vector is $\varOmega$, the set of all binary vectors indexed by all pairs (i, j). For any vector $w \in \varOmega$, we write $\#w$ to represent the number of 1’s that appear in w. Let $\varOmega _{\le } = \{w: \#w \le \frac{1}{\sqrt{\epsilon '}} \}$ and its complement set by $\varOmega _>$.

We define a random variable ${\textsf {N}} = \sum _{i\ne j} {\textsf {I}}_{i,j}$: The number of $\texttt {E}$ events holds. As $\texttt {E}_{i,j}$ holds with probability at most $\epsilon$,

$$\begin{aligned} q(q-1) \epsilon&\ge {\textsf {Ex} _{}\left[ {{\textsf {N}}}\right] } \nonumber \\&= \sum _w \# w \cdot {\Pr _{}\left[ {{\textsf {I}} = w}\right] } \nonumber \\&\ge \sum _{w \in \varOmega _{\le }} \# w \cdot {\Pr _{}\left[ {{\textsf {I}} = w}\right] } + \frac{{\Pr _{}\left[ {{\textsf {I}} \in \varOmega _{>}}\right] }}{\sqrt{\epsilon '}}. \end{aligned}$$

(34)

Let $\texttt {EEF}$ denote the event that there exists distinct i, j, k and l such that $\texttt {E}_{i,j}\ \wedge \ \texttt {E}_{k,l}\ \wedge \ \texttt {F}_{i,j,k,l}$. Now we proceed for bounding the probability of the event.

$$\begin{aligned} {\Pr _{}\left[ {\texttt {EEF}}\right] }&= \sum _w {\Pr _{}\left[ {\texttt {EEF} \ \wedge \ {\textsf {I}} = w}\right] } \\&= \sum _w {\Pr _{}\left[ {{\textsf {I}} = w}\right] } \times {\Pr _{}\left[ {\texttt {EEF} \wedge {\textsf {I}} = w\ |\ {\textsf {I}} = w}\right] } \\&\le \sum _w {\Pr _{}\left[ {{\textsf {I}} = w}\right] } \times \min \{1, (\#w)^2\cdot \epsilon ' \} \\&= {\Pr _{}\left[ {{\textsf {I}} \in \varOmega _>}\right] } + \sum _{w \in \varOmega _{\le }} {\Pr _{}\left[ {{\textsf {I}} = w}\right] } \cdot (\#w)^2\cdot \epsilon ' \\&\le {\Pr _{}\left[ {{\textsf {I}} \in \varOmega _>}\right] } + \sum _{w \in \varOmega _{\le }} {\Pr _{}\left[ {{\textsf {I}} = w}\right] } \cdot \#w\cdot \sqrt{\epsilon '} \\&= \sqrt{\epsilon '} \cdot \left( \sum _{w \in \varOmega _{\le }} \# w \cdot {\Pr _{}\left[ {{\textsf {I}} = w}\right] } + \frac{{\Pr _{}\left[ {{\textsf {I}} \in \varOmega _{>}}\right] }}{\sqrt{\epsilon '}} \right) \\&\le q(q-1) \epsilon \cdot \sqrt{\epsilon '}. \end{aligned}$$

The first inequality follows exactly by the same reason argued in the proof of Lemma 4.1. The last inequality follows from Eq. (34). This completes the proof. $\square$

Proof of Mirror Theory in Tweakable Settings

The induction is defined on the number of components. Apropos of this, we consider some new parameters. For $i \in [c_1+c_2+c_3]$:

• $X_i$ denotes the number of Y vertices in the previous $i-1$ components.

• $U_i$ denotes the number of V vertices in the previous $i-1$ components.

• $\xi _i$ denotes the size (number of vertices) of the ith component. We actually use $\eta _i:=\xi _i-1$ (number of edges in the ith component).

• for $j \in [\eta _i]$ and $r = \sum _{k=1}^{i-1}\eta _k+j$,

  • $\lambda ^i_j := \lambda _r$ ($\lambda$ value corresponding to the jth equation of ith component).

  • $\delta ^i_j := \mu (\lambda ^{r-1},\lambda ^i_j)$, where $\delta ^1_1 = 0$ by convention.

• ${\mathfrak {h}}_i$ denotes the number of solutions for the sub-system consisting of the first i components of ${\mathcal {L}}$, denoted ${\mathcal {L}}_{|i}$. Note that $h_i = {\mathfrak {h}}_i$ for $i \in [c_1]$, and $h_q = {\mathfrak {h}}_{c_1+c_2+c_3}$.

• $H_i := \prod _{j \in [\eta _i]}(2^n)_{\mu (\lambda ^{s},\lambda ^i_j)} \cdot {\mathfrak {h}}_i$, where $s = \sum _{k=1}^{i}\eta _k$.

• $J_i := {\left\{ \begin{array}{ll} (2^n)_{X_i+1}(2^n)_{U_i+1} &{} i\text {th component is isolated,}\\ (2^n)_{X_i+1}(2^n)_{U_i+\eta _i} &{} i\text {th component is a } {{\mathcal {Y}}}_{\text {-}\star },\\ (2^n)_{X_i+\eta _i}(2^n)_{U_i+1} &{} i\text {th component is a } {{\mathcal {V}}}_{\text {-}\star }. \end{array}\right. }$

Proof Sketch: Inspired by Patarin’s mirror theory argument [37, 39], we will study the relation between $H_i$ and $J_i$ for all $i \in [c_1+c_2+c_3]$. Our goal is to bound ${\mathfrak {h}}_{c_1+c_2+c_3}$ in terms of $H_{c_1+c_2+c_3}$ and $J_{c_1+c_2+c_3}$. We show that $H_{c_1+c_2+c_3} \ge (1-\epsilon ) J_{c_1+c_2+c_3}$, where $\epsilon = O\left( q^2/2^{2n} + \sum _{i=1}^{c_2+c_3}\eta ^2_{c_1+i}q^2/2^{2n}\right)$, which immediately gives the bound for ${\mathfrak {h}}_{c_1+c_2+c_3}$. This is precisely the motivation behind the definition of H and J.

The proof is given in two steps. First, in Sect. D.1, we bound the number of solutions for the sub-system of equations corresponding to isolated edges, i.e., the first $c_1$ components. The idea is to apply induction on $H_i/J_i$ for $i \in [c_1]$.

Given the number of solutions for the first $c_1$ components, we then bound the number of solutions for the remaining $c_2+c_3$ components (corresponding to star components) in section D.2, which essentially gives a bound for the complete system ${\mathcal {L}}$. Again, $H_{i'}/J_{i'}$ is analyzed for $i' = c_1+i$ and $i \in [c_2+c_3]$. However, we keep the expression in terms of q and $\eta$ intact.

1.1 Bound for Sub-system Corresponding to Isolated Edges

As noted before, we want to bound ${\mathfrak {h}}_{i}$ by induction on i, i.e., we want to evaluate ${\mathfrak {h}}_{i+1}$ from ${\mathfrak {h}}_i$. Since isolated components have only one edge, we simply write $\lambda _i$ and $\delta _i$ instead of $\lambda ^i_1$ and $\delta ^i_1$. We first give two supplementary results in Lemmas D.1 and D.2, which will be used later on to prove the main result.

Lemma D.1

For $i \in [q_1]$,

$$\begin{aligned} {\mathfrak {h}}_{i+1} = {\mathfrak {h}}_i \left( 2^n - 2i + \delta _{i+1}\right) + \sum _{(j,k) \in {\mathcal {M}}} {\mathfrak {h}}'_i(j,k,\lambda _{i+1}), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {M}}= \{(j,k): j,k \in [i], j \ne k, \lambda _{i+1} \ne \lambda _{j}, \lambda _{i+1} \ne \lambda _{k}\}, \end{aligned}$$

and ${\mathfrak {h}}'_i(j,k,\lambda _{i+1})$ denotes the number of solutions of ${\mathcal {L}}'_{|i}(j,k,\lambda _{i+1}) := {\mathcal {L}}_{|i} \cup \{Y_j \oplus V_k = \lambda _{i+1}\}$, for some $j,k \in [i]$.

Proof

Let ${\mathcal {S}}_i$ denote the solution space of ${\mathcal {L}}_{|i}$, i.e., ${\mathfrak {h}}_i = |{\mathcal {S}}_i|$. For a fix $(y^i,v^i) \in {\mathcal {S}}_i$, we want to compute the number of $(y_{i+1},v_{i+1})$ pairs such that $(y^{i+1},v^{i+1}) \in {\mathcal {S}}_{i+1}$. Now, some pair $(x,x \oplus \lambda _{i+1})$ is valid if $x \ne y_j$ and $x \oplus \lambda _{i+1} \ne v_k$, for $j,k \in [i]$. This means that $x \notin {\mathcal {Y}}\cup {\mathcal {V}}$, where ${\mathcal {Y}}= \{y_j:j \in [i]\}$ and ${\mathcal {V}}= \{v_j \oplus \lambda _{i+1}:j \in [i]\}$. As all $y_j$ values are pairwise distinct and $v_j$ values are pairwise distinct, we must have $|{\mathcal {Y}}| = |{\mathcal {V}}| = i$. Thus, we have

$$\begin{aligned} {\mathfrak {h}}_{i+1}&= \sum _{(y^i,v^i) \in {\mathcal {S}}_i}(2^n - |{\mathcal {Y}}\cup {\mathcal {V}}|)\nonumber \\&= \sum _{(y^i,v^i) \in {\mathcal {S}}_i}(2^n - |{\mathcal {Y}}| - |{\mathcal {V}}| + |{\mathcal {Y}}\cap {\mathcal {V}}|)\nonumber \\&= {\mathfrak {h}}_i \cdot (2^n - 2i) + \sum _{(y^i,v^i) \in {\mathcal {S}}_i} |{\mathcal {Y}}\cap {\mathcal {V}}|\nonumber \\&= {\mathfrak {h}}_i \cdot (2^n - 2i) + \sum _{(y^i,v^i) \in {\mathcal {S}}_i} \sum _{j,k \in [i]}\phi (j,k)\nonumber \\&{\mathop {=}\limits ^{1}} {\mathfrak {h}}_i \cdot (2^n - 2i) + \sum _{j,k \in [i]}{\mathfrak {h}}'_i(j,k,\lambda _{i+1})\nonumber \\&{\mathop {=}\limits ^{2}} {\mathfrak {h}}_i \cdot (2^n - 2i) + {\mathfrak {h}}_i \cdot \delta _{i+1} + \sum _{(j,k) \in {\mathcal {M}}} {\mathfrak {h}}'_i(j,k,\lambda _{i+1})\nonumber \\&= {\mathfrak {h}}_i \cdot (2^n - 2i + \delta _{i+1}) + \sum _{(j,k) \in {\mathcal {M}}} {\mathfrak {h}}'_i(j,k,\lambda _{i+1}), \end{aligned}$$

(35)

where $\phi (j,k)$ is the indicator variable that takes the value of 1 when $y_j \oplus v_k = \lambda _{i+1}$, and 0 otherwise. Equality 1 follows from the definition of ${\mathfrak {h}}'_i(j,k,\lambda _{i+1})$, and equality 2 follows from the fact that exactly $\delta _{i+1}$ (j, k) pairs exist such that $k = j$, $\lambda _{i+1} = \lambda _j$, and $y_j \oplus v_j = \lambda _{i+1}$. For these, the number of solutions is exactly the same as ${\mathfrak {h}}_i$ (since $Y_j \oplus V_k = \lambda _{i+1}$ is already in ${\mathcal {L}}_{|i}$). The remaining valid (j, k) pairs must have $\lambda _j,\lambda _k \ne \lambda _{i+1}$; else, they contradict ${\mathcal {L}}$. The set of these remaining (j, k) pairs is the set ${\mathcal {M}}$. $\square$

The following corollary of Lemma D.1 will be quite useful. The proof is immediate from the proof of Lemma D.1.

Corollary D.1

For $i \ge 1$, let ${\widehat{{\mathcal {L}}}}_{i+1}$ be a system of $i+1$ equations such that $\xi _{\max }({\widehat{{\mathcal {L}}}}_{i+1}) = 2$. Then, for any sub-system ${\widehat{{\mathcal {L}}}}_i$ consisting of i equations from ${\widehat{{\mathcal {L}}}}_{i+1}$, we have

$$\begin{aligned} (2^n-2i){\widehat{{\mathfrak {h}}}}_i \le {\widehat{{\mathfrak {h}}}}_{i+1} \le (2^n-i){\widehat{{\mathfrak {h}}}}_{i}, \end{aligned}$$

where ${\widehat{{\mathfrak {h}}}}_i$ and ${\widehat{{\mathfrak {h}}}}_{i+1}$ denote the number of solutions of ${\widehat{{\mathcal {L}}}}_i$ and ${\widehat{{\mathcal {L}}}}_{i+1}$, respectively.

Lemma D.2

For all $(j,k) \in {\mathcal {M}}$, and for all $\beta \in \{0,1\}^n$,

$$\begin{aligned} {\mathfrak {h}}_i'(j,k,\beta ) \ge \frac{{\mathfrak {h}}_i}{2^n - i + 1} \cdot \left( 1 - \frac{2(i - 2)}{2^n - 2(i - 2)}\right) . \end{aligned}$$

Proof

We are interested in ${\mathfrak {h}}_i'(j,k,\beta )$, which is the number of solutions of ${\mathcal {L}}'_{|i}(j,k,\beta )$, $j,k \in {\mathcal {M}}$. The sub-system containing j and k equations is of the form

$$\begin{aligned} Y_j \oplus V_j = \lambda _j,\quad Y_j \oplus V_k = \beta ,\quad Y_k \oplus V_k = \lambda _k, \end{aligned}$$

where once we fix $Y_j = y_j$, all other unknowns are completely determined by linearity. Thus, ${\mathfrak {h}}_i'(j,k,\beta )$ is at most ${\widehat{{\mathfrak {h}}}}_{i-1}$, where ${\widehat{{\mathfrak {h}}}}_{i-1}$ is the number of solutions of ${\widehat{{\mathcal {L}}}}_{|i-1} := {\mathcal {L}}'_{|i}(j,k,\beta ){\setminus }\{Y_j \oplus V_k = \beta ,Y_k \oplus V_k = \lambda _k\}$, the system obtained by removing the equations $Y_j \oplus V_k = \beta$ and $Y_k \oplus V_k = \lambda _k$ from ${\mathcal {L}}'_{|i}(j,k,\beta )$. Now a solution among the ${\widehat{{\mathfrak {h}}}}_{i-1}$ solutions of ${\widehat{{\mathcal {L}}}}_{|i-1}$ is not valid to be counted in ${\mathfrak {h}}_i'(j,k,\beta )$, if there exists $\ell \in [i]{\setminus }\{k\}$, such that $y_j \oplus v_\ell = \beta$ or $y_j \oplus v_\ell = \beta \oplus \lambda _{k} \oplus \lambda _\ell$. The first case leads to $V_k = V_\ell$, and the second case leads to $Y_k = Y_\ell$, where $k \ne \ell$ is obvious. Let ${\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta ) := {\widehat{{\mathcal {L}}}}_{|i-1} \cup \{Y_j \oplus V_\ell = \beta \}$ and ${\widehat{h}}'_{i-1}(j,\ell ,\beta )$ be the number of solutions ${\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta )$. Therefore, the two cases correspond to the terms ${\widehat{{\mathfrak {h}}}}'_{i-1}(j,\ell ,\beta )$ and ${\widehat{{\mathfrak {h}}}}'_{i-1}(j,\ell ',\beta \oplus \lambda _k \oplus \lambda _{\ell '})$, whence we have

$$\begin{aligned} {\mathfrak {h}}_i'(j,k,\beta ) \ge {\widehat{{\mathfrak {h}}}}_{i-1} - \sum _{\ell \in [i]{\setminus }\{j,k\}} {\widehat{{\mathfrak {h}}}}_{i-1}'(j,\ell ,\beta ) - \sum _{\ell ' \in [i]{\setminus }\{j,k\}} {\widehat{{\mathfrak {h}}}}_{i-1}'(j,\ell ',\beta \oplus \lambda _{k}\oplus \lambda _{\ell '}).\\ \end{aligned}$$

Let ${\widehat{{\mathcal {L}}}}_{|i-2,\ell } := {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta ){\setminus }\{Y_j \oplus V_{\ell } = \beta ,Y_{\ell } \oplus V_{\ell } = \lambda _{\ell }\}$ and ${\widehat{{\mathcal {L}}}}_{|i-2,\ell '} := {\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ',\beta \oplus \lambda _{k}\oplus \lambda _{\ell '}){\setminus }\{Y_j \oplus V_{\ell '} = \beta \oplus \lambda _{k}\oplus \lambda _{\ell '},Y_{\ell '} \oplus V_{\ell '} = \lambda _{\ell '}\}$. Let ${\widehat{{\mathfrak {h}}}}_{i-2,\ell }$ and ${\widehat{{\mathfrak {h}}}}_{i-2,\ell '}$ be the number of solutions for ${\widehat{{\mathcal {L}}}}_{|i-2,\ell }$ and ${\widehat{{\mathcal {L}}}}_{|i-2,\ell '}$. Using similar line of argument as above, we bound ${\widehat{{\mathfrak {h}}}}_{i-1}'(j,\ell ,\beta ) \le {\widehat{{\mathfrak {h}}}}_{i-2,\ell }$ and ${\widehat{{\mathfrak {h}}}}_{i-1}'(j,\ell ',\beta \oplus \lambda _k \oplus \lambda _{\ell '}) \le {\widehat{{\mathfrak {h}}}}_{i-2,\ell '}$. Finally, we have

$$\begin{aligned} {\mathfrak {h}}_i'(j,k,\beta )&\ge {\widehat{{\mathfrak {h}}}}_{i-1} - \sum _{\ell \in [i]{\setminus }\{j,k\}} {\widehat{{\mathfrak {h}}}}_{i-2,\ell } - \sum _{\ell ' \in [i]{\setminus }\{j,k\}} {\widehat{{\mathfrak {h}}}}_{i-2,\ell '}\\&\ge {\widehat{{\mathfrak {h}}}}_{i-1} - (i-2){\widehat{{\mathfrak {h}}}}_{i-2,\ell } - (i-2){\widehat{{\mathfrak {h}}}}_{i-2,\ell '}\\&{\mathop {\ge }\limits ^{1}} {\widehat{{\mathfrak {h}}}}_{i-1} \left( 1 - \frac{2(i-2)}{2^n - 2(i-2)}\right) \\&{\mathop {\ge }\limits ^{2}} \frac{{\mathfrak {h}}_{i}}{2^n- i + 1} \left( 1 - \frac{2(i-2)}{2^n - 2(i-2)}\right) ,\\ \end{aligned}$$

where inequalities 1 and 2 follow from Corollary D.1. Note that we switch from ${\widehat{{\mathfrak {h}}}}_{i-2,\ell }$ and ${\widehat{{\mathfrak {h}}}}_{i-2,\ell '}$ to ${\widehat{{\mathfrak {h}}}}_{i-1}$ by reintroducing the equation $Y_\ell \oplus V_\ell = \lambda _\ell$ and $Y_{\ell '} \oplus V_{\ell '} = \lambda _{\ell '}$, respectively, and from ${\widehat{{\mathfrak {h}}}}_{i-1}$ to ${\mathfrak {h}}_i$ by reintroducing the equation $Y_k \oplus V_k = \lambda _k$. The readers may use Fig. 5 to get a pictorial view of the switchings between different systems of equations. $\square$

Fig. 5

Switchings used in the proof of Lemma D.2. From left to right: ${\mathcal {L}}'_{|i}(j,k,\beta )$ is the system ${\mathcal {L}}_{|i}\cup \{Y_j \oplus V_k = \beta \}$; ${\widehat{{\mathcal {L}}}}_{|i-1}$ is obtained by removing the equations involving $V_k$ from ${\mathcal {L}}'_{|i}(j,k,\beta )$; ${\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta )$ is the system ${\widehat{{\mathcal {L}}}}_{|i-1}\cup \{Y_j \oplus V_\ell = \beta \}$; ${\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ',\beta ')$ is the system ${\widehat{{\mathcal {L}}}}_{|i-1}\cup \{Y_j \oplus V_{\ell '} = \beta '\}$, where $\beta ' = \beta \oplus \lambda _k \oplus \lambda _{\ell '}$; ${\widehat{{\mathcal {L}}}}_{|i-2,\ell }$ is obtained by removing the equations involving $V_\ell$ from ${\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta )$. Note that there should have been two ${\widehat{{\mathcal {L}}}}_{|i-2}$ switchings, one each for ${\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ,\beta )$ and ${\widehat{{\mathcal {L}}}}'_{|i-1}(j,\ell ',\beta ')$. We have drawn just once for economical reasons. Similar clarification applies to switchings from ${\widehat{{\mathcal {L}}}}_{|i-2}$ to ${\widehat{{\mathcal {L}}}}_{|i-1}$ (we only show for $\ell$)

Remark 1

In [37, Theorem 11], a result similar to Lemma D.2 has been proved for random function scenario. While the proof of that theorem is correct, there is a notational issue which is worth pointing out. The ${\mathfrak {h}}'$ notation is used in an unparametrized fashion, with an explicit hint in [37, Theorem 8] that this is done for simplification. But this simplification leads to a rather peculiar technical issue in [37, Theorem 11], where both lower and upper bounds are required on ${\mathfrak {h}}'$ values, requiring different switchings. Without the parametrization, it is difficult to understand (and verify) the switchings.

Remark 2

The proof of Lemma D.2 should also give an idea of the proof complexity. Since we only want $\epsilon = O(q^4/2^{3n})$, we needed a somewhat crude estimate of ${\mathfrak {h}}'$ values. In actual mirror theory as we move toward $\epsilon = O(q/2^n)$, we have to make a good estimate of ${\mathfrak {h}}'$ values, which does not seem easy.

Now, we state the main result of this section.

Lemma D.3

For $q_1 < 2^{n-2}$, we have

$$\begin{aligned} \frac{H_{q_1}}{J_{q_1}} \ge \left( 1 - \frac{13q_1^4}{2^{3n}} - \frac{2q_1^2}{2^{2n}}\right) . \end{aligned}$$

Proof

We prove by induction on $i \in [q_1]$, the number of components. First, $H_1 = 2^{2n} = J_1$. So the statement is true for $i = 1$. By definition, the ratio $\frac{H_{i+1}}{H_i} = (2^n-\delta _{i+1}) \cdot \frac{{\mathfrak {h}}_{i+1}}{{\mathfrak {h}}_i}$, and $J_{i+1} = (2^n - i)^2 J_i$. So we have

$$\begin{aligned} \frac{H_{i+1}}{J_{i+1}} = \frac{(2^n-\delta _{i+1})\frac{{\mathfrak {h}}_{i+1}}{{\mathfrak {h}}_i}}{(2^n-i)^2}\frac{H_i}{J_i}. \end{aligned}$$

(36)

From Lemmas D.1 and D.2, we have

$$\begin{aligned} {\mathfrak {h}}_{i+1} \ge {\mathfrak {h}}_i \left( \left( 2^n - 2i + \delta _{i+1}\right) + \frac{|{\mathcal {M}}|}{2^n - i + 1}\left( 1-\frac{2(i-2)}{2^n - 2(i-2)}\right) \right) . \end{aligned}$$

(37)

Recall that ${\mathcal {M}}= \{(j,k):j,k \in [i],j \ne k,\lambda _j,\lambda _k \ne \lambda _{i+1}\}$. As there are $\delta _{i+1}$$i' \in [i]$ such that $\lambda _{i+1} = \lambda _{i'}$, we must have $|{\mathcal {M}}| \ge (i - \delta _{i+1})(i-\delta _{i+1}-1)$. On substituting this value for $|{\mathcal {M}}|$ in Eq. (37), and using the resulting lower bound for ${\mathfrak {h}}_{i+1}$ in Eq. (36), we get

Let the boxed expression be A. We first simplify this term.

$$\begin{aligned} A&\ge \dfrac{(2^n-\delta _{i+1})\left( (2^n - 2i + \delta _{i+1}) + \frac{(i - \delta _{i+1})(i - \delta _{i+1} - 1)}{2^n - i + 1}\left( 1 - \frac{2(i-2)}{2^n - 2(i-2)}\right) \right) }{(2^n-i)^2}\\&{\mathop {\ge }\limits ^{1}} \dfrac{(2^n-\delta _{i+1})(2^n - 2i + \delta _{i+1}) + \frac{(2^n-\delta _{i+1})(i - \delta _{i+1})(i - \delta _{i+1} - 1)}{2^n} - \frac{16}{3}\frac{i^3}{2^{n}}}{(2^n-i)^2}\\&{\mathop {\ge }\limits ^{2}} 1 - \dfrac{(i-\delta _{i+1}) + \frac{(i-\delta _{i+1})^2\delta _{i+1}}{2^n} - \frac{(i - \delta _{i+1})\delta _{i+1}}{2^n} + \frac{16}{3}\frac{i^3}{2^{n}}}{(2^n-i)^2}\\&{\mathop {\ge }\limits ^{3}} 1 - \frac{13i^3}{2^{3n}} - \frac{2i}{2^{2n}}. \end{aligned}$$

At inequality 1, we use $i \le q_1 \le 2^{n-2}$, $(i-2),(i-\delta _{i+1}) < i$, and $(2^n-\delta _{i+1}),(2^n-i+1) < 2^n$; inequality 2 is just a simplification; and at inequality 3, we use $(i-\delta _{i+1}),\delta _{i+1} \le i$ and $(2^n-i)^2 \le 2^{n-1}$. Now, we have

$$\begin{aligned} \frac{H_{i+1}}{J_{i+1}}&\ge \left( 1 - \frac{13i^3}{2^{3n}} - \frac{2i}{2^{2n}}\right) \times \frac{H_i}{J_i}\\&{\mathop {\ge }\limits ^{1}} \left( 1 - \frac{13i^3}{2^{3n}} - \frac{2i}{2^{2n}}\right) ^i\\&\ge \left( 1 - \frac{13i^4}{2^{3n}} - \frac{2i^2}{2^{2n}}\right) . \end{aligned}$$

Inequality 1 follows from recursive application of the induction hypothesis. The result follows by induction. $\square$

1.2 Bound for Sub-system Corresponding to Star Components

At this point, we have the bound for the sub-system corresponding to the $q_1$ isolated edges, and we want to extend it to get the bound on ${\mathfrak {h}}_{q_1+c_2+c_3}$. For simplicity, we let $i' = q_1+i = c_1+i$. Thus, $c_1+c_2+c_3 = (c_2+c_3)'$. We follow exactly the same approach as before in case of isolated edges.

For $i'-1 \ge 0$, we analyze the ratio $\frac{H_{i'}}{J_{i'}}$. Note that $J_{i'}$ depends on the type of $i'$th component (${{\mathcal {Y}}}_{\text {-}\star }$ or ${{\mathcal {V}}}_{\text {-}\star }$). However, it can be easily seen that the two expressions are symmetric. Without loss of generality, we assume that the $i'$th component is ${{\mathcal {Y}}}_{\text {-}\star }$. Then, we have

Let the boxed expression be A. We first simplify this term. In Lemma D.5, we show that

$$\begin{aligned} \frac{{\mathfrak {h}}_{i'}}{{\mathfrak {h}}_{i'-1}} \ge \left( 2^n-X_{i'}-\eta _{i'}U_{i'} + \sum _{j=1}^{\eta _{i'}} \delta ^{i'}_j\right) . \end{aligned}$$

Thus, we have

$$\begin{aligned} A&\ge \dfrac{\prod _{j=1}^{\eta _{i'}}(2^n-\delta ^{i'}_j) (2^n - X_{i'} - \eta _{i'}U_{i'} + \sum _{k=1}^{\eta _{i'}}\delta ^{i'}_k)}{(2^n-X_{i'})(2^n-U_{i'})_{\eta _{i'}}}\nonumber \\&\ge 1 - \dfrac{{\mathop {\overbrace{(2^n-X_{i'})(2^n-U_{i'})_{\eta _{i'}}}}\limits ^{B}} - {\mathop {\overbrace{\prod _{j=1}^{\eta _{i'}}(2^n-\delta ^{i'}_j)(2^n - X_{i'} - \eta _{i'}U_{i'} + \sum _{k=1}^{\eta _{i'}} \delta ^{i'}_k)}}\limits ^{C}}}{(2^n-X_{i'}) (2^n-U_{i'})_{\eta _{i'}}}. \end{aligned}$$

(38)

We need both lower and upper bounds on B. Using the facts that $X_{i'},U_{i'}+\eta _{i'} < q$, and $\xi _{\max }q < 2^{n-1}$, we get $B \ge 2^{n(\eta _{i'}+1)-1}$. Now, we derive an upper bound on B.

$$\begin{aligned} B&= (2^n-X_{i'})(2^n-U_{i'})_{\eta _{i'}}\nonumber \\&\le (2^n-X_{i'})(2^n-U_{i'})^{\eta _{i'}}\nonumber \\&\le (2^n-X_{i'}) \left( 2^{n\eta _{i'}} - \eta _{i'}U_{i'}2^{n(\eta _{i'}-1)} + \eta ^2_{i'}U^2_{i'}2^{n(\eta _{i'}-2)}\right) \nonumber \\&\le 2^{n(\eta _{i'}+1)} -\eta _{i'}U_{i'}2^{n\eta _{i'}} + \eta ^2_{i'}U^2_{i'}2^{n(\eta _{i'}-1)} - X_{i'}2^{n\eta _{i'}} + \eta _{i'}X_{i'}U_{i'}2^{n(\eta _{i'}-1)}. \end{aligned}$$

(39)

We also need a lower bound on C.

$$\begin{aligned} C&= \prod _{j=1}^{\eta _{i'}}\left( 2^n-\delta ^{i'}_j\right) \left( 2^n-X_{i'}-\eta _{i'}U_{i'} + \sum _{k=1}^{\eta _{i'}}\delta ^{i'}_k\right) \nonumber \\&\ge \left( 2^{n\eta _{i'}}-\sum _{j=1}^{\eta _{i'}} \delta ^{i'}_j2^{n(\eta _{i'}-1)}\right) \left( 2^n-X_{i'}-\eta _{i'}U_{i'} + \sum _{k=1}^{\eta _{i'}}\delta ^{i'}_k\right) \nonumber \\&\ge 2^{n(\eta _{i'}+1)} - X_{i'}2^{n\eta _{i'}} - \eta _{i'}U_{i'}2^{n\eta _{i'}} - \left( \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j\right) ^22^{n(\eta _{i'}-1)}. \end{aligned}$$

(40)

On substituting the bounds of B and C in Eq. (38), we get

$$\begin{aligned} A&\ge \dfrac{\eta ^2_{i'}U^2_{i'}2^{n(\eta _{i'}-1)}+\eta _{i'}X_{i'}U_{i'}2^{n(\eta _{i'}-1)}+\left( \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j\right) ^22^{n(\eta _{i'}-1)}}{2^{n(\eta _{i'}+1)-1}}\nonumber \\&{\mathop {\ge }\limits ^{1}} \dfrac{\eta ^2_{i'}q^22^{n(\eta _{i'}-1)}+\eta _{i'}q^22^{n(\eta _{i'}-1)}+q^22^{n(\eta _{i'}-1)}}{2^{n(\eta _{i'}+1)-1}}\nonumber \\&{\mathop {\ge }\limits ^{2}} \frac{4\eta ^2_{i'}q^2}{2^{2n}}. \end{aligned}$$

(41)

At inequality 1, we use the fact that $X_{i'},Y_{i'} \le q$ and $\sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j < q$ ($\lambda ^{i'}_j$ can occur at most once in any component). At inequality 2, we use the fact that $\eta ^2_{i'} > \eta _{i'}+1$ as $\eta _{i'} > 2$. Therefore, we have

$$\begin{aligned} \frac{H_{i'}}{J_{i'}} \ge \left( 1 - \frac{4\eta ^2_{i'}q^2}{2^{2n}}\right) \times \frac{H_{i'-1}}{J_{i'-1}}. \end{aligned}$$

In combination with Lemma D.3, this immediately gives the bound on $\frac{H_{c_1+c_2+c_3}}{J_{c_1+c_2+c_3}}$ in Lemma D.4.

Lemma D.4

For $q \le 2^{n-2}$ and $\xi _{\max } \le 2^n/2q$, we have

$$\begin{aligned} \frac{H_{c_1+c_2+c_3}}{J_{c_1+c_2+c_3}} \ge \left( 1 - \frac{13q^4}{2^{3n}} - \frac{2q^2}{2^{2n}} - \left( \sum _{i=1}^{c_2+c_3}\eta ^2_{c_1+i}\right) \frac{4q^2}{2^{2n}}\right) . \end{aligned}$$

Theorem 5.1 follows from the definition of H, J and Lemma D.4.

Lemma D.5

$\displaystyle {\mathfrak {h}}_{i'} \ge \left( 2^n - X_{i'} - \eta _{i'}U_{i'} + \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j\right) \cdot {\mathfrak {h}}_{i'-1}.$

Proof

Let ${\mathcal {S}}_{i'-1}$ denote the solution space of ${\mathcal {L}}_{|i'-1}$. Let $r = \sum _{j=1}^{i'-1}\eta _{j}$. For a fixed $(y^r,v^r) \in {\mathcal {S}}_{i'-1}$, we want to compute the number of solutions for ${\mathcal {L}}_{|i'}$. Since this is a ${{\mathcal {Y}}}_{\text {-}\star }$ component, it is sufficient to choose an assignment for $Y_{i'}$ (center of the $i'$th component) value and $V^{i'}_j = Y_{i'} \oplus \lambda ^{i'}_{j}$. Now, an assignment x is invalid if $x \in {\mathcal {Y}}\cup {\mathcal {V}}$, where ${\mathcal {Y}}= \{y_j:j \in [r]\}$ and ${\mathcal {V}}= \{v_j\oplus \lambda ^{i'}_k: j\in [r],k \in [\eta _{i'}]\}$. Clearly, $|{\mathcal {Y}}| = X_{i'}$ and $|{\mathcal {V}}| \le \eta _{i'}U_{i'}$. Further, exactly $\sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j$ previous equations share $\lambda$ value with some equation in the $i'$th component, whence $|{\mathcal {Y}}\cap {\mathcal {V}}| \ge \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j$. Thus, we have

$$\begin{aligned} {\mathfrak {h}}_{i'}&= \sum _{(y^{r},v^{r}) \in {\mathcal {S}}_{i'}}(2^n - |{\mathcal {Y}}\cup {\mathcal {V}}|)\\&= \sum _{(y^{r},v^{r}) \in {\mathcal {S}}_{i'}}(2^n - |{\mathcal {Y}}| - |{\mathcal {V}}| + |{\mathcal {Y}}\cap {\mathcal {V}}|)\\&\ge \sum _{(y^{r},v^{r}) \in {\mathcal {S}}_{i'}}\left( 2^n - X_{i'} - \eta _{i'}U_{i'} + \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j\right) \\&= \left( 2^n - X_{i'} - \eta _{i'}U_{i'} + \sum _{j=1}^{\eta _{i'}}\delta ^{i'}_j\right) \cdot {\mathfrak {h}}_{i'-1}. \end{aligned}$$

$\square$

Proof of Lemma 6.1

Property 1 holds by definition and the nonexistence of bad hash key condition 1. Property 2 holds due to the nonexistence of bad hash key conditions 2 and 3. Property 3 holds due to the nonexistence of bad hash key conditions 4, 5, 6 and 7. Property 4 holds due to nonexistence of bad hash key conditions 4 and 5. It is easy to verify that given Properties 1, 2, 3 and 4, Fig. 4 enumerates all possible types of components of ${\mathcal {G}}$. $\square$

Proof of Security of $\textsf {DbHtS-p}$

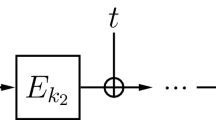
The analysis of $\textsf {DbHtS-p}$ would be similar to the analysis of CLRW2 presented in this paper. The variables arising in $\textsf {DbHtS-p}$ computation are analogously notated as in CLRW2 (see Fig. 6). Specifically, we have the following connection between the notations for $\textsf {DbHtS-p}$ and CLRW2:

• $x^q$ and $u^q$ in $\textsf {DbHtS-p}$ correspond to $x^q$ and $u^q$ in CLRW2. Here, $x^q = h_1(m^q)$ and $u^q = h_2(m^q)$.

• $y^q$ and $v^q$ in $\textsf {DbHtS-p}$ correspond to $y^q$ and $v^q$ in CLRW2.

• Similar to CLRW2, in $\textsf {DbHtS-p}$${x^q}\leftrightsquigarrow {y^q}$ and ${u^q}\leftrightsquigarrow {v^q}$. Note that in $\textsf {DbHtS-p}$$v^q = {E}_{k_2}(u^q)$, whereas in CLRW2$u^q = {E}_{k_2}(v^q)$. However, this does not affect the permutation compatibility property.

• $\lambda ^q$ in $\textsf {DbHtS-p}$ corresponds to $\lambda ^q$ in CLRW2. Therefore, $v^q \oplus y^q = \lambda ^q$.

Fig. 6

$\textsf {DbHtS-p}$ construction

Initial Setup: The first step of replacing the block cipher instantiations with independent uniform random permutations $\Pi _1$ and $\Pi _2$ incurs a cost of $2\mathbf {Adv}^{{\textsf {prp}}}_{{E}}(q,t')$. For the sake of simplicity, we call the resulting construction $\textsf {DbHtS-p}$.

Oracle Description and Sampling Mechanism: The real and ideal oracles can be described in a similar manner as in case of CLRW2, except a small change. For all $i \in [q]$, ${\lambda }_i \leftarrow \!\!{\$}\,\{0,1\}^n$ in the ideal world, and ${\lambda }_i = \textsf {DbHtS-p} (m_i)$ in the real world.

Definition of Bad Transcript and its Analysis: We again use the same set of bad transcripts and bound the probability of realizing a bad transcript, denoted ${\epsilon _{{\textsf {bad}}}}$, as

$$\begin{aligned} {\epsilon _{{\textsf {bad}}}} \le q^2\epsilon ^2 + \frac{q^2\epsilon }{2^n} + 2q^2\epsilon ^{1.5} + \frac{16q^4\epsilon }{2^{2n}} + \frac{9q^4\epsilon ^2}{2^{n}}. \end{aligned}$$

(42)

Here, the only notable difference is the bound on ${\Pr _{}\left[ {{\texttt {H}}_2}\right] }$ and ${\Pr _{}\left[ {\texttt {H}_3}\right] }$. Since now the ${\lambda }$ values are uniform at random, ${\Pr _{}\left[ {{\texttt {H}}_2}\right] } \le {q \atopwithdelims ()2}\epsilon 2^{-n}$ and ${\Pr _{}\left[ {\texttt {H}_3}\right] } \le {q \atopwithdelims ()2}\epsilon 2^{-n}$. All other bad events are bounded identically to the bad events in case of CLRW2.

Good Transcript Analysis: For a fixed good transcript $\omega$, in the real world the interpolation probability is bounded as in case of CLRW2, i.e.,

(43)

In the ideal world, using Corollary 5.1 we get

(44)

where $p_1 = q_1+c_2+q_3$, $p_2=q_1+q_2+c_3$, and

$$\begin{aligned} \zeta (\omega ) = \left( 1 - \frac{13q^4}{2^{3n}} - \frac{2q^2}{2^{2n}} - \left( \sum _{i=1}^{c_2+c_3}\eta ^2_{c_1+i}\right) \frac{4q^2}{2^{2n}}\right) . \end{aligned}$$

On dividing Eq. (43) by (44) and doing some simplification, we get

Using Lemma 2.1, we get

$$\begin{aligned} \mathbf {Adv}^{{\textsf {prf}}}_{\textsf {DbHtS-p}}(q)&\le \frac{2q^2}{2^{2n}} + \frac{13q^4}{2^{3n}} + \frac{4q^2}{2^{2n}}{\textsf {Ex} _{}\left[ {\sum _{i=1}^{c_2+c_3}\eta ^2_{c_1+i}}\right] } + {\epsilon _{{\textsf {bad}}}}\nonumber \\&\le \frac{2q^2}{2^{2n}} + \frac{13q^4}{2^{3n}} + \frac{16q^4\epsilon }{2^{2n}} + {\epsilon _{{\textsf {bad}}}}. \end{aligned}$$

(45)

The result follows from Eqs. (42) and (45). $\square$

Note that the application of alternating events/collisions lemma (or a similar result) seems indispensable, even if one assumes that the fundamental theorem of mirror theory holds.