A new generalization of lifetime distributions

Abstract

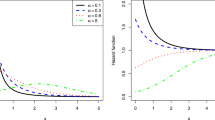
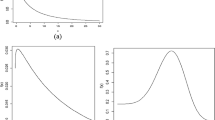
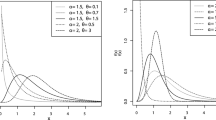
In the current study, we set out to extend the three-parameter Modified Weibull (MW) distribution in an attempt to propose a four-parameter distribution named the Modified Weibull Poisson (MWP) distribution including such noticeable submodels as Exponential Poisson, Weibull Poisson, and Rayleigh Poisson known as the distributions subsumed under the umbrella term MWP. Depending on its parameter values, this overarching distribution was demonstrated by this work to exhibit some hazard rates like decreasing, increasing, bathtub, and upside-down bathtub ones. In addition to the hazard rates of the MWP, the mathematical properties as well as the properties of maximum likelihood estimations were brought to the forefront, and the very capability of the quantile measures to be explicitly expressed in terms of the Lambert W function was vigorously discussed. To shed light on the functioning of the maximum likelihood estimators and their asymptomatic results for the finite sample sizes, some numerical experiments were carried out leading to two data sets intended chiefly to illustrate or explicate the higher levels of importance and flexibility of the MWP in comparison with its standard counterparts, namely the Weibull, Gamma, and MW distributions.

Appendix

The Fisher observed information matrix for the parameter vector $\varvec{\theta }$ whose elements are given by:

$$\begin{aligned} U_{\alpha \alpha }&= -n\alpha ^{-2}+\lambda \sum \limits _{i=1}^n \left( {x_i^\gamma e^{\beta x_i }} \right) ^{2}e^{-u_i },\\ U_{\alpha \beta }&= U_{\beta \alpha } =-\alpha ^{-1}\sum \limits _{i=1}^n x_i u_i \left[ {1+\lambda \left( {1-u_i } \right) e^{-u_i }} \right] ,\\ U_{\alpha \gamma }&= U_{\gamma \alpha } =-\alpha ^{-1}\sum \limits _{i=1}^n u_i \left[ {1+\lambda e^{-u_i } \left( {1-u_i } \right) } \right] \log x_i , U_{\alpha \lambda } =U_{\lambda \alpha } \\&= -\alpha ^{-1}\sum \limits _{i=1}^n u_i e^{-u_i }\\ U_{\beta \beta }&= -\sum \limits _{i=1}^n x_i^2 \left( {\gamma +\beta x_i } \right) ^{-2}-\sum \limits _{i=1}^n x_i^2 u_i \left[ {1+\lambda e^{-u_i } \left( {1-u_i } \right) } \right] ,\\ U_{\gamma \beta }&= U_{\beta \gamma } =-\sum \limits _{i=1}^n x_i \left( {\gamma +\beta x_i } \right) ^{-2}-\sum \limits _{i=1}^n x_i u_i \left[ {1+\lambda e^{-u_i } \left( {1-u_i } \right) } \right] \log x_i ,\\ U_{\beta \lambda }&= U_{\lambda \beta } =-\sum \limits _{i=1}^n x_i u_i e^{-u_i },\\ U_{\gamma \gamma }&= -\sum \limits _{i=1}^n \left( {\gamma +\beta x_i } \right) ^{-2}-\sum \limits _{i=1}^n u_i \left[ {1+\lambda e^{-u_i } \left( {1-u_i } \right) } \right] \left( {\log x_i } \right) ^{2}\\ U_{\gamma \lambda }&= U_{\lambda \gamma } =-\sum \limits _{i=1}^n u_i e^{-u_i }\log x_i \hbox { and } U_{\lambda \lambda } =-n\lambda ^{-2}+ne^{-\lambda }\left( {1-e^{-\lambda }} \right) ^{-2}\\ \end{aligned}$$

Using the $X^{\gamma }e^{\beta X}\sim EP(\alpha ,\lambda )$, the Fisher information matrix can be obtained as:

$$\begin{aligned} E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \alpha ^{2}}} \right)&= n\alpha ^{-2}-0.25 n\lambda e^{-\lambda }\alpha ^{-2}\left( {1-e^{-\lambda }} \right) ^{-1} F_{3,3} \left( {\left[ {2,2,2} \right] , \left[ {3,3,3} \right] ,\lambda } \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \alpha \partial \beta }} \right)&= n I\left( {\gamma +1,0,1,0} \right) +n\lambda I\left( {\gamma +1,0,1,1} \right) -n\lambda I\left( {2\gamma +1,0,2,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \alpha \partial \gamma }} \right)&= nI\left( {\gamma ,1,1,0} \right) +n\lambda I\left( {\gamma ,1,1,1} \right) -n\alpha \lambda I\left( {2\gamma ,1,2,0} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \alpha \partial \lambda }} \right)&= 0.25 n\lambda e^{-\lambda } \left[ {\alpha \left( {1-e^{-\lambda }} \right) } \right] ^{-1}F_{2,2} \left( {\left[ {2,2} \right] , \left[ {3,3} \right] ,\lambda } \right) ,\\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \beta \partial \lambda }} \right)&= nI(\left( {\gamma +1,0,1,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \beta ^{2}}} \right)&= nJ\left( {2,2} \right) +n\alpha I\left( {\gamma +2,0,1,0} \right) +n\alpha \lambda I\left( {\gamma +2,0,1,1} \right) \\&-n\alpha \lambda I\left( {2\gamma +2,0,2,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \beta \partial \gamma }} \right)&= n J\left( {1,2} \right) +n\alpha I\left( {\gamma +1,1,1,0} \right) +n\alpha \lambda I\left( {\gamma +1,1,1,1} \right) \\&+n\alpha \lambda I\left( {2\gamma +1,1,2,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \gamma ^{2}}} \right)&= n J\left( {0,2} \right) +n\alpha I\left( {\gamma ,2,1,0} \right) +n\alpha \lambda I\left( {\gamma ,2,1,1} \right) \\&-n\alpha ^{2}\lambda I\left( {2\gamma ,2,2,1} \right) \\ E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \gamma \partial \lambda }} \right)&= n\alpha I(\left( {\gamma ,1,1,1} \right) , E\left( {-\frac{\partial ^{2}\ell \left( \theta \right) }{\partial \lambda ^{2}}} \right) =n\lambda ^{-2}-ne^{-\lambda }\left( {1-e^{-\lambda }} \right) ^{-1}, \end{aligned}$$

where $F_{v,w} \left( {\left[ {a_1 ,\ldots ,a_v } \right] , \left[ {b_1 ,\ldots ,b_w } \right] ,\gamma } \right)$ is the generalized hypergeometric function with the following definition provided by Gradshteyn and Ryzhik (2000).

$$\begin{aligned} F_{v,w} \left( {\left[ {a_1 ,\ldots ,a_v } \right] , \left[ {b_1 ,\ldots ,b_w } \right] ,\gamma } \right) =\sum \limits _{k=0}^\infty \frac{\gamma ^{k}\mathop \prod \nolimits _{i=1}^v {\Gamma }\left( {a_i +k} \right) {\Gamma }^{-1}(a_i )}{{\Gamma }\left( {k+1} \right) \mathop \prod \nolimits _{i=1}^w {\Gamma }\left( {b_i +k} \right) {\Gamma }^{-1}(b_i )}, \end{aligned}$$

and $I\left( {i,j,k,l} \right) =E\left[ {X^{i}\left( {\log X} \right) ^{j} e^{k\beta X-l\alpha X^{\gamma }e^{\beta X}}} \right]$, $J\left( {i,j} \right) =E\left[ {X^{i}\left( {\gamma +\beta X} \right) ^{-j}} \right]$ are expectations which can be computed numerically.