Abstract
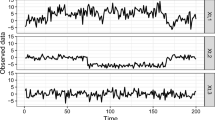
In this paper, we propose a procedure for detecting multiple change-points in a mean-shift model, where the number of change-points is allowed to increase with the sample size. A theoretic justification for our new method is also given. We first convert the change-point problem into a variable selection problem by partitioning the data sequence into several segments. Then, we apply a modified variance inflation factor regression algorithm to each segment in sequential order. When a segment that is suspected of containing a change-point is found, we use a weighted cumulative sum to test if there is indeed a change-point in this segment. The proposed procedure is implemented in an algorithm which, compared to two popular methods via simulation studies, demonstrates satisfactory performance in terms of accuracy, stability and computation time. Finally, we apply our new algorithm to analyze two real data examples.






Similar content being viewed by others
References
Auger I, Lawrence C (1989) Algorithms for the optimal identification of segment neighborhoods. Bull Math Biol 51:39–54
Barry D, Hartigan JA (1992) Product partition models for change-point problems. Ann Stat 20:260–279
Barry D, Hartigan JA (1993) A Bayesian analysis for change point problems. J Am Stat Assoc 35:309–319
Chen J, Gupta AK (2012) Parametric statistical change point analysis with applications to genetics medicine and finance, 2nd edn. Birkhäuser, Boston
Csörgő M, Horváth L (1997) Limit theorems in change-point analysis. Wiley, Chichester
Erdman C, Emerson JW (2007) bcp: an R package for performing a Bayesian analysis of change point problems. J Stat Softw 23:1–13
Erdman C, Emerson JW (2008) A fast Bayesian change point analysis for the segmentation of microarray data. Bioinformatics 24:2143–2148
Harchaoui Z, Lévy-Leduc C (2008) Catching change-points with Lasso. Adv Neural Inf Process Syst 20:617–624
Harchaoui Z, Lévy-Leduc C (2010) Multiple change-point estimation with a total variation penalty. J Am Stat Assoc 105:1480–1493
Jackson B, Sargle J, Barnes D, Arabhi S, Alt A, Gioumousis P, Gwin E, Sangtrakulcharoen P, Tan L, Tsai TT (2005) An algorithm for optimal partitioning of data on an interval. IEEE Signal Process Lett 12:105–108
Jin B, Shi X, Wu Y (2013) A novel and fast methodology for simultaneous multiple structural break estimation and variable selection for nonstationary time series models. Stat Comput 23:221–231
Killick R, Eckley IA (2014) changepoint: an R package for changepoint analysis. J Stat Softw 58(3):1–19
Killick R, Eckley IA, Haynes K (2014) changepoint: An R package for changepoint analysis. R package version 1(1):5
Killick R, Fearnhead P, Eckley IA (2012) Optimal detection of changepoints with a linear computational cost. J Am Stat Assoc 107:1590–1598
Lin D, Foster DP, Ungar LH (2011) VIF regression: a fast regression algorithm for large data. J Am Stat Assoc 106:232–247
Matteson DS, James NA (2013) A nonparametric approach for multiple change point analysis of multivariate data. J Am Stat Assoc 109:334–345
Olshen A, Venkatraman E, Lucito R, Wigler M (2004) Circular binary segmentation for the analysis of array-based DNA copy number data. Biostatistics 5:557–572
Qu L, Tu Y (2006) Change point estimation of bilevel functions. J Mod Appl Stat Methods 5:347–355
Rigaill G (2010) Pruned dynamic programming for optimal multiple change-point detection. Technical Report, arXiv:1004.0887v1
Scott AJ, Knott M (1974) A cluster analysis method for grouping means in the analysis of variance. Biometrics 30:507–512
Seshan VE, Olshen A (2015) DNAcopy: DNA copy number data analysis. R package version 1(40)
Shi X, Wang X, Wei W, Wu Y (2015) VIFCP: detecting change-points via VIFCP method. R package version 1.0
Stransky N, Vallot C, Reyal F, Bernard-Pierrot I, Diez de Medina SG, Segraves R, de Rycke Y, Elvin P, Cassidy A, Spraggon C, Graham A, Southgate J, Asselain B, Allory Y, Abbou CC, Albertson DG, Thiery J-P, Chopin DK, Pinkel D, Radvanyi F (2006) Regional copy number-independent deregulation of transcription in cancer. Nat Genet 38:1386–1396
Acknowledgments
The authors would like to thank the associate editor and two anonymous reviewers for the critical comments and constructive suggestions which have led to the improvement of this paper. The authors would also like to thank Professor Trueman MacHenry for polishing the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
The research was partially supported by Natural Sciences and Engineering Research Council of Canada.
Appendix: Proof of Theorem 1
Appendix: Proof of Theorem 1
Since \(\varepsilon _i\), \(i=1,2,\ldots \), are iid zero-mean variables with variance \(\sigma ^2\), it follows from the definition of \(\rho _{i+1}\) in (8) and the idempotence of \( I- X^{(i+1)}[( X^{(i+1)})^T X^{(i+1)}]^{-1}( X^{(i+1)})^T\) that the variance of \(\rho _{i+1}^{-1}(\varvec{x}_{\mathrm{new}}^{(i+1)})^T\{I- X^{(i+1)}[( X^{(i+1)})^T X^{(i+1)}]^{-1}( X^{(i+1)})^T\}{\varvec{\varepsilon }}^{(i+1)}\) is still \(\sigma ^2\). By the central limit theorem, we obtain that
Note that \( ( X^{(i+1)})^T X^{(i+1)}\) can be expressed as \(( U^{(i+1)})^T \varLambda ^{(i+1)} U^{(i+1)}\), where \(U^{(i+1)}\) is the lower triangular matrix of order \(k+1\) whose nonzero entries are all 1’s, and \(\varLambda ^{(i+1)}\) is a diagonal matrix with diagonal entries being \(k_1-k_0,\ k_2-k_1,\ \ldots ,\ k_m-k_{m-1},\ 1+(i+1)l-k_m\). Since the change-points are well-separated, i.e., \(k_r-k_{r-1}=O(n)\), \((\varLambda ^{(i+1)})^{-1}\) is of order O(1 / n), we have that \([( X^{(i+1)})^T X^{(i+1)}]^{-1}\) is also of order O(1 / n).
Next, we prove that \(\rho _{i+1}\) defined in (8) is asymptotically equal to \(\sqrt{l}\). Note that \(\varvec{x}_{\mathrm{new}}^{(i+1)}={{\varvec{\ell }}}_{il,l}\) is the vector with only the last l elements being ones, and all other elements are zeros. It can be seen that \((\varvec{x}_{\mathrm{new}}^{(i+1)})^T\varvec{x}_{\mathrm{new}}^{(i+1)}=l\) and \((\varvec{x}_{\mathrm{new}}^{(i+1)})^T X^{(n+1)}=O(l)\). Therefore, as \(n\rightarrow \infty \), it is readily seen from \([( X^{(i+1)})^T X^{(i+1)}]^{-1}=O(1/n)\) that
Under the null hypothesis, there exists no change-point in the interval \([1+il,(i+1)l]\). It can be shown that the last l elements of the correction vector \({\varvec{\eta }}^{(i+1)}\) are zeros, which implies that \((\varvec{x}_{\mathrm{new}}^{(i+1)})^T{\varvec{\eta }}^{(i+1)}=0\). Since \((\varvec{x}_{\mathrm{new}}^{(i+1)})^T X^{(i+1)}=O(l)\), \((X^{(i+1)})^T{\varvec{\eta }}^{(i+1)}=o_p(bl)\), \([ (X^{(i+1)})^T X^{(i+1)}]^{-1}=O(1/n)\) and \(\rho _{i+1}/\sqrt{l}\rightarrow 1\), by Assumption A1, it follows that
In view of the fact that \(\beta _{\mathrm{new}}^{(i+1)}=0\), i.e., there is no change-point in \([1+il,(i+1)l]\), and \(\rho _{i+1}\rightarrow \infty \), by (7) and (9), we obtain that
This proves Theorem 1(a).
Under the alternative hypothesis, there exists a change-point, say \(k_m\), in the segment \([1+il,(i+1)l]\). Moreover, \(k_m-il\) many of the last l elements of the correction vector \({\varvec{\eta }}^{(i+1)}\) are equal to \(\beta _{\mathrm{new}}^{(i+1)}\), and \(\beta _{\mathrm{new}}^{(i+1)} \not =0\), which implies \((\varvec{x}_{\mathrm{new}}^{(i+1)})^T{\varvec{\eta }}^{(i+1)}=\beta _{\mathrm{new}}^{(i+1)}\left( k_m-il\right) \).
Moreover, we have
from the Proof of Theorem 1(a). In view of (11), we obtain that
Applying these results to (7) yields
Furthermore, if the change-point \(k_m\) is located in the artificial interval \([1+(i-1)l,il]\) (i.e., the change-point was previously undetected), then the correction vector \({\varvec{\eta }}^{(i+1)}\) has zero components in the last l rows, which implies that \((\varvec{x}_{\mathrm{new}}^{(i+1)})^T{\varvec{\eta }}^{(i+1)}=0\). A similar argument as above yields that \(\hat{\beta }_{\mathrm{new}}^{(i+1)}=\beta _{\mathrm{new}}^{(i+1)}+o_p(1).\) This ends the proof of Theorem 1(b).
Rights and permissions
About this article
Cite this article
Shi, X., Wang, XS., Wei, D. et al. A sequential multiple change-point detection procedure via VIF regression. Comput Stat 31, 671–691 (2016). https://doi.org/10.1007/s00180-015-0587-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-015-0587-5