Investigating GQL-based inferential approaches for non-stationary BINAR(1) model under different quantum of over-dispersion with application

Abstract

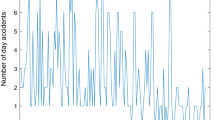
In particular, this paper addresses solutions to the computational challenges encountered in estimating parameters in non-stationary over-dispersed bivariate integer-valued autoregressive of order 1 (BINAR(1)) model with Negative Binomial (NB) innovations. In this BINAR(1) model, the cross-correlation is induced through the paired NB innovations which follows a recently introduced bivariate NB model under different over-dispersion indices. The estimation of the model parameters is conducted via a two-phased generalized quasi-likelihood (GQL) approach but the second GQLs auto-covariance structure constitutes of higher-order moment entries which are not readily available in closed form. In this context, two GQL approaches: GQL$_{MVN}$ based on approximating the higher-order covariances through the multivariate normality structure and GQL$_{BT}$ based on deriving the exact higher-order covariances by some novel high-dimensional thinning properties are proposed and compared. The asymptotic properties of the respective GQLs are derived. Monte-Carlo simulation experiments are implemented to investigate on the performance of the GQLs, the consistency and the asymptotic efficiency of the estimates. The proposed model and the estimation methodologies are applied to a real-life time series data in the Transport sector in Mauritius. The root mean square error based on some out-sample statistics are also computed to assess the reliability of the model.

Appendices

A

Proof of Lemma 1

$$\begin{aligned} Cov(Y_{t},R_{t})&=Cov(\alpha _{t}\circ Y_{t-1}+R_{t},R_{t}) \end{aligned}$$

(19)

$$\begin{aligned}&=Cov(\alpha _{t}\circ Y_{t-1},R_{t})+Cov(R_{t},R_{t})\nonumber \\&=Var(R_{t}) \end{aligned}$$

(20)

$$\begin{aligned} Cov(Y_{t},R_{u})&=Cov(\alpha _{t}\circ Y_{t-1}+R_{t},R_{u}) \end{aligned}$$

(21)

$$\begin{aligned}&=Cov(\alpha _{t}\circ Y_{t-1},R_{u})+Cov(R_{t},R_{u})\nonumber \\&=0 \end{aligned}$$

(22)

$\square$

Derivation of serial- and cross-covariances:

$$\begin{aligned} \text {Cov}\left( Y_{t}^{[k]},Y_{t+h}^{[k]}\right)&=\text {Cov}\left( Y_{t}^{[k]},\alpha _{k,t+h} \circ Y_{t+h-1}^{[k]}+R_{t+h}^{[k]}\right) \nonumber \\&=\rho _{k}\text {Cov}\left( Y_{t}^{[k]}, Y_{t+h-1}^{[k]})+\text {Cov}(Y_{t}^{[k]},R_{t+h}^{[k]}\right) \nonumber \\&= \rho _{k} Cov\left( Y_t^{[k]},Y_{t+h-1}^{[k]}\right) \nonumber \\&=\rho _{k}^{h}\text {Cov}\left( Y_{t}^{[k]}, Y_{t}^{[k]}\right) \nonumber \\&=\rho _{k}^{h}\mu _{t}^{[k]}\left( 1+c_{k}^{*}{\mu _{t}^{[k]}}\right) \end{aligned}$$

(23)

and hence the lag-h serial correlation is derived as

$$\begin{aligned} \text {Corr}\left( Y_{t}^{[k]},Y_{t+h}^{[k]}\right) =\rho _{k}^{h}\frac{\sqrt{\mu _{t}^{[k]}(1+c_{k}^{*}{\mu _{t}^{[k]}})}}{\sqrt{\mu _{t+h}^{[k]}(1+c_{k}^{*}{\mu _{t+h}^{[k]}})}}. \end{aligned}$$

(24)

Using the independency between the innovation terms $R_t^{[1]}$ and $R_t^{[2]}$ and the random variables $Y_{t-1}^{[1]}$, $Y_{t-1}^{[2]}$, $\alpha _{1,t}$, $\alpha _{2,t}$ and the counting sequences, we have that the cross-covariance between the two series is given by

$$\begin{aligned} \text {Cov}\left( Y^{[1]}_{t},Y^{[2]}_{t}\right)&=\text {Cov}\left( \alpha _{1,t}\circ Y_{t-1}^{[1]}+R^{[1]}_{t},\alpha _{2,t}\circ Y_{t-1}^{[2]}+R^{[2]}_{t}\right) \nonumber \\&=\text {Cov}\left( \alpha _{1,t}\circ Y_{t-1}^{[1]},\alpha _{2,t} \circ Y_{t-1}^{[2]}\right) +\text {Cov}\left( R^{[1]}_{t},R^{[2]}_{t}\right) \nonumber \\&=\rho _{1}\rho _{2}\text {Cov}\left( Y^{[1]}_{t-1},Y^{[2]}_{t-1}\right) +\text {Cov}\left( R^{[1]}_{t},R^{[2]}_{t}\right) \nonumber \\&=\rho _{1}\rho _{2}\text {Cov}\left( Y^{[1]}_{t-1},Y^{[2]}_{t-1}\right) +c_1^{} c_2^{} \nu \lambda _t^{[1]} \lambda _t^{[2]}. \end{aligned}$$

(25)

At the end of this section, we derive the covariances Cov$(Y_t^{[1]}, Y_{t+h}^{[2]})$ and Cov$(Y_t^{[2]}, Y_{t+h}^{[1]})$. The first one is derived as

$$\begin{aligned} \text {Cov}\left( Y^{[1]}_{t},Y^{[2]}_{t+h}\right)&=\text {Cov}\left( Y_{t}^{[1]},\alpha _{2,t}\circ Y_{t+h-1}^{[2]}+R_{t+h}^{[2]}\right) \nonumber \\&=\text {Cov}\left( Y_{t}^{[1]},\alpha _{2,t}\circ Y_{t+h-1}^{[2]}\right) +\text {Cov}\left( Y_{t}^{[1]},R_{t+h}^{[2]}\right) \nonumber \\&=\rho _{2}\text {Cov}\left( Y_{t}^{[1]},Y_{t+h-1}^{[2]}\right) \nonumber \\&=\rho _{2}^{h}\text {Cov}\left( Y^{[1]}_{t} Y^{[2]}_{t}\right) . \end{aligned}$$

(26)

Similarly, we obtain that

$$\begin{aligned} \text {Cov}\left( Y^{[1]}_{t+h},Y^{[2]}_{t}\right) =\rho _{1}^{h}\text {Cov}\left( Y^{[1]}_{t}, Y^{[2]}_{t}\right) . \end{aligned}$$

(27)

Proof of Lemma 3

• (a) For given $Y_{t-1}^{[1]}$ and $Y_{t-1}^{[2]}$, the product $W_{1,t}W_{2,t}$ is independent of the product $R_{t}^{[1]}R_{t}^{[2]}$, which implies that the corresponding covariance is 0.

• (b) For given $Y_{t-1}^{[1]}$ and $Y_{t-1}^{[2]}$, the random variables $W_{k,t}$ and $W_{j,t}$ are mutually independent random variables independent of the random variables $R_t^{[1]}$ and $R_t^{[2]}$. Using this and the property of the binomial thinning operator that $E(\alpha _{k,t}\circ Y_{t-1}^{[k]}|Y_{t-1}^{[k]})= \rho _{k} Y_{t-1}^{[k]}$, we have that

  $$\begin{aligned} Cov(W_{k,t}R_t^{[j]}, W_{j,t}R_t^{[k]}|Y_{t-1}^{[1]}, Y_{t-1}^{[2]})= & {} \prod _{i=1}^2 E(W_{i,t}| Y_{t-1}^{[i]}) Cov(R_t^{[1]},R_t^{[2]})\\= & {} \nu \prod _{i=1}^2 \rho _{i} c_i \lambda _t^{[i]} Y_{t-1}^{[i]}. \end{aligned}$$

• (c) The proof follows from the conditional independency of the random variables $W_{k,t}$ and $R_t^{[1]}$ and $R_t^{[2]}$ for given $Y_{t-1}^{[1]}$ and $Y_{t-1}^{[2]}$, and the fact that the covariance between the random variables $R_t^{[j]}$ and $R_t^{[1]} R_t^{[2]}$ is given by

  $$\begin{aligned} Cov(R_t^{[j]}, R_t^{[1]} R_t^{[2]}) = \lambda _t^{[1]} \lambda _t^{[2]} (1+\nu c_1 c_2 +c_j \lambda _t^{[j]} + \nu c_1 c_2 \lambda _t^{[j]} + 2 \nu c_j^2 c_k \lambda _t^{[j]}). \end{aligned}$$

• (d) From the conditional independency of the random variables $W_{1,t}$, $W_{2,t}$ and $R_t^{[j]}$ for given $Y_{t-1}^{[1]}$ and $Y_{t-1}^{[2]}$, we have first that

$$\begin{aligned} Cov\left( W_{k,t}R_t^{[j]}, W_{j,t}R_t^{[k]}|Y_{t-1}^{[1]}, Y_{t-1}^{[2]}\right)= & {} E\left( W_{j,t} | Y_{t-1}^{[j]}) E(R_t^{[j]}\right) Var\left( W_{k,t}|Y_{t-1}^{[k]}\right) \\= & {} \rho _{j} \lambda _t^{[j]} Y_{t-1}^{[j]} Var\left( W_{k,t}|Y_{t-1}^{[k]}\right) . \end{aligned}$$

To derive the conditional variance $Var(W_{k,t}|Y_{t-1}^{[k]})$, we first derive the conditional second order moment $E(W_{k,t}^2|Y_{t-1}^{[k]})$. We have that

$$\begin{aligned} E\left( W_{k,t}^2\big |Y_{t-1}^{[k]}\right)= & {} E\left( E\left( W_{k,t}^2\big |\alpha _{k,t},Y_{t-1}^{[k]}\right) \big | Y_{t-1}^{[k]}\right) \\= & {} E\left( \left( \alpha _{k,t}-\alpha _{k,t}^2\right) Y_{t-1}^{[k]}+\alpha _{k,t}^2 {Y_{t-1}^{[k]}}^2\big |Y_{t-1}^{[k]}\right) \\= & {} \frac{\rho _{k}(1-\rho _{k})}{1+c_k} Y_{t-1}^{[k]} + \frac{\rho _{k}(c_k + \rho _{k})}{1+c_k} {Y_{t-1}^{[k]}}^2. \end{aligned}$$

Using this result we obtain that the conditional variance is given by $Var(W_{k,t}|Y_{t-1}^{[k]}) = \frac{\rho _{k}(1-\rho _{k})}{1+c_k} Y_{t-1}^{[k]} (1+c_k Y_{t-1}^{[k]})$. Replacing this result in the above expression for the conditional covariance we prove this last statement. $\square$

Proof of Lemma 4

Proof

• (a) Using the results from the previous lemma we have that

  $$\begin{aligned}&Var\left( W_{k,t} R_t^{[j]}\big |Y_{t-1}^{[k]}\right) = E\left( W_{k,t}^2\big |Y_{t-1}^{[k]}\right) E\left( {R_t^{[j]}}^2\right) - \left( E(W_{k,t}\big |Y_{t-1}^{[k]}\right) E\left( {R_t^{[j]}})\right) ^2 \\&\quad = \lambda _t^{[j]} \left( 1+\lambda _t^{[j]} + c_j \lambda _t^{[j]}\right) \left[ \frac{\rho _{k}(1-\rho _{k})}{1+c_k} Y_{t-1}^{[k]} + \frac{\rho _{k}(c_k + \rho _{k})}{1+c_k} {Y_{t-1}^{[k]}}^2\right] \\&\qquad -\rho _{k}^2 {\lambda _t^{[j]}}^2 {Y_{t-1}^{[k]}}^2. \end{aligned}$$

• (b) This statement follows from the conditional independency of the random variables $W_{1,t}$ and $W_{2,t}$ for given $Y_{t-1}^{[1]}$ and $Y_{t-1}^{[2]}$.

• (c) Follows from the definition of the bivariate negative binomial distribution of Ng et al. (2010).

$\square$