A Bayesian approach to the analysis of asymmetric association for two-way contingency tables

Abstract

Recently, a subcopula-based asymmetric association measure was developed for the variables in two-way contingency tables. Here, we develop a fully Bayesian method to implement this measure, and examine its performance using simulation data and several real data sets of colorectal cancer. We use coverage probabilities and lengths of the interval estimators to compare the Bayesian approach and a large-sample method of analysis. In simulation studies, we find that the Bayesian method outperforms the large-sample method on average, and provides either similar or improved results for the real data analyses.

Appendix

1.1 1 Asymptotic distribution of the subcopula-based asymmetric association measures

The asymptotic distributions of the estimators for the subcopula-based asymmetric association measures provided in Eqs. (4) and (5) are developed in the following theorem.

Theorem 1

(Wei and Kim 2017) Let ${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}$ be the estimator for the asymmetric measure ${\rho }^{2}_{_{({X \rightarrow Y})}}$ defined in Eq. (4). Then,

$$\begin{aligned} \sqrt{n}\left( {\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}-\rho ^{2}_{_{({X \rightarrow Y})}}\right) \overset{D}{\rightarrow } N\left( 0,\nabla h_1({\varvec{p}})^{T}\left( diag({\varvec{p}})-{\varvec{p}} {\varvec{p}}^T\right) \, \nabla h_1({\varvec{p}})\right) , \end{aligned}$$

(17)

where ${\varvec{p}}\,=\,(p_{11}, p_{12},\ldots , {p}_{I(J-1)}, {p_{IJ}})^T$,

$\nabla h_1({\varvec{p}}) {=} \begin{bmatrix} \frac{\partial {{\rho }^{2}_{_{({X \rightarrow Y})}}}}{\partial p_{11}} , \frac{\partial {{\rho }^{2}_{_{({X \rightarrow Y})}}}}{\partial p_{12}} , \,\ldots \, ,\frac{\partial {{\rho }^{2}_{_{({X \rightarrow Y})}}}}{\partial p_{IJ}} \end{bmatrix}^{T}$, and $\frac{\partial {\rho }^{2}_{_{({X \rightarrow Y})}}}{\partial p_{st}}$ is given in Eq. (A.4)–(A.8) in Wei and Kim (2017), for $s=1,\ldots ,I,$ and $t=1,\ldots ,J$. Let $\nabla h_2({\varvec{p}}) = \begin{bmatrix} \frac{\partial {{\rho }^{2}_{_{({Y \rightarrow X})}}}}{\partial p_{11}} , \frac{\partial {{\rho }^{2}_{_{({Y \rightarrow X})}}}}{\partial p_{12}} , \,\ldots \, ,\frac{\partial {{\rho }^{2}_{_{({Y \rightarrow X})}}}}{\partial p_{IJ}} \end{bmatrix}^{T}$, and $\frac{\partial {\rho }^{2}_{_{({Y \rightarrow X})}}}{\partial p_{st}}$ is given in Eq. (A.9)–(A.14) in Wei and Kim (2017). Then, the asymptotic distribution of ${\hat{\rho }}^{2}_{_{({Y \rightarrow X})}}$ can be obtained by substituting $\nabla h_2({\varvec{p}})$ for $\nabla h_1({\varvec{p}})$ in Equation (17).

Based on Theorem 1, the following corollary is derived for the asymptotic distribution of the difference between the estimators of the asymmetric measures, (${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}-{\hat{\rho }}^{2}_{_{({Y \rightarrow X})}}$):

Corollary 1

Let ${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}$ and ${\hat{\rho }}^{2}_{_{({Y \rightarrow X})}}$ be the estimators for the asymmetric measures ${\rho }^{2}_{_{({X \rightarrow Y})}}$ and ${\rho }^{2}_{_{({Y \rightarrow X})}}$ defined in Eq. (4) and (5). Then,

$$\begin{aligned}&\sqrt{n}\left( ({\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}-{\hat{\rho }}^{2}_ {_{({Y \rightarrow X})}})-(\rho ^{2}_{_{({X \rightarrow Y})}}-\rho ^{2}_{_{({Y \rightarrow X})}})\right) \overset{D}{\rightarrow }\nonumber \\&\quad N\left( 0, (\nabla h_1({\varvec{p}})-\nabla h_2({\varvec{p}}))^{T}\left( diag({\varvec{p}})-{\varvec{p}} {\varvec{p}}^T\right) \, (\nabla h_1({\varvec{p}})-\nabla h_2({\varvec{p}}))\right) ,\qquad \end{aligned}$$

(18)

where ${\varvec{p}}$, $\nabla h_1({\varvec{p}})$, and $\nabla h_2({\varvec{p}})$ are given in Theorem 1.

From the Theorem 1 and Corollary 1, the large-sample confidence intervals for $\rho ^{2}_{_{({X \rightarrow Y})}}$, $\rho ^{2}_{_{({Y \rightarrow X})}}$, and ($\rho ^{2}_{_{({X \rightarrow Y})}} - \rho ^{2}_{_{({Y \rightarrow X})}}$) can be obtained.

Fig. 3

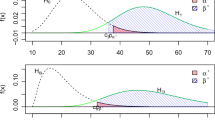
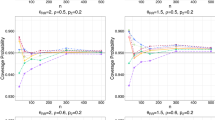
$\hat{p}_{_{BCI}}$(square), $\hat{p}_{_{HPD}}$(dot), $\hat{p}_{_{WKI}}$(triangle) and the associated $95\%$ confidence intervals for $\hat{p}_{_{BCI}}$(dotted lines), $\hat{p}_{_{HPD}}$(solid lines) and $\hat{p}_{_{WKI}}$(dashed lines) for $3\times 2$ table (top panel), $2\times 3$ table (middle panel), and $3\times 3$ table (bottom panel), with $\sigma ^2=0.1$ and sample size $n=200$, 400, 800, and 1600 under weak, moderate and strong association

Fig. 4

$\hat{p}_{_{BCI}}$(square), $\hat{p}_{_{HPD}}$(dot), $\hat{p}_{_{WKI}}$(triangle) and the associated $95\%$ confidence intervals for $\hat{p}_{_{BCI}}$(dotted lines), $\hat{p}_{_{HPD}}$(solid lines) and $\hat{p}_{_{WKI}}$(dashed lines) for $3\times 2$ table (top panel), $2\times 3$ table (middle panel), and $3\times 3$ table (bottom panel), with $\sigma ^2=10^6$ and sample size $n=200$, 400, 800, and 1600 under weak, moderate and strong association

1.2 2 Sensitivity analysis results

The following are figures for the results of the sensitivity analysis in Sect. 4.2 (see Figs. 3 and 4).

1.3 3 Diagnostic Plots

Here, we provide history plots, autocorrelation function and partial autocorrelation function plots for select parameters in both the simulation studies and real data studies (Figs. 5, 6, 7). See Sect. 3.4 for details. Plots for additional parameters are provided in Section S2 of the Supplementary Material.

Fig. 5

History plots for select parameters of simulation studies and real data analysis. a–c is for simulation data and $\sigma ^2 = 1$: a ${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}$ for n=200, $3\times 2$ table, weak association. b ${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}$ for n=400, $2\times 3$ table, moderate association. c ${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}$ for n=1600, $3\times 3$ table, strong association. d–f is for real data: d ${\hat{\rho }}^2_{({\text {CIMP}} \rightarrow {\text {BRAF}})}$. e ${\hat{\rho }}^2_{({\text {KRAS}} \rightarrow {\text {CIMP}})}$. f ${\hat{\rho }}^2_{(p53 \rightarrow {\text {CIMP}})}$

Fig. 6

Autocorrelation Plots and Partial Autocorrelation Plots for select parameters of the simulation studies. a ${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}$ for n=200, $3\times 2$ table, weak association. b ${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}$ for n=400, $2\times 3$ table, moderate association. c ${\hat{\rho }}^{2}_{_{({X \rightarrow Y})}}$ for n=1600, $3\times 3$ table, strong association

Fig. 7

Autocorrelation Plots and Partial Autocorrelation Plots for select parameters of the real data analysis. a ${\hat{\rho }}^2_{({\text {CIMP}} \rightarrow {\text {BRAF}})}$. b ${\hat{\rho }}^2_{({\text {KRAS}} \rightarrow {\text {CIMP}})}$. c ${\hat{\rho }}^2_{(p53 \rightarrow {\text {CIMP}})}$