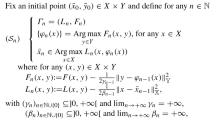Nonconvergence to saddle boundary points under perturbed reinforcement learning

Abstract

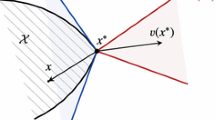
For several reinforcement learning models in strategic-form games, convergence to action profiles that are not Nash equilibria may occur with positive probability under certain conditions on the payoff function. In this paper, we explore how an alternative reinforcement learning model, where the strategy of each agent is perturbed by a strategy-dependent perturbation (or mutations) function, may exclude convergence to non-Nash pure strategy profiles. This approach extends prior analysis on reinforcement learning in games that addresses the issue of convergence to saddle boundary points. It further provides a framework under which the effect of mutations can be analyzed in the context of reinforcement learning.

Appendices

Appendix 1: Proof of proposition 2

We first define the canonical path space $\varOmega$ generated by the reinforcement learning process, as discussed in the beginning of Sect. 5. We denote $\mathbb {P}$ the probability operator and we implicitly assume that computation of probabilities is performed in an appropriately generated $\sigma$-algebra.

Let us assume that action profile $\alpha =(\alpha _1,\ldots \alpha _n)\in \mathcal {A}$ has been selected at time $k=0$. This implies that $x_{i\alpha _i}(0)>0$, since actions are selected according to the strategy distribution $\sigma _i(0)=x_i(0)$. The corresponding payoff profile will be $R(\alpha )=(R_1(\alpha ),\ldots ,R_n(\alpha ))$, where according to Assumption 1, $R_i(\alpha )>0$ for all $i\in \mathcal {I}$. Let us define the following event:

$$\begin{aligned} A_\tau \triangleq \left\{ \omega \in \varOmega : \psi _k(\omega ) \triangleq \alpha (k) = \alpha \text{ for } \text{ all } k \le \tau \right\} , \end{aligned}$$

$\tau = 1,2,\ldots$. Thus, $A_\tau$ corresponds to the case where the same action profile has been performed for all times $k\le \tau$. Note that the sequence of events $\{A_\tau \}$ is decreasing, since $A_\tau \supseteq A_{\tau +1}$ for all $\tau =1,2,\ldots$. Define also the event

$$\begin{aligned} A_\infty \triangleq \bigcap _{\tau =1}^{\infty }A_\tau \equiv \{\alpha (\tau )=\alpha ,\forall \tau \}. \end{aligned}$$

Therefore, from continuity from above, we have:

$$\begin{aligned} \mathbb {P}[A_\infty ] = \lim _{\tau \rightarrow \infty }\mathbb {P}[A_\tau ] = \lim _{\tau \rightarrow \infty } \prod _{k=1}^\tau \prod _{i\in \mathcal {I}}x_{i\alpha _i}(k) \triangleq \chi (\alpha ). \end{aligned}$$

The above upper bound $\chi (\alpha )$ is non-zero if and only if

$$\begin{aligned} \sum _{k=1}^{\infty }\log (x_{i\alpha _i}(k))> -\infty \text{ for } \text{ each } i\in \mathcal {I}. \end{aligned}$$

(25)

Let us define the new variable $y_i(k)\triangleq 1-x_{i\alpha _i}(k) = \sum _{j\in \mathcal {A}_i\backslash {\alpha _i}}x_{ij}(k),$ which corresponds to the probability of agent $i$ selecting any action other than $\alpha _i$. Condition (25) is equivalent to

$$\begin{aligned} -\sum _{k=0}^{\infty }\log (1-y_i(k)) < \infty , \quad \text{ for } \text{ each } i\in \mathcal {I}. \end{aligned}$$

(26)

We also have that

$$\begin{aligned} \lim _{k\rightarrow \infty }\frac{-\log (1-y_i(k))}{y_i(k)} = \lim _{k\rightarrow \infty }\frac{1}{1-y_i(k)} > \rho \end{aligned}$$

for some finite $\rho >0$, since $0\le y_i(k) \le 1$. Thus, from the limit comparison test, we conclude that condition (26) holds, if and only if $\sum _{k=1}^{\infty }y_i(k) < \infty ,$ for each $i\in \mathcal {I}.$ Since $\epsilon (k)=1/(k^\nu +1)$, for $1/2<\nu \le {1}$, we have:

$$\begin{aligned} \frac{y_i(k+1)}{y_i(k)} = 1 - \frac{R_i(\alpha )}{k^\nu +1} \le 1 - \frac{R_i(\alpha )}{k+1}. \end{aligned}$$

By Raabe’s criterion, the series $\sum _{k=0}^{\infty }y_i(k)$ is convergent if

$$\begin{aligned} \lim _{k\rightarrow \infty }k\left( \frac{y_i(k)}{y_i(k+1)}-1\right) >1. \end{aligned}$$

Since

$$\begin{aligned} k\left( \frac{y_i(k)}{y_i(k+1)}-1\right) \ge k\left( \frac{1}{1-\frac{R_i(\alpha )}{k+1}}-1\right) = k\frac{R_i(\alpha )}{k+1-R_i(\alpha )} = \frac{R_i(\alpha )}{1+\frac{1-R_i(\alpha )}{k}} \end{aligned}$$

we conclude that the series $\sum _{k=0}^{\infty }y_i(k)$ is convergent if $R_i(\alpha )>1$ for each $i\in \mathcal {I}$. In other words, the action profile $\alpha$ will be performed for all future times with positive probability if $R_i(\alpha )>1$ for all $i\in \mathcal {I}$. Furthermore, if $R_i(\alpha )>1$ for all $i\in \mathcal {I}$ and for all $\alpha \in \mathcal {A}$, then the probability that the same action profile will be played for all future times is uniformly bounded away from zero over all initial conditions.

Appendix 2: Proof of proposition 2

For any agent $i\in \mathcal {I}$ and any action $s\in \mathcal {A}_i$, the corresponding entry of the vector field of ODE (16), evaluated at strategy $\tilde{x}$, is

$$\begin{aligned} \overline{g}_{is}^{\lambda }(\tilde{x}) = U_{is}(\tilde{x})[(1-\zeta _i)\tilde{x}_{is}+\zeta _i/\left| \mathcal {A}_i \right| ] - \sum _{q\in \mathcal {A}_i}U_{iq}(\tilde{x})[(1-\zeta _i)\tilde{x}_{iq}+ \zeta _i/\left| \mathcal {A}_i \right| ]\tilde{x}_{is},\nonumber \\ \end{aligned}$$

(27)

where $\zeta _i=\zeta _i(\tilde{x}_i,\lambda )$. Consider any pure strategy profile $x^{*}$, and take $\tilde{x}=x^{*} + {\nu }$, for some $\nu =(\nu _1,\nu _2,\ldots ,\nu _n)\in \mathbb {R}^{\left| \mathcal {A}_1 \right| }\times \ldots \times \mathbb {R}^{\left| \mathcal {A}_n \right| }$ such that $\nu _i\in \mathrm{null}\{\mathbf {1}^{\mathrm T}\}$ and $\tilde{x}_i=x^*_i+\nu _i \in \varDelta (\left| \mathcal {A}_i \right| )$ for all $i\in \mathcal {I}$. Substituting $\tilde{x}$ into (27), yields

$$\begin{aligned}&\overline{g}_{is}^{\lambda }(\nu ,\lambda ) = U_{is}(\tilde{x})\left[ (1-\zeta _i)(x_{is}^*+ \nu _{is}) + \zeta _i/\left| \mathcal {A}_i \right| \right] \\&\quad - \sum _{q\in \mathcal {A}_i}U_{iq}(\tilde{x})\left[ (1-\zeta _i)(x_{iq}^*+ \nu _{iq})+ \zeta _i/\left| \mathcal {A}_i \right| \right] (x_{is}^*+ \nu _{is}). \end{aligned}$$

where $\zeta _i=\zeta _i(x_i^*+\nu _i,\lambda )$.

Due to property (4) of Assumption 2, the perturbation function satisfies

$$\begin{aligned} \left. \frac{\partial {\zeta _i(\nu _i,\lambda )}}{\partial {\nu _{ij}}}\right| _{(0,0)} = 0, \quad \text{ for } \text{ all } j\in \mathcal {A}_i. \end{aligned}$$

Furthermore, $\overline{g}_{is}^{\lambda }(0,0)=0$, since $x^*$ is a stationary point of the unperturbed dynamics. Thus, the partial derivatives of $\overline{g}_{is}^{\lambda }$ evaluated at $(0,0)$ are:

$$\begin{aligned} \left. \frac{\partial {\overline{g}_{is}^{\lambda }(\nu ,\lambda )}}{\partial {\nu _{is}}}\right| _{(0,0)} = U_{is}({x}^*)(1-x_{is}^*) - \sum _{q\in \mathcal {A}_i}U_{iq}({x}^*)x_{iq}^*, \\ \left. \frac{\partial {\overline{g}_{is}^{\lambda }(\nu ,\lambda )}}{\partial {\nu _{iq}}}\right| _{(0,0)} = -U_{iq}({x}^*)x_{is}^*, \quad \text{ for } \text{ all } q\in \mathcal {A}_i\backslash {s}. \end{aligned}$$

Note also that for any $\ell \in \mathcal {I}\backslash {i}$ and $m\in \mathcal {A}_{\ell }$, we have

$$\begin{aligned} \left. \frac{\partial {\overline{g}_{is}^{\lambda }(\nu ,\lambda )}}{\partial {\nu _{\ell m}}}\right| _{(0,0)} = \left. \frac{\partial U_{is}(\tilde{x})}{\partial {\nu _{\ell m}}}\right| _{(0,0)}x_{is}^* - \sum _{q\in \mathcal {A}_i} \left. \frac{\partial U_{iq}(\tilde{x})}{\partial {\nu _{\ell m}}}\right| _{(0,0)}x_{iq}^*x_{is}^*. \end{aligned}$$

Since $x^*$ corresponds to a pure strategy state, for each $i\in \mathcal {I}$ there exists $j^*=j^*(i)$ such that $x_i^*=e_{j^*}$, i.e., $x_{ij^*}=1$ and $x_{is}^*=0$ for all $s\ne j^*$. For this pure strategy state and for any $s\in \mathcal {A}_i\backslash {j^*}$ we have

$$\begin{aligned} \left. \frac{\partial {\overline{g}_{is}^{\lambda }(\nu ,\lambda )}}{\partial {\nu _{is}}}\right| _{(0,0)} = U_{is}(x^*) - U_{ij^*}(x^*), \end{aligned}$$

and

$$\begin{aligned} \left. \frac{\partial {\overline{g}_{is}^{\lambda }(\nu ,\lambda )}}{\partial {\nu _{iq}}}\right| _{(0,0)} = 0 \quad \forall q\in \mathcal {A}_i\backslash {s}, \quad \left. \frac{\partial {\overline{g}_{is}^{\lambda }(\nu ,\lambda )}}{\partial {\nu _{\ell m}}}\right| _{(0,0)} = 0 \quad \forall \ell \in \mathcal {I}\backslash {i}, m\in \mathcal {A}_{\ell }. \end{aligned}$$

Given that $\nu _i\in \mathrm{null}\{\mathbf {1}^{\mathrm T}\}$ and $\partial {\overline{g}_{is}^{\lambda }(\nu ,\lambda )}/\partial {\nu _{ij^*}}=0$ for all $s\ne j^*$, the behavior of $\overline{g}^{\lambda }(\cdot ,\cdot )$ with respect to $\nu$ about the point $(0,0)$ is described by the following Jacobian matrix:

$$\begin{aligned}&\left. \nabla _{\nu }\overline{g}^{\lambda }(\nu ,\lambda )\right| _{(0,0)} = \\&\left( \begin{array} {ccc} \hbox {diag}\left\{ U_{1s}(x^*)-U_{1j^*}(x^*)\right\} _{s\ne j^*} &{} &{} 0 \\ &{} \ddots &{} \\ 0 &{} &{} \hbox {diag}\left\{ U_{ns}(x^*)-U_{nj^*}(x^*)\right\} _{s\ne j^*} \end{array}\right) . \end{aligned}$$

The above Jacobian matrix has full rank if for each $i\in \mathcal {I}$

$$\begin{aligned} U_{is}(x^*)-U_{ij^*}(x^*)\ne {0} \quad \text{ for } \text{ all } s\ne j^*. \end{aligned}$$

In this case, by the implicit function theorem, there exists a neighborhood $D$ of $\lambda =0$ and a unique differentiable function $\nu ^*:D\rightarrow \mathbb {R}^{\left| \mathcal {A} \right| }$ such that $\nu ^*(0)=0$ and $\overline{g}^{\lambda }(\nu ^*(\lambda ),\lambda )=0,$ for any $\lambda \in {D}$.

To characterize exactly the stationary points for small values of $\lambda$, we need to also compute the gradient of the mean-field with respect to the perturbation parameter $\lambda$. Note that:

$$\begin{aligned} \left. \frac{\partial {\overline{g}_{is}^{\lambda }(\nu ,\lambda )}}{\partial {\lambda }} \right| _{(0,0)} = \frac{U_{is}(\tilde{x})}{\left| \mathcal {A}_i \right| }\left. \frac{\partial {\zeta _i}}{\partial {\lambda }}\right| _{(0,0)} =\frac{U_{is}(\tilde{x})}{\left| \mathcal {A}_i \right| }, \end{aligned}$$

since the partial derivative of $\zeta _i$ with respect to $\lambda$ when evaluated at $(0,0)$ is 1. Thus,

$$\begin{aligned} \left. \nabla _{\lambda }\overline{g}^{\lambda }(\nu ,\lambda )\right| _{(0,0)} = \left( \begin{array} {c} \hbox {col}\left\{ U_{1s}(x^*)/{\left| \mathcal {A}_1 \right| }\right\} _{s\ne j^*} \\ \vdots \\ \hbox {col}\left\{ U_{ns}(x^*)/{\left| \mathcal {A}_n \right| }\right\} _{s\ne j^*} \end{array}\right) . \end{aligned}$$

Again, by implicit function theorem, we have that

$$\begin{aligned} \nabla _{\lambda }\nu ^*(\lambda )|_{\lambda =0}=- \left( \nabla _{\nu }{\overline{g}}^{\lambda }(\nu ,\lambda )|_{(0,0)}\right) ^{-1} \nabla _{\lambda }\overline{g}^{\lambda }(\nu ,\lambda )|_{(0,0)} \end{aligned}$$

which implies that for any $i\in \mathcal {I}$ and for any $s\ne j^*$

$$\begin{aligned} \left. \frac{d\nu _{is}^*(\lambda )}{d\lambda }\right| _{\lambda =0} = -\frac{1}{(U_{is}(x^*)-U_{ij^*}(x^*))}. \end{aligned}$$

Since $\nu _{is}^*(0)=0$ and $x_{is}^*=0$, in order for the solution $\tilde{x}=x^*+\nu ^*(\lambda )$ to be in $\varvec{\Delta }^o$, we also need the condition $d\nu _{is}^*(\lambda )/d\lambda |_{\lambda =0}>0$ to be satisfied for all $s\ne j^*$. Since $U_{is}(x^*)>0$ by Assumption 1, this condition is equivalent to

$$\begin{aligned} U_{is}(x^*)-U_{ij^*}(x^*)<0 \end{aligned}$$

for all $i\in \mathcal {I}$ and any $s\ne j^*$. This is also equivalent to $x^*$ being a strict Nash equilibrium. Thus, the conclusion follows.

If $x^*$ corresponds to an action profile which is not a Nash equilibrium, then there exist $i\in \mathcal {I}$ and $s\ne j^*$ such that $U_{is}(x^*)-U_{ij^*}(x^*)>{0}$. For any $\beta \in (0,1)$ which is sufficiently close to one, there exist $\delta _0=\delta _0(\beta )$ such that $\zeta _i(x_i,\lambda )\equiv {0}$, $i\in \mathcal {I}$, for any $x\in \varvec{\Delta }\backslash \mathcal {B}_{\delta }(x^*)$, $\lambda >0$ and $\delta \ge \delta _0$. For any $x\in \mathcal {B}_{\delta }(x^*)$, $\delta \ge \delta _0$, the vector field becomes

$$\begin{aligned} \overline{g}_{is}^{\lambda }(x) \approx [U_{is}(x)-U_{ij^*}(x)]x_{is} + U_{is}(x)\zeta _i(x_i,\lambda )/\left| \mathcal {A}_i \right| \end{aligned}$$

(28)

plus higher order terms of $\lambda$ and $\delta$, for all $s\ne j^*$. Since the Nash condition is violated in the direction of $s$, $U_{is}(x)-U_{ij^*}(x)=c+O(\delta )$, for some $c>{0}$, where $O(\delta )$ denotes a quantity of order of $\delta$. Furthermore, by Assumption 1 of strictly positive rewards, $U_{is}(x)>0$ for all $s\in \mathcal {A}_i$ and $x\in \mathcal {B}_{\delta }(x^*)$. Therefore, for any $\delta \ge \delta _0$ and for sufficiently small $\lambda >0$, the vector field $\overline{g}_{is}^{\lambda }(x)>0$ for any $x\in \mathcal {B}_{\delta }(x^*)$, which implies that there is no stationary point of the vector field in $\mathcal {B}_{\delta }(x^*)$.