Skip to main content
SpringerLink
Log in

Error reduction of the adaptive conforming and nonconforming finite element methods with red–green refinement

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

In this paper, we analyze the convergence of the adaptive conforming and nonconforming \(P_1\) finite element methods with red–green refinement based on standard Dörfler marking strategy. Since the mesh after refining is not nested into the one before, the usual Galerkin-orthogonality or quasi-orthogonality for newest vertex bisection does not hold for this case. To overcome such a difficulty, we develop some new quasi-orthogonality instead under certain condition on the initial mesh (Condition A). Consequently, we show convergence of the adaptive methods by establishing the reduction of some total errors. To weaken the condition on the initial mesh, we propose a modified red–green refinement and prove the convergence of the associated adaptive methods under a much weaker condition on the initial mesh (Condition B). Furthermore, we also develop an initial mesh generator which guarantee that all the interior triangles are equilateral triangles (satisfy Condition A) and the other triangles containing at least one vertex on the boundary satisfy Condition B.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

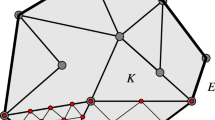
  1. We give up the symbol \(\nabla _h\) which was used in the previous literature (\(h\) seems corresponding to the current mesh \(\mathcal{T }_h\)). Because, for non-nested red–green refinement, there will be some triangles in our proofs which neither belongs to the current mesh \(\mathcal{T }_h\) nor the previous mesh \(\mathcal{T }_H\). This means the meaning of \(\nabla _h u_H\) will be puzzling. For example, see the four triangles in the parallelogram \(\overline{A_1A_2A_4A_6}\) in Fig.  4. Therefore, herein we use another symbol \(\tilde{\nabla }\) to stand for piecewise gradient.

  2. Since two level meshes are not nested. Some quantities like \(\tilde{\nabla } v|_T\) or \(\tilde{\nabla } v|_E\) in the proof of Lemmas and 5.3 may be piecewise constant on some triangle \(T\) or edge \(E\). Hence we define the edge jump for general piecewise linear functions not merely on nonconforming \(P_1\) functions. However there is no confusion since the edge jump is well-defined.

  3. The “PLTMG” package after the version 8.0 has changed data structures to use the longest-edge bisection while the previous versions is based on the red–green refinement.

References

  1. Ainsworth, M., Oden, J.T.: A posteriori error estimation in finite element analysis. In: Pure and Applied Mathematics. Wiley, New York (2000)

    Book  Google Scholar 

  2. Babuska, I., Rheinboldt, W.C.: Error estimates for adaptive finite element computations. SIAM J. Numer. Anal. 15, 736–754 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  3. Baker, B.S., Grosse, E., Rafferty, C.S.: Nonobtuse triangulation of polygons. Discrete Comput. Geom. 3(2), 147–168 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bank, R.E., Sherman, A.H., Weiser, A.: Refinement algorithms and data structures for regular Local mesh refinement, scientific computing. In: Stepleman, R.S. (ed.) Applications of Mathematics and Computing to the Physical Sciences, pp. 3–17. North-Holland, Amsterdam (1983)

  5. Bank, R.E.: The efficient implementation of local mesh refinement algorithms. In: Babuska, I., Chandra, J., Flaherty, J.E. (eds.) Adaptive Computational Methods for Partial Differential Equations. SIAM, Philadelphia (1983)

    Google Scholar 

  6. Becker, R., Mao, S., Shi, Z.C.: A convergent nonconforming adaptive finite element method with quasi-optimal complexity. SIAM J. Numer. Anal. 47(6), 4639–4659 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bern, M., Eppstein, D., Gilbert, J.: Provably good mesh generation. J. Comput. Syst. Sci. 48(3), 384–409 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  8. Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, 2nd edn. Springer, Berlin (2002)

    Book  MATH  Google Scholar 

  9. Carstensen, C., Hu, J.: A unifying theory of a posteriori error control for nonconforming finite element methods. Numer. Math. 107, 473–502 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Carstensen, C., Hoppe, R.H.W.: Convergence analysis of an adaptive nonconforming finite element methods. Numer. Math. 103, 251–266 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. Cascon, J.M., Kreuzer, Ch., Nochetto, R.H., Siebert, K.G.: Quasi-optimal convergence rate for an adaptive finite element method. SIAM J. Numer. Anal. 46, 2524–2550 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cervenka, J.: URL: http://www.iue.tuwien.ac.at/phd/cervenka/node14.html

  13. Ciarlet, P.G.: The Finite Element method for Elliptic Problems. North-Holland, Amsterdam (1978)

    MATH  Google Scholar 

  14. Crouzeix, M., Raviart, P.A.: Conforming and nonconforming finite element methods for solving the stationary Stokes equations. RAIRO Anal. Numer. 7, 33–76 (1973)

    MathSciNet  Google Scholar 

  15. Dari, E., Durén, R.G., Padra, C., Vampa, V.: A posteriori error estimators for nonconforming finite element methods. RAIRO Modél. Math. Anal. Numér. 30, 385–400 (1996)

    MATH  Google Scholar 

  16. Dörfler, W.: A convergent adaptive algorithm for Poisson’s equation. SIAM J. Numer. Anal 33, 1106–1124 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  17. Du, Q., Faber, V., Gunzburger, M.: Centroidal Voronoi tessellations: applications and algorithms. SIAM Rev. 41, 637–676 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  18. Du, Q., Wang, D.: Recent progress in robust and quality Delaunay mesh generation. J. Comput. Appl. Math. 195, 8–23 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  19. Fleischmann P.: URL: http://www.iue.tuwien.ac.at/phd/fleischmann/node23.html

  20. Hu, J., Shi, Z.C., Xu, J.C.: Convergence and optimality of the adaptive Morley element method. Numer. Math 121, 731–752 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  21. Leitner, E., Selberherr, S.: Three-dimensional grid adaptation using a mixed-element decomposition method. In: Ryssel, H., Pichler, P. (eds.) Simulation of Semiconductor Devices and Processes, vol. 6, pp. 464–467. Wien, Austria (1995)

    Chapter  Google Scholar 

  22. Mao, S.P., Zhao, X.Y., Shi, Z.C.: Convergence of a standard adaptive nonconforming finite element method with optimal complexity. Appl. Numer. Math. 60, 673–688 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  23. Mekchay, K., Nochetto, R.H.: Convergence of adaptive finite element methods for general second order linear elliptic PDE. SIAM J. Numer. Anal. 43, 1803–1827 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  24. Molino, N., Bridson, R., Teran, J., Fedkiw, R.: A crystalline, red green strategy for meshing highly deformable objects with tetrahedra. In: 12th International Meshing Roundtable, Sandia National Laboratories, pp. 103–114 (2003)

  25. Morin, P., Nochetto, R.H., Siebert, K.G.: Data oscillation and convergence of adaptive FEM. SIAM J. Numer. Anal. 38, 466–488 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  26. Morin, P., Nochetto, R.H., Siebert, K.G.: Convergence of adaptive finite element methods. SIAM Rev. 44, 631–658 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  27. Stevenson, R.: Optimality of a standard adaptive finite element method. Foundat. Comput. Math. 7(2), 245–269 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  28. Stevenson, R.: The completion of locally refined simplicial partitions created by bisection. Department of Mathematics, Utrecht University, Tech. Report (2006)

  29. Taakili, A., Becker, R.: URL: http://web.univ-pau.fr/becker/ConchaBase/ConchaBasePool/RedGreen/

  30. Verfürth, R.: A review of a posteriori error estimation and adaptive mesh-refinement techniques. Wiley-Teubner, Chichester (1996)

  31. Zhao, X.Y., Hu, J., Shi, Z.C.: Convergence analysis of the adaptive finite element method with the red-green refinement. Sci. China Math. 53, 499–512 (2010)

    Article  MathSciNet  Google Scholar 

  32. Zhao, X.Y., Mao, S.P., Shi, Z.C.: Adaptive Finite Element Methods on quadrilateral meshes without hanging nodes. SIAM J. Sci. Comput. 32, 2099–2120 (2010)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors are very thankful to Professor Qiang Du who made many valuable discussions in Algorithm 5, and to the Department of Mathematics, Pennsylvania State University for the hospitality during the second-named author’s visit, and also to the anonymous referees who made many valuable comments and corrections of the English and typesetting mistakes.

Author information

Authors and Affiliations

  1. LSEC, Institute of Computational Mathematics and Scientific/Engineering Computing, NCMIS, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, People’s Republic of China

    Zhongci Shi & Xuying Zhao

  2. Beijing Computational Science Research Center, Beijing, 100084, People’s Republic of China

    Xuying Zhao

Authors
  1. Zhongci Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xuying Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xuying Zhao.

Additional information

Supported by the National Center for Mathematics and Interdisciplinary Sciences, CAS. The second-named author was supported by the National Nature Science Foundation of China under Grant 11201462, and China Postdoctoral Science Foundation under Grant 20110490279.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shi, Z., Zhao, X. Error reduction of the adaptive conforming and nonconforming finite element methods with red–green refinement. Numer. Math. 123, 553–584 (2013). https://doi.org/10.1007/s00211-012-0495-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-012-0495-3

Mathematics Subject Classification

Search

Navigation