Precise and fast computation of Jacobian elliptic functions by conditional duplication

Abstract

We developed a new method to compute the cosine amplitude function, $c\equiv \mathrm{cn}(u|m)$, by using its double argument formula. The accumulation of round-off errors is effectively suppressed by the introduction of a complementary variable, $b\equiv 1-c$, and a conditional switch between the duplication of $b$ and $c$. The sine and delta amplitude functions, $s \equiv \mathrm{sn}(u|m)$ and $d \equiv \mathrm{dn}(u|m)$, are evaluated from thus computed $b$ or $c$ by means of their identity relations. The new method is sufficiently precise as its errors are less than a few machine epsilons. Also, it is significantly faster than the existing procedures. In case of single precision computation, it runs more than 50 times faster than Bulirsch’s sncndn based on the Gauss transformation and 2.7 times faster than our previous method based on the simultaneous duplication of $s,c$ and $d$. The ratios change to 7.6 and 3.5 respectively in case of the double precision environment.

Appendices

Appendix

A Background of new method

1.1 A.1 Reason to choose cosine amplitude function as base

The identity relations among the three Jacobian elliptic functions are written as

$$\begin{aligned} s^2+c^2=m s^2+d^2=1, \end{aligned}$$

(26)

as shown in the formula 121.00 of [4]. In principle, any of three or its variation can be a base to compute all three simultaneously. However, we selected $c$ among several possibilities because of the following reasons.

First, the computation of $s$ and $c$ from $d$ given as

$$\begin{aligned} s=\sqrt{{\frac{1-d^2}{m}}},\quad c=\sqrt{{\frac{m_c-d^2}{m}}}. \end{aligned}$$

(27)

faces a significant loss of information when $m$ is small. Meanwhile, that of $c$ and $d$ from $s$ and that of $s$ and $d$ from $c$ experience no such loss. Thus, we did not adopt this choice.

Second, the above loss of information is avoided if we introduce a new variable defined as

$$\begin{aligned} e \equiv {\frac{1-d}{m}}. \end{aligned}$$

(28)

In fact, $s,c$, and $d$ are computed from $e$ as

$$\begin{aligned} s=\sqrt{e (2+me)},\quad c=\sqrt{1-e(2+me)},\quad d=1+me. \end{aligned}$$

(29)

We did not take this option since the above computation of $c$ from $e$ suffers a difficult cancellation problem when $e$ is large.

Third, the duplication of $s$ by using itself requires a square root operation as

$$\begin{aligned} s_{n+1}={\frac{s_n \sqrt{(1-y_n)(1-m y_n)}}{1-m y_n^2}}, \end{aligned}$$

(30)

where $y_n \equiv s_n^2$. Refer to the second part of the formula 124.02 of [4]. This is a disadvantage in terms of the computational speed when noting the fact that the similar duplications of $c$ and $d$ require no square root operations. Then, we did not select this alternative.

Finally, the inconvenience caused by the above direct duplication of $s$ can be avoided by choosing $y$ as a base variable as

$$\begin{aligned} y_{n+1}={\frac{y_n(1-y_n)(1-m y_n)}{(1-m y_n^2)^2}}. \end{aligned}$$

(31)

The resulting formulation is almost the same as we presented in the main text. However, it requires one more square root operation than the new method in the final computation of function values from $y$. Therefore, we did not adopt this way.

1.2 A.2 Maclaurin series of complementary variable

When the argument $u$ is sufficiently small, we evaluate $b$ by its Maclaurin series,

$$\begin{aligned} b={\frac{u^2}{2}}\left(1+2\sum _{\ell =1}^{\infty }{\frac{b_\ell (m)(-u^2)^\ell }{(2\ell +2)!}}\right), \end{aligned}$$

(32)

where $b_{\ell } (m)$ is an $\ell$-th order polynomial of $m$ with integer coefficients. The first three of them are given in the formula 907.02 of [4] as

$$\begin{aligned} b_1 (m)\!=\!1+4m,\quad b_2(m)\!=\!1+44m+16 m^2,\quad b_3 (m)\!=\!1\!+\!408m\!+\!912m^2\!+\! 64 m^3.\nonumber \\ \end{aligned}$$

(33)

We already used $b_1(m)$ and $b_2(m)$ in Eq. (7). The higher order polynomials, $b_4(m)$ through $b_6(m)$, can be found in Table 2 of [7].

1.3 A.3 Truncation of Maclaurin series

Let us calculate the critical value of $u$ needed in discussing the smallness of the argument in applying the Maclaurin series expansion of $b$. Assume that we truncate the series so as to include the first $L$ terms, namely up to the term containing $b_{L-1}(m)$. We define the critical value such that the relative magnitude of the next term in the series expansion is smaller than $\epsilon$, the machine epsilon in the adopted computing environment. Solving this condition with respect to $u$, we obtain the expression of the critical value as

$$\begin{aligned} u_S (m)=\root 2 L \of {{\frac{(2 L + 2)! \epsilon }{2 b_L (m)}}}. \end{aligned}$$

(34)

This is a complicated function of $m$. See Fig. 3 for the case $L=3$ in the double precision environment. For the reduction purpose, it is not necessary to know the precise value of $u_S(m)$. This is because the argument reduction is conducted by halving, and therefore there remains a room of factor 2. Thus, we approximate $u_S(m)$ by a linear function of $m$ giving its lower bound in order to decrease significantly the computational time of the judgment to terminate the argument reduction.

Fig. 3

Approximation of critical value function. Shown are the parameter dependence of $u_S(m)$ and its linear approximate, $u_T(m)$, for the case $L=3$ in the double precision environment

Since $u_S(m)$ is convex downward, we approximate its lower bound by its tangent at the middle point $m=1/2$ as

$$\begin{aligned} u_T(m) \equiv u_S \left({\frac{1}{2}}\right)+\left({\frac{du_S}{dm}}\right)_{m=1/2}\left(m- {\frac{1}{2}}\right). \end{aligned}$$

(35)

Table 2 provides the two coefficients of $u_T(m)$ for various values of $L$ in the single and double precision environments. The case for $L=1$ in the single precision and that for $L=3$ in the double precision are explicitly given in Eqs. (4) and (5), respectively. The reasons of these selection will be explained later in Appendix A.12. Figure 3 shows the manner of approximation for the latter case.

Table 2 Critical arguments to truncate series expansion of complementary cosine amplitude

1.4 A.4 Number of duplications

Now that the policy of truncation is fixed in the previous subsection, we can estimate the number of duplications. As their specimen, we show their maximum corresponding to the case when $u=K/2$;

$$\begin{aligned} N_\mathrm{MAX}=\left[\log _2\left({\frac{K}{2 u_T}}\right)\right]_\mathrm{floor}+1, \end{aligned}$$

(36)

where $[x]_\mathrm{floor}$ is the floor function.

Figure 4 shows $N_\mathrm{MAX}$ as functions of $m$ for various $L$ in the double precision environment. We omit the cases for $L \ge 6$ since they are almost the same as that for $L=5$. Although it is hardly visible from this figure, $N_\mathrm{MAX}$ significantly grows when $m \rightarrow 1$. Then, it becomes around 50 % larger than its value when $m=0$. For example, the number for $L=3$ reaches 12 when $m_c \approx 1.11 \times 10^{-16}$. In the case of single precision environment, similar investigation shows that the number for $L=1$ ranges from 8 when $m=0$ to 14 when $m_c \approx 1.19 \times 10^{-7}$.

Fig. 4

Maximum number of duplications of $b$ in double precision environment. Shown are $N_\mathrm{MAX}$, the maximum number of duplications of $b$ as functions of $m$. The results in the double precision environment are plotted for some values of $L$, the number of terms in the truncated Maclaurin series

1.5 A.5 Error propagation of duplication

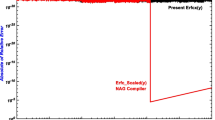
One may think that the introduction of complementary variable $b$ is not necessary since $c$ itself has a rational double argument formula, Eq. (13), and therefore it can be duplicated by itself without calling square root operations. However, we experimentally find that its naive duplication faces a serious accumulation of round-off errors as already shown in Fig. 1. This is understood by examining the error propagation of the duplication procedure. Ignoring higher order effects, we approximate the error propagation of Eq. (13) as

$$\begin{aligned} \Delta c_{n+1}=J_n\Delta c_n+\delta c_{n+1},\quad (n=0,\ldots , N-1) \end{aligned}$$

(37)

with the initial condition $\Delta c_0 = \delta c_0$. Here $\Delta$ and $\delta$ denote the global and local errors, respectively, and $J_n$ is the amplification factor obtained as the partial derivative of the right hand side of Eq. (13) with respect to $c_n$ as

$$\begin{aligned} J_n={\frac{4 c_n(m_c+m x_n^2)}{[m_c+m x_n(2-x_n)]^2}}. \end{aligned}$$

(38)

Unless $m \approx 1$ and $u$ is not so small, the factor is as large as around 4. This results a significant amplification of local errors, especially that of the initial one, $\Delta c_0$.

1.6 A.6 Expected error of cosine amplitude

Consider an extreme case when $u=K/2$. It requires the maximum number of duplications. Assume that numerical computation is conducted in the double precision environment where the machine epsilon is $\epsilon \approx 1.11 \times 10^{-16}$. Choose the first $L$ terms in the Maclaurin series of $c$ in order to evaluate it for the reduced argument. Such an example is $c\approx 1-u^2/2$ when $L=2$. For simplicity, we assume that the local errors of $c$ are all correlated and their relative magnitudes are equal to $\epsilon$. Namely, we approximate them as $\delta _n=c_n\epsilon$. Thus, the final error of $c$ is estimated as

$$\begin{aligned} \Delta c_N=\epsilon \left[c_N+\sum _{n=0}^{N-1}c_n\left( \prod _{j=n}^{N-1}J_j\right)\right], \end{aligned}$$

(39)

where $N$ means its maximum calculated by a formula similar to that of $b$ given in Eq. (36). The resulting $\Delta c_N$ is a function of $m$ only. This is because (1) $u=K(m)/2$ is a function of $m$, (2) $u_n \equiv 2^{n-N} u$ is so, (3) $c_n=\mathrm{cn}(u_n|m)$ is so, and (4) $J_n$ is so.

Figure 5 shows thus-estimated $\Delta c_N$ as a function of $m$ for some values of $L$. The jumps in the curves are due to the change in $N$. Although it is hardly seen from the figure, we frequently encounter with such jumps of a similar zigzag pattern with a similar height when $m \rightarrow 1$. This discontinuous feature does not significantly change the error magnitude. We omit the curves obtained by the duplication of $c$ for $L=1$ and $L>4$. This is because the results for $L=1$ is as large as of the order of unity. Meanwhile, those for $L>4$ do not differ significantly from those of $L=3$ and $L=4$. In fact, the curve for $L=5$ lies between those of $L=3$ and $L=4$.

Fig. 5

Expected maximum error of duplication in double precision environment. Illustrated are the expected maximum errors of the cosine amplitude function, $c$, and its complement, $b\equiv 1-c$. They are the relative errors for $u=K/2$, the maximum argument to be considered. The results in the double precision environment are plotted as functions of $m$ for some values of $L$

The figure reveals that the accumulated absolute error of $c$ amounts to $10^{-11}$ or so even if we choose a relatively large value of $L$ as four. A similar investigation shows that the expected maximum error becomes around $10^{-5}$ at least in the single precision environment. The essential point of the problem is the fact that the initial error of the variable to be duplicated is of the order of $\epsilon$ despite that the amplification factor is as large as 4.

1.7 A.7 Expected error of complementary variable

Let us examine the error of the complementary variable, $b$. The manner of the error propagation is unchanged from that of $c$ since the amplification factor is exactly the same. However, the magnitude of the initial value of the variable to be duplicated is reduced significantly from $c_0 \approx 1$ to $b_0 \approx u_0^2/2$. This leads to a substantial change. In order to illustrate this clearly, we take the same worst case as we discussed in case of $c$, namely the case when $u=K/2$.

Again choose the first $L$ terms in the Maclaurin series of $b$. The initial value, $b_0$, is significantly small as $u_c^2/2$ or so. Then, its round-off error would be of the order of $u_c^2\epsilon /2$. Also, the locally-produced errors, $\delta b_n$, are reduced since we assume that they are in proportion to $b_n$, and therefore less than $\delta c_n$ significantly. Further, the number of duplications differ somewhat from the case of $c$ although its effect is small.

Figure 5 also illustrates thus-estimated global error, $\Delta b_n$, as a function of $m$. The global errors are ${<}10\epsilon$ for $L=1$ and ${<}5\epsilon$ when $L=2$. We omitted the curves for $L>2$ since their differences from that for $L=2$ are hardly visible at this scale. In the single precision environment, we confirm that the expected errors rarely depends on $L$.

Thus the issue of round-off error amplification is positively resolved by the introduction of the complementary variable. Nevertheless, there is a pitfall in the usage of the translated double argument formula, Eq. (8).

1.8 A.8 Cancellation problem of complementary variable

During the duplications of $b$, there exists a chance such that $b_n$ grows significantly, and therefore the computation of $b_{n+1}$ suffers a cancellation problem. If we take no care of it, the resulting errors grow so much as already shown in Fig. 1.

Let us examine the source of the problem. The domain of $y_n$ is $0<y_n<1$ since $0<b_n<1$. Then, there are two possible origins of cancellation; the computation of $1-m y_n$ and $1-my_n^2$. The cancellation in the latter happens only when that in the former occurs. This is because $1-m y_n<1-m y_n^2$ since $0<y_n<1$. Thus, we concentrate ourselves to the former problem.

The loss of information associated with the subtraction, $1-my$, is negligible as long as $my<1/2$. Note that

$$\begin{aligned} y=\left. \mathrm{sn}^2 \left({\frac{u}{2}}\right|m\right), \end{aligned}$$

(40)

where the denominator $2$ is due to the fact that $y$ corresponds to the argument before the duplication. Also, note that the inverse sine amplitude function is expressed in terms of the incomplete elliptic integral of the first kind as

$$\begin{aligned} \mathrm{sn}^{-1}(s|m)=F(\sin ^{-1}s|m). \end{aligned}$$

(41)

Refer to the formula 130.02 of [4]. Then, the marginal condition, $my=1/2$, is translated in terms of the argument, $u$, as

$$\begin{aligned} u=u_B \equiv \left. 2F\left(\sin ^{-1}\left\{ {\frac{1}{\sqrt{2m}}} \right\} \right|m\right). \end{aligned}$$

(42)

Figure 6 illustrates thus-defined $u_B$ as well as $K/2$ as functions of $m$. An information loss may happen if $u>u_B$ while the argument we consider satisfies the condition, $u<K/2$. The figure shows that the crossing of these two curves happens when $m\approx 1$ and when $u$ is sufficiently large. At any rate, there is no worry of information loss when $u<u_B$.

Fig. 6

Critical curves in computing cosine amplitude function by duplication. Shown are some curves needed in discussing the information loss in the duplication procedures. The curves are (1) $K$ and $K/2$ showing the domains of the argument $u$ to be considered, (2) $u_C$ indicating the marginal curve when one bit loss is expected in the duplication of $c$, (3) $u_B$ indicating the similar curve in the duplication of $b$, and (4) $u_A$ approximating $u_B$ in the region $u_B < K/2$, namely when $m>m_X\approx 0.986741$. The curve $u_B$ is well-defined only when $m>1/2$

1.9 A.9 Criterion for switch of variables

Since $u_B$ is a complicated function of $m$, we replace it by its lower bound for the judging purpose. We numerically solved the equation, $u_B=K/2$, and obtained the value of $m$ of the cross point as

$$\begin{aligned} m_X \approx 0.986741. \end{aligned}$$

(43)

Noting that $u_B$ is convex downward, we approximate its lower bound by a tangent contacting it at the mid point of the considered region, $m_X<m<1$. Using Mathematica [22], we arrived the expression of the linear function as

$$\begin{aligned} u_A\equiv 1.76269+1.16357m_c, \end{aligned}$$

(44)

where we rounded the numerical values for simplicity. It is already plotted in Fig. 6. The narrowness of the region considered significantly reduces the approximation error as small as less than $5 \times 10^{-5}$. This critical value function is used in excluding efficiently the cases of no necessity of watching the possible cancellations in the new method.

1.10 A.10 Cancellation problem of cosine amplitude

Next, we shall examine the possibility of information loss in the duplication of $c$, especially that after the switch of variables. See Eq. (13) carefully. The denominator of its right hand side suffers no loss of information. This is partly because it is written as a sum of two positive terms, $m_c$ and $mx_n(2-x_n)$, and partly because the factor, $2-x_n$, in the second term faces no cancellation since $x_n<1$. Meanwhile, a bit loss in the computation of the numerator can happen when

$$\begin{aligned} (m x_n+2m_c)x_n<2 m_c. \end{aligned}$$

(45)

The marginal condition is a quadratic equation of $x_n$. It is solved in terms of $c$ as

$$\begin{aligned} c_n=c_C\equiv \sqrt{{\frac{2 m_c}{m_c+\sqrt{m_c(2-m_c)}}}}, \end{aligned}$$

(46)

where the ambiguity of the sign in front of the square root of the denominator is resolved by the fact $x_n>0$. This critical value is translated in terms of the argument as

$$\begin{aligned} u=u_C \equiv 2F(\cos ^{-1}c_C|m). \end{aligned}$$

(47)

Again the factor 2 in front of the incomplete elliptic integral is due to the fact that it corresponds to the value before the duplication. At any rate, $u_C$ is also plotted in Fig. 6 as well as $K\!$.

One bit loss can happen when $c<c_C$, and therefore when $u>u_C$. If we set the argument domain as $0<u<K$, then the information loss occurs for all values of $m$ in the duplication of $c$. The chance significantly decreases when the domain of $u$ is reduced to be the standard one as $0<u<K/2$. This is one of the reasons why we limit ourselves to the standard domain. Note that $u<u_C$ when $m>m_X$. Namely, no information loss occurs in the duplication of $c$ after the switch from that of $b$. In conclusion, the cancellation problem is positively solved by the introduction of a switch between the duplications of $b$ and $c$.

1.11 A.11 Expected error of cosine amplitude after switch of variables

The cancellation problems are overcome by a suitable switch of variables to be duplicated as seen in the previous subsections. However, this revives a question of the amplification of round-off errors in $c$ after the switching. Then, we reexamine this issue.

Denote by $j$ the index just before the switching. Then, the initial error, $\Delta c_j$, is assumed to be of the same level as $\Delta b_j$. This is because the subtraction, $c_j=1-b_j$, causes no cancellation since

$$\begin{aligned} y_j<{\frac{1}{2 m_X}} \approx 0.507, \end{aligned}$$

(48)

and therefore

$$\begin{aligned} b_j={\frac{y_j}{1+\sqrt{1-y_j}}}<0.298. \end{aligned}$$

(49)

We expect that $\Delta c_j$ is as small as being a few machine epsilons or less. Assuming this feature and conducting the similar calculations of the amplification process, we obtained the expected errors of $\Delta c_N$ as plotted in Fig. 7.

Fig. 7

Expected maximum error of duplication of $c$ after switch of variables. Illustrated are $\Delta c$ when $m>m_X$. The errors in the single and double precision environments are plotted as functions of $m_c$ in a log-log scale. The jumps in the curves are due to the change in the necessary number of duplications after the shift of the variable to be duplicated from $b$ to $c$

This time, the smallness of $m_c$ being ${<}0.014$ significantly reduces the amplification factor. Also, the intermediate function values, $c_n$, themselves become small when $n \ge j$. As a result, the expected final error, $\Delta c_N$, reduces significantly as shown in the figure. The situation is the same in the single precision environment as illustrated.

1.12 A.12 Optimization of order of approximation polynomial

As described in the previous subsections, except for the case $L=1$ in the double precision environment, the precision of the duplicated variables is expected to be at the machine epsilon level as long as an appropriate switching of variables is conducted. Then, the rest question is which value of $L$ is most preferable in the sense to minimize the total computing time. If $L$ is too small, then the number of duplications becomes large. Thus, the total computing time increases. On the other hand, if $L$ is too large, the truncated series is too lengthy. Then, the total computing time becomes large. Therefore, there is an optimal solution in the sense of computational time. This depends on the balance between the computational labor of each duplication and the truncated polynomial evaluation.

In order to investigate this issue, we prepared Table 3 showing the $L$-dependence of the averaged CPU times of the new method. For each $L$, we adopt the corresponding $u_T(m)$ as the criterion to terminate the argument reduction. The table indicates that the optimal order in the sense of computational time is 1 and 3 in the single and double precision environments, respectively. Although we illustrated here the result for the measurement using the Intel Core Duo processor, we confirm that the optimal condition does not change by the choice of recent CPU chips.

Table 3 Order dependence of averaged CPU time