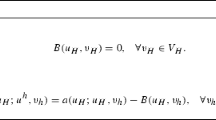Abstract
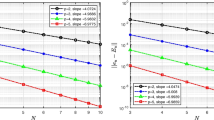
Consider the Poisson equation in a polytopal domain \(\Omega \subset {\mathbb {R}}^d\) (\(d=2, 3\)) as the model problem. We study interior energy error estimates for the weak Galerkin finite element approximation to elliptic boundary value problems. In particular, we show that the interior error in the energy norm is bounded by three components: the best local approximation error, the error in negative norms, and the trace error on the element boundaries. This implies that the interior convergence rate can be polluted by solution singularities on the domain boundary, even when the solution is smooth in the interior region. Numerical results are reported to support the theoretical findings. To the best of our knowledge, this is the first local energy error analysis that applies to general meshes consisting of polytopal elements and hanging nodes.

Similar content being viewed by others
References
Adams, R.: Sobolev Spaces, Pure and Applied Mathematics, vol. 65. Academic Press, New York, London (1975)
Apel, T., Nicaise, S.: The finite element method with anisotropic mesh grading for elliptic problems in domains with corners and edges. Math. Methods Appl. Sci. 21(6), 519–549 (1998)
Băcuţă, C., Nistor, V., Zikatanov, L.T.: Improving the rate of convergence of ‘high order finite elements’ on polygons and domains with cusps. Numer. Math. 100(2), 165–184 (2005)
Brenner, S .C., Scott, L .R.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, vol. 15, second edition edn. Springer, New York (2002)
Costabel, M., Dauge, M.: Weighted regularization of maxwell equations in polyehdral domains. a rehabilitation of nodal finite elements. Numer. Math. 93, 239–277 (2002)
Costabel, M., Dauge, M., Nicaise, S.: Corner singularities of Maxwell interface and eddy current problems. In: Gohberg, I., Wendland, W., Ferreira dos Santos, A., Speck, FO., Teixeira, F.S. (eds.) Operator Theoretical Methods and Applications to Mathematical Physics. Operator Theory: Advances and Applications, vol. 147, pp. 241–256. Birkhäuser, Basel (2004)
Costabel, M., Dauge, M., Schwab, C.: Exponential convergence of \(hp\)-FEM for Maxwell equations with weighted regularization in polygonal domains. Math. Models Methods Appl. Sci. 15(4), 575–622 (2005)
Dauge, M.: Elliptic Boundary Value Problems on Corner Domains. Lecture Notes in Mathematics, vol. 1341. Springer, Berlin (1988)
Grisvard, P.: Elliptic Problems in Nonsmooth Domains, Volume 24 of Monographs and Studies in Mathematics. Pitman (Advanced Publishing Program), Boston (1985)
Grisvard, P.: Singularities in Boundary Value Problems. Research Notes in Applied Mathematics, vol. 22. Springer, New York (1992)
Guo, B., Babuška, I.: Regularity of the solutions for elliptic problems on nonsmooth domains in \(\mathbf{R}^3\). I. Countably normed spaces on polyhedral domains. Proc. R. Soc. Edinb. Sect. A 127(1), 77–126 (1997)
Jin, G., Li, H., Zhang, Q., Zou, Q.: Linear and quadratic finite volume methods on triangular meshes for elliptic equations with singular solutions. Int. J. Numer. Anal. Model. 13(2), 244–264 (2016)
Kondrat’ev, V.A.: Boundary value problems for elliptic equations in domains with conical or angular points. Transl. Mosc. Math. Soc. 16, 227–313 (1967)
Li, H.: The \(W^1_p\) stability of the Ritz projection on graded meshes. Math. Comput. 86(303), 49–74 (2017)
Li, H.: An anisotropic finite element method on polyhedral domains: interpolation error analysis. Math. Comput. https://doi.org/10.1090/mcom/3290
Li, H., Mazzucato, A., Nistor, V.: Analysis of the finite element method for transmission/mixed boundary value problems on general polygonal domains. Electron. Trans. Numer. Anal. 37, 41–69 (2010)
Maz’ya, V., Rossmann, J.: Elliptic Equations in Polyhedral Domains. Mathematical Surveys and Monographs, vol. 162. American Mathematical Society, Providence (2010)
Mu, L., Wang, J., Wang, Y., Ye, X.: A weak Galerkin mixed finite element method for biharmonic equations. Numer. Solut. Partial Differ. Equ. Theory Algorithms Appl. 45, 247–277 (2013)
Mu, L., Wang, J., Ye, X.: Weak Galerkin finite element methods on polytopal meshes. Int. J. Numer. Anal. Model. 12, 31–53 (2015)
Mu, L., Wang, J., Ye, X.: A Weak Galerkin finite element method with polynomial reduction. J. Comput. Appl. Math. 285, 45–58 (2015)
Nicaise, S., Li, H., Mazzucato, A.: Regularity and a priori error analysis of a Ventcel problem in polyhedral domains. Math. Methods Appl. Sci. 40(5), 1625–1636 (2017)
Nitsche, J., Schatz, A.: Interior estimates for Ritz-Galerkin methods. Math. Comput. 28, 937–958 (1974)
Schatz, A., Wahlbin, L.: Maximum norm estimates in the finite element method on plane polygonal domains. I. Math. Comput. 32(141), 73–109 (1978)
Schatz, A., Wahlbin, L.: Maximum norm estimates in the finite element method on plane polygonal domains II. Refinements Math. Comput. 33(146), 465–492 (1979)
Schötzau, D., Schwab, C., Wihler, T.: \(hp\)-dGFEM for second-order mixed elliptic problems in polyhedra. Math. Comput. 85, 1051–1083 (2016)
Wahlbin, L.: On the sharpness of certain local estimates for \( H^{1}\) projections into finite element spaces: influence of a re-entrant corner. Math. Comput. 42(165), 1–8 (1984)
Wahlbin, L.B.: Superconvergence in Galerkin Finite Element Methods. Lecture Notes in Mathematics, vol. 1605. Springer, Berlin (1995)
Wang, J., Ye, X.: A weak Galerkin finite element method for second-order elliptic problems. J. Comput. Appl. Math. 241, 103–115 (2013)
Wang, J., Ye, X.: A weak Galerkin mixed finite element method for second order elliptic problems. Math. Comput. 83, 2101–2126 (2014)
Author information
Authors and Affiliations
Corresponding author
Additional information
Hengguang Li: This research was supported in part by the National Science Foundation Grant DMS-1418853, by the Natural Science Foundation of China Grant 11628104, and by the Wayne State University Grants Plus Program.
Lin Mu: This research was supported in part by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Applied Mathematics program under award number ERKJE45; and by the Laboratory Directed Research and Development program at the Oak Ridge National Laboratory, which is operated by UT-Battelle, LLC., for the U.S. Department of Energy under Contract DE-AC05-00OR22725.
Xiu Ye: This research was supported in part by the National Science Foundation Grant DMS-1620016.
Appendix A
Appendix A
The proof of Lemma 4.4.
Proof
It follows from (4.8), (2.7), and \(\mathrm{supp}(\omega _1)\subseteq D_1\), that
Below, we obtain estimates for each \(I_i\), \(1\le i\le 5\).
Recall \(\mathrm{supp}(\omega _1v)\subseteq D_1\). Then, using (2.11), (2.13), (2.14), (4.3), (3.3), and the inverse inequality, we have
Using the boundedness of \(\omega _1\), (3.2), and the Cauchy-Schwarz inequality, we have
and
Now, we estimate \(I_4\) and \(I_5\). Note that \(v_b=0\) on \(\partial \tilde{D}_2\). Therefore,
Then, we have
By the Cauchy-Schwarz inequality, the trace inequality (3.1), the boundedness of \(\omega _1\), (2.5), the inverse inequality, and (3.2), we have
Similarly, for \(A_4\), we have
Now, for \(A_1\), we first have
For the second term \(A_{12}\), using the Cauchy-Schwarz inequality, the trace inequality (3.1), the boundedness of \(\omega _1\), (2.5), the fact \(\partial ^\alpha (\nabla _wv)=0\) on T for \(|\alpha |=k\), and the inverse inequality, we obtain
The estimate on \(A_{11}\) is more involved. Note that by (4.14), we have
Therefore, considering \(A_{11}\) and \(I_5\) together, by the Cauchy-Schwarz inequality, the trace inequality (3.1), the boundedness of \(\omega _1\), and (2.5), we obtain
Thus, by the inverse inequality, (3.3), and the fact \(\partial ^\alpha (\nabla _wz)=0\) on T for \(|\alpha |=k\), we have
It follows from the Cauchy-Schwarz inequality, the trace inequality, (2.3), (2.4), and the inverse inequality that
which implies
In addition, the triangle inequality implies
Combining all the estimates (A.1)–(A.12), we have completed the proof for (4.15). \(\square \)
Rights and permissions
About this article
Cite this article
Li, H., Mu, L. & Ye, X. Interior energy error estimates for the weak Galerkin finite element method. Numer. Math. 139, 447–478 (2018). https://doi.org/10.1007/s00211-017-0940-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-017-0940-4