Skip to main content
SpringerLink
Log in

On the Rate of Convergence of Fictitious Play

  • Published:
Theory of Computing Systems Aims and scope Submit manuscript

Abstract

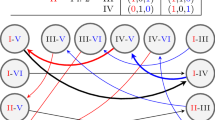
Fictitious play is a simple learning algorithm for strategic games that proceeds in rounds. In each round, the players play a best response to a mixed strategy that is given by the empirical frequencies of actions played in previous rounds. There is a close relationship between fictitious play and the Nash equilibria of a game: if the empirical frequencies of fictitious play converge to a strategy profile, this strategy profile is a Nash equilibrium. While fictitious play does not converge in general, it is known to do so for certain restricted classes of games, such as constant-sum games, non-degenerate 2×n games, and potential games. We study the rate of convergence of fictitious play and show that, in all the classes of games mentioned above, fictitious play may require an exponential number of rounds (in the size of the representation of the game) before some equilibrium action is eventually played. In particular, we show the above statement for symmetric constant-sum win-lose-tie games.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. A two-player game with totally ordered sets of actions is said to have strategic complementarities if the advantage of switching to a higher action, according to the ordering, increases when the opponent chooses a higher action, and diminishing returns if the advantage of increasing one’s action is decreasing.

  2. The proof of this claim later turned out to be flawed [5].

References

  1. Bellman, R.: On a new iterative algorithm for finding the solutions of games and linear programming problems. Research Memorandum P-473, The RAND Corporation (1953)

  2. Berger, U.: Fictitious play in 2×n games. J. Econ. Theory 120, 139–154 (2005)

    Article  MATH  Google Scholar 

  3. Berger, U.: Brown’s original fictitious play. J. Econ. Theory 135, 572–578 (2007)

    Article  MATH  Google Scholar 

  4. Berger, U.: Learning in games with strategic complementarities revisited. J. Econ. Theory 143, 292–301 (2008)

    Article  MATH  Google Scholar 

  5. Berger, U.: The convergence of fictitious play in games with strategic complementarities: a comment. MPRA Paper No. 20241, Munich Personal RePEc Archive, 2009

  6. Brandt, F., Fischer, F.: On the hardness and existence of quasi-strict equilibria. In: Monien, B., Schroeder, U.-P. (eds.) Proceedings of the 1st International Symposium on Algorithmic Game Theory. Lecture Notes in Computer Science, vol. 4997, pp. 291–302. Springer, Berlin (2008)

    Chapter  Google Scholar 

  7. Brown, G.W.: Iterative solutions of games by fictitious play. In: Koopmans, T.C. (ed.) Activity Analysis of Production and Allocation, pp. 374–376. Wiley, New York (1951)

    Google Scholar 

  8. Conitzer, V.: Approximation guarantees for fictitious play. In: Proceedings of the 47th Annual Allerton Conference on Communication, Control, and Computing, pp. 636–643 (2009)

    Google Scholar 

  9. Conitzer, V., Sandholm, T.: AWESOME: a general multiagent learning algorithm that converges in self-play and learns a best response against stationary opponents. Mach. Learn. 67(1–2), 23–43 (2007)

    Article  Google Scholar 

  10. Dantzig, G.B.: A proof of the equivalence of the programming problem and the game problem. In: Koopmans, T.C. (ed.) Activity Analysis of Production and Allocation, pp. 330–335. Wiley, New York (1951)

    Google Scholar 

  11. Fudenberg, D., Levine, D.: Consistency and cautious fictitious play. J. Econ. Dyn. Control 19, 1065–1089 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  12. Ganzfried, S., Sandholm, T.: Computing an approximate jam/fold equilibrium for 3-player no-limit Texas Hold’em tournaments. In: Proceedings of the 7th International Joint Conference on Autonomous Agents and Multi-Agent Systems, pp. 919–925 (2008)

    Google Scholar 

  13. Gjerstad, S.: The rate of convergence of continuous fictitious play. J. Econ. Theory 7, 161–178 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  14. Goldberg, P.W., Savani, R., Sørensen, T.B., Ventre, C.: On the approximation performance of fictitious play in finite games. Int. J. Game Theory (2013). doi:10.1007/s00182-012-0362-6

    Google Scholar 

  15. Hahn, S.: The convergence of fictitious play in 3×3 games with strategic complementarities. Econ. Lett. 64, 57–60 (1999)

    Article  MATH  Google Scholar 

  16. Hannan, J.: Approximation to Bayes risk in repeated plays. In: Dresher, M., Tucker, A.W., Wolfe, P. (eds.) Contributions to the Theory of Games, vol. 3, pp. 97–139. Princeton University Press, Princeton (1957)

    Google Scholar 

  17. Karlin, S.: Mathematical Methods and Theory in Games, Programming, and Economics, vol. 1–2. Addison-Wesley, Reading (1959)

    Google Scholar 

  18. Luce, R.D., Raiffa, H.: Games and Decisions: Introduction and Critical Survey. Wiley, New York (1957)

    MATH  Google Scholar 

  19. Miyasawa, K.: On the convergence of the learning process in a 2×2 nonzero sum two-person game. Research Memorandum 33, Econometric Research Program, Princeton University, 1961

  20. Monderer, D., Sela, A.: A 2×2 game without the fictitious play property. Games Econ. Behav. 14, 144–148 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  21. Monderer, D., Shapley, L.S.: Potential games. Games Econ. Behav. 14(1), 124–143 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  22. Monderer, D., Shapley, L.S.: Fictitious play property for games with identical interests. J. Econ. Theory 68, 258–265 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  23. Nachbar, J.H.: “Evolutionary” selection dynamics in games: convergence and limit properties. Int. J. Game Theory 19, 59–89 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  24. Powers, R., Shoham, Y.: New criteria and a new algorithm for learning in multi-agent systems. In: Advances in Neural Information Processing Systems 17, pp. 1089–1096. MIT Press, Cambridge (2004)

    Google Scholar 

  25. Rabinovich, Z., Gerding, E., Polukarov, M., Jennings, N.R.: Generalised fictitious play for a continuum of anonymous players. In: Proceedings of the 21st International Joint Conference on Artificial Intelligence, pp. 245–250 (2009)

    Google Scholar 

  26. Robinson, J.: An iterative method of solving a game. Ann. Math. 54(2), 296–301 (1951)

    Article  MATH  Google Scholar 

  27. Shapiro, H.: Note on a computation model in the theory of games. Commun. Pure Appl. Math. 11, 587–593 (1958)

    Article  MATH  Google Scholar 

  28. Shapley, L.: Some topics in two-person games. In: Dresher, M., Shapley, L.S., Tucker, A.W. (eds.) Advances in Game Theory. Annals of Mathematics Studies, vol. 52, pp. 1–29. Princeton University Press, Princeton (1964)

    Google Scholar 

  29. von Neumann, J.: Zur Theorie der Gesellschaftspiele. Math. Ann. 100, 295–320 (1928)

    Article  MathSciNet  MATH  Google Scholar 

  30. von Neumann, J.: A numerical method to determine optimum strategy. Nav. Res. Logist. Q. 1(2), 109–115 (1954)

    Article  Google Scholar 

  31. Zhu, W., Wurman, P.R.: Structural leverage and fictitious play in sequential auctions. In: Proceedings of the 18th National Conference on Artificial Intelligence, pp. 385–390 (2002)

    Google Scholar 

Download references

Acknowledgements

This material is based on work supported by the Deutsche Forschungsgemeinschaft under grants BR 2312/3-2, BR 2312/3-3, BR 2312/7-1, and FI 1664/1-1, and by the European Research Council under Advanced Grant 291528. The authors would like to thank Vincent Conitzer, Paul Goldberg, Peter Bro Miltersen, and Troels Bjerre Sørensen for valuable discussions.

Author information

Authors and Affiliations

  1. Institut für Informatik, Technische Universität München, 85748, Garching, Germany

    Felix Brandt

  2. Statistical Laboratory, University of Cambridge, Cambridge, CB3 0WB, UK

    Felix Fischer

  3. Department of Computer Science, University of Oxford, Oxford, OX1 3QD, UK

    Paul Harrenstein

Authors
  1. Felix Brandt
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Felix Fischer
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Paul Harrenstein
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Paul Harrenstein.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Brandt, F., Fischer, F. & Harrenstein, P. On the Rate of Convergence of Fictitious Play. Theory Comput Syst 53, 41–52 (2013). https://doi.org/10.1007/s00224-013-9460-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00224-013-9460-5

Keywords

Search

Navigation