Abstract
Over the past two decades, de Alfaro and Henzinger’s interface automata (IA) have become a popular formal framework for the component-based specification of concurrent systems. IA’s parallel composition assumes that a component may wait on inputs but never on outputs, implying that an output must be consumed immediately or a communication error occurs. By now, the literature contains a number of semantics for IA: linear-time semantics based on traces observing communication errors, quiescence and/or divergence, as well as branching-time semantics based on alternating simulation. This article surveys these semantics from Rob van Glabbeek’s linear-time branching-time perspective, which does not consider settings with communication errors. We shed light onto the subtleties implied by IA’s pruning of all behaviour that might lead a component to autonomously enter an error state, and investigate when exactly de Alfaro and Henzinger’s restriction of input-determinism is needed. In addition, we introduce several new semantics for IA, in particular the linear-time ready semantics and the branching-time ready simulation.
Similar content being viewed by others
1 Introduction
Modern software systems are assembled from components that need to interoperate properly in order to ensure a system’s correctness. Behavioural interfaces allow one to specify contracts between concurrent components [5] and, thus, to statically reason about component compatibility. This is of particular relevance during early system design and also when integrating legacy components.
The theoretical foundations of such interfaces have been studied intensively in the concurrency theory community [4, 9,10,11, 19, 21, 29, 35, 38], especially since the inception of interface automata (IA) by de Alfaro and Henzinger [12, 13]. These automata are based on labelled transition systems but distinguish a component’s input and output actions, and define a parallel composition whereby a component may wait on inputs but never on outputs. Therefore, a communication error occurs if one component receives a message for which it is not ready. In case no potential system environment may restrict the system components’ behaviour so that all errors are avoided, the components are deemed to be incompatible.
Behavioural preorders for IA Over the years, IA have been equipped with a number of behavioural relations for interface refinement and implementation. Originally, de Alfaro and Henzinger presented the IA-setting with branching-time preorders based on co-inductive notions of alternating simulation [12, 13]: a component satisfies an interface if it implements all input behaviour prescribed by the interface and if the interface permits all output behaviour executed by the implementing component, thereby preserving compatibility wrt. arbitrary system environments. Later, Göhrle [21] studied preorders that vary the degree to which internal behaviour surrounding input and output actions is abstracted and that lie in-between the two preorders proposed by de Alfaro and Henzinger.
More recently, various fully-abstract, linear-time preorders based on decorated traces have been developed for IA: the error semantics of [10, 11], the quiescence and the divergence semantics of [38], and the CJK-semantics of [11]. Strictly speaking, these preorders have been studied in the setting of Error-IO Transition Systems (EIO) [10, 38], which are input-enabled interface automata with explicit error states. EIO and IA are essentially the same model: the error states in EIO are eliminated in IA by pruning locally reachable errors, i.e., states from which a component can autonomously reach some error state via output and internal transitions only.
Contributions This article surveys and extends the above works and is intended for concurrency theoreticians to gain an overview and better understanding of the subtle semantic issues introduced by the notions of communication errors and component compatibility. We first recall the above preorders on EIO and IA, together with their precongruence properties and, where applicable, full-abstraction properties. Then, we study these preorders for a general notion of parallel composition that considers multicast synchronization and enables action internalisation via a separate hiding operator, whereas some of the preorders, e.g., the original IA-preorders proposed by de Alfaro and Henzinger [12, 13] have so far been studied only for a binary, internalising parallel composition operator.
As a first contribution, we arrange all these preorders in a linear-time branching-time spectrum, as inspired by van Glabbeek’s seminal works on the spectrum for behavioural relations on ordinary labelled transition systems [41,42,43]. We add to the IA-spectrum a number of new preorders: ready semantics to the linear-time part, as well as ready simulation and several bi-variant variations [3] of alternating simulation, including IA-bisimulation, to the branching-time part. Our final IA-spectrum (see Figs. 6, 13) depicts all implications between the studied 16 preorders, and counterexamples are provided wherever implications fail to hold.
As a second contribution, we discuss various design decisions and properties of the preorders. For the linear-time preorders, we show that the pruning of locally reachable errors does not change an interface’s semantics. We also take a closer look at the CJK-semantics and a variation of quiescence semantics. Regarding the branching-time preorders, we present characterizations of both IA-preorders by de Alfaro and Henzinger in terms of standard simulations.
The main insight is that the original preorder for IA, to which we refer as IA-refinement [12], also supports associativity for parallel composition, even for interfaces that are not input-deterministic. That associativity fails in [12] is solely owed to the incomplete notion of pruning employed therein. Hence, there is no need to restrict IA to input-deterministic interfaces as is done, e.g., in [13], and we recommend future investigations into IA to be based on the coarser IA-refinement preorder rather than on the alternating simulation of [13]. For those who prefer the latter preorder, we show how it can be generalized to arbitrary, i.e., not necessarily input-deterministic IA.
Related work A linear-time branching-time spectrum for behavioral specification theories is presented by Fahrenberg and Legay [18]. They employ disjunctive modal transition systems [28] to define a spectrum of refinement preorders, including failure semantics [7] and ready simulation [6], each giving rise to a specification theory for some equivalence—but not preorder—in van Glabbeek’s Linear-Time Branching-Time Spectrum I (without internal actions) [41, 43]. Moreover, Fahrenberg and Legay do not specifically consider interface theories: neither IA and its parallel composition, nor a notion of communication error, nor alternating simulation and related behavioural relations are studied.
Structure of this article The next section introduces IA informally, and points out the main aspects of parallel composition, communication error, pruning and compatibility. Sect. 3 then defines the formal framework considered by us, i.e., Interface Automata and Error-IO Transition Systems and their parallel and hiding operators. The subsequent Sects. 4 and 5 develop the linear-time and resp. branching-time part of our IA-spectrum, as announced above, and explores how exactly these two parts are connected. Finally, Sect. 6 briefly discusses two fields closely related to IA, namely interface theories and certain parts of model-based testing, while Sect. 7 presents our conclusions and suggestions for future work.
2 Interface automata by example
We introduce IA by an example that demonstrates the utility of de Alfaro and Henzinger’s setting [12, 13] for reasoning about component compatibility in concurrent systems. The essential feature of the setting is that, in the definition of parallel composition, one identifies error states and removes them in a suitable manner. If this leads to the removal of the initial state of the composition, the components are deemed to be incompatible, i.e., they cannot be used in combination in any system environment.
Consider the example depicted in Fig. 1, which is taken from [30] and adapted from [13]. It shows a simple networking protocol consisting of a Client that repeatedly sends messages (output action send!) and expects to receive a positive response (input action ok?). While Client can also listen to retry messages (input retry?), it always ignores these. The transport layer protocol is modelled by component TryOnce that receives messages (input send?), sends them over the network (output trnsmt!), and receives either a positive acknowledgement (input ack?) and relays this (output ok!), or a negative acknowledgement (input nack?) after which the component resets the lower layer (output reset!) and sends a retry request to the client (output retry!).
We now consider the parallel composition \({\textit{Client}} |{\textit{TryOnce}}\) of Client and TryOnce. For this, one first carries out a standard composition \({\textit{Client}} \otimes {\textit{TryOnce}}\), called product, where an output action synchronizes with an equally named input action, resulting in the output action. This way, a third component can listen to and synchronize with the same output, i.e., a multicast synchronization is possible. Then, in our example, state E is identified as an error state because TryOnce sends a retry, which Client refuses to accept. Such a communication mismatch has to be avoided and, because a component controls its output actions, the source of transition reset! has to be avoided as well. In general, a state is deemed illegal if it can reach an error state autonomously, i.e., by locally controlled actions. The idea of pruning in [12, 13] is to obtain \({\textit{Client}} |{\textit{TryOnce}}\) by removing all illegal states, whereby also the input transition nack? is cut. The resulting pruned automaton can also be seen as an operating guideline on how to use the two components working in parallel. Here, the guideline states that this automaton should not be confronted with input nack? after trnsmt!.
Component TryOften (with the same inputs and outputs as TryOnce) and its parallel composition with Client, using the pruning of [12], and component Lower (with inputs \(\{{\textit{trnsmt, reset}}\}\) and outputs \(\{{\textit{ack, nack}}\}\)
Unfortunately, the pruning of de Alfaro and Henzinger [12] leads to an associativity problem of parallel composition. To see this, we extend TryOnce to TryOften by adding a second transition nack?, as shown in Fig. 2. Thereby, TryOften can nondeterministically decide how often to re-transmit a message before forcing a reset. Furthermore, we add a lower-level component Lower that forwards a transmission to the communication medium, returns a positive or negative acknowledgement after some internal activity (non-observable action \(\tau \)), and accepts reset requests in its initial state. If we compose Client and TryOften, we obtain the same systems as in Fig. 1 as the product and also as the parallel composition, except for the additional nack?-transition. We use the operator \(\widehat{|}\) in \({\textit{Client}} \,\widehat{|}\, {\textit{TryOften}}\) to indicate that this composition is unsatisfactory. If we further add Lower as third component, there are no error states (see Fig. 3, left), i.e., Client, TryOften and Lower are deemed to be compatible. However, when we first compose TryOften with Lower, we obtain the error-free IA depicted in the middle of Fig. 3 and, then, the product with Client as shown on the right-hand side of the figure. Here, the initial state can reach the error state autonomously by local actions; note that \(\tau \) is locally-controlled, too. Thus, with this bracketing, the three components are incompatible and their parallel composition is undefined. Consequently, \(\widehat{|}\) is not associative.
This associativity defect, which was first discovered in [10], is rooted in the non-deterministic choice on input nack?, which was avoided by de Alfaro and Henzinger in their later work [13] by restricting the IA-setting to input-deterministic components. Additionally, they replaced the original refinement relation of [12] by a stricter one, which is however unrelated to the associativity defect. In fact, the restriction to input-deterministic components in [13] is unnecessary, because the conceptual mistake lies in the notion of pruning. Recall that cutting the nack?-transition in \({\textit{Client}} \otimes {\textit{TryOnce}}\), and similar in \({\textit{Client}} \otimes {\textit{TryOften}}\) (not shown in the figures), should indicate that the environment must refrain from sending nack in the state after trnsmt!. However, the pruning of [12] incompletely reflects this requirement, because the second nack?-transition in \({\textit{Client}} \otimes {\textit{TryOften}}\) is not pruned. To obtain a proper pruning, one must always prune all transitions of an input at a state, if one prunes one transition of this input at the state. In our example, the nack?-transition remaining in Fig. 2 in the middle is then also pruned, so that the composition with the third component Lower is incompatible due to that component’s output nack!. In the following, we use the ordinary symbol | for the parallel composition with proper pruning. Observe that, in Fig. 1, the kind of pruning does not matter and one may use either | or \(\widehat{|}\) there.
Completing our example to illustrate the associativity defect of the pruning of [12]
To conclude, the above discussion leads to the following understanding of parallel product and composition. The product of, e.g., Client and TryOnce describes how the two automata interact with each other, while their composition is more concise and describes the behaviour only as far as needed. At the same time, the composition captures more clearly the requirements imposed upon the system environment, in which the composition may be placed. For fundamental studies of this specification setting, the EIO variant of IA with explicit error states was introduced (cf. [10, 11]).
3 The interface automata setting
This section presents the formal framework in which the linear-time and branching-time preorders studied in the literature were developed: the interface automata (IA) of de Alfaro and Henzinger [12] and the equally expressive Error-IO Transition Systems (EIO) of Bujtor and Vogler [10] (cf. also [11]). A particular focus is placed on the parallel composition of such automata and the pruning in IA; as just explained, our pruning subtly but importantly deviates from the one employed in [12]. Generalizing the standard definition, we also equip IA with an associative multicast parallel operator; our additional hiding operator allows for the internalization of actions that implicitly occurs in [12, 13] when actions synchronize.
Definition 1
(Interface automata) An Interface Automaton (IA) is a tuple \((P, I, O, \, {\mathop {\longrightarrow }\limits ^{}}, p_0)\), where
-
P is the set of states;
-
I and O are disjoint sets of input and output actions, resp., not containing the special, non-observable action \(\tau \), where \(A =_{\text {df}}I \cup O\) is called the automaton’s action set or alphabet and (I, O) its signature;
-
\({\mathop {\longrightarrow }\limits ^{}} \,\subseteq P \times A_{\tau } \times P\) is the transition relation, where \(X_\tau =_{\text {df}}X \cup \{\tau \}\) for \(X \subseteq A\);
-
\(p_0 \in P\) is the initial state.
An IA is input-deterministic if \((p, i, p')\), \((p, i, p'') \in \,{\mathop {\longrightarrow }\limits ^{}}\) with \(i \in I\) implies \(p'=p''\).
Note that the IAs studied by us are not by definition input-deterministic. In the following, we denote an IA as above also by P, i.e., we identify an IA by its state set. We often use p and \(p'\) as representatives of the state set P, as well as i, o, \(\omega \), a and \(\alpha \) as representatives of the action sets I, O, \(O_\tau \), A and \(A_\tau \), resp. If \(\alpha = \tau \), then \({\hat{\alpha }} =_{\text {df}}\epsilon \); otherwise, \({\hat{\alpha }} =_{\text {df}}\alpha \). In addition, we let \(p {\mathop {\longrightarrow }\limits ^{\alpha }} p'\) denote the transition \((p, \alpha , p') \in \,{\mathop {\longrightarrow }\limits ^{}}\), while \(p \,{\mathop {\longrightarrow }\limits ^{\alpha }}\) means that such a transition exists for some \(p'\), i.e., \(\alpha \) is enabled at p. A state is stable if it does not enable \(\tau \). Unless defined otherwise, an IA P always has the components P, I, O, \({\mathop {\longrightarrow }\limits ^{}}\), and \(p_0\), and similarly \(P_1\) has components \(P_1\), \(I_1\), etc. In figures, we sometimes display i? for an input i and o! for an output o.
Extending our transition notation to action sequences, we write \(p{\mathop {\longrightarrow }\limits ^{w}} p'\) if there exists a run \(p {\mathop {\longrightarrow }\limits ^{\alpha _1}} p_1 {\mathop {\longrightarrow }\limits ^{\alpha _2}} p_2 \cdots {\mathop {\longrightarrow }\limits ^{\alpha _n}} p_n = p'\) such that \(w=\alpha _1\alpha _2 \cdots \alpha _n\) where \(\alpha _i \in A_\tau \) for \(1 \le i \le n\); analogously, a run can also be infinite. A state p is reachable if \(p_0 {\mathop {\longrightarrow }\limits ^{w}} p\) for some w; it is locally reachable if it is reachable by local actions only, i.e., if \(w \in O_\tau ^*\). The projection \(w|_B\) of w onto \(B \subseteq A\) arises by deleting from w all actions that are not in B. Now, \(p {\mathop {\Longrightarrow }\limits ^{w}} p'\) if \(w \in A^*\) and \(\exists w' \in A_\tau ^*.\; w'|_A=w\) and \(p {\mathop {\longrightarrow }\limits ^{w'}} p'\); we say that the run according to \(p {\mathop {\longrightarrow }\limits ^{w'}} p'\) underlies \(p {\mathop {\Longrightarrow }\limits ^{w}} p'\), or just w if the context is clear. As above, we write \(p{\mathop {\longrightarrow }\limits ^{w}}\) for \(\exists p'.\, p{\mathop {\longrightarrow }\limits ^{w}} p'\) and \(p{\mathop {\Longrightarrow }\limits ^{w}}\) for \(\exists p'.\, p{\mathop {\Longrightarrow }\limits ^{w}} p'\). The language \({\text {L}}({P})\) of P consists of all traces of P and is the set \(\{ w \in A^* \,|\, p_0 {\mathop {\Longrightarrow }\limits ^{w}} \}\).
Error-IO transition systems are input-enabled IA with explicit error states, for which we adopt the conventions above:
Definition 2
(Error-IO transition system) An Error-IO Transition System (EIO) is a tuple \((P, I, O, {\mathop {\longrightarrow }\limits ^{}}, p_0, E)\), where \((P, I, O, {\mathop {\longrightarrow }\limits ^{}}, p_0\)) is an IA and \(E \subseteq P\) is the set of error states. In addition, we require that P is input-enabled, i.e., for all \(p \in P\) and \(i \in I\), there exists some \(p' \in P\) with \(p {\mathop {\longrightarrow }\limits ^{i}} p'\).
In essence, EIO and IA are the same model: a missing input transition at a state in an IA corresponds in EIO to an input transition to an error state. IA is convenient for simulation-based semantics where, simply, a missing input does not have to be matched. However, making errors explicit in EIO removes any prejudice present in the IA-setting as to how exactly error states arising in a parallel composition are avoided. This is why linear-time semantics with their full-abstraction results have been based on EIO. Furthermore, adopting input-enabledness in EIO (as in [11]) lends itself to an easier description of linear-time semantics. Observe that input-transitions to an error state in an EIO do not have to be implemented, and in fact cannot be implemented; this differs from the treatment of input-enabledness in the IO-automata model of Lynch [31].
We now introduce (proper) pruning for EIO, which enables one to translate between EIO and IA:
Definition 3
(Pruning) Let P be an EIO. Then, \(e\in E\) is canonical if it is the only error state, has exactly a loop for each input as its outgoing transitions and, if \(p {\mathop {\longrightarrow }\limits ^{\alpha }} e\), then \(\alpha \in I\) and p has no other \(\alpha \)-transitions.
A state p is illegal if an error state can be locally reached from p, i.e., reached via output- and \(\tau \)-transitions only. We obtain EIO \(\textit{prune}({P})\) from P in two steps: first, we remove all illegal states and, additionally, each input transition \(p {\mathop {\longrightarrow }\limits ^{i}} p'\) for which there is some illegal state \(p''\) with \(p {\mathop {\longrightarrow }\limits ^{i}} p''\). Second, we add a new error state \(e\) with ingoing transitions that ensure input-enabledness and make \(e\) canonical. If \(p_0\) is illegal, then \(e\) is also initial.
In [10], it is shown that, when applying this proper pruning, each EIO P is equivalent to \(\textit{prune}({P})\) according to our first linear-time refinement (cf. Sect. 4.2). We prove in Sect. 4 that this also holds for the other linear-time refinements.
Remark 4
(Translating between EIO and IA) IAs can be understood as special EIOs by adding a canonical error state as above. Thus, an input i missing at some state p of an IA is translated to the transition \(p {\mathop {\longrightarrow }\limits ^{i}} e\). Conversely, one can normalise an EIO P to \(\textit{prune}({P})\) and then remove the canonical error state and the adjacent transitions to get a corresponding IA. If \(\textit{prune}({P})\) only consists of the error state, it corresponds to the “undefined IA” that arises from an undefined parallel composition.
All previously known linear-time preorders (see Sect. 4) have been defined on EIOs in the literature, while all branching-time preorders (see Sect. 5) are defined on IAs. By the above remark, we may still compare linear-time to branching-time preorders, by lifting the preorders from IA to EIO or vice versa.
Definition 5
(Hiding) For an EIO \((P, I, O, {\mathop {\longrightarrow }\limits ^{}}, p_0, E)\) and \(H \subseteq O\), the hiding of H in P is the EIO \(P{\setminus }H =_{\text {df}}(P, I, O{\setminus }H, {\mathop {\longrightarrow }\limits ^{}}_H, p_0, E)\), where
-
1.
\(p {\mathop {\longrightarrow }\limits ^{\alpha }}_H p'\) if \(p {\mathop {\longrightarrow }\limits ^{\alpha }} p'\) and \(\alpha \notin H\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{\tau }}_H p'\) if \(p {\mathop {\longrightarrow }\limits ^{o}} p'\) for some \(o \in H\).
We now define parallel composition on EIO, which is a multicast because an output of one EIO can synchronize with inputs from several other EIOs in its environment. This differs from broadcast in that all potential receivers must be ready to synchronize. Naturally, the receivers synchronize on their common inputs.
Definition 6
(EIO-parallel composition) Two EIOs \(P_1\) and \(P_2\) are composable if \(O_1 \cap O_2 = \emptyset \). In this case, the EIO-parallel composition \(P_{12} =_{\text {df}}P_1 \Vert P_2\) is \((S, I, O, {\mathop {\longrightarrow }\limits ^{}}, \, s_0, E)\), where \(S =_{\text {df}}P_1 \times P_2\), \(I =_{\text {df}}(I_1{\setminus }O_2) \cup (I_2{\setminus }O_1)\), \(O =_{\text {df}}O_1 \cup O_2\), \(s_0 =_{\text {df}}(p_{01}, p_{02})\), \(E =_{\text {df}}(E_1 \times P_2) \cup (P_1 \times E_2)\), and the transition relation \({\mathop {\longrightarrow }\limits ^{}}\) is the least relation satisfying the following rules:
We call \(P_1\) a partner of \(P_2\) if \(I_2 \subseteq O_1\) and \(O_2 = I_1\); intuitively, \(P_1\) fully synchronizes with \(P_2\) but might have additional outputs.
The definition of IA-parallel composition is given in two steps, as usual [12, 13]:
Definition 7
(IA-parallel composition) The parallel product \(\otimes \) on composable IAs \(P_1\), \(P_2\) is defined as the EIO-parallel composition above, except that  , i.e., one component of an error state offers an output to the other that the other cannot receive. The IA-parallel composition \(P_1 |P_2\) is obtained by applying the pruning of Definition 3 without adding an error state. If the initial state is illegal, then the parallel composition is undefined. Otherwise, we call \(P_1\) and \(P_2\) compatible.
, i.e., one component of an error state offers an output to the other that the other cannot receive. The IA-parallel composition \(P_1 |P_2\) is obtained by applying the pruning of Definition 3 without adding an error state. If the initial state is illegal, then the parallel composition is undefined. Otherwise, we call \(P_1\) and \(P_2\) compatible.
The defined parallel operators are obviously commutative wrt. isomorphism, and they are associative, too:
Proposition 8
(Associativity) \((P_1 \Vert P_2) \Vert P_3\) and \(P_1 \Vert (P_2 \Vert P_3)\) are isomorphic, for all pairwise composable EIOs \(P_1\), \(P_2\), \(P_3\). The analogous holds for \(|\) if \(P_1\), \(P_2\), \(P_3\) are IAs – provided one of the two composed IAs is defined, in which case the other is as well.
Proof
Associativity on EIOs can be established by adapting the proof of Theorem 16 in [10]. If the parallel compositions are defined, associativity on IAs is a consequence of a corresponding result in the setting of Modal Interface Automata (MIA) [9, Thm. 12]: one translates every IA-transition into a must-transition in the MIA-setting and adds a disconnected error state. (Note that this does not preserve refinements.)
In more detail, consider \((P_1 |P_2) |P_3\) and let \(P'_1\), \(P'_2\) and \(P'_3\) be the resp. translations to MIA. \(P'_1 |P'_2\) is the same as \(P_1 |P_2\) except for the error state and the fact that, in the former, if some input i is cut at a state \(p_1 |p_2\), then there is a so-called may-transition with label i from \(p_1 |p_2\) to the error state. Thus, we get \(P_1 |P_2\) back from \(P'_1 |P'_2\) by omitting such may-transitions and the error state.
The same is true for \((P_1 |P_2) |P_3\), as we argue now. The only additional problem is that \(p_1 |p_2\) has the above i-may-transition in the MIA and no i-transition in the IA. If state \(p_1 |p_2\) of \(P_1' |P_2'\) is composed with some \(p_3\) of \(P'_3\), there are several cases to consider. First, if \(i \in A_3\) is not enabled at \(p_3\), then \((p_1 |p_2, p_3)\) as state of \((P'_1 |P'_2) \otimes P'_3\) has no i-transition, which fits \((P_1 |P_2) \otimes P_3\). Second, if \(i \in I_3\) is enabled at \(p_3\) or \(i \notin A_3\), then \((p_1 |p_2, p_3)\) has an i-may-transition to the error state, which fits \((P_1 |P_2) \otimes P_3\) after the translation back. Third, if \(i \in O_3\) is enabled at \(p_3\), then \((p_1 |p_2, p_3)\) is an error state as in the IA-case.
Thus, associativity for IA follows because one can translate the two isomorphic MIA-compositions back to the two IA-compositions by removing the corresponding may-transitions and error states, so the latter two are isomorphic as well. \(\square \)
Remark 9
For all IAs \(P_1\), \(P_2\), we have that \(P_1 |P_2\), if defined, is identical to the IA obtained in the following way. First, we consider \(P_1\), \(P_2\) as EIOs according to Remark 4, apply EIO-parallel composition to obtain \(P_{12}\), and translate this result back into an IA by pruning without adding the canonical error state.
To see this coincidence, consider a transition \((p_1,p_2) {\mathop {\longrightarrow }\limits ^{a}} (p_1',p_2') \in E_{12}\) entering an error state in \(P_{12}\). The first case is that a is an input. W.l.o.g. assume \(p_1 {\mathop {\longrightarrow }\limits ^{a}} e_1 \in E_1\) and either \(a \notin A_2\) or \(a \in I_2\). Then, \(p_1\) cannot perform a in the IA \(P_1\) and, thus, \((p_1,p_2)\) cannot perform a in \(P_1 |P_2\). The same holds in the pruned \(P_{12}\). The second case is that a is an output. W.l.o.g. \(a \in O_1 \cap I_2\), \(p_1 {\mathop {\longrightarrow }\limits ^{a}} p_1'\) and \(p_2 {\mathop {\longrightarrow }\limits ^{a}} e_2\). In this case, \((p_1,p_2)\) is illegal in \(P_{12}\) and an error in \(P_1 \otimes P_2\). Consequently, the illegal states in the IA-setting are the illegal states in the EIO-setting without the error states. This shows that \(\Vert \) on EIO coincides with \(|\) on the subclass IA of EIO.
In the original papers on IA [12, 13], parallel composition is only applied to strongly composable IAs \(P_1\), \(P_2\)—i.e., they are composable and \(I_1 \cap I_2 = \emptyset \)—and immediately followed by hiding of the synchronized actions. This can be expressed in our setting as \((P_1 |P_2) / {H}\), where \(H =_{\text {df}}(I_1 \cap O_2) \cup (I_2 \cap O_1)\). Thus, the precongruence results for IA-parallel composition and hiding imply the precongruence property for the original IA-operator. In contrast to IA-parallel composition, observe that, with the original operator, only two components synchronize on a common action.
4 Linear-time preorders
This section investigates the linear-time spectrum for EIO. We largely follow [38] by studying the error semantics of [10, 11], the quiescence and divergence semantics of [38] and the CJK-semantics of [11], and we also consider our new ready semantics. For each case, we show how to determine the semantics for a parallel composition and for an application of hiding from the semantics of the underlying components. This implies that the refinement preorders accompanying the semantics are precongruences; indeed, full-abstraction results are known for error, quiescence and divergence semantics [38]. New contributions by us are, besides the addition of ready semantics (see Sect. 4.6), the equivalence results on pruning, a closer look at the CJK-semantics (see Sect. 4.5) and a variation of quiescence semantics (see Sect. 4.3).
4.1 Basic requirements, preorders and properties
The preorders to be considered for our linear-time spectrum compare EIOs having the same signature and, thus, the same interaction potential. Our basic requirement of a preorder is that a refinement, i.e., the smaller EIO, avoids errors whenever the specification, i.e., the larger EIO, avoids errors; here, avoiding an error means that an error state is not locally reachable, as discussed above. We write \(\sqsubseteq _E^B\) for the basic preorder that obeys just this preservation property.
In addition, for a preorder to be practically applicable, one expects that it enables compositional reasoning, i.e., that it is a precongruence. Ideally, a refinement precongruence does, at the same time, not unnecessarily distinguish EIOs, i.e., it is fully-abstract wrt. the initial, basic preorder and the EIO operators. Mathematically, this means with regards to \(\sqsubseteq _E^B\) that the desired fully-abstract preorder characterizes the coarsest precongruence \(\sqsubseteq _E^C\) contained in \(\sqsubseteq _E^B\). Below we first establish full-abstraction wrt. parallel composition, and then show the precongruence property wrt. hiding, i.e., full abstraction also holds for full EIO.
While avoiding errors is obviously the basic observable on which a system designer wishes to base a preorder for interfaces, one may also consider two further observables that are extensively studied in the concurrency literature [42]: quiescence and divergence. This leads to the two basic preorders \(\sqsubseteq _{\text {Qui}}^B\) and \(\sqsubseteq _{\text {Div}}^B\) and their fully-abstract counterparts \(\sqsubseteq _{\text {Qui}}^C\) and \(\sqsubseteq _{\text {Div}}^C\), resp., which are studied below for EIO. Intuitively, a state avoids quiescence, if it cannot locally reach a state that has only input transitions, i.e., in which the system cannot progress on its own. The state avoids divergence, if it cannot locally reach a state that is divergent, i.e., in which an infinite run of \(\tau \)-transitions starts. Hence, we obtain the following definition [38]:
Definition 10
(Faults and preorders) In addition to the errors contained in the definition of EIO, we consider the two following sets of observable faults for an EIO P: the set \({\text {Qui}}({P})\) of quiescent states given by  and the set \({\text {Div}}({P})\) of divergent states defined by \(\{ p \in P \;|\; p \text { has an infinite run of} \, \tau \text {-transitions} \}\). We say that P avoids errors/quiescence/divergence, if no error/quiescent/divergent state is locally reachable.
and the set \({\text {Div}}({P})\) of divergent states defined by \(\{ p \in P \;|\; p \text { has an infinite run of} \, \tau \text {-transitions} \}\). We say that P avoids errors/quiescence/divergence, if no error/quiescent/divergent state is locally reachable.
For EIOs \(P_1\), \(P_2\) with the same signature, we write (i) \(P_1 \sqsubseteq _E^BP_2\), (ii) \(P_1 \sqsubseteq _{\text {Qui}}^BP_2\) and (iii) \(P_1 \sqsubseteq _{\text {Div}}^BP_2\) whenever \(P_1\) avoids (i) errors, (ii) errors and quiescence, (iii) errors and quiescence and divergence, resp., provided \(P_2\) does. As explained above, \(\sqsubseteq _E^C\), \(\sqsubseteq _{\text {Qui}}^C\) and \(\sqsubseteq _{\text {Div}}^C\) are the fully-abstract preorders for EIO-parallel composition and \(\sqsubseteq _E^B\), \(\sqsubseteq _{\text {Qui}}^B\) and \(\sqsubseteq _{\text {Div}}^B\), resp.
The characterizations of the desired fully-abstract preorders rely on traces that are often obtained via pruning and continuation operations [10]:
Definition 11
(Pruning and continuation functions) Let P be an EIO, \(\epsilon \) the empty word and \({{\mathscr {P}}}({M})\) the power set of a set M.
-
\(\textit{prune}({}) : A^* \rightarrow A^*\), \(uv \mapsto u\) with \(v \in O^*\) and either \(u=\epsilon \) or \(u \in A^* \cdot I\);
-
\(\textit{cont}({}) : A^* \rightarrow {{\mathscr {P}}}({A^*})\), \(w \mapsto \{ wu \,|\, u \in A^* \}\);
-
\(\textit{cont}({}): {{\mathscr {P}}}({A^*}) \rightarrow {{\mathscr {P}}}({A^*})\), \(L \mapsto \bigcup \{ \textit{cont}({w}) \,|\, w \in L \}\).
Intuitively, pruning is needed because a trace reaching an error state directly is as good as a trace that reaches a state that can locally reach an error state. Another operation on traces required in the sequel is parallel composition:
Definition 12
(Parallel composition on action sequences) Let \(P_1\), \(P_2\) be EIOs.
-
The parallel composition \(w_1 \Vert w_2\) of words \(w_1 \in A_1^*\) and \(w_2 \in A_2^*\) is defined to be the set \(\{w \in (A_1 \cup A_2)^* \;|\; w|_{A_1} = w_1\) and \(w|_{A_2} = w_2 \}\).
-
The parallel composition \(W_1 \Vert W_2\) of two languages, i.e., sets of words, \(W_1 \subseteq A_1^*\) and \(W_2 \subseteq A_2^*\) is the set \(\bigcup \{w_1 \Vert w_2 \;|\; w_1 \in W_1\) and \(w_2 \in W_2 \}\).
Obviously, the traces of a parallel composition are in close correspondence with the traces of each parallel component:
Lemma 13
Let \(P_1\), \(P_2\) be composable EIOs and \(P_{12}\) be their parallel composition.
-
1.
Let \(w \in A_{12}^*\), \(w_1 = w|_{A_1}\), \(w_2 = w|_{A_2}\), and consider \((p_1,p_2)\), \((p_1',p_2') \in P_{12}\). Then, \((p_1,p_2) {\mathop {\Longrightarrow }\limits ^{w}} (p_1',p_2')\) if and only if \(p_1 {\mathop {\Longrightarrow }\limits ^{w_1}} p_1'\) and \(p_2 {\mathop {\Longrightarrow }\limits ^{w_2}} p_2'\);
-
2.
\({\text {L}}({P_{12}}) = {\text {L}}({P_1}) \,\Vert \, {\text {L}}({P_2})\).
We call the second and third (underlying) run in the above first part the projections of the first run.
4.2 Preserving freedom from errors
Our technical considerations start off with the basic case of error avoidance, reciting the results of [10, 38] (cf. also [11]). The following trace languages are required for characterizing the fully-abstract precongruence \(\sqsubseteq _E^C\):
Definition 14
(Error semantics) Let P be an EIO. We define the following:
-
Strict error traces: \({\text {StET}}({P}) =_{\text {df}}\{ w \in A^* \,|\, \exists p'.\, p_0 {\mathop {\Longrightarrow }\limits ^{w}} p' \in E \}\);
-
Pruned error traces: \({\text {PrET}}({P}) =_{\text {df}}\{ \textit{prune}({w}) \,|\, w \in {\text {StET}}({P}) \}\);
-
Error traces: \({\text {ET}}({P}) =_{\text {df}}\textit{cont}({{\text {PrET}}({P})})\);
-
Error-flooded language: \({\text {EL}}({P}) =_{\text {df}}{\text {L}}({P}) \cup {\text {ET}}({P})\).
We call \(({\text {ET}}({P}), {\text {EL}}({P}))\) the error semantics of P. For EIOs \(P_1\), \(P_2\) with the same signature, we write \(P_1\sqsubseteq _EP_2\) if \({\text {ET}}({P_1}) \subseteq {\text {ET}}({P_2})\) and \({\text {EL}}({P_1})\subseteq {\text {EL}}({P_2})\). From the semantics’ name, we derive that \(P_1\) is an error-refinement of \(P_2\), and EIOs error-refining each other are error-equivalent, and similarly for the other linear-time semantics.
The error semantics adds to the error traces only the error-flooded language. Thus, \(\sqsubseteq _E\) corresponds to language inclusion in the standard linear-time branching-time spectrum [41,42,43]. As a purely denotational model, error semantics has already been introduced by Dill [16]. Note that \(\sqsubseteq _E\) strictly refines \(\sqsubseteq _E^B\): on the one hand, we show below that \(\sqsubseteq _E^C\) and \(\sqsubseteq _E\) coincide. On the other hand, consider the EIO consisting of a single, initial, non-error state with an o-loop and a similar EIO without any transition. Obviously, the former is related to the latter according to \(\sqsubseteq _E^B\) but not according to \(\sqsubseteq _E\).
The above definition reflects our intuitive understanding of a refinement semantics that preserves error avoidance, where both the direct reachability of errors (cf. strict error traces) and their indirect reachability via states that can locally reach error states (cf. pruned error traces) are relevant. Once some error manifests itself, any further behaviour does not matter, so that all continuations of error traces must also be considered to be error traces, leading to an error-flooded language and a notion of error semantics for which the following properties and, in particular, full-abstraction hold [10]:
Theorem 15
(Error semantics for EIO-parallel composition) For composable EIOs \(P_1\), \(P_2\) and their parallel composition \(P_{12}\):
-
1.
\({\text {ET}}({P_{12}}) = \textit{cont}({\textit{prune}({({\text {ET}}({P_1}) \Vert {\text {EL}}({P_2})) \cup ({\text {EL}}({P_1}) \Vert {\text {ET}}({P_2}))})})\);
-
2.
\({\text {EL}}({P_{12}}) = ({\text {EL}}({P_1}) \Vert {\text {EL}}({P_2})) \cup {\text {ET}}({P_{12}})\).
Hence, \(\sqsubseteq _E\) is a precongruence wrt. EIO-parallel composition. Furthermore, \(\sqsubseteq _E\) is fully-abstract, i.e., it coincides with \(\sqsubseteq _E^C\).
The precongruence result is implied by the first two items since \(\textit{cont}({})\), \(\textit{prune}({})\) and \(\Vert \) are monotonic on languages. The same argument applies in analogous situations below. We leave out the full-abstraction proof here; an example of such a proof is given below for the more involved quiescence semantics (see Theorem 21).
Theorem 16
(Error precongruence for hiding) Let P be an EIO and \(H \subseteq O\). Then,
-
1.
\({\text {L}}({P/ {H}}) = \{w \in (A{\setminus }H)^* \,|\, \exists w' \in {\text {L}}({P}).\; w'|_{A{\setminus }H} = w \}\);
-
2.
\({\text {ET}}({P/ {H}}) = \{w\in (A{\setminus }H)^* \,|\, \exists w' \in {\text {ET}}({P}).\; w'|_{A{\setminus }H} = w \}\);
-
3.
\({\text {EL}}({P/ {H}}) = \{ w \in (A{\setminus }H)^* \,|\, \exists w' \in {\text {EL}}({P}).\; w'|_{A{\setminus }H} = w \}\).
Hence, \(\sqsubseteq _E\) is a precongruence wrt. hiding, too.
This precongruence result is implied by the fact that hiding turns outputs into internal \(\tau \)s and, thus, preserves local reachability. The next theorem has been shown in [10]; we prove it here for the present variant of EIOs that requires input-enabledness:
Theorem 17
(Pruning) Each EIO P is error-equivalent to \(\textit{prune}({P})\).
Proof
Assume that \(p_0\) is not illegal; otherwise, the claim is clear. To show \({\text {ET}}({P}) \subseteq {\text {ET}}({\textit{prune}({P})})\), it suffices to consider a prefix-minimal \(w \in {\text {ET}}({P})\), because both sides are continuation-closed. Obviously, \(w \in {\text {PrET}}({P})\) and a suitable underlying run ends with \(p {\mathop {\longrightarrow }\limits ^{i}} p'\), where \(i \in I\) and \(p'\) is illegal while p is not. Because all i-transitions exiting p are removed to obtain \(\textit{prune}({P})\), we get a new \(p {\mathop {\longrightarrow }\limits ^{i}} e\). Thus, \(w \in {\text {ET}}({\textit{prune}({P})})\) and the first inclusion is established. Next, consider some \(w \in {\text {L}}({P})\). Either, some run underlying w is still in \(\textit{prune}({P})\) and \(w \in {\text {L}}({\textit{prune}({P})})\). Or, some transition of the run is missing and redirected to \(e\); then, some prefix of w and, thus, also w is in \({\text {EL}}({\textit{prune}({P})})\).
For the reverse inclusions, first consider a prefix-minimal \(w \in {\text {ET}}({\textit{prune}({P})})\). An underlying run ends with \(p{\mathop {\longrightarrow }\limits ^{i}} e\), where \(i \in I\) and \(p \ne e\). This run also exists in P up to the last transition and \(p {\mathop {\longrightarrow }\limits ^{i}} p'\) for some illegal \(p'\), implying \(w \in {\text {ET}}({P})\). Second, each run of \(\textit{prune}({P})\) exists in P as well, except if some transition along the run ends in \(e\) in \(\textit{prune}({P})\) and in some illegal \(p'\) in P. This implies \({\text {L}}({\textit{prune}({P})}) \subseteq {\text {EL}}({P})\). \(\square \)
Consequently, we may essentially work on EIOs without error states.
We conclude by remarking on how component compatibility is reflected in linear-time semantics. In fact, this notion is not so relevant for EIO, because parallel composition is always defined for composable EIOs. In Sect. 2, we have explained that components are incompatible if the initial state of their composition is illegal. Here, we have that the initial state of an EIO P is illegal if and only if \(\epsilon \in {\text {ET}}({P})\). Error-refinement preserves compatibility: if \(P_1 \sqsubseteq _EP_2\) and \(P_2\), Q are compatible, then \(\epsilon \notin {\text {ET}}({P_2 \Vert Q}) \supseteq {\text {ET}}({P_1 \Vert Q})\); hence, \(P_1\), Q are compatible, too.
4.3 Preserving freedom from quiescence
This section adds quiescence as an observable fault [38], which requires us to extend error semantics by quiescence traces, or qsc-traces for short. Analogous to our various kinds of error traces, we consider strict qsc-traces and error-flooded qsc-traces:
Definition 18
(Quiescence semantics) Let P be an EIO. We define the following:
-
Strict qsc-traces: \({\text {StQT}}({P}) =_{\text {df}}\{ w \in A^* \,|\, \exists p'.\, p_0 {\mathop {\Longrightarrow }\limits ^{w}} p' \in {\text {Qui}}({P}) \}\);
-
(Error-flooded) qsc-traces: \({\text {QET}}({P}) =_{\text {df}}{\text {StQT}}({P}) \cup {\text {ET}}({P})\).
We call \(({\text {ET}}({P}), {\text {QET}}({P}), {\text {EL}}({P}))\) the quiescence semantics of P. For EIOs \(P_1\), \(P_2\) with the same signature, we write \(P_1 \sqsubseteq _{\text {Qui}}P_2\) if \(P_1 \sqsubseteq _EP_2\) and \({\text {QET}}({P_1}) \subseteq {\text {QET}}({P_2})\).
For this refinement preorder, we now show some details how to prove full abstraction. The following lemma is easily seen with Lemma 13. Observe that if, say, \(p_1\) enables an output o, so does \((p_1,p_2)\) by input-enabledness.
Lemma 19
Let \(P_1\), \(P_2\) be EIOs and \(P_{12}\) be their parallel composition.
-
1.
A state \((p_1,p_2)\) in the parallel composition \(P_{12}\) is quiescent if and only if the states \(p_1\) and \(p_2\) are quiescent in \(P_1\) and \(P_2\), resp.
-
2.
Let \(w \in A_{12}^*\), as well as \(w_1 = w|_{A_1}\) and \(w_2 = w|_{A_2}\). Then, \(w \in {\text {StQT}}({P_{12}})\) if and only if \(w_1 \in {\text {StQT}}({P_1})\) and \(w_2 \in {\text {StQT}}({P_2})\).
This lemma is essential for proving that \(\sqsubseteq _{\text {Qui}}\) is compositional for parallel composition [38]:
Theorem 20
(Quiescence semantics for EIO-parallel composition) For composable EIOs \(P_1\), \(P_2\) and their composition \(P_{12}\):
-
1.
\({\text {ET}}({P_{12}}) = \textit{cont}({\textit{prune}({({\text {ET}}({P_1}) \Vert {\text {EL}}({P_2})) \cup ({\text {EL}}({P_1}) \Vert {\text {ET}}({P_2}))})})\);
-
2.
\({\text {QET}}({P_{12}}) = ({\text {QET}}({P_1}) \Vert {\text {QET}}({P_2})) \cup {\text {ET}}({P_{12}})\);
-
3.
\({\text {EL}}({P_{12}}) = ({\text {EL}}({P_1}) \Vert {\text {EL}}({P_2})) \cup {\text {ET}}({P_{12}})\).
Hence, \(\sqsubseteq _{\text {Qui}}\) is a precongruence wrt. EIO-parallel composition.
Proof
The first and the third part have been shown already for the previous setting in [38]; we recall the proof for the second part and note that \({\text {ET}}({P_{12}})\) is contained in both sides. For the inclusion, we only have to consider some \(w \in {\text {StQT}}({P_{12}})\), and this is in \({\text {QET}}({P_1}) \Vert {\text {QET}}({P_2})\) by Lemma 19(2). For the reverse inclusion, it suffices to consider some \(w_1 \in {\text {QET}}({P_1})\) and \(w_2 \in {\text {QET}}({P_2})\). If \(w_1\), say, is an error trace, then \(w_1 \Vert w_2\) is in \({\text {ET}}({P_1}) \Vert {\text {EL}}({P_2}) \subseteq {\text {ET}}({P_{12}})\) by the first part. Otherwise, \(w_1 \Vert w_2\) consists of strict qsc-traces, again by Lemma 19(2).
The precongruence result follows by monotonicity of \(\textit{cont}({})\), \(\textit{prune}({})\) and \(\Vert \). \(\square \)
It is relatively easy to show that \(\sqsubseteq _{\text {Qui}}\) is as fine as \(\sqsubseteq _{\text {Qui}}^C\), see the treatment of the reverse implication in the next proof. What is missing then is a proof that a precongruence wrt. EIO-parallel composition that refines \(\sqsubseteq _{\text {Qui}}^B\) is as fine as \(\sqsubseteq _{\text {Qui}}\), i.e., that \(\sqsubseteq _{\text {Qui}}\) is fully-abstract. What we prove is actually stronger: it suffices to be interested in a relation that is compositional wrt. \(\Vert \) just for partners and that refines \(\sqsubseteq _{\text {Qui}}^B\) just on systems without inputs. On such systems, which result from the composition with a partner, local reachability coincides with reachability. That we do not want to introduce a reachable error or quiescence in a refinement step if there was none initially, is possibly even more convincing than the same for local reachability. To prove the implication, we only use that \(\sqsubseteq _{\text {Qui}}^C\) has the two properties just declared to be sufficient [38]:
Theorem 21
(Full abstraction for quiescence semantics) For EIOs \(P_1\), \(P_2\) with the same signature, (1) \(P_1 \sqsubseteq _{\text {Qui}}^CP_2\) if and only if \(P_1 \sqsubseteq _{\text {Qui}}P_2\). Further, (2) \(P_1 \sqsubseteq _{\text {Qui}}P_2\) holds if \(U \Vert P_1 \sqsubseteq _{\text {Qui}}^BU \Vert P_2\) for all partners U.
Proof
(1) “\(\Longleftarrow \)”: If \(P_1 \sqsubseteq _{\text {Qui}}P_2\) and \(P_1\) can reach an error locally, we have \(\epsilon \in {\text {ET}}({P_1})\); hence, \(\epsilon \in {\text {ET}}({P_2})\) and \(P_2\) can reach an error locally. If \(P_1 \sqsubseteq _{\text {Qui}}P_2\) and \(P_1\) can reach a quiescent state locally with some \(w \in {\text {QET}}({P_1})\), i.e., \(w \in O_1^*\), then \(w \in {\text {QET}}({P_2})\) and \(P_2\) can reach a quiescent or error state locally. Thus, \(\sqsubseteq _{\text {Qui}}\) is contained in \(\sqsubseteq _{\text {Qui}}^B\). Because \(\sqsubseteq _{\text {Qui}}\) is a precongruence wrt. \(\Vert \) and \(\sqsubseteq _{\text {Qui}}^C\) is the coarsest precongruence wrt. \(\Vert \), \(\sqsubseteq _{\text {Qui}}\) is contained in \(\sqsubseteq _{\text {Qui}}^C\).
(1) “\(\Longrightarrow \)”: For this part, we use the second statement, which we prove below. Due to \(\sqsubseteq _{\text {Qui}}^C\) being a precongruence, we have \(U \Vert P_1 \sqsubseteq _{\text {Qui}}^CU \Vert P_2\) for all partners U. Because \(\sqsubseteq _{\text {Qui}}^C\) is contained in \(\sqsubseteq _{\text {Qui}}^B\), this implies \(U \Vert P_1\sqsubseteq _{\text {Qui}}^BU \Vert P_2\) for all partners U. With the second statement, we get \(P_1 \sqsubseteq _{\text {Qui}}P_2\).
(2) Next, we give an impression of how to prove the second statement. We restrict ourselves to partners with \(I_U = O_1\) and \(O_U = I_1 \cup \{o\}\) for a fresh action o. This action allows the partner to prevent quiescence. In fact, \({\text {ET}}({P_1}) \subseteq {\text {ET}}({P_2})\) and \({\text {EL}}({P_1}) \subseteq {\text {EL}}({P_2})\) are shown in [38] with partners that enable o in each state such that quiescence does not play a role. We only recall the proof for \({\text {QET}}({P_1})\subseteq {\text {QET}}({P_2})\) [38]:
Due to ET-inclusion, it suffices to prove that any \(w = a_1\cdots a_n \in {\text {StQT}}({P_1})\) with \(n \ge 0\) is also in \({\text {QET}}({P_2})\). We construct the partner EIO U as shown in Fig. 4, where \(E_U = \emptyset \). Clearly, w reaches a quiescent state in \(U \Vert P_1\) and consists of outputs only. By assumption, also \(U \Vert P_2\) can locally reach an error state or quiescent state.
-
(a)
If an error is reached locally, U and \(P_2\) each perform some \(a_1 \cdots a_i u\) with some \(u \in I_U^*=O_1^*\) in the respective run. With this, \(P_2\) reaches a state in \(E_2\), because U does not have any errors. Thus, \(\textit{prune}({a_1 \cdots a_i u}) = \textit{prune}({a_1 \cdots a_i}) \in {\text {PrET}}({P_2}) \subseteq {\text {ET}}({P_2})\). This implies that \(a_1 \cdots a_i\) and also w are in \({\text {ET}}({P_2}) \subseteq {\text {QET}}({P_2})\).
-
(b)
If a quiescent state is reached locally, \(P_2\) performs w and reaches a quiescent state itself. Hence, \(w \in {\text {StQT}}({P_2}) \subseteq {\text {QET}}({P_2})\).
\(\square \)
Partner EIO U in the proof of Theorem 21, where \(a? \not = a_i\) represents all \(a \in I_U{\setminus }\{a_i\}\) and q is the only quiescent state
Quiescence is the counterpart of deadlock in standard LTS, and quiescence semantics and failure semantics [7] are just right to avoid these in the resp. settings. Hence, we can regard the former semantics as the counterpart of the latter. In failure semantics, each trace is combined with a set of visible actions that are impossible in some state that can be reached by the trace. Such a set is not needed here, because synchronization is of a different nature in the IA-setting. More precisely, the above semantics corresponds to stable failures, where sets are only considered for stable states. Quiescence semantics can also be seen as the counterpart of completed traces as defined by van Glabbeek [42].
Because hiding transforms one local action to another, the quiescence status of a state is not changed. Therefore, the following result holds (cf. Theorem 17 and [38]):
Theorem 22
(Quiescence precongruence for hiding) For EIO P and \(H \subseteq O\):
-
1.
\({\text {ET}}({P/ {H}}) = \{ w \in (A{\setminus }H)^* \,|\, \exists w' \in {\text {ET}}({P}).\; w'|_{A{\setminus }H} = w \}\);
-
2.
\({\text {EL}}({P/ {H}}) = \{ w \in (A{\setminus }H)^* \,|\, \exists w' \in {\text {EL}}({P}).\; w'|_{A{\setminus }H} = w \}\);
-
3.
\({\text {StQT}}({P/ {H}}) = \{ w \in (A{\setminus }H)^* \,|\, \exists w' \in {\text {StQT}}({P}).\; w'|_{A{\setminus }H} = w \}\);
-
4.
\({\text {QET}}({P/ {H}}) = \{w \in (A{\setminus }H)^* \,|\, \exists w' \in {\text {QET}}({P}).\; w'|_{A{\setminus }H} = w \}\).
Hence, \(\sqsubseteq _{\text {Qui}}\) is a precongruence wrt. hiding.
Analogous to the situation in error semantics, we add to the results of [38] that pruning an EIO preserves its quiescence semantics:
Theorem 23
(Pruning) Each EIO P is quiescence-equivalent to \(\textit{prune}({P})\).
Proof
In view of Theorem 17, we only have to deal with the QET-sets. As in the proof of that theorem, we assume that \(p_0\) is not illegal. For a strict qsc-trace w of P, a suitable underlying run still exists in \(\textit{prune}({P})\), or it is cut because a prefix of w can lead to an illegal state. Thus, \(w \in {\text {QET}}({\textit{prune}({P})})\). Conversely, a run in \(\textit{prune}({P})\) underlying a strict qsc-trace \(w \notin {\text {ET}}({\textit{prune}({P})})\) also exists in P. \(\square \)
The authors of [11] use the same definition of quiescent state as we do, but regard it as necessary to consider divergence when dealing with quiescence. Their intuition could be that a system can be stuck in a divergent state, just as it can be in a state with only inputs. This view could be supported by the notion of complete traces in [44], which includes strict div-traces. With such a view, divergence and our quiescence are regarded as faults, and the coarsest precongruence is \(\sqsubseteq _{\text {Div}}\), presented in Sect. 4.4.
Another variant is to define a state \(p \in P\) as quiescent if there is no output o with \(p {\mathop {\Longrightarrow }\limits ^{o}}\). Due to \(\tau \)-transitions, such a p might not be quiescent in our sense, so we call it weakly quiescent. Let \({\text {wQui}}({P})\) be the set of these states. Starting from \({\text {wQui}}({P})\), we can modify the definitions of \({\text {StQT}}({P})\), \({\text {QET}}({P})\) and \(\sqsubseteq _{\text {Qui}}\) to obtain \({\text {wStQT}}({P})\), \({\text {wQET}}({P})\) and \(\sqsubseteq _{\text {wQui}}\). Similarly, we can define weak versions of \(\sqsubseteq _{\text {Qui}}^B\) and \(\sqsubseteq _{\text {Qui}}^C\). Because we have given all quiescence-relevant proofs for Theorems 20 and 21, it should not be hard to check that the easy Lemma 19 as well as the ‘weak versions’ of the two theorems hold. Thus, we have also a full-abstraction result for this variant of quiescence. Unfortunately, this is not really satisfactory, because \(\sqsubseteq _{\text {wQui}}\) is not a precongruence for hiding, as can be seen from P, \(P'\) in Fig. 5. Both EIOs have no errors and the same traces, as well as \({\text {wStQT}}({P}) = {\text {wStQT}}({P'})\). After hiding o, however, \(\epsilon \in {\text {wStQT}}({P})\) but \(\epsilon \notin {\text {wStQT}}({P'})\). Developing a fully-abstract precongruence for parallel composition and hiding with this variant of quiescence is an open problem.
4.4 Preserving freedom from divergence
Lastly, we add divergence as a third observable for a fault in EIO and, therefore, consider divergent traces, too [38]. Note that divergent behaviour of some component cannot be prevented when placing the component in any environment and, thus, not only errors but also divergences are catastrophic. Consequently, in addition to strict divergent traces, their pruned and continuation variants are also of interest:
Definition 24
(Divergent traces) Let P be an EIO. We define the following:
-
Strict div-traces: \({\text {StDT}}({P}) =_{\text {df}}\{w \in A^* \,|\, \exists p'.\, p_0 {\mathop {\Longrightarrow }\limits ^{w}} p' \in {\text {Div}}({P}) \}\);
-
Pruned div-traces: \({\text {PrDT}}({P}) =_{\text {df}}\{ \textit{prune}({w}) \,|\, w \in {\text {StDT}}({P}) \}\);
-
Div-traces \({\text {DT}}({P}) =_{\text {df}}\textit{cont}({{\text {PrDT}}({P})})\).
This leads to the definition of divergence semantics [38], for which the quiescence semantics from above needs to be modified by flooding with div-traces:
Definition 25
(Divergence semantics) Let P be an EIO. We define the following:
-
Error-div-traces: \({\text {EDT}}({P}) =_{\text {df}}{\text {DT}}({P}) \cup {\text {ET}}({P})\);
-
Flooded qsc-traces: \({\text {QDT}}({P}) =_{\text {df}}{\text {StQT}}({P}) \cup {\text {EDT}}({P})\);
-
Flooded language: \({\text {EDL}}({P}) =_{\text {df}}{\text {L}}({P}) \cup {\text {EDT}}({P})\).
We call \(({\text {EDT}}({P}), {\text {QDT}}({P}), {\text {EDL}}({P}))\) the divergence semantics of P. For EIOs \(P_1\), \(P_2\) with the same signature, we write \(P_1 \sqsubseteq _{\text {Div}}P_2\) if \({\text {EDT}}({P_1}) \subseteq {\text {EDT}}({P_2})\), \({\text {QDT}}({P_1}) \subseteq {\text {QDT}}({P_2})\) and \({\text {EDL}}({P_1}) \subseteq {\text {EDL}}({P_2})\).
The divergence semantics here is the counterpart to the failure-divergence semantics of [7]. Although the new refinement is closely related to the previous ones, the sets in the semantics above are all different from the previous sets because of the flooding due to divergence. We now report on compositionality and full abstraction for \(\sqsubseteq _{\text {Div}}\) [38]:
Theorem 26
(Divergence semantics for EIO-parallel composition) For composable EIOs \(P_1\), \(P_2\) and their composition \(P_{12}\):
-
1.
\({\text {EDT}}({P_{12}}) = \textit{cont}({\textit{prune}({({\text {EDT}}({P_1}) \Vert {\text {EDL}}({P_2})) \cup ({\text {EDL}}({P_1}) \Vert {\text {EDT}}({P_2}))})})\);
-
2.
\({\text {QDT}}({P_{12}}) = ({\text {QDT}}({P_1}) \Vert {\text {QDT}}({P_2})) \cup {\text {EDT}}({P_{12}})\);
-
3.
\({\text {EDL}}({P_{12}}) = ({\text {EDL}}({P_1}) \Vert {\text {EDL}}({P_2})) \cup {\text {EDT}}({P_{12}})\).
Hence, \(\sqsubseteq _{\text {Div}}\) is a precongruence wrt. EIO-parallel composition. Furthermore, \(\sqsubseteq _{\text {Div}}\) is fully-abstract, i.e., it coincides with \(\sqsubseteq _{\text {Div}}^C\).
In a divergence-sensitive setting, precongruence for hiding usually needs some finiteness condition. For simplicity, we restrict ourselves to finite EIOs and to the hiding of single outputs as in [38]. Hiding of finite sets can be obtained by repeating such hiding. We write \(P / {o}\) for \(P / {\{o\}}\), where \(o \in O\). Note that, in the following result, \({\text {EDT}}({P/ {o}})\) is obtained from \({\text {EDL}}({P})\); it is larger than just \(\{ w \,|\, \exists w' \in {\text {EDT}}({P}).\, w'|_{A{\setminus }\{o\}} = w \}\). Due to the latter, the other two sets need a new flooding:
Theorem 27
(Divergence precongruence for hiding) Let P be a finite EIO and \(o \in O\). Then,
-
1.
\({\text {EDT}}({P/ {o}}) = \textit{cont}({\textit{prune}({ \{w \,|\, \exists w'.\; w'|_{A{\setminus }\{o\}} = w \text { and } \forall n\ge 0.\; w'o^n \in {\text {EDL}}({P}) \} }) })\);
-
2.
\({\text {EDL}}({P/ {o}}) = \{w \,|\, \exists w'\in {\text {EDL}}({P}).\; w'|_{A{\setminus }\{o\}} = w \} \cup {\text {EDT}}({P/ {o}})\);
-
3.
\({\text {QDT}}({P/ {o}}) = \{ w \,|\, \exists w' \in {\text {QDT}}({P}).\; w'|_{A{\setminus }\{o\}} = w \} \cup {\text {EDT}}({P/ {o}})\).
Hence, \(\sqsubseteq _{\text {Div}}\) is a precongruence wrt. hiding.
The finiteness requirement on EIO P in this theorem may be replaced by the weaker requirement that P is image-finite. We have chosen finiteness because this is also assumed in [38] and, throughout, in [11].
Divergence semantics yields a new, analogous theorem regarding pruning insensitivity as above for error semantics and quiescence semantics:
Theorem 28
(Pruning) Each EIO P is divergence-equivalent to \(\textit{prune}({P})\).
Proof
Again, we assume that \(q_0\) is not illegal. For the EDT-semantics, we already know that pruning preserves the ET-semantics. For a prefix-minimal \(w \in {\text {DT}}({P})\), a suitable underlying run still exists in \(\textit{prune}({P})\), or it is cut because a prefix of w can lead to an illegal state. Thus, \(w \in {\text {EDT}}({\textit{prune}({P})})\). A run in \(\textit{prune}({P})\) underlying a strict div-trace \(w \notin {\text {ET}}({\textit{prune}({P})})\) also exists in P. Together, pruning preserves the EDT-semantics.
For a strict qsc-trace w of P, we can argue as in the proof of Theorem 23 that \(w \in {\text {QET}}({\textit{prune}({P})}) \subseteq {\text {QDT}}({\textit{prune}({P})})\). A run in \(\textit{prune}({P})\) underlying a strict qsc-trace \(w \notin {\text {ET}}({\textit{prune}({P})})\) also exists in P, and preservation of the QDT-semantics follows.
The arguments for preservation of the L-semantics are the same as in the proof of Theorem 17, again because the ET-semantics is contained in the EDT-semantics. \(\square \)
We end this section by discussing the implications of the weak quiescence variant on the divergence semantics; recall the definitions at the end of Sect. 4.3.
Remark 29
Adapting the divergence semantics to this weak variant, we let \({\text {QDT}}({P})\) be built upon \({\text {wStQT}}({P})\) instead of \({\text {StQT}}({P})\), resulting in \({\text {wQDT}}({P})\). This semantics can only differ from divergence semantics, if there is some \(w \in {\text {wStQT}}({P}){\setminus }{\text {StQT}}({P})\) due to some \(p_0 {\mathop {\Longrightarrow }\limits ^{w}} p \in {\text {wQui}}({P})\). Because \(p \notin {\text {Qui}}({P})\) by choice of w, it has a \(\tau \)-transition to some \(p'\). However, due to \(p \in {\text {wQui}}({P})\), it cannot reach by \(\tau \)-transitions a state that enables an output. The same applies to \(p'\), so we have \(p_0 {\mathop {\Longrightarrow }\limits ^{w}} p' \in {\text {wQui}}({P})\). Repeating this argument, p is seen to be divergent. We conclude that \(w \in {\text {QDT}}({P})\), so the weak variant of divergence semantics coincides with the one of Definition 25. Similarly, \(\sqsubseteq _{\text {Div}}^B\) does not change for weak quiescence, and full abstraction holds for the variant because we would only change the text of the definitions but not the relations.
4.5 CJK-semantics
Another quiescence- and divergence-sensitive precongruence is presented by Chilton et al. [11] and denoted here by \(\sqsubseteq _{\text {CJK}}\). This is based on sets like \({\text {ET}}({\cdot })\) and \({\text {EL}}({\cdot })\), too, but \({\text {ET}}({\cdot })\) is not closed under pruning, and this difference carries over to the other semantic sets like \({\text {EL}}({\cdot })\). To compensate this, refinement is not component-wise inclusion. Here, we give a new characterization of \(\sqsubseteq _{\text {CJK}}\) in the style of the above precongruences:
Definition 30
(CJK-semantics) Let P be an EIO. We define the following:
-
Error-flooded strict div-traces: \({\text {ESDT}}({P}) =_{\text {df}}{\text {StDT}}({P}) \cup {\text {ET}}({P})\);
-
ESD-flooded strict qsc-traces: \({\text {ESDQ}}({P}) =_{\text {df}}{\text {StQT}}({P}) \cup {\text {ESDT}}({P})\).
\(({\text {ET}}({P}), {\text {ESDT}}({P}), {\text {ESDQ}}({P}), {\text {EL}}({P}))\) is the CJK-semantics of P. For EIOs \(P_1, P_2\) with the same signature, we write \(P_1 \sqsubseteq _{\text {CJK}}P_2\) for the resp. component-wise inclusion.
Observe that, as CJK-refinement works with strict div-traces, it is finer than \(\sqsubseteq _{\text {Div}}\) where div-traces are closed under pruning and continuation. Our new characterization leads to new equations in the next theorem; they look quite similar to those in [11], but the proof obligations are a bit different so that we provide the theorem’s proof.
Theorem 31
(CJK-semantics for EIO-parallel composition) For two composable EIOs \(P_1\), \(P_2\) and their composition \(P_{12}\):
-
1.
\({\text {ESDT}}({P_{12}}) = ({\text {ESDT}}({P_1}) \Vert {\text {EL}}({P_2})) \cup ({\text {EL}}({P_1}) \Vert {\text {ESDT}}({P_2})) \cup {\text {ET}}({P_{12}})\);
-
2.
\({\text {ESDQ}}({P_{12}}) = ({\text {ESDQ}}({P_1}) \Vert {\text {ESDQ}}({P_2})) \cup {\text {ESDT}}({P_{12}})\).
Hence, \(\sqsubseteq _{\text {CJK}}\) is a precongruence wrt. EIO-parallel composition.
Proof
We start with the first equation and note that both sides contain \({\text {ET}}({P_{12}})\). For inclusion, consider a strict div-trace of \(P_1 \Vert P_2\). It projects to a strict div-trace of one component and a trace of the other, so it is contained in the right-hand side. For the reverse inclusion, consider w.l.o.g. some \(w \in {\text {ESDT}}({P_1}) \Vert {\text {EL}}({P_2})\) that is not an error trace. Then, \(w|_{A_1}\) is a strict div-trace and \(w|_{A_2}\) is a trace, so w is a strict div-trace. The proof of the second equation is similar, except that a strict qsc-trace projects to two strict qsc-traces, and w is not an error trace or a strict div-trace. \(\square \)
At this stage, we can discuss the patterns that appear when determining the semantic sets of a parallel composition. A strict error trace (div-trace) of the composition projects to a strict error trace (div-trace) of one component and a trace of the other. This explains subsets such as \({\text {ET}}({P_1}) \Vert {\text {EL}}({P_2})\), \({\text {EDT}}({P_1}) \Vert {\text {EDL}}({P_2})\) and \({\text {ESDT}}({P_1}) \Vert {\text {EL}}({P_2})\). The resulting sets are not necessarily closed under pruning, so \({\text {EDT}}({P_{12}})\) and \({\text {ET}}({P_{12}})\) have to be closed under pruning and then under continuation. For a trace or strict qsc-trace, both projections must be traces or strict qsc-traces, leading to \({\text {EL}}({P_1}) \Vert {\text {EL}}({P_2})\), \({\text {EDL}}({P_1}) \Vert {\text {EDL}}({P_2})\), \({\text {QET}}({P_1}) \Vert {\text {QET}}({P_2})\), \({\text {QDT}}({P_1}) \Vert {\text {QDT}}({P_2})\) and \({\text {ESDQ}}({P_1}) \Vert {\text {ESDQ}}({P_2})\).
The resp. semantic sets are flooded with the pruning- and continuation-closed sets \({\text {ET}}({\cdot })\) or \({\text {EDT}}({\cdot })\). But though, e.g., \({\text {EL}}({P_1}) \Vert {\text {EL}}({P_2})\) contains \(({\text {ET}}({P_1}) \Vert {\text {EL}}({P_2})) \cup ({\text {EL}}({P_1}) \Vert {\text {ET}}({P_2}))\), it might fail to contain all pruned error traces of the composition. Hence, \({\text {ET}}({P_{12}})\) (\({\text {EDT}}({P_{12}})\)) has to be added to get \({\text {EL}}({P_{12}})\) (\({\text {EDL}}({P_{12}})\)), and the case of \({\text {ESDT}}({P_{12}})\) is similar. For \({\text {QET}}({P_{12}})\) and \({\text {QDT}}({P_{12}})\), even some strict error or div-traces may be missing, because these semantic sets might not cover the language. The same argument (for strict div-traces) shows that, for \({\text {ESDQ}}({P_{12}})\), adding \({\text {ET}}({P_{12}})\) might not suffice.
Hiding can be handled similarly to the resp. results above; see [11] for details. Again, pruning of an EIO preserves the semantics. For the proof, one can argue for strict div- and qsc-traces as for strict qsc-traces in the proof of Theorem 23.
Theorem 32
(Pruning) Each EIO P is CJK-equivalent to \(\textit{prune}({P})\).
4.6 Ready semantics
This section adds to the class of linear-time refinements for IA a counterpart to standard ready semantics [42]. In that semantics, for each run, its trace is combined with the set of visible actions offered in the state that is reached by the run. Due to input-enabledness, only local actions are relevant here. But also without the assumption, one should proceed this way: inputs that are missing in a state give rise to error traces and, thus, have some visibility already. Inputs that are possible in a state but missing in another state reached by the same trace, are not so relevant, because the environment would risk an error when providing such an input; we assume that the environment does not do this. Thus, and consistent with the above notion of quiescence, we include all actions that, in the resp. state, can prevent such a quiescence.
Definition 33
(Ready semantics) Let P be an EIO. We define the following:
-
Strict ready pairs: \({\text {StRP}}({P}) =_{\text {df}}\{ (w,X) \in A^* \times {{\mathscr {P}}}({O_\tau }) \,|\, \exists p'.\, p_0{\mathop {\Longrightarrow }\limits ^{w}} p'\) and \(X = {\mathbb {R}}({p'}) \}\), where \({\mathbb {R}}({p'}) =_{\text {df}}\{ \omega \in O_{\tau } \,|\, p' {\mathop {\longrightarrow }\limits ^{\omega }} \}\) is called the ready set of \(p'\);
-
(Error-flooded) ready pairs: \({\text {RP}}({P}) =_{\text {df}}{\text {StRP}}({P}) \cup \{ (w, X) \,|\, w \in {\text {ET}}({P}),\, X \subseteq O_{\tau } \}\).
We call \(({\text {ET}}({P}), {\text {RP}}({P}))\) the ready semantics of P. Note that \({\text {EL}}({P})\) can be derived as \(\{w \in A^* \,|\, \exists X \subseteq O_{\tau }.\, (w,X) \in {\text {RP}}({P}) \}\). For EIOs \(P_1\), \(P_2\) with the same signature, we write \(P_1\sqsubseteq _{\text {Rd}}P_2\) if \({\text {ET}}({P_1}) \subseteq {\text {ET}}({P_2})\) and \({\text {RP}}({P_1}) \subseteq {\text {RP}}({P_2})\).
Ready semantics allows for compositional reasoning, too:
Theorem 34
(Ready semantics for EIO-parallel composition) For composable EIOs \(P_1\), \(P_2\) and their composition \(P_{12}\):
-
1.
\({\text {ET}}({P_{12}}) = \textit{cont}({\textit{prune}({({\text {ET}}({P_1}) \Vert {\text {EL}}({P_2})) \cup ({\text {EL}}({P_1}) \Vert {\text {ET}}({P_2}))})})\);
-
2.
\({\text {RP}}({P_{12}}) = {\text {ET}}({P_{12}}) \cup \{ (w,X) \,|\, \exists X_1, X_2.\; X = X_1 \cup X_2,\; (w|_{A_1}, X_1) \in {\text {RP}}({P_1}) \text { and} (w|_{A_2}, X_2) \in {\text {RP}}({P_2}) \}\).
Hence, \(\sqsubseteq _{\text {Rd}}\) is a precongruence wrt. EIO-parallel composition.
Proof
For the second equation, consider some (w, X) in the left-hand side and the projections \(w_1\) and \(w_2\) of w. If \(w \in {\text {ET}}({P_{12}})\), all possible pairs with w are contained in both sides. Otherwise, \((w,X) \in {\text {RP}}({P_{12}})\) due to some \((p_{01},p_{02}) {\mathop {\Longrightarrow }\limits ^{w}} (p_1,p_2)\). Then, \(p_{01} {\mathop {\Longrightarrow }\limits ^{w_1}} p_1\) and \(p_{02} {\mathop {\Longrightarrow }\limits ^{w_2}}p_2\) by Lemma 13. Because the ready set X of \((p_1,p_2)\) is the union of the ready sets of \(p_1\) and \(p_2\) by input-enabledness, (w, X) is contained in the right-hand side as well.
If \((w_1,X_1)\) and \((w_2,X_2)\) satisfy the conditions on the right-hand side, each \(w_i\) is contained in the resp. flooded language. If one of them is an error trace, then w is as well. Otherwise, there are suitable runs \(p_{01} {\mathop {\Longrightarrow }\limits ^{w_1}} p_1\) and \(p_{02} {\mathop {\Longrightarrow }\limits ^{w_2}} p_2\) and, in both cases, we are done as above. \(\square \)
Because only outputs are hidden when applying our hiding operator, each ready set is modified by deleting hidden outputs and adding \(\tau \) if some output is deleted. This also works for a ready pair in which the trace is an error trace; adding \(\tau \) is not necessary here.
Theorem 35
(Ready precongruence for hiding) Let P be an EIO and \(H \subseteq O\). Then,
-
1.
\({\text {ET}}({P/ {H}}) = \{ w \in (A{\setminus }H)^* \,|\, \exists w'\in {\text {ET}}({P}).\; w'|_{A{\setminus }H} = w \}\);
-
2.
\({\text {RP}}({P/ {H}}) = \{ (w,X) \,|\, \exists (w',X')\in {\text {RP}}({P}).\, w'|_{A{\setminus }H} = w, \text { and } X = (X'{\setminus }H) \cup \{\tau \}, \text { if} \, X' \cap H \ne \emptyset , \text { and } X = X'{\setminus }H, \text { otherwise} \}\).
Hence, \(\sqsubseteq _{\text {Rd}}\) is a precongruence wrt. hiding.
Again, pruning of an EIO preserves the semantics:
Theorem 36
(Pruning) Each EIO P is ready-equivalent to \(\textit{prune}({P})\).
Proof
Analogously to above, we just have to deal with the strict ready pairs and assume that \(p_0\) is not illegal. Also, it suffices to consider a pair in which the trace is not an error trace. The underlying runs are the same in both EIOs, and the transitions exiting from the reached state are only modified if they are inputs. \(\square \)
4.7 The linear-time IA-spectrum
The resulting overall spectrum of linear-time preorders on EIO is shown in Fig. 6:
Theorem 37
(Linear-time IA spectrum) All inclusions between \(\sqsubseteq _E\), \(\sqsubseteq _{\text {Qui}}\), \(\sqsubseteq _{\text {Div}}\), \(\sqsubseteq _{\text {CJK}}\) and \(\sqsubseteq _{\text {Rd}}\) are depicted in Fig. 6 as arrows; note that these inclusions are strict.
Proof
The inclusions of the preorders except for \(\sqsubseteq _{\text {Rd}}\) have been established in [38]. In case an inclusion holds, this is because the semantic sets needed in the larger preorder can be determined from the sets employed by the smaller preorder. This is also the case for the inclusion of \(\sqsubseteq _{\text {Rd}}\) in \(\sqsubseteq _{\text {Qui}}\): from \({\text {RP}}({P})\), one can read off \({\text {EL}}({P})\) as noted above, and \({\text {QET}}({P}) = \{ w \,|\, (w, \emptyset ) \in {\text {RP}}({P}) \}\).
The proofs that the missing inclusions fail to hold, are by example. In particular, \(\sqsubseteq _{\text {Qui}}\) is not included in \(\sqsubseteq _{\text {Rd}}\) as can be seen from EIOs \(Q_1\) and \(Q_2\) in Fig. 7, for which \(Q_1 \sqsubseteq _{\text {Qui}}Q_2\) but \(Q_1 \not \sqsubseteq _{\text {Rd}}Q_2\) due to the ready pair \((\epsilon , \{o\})\). Observe that no state is quiescent or an error. To check that no other preorder implies \(\sqsubseteq _{\text {Rd}}\), it suffices to show that \(\sqsubseteq _{\text {CJK}}\) is not included in \(\sqsubseteq _{\text {Rd}}\). Consider EIOs \(Q_3\) and \(Q_4\) in Fig. 7, for which \(Q_3 \sqsubseteq _{\text {CJK}}Q_4\) because the additional strict quiescent trace \(\epsilon \) in \(Q_3\) is covered by the divergence \(\epsilon \). However, \(Q_3 \not \sqsubseteq _{\text {Rd}}Q_4\) due to the ready pair \((\epsilon , \emptyset )\). It remains to show that \(\sqsubseteq _{\text {Rd}}\) is not included in \(\sqsubseteq _{\text {Div}}\). For this, we refer to the EIOs \(Q_5\) and \(Q_6\) in Fig. 7, where \(Q_5 \sqsubseteq _{\text {Rd}}Q_6\) but \(Q_5 \not \sqsubseteq _{\text {Div}}Q_6\). Note that \(Q_6\) also has the ready pair \((\epsilon , \{\tau \})\) by staying in its initial state.
The other counterexamples for failing inclusions are given in [38]. It might be instructive to recall why \(\sqsubseteq _{\text {Div}}\) is not included in any of the other preorders. Simply take \(Q_5\) and the div-equivalent EIO consisting of a single, initial error-state. \(\square \)
5 Branching-time preorders
This section develops the branching-time spectrum for IA. It first recalls de Alfaro and Henzinger’s original IA-refinement [12], as well as their notion of alternating simulation that they adopted four years later in [13]. Whereas the former preorder is defined on general IA, the latter requires input-determinism in order to be a precongruence for parallel composition. Possibly, the former preorder was abandoned by de Alfaro and Henzinger as parallel composition is not associative in the setting of [12], unless our proper pruning is applied or, alternatively, the setting is restricted to input-deterministic IA as in [13] (cf. Sect. 2). Below, we first characterize both preorders in terms of standard simulations (see Theorems 42, 45), discuss a couple of preorders studied by Göhrle [21] that lie in-between, and adapt ready simulation to the IA-setting. We then introduce several bi-variant variations [3] of alternating simulation, including IA-bisimulation. We conclude this section by proving that (almost) all considered preorders are precongruences for IA, possibly under some restrictions, and by presenting the branching-time IA-spectrum, for which we also study its relationships with the linear-time spectrum of Sect. 4.
We start off by introducing several kinds of initial action set for a state p in a given IA P, which are needed in the definitions of the branching-time preorders:
Intuitively, \({\mathbb {I}}_\forall ({p})\) and \({\mathbb {O}}_\exists ({p})\) capture the guaranteed inputs and possible outputs of p, resp., while \({\text {I}}({p}) \supseteq {\mathbb {I}}_\forall ({p})\) contains all inputs that are immediately enabled at p.
5.1 Original IA-refinement
We revisit the first refinement preorder devised by de Alfaro and Henzinger for IA [12], which we call IA-refinement \(\preceq _{\text {IA}}\). Our definition adopts the phrasing employed by Chilton et al. [11]:
Definition 38
(IA-refinement) For IAs P, Q with the same signature, \({{\mathscr {R}}} \,\subseteq P \times Q\) is an IA-simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\({\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p})\);
-
2.
\({\mathbb {O}}_\exists ({p}) \subseteq {\mathbb {O}}_\exists ({q})\);
-
3.
\(p \Longrightarrow {\mathop {\longrightarrow }\limits ^{a}} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{a}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(a \in {\mathbb {I}}_\forall ({q}) \cup {\mathbb {O}}_\exists ({p})\).
P IA-refines Q, in signs \(P \preceq _{\text {IA}}Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some IA-simulation \({{\mathscr {R}}}\).
IA-refinement is a preorder and defined on the basis of a simulation with a couple of non-standard features. First, the step of the implementation side requires one to also consider steps with leading \(\tau \)s; although \(\tau \)-transitions do not have to be matched explicitly, in general many more matches have to be found than is usual for a simulation. Furthermore, the step on the specification side does not allow trailing \(\tau \)s. Second, there is an unusual superset inclusion on \({\mathbb {I}}_\forall ({\cdot })\). The idea is that \({\mathbb {I}}_\forall ({\cdot })\) contains the guaranteed inputs, and only the guaranteed inputs in the specification are simulated. This is because the environment cannot rely on other inputs, i.e., those that can be dropped after some \(\tau \)-transitions. The environment does not send such an input in order not to cause an error and, thus, the implementation does not have to provide it. Finally, observe that the second condition follows from the third, so we ignore the former in the following. We can also ignore \({\mathbb {O}}_\exists ({p})\), replacing it by the output alphabet O in the third condition.
Next, we define a standard simulation combined with the idea of guaranteed inputs, called (input) acceptance refinement \(\preceq _{\text {acc}}\), which turns out to characterize IA-simulation. Our definition closely resembles I4-refinement \(\preceq _{\text {sacc}}^4\) of Göhrle’s Master’s thesis [21]. Indeed, his definition differs only in the first condition from ours, where he demands \({\mathbb {I}}_\forall ({q}) \subseteq {\text {I}}({p})\).
Definition 39
(Acceptance refinement) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is an (input) acceptance simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\({\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p})\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in {\mathbb {I}}_\forall ({q})\);
-
3.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \).
P acc-refines Q, in signs \(P \preceq _{\text {acc}}Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some acceptance simulation \({{\mathscr {R}}}\).
The term acceptance refinement uses acceptance sets, which is the name Hennessy adopted for ready sets in the following context with standard labelled transition systems [23]: he requires that an implementation state has a larger ready set than the specification state that it refines. Hence, if the implementation refuses an action set, then the specification also refuses this action set. This leads to a compact representation for checking failures inclusion [7].
For the proof of the coincidence of IA-refinement and acceptance refinement, we employ a saturation on simulation relations:
Definition 40
(Saturation) For IAs P, Q and \({{\mathscr {R}}} \subseteq P \times Q\), we define:
\({{\mathscr {R}}}_L\) and \({{\mathscr {R}}}_R\) are called the left-saturation and right-saturation of \({{\mathscr {R}}}\), resp.
Lemma 41
If \({{\mathscr {R}}}\) is an IA-simulation, then so are \({{\mathscr {R}}}_{L}\) and \({{\mathscr {R}}}_{R}\).
Proof
Regarding \({{\mathscr {R}}}_{L}\), consider: (1) \({\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p}) \subseteq {\mathbb {I}}_\forall ({p''})\); (3) if \(p'' \Longrightarrow {\mathop {\longrightarrow }\limits ^{a}} p'\), then \(p \Longrightarrow {\mathop {\longrightarrow }\limits ^{a}} p'\). An analogous proof works for \({{\mathscr {R}}}_R\). \(\square \)
We can now prove the desired characterization result, which was not noticed by Göhrle [21]:
Theorem 42
(Coincidence I) \(\preceq _{\text {IA}}\;=\; \preceq _{\text {acc}}\).
Proof
For inclusion “\(\subseteq \)”, consider some IA-simulation \({{\mathscr {R}}}\) and its saturation \({{\mathscr {R}}}_{L}\) according to Definition 40. Assume \((p'',q) \in {{\mathscr {R}}}_{L}\) due to \((p,q) \in {{\mathscr {R}}}\) and further \(p'' {\mathop {\longrightarrow }\limits ^{\alpha }} p'\). For \(\alpha \ne \tau \), a suitable match exists due to the third condition of Definition 38. If \(\alpha = \tau \), then \(p \Longrightarrow p'\) and \((p',q) \in {{\mathscr {R}}}_{L}\) by saturation. Hence, \({{\mathscr {R}}}_{L}\) is an acceptance simulation.
Regarding inclusion “\(\supseteq \)”, let \({{\mathscr {R}}}\) be an acceptance simulation and consider its right-saturation \({{\mathscr {R}}}_{R}\). Assume \((p,q'') \in {{\mathscr {R}}}_R\) due to \((p,q) \in {{\mathscr {R}}}\). First, we note that \({\mathbb {I}}_\forall ({q''}) \subseteq {\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p})\). Now, let \(p \Longrightarrow p''' {\mathop {\longrightarrow }\limits ^{a}} p'\) for \(a \in {\mathbb {I}}_\forall ({q}) \cup O\). By repeated application of acceptance simulation, one obtains \(q \Longrightarrow q''' \Longrightarrow {\mathop {\longrightarrow }\limits ^{a}} q'''' \Longrightarrow q'\) for some \(q'''\), \(q''''\) and \(q'\) with \((p''',q'''), (p',q') \in {{\mathscr {R}}}\). Note that \(a \in {\mathbb {I}}_\forall ({q'''})\) if \(a \in {\mathbb {I}}_\forall ({q})\). Hence, \(q'' \Longrightarrow {\mathop {\longrightarrow }\limits ^{a}} q''''\) and \((p',q'''') \in {{\mathscr {R}}}_R\), and \({{\mathscr {R}}}_{R}\) is an IA-simulation. \(\square \)
5.2 Standard IA-refinement
Today’s understanding of the IA-setting considers alternating simulation \(\preceq _{\text {alt}}\) [13] as the refinement preorder on IA:
Definition 43
(Alternating simulation) For input-deterministic IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is an alternating simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\(q {\mathop {\longrightarrow }\limits ^{i}} q'\) implies \(\exists p'.\; p {\mathop {\longrightarrow }\limits ^{i}} p'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in I\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \).
P alt-refines Q, in signs \(P \preceq _{\text {alt}}Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some alternating simulation \({{\mathscr {R}}}\).
Note that this preorder is only defined on input-deterministic IA. This is because, otherwise, alt-refines is not a precongruence for parallel composition, independent of the pruning used. As an example, consider the IAs P, Q, R in Fig. 8 (cf. [30]), where P violates input-determinism in its initial state. We would have \(P \preceq _{\text {alt}}Q\) because P can obviously match Q’s i?-transition. However, the additional i?-branch of P means that \(P |R\) is undefined due to backward propagation, whereas \(Q |R\) is defined.
We show how compositionality can be fixed by providing an alternative definition, which yields a preorder that coincides with alternating simulation on input-deterministic IAs, but is a precongruence for all IAs. The trick is to define a pure simulation that matches only the inputs that are enabled in the specification, as demanded by the first condition of alternating simulation. Our resulting strict acceptance refinement \(\preceq _{\text {sacc}}\) does this by adding a condition on initial input action sets, this time concerning all initial input actions \({\text {I}}({\cdot })\) instead of only the guaranteed input actions \({\mathbb {I}}_\forall ({\cdot })\) as above. We call our preorder strict, because more inputs have to be matched than in acceptance refinement.
Definition 44
(Strict acceptance refinement) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is a strict acceptance simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\({\text {I}}({q}) \subseteq {\text {I}}({p})\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q {\mathop {\longrightarrow }\limits ^{i}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in {\text {I}}({q})\);
-
3.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \).
P sacc-refines Q, in signs \(P \preceq _{\text {sacc}}Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some strict acceptance simulation \({{\mathscr {R}}}\).
This definition was studied by Göhrle [21] under the name I1-refinement, where also the desired coincidence result was proved:
Theorem 45
(Coincidence II) \(\preceq _{\text {alt}}\;=\; \preceq _{\text {sacc}}\) on input-deterministic IAs.
Proof
We show that the two types of simulations are the same. For establishing inclusion “\(\subseteq \)”, the first condition of alternating simulation implies the first condition of strict acceptance simulation. Further, let \(p {\mathop {\longrightarrow }\limits ^{i}} p'\) be the i-transition of p for some \(i \in {\text {I}}({q})\); this transition is unique due to input-determinism. Then, q has a unique i-transition \(q {\mathop {\longrightarrow }\limits ^{i}} q'\). Hence, the first condition of alternating simulation also implies the second condition of strict acceptance simulation.
Regarding inclusion “\(\supseteq \)”, let \(q {\mathop {\longrightarrow }\limits ^{i}} q'\) be the unique i-transition of q. The first condition of strict acceptance simulation implies that p has a (unique) i-transition \(p {\mathop {\longrightarrow }\limits ^{i}} p'\); these match each other by the second condition. \(\square \)
5.3 Further simulations: I2-, I3-refinement and ready simulation
Göhrle also introduced the preorders I2-refinement and I3-refinement [21], which lie in-between I1- and I4-refinement. In the definitions of his refinements, he successively replaced the conditions of I1 (sacc-simulation) by those of I4 (acc-simulation). This time, a more generous use of \(\tau \)s when matching a transition makes a difference.
Definition 46
(I2-refinement) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is an I2-simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\({\text {I}}({q}) \subseteq {\text {I}}({p})\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q {\mathop {\longrightarrow }\limits ^{i}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in {\text {I}}({q})\);
-
3.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \).
P I2-refines Q, in signs \(P \preceq _{\text {sacc}}^2Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some I2-simulation \({{\mathscr {R}}}\).
Hence, I2-refinement is defined analogously to sacc-simulation, but it allows an \(\omega \)-transition to be matched by a weak \(\omega \)-transition that does not only permit leading but also trailing \(\tau \)s. I3-refinement now relaxes the matching of inputs by permitting leading and trailing \(\tau \)s:
Definition 47
(I3-Refinement) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is an I3-simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\({\text {I}}({q}) \subseteq {\text {I}}({p})\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in {\text {I}}({q})\);
-
3.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \).
P I3-refines Q, in signs \(P \preceq _{\text {sacc}}^3Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some I3-simulation \({{\mathscr {R}}}\).
The following result was established in [21], when considering the coincidence of \(\preceq _{\text {acc}}\) with \(\preceq _{\text {sacc}}^4\) (cf. Theorem 58):
Theorem 48
\(\preceq _{\text {sacc}}\;\subsetneq \; \preceq _{\text {sacc}}^2\;\subsetneq \; \preceq _{\text {sacc}}^3\;\subsetneq \; \preceq _{\text {acc}}\,\).
Example illustrating the strict inclusion of I3-refinement in I4-refinement [21]
Göhrle showed that all these inclusions are indeed strict. Most important for our branching-time spectrum is the fact that \(\preceq _{\text {sacc}}\,\subsetneq \, \preceq _{\text {acc}}\). To demonstrate this, we state in Fig. 9 an example that highlights the difference between I3- and I4-refinement; note that \({\text {I}}({q_0}) = \{i\}\) and \({\mathbb {I}}_\forall ({q_0})= \emptyset \).
Finally, we adapt ready simulation \(\preceq _{\text {rs}}\) [6] to our IA-setting, which requires related states to have the same ready sets. In particular, all branching-time preorders discussed so far allow one to omit any specified output in an implementation. This is often unsatisfactory in practice, and ready simulation is our first proposal of a preorder that remedies the shortcoming:
Definition 49
(Ready simulation) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is a ready simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\({\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p})\);
-
2.
\({\mathbb {R}}({p}) = {\mathbb {R}}({q})\);
-
3.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in {\mathbb {I}}_\forall ({q})\);
-
4.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \).
P rs-refines Q, in signs \(P \preceq _{\text {rs}}Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some ready simulation \({{\mathscr {R}}}\).
This preorder refines acc-refinement by adding the condition on ready sets, which are defined as in Sect. 4. So far, outputs could be removed in a refinement step, whereas here we require the same outputs (and \(\tau \)s) to be enabled, without insisting that all subsequent behaviour is preserved. Inclusion of \(\tau \) in a ready set fits our notion of quiescence, so that rs-refinement refines the linear-time ready semantics.
5.4 Bivariant simulations and IA-bisimulation
In the \(\tau \)-free setting of [3], simulations are studied where some actions are simulated in one direction, some in the opposite direction, and others in both directions; the latter are called bivariant. As another proposal for not losing desired outputs during refinement, we define the new preorders (strict) output-bivariant refinement that strengthen (strict) acceptance refinement by requiring that specified outputs are kept; in contrast to rs-refinement, also their subsequent behaviour must be preserved. Observe that strict output-bivariant refinement differs from output-bivariant refinement in the same way that sacc-refinement differs from acc-refinement.
Definition 50
(Output-bivariant refinement) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is an output-bivariant simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\({\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p})\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in {\mathbb {I}}_\forall ({q})\);
-
3.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}}\Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \);
-
4.
\(q {\mathop {\longrightarrow }\limits ^{\omega }} q'\) implies \(\exists p'.\; p \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}}\Longrightarrow p'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \).
P obs-refines Q, in signs \(P \preceq _{\text {obs}}Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some output-bivariant simulation \({{\mathscr {R}}}\).
Definition 51
(Strict output-bivariant refinement) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is a strict output-bivariant simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\({\text {I}}({q}) \subseteq {\text {I}}({p})\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q {\mathop {\longrightarrow }\limits ^{i}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in {\text {I}}({q})\);
-
3.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \);
-
4.
\(q {\mathop {\longrightarrow }\limits ^{\omega }} q'\) implies \(\exists p'.\; p \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} p'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \).
P sobs-refines Q, in signs \(P \preceq _{\text {sobs}}Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some strict output-bivariant simulation \({{\mathscr {R}}}\).
In [37], sobs-refinement was studied in a restricted Petri net setting, which adopts certain determinism requirements, and was called correct STG-decomposition. This decomposition allows efficient asynchronous circuits to be developed from large, monolithic specifications. Here, the compatibility as in IA is crucial, because asynchronous circuits cannot deal with unexpected inputs [16].
Analogously to output-bivariance, we define a version where inputs are bivariant. This is essentially sacc-refinement with the additional condition on matching a specification’s inputs. Because the matching of such inputs should be direct, i.e., without leading and trailing \(\tau \)s, we only define a strict variant, called input-bivariant refinement \(\preceq _{\text {ibs}}\). Note that the added condition is stronger than the condition \({\text {I}}({q}) \subseteq {\text {I}}({p})\) of sacc-refinement, which can thus be omitted. Obviously, \(\preceq _{\text {ibs}}\,\subseteq \, \preceq _{\text {sacc}}\).
Definition 52
(Input-bivariant refinement) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is an input-bivariant simulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q {\mathop {\longrightarrow }\limits ^{i}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in {\text {I}}({q})\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(\omega \in O_\tau \);
-
3.
\(q {\mathop {\longrightarrow }\limits ^{i}} q'\) implies \(\exists p'.\; p {\mathop {\longrightarrow }\limits ^{i}} p'\) and \((p',q') \in {{\mathscr {R}}}\), for all \(i \in I\).
P ibs-refines Q, in signs \(P \preceq _{\text {ibs}}Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some input-bivariant simulation \({{\mathscr {R}}}\).
Problem regarding the allowance of trailing \(\tau \)s in the third condition of Definition 52
Observe that allowing trailing \(\tau \)s in the third condition above would not only deviate from alternating simulation, the resulting refinement would also fail to be transitive and, thus, to be a preorder. Consider the example in Fig. 10: input i of P matches the first i of Q, and Q matches with the lower branch of R. Now, the first i in the upper branch of R is matched by \(i\tau \) in Q, but cannot be matched in P. Hence, if additional \(\tau \)s are allowed to match some action in one direction, also single \(\tau \)s should be matched in this direction.
The strongest behavioural relation typically studied in a linear-time branching-time spectrum [42] is the equivalence bisimilarity a.k.a. observation equivalence [32, 34], i.e., a mutually recursive simulation. Our variant \(\approx \) of bisimilarity does not permit extra \(\tau \)s when matching inputs and only leading \(\tau \)s when matching outputs, so that \(\approx \) refines sacc-refinement and our bivariant refinements:
Definition 53
(IA-bisimilarity) For IAs P, Q with the same signature, \({{\mathscr {R}}} \subseteq P \times Q\) is an IA-bisimulation if the following conditions hold for all \((p,q) \in {{\mathscr {R}}}\):
-
1.
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(\exists q'.\; q {\mathop {\longrightarrow }\limits ^{i}} q'\) and \((p',q') \in {{\mathscr {R}}}\);
-
2.
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) implies \(\exists q'.\; q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q'\) and \((p',q') \in {{\mathscr {R}}}\);
-
3.
\(q {\mathop {\longrightarrow }\limits ^{i}} q'\) implies \(\exists p'.\; p {\mathop {\longrightarrow }\limits ^{i}} p'\) and \((p',q') \in {{\mathscr {R}}}\).
-
4.
\(q {\mathop {\longrightarrow }\limits ^{\omega }} q'\) implies \(\exists p'.\; p \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} p'\) and \((p',q') \in {{\mathscr {R}}}\).
P is IA-bisimilar to Q, in signs \(P \approx Q\), if \((p_0,q_0) \in {{\mathscr {R}}}\) for some IA-bisimulation \({{\mathscr {R}}}\).
5.5 Precongruence results
We now give a concise proof that the branching-time preorders presented above are (mostly) precongruences. The precongruence results for de Alfaro and Henzinger’s preorders were stated in [12, 13], resp., for a binary parallel composition where synchronized actions are hidden. The precongruence proofs can be found, e.g., in Göhrle’s work [21] for a slightly different but equivalent characterization of IA-refinement (cf. Theorems 42, 58), and in [30] for alternating simulation. These results are re-proved here for our multicast parallel operator \(|\), and the result for alternating simulation is extended to our notion of sacc-refinement (cf. Theorem 45). Because of Theorems 42 and 45, we do not consider IA-refinement and alternating simulation in the following theorem:
Theorem 54
(Precongruence for IA-parallel composition) Let \(\preceq \) be any one of the preorders except for \(\preceq _{\text {sacc}}^3\) and \(\preceq _{\text {obs}}\). Then, for all IAs P, Q, R, where Q, R are composable and compatible and \(P \preceq Q\), we have that P, R are composable and compatible and that \(P |R \preceq Q |R\). For \(\preceq _{\text {sobs}}\), this only holds if Q is input-deterministic.
Before proving this theorem, we first note that Göhrle also showed that I2- and I3-refinement are precongruences for the binary parallel operator [21]. However, I3-refinement is only a precongruence, if the pruning involved is further strengthened (cf. also [8]); it also fails to be a precongruence for the operator \(|\) studied here. This can be seen in Göhrle’s example that is reproduced in Fig. 11, where \(P \preceq _{\text {sacc}}^3Q\) since P’s i?-transition can be matched by the \(\tau \)- and the i-transition of Q. However, when composing both IAs with IA R that has no behaviour but input alphabet \(\{o\}\), the o!-transition raises an error and, thus, the preceding i?-transition is cut by pruning. Hence,  .
.
Regarding our output-bivariant preorders, the example IAs P, \(Q_1\), R in Fig. 12 testify to the precongruence defect of \(\preceq _{\text {sobs}}\) (and \(\preceq _{\text {obs}}\)) in the general case. The problem is that the choice between the initial a?-transitions of \(Q_1\) does not matter for \(\preceq _{\text {sobs}}\) (and \(\preceq _{\text {obs}}\)); however, after synchronization, these inputs are essentially turned into outputs and the lower a!-transition has to be matched. While this defect disappears for \(\preceq _{\text {sobs}}\) when restricting the specification side to input-deterministic IAs, the same is not true for \(\preceq _{\text {obs}}\). This can be seen (a) from IAs P, \(Q_2\), R, where \(Q_2\) matches P’s a?-transition by the a- and the upper trailing \(\tau \)-transition of \(Q_2\), and (b) from IAs P, \(Q_3\), R, where \(Q_3\) matches P’s a?-transition by the leading \(\tau \)- and the upper a-transition of \(Q_3\). To avoid this problem, one would need to significantly change the second condition of Definition 50, which seems to be too drastic to us.
The proof of Theorem 54 makes use of the following two lemmas. The first lemma collects properties that are shared among several preorders, for ease of reference:
Lemma 55
Let \(\preceq \) be any one of the preorders except for \(\preceq _{\text {sacc}}^3\) and \(\preceq _{\text {obs}}\), and let \({{\mathscr {R}}}\) be a \(\preceq \)-simulation for IAs P, Q such that \((p,q) \in {{\mathscr {R}}}\).
-
1.
If \(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) then, in all cases, \(\exists q'.\, q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow q'\) with \((p',q') \in {{\mathscr {R}}}\).
-
2.
If \(p {\mathop {\longrightarrow }\limits ^{i}} p'\) then, in all cases, \(\exists q'.\, q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow q'\) with \((p',q') \in {{\mathscr {R}}}\) or, alternatively,
 .
. -
3.
If
 , then
, then  .
. -
4.
If \(\preceq \) is \(\preceq _{\text {sacc}}^2\) or requires one to match \(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) with some \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q'\), then it also requires one to match \(p {\mathop {\longrightarrow }\limits ^{i}} p'\) with \(q {\mathop {\longrightarrow }\limits ^{i}} q'\) for \(i \in {\text {I}}({q})\). If \(\preceq \) is not \(\preceq _{\text {sacc}}^2\) and the first match is some \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow q'\), then the second one is some \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow q'\) for \(i \in {\mathbb {I}}_\forall ({q})\).
-
5.
If \({\mathbb {I}}_\forall ({\cdot })\) matters, then a transition \(p {\mathop {\longrightarrow }\limits ^{i}} p'\) with \(i \in {\mathbb {I}}_\forall ({q})\) is matched with some \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow q'\); otherwise, the match is some \(q {\mathop {\longrightarrow }\limits ^{i}} q'\) for \(i \in {\text {I}}({q})\).
Proof
Let \(\preceq \), \({{\mathscr {R}}}\) and \((p,q) \in {{\mathscr {R}}}\) be as stated in the lemma.
-
1.
Obvious. (Note that this claim also holds for the preorders that do not allow trailing \(\tau \)s.)
-
2.
We could have \(i \notin {\text {I}}({q})\) if \({\text {I}}({\cdot })\) matters, or \(i \notin {\mathbb {I}}_\forall ({q})\) if \({\mathbb {I}}_\forall ({\cdot })\) matters. In both cases, the second alternative holds. Otherwise, there exists some \(q'\) such that \(q {\mathop {\longrightarrow }\limits ^{i}} q'\) or \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow q'\) with \((p',q') \in {{\mathscr {R}}}\), so the first alternative holds.
-
3.
We have
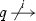 if \({\text {I}}({q}) \subseteq {\text {I}}({p})\) or Definition 52(3) or 53(3) applies. Otherwise, we get
if \({\text {I}}({q}) \subseteq {\text {I}}({p})\) or Definition 52(3) or 53(3) applies. Otherwise, we get  for some \(q'\) due to \({\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p})\).
for some \(q'\) due to \({\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p})\). -
4.
For \(\approx \) and the first part of the statement, observe that \(p {\mathop {\longrightarrow }\limits ^{i}} p'\) implies \(i \in {\text {I}}({q})\) by Definition 53(1).
-
5.
See the proof for (4).
\(\square \)
Lemma 56
Let \(\preceq \) be any one of the above preorders except for \(\preceq _{\text {sacc}}^3\) and \(\preceq _{\text {obs}}\), and let P, Q, R be IAs with \(P \preceq Q\) due to the \(\preceq \)-simulation \({{\mathscr {R}}}\) and such that Q, R are composable. If \(((p,r),(q,r)) \in \widehat{{{\mathscr {R}}}} =_{\text {df}}\{ ((p,r),(q,r)) \;|\; (p,q) \in {{\mathscr {R}}} \}\) and (p, r) is illegal, then so is (q, r).
Proof
First observe that P, R are composable because P, Q have the same signature (I, O). We now proceed by induction on the length of a run from (p, r) to an error state of \(P \otimes R\). In the base case, (p, r) is an error state and there are two sub-cases to distinguish:
-
\(p {\mathop {\longrightarrow }\limits ^{a}}\) and
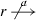 with \(a \in O \cap I_R\): Then, \(q \Longrightarrow q' {\mathop {\longrightarrow }\limits ^{a!}}\) for some \(q'\) by Lemma 55(1). Hence, \((q,r) \Longrightarrow (q',r)\) and \((q',r)\) is an error. Thus, (q, r) is illegal.
with \(a \in O \cap I_R\): Then, \(q \Longrightarrow q' {\mathop {\longrightarrow }\limits ^{a!}}\) for some \(q'\) by Lemma 55(1). Hence, \((q,r) \Longrightarrow (q',r)\) and \((q',r)\) is an error. Thus, (q, r) is illegal. -
 and \(r {\mathop {\longrightarrow }\limits ^{a}}\) with \(a \in I \cap O_R\): By Lemma 55(3), there exists some \(q'\) such that
and \(r {\mathop {\longrightarrow }\limits ^{a}}\) with \(a \in I \cap O_R\): By Lemma 55(3), there exists some \(q'\) such that  , and (q, r) is illegal as above.
, and (q, r) is illegal as above.
For the induction step, consider the first transition \((p,r) {\mathop {\longrightarrow }\limits ^{\omega }} (p',r')\) of a run of local transitions to an error state, i.e., \((p',r')\) is illegal due to a shorter run. There are three sub-cases:
-
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\), \(r' = r\) and \(\omega \in O_\tau {\setminus }A_R\): Then, \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow q'\) for a \(q'\) with \((p',q') \in {{\mathscr {R}}}\) by Lemma 55(1). Hence, \((q,r) \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow (q',r)\) with \(((p',r),(q',r)) \in \widehat{{{\mathscr {R}}}}\). State \((q',r)\) is illegal by induction hypothesis, and so is (q, r).
-
\(p' = p\), \(r {\mathop {\longrightarrow }\limits ^{\omega }} r'\) and \(\omega \in {O_{R\tau }{\setminus }A}\): Then, \((q,r) {\mathop {\longrightarrow }\limits ^{\omega }} (q,r')\) and \(((p,r'),(q,r')) \in \widehat{{{\mathscr {R}}}}\), and we are done as above.
-
\(p {\mathop {\longrightarrow }\limits ^{a}} p'\), \(r {\mathop {\longrightarrow }\limits ^{a}} r'\), \(a \in O \cup O_R\): Here, we have to distinguish two sub-cases.
-
\(a \in O \cap I_R\): \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{a!}} \Longrightarrow q'\) for some \(q'\) and \((p',q') \in {{\mathscr {R}}}\) by Lemma 55(1). Hence, \((q,r) \Longrightarrow {\mathop {\longrightarrow }\limits ^{a!}} \Longrightarrow (q',r')\) and \(((p',r'),(q',r')) \in \widehat{{{\mathscr {R}}}}\), so we are done as above.
-
\(a \in I \cap O_R\): By Lemma 55(2), we might have \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{a?}} \Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\) for some \(q'\). Then, \((q,r) \Longrightarrow {\mathop {\longrightarrow }\limits ^{a!}} \Longrightarrow (q',r')\) with \(((p',r'),(q',r')) \in \widehat{{{\mathscr {R}}}}\), and we are done. Otherwise,
 for some \(q'\), and (q, r) is illegal as in the second base case.
for some \(q'\), and (q, r) is illegal as in the second base case.
-
\(\square \)
Proof of Theorem 54
The following proof mainly works for \(\preceq _{\text {obs}}\) and \(\preceq _{\text {sobs}}\), too. In each of these cases, one proof part fails as indicated below; for \(\preceq _{\text {sobs}}\), the defect disappears when requiring input-determinism of the specification Q. Now, let \(\preceq \) be one of the refinements mentioned in the theorem and consider \({{\mathscr {R}}}\) and \(\widehat{{{\mathscr {R}}}}\) as in Lemma 56. The theorem’s statement on composability is trivial because P, Q have the same signature (I, O). Further, we write \((I_{QR}, O_{QR})\) for the signature of \(Q \otimes R\). Lemma 56 shows the theorem’s statement regarding compatibility.
Now, we restrict \(\widehat{{{\mathscr {R}}}}\) to those pairs ((p, r), (q, r)) where \(q |r\), and hence \(p |r\), is defined; we call the restriction \({{\mathscr {R}}}'\). The sequel considers some \(((p,r),(q,r)) \in {{\mathscr {R}}}'\) and has a sub-case for each requirement appearing in the definition of at least one of our relations:
-
(\(P\omega \)) Assume \(p |r {\mathop {\longrightarrow }\limits ^{\omega }} p' |r'\). Then, \(\preceq \) requires \(q |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q' |r'\) (or \(q |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow q' |r'\), which can mostly be handled analogously) for some \(q'\) with \((p',q') \in {{\mathscr {R}}}\). There are four sub-cases needed to show this:
-
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\), \(r' = r\) and \(\omega \notin A_R\): Then, we have \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q'\) for some \(q'\) with \((p',q') \in {{\mathscr {R}}}\), implying \(q |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q' |r\), where all states on this run are defined since \(q |r\) is.
-
\(r {\mathop {\longrightarrow }\limits ^{\omega }} r'\), \(p' = p\) and \(\omega \notin A\): Easier.
-
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\), \(r {\mathop {\longrightarrow }\limits ^{\omega }} r'\) and \(\omega \in O \cap I_R\): Similar to the first sub-case.
-
\(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\), \(r {\mathop {\longrightarrow }\limits ^{\omega }} r'\) and \(\omega \in I \cap O_R\): If
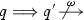 , then we would have \((q,r) \Longrightarrow (q',r)\). The latter state would be an error, contradicting that \(q |r\) is defined. Thus, \(\omega \in {\mathbb {I}}_\forall ({q}) \subseteq {\text {I}}({q})\).
, then we would have \((q,r) \Longrightarrow (q',r)\). The latter state would be an error, contradicting that \(q |r\) is defined. Thus, \(\omega \in {\mathbb {I}}_\forall ({q}) \subseteq {\text {I}}({q})\).By Lemma 55(4), there is \(q {\mathop {\longrightarrow }\limits ^{\omega }} q'\) with \((p',q') \in {{\mathscr {R}}}\). Hence (also for \(\preceq _{\text {sacc}}^2\)), we have \(q |r {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} q' |r'\) (cf. the first sub-case) and are done.
In the case in brackets, there is some \(q'\) with \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{\omega }} \Longrightarrow q'\) and \((p',q') \in {{\mathscr {R}}}\). Thus, we obtain \(q |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow q' |r'\) (cf. the first sub-case).
-
-
(\({\mathbb {I}}_\forall ({\cdot })\)) Assume that \(\preceq \) requires \({\mathbb {I}}_\forall ({q |r}) \subseteq {\mathbb {I}}_\forall ({p |r})\). In a product like \(P \otimes R\), we have \({\mathbb {I}}_\forall ({(p,r)}) = (({\mathbb {I}}_\forall ({p}){\setminus }I_R \cup {\mathbb {I}}_\forall ({r}) \setminus I) \cap I_{QR}) \cup ({\mathbb {I}}_\forall ({p}) \cap {\mathbb {I}}_\forall ({r}))\); in particular, note that some \(i \in {\mathbb {I}}_\forall ({p}){\setminus }I_R\) could be an output of the composition, so we need to intersect with \(I_{QR}\). Therefore, \({\mathbb {I}}_\forall ({q |r}) \subseteq {\mathbb {I}}_\forall ({p |r})\) could only fail for some \(i \in I_{QR}\) if
 due to pruning, although \(i \in {\mathbb {I}}_\forall ({(p,r)}) \subseteq {\mathbb {I}}_\forall ({(p',r')})\). This only happens if \((p',r') {\mathop {\longrightarrow }\limits ^{i}} (p'',r'')\) for some illegal \((p'',r'')\). From (\(P\omega \)), we get \(q |r \Longrightarrow q' |r'\) with \((p',q') \in {{\mathscr {R}}}\). Further, consider the following three sub-cases:
due to pruning, although \(i \in {\mathbb {I}}_\forall ({(p,r)}) \subseteq {\mathbb {I}}_\forall ({(p',r')})\). This only happens if \((p',r') {\mathop {\longrightarrow }\limits ^{i}} (p'',r'')\) for some illegal \((p'',r'')\). From (\(P\omega \)), we get \(q |r \Longrightarrow q' |r'\) with \((p',q') \in {{\mathscr {R}}}\). Further, consider the following three sub-cases:-
If the i-transition is due to \(r'\) only, we have \(p'' = p'\) and \((q',r') {\mathop {\longrightarrow }\limits ^{i}} (q',r'')\). Because \((p',r'')\) is illegal and \(((p',r''),(q',r'')) \in \widehat{{{\mathscr {R}}}}\), the latter pair is also illegal and also \(i \notin {\mathbb {I}}_\forall ({q |r})\).
-
If the i-transition is due to \(p'\) only, i.e., if \(r'' = r'\) and \(p' {\mathop {\longrightarrow }\limits ^{i}} p''\), we may have
 by Lemma 55(2). Then,
by Lemma 55(2). Then,  and \(i \notin {\mathbb {I}}_\forall ({q |r})\).
and \(i \notin {\mathbb {I}}_\forall ({q |r})\).Otherwise, \(q' \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow q''\) and \((p'',q'') \in {{\mathscr {R}}}\). Hence, \((q',r') \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow (q'',r')\) and \(((p'',r'),(q'',r')) \in \widehat{{{\mathscr {R}}}}\). Again, \((q'',r')\) is illegal, and so is the state after the i-transition. The state before the i-transition is not illegal because \(q' |r'\) is defined. Thus, \(i \notin {\mathbb {I}}_\forall ({q |r})\).
-
If \(p' {\mathop {\longrightarrow }\limits ^{i}} p''\) and \(r' {\mathop {\longrightarrow }\limits ^{i}} r''\), we can argue as in the previous sub-case.
-
-
(\({\text {I}}({\cdot })\)) Assume \(\preceq \) requires \({\text {I}}({q |r}) \subseteq {\text {I}}({p |r})\). This case is similar but much simpler than Case (\({\mathbb {I}}_\forall ({\cdot })\)) above, because \(p = p'\), \(r = r'\) and, in the second and third sub-case of (\({\mathbb {I}}_\forall ({\cdot })\)), one just has to apply Lemma 55(5) instead of (2), leading directly to the “otherwise” case.
-
(Pi) Let \(p |r {\mathop {\longrightarrow }\limits ^{i}} p' |r'\), and assume that \(\preceq \) requires the proof that \(q |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow q' |r'\) for \(i \in {\mathbb {I}}_\forall ({q |r})\) (or just \(q |r {\mathop {\longrightarrow }\limits ^{i}} q' |r'\) for \(i \in {\text {I}}({q |r})\)) by Lemma 55(5), for some \(q'\) with \((p',q') \in {{\mathscr {R}}}\). There are three sub-cases:
-
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\), \(r' = r\) and \(i \notin A_R\): We have \(i \in {\mathbb {I}}_\forall ({q})\) by \(i \in {\mathbb {I}}_\forall ({q |r})\), and further \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow q'\) with \((p',q') \in {{\mathscr {R}}}\). Then, \(q |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} \Longrightarrow q' |r\). The states before the i-transition exist because \(q |r\) is defined, and the states after because \(i \in {\mathbb {I}}_\forall ({q |r})\).
The other variant with \(q |r {\mathop {\longrightarrow }\limits ^{i}} q' |r\) is easier, where the latter state exists by \(i \in {\text {I}}({q |r})\).
-
\(r {\mathop {\longrightarrow }\limits ^{i}} r'\), \(p' = p\) and \(i \notin A\): Then, \((q,r) {\mathop {\longrightarrow }\limits ^{i}} (q,r')\) and state \(q |r'\) is defined by \(i \in {\text {I}}({q |r}) \supseteq {\mathbb {I}}_\forall ({q |r})\).
-
\(p {\mathop {\longrightarrow }\limits ^{i}} p'\) and \(r {\mathop {\longrightarrow }\limits ^{i}} r'\): Essentially as in the first sub-case.
-
-
(\(Q\omega \)) Assume \(q |r {\mathop {\longrightarrow }\limits ^{\omega }} q' |r'\) and that, as in \(\preceq _{\text {obs}}\), preorder \(\preceq \) requires \(p |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow p' |r'\) (or \(p |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} p' |r'\), for \(\preceq _{\text {sobs}}\) and \(\approx \)) for some \(p'\) with \((p',q') \in {{\mathscr {R}}}\). We distinguish four sub-cases:
-
\(q {\mathop {\longrightarrow }\limits ^{\omega }} q'\), \(r' = r\) and \(\omega \notin A_R\): Then, \(p \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow p'\) with \((p',q') \in {{\mathscr {R}}}\) (the other case is almost the same). Thus, \(p |r \Longrightarrow {\mathop {\longrightarrow }\limits ^{{\hat{\omega }}}} \Longrightarrow p' |r\) and \((p' |r, q' |r) \in {{\mathscr {R}}}'\), and all states are defined since \(p |r\) is.
-
\(r {\mathop {\longrightarrow }\limits ^{\omega }} r'\), \(q' = q\) and \(\omega \notin A\): Easier.
-
\(q {\mathop {\longrightarrow }\limits ^{\omega }} q'\), \(r {\mathop {\longrightarrow }\limits ^{\omega }} r'\) and \(\omega \in O \cap I_R\): As in the first sub-case.
-
\(q {\mathop {\longrightarrow }\limits ^{\omega }} q'\), \(r {\mathop {\longrightarrow }\limits ^{\omega }} r'\) and \(\omega \in I \cap O_R\): For \(\approx \), we have \(p {\mathop {\longrightarrow }\limits ^{\omega }} p'\) with \((p',q') \in {{\mathscr {R}}}\); hence, \(p |r {\mathop {\longrightarrow }\limits ^{\omega }} p' |r'\) as above. For \(\preceq _{\text {sobs}}\), in case that P is input-deterministic, p has an \(\omega \)-transition, and this must match \(q {\mathop {\longrightarrow }\limits ^{\omega }} q'\) in the same way. (Note that this sub-case fails for \(\preceq _{\text {sobs}}\) in general and also for \(\preceq _{\text {obs}}\).)
-
-
(Qi) Let \(q |r {\mathop {\longrightarrow }\limits ^{i}} q' |r'\) and assume, as is the case for \(\preceq _{\text {ibs}}\) and \(\approx \), that \(\preceq \) requires \(p |r {\mathop {\longrightarrow }\limits ^{i}} p' |r'\) for some \(p'\) with \((p',q') \in {{\mathscr {R}}}\). Hence, we have three sub-cases:
-
\(q {\mathop {\longrightarrow }\limits ^{i}} q'\), \(r' = r\) and \(i \notin A_R\): Then, there exists some \(p'\) such that \(p {\mathop {\longrightarrow }\limits ^{i}} p'\) and \((p',q') \in {{\mathscr {R}}}\). Thus, \(p |r {\mathop {\longrightarrow }\limits ^{i}} p' |r'\) and the latter state is defined by Lemma 56.
-
\(r {\mathop {\longrightarrow }\limits ^{i}} r'\), \(q' = q\) and \(i \notin A\): Obvious.
-
\(q {\mathop {\longrightarrow }\limits ^{i}} q'\), \(r {\mathop {\longrightarrow }\limits ^{i}} r'\) and \(i \in I \cap I_R\): Similar to the first sub-case.
-
-
(\({\mathbb {R}}({\cdot })\)) For \(\preceq _{\text {rs}}\), observe that \({\mathbb {R}}({q |r}) = {\mathbb {R}}({q}) \cup {\mathbb {R}}({r})\) because, if an output o of, say, Q is in \({\mathbb {R}}({q})\) and \({\text {I}}({r})\), then r must provide its input o; otherwise, (q, r) would be an error state. Now, \({\mathbb {R}}({q |r}) = {\mathbb {R}}({q}) \cup {\mathbb {R}}({r}) = {\mathbb {R}}({p}) \cup {\mathbb {R}}({r}) = {\mathbb {R}}({p |r})\).
\(\square \)
We finish this section by establishing the precongruence property for hiding:
Theorem 57
(Precongruence for hiding) Let \(\preceq \) be any one of the above branching-time preorders. Then, \(P / {H} \preceq Q / {H}\) for all IAs P, Q with \(P \preceq Q\) and all \(H \subseteq O\).
Proof
Assume that \(P \preceq Q\) holds due to \(\preceq \)-simulation \({{\mathscr {R}}}\). We show that \({{\mathscr {R}}}\) is also suitable to prove the theorem’s statement. First observe that all conditions, except for condition \({\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({p})\), are obviously preserved. Hence, we establish this remaining condition:
If \(i \in {\mathbb {I}}_\forall ({p})\) is lost in \(P / {H}\), then there is some run in P from p to \(p'\) with actions in \(H \cup \{\tau \}\) such that  . This run is matched by q to reach some state \(q'\) with \((p',q') \in {{\mathscr {R}}}\). By Lemma 55(3), there exists some \(q''\) such that
. This run is matched by q to reach some state \(q'\) with \((p',q') \in {{\mathscr {R}}}\). By Lemma 55(3), there exists some \(q''\) such that  . Thus, \(i \notin {\mathbb {I}}_\forall ({q})\) in \(Q / {H}\). \(\square \)
. Thus, \(i \notin {\mathbb {I}}_\forall ({q})\) in \(Q / {H}\). \(\square \)
5.6 The branching-time IA-spectrum
Overall, our spectrum of branching-time preorders on IA is as shown in Fig. 13; again, arrows display inclusions between the preorders. I4-refinement is not depicted, because it coincides with acc-refinement. Recall that the definition of Göhrle’s \(\preceq _{\text {sacc}}^4\) [21] only differs from \(\preceq _{\text {acc}}\) in the first condition, where he demands \({\mathbb {I}}_\forall ({q}) \subseteq {\text {I}}({p})\).
Theorem 58
\(\preceq _{\text {sacc}}^4\,=\, \preceq _{\text {acc}}\) on all IAs.
Proof
Clearly, each acceptance simulation is an I4-simulation. Conversely, consider some I4-simulation \({{\mathscr {R}}}\) with \((p,q) \in {{\mathscr {R}}}\) and some input \(i \in {\mathbb {I}}_\forall ({q}){\setminus }{\mathbb {I}}_\forall ({p})\). Then, there is some \(p'\) such that \(p \Longrightarrow p'\) but  . Now, \(p \Longrightarrow p'\) can be matched according to I4-simulation by \(q \Longrightarrow \Longrightarrow \cdots \Longrightarrow q'\) for some \(q'\) satisfying \((p',q') \in {{\mathscr {R}}}\). Hence, \(i \in {\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({q'})\) but \(i \notin {\text {I}}({p'})\), which is a contradiction to the first condition of I4-simulation. Thus, \({{\mathscr {R}}}\) is an acceptance simulation. \(\square \)
. Now, \(p \Longrightarrow p'\) can be matched according to I4-simulation by \(q \Longrightarrow \Longrightarrow \cdots \Longrightarrow q'\) for some \(q'\) satisfying \((p',q') \in {{\mathscr {R}}}\). Hence, \(i \in {\mathbb {I}}_\forall ({q}) \subseteq {\mathbb {I}}_\forall ({q'})\) but \(i \notin {\text {I}}({p'})\), which is a contradiction to the first condition of I4-simulation. Thus, \({{\mathscr {R}}}\) is an acceptance simulation. \(\square \)
The strict inclusions between sacc- and acc-refinement have been the subject of Theorem 48 above. The other implications follow because, in each case, a condition is added for the finer refinement. The only exception is the implication from sobs-refinement to obs-refinement:
Theorem 59
\(\preceq _{\text {sobs}}\,\subsetneq \preceq _{\text {obs}}\,\).
Proof
For the proof, we define an OB4-simulation just as an output-bivariant simulation, except that we require \({\mathbb {I}}_\forall ({q}) \subseteq {\text {I}}({p})\) in the first condition. Clearly, each strict output-bivariant simulation \({{\mathscr {R}}}\) is an OB4-simulation, because the allowed matchings are more generous and \({\mathbb {I}}_\forall ({q}) \subseteq {\text {I}}({q})\); the latter also implies that fewer inputs have to be matched in the OB4-simulation. Now, we repeat the arguments in the proof of Theorem 58 for OB4 in place of I4, obtaining that \({{\mathscr {R}}}\) is an output-bivariant simulation. Inequality follows from Lemma 60(d) below. \(\square \)
Also the other inclusions omitted in Fig. 13 fail:
Lemma 60
(Failing implications) The following properties hold:
-
(a)
\(\preceq _{\text {rs}}\) is not included in \(\preceq _{\text {sacc}}^3\);
-
(b)
\(\preceq _{\text {rs}}\) is not included in \(\preceq _{\text {obs}}\);
-
(c)
\(\approx \) is not included in \(\preceq _{\text {rs}}\);
-
(d)
\(\preceq _{\text {obs}}\) is not included in \(\preceq _{\text {sacc}}^3\);
-
(e)
\(\preceq _{\text {ibs}}\) is not included in \(\preceq _{\text {obs}}\);
-
(f)
\(\preceq _{\text {sobs}}\) is not included in \(\preceq _{\text {ibs}}\).
Proof
First, we prove Parts (a)–(c): (a) Consider P, Q of Fig. 9, where \(P \preceq _{\text {rs}}Q\) due to \(i \notin {\mathbb {I}}_\forall ({q_0})\), such that the i-transition of \(p_0\) does not have to be matched. However, \(P \not \preceq _{\text {sacc}}^3Q\), as pointed out before. (b) Let \(P_1\), \(P_2\) as in Fig. 14. Then, \(P_1 \preceq _{\text {rs}}P_2\) due to the upper branch of \(P_2\), but \(P_1 \not \preceq _{\text {obs}}P_2\) since the lower branch cannot be matched. (c) For IAs \(P_3\), \(P_4\) in Fig. 14, \(P_3 \approx P_4\), but \(P_3 \not \preceq _{\text {rs}}P_4\) because \(o \notin {\mathbb {R}}({p_0})\).
Second, we consider Parts (d) and (e): (d) The same example as in Part (a) applies; \(P \preceq _{\text {obs}}Q\) holds for the same reason. (e) Consider the example of Part (b) again, which does not have any inputs.
Last, for Part (f) and \(P_5\), \(P_6\) in Fig. 14, obviously \(P_5 \preceq _{\text {sobs}}P_6\), but \(P_5 \not \preceq _{\text {ibs}}P_6\) due to the lower branch of \(P_6\). \(\square \)
The above properties of our preorders yield the branching-time spectrum for IA:
Theorem 61
(Branching-time IA spectrum) All inclusions between our branching-time preorders are depicted in Fig. 13 as arrows; in particular, these inclusions are strict.
Proof
We have shown above that the indicated implications hold. Parts (a)–(c) of Lemma 60 settle the missing implications around \(\preceq _{\text {rs}}\). Parts (d) and (e) testify to the missing implications for \(\preceq _{\text {obs}}\), but Part (e) also shows that \(\preceq _{\text {ibs}}\) is not included in \(\preceq _{\text {sobs}}\). By Part (f), the proof is finished. \(\square \)
Finally, we remark that, when restricting ourselves to input-deterministic IAs, strict acceptance refinement and input-bivariant refinement coincide:
Proposition 62
\(\preceq _{\text {sacc}}\;=\; \preceq _{\text {ibs}}\) on input-deterministic IAs.
5.7 Completing the spectrum
We conclude the technical part of this article by connecting our branching-time spectrum for IA to the linear-time spectrum studied in Sect. 4, recalling that any IA can be understood as an EIO (see Remark 4).
Theorem 63
\(\preceq _{\text {acc}}\;\subseteq \;\, \sqsubseteq _E\,\).
Proof
Let P, Q be IAs satisfying \(P \preceq _{\text {acc}}Q\), and let \(P'\), \(Q'\) be the corresponding EIOs with an additional, canonical error state. Consider a prefix-minimal error trace wi of \(P'\), which must end with an input transition to the error state. The same run exists in P, except for the last i-transition. In principle, due to acc-refinement, a run with the same w exists in Q. This fails only if an intermediate \(i'\)-transition along the run in P is not matched in Q because it is not guaranteed in the resp. state q in Q. In this case, we extend the run in Q from q to a state \(q'\) that does not enable \(i'\). Thus, \(q'\) has an \(i'\)-transition to the error state of \(Q'\), and we have a prefix \(w'\) of w that is an error trace in \(Q'\). If the translated run exists, i cannot be guaranteed in the last state, because i is missing in P. Now, we repeat the argument for this last state and obtain that wi is an error trace of \(Q'\).
A similar argument holds for the languages: for a trace w in \(P'\), we either find the same trace in \(Q'\) or an error trace that is a prefix of w. \(\square \)
Next, we consider our two ready preorders:
Theorem 64
(IA-spectrum) \(\preceq _{\text {rs}}\;\subseteq \;\, \sqsubseteq _{\text {Rd}}\,\).
Proof
Let \(P \preceq _{\text {rs}}Q\) due to \({{\mathscr {R}}}\), and consider \(wi \in {\text {StET}}({P}) = {\text {PrET}}({P})\) due to \(p_0 {\mathop {\Longrightarrow }\limits ^{w}} p {\mathop {\longrightarrow }\limits ^{i}} e\). We proceed by induction on the length of the underlying run. Assume that \(p_0 {\mathop {\Longrightarrow }\limits ^{v}} p'\) due to a prefix of this run, and we have \(q_0 {\mathop {\Longrightarrow }\limits ^{v}} q'\) for some \(q'\) with \((p',q') \in {{\mathscr {R}}}\) due to induction or because \(p' = p_0\) and \(q' = q_0\). Let \(p' {\mathop {\longrightarrow }\limits ^{\alpha }} p''\) be the next transition. If \(\alpha \in O_\tau \), then \(q' {\mathop {\Longrightarrow }\limits ^{{\hat{\alpha }}}} q''\) for some \(q''\) satisfying \((p'',q'') \in {{\mathscr {R}}}\). The same holds for \(\alpha \in I\), except if \(\alpha \notin {\mathbb {I}}_\forall ({q'})\). In the latter case, \(v\alpha \in {\text {ET}}({Q})\) for the prefix \(v\alpha \) of w, and we are done. If the latter never happens, we get \(q_0 {\mathop {\Longrightarrow }\limits ^{w}} q\) with \((p,q) \in {{\mathscr {R}}}\), and \(i \notin {\mathbb {I}}_\forall ({q})\) due to \( i \notin {\mathbb {I}}_\forall ({p})\). Thus, \(q \Longrightarrow {\mathop {\longrightarrow }\limits ^{i}} e\) and \(wi \in {\text {ET}}({Q})\). Now, it suffices to consider some \((w, X) \in {\text {StRP}}({P})\) due to \(p_0 {\mathop {\Longrightarrow }\limits ^{w}} p\). As above, \((w, X) \in {\text {RP}}({Q})\) due to flooding or \(q_0 {\mathop {\Longrightarrow }\limits ^{w}} q\) with \((p,q) \in {{\mathscr {R}}}\) and \({\mathbb {R}}({q}) = {\mathbb {R}}({p}) = X\). \(\square \)
However, many inclusions between the preorders presented in this article are invalid, due to following lemma:
Lemma 65
(Failing implications) The following properties hold:
-
(a)
\(\preceq _{\text {rs}}\) is not included in \(\sqsubseteq _{\text {Div}}\);
-
(b)
\(\approx \) is not included in \(\sqsubseteq _{\text {Div}}\);
-
(c)
\(\approx \) is not included in \(\sqsubseteq _{\text {Qui}}\);
-
(d)
\(\sqsubseteq _{\text {CJK}}\) is not included in \(\preceq _{\text {acc}}\);
-
(e)
\(\sqsubseteq _{\text {Rd}}\) is not included in \(\preceq _{\text {acc}}\).
Proof
Regarding Parts (a)–(c), consider IAs \(R_1\), \(R_2\) in Fig. 15. These are bisimilar, and \(R_1 \preceq _{\text {rs}}R_2\) due to \(R_2\) staying put in the initial state. However, \(R_1 \not \sqsubseteq _{\text {Div}}R_2\) due to \(R_1\) being divergent, and \(R_2 \not \sqsubseteq _{\text {Qui}}R_1\) because only \(R_2\) has a quiescent trace.
Regarding Part (d), examine IAs \(R_3\), \(R_4\) of Fig. 15. They have the same language and quiescent traces, no (strict) divergent traces, and the same error traces due to the missing input transitions to the implicit canonical error state. Hence, they are CJK-equivalent, but the i-transition of \(R_3\) cannot be properly simulated by \(R_4\), i.e., \(R_3 \not \preceq _{\text {acc}}R_4\).
Regarding Part (e), the IAs \(R_5\), \(R_6\) in Fig. 15 satisfy \(R_5 \sqsubseteq _{\text {Rd}}R_6\) but \(R_5 \not \preceq _{\text {acc}}R_6\), analogous to the argument above for Part (d). \(\square \)
This lemma now allows us to conclude this section with the desired theorem for corroborating our IA-spectrum:
Theorem 66
(IA-spectrum) All inclusions between the linear-time and branching-time refinement are depicted using dashed arrows in Fig. 6; in particular, these inclusions are strict.
Proof
The positive statements are proved in Theorems 63 and 64. Furthermore, \(\preceq _{\text {rs}}\) does not imply any other linear-time preorders by Lemma 65(a). The other branching-time preorders do not imply any linear-time preorder except \(\sqsubseteq _E\), and the linear-time preorders do not imply any branching-time preorder. \(\square \)
6 Discussion
De Alfaro and Henzinger’s IA-setting and its preorders IA-simulation and alternating simulation have influenced the field of interface theories and are closely related to a research direction in model-based testing. In the former field, the majority of recent interface theories are based on Modal Transition Systems (MTS) and the modal refinement preorder [28], which is more expressive than IA [29]. In the latter field, the ioco approach [39] uses a trace-comparing relation not unlike alternating simulation.
MTS-based interface theories Refinement in the IA-setting is characterized by allowing the addition of inputs and the removal of outputs, which implies that, e.g., the single-state interface with a self-loop for every input action and no further transition refines any interface. Thus, output actions in IA specify permitted but not required behaviour. This is why recent research [4, 9, 19, 29, 35] has focused on combining IA [13] and Modal Transition Systems (MTS) [28]; MTS allows one to specify required and optional behaviour, for any action. Taking stepwise decisions on the optional behaviour permits a component-based, incremental design, which is supported in MTS by the compositional modal refinement preorder.
This research on combining IA and MTS has led to Modal Interface Automata (MIA) [9], which resolves the conflict between unspecified inputs being allowed in IA but forbidden in MTS and does away with the input-determinism requirement of IA. MIA fixes various shortcomings of earlier works: modal refinement in the IOMTS-setting of Larsen et al. [29] is not a precongruence for parallel composition; the MI-setting of Raclet et al. [35] considers deterministic interfaces only; the MIO-setting of Bauer et al. [4] adopts pessimistic compatibility that deems a composition undefined as soon as some error can potentially occur in some system environment. Not unlike EIO [10, 38], there is also an error-aware variant EMIA [19] of MIA, which leaves error states explicit and does not prune them away. Thereby, one may distinguish potential errors that can be resolved by refinement, from actual, unresolvable errors that arise when an output is required but the corresponding input is forbidden.
Finally, it should be noted that all MTS-based theories mentioned above are interface theories in the sense that they are equipped also with a conjunction and a quotienting operator. Conjunction is necessary when reasoning about a component that must satisfy several interfaces, while quotienting enables one to calculate residual interfaces when given some partial system implementation.
The ioco approach This approach [39] for model based testing is somewhat related to interface automata, because it allows one to implement unspecified inputs and to ignore specified outputs, at least to some degree. One difference is that the ioco-relation compares an implementation to a specification, i.e., the approach does not aim at stepwise refinement. Furthermore, an implementation is required to be input-enabled. Another and essential difference is that it suffices to provide an input via some preceding \(\tau \)s; there is no concept of communication error and, in particular, no concern about an input not being provided immediately (cf. [40]).
An additional feature of the ioco-setting is that each quiescent state is decorated with a \(\delta \)-labelled loop. (Usually, these loops are left implicit.) For \(\delta \)-decorated models without \(\tau \), it is shown in [1], for an input-deterministic implementation P and a deterministic specification Q, that P ioco-implements Q if and only if \(P \preceq _{\text {alt}}Q\). Conceptually, the ioco-relation compares traces of P and Q and, under the restrictions mentioned, it coincides with quiescence-, divergence- and CJK-refinement due to the \(\delta \)-transitions. This does not hold without determinism, because our strict quiescence traces just end in a quiescent state, whereas a trace in the ioco-approach can additionally inform about quiescent states passed along the way.
Motivated by the ioco-approach, a refinement based on alternating simulation is introduced in [22] under the name of iocos, which stands for ioco-simulation. The referenced paper considers \(\delta \)-decorated IAs without \(\tau \) as models (and without distinguishing implementations and specifications) and defines a natural variation of ioco for these models. The new iocos coincides with \(\preceq _{\text {IA}}\), except for the additional discrimination due to \(\delta \). It is shown in [22] that iocos is finer than ioco and that it can be characterized with a testing scenario; a general parallel composition is not considered.
The very recent paper [26] also looks at stepwise refinement in relation to the ioco-approach and alternating simulation in a setting without parallel composition, precongruence results and internal actions. It introduces input-failure refinement, which is another characterization of error-refinement as in [10, 11], although this result is not formally stated or proven. Taking also \(\delta \) into account, this refinement fits another variant of ioco in the literature called uioco.
7 Conclusions and future work
De Alfaro and Henzinger’s Interface automata (IA) [12] are a popular framework for formally reasoning about the compatibility of concurrently interacting components, for which a sizeable number of behavioural preorders have been proposed in the literature over the years. In this article, we characterized and compared these preorders, both trace-based and simulation-based preorders, so as to arrive at a linear-time branching-time spectrum for IA, in analogy to the linear-time branching-time spectrum of van Glabbeek for ordinary labelled transition systems [42]. This was done via a uniform and general notion of parallel composition that constitutes a multicast communication mechanism for synchronizing components, as well as a hiding operator for action scoping. Alongside, we also explored several new preorders for IA, based on ready semantics, ready simulation and bi-variant simulation.
An important insight obtained by our work was that the problem in the original publication on IA [12], namely that parallel composition is not associative, disappears if a proper pruning of states that can locally reach an error state is applied, even for interfaces that are not input-deterministic. Complementing the work of Göhrle [21], we characterized this original preorder of [12], which is coarser than strict acceptance refinement, as a simulation-preorder called acceptance refinement. Thereby, our framework of general interface automata and acceptance refinement paves the way for further investigations into semantic theories for interface automata, without the need for input-determinism.
Future work We propose to complete the presented IA-spectrum by using van Glabbeek’s Linear-Time Branching-Time Spectrum II [42] as guidance. Our spectrum is currently missing, among other behavioural relations, ready trace semantics [33] and possible futures semantics [36] in the lower, linear-time half and branching bisimulation [45] in the upper, branching-time half. These have not yet been considered in the IA-literature.
Some of the linear-time preorders studied in this article, namely error semantics, quiescence semantics and divergence semantics, are supported by full-abstraction results. Such results are closely related to observational justifications via testing or button pushing scenarios [15, 41, 42], which are missing for the remaining linear-time and all branching-time preorders. It would be nice to improve the situation, e.g., using ideas of Abramsky [2].
Concerning the applicability of interface theories, we note that reasoning about communication errors is already employed in the design of asynchronous circuits, which are vulnerable to unexpected inputs (see, e.g., [16, 17]). We suggest that IA is developed further towards practical applications in software engineering, for which one would need to consider at least extensions of the model with data (see, e.g., [14, 20, 24]). As a final note, programming languages such as Go have been extended with session types; these check for communication safety, which is related to communication error in IA [25, 27].
Dedication We dedicate this article to Rob van Glabbeek, an exceptional researcher and outstanding colleague, on the occasion of his 60th birthday. Foremost, we thank him for the many fruitful discussions that we had on various topics in concurrency theory. We are also grateful for Rob’s strong dedication to the scientific community, which led him to establish, with his own time and financial resources, the Electronic Proceedings in Theoretical Computer Science (EPTCS) series, an international, refereed open access venue for the rapid electronic publication of workshop and conference proceedings and other scientific works.
Change history
08 July 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00236-021-00406-w
References
Aarts, F., Vaandrager, F.: Learning I/O automata. In: CONCUR, volume 6269 of LNCS, pp. 71–85. Springer (2010)
Abramsky, S.: Observation equivalence as a testing equivalence. Theoret. Comput. Sci. 53, 225–241 (1987)
Aceto, L., Fábregas, I., de Frutos-Escrig, D., Ingólfsdóttir, A., Palomino, M.: On the specification of modal systems: a comparison of three frameworks. Sci. Comput. Program. 78(12), 2468–2487 (2013)
Bauer, S., Mayer, P., Schroeder, A., Hennicker, R.: On weak modal compatibility, refinement, and the MIO Workbench. In: TACAS, volume 6015 of LNCS, pp. 175–189. Springer (2010)
Benveniste, A., Caillaud, B., Nickovic, D., Passerone, R., Raclet, J.-B., Reinkemeier, P., Sangiovanni-Vincentelli, A., Damm, W., Henzinger, T.A., Larsen, K.G.: Contracts for system design. Found. Trends EDA 12(2–3), 124–400 (2018)
Bloom, B.: Ready Simulation, Bisimulation, and the Semantics of CCS-like Languages. PhD thesis, MIT (1990)
Brookes, S.D., Hoare, C.A.R., Roscoe, A.W.: A theory of communicating sequential processes. J. ACM 31(3), 560–599 (1984)
Bujtor, F.: Modal Interface Automata: A Theory for Heterogeneous Specification of Parallel Systems. PhD thesis, Univ. Augsburg, Germany (October 2018). https://opus.bibliothek.uni-augsburg.de/opus4/files/43805/Bujtor_Diss.pdf. Accessed 2 Feb 2020
Bujtor, F., Fendrich, S., Lüttgen, G., Vogler, W.: Nondeterministic modal interfaces. Theoret. Comput. Sci. 642(C), 24–53 (2016)
Bujtor, F., Vogler, W.: Error-pruning in interface automata. Theoret. Comput. Sci. 597, 18–39 (2015)
Chilton, C., Jonsson, B., Kwiatkowska, M.: An algebraic theory of interface automata. Theoret. Comput. Sci. 549, 146–174 (2014)
de Alfaro, L., Henzinger, T.A.: Interface automata. In: ESEC/FSE, pp. 109–120. ACM (2001)
de Alfaro, L., Henzinger, T.A.: Interface-based design. In: Engineering Theories of Software Intensive Systems, pp. 83–104. Springer (2005)
de Alfaro, L., da Silva, L.D., Faella, M., Legay, A., Roy, P., Sorea, M.: Sociable interfaces. In: FroCoS, volume 3717 of LNCS, pp. 81–105. Springer (2005)
De Nicola, R., Hennessy, M.: Testing equivalences for processes. Theoret. Comput. Sci. 34, 83–133 (1984)
Dill, D.L.: Trace Theory for Automatic Hierarchical Verification of Speed-Independent Circuits. MIT Press, Cambridge (1989)
Ebergen, J.C.: Arbiters: an exercise in specifying and decomposing asynchronously communicating components. Sci. Comput. Program. 18(3), 223–245 (1992)
Fahrenberg, U., Legay, A.: A linear-time–branching-time spectrum for behavioral specification theories (May 2019). Preprint submitted to J. Log. Algebr. Meth. Program. Available as arXiv:1604.06503v4
Fendrich, S., Lüttgen, G.: A generalised theory of interface automata, component compatibility and error. Acta Inf. 56(4), 287–319 (2019)
Gareis, J., Lüttgen, G., Schinko, A., Vogler, W.: Interface automata for shared memory. In: Models, Mindsets, Meta: The What, the How, and the Why Not? Essays Dedicated to Bernhard Steffen on the Occasion of His 60th Birthday, volume 11200 of LNCS, pp. 151–166. Springer (2018)
Göhrle, S.: Input-Verweigerungs-Simulation für Interface-Automaten. Master’s thesis, Univ. Augsburg, Germany (2014)
Gregorio-Rodríguez, C., Llana, L., Martínez-Torres, R.: Input-output conformance simulation (iocos) for model based testing. In: FMOODS/FORTE, volume 7892 of LNCS, pp. 114–129. Springer (2013)
Hennessy, M.: Algebraic Theory of Processes. MIT Press, Cambridge (1988)
Holík, L., Isberner, M., Jonsson, B.: Mediator synthesis in a component algebra with data. In: Correct System Design, volume 9360 of LNCS, pp. 238–259. Springer (2015)
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. SIGPLAN Not. 43(1), 273–284 (2008)
Janssen, R., Vaandrager, F.W., Tretmans, J.: Relating alternating relations for conformance and refinement. In: IFM, volume 11918 of LNCS, pp. 246–264. Springer (2019)
Lange, J., Ng, N., Toninho, B., Yoshida, N.: A static verification framework for message passing in Go using behavioural types. In: ICSE, pp. 1137–1148. ACM (2018)
Larsen, K.G.: Modal specifications. In: Automatic Verification Methods for Finite State Systems, volume 407 of LNCS, pp. 232–246. Springer (1990)
Larsen, K.G., Nyman, U., Wasowski, A.: Modal I/O automata for interface and product line theories. In: ESOP, volume 4421 of LNCS, pp. 64–79. Springer (2007)
Lüttgen, G., Vogler, W.: Modal interface automata. Log. Methods Comput. Sci. 9(3:4), 1–28 (2013)
Lynch, N.A.: Distributed Algorithms. Morgan Kaufmann, Burlington (1996)
Milner, R.: Communication and Concurrency. Prentice Hall, Upper Saddle River (1989)
Olderog, E.-R., Hoare, C.A.R.: Specification-oriented semantics for communicating processes. Acta Inf. 23(1), 9–66 (1986)
Park, D.: Concurrency and automata on infinite sequences. In: Theoretical Computer Science, volume 104 of LNCS, pp. 167–183. Springer (1981)
Raclet, J.-B., Badouel, E., Benveniste, A., Caillaud, B., Legay, A., Passerone, R.: A modal interface theory for component-based design. Fundam. Inform. 108(1–2), 119–149 (2011)
Rounds, W.C., Brookes, S.D.: Possible futures, acceptances, refusals, and communicating processes. In: FOCS, pp. 140–149. IEEE (1981)
Schäfer, M., Vogler, W.: Component refinement and CSC-solving for STG decomposition. Theoret. Comput. Sci. 388(1–3), 243–266 (2007)
Schinko, A., Vogler, W.: Fault-free refinements for interface automata. Sci. Ann. Comp. Sci. 28, 289–337 (2018)
Tretmans, J.: Model-based testing and some steps towards test-based modelling. In: SFM, volume 6659 of LNCS, pp. 297–326. Springer (2011)
van der Bijl, M., Rensink, A., Tretmans, J.: Compositional testing with IOCO. In: FATES, volume 2931 of LNCS, pp. 86–100. Springer (2004)
van Glabbeek, R.: The linear time—branching time spectrum. In: CONCUR, volume 458 of LNCS, pp. 278–297. Springer (1990)
van Glabbeek, R.: The linear time—branching time spectrum II. In: CONCUR, volume 715 of LNCS, pp. 66–81. Springer (1993)
van Glabbeek, R.: The linear time—branching time spectrum I. In: Handbook of Process Algebra, pp. 3–99. North-Holland/Elsevier (2001)
van Glabbeek, R.: The coarsest precongruences respecting safety and liveness properties. In: TCS, volume 323 of IFIP Advances in Information and Communication Technology, pp. 32–52. Springer (2010)
van Glabbeek, R., Weijland, W.P.: Branching time and abstraction in bisimulation semantics. J. ACM 43(3), 555–600 (1996)
Acknowledgements
We thank Ayleen Schinko and Simon Göhrle for their past contributions to a number of results presented in this article. Moreover, we are grateful to the reviewers for their insightful suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was partially supported by the DFG-project Foundations of Heterogenous Specifications Using State Machines and Temporal Logic (Grant Nos. LU 1748/3-2 and VO 615/12-2).
The original online version of this article was revised due to retrospective open access.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vogler, W., Lüttgen, G. A linear-time branching-time perspective on interface automata. Acta Informatica 57, 513–550 (2020). https://doi.org/10.1007/s00236-020-00369-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-020-00369-4

















 .
. , then
, then  .
.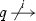 if
if  for some
for some 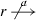 with
with  and
and  , and (q, r) is illegal as above.
, and (q, r) is illegal as above. for some
for some 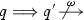 , then we would have
, then we would have  due to pruning, although
due to pruning, although  by Lemma
by Lemma  and
and 

