Abstract
For each two-way alternating finite automaton (a fa) A with s states, we directly build a a fa \(A^c \) with \(O(s^6)\) states which accepts exactly those inputs that are not accepted by A. This improves upon the previously best-known construction, which was both more expensive and more complicated, as it required \(O(s^7)\) states and involved building and simulating an intermediate linear-bounded automaton.












Similar content being viewed by others
Notes
The side notes in small font on the right margin of each line of pseudocode will be useful in Sect. 5, when we discuss implementation and efficiency. For now, they can be ignored.
In pseudocode, such existential branching is captured by the statement “\(\smash {\underline{\mathbf{guess }}}\) one of:,” followed by a list of •-marked code snippets: the current branch of the a fa forks into one new branch for each snippet, and accepts iff at least one of these branches accepts. When the branching is over (not multiple code snippets, but) multiple values of a variable v, then we use the statement “\(\smash {\underline{\mathbf{guess }}}\) one v”: the a fa forks into one new branch for each possible value of v, and the statement accepts iff at least one of these branches accepts. Likewise, universal branching is captured by the statements “\(\smash {\underline{\mathbf{select }}}\) one of:” and “\(\smash {\underline{\mathbf{select }}}\) one v,” which are interpreted similarly, except now the current branch accepts iff all of the new branches do. To help understand this terminology, we stress that our pseudocode is written from the perspective (not of the entire computation, but) of a single computation branch: it describes what a single branch must do when it participates (together with other branches) in the execution of a procedure. From this perspective, other usual phrases for describing existential and universal branching, like “check/verify existentially one of:” and “check/verify universally/in parallel each of:” (which are suitable from the perspective of the entire computation), are not appropriate: e.g., a single branch cannot do multiple things “in parallel,” as this requires spawning other branches; but it can certainly guess which one of many snippets is the “right” one and execute it, or select among many snippets the one “assigned” to it and execute it.
By the analysis of Sect. 5, it will be clear that l:2 in this snippet needs \(\varTheta (s^7)\) states.
Note that, in contrast, calls to procedures do not require a call stack, for two reasons: first, because the called procedure does not need to return any value; and second, because (as the reader can verify by inspection) no procedure call is ever followed by other steps in the calling procedure. Hence, the automaton can execute the called procedure independently from the calling one, i.e., without storing any information about it, as it will never need to return to it.
References
Birget, J.-C.: Partial orders on words, minimal elements of regular languages, and state complexity. Theoret. Comput. Sci. 119, 267–291 (1993)
Geffert, V.: Complement for two-way alternating automata. In: Proceedings of the International Computer Science Symposium in Russia, pp. 132–144 (2018)
Geffert, V., Kapoutsis, C., Zakzok, M.: Complement for two-way alternating automata. Acta Informatica (2020). https://doi.org/10.1007/s00236-020-00373-8
Geffert, V., Mereghetti, C., Pighizzini, G.: Complementing two-way finite automata. Inf. Comput. 205(8), 1173–1187 (2007)
Geffert, V., Okhotin, A.: Transforming two-way alternating finite automata to one-way nondeterministic automata. In: Proceedings of the International Symposium on Mathematical Foundations of Computer Science, pp. 291–302 (2014)
Goldstine, J., Kappes, M., Kintala, C.M.R., Leung, H., Malcher, A., Wotschke, D.: Descriptional complexity of machines with limited resources. J. Univ. Comput. Sci. 8(2), 193–234 (2002)
Kapoutsis, C.: Removing bidirectionality from nondeterministic finite automata. In: Proceedings of the International Symposium on Mathematical Foundations of Computer Science, pp. 544–555 (2005)
Kapoutsis, C.: Algorithms and lower bounds in finite automata size complexity. Ph.D. Thesis, Massachusetts Institute of Technology (2006)
Kapoutsis, C.: Minicomplexity. J. Autom. Lang. Comb. 17(2–4), 205–224 (2012)
Kapoutsis, C., Zakzok, M.: Alternation in two-way finite automata. Theor. Comput. Sci. (2020). https://doi.org/10.1016/j.tcs.2020.12.011
Meyer, A.R., Fischer, M.J.: Economy of description by automata, grammars, and formal systems. In: Proceedings of the Symposium on the Foundations of Computer Science, pp. 188–191 (1971)
Rabin, M.O., Scott, D.: Remarks on finite automata. In: Proceedings of the Summer Institute of Symbolic Logic, pp. 106–112. Cornell (1957)
Rabin, M.O., Scott, D.: Finite automata and their decision problems. IBM J. Res. Dev. 3, 114–125 (1959)
Sakoda, W.J., Sipser, M.: Nondeterminism and the size of two-way finite automata. In: Proceedings of the Symposium on the Theory of Computing, pp. 275–286 (1978)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author was supported by the Slovak Grant Agency for Science (VEGA) under contract 1/0177/21 Descriptional and Computational Complexity of Automata and Algorithms and by the Slovak Research and Development Agency under contract APVV-15-0091 Efficient Algorithms, Automata, and Data Structures. The last two authors were supported by Qatar Foundation, through CMUQ’s Seed Research program and under project Minicomplexity. The statements made herein are solely the responsibility of the authors.
Appendix: Notes
Appendix: Notes
(1) So, here we are describing a fa computations following the run view of [10].
(2) Indeed, every accepting terminal configuration (q, i) is an accepting configuration, because the single-node tree with root (q, i) is already an accepting run. And every rejecting terminal configuration (q, i) is a non-accepting configuration, because an accepting run from it would have root (q, i) (by (A3)); this root would be a leaf (by (A2), as (q, i) is terminal); and thus (A5) would fail (as this leaf would not be an accepting terminal configuration), so this tree would not be an accepting run.
(3) Proof of Lemma 1
Pick any a fa \(A=(S,{\,\cdot \,},\delta ,q_s ,F,U)\). Let \(A':=(S\cup \{q_r \},{\,\cdot \,},\delta ',q_s ,F,U)\) be the a fa that we get from A when we add a fresh non-final existential state \(q_r \) with no outgoing transitions, i.e., with no transitions of the form \((q_r ,{\,\cdot \,},{\,\cdot \,},{\,\cdot \,})\); and redirect to it all “reflexive” transitions, i.e., replace every transition of the form \((q,a,q,\textsc {i} )\) by the corresponding transition \((q,a,q_r ,\textsc {i} )\). Clearly, \(A'\) is irreflexive. To show that it is also equivalent to A, we fix an arbitrary input w and prove that
Before doing so, let \(n:=|w|\) and \(0\le i\le n{+}2\), and observe that:
-
(a)
Every configuration \((q_r ,i)\) is terminal and rejecting: either because it is outer and \(q_r \) is non-final; or because is it inner and \(\delta '(q_r ,w_i)=\emptyset \) and \(q_r \) is existential.
-
(b)
\(|\delta '(q,a)|=|\delta (q,a)|\) for all q, a: either because \(\delta \) does not have the reflexive transition \((q,a,q,\textsc {i} )\), and thus \(\delta '(q,a)=\delta (q,a)\); or because it does, and so \((q,a,q,\textsc {i} )\) is replaced by \((q,a,q_r ,\textsc {i} )\), hence \(\delta '(q,a)\) is \(\delta (q,a)\) with \((q,\textsc {i} )\) replaced by \((q_r ,\textsc {i} )\).
-
(c)
Every configuration (q, i) with \(q\in S\) is terminal in \(A'\) iff it is terminal in A, by observation (b); and, if it is terminal, then it is accepting in \(A'\) iff it is accepting in A, since \(A,A'\) share the same sets of final and universal states.
Using these observations, we prove each direction of (7) separately.
\([\Rightarrow ]\) Suppose \(A'\) accepts w. Let \(T'\) be an accepting run from \((q_s ,0)\). We claim that (i) \(T'\) uses no configuration of the form \((q_r ,{\,\cdot \,})\), and thus (ii) \(T'\) is also an accepting run of A on w. So, A accepts w, and we are done.
To justify (i), suppose \(T'\) contains node \((q_r ,i)\) for some i. Since \((q_r ,i)\) is terminal (by (a)), this node is a leaf. Since \((q_r ,i)\) is rejecting (again by (a)), one of the leaves of \(T'\) is not an accepting terminal configuration, so \(T'\) fails the last of conditions (A1)–(A5) (from p. 4) and is not an accepting run, which is a contradiction.
To justify (ii), we verify (A1)–(A5). First, \(T'\) is indeed a tree of configurations of A (since it uses only states from S, by (i)) and is clearly finite (cf. (A1)) and rooted at the start configuration of A (cf. (A3)). Moreover, every edge in \(T'\) is caused by a \(\delta '\)-transition which is also in \(\delta \) (or else that transition would be the replacement \((q,a,q_r ,\textsc {i} )\) of some reflexive transition of A, so it would introduce \(q_r \) into \(T'\), contradicting (i)), so every parent indeed \(\delta \)-yields each of its children (cf. (A2)). Finally, every leaf is an accepting terminal configuration of A (cf. (A5)), by (c) and since it is accepting terminal in \(A'\); and every internal node (q, i) is either existential with exactly 1 child or universal with exactly \(|\delta (q,w_i)|\) children (cf. (A4)), by (b) and since \(T'\) is an accepting run of \(A'\).
\([\Leftarrow ]\) Suppose A accepts w. Let T be an accepting run from \((q_s ,0)\) that is smallest, in the sense that it has the smallest possible number of nodes. We say that an edge \((q,i)\rightarrow (p,j)\) in T is “reflexive” if so is the underlying transition \((q,w_i,p,j{-}i)\in \delta \), i.e., if \((q,i)=(p,j)\). We claim that (i) T contains no reflexive edges, and thus (ii) T is also an accepting run of \(A'\) on w. So, \(A'\) accepts w, and we are done.
To justify (i), suppose T uses a reflexive transition \((q,{\,\cdot \,},q,\textsc {i} )\) to create a reflexive edge from a parent \(u=(q,i)\) to an identical child \(v=(q,i)\). Consider the tree \(\smash {\tilde{T}}\) derived from T when we replace the subtree rooted at u with the subtree rooted at v. Easily, \(\smash {\tilde{T}}\) is still an accepting run of A from \((q_s ,0)\). Moreover, it has strictly fewer nodes than T, contradicting the selection of T as smallest.
To justify (ii), we verify (A1)–(A5). First, T is indeed a tree of configurations of \(A'\) (since all states of A are also in \(A'\)) and is clearly finite (cf. (A1)) and rooted at the start configuration of \(A'\) (cf. (A3)). Moreover, every edge in T is caused by a \(\delta \)-transition which is also in \(\delta '\) (or else that transition would be among the reflexive ones that we replaced, and thus the edge would be reflexive, contradicting (i)), so every parent indeed \(\delta '\)-yields each of its children (cf. (A2)). Finally, every leaf is an accepting terminal configuration of \(A'\) (cf. (A5)), by (c) and since it is accepting terminal in A; and every internal node (q, i) is either existential with exactly 1 child or universal with exactly \(|\delta '(q,w_i)|\) children (cf. (A4)), by (b) and since T is an accepting run of A.
(4) Proof of Lemma 2
Let \(A=(S,\varSigma ,\delta ,q_s ,F,U)\) be any irreflexive a fa. We introduce the new a fa \(A':=(S\cup S',\varSigma ,\delta ',q_s ,F,U\cup U')\), where \(S':=\{q'\mid q\in S\}\) and \(U':=\{q'\mid q\in U\}\) and \(\delta '\) consists of the transitions:
We prove that \(A'\) is asymmetric and equivalent to A.
Asymmetry. Toward a contradiction, suppose \(A'\) is not asymmetric. Then there exist input w and configurations (q, i) and (p, j) such that the configuration graph of A on w contains both arrows between them.
-
If \(q\in S\), then consider the arrow \((q,i)\rightarrow (p,j)\). This is caused by a transition \((q,w_i,p,j-i)\), which is of the form (8) (as \(q\in S\)), and so \(p=q'\) and \(j-i=\textsc {i} =0\). Hence, the other arrow \((p,j)\rightarrow (q,i)\) is really \((q',i)\rightarrow (q,i)\) and is caused by a transition \((q',w_i,q,\textsc {i} )\); since this is of type (9), it implies that \(\delta \) contains the reflexive transition \((q,w_i,q,\textsc {i} )\), and thus A is not irreflexive —a contradiction.
-
If \(p\in S\), then by a similar argument we conclude that \(\delta \) contains the reflexive transition \((p,w_j,p,\textsc {i} )\), and thus A is not irreflexive —a contradiction.
Hence, \(q,p\in S'\). But then the arrows between (q, i) and (p, j) imply that \(\delta \) contains transitions between states in \(S'\), which is again a contradiction (by (8) and (9)).
Equivalence. Pick any w. We prove that \(A'\) accepts w iff A does, by showing how to convert an accepting run of one automaton to an accepting run of the other.
Let T be an accepting run of A from \((q_s ,0)\). Consider the tree \(T'\) of configurations of \(A'\) that we get from T when we replace every node (q, i) which is an inner configuration by the edge \((q,i)\rightarrow (q',i)\) (so that all children of (q, i) become children of \((q',i)\), which in turn becomes the unique child of (q, i)). Note that, when the node (q, i) is a leaf (and thus (q, i) is an accepting terminal configuration), then either (a) no replacement takes place, if (q, i) is an outer configuration; or (b) the replacement involves no children, if (q, i) is inner with \(q\in U\) and \(\delta (q,w_i)=\emptyset \).
We claim that \(T'\) is an accepting run of \(A'\) from \((q_s ,0)\). Indeed, it is clearly finite (see (A1) in p. 4) with root \((q_s ,0)\) (see (A3)). Moreover, every leaf is an accepting terminal configuration (see (A5)):
-
If it is an old leaf (case (a) above), then it is an outer accepting terminal configuration of A, namely \((q,n{+}2)\) with \(q\in F\). Hence, it is also an (outer) accepting terminal configuration in \(A'\), as desired.
-
If it is a new leaf \((q',i)\) hanging under and old leaf (q, i) (case (b) above), then \(i\le n{+}1\) and \(q\in U\) and \(\delta (q,w_i)=\emptyset \). Hence, it is also \(q'\in U'\) and \(\delta '(q',w_i)=\emptyset \) (as \(q'\) inherits both the type and the transitions (9) of q). So, \((q',i)\) is again an (inner) accepting terminal configuration of \(A'\).
Finally, every parent node has the correct number of children (see (A4)) and yields each one of them (see (A2)):
-
If it is an old node (q, i), then it has \((q',i)\) as only child. By transitions (8), this is indeed yielded by (q, i); and is the correct number, both when q is existential (obviously) and when q is universal (since \(|\delta '(q,w_i)|=|\{(q',\textsc {i} )\}|=1\)).
-
If it is a new node \((q',i)\), then its children as those of its parent (q, i) in T. By transitions (9), these are indeed yielded by \((q',i)\) (since they were yielded by (q, i) in T) and are the correct number (since they were the correct number for (q, i) in T, and since \(q'\) inherits the type of q).
Overall, we see that \(T'\) indeed satisfies all necessary conditions.
Conversely, let \(T'\) be an accepting run of \(A'\) from \((q_s ,0)\). We know all transitions of \(A'\) switch from states in S to states in \(S'\) (type (8)) or vice versa (type (9)). Hence, since the root \((q_s ,0)\) of \(T'\) at level 0 uses a state from S, it follows that every node at an even (resp., odd) level uses a state from S (resp., from \(S'\)).
Consider any internal even-level node (q, i). Since \(q\in S\), the only transition of the form \((q,w_i,{\,\cdot \,},{\,\cdot \,})\) in \(\delta '\) is the transition \((q,w_i,q',\textsc {i} )\) of type (8). Hence, the only possible child for (q, i) is the configuration \((q',i)\) yielded by this transition; and so it is the unique child of (q, i) in \(T'\) (even when q is universal). In turn, \((q',i)\) has zero or more children (p, j), each yielded by a transition \((q',w_i,p,j{-}i)\) of type (9), which is in \(\delta '\) because of a corresponding transition \((q,w_i,p,j{-}i)\in \delta \). Therefore, (q, i) yields (p, j) in A. Moreover, in case q is universal, we know \(q'\) is also universal, so the children (p, j) of \((q',i)\) in \(T'\) are all configurations that \((q',i)\) can yield in \(A'\) (via transitions of type (9)), and thus also all configurations that (q, i) can yield in A (since transitions of type (9) replicate those from A).
Now consider the tree T that we get from \(T'\) when we first add an edge from every internal even-level node (q, i) to each one of its grandchildren (p, j), bypassing the odd-level child \((q',i)\); and then remove all these odd-level nodes. We claim that T is an accepting run of A from \((q_s ,0)\) on w. Indeed, it is a tree of configurations of A on w (since only even-level nodes survived, and these use only states from S), which is clearly finite (see (A1)) with root \((q_s ,0)\) (see (A3)). Moreover, every parent (q, i) yields all of its children (p, j) (see (A2)) and has the correct number of them (see (A4)), by the analysis of the previous paragraph. Finally, every leaf (q, i) is an accepting terminal configuration (see (A5)), either because it was also a leaf in \(T'\), and thus \(i=n{+}2\) and \(q\in F\) (the only way for an even-level node in \(T'\) not to have children, given the transitions of type (8)); or because it was the parent of a leaf \((q',i)\), and thus \(i\le n{+}1\) (or else (q, i) could not produce this child) and \(q'\) is universal with \(\delta '(q',w_i)=\emptyset \) (the only way for such \((q',i)\) not to have children), and thus q is universal with \(\delta (q,w_i)=\emptyset \) (since \(q'\) copies the type of q, and transitions of type (9) copy those from A). \(\square \)
(5) Proof of Lemma 3
Pick any a fa \(A=(S,\varSigma ,\delta ,q_s ,F,U)\). Consider the a fa
and \(\delta '\) is what we get from \(\delta \) when we apply the following changes:
-
(i)
We add the transition \((p_s ,{\vdash },q_s ,\textsc {i} )\). Hence, \(A'\) always starts by switching to the old start state and staying on \({\vdash }\), from where it starts simulating A (Fig. 13(1)).
-
(ii)
We add the transition \((p_f ,{\dashv },p_f ,\textsc {r} )\); and replace every transition \((q,{\dashv },p,\textsc {r} )\) where \(p\in F\) with the transition \((q,{\dashv },p_f ,\textsc {i} )\). Hence, every single step of A from \({\dashv }\) into a final state off \({\dashv }\) is simulated in \(A'\) by two steps with the same effect: first, an idle one into \(p_f \); and then an r-moving one into \(p_f \) off \({\dashv }\) (Fig. 13-(2,3)).
-
(iii)
We add the transition \((p_f ,a,p_f ,\textsc {r} )\) for every \(a\ne {\dashv }\); and, for every universal \(q\in S\) and symbol a with \(\delta (q,a)=\emptyset \), we add the transition \((q,a,p_f ,\textsc {i} )\). Hence, whenever A accepts inside the input by halting at a universal state, \(A'\) performs enough steps so that it eventually accepts at \(p_f \) off \({\dashv }\): first, an idle step into \(p_f \); and then enough r-moves through \(p_f \) (Fig. 13(2,5)).
-
(iv)
We add the transition \((p_s ,a,p_s ,\textsc {r} )\) for every \(a\ne {\vdash }\); and, for every existential \(q\in S\) and symbol a with \(\delta (q,a)=\emptyset \), we add the transition \((q,a,p_s ,\textsc {r} )\). Hence, whenever A rejects inside the input by halting at an existential state, \(A'\) performs enough steps so that it eventually rejects at \(p_s \) off \({\dashv }\): first, an r-move into \(p_s \); and then enough r-moves through \(p_s \) (Fig. 13(1,4)).
This concludes the definition of the new automaton. We claim that \(A'\) is in enf; that it is asymmetric, if A is; and that it is equivalent to A.
Converting the a fa of Fig. 1 into enf, assuming that \(q_2\) is existential, \(q_3\) is universal, and \(q_4\) is final; that \(\delta \) contains the tuple \((q_1,{\dashv },q_4,\textsc {r} )\); and that \(\delta (q_2,a)=\emptyset =\delta (q_3,a)\) when \(a\in \{{\vdash },\texttt {b},{\dashv }\}\). The two new rows show the fresh states \(p_s \) and \(p_f \). The arrows show the fresh transitions: (1) the idle move on \({\vdash }\) from the new start state to the old one, and the r-moves on all other symbols from \(p_s \) to itself; (2) the r-moves on all symbols from \(p_f \) to itself; (3) the idle move on \({\dashv }\) from \(q_1\) to \(p_f \) that replaces \((q_1,{\dashv },q_4,\textsc {r} )\); (4) the r-moves to \(p_s \) from the (existential, and thus) rejecting inner terminal configurations \((q_2,{\,\cdot \,})\); and (5) the idle moves to \(p_f \) from the (universal, and thus) accepting inner terminal configurations \((q_3,{\,\cdot \,})\)
Endmarker normal form. Conditions (E1) and (E3) are met because of (10); (E4) is met because of (ii) and since the transition \((p_f ,{\dashv },p_f ,\textsc {r} )\) added therein is the only transition of the form \(({\,\cdot \,},{\dashv },p_f ,\textsc {r} )\) that we ever add; and (E2) is met because of (iii) and (iv) (for the states in S), and (i) and (iv) (for \(p_s \)), and (ii) and (iii) (for \(p_f \)).
Asymmetry. Suppose A is asymmetric. Toward a contradiction, suppose \(A'\) is not. Then there exists w and two configurations (q, i) and (p, j) of \(A'\) on w that yield each other. Consider the underlining transitions \(e_1:=(q,w_i,p,j{-}i)\) and \(e_2:=(p,w_j,q,i{-}j)\). At least one of the two must be new, namely added in (i)–(iv) above (or else they are both in \(\delta \), contradicting the asymmetry of A). Without loss of generality, assume \(e_1\) is new. We take cases as to which of (i)–(iv) added it.
-
If (i): Then \(e_1\) has the form \((p_s ,{\,\cdot \,},{\,\cdot \,},\textsc {i} )\), and thus \(e_2\) has the form \(({\,\cdot \,},{\,\cdot \,},p_s ,\textsc {i} )\). However, all transitions into \(p_s \) are r-moving.
-
If (ii) or (iii): Then \(e_1\) has the form \(({\,\cdot \,},{\,\cdot \,},p_f ,\textsc {r} )\) or \(({\,\cdot \,},{\,\cdot \,},p_f ,\textsc {i} )\), and thus \(e_2\) has the form \((p_f ,{\,\cdot \,},{\,\cdot \,},\textsc {l} )\) or \((p_f ,{\,\cdot \,},{\,\cdot \,},\textsc {i} )\). However, all transitions from \(p_f \) are r-moving.
-
If (iv): Then \(e_1\) has the form \(({\,\cdot \,},{\,\cdot \,},p_s ,\textsc {r} )\), and thus \(e_2\) has the form \((p_s ,{\,\cdot \,},{\,\cdot \,},\textsc {l} )\). However, all transitions from \(p_s \) are idle or r-moving.
Overall, all cases lead to contradiction. So, \(A'\) is indeed asymmetric.
Equivalence. Pick any w. We prove that \(A'\) accepts w iff A does, by showing how to convert an accepting run of one automaton to an accepting run of the other.
Let T be an accepting run of A from \((q_s ,0)\). Its root is \((q_s ,0)\) and each leaf (p, j) is either outer, with \(i=n{+}2\) and \(p\in F\); or inner, with \(i\le n{+}1\) and \(p\in U\). Consider the tree \(T'\) that we get from T when we add the following edge to the root
replace every edge \((q,n{+}1)\rightarrow (p,n{+}2)\) to an outer leaf with the two edges
and replace every edge \((q,i)\rightarrow (p,j)\) to an inner leaf with the path
Is it easy to verify that \(T'\) is an accepting run of \(A'\) from \((p_s ,0)\). Specifically, (A2) (p. 4) holds because of the transitions introduced by (i) (for the edge in (11)) and (ii) (for the edges in (12) and the last edge in (13)) and (iii) (for the new edges in (13), except the last one), and because, apart from the transitions replaced in (ii), all other transitions of \(\delta \) are also in \(\delta '\); and (A4) holds because \(p_s \) and \(p_f \) are existential, and every universal configuration that used to be terminal now has only 1 child.
Conversely, let \(T'\) by an accepting run of \(A'\) from \((p_s ,0)\). We know the root is \((p_s ,0)\) (by (A3)), and its only child is \((q_s ,0)\) (since the only transition from \(p_s \) on \({\vdash }\) is the one added in (i)). We also know that every leaf is a copy of \((p_f ,n{+}2)\) (because it must be an accepting terminal configuration, by (A5); but all terminal configurations are outer, by (E2); and the only final state is \(p_f \), by (E3)) and unique child of a node \((p_f ,n{+}1)\) (by (E4)), which in turn is either a child of a node \((q,n{+}1)\), because of a transition that was added in (ii) on the basis of a transition \((q,{\dashv },p,\textsc {r} )\in \delta \) with \(p\in F\); or the last node of a path \((q,i)\rightarrow (p_f ,j)\rightarrow (p_f ,j{+}1)\rightarrow \cdots \rightarrow (p_f ,n{+}1)\) that is caused by transitions added in (iii), because \(q\in U\) and \(\delta (q,w_i)=\emptyset \). Overall, every maximal path in \(T'\) starts with \((p_s ,0)\rightarrow (q_s ,0)\) and finishes either with
where \(\delta (q,w_i)\ni (p,\textsc {r} )\) for some \(p\in F\); or with
where \(q\in U\) and \(\delta (q,w_i)=\emptyset \).
Now consider the tree T that we get from \(T'\) when we remove the root and replace every path of the form (14) with \((q,n{+}1)\rightarrow (p,n{+}2)\); and every path of the form (15) with the node (q, i). We claim that T is an accepting run of A from \((q_s ,0)\). Indeed, it is clearly finite (see (A1)) with root \((q_s ,0)\) (see (A3)). The replacement of the paths (14) and (15) ensures that every leaf is an accepting terminal configuration (see (A5)), as it is now either of the form \((p,n{+}2)\) for \(p\in F\); or of the form (q, i) with \(q\in U\) and \(\delta (q,w_i)=\emptyset \). Finally, these two changes remove from \(T'\) all occurrences of \(p_s \) and \(p_f \); so, every remaining edge is between two “old” configurations (i.e., configurations of A) and is thus caused by an “old” transition (i.e., from \(\delta \)); therefore, T also satisfies (A2) and (A4). \(\square \)
(6) The full code of function inarrows-aft:


(7) The full code of function inarrows-btw:
(8) Proof of  .
.
\([\Leftarrow ]\) Obvious. \([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the outstep  . This is possible only if (p, k) and \((x,k{+}d)\) are neighbors, so G contains at least one of the two arrows \(p\rightarrow x_d\) and \(x_d\rightarrow p\). (In fact, it contains exactly one, since A is asymmetric.) If it contains the first arrow, then the outstep is backtracking, so
. This is possible only if (p, k) and \((x,k{+}d)\) are neighbors, so G contains at least one of the two arrows \(p\rightarrow x_d\) and \(x_d\rightarrow p\). (In fact, it contains exactly one, since A is asymmetric.) If it contains the first arrow, then the outstep is backtracking, so
 holds; if it contains the second arrow, then the outstep is advancing, so
holds; if it contains the second arrow, then the outstep is advancing, so  holds.
holds.
(9) Proof of  , when \(x_d\) is the first in-neighbor of p (Fig. 6a).
, when \(x_d\) is the first in-neighbor of p (Fig. 6a).
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the advancing outstep  . Then this is the first step in the search of the in-neighbors of p. Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does break the threshold of p, so it contains a critical step
. Then this is the first step in the search of the in-neighbors of p. Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does break the threshold of p, so it contains a critical step  into it, where \(y_b\) some (out-neighbor of p, and thus some) state–direction pair.
into it, where \(y_b\) some (out-neighbor of p, and thus some) state–direction pair.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a critical instep  , from some \(y_b\). Then this step breaks the threshold of p, causing the start of the search of its in-neighbors. In particular, it causes the advancing outstep from p to its first in-neighbor, namely to \(x_d\). So, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the advancing outstep
, from some \(y_b\). Then this step breaks the threshold of p, causing the start of the search of its in-neighbors. In particular, it causes the advancing outstep from p to its first in-neighbor, namely to \(x_d\). So, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the advancing outstep  .
.
(10) Proof of  , when \(y_b,x_d\) are successive in-neighbors of p (Fig. 6b).
, when \(y_b,x_d\) are successive in-neighbors of p (Fig. 6b).
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the advancing outstep  . This starts the search of the in-neighbor \(x_d\) of p, which we know happens only after \({\widetilde{{\scriptstyle \mathcal {W}}}}\) has concluded the search of all previous in-neighbors. In particular, it happens only after the search of \(y_b\) is over. Therefore, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the step
. This starts the search of the in-neighbor \(x_d\) of p, which we know happens only after \({\widetilde{{\scriptstyle \mathcal {W}}}}\) has concluded the search of all previous in-neighbors. In particular, it happens only after the search of \(y_b\) is over. Therefore, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the step  which finishes that search.
which finishes that search.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step  . This concludes the search of the in-neighbor \(y_b\) of p, which we know is followed by the search of the next in-neighbor of p, namely of \(x_d\). So, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the initiating step
. This concludes the search of the in-neighbor \(y_b\) of p, which we know is followed by the search of the next in-neighbor of p, namely of \(x_d\). So, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the initiating step  of that search.
of that search.
(11) Proof of  (Fig. 6c, d).
(Fig. 6c, d).
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the backtracking step  . Then it also contains the matching advancing step
. Then it also contains the matching advancing step  . If this is non-critical, then
. If this is non-critical, then  holds. Otherwise,
holds. Otherwise,  is critical, and the first conjunct of
is critical, and the first conjunct of  is immediately true. The second conjunct is also immediately (and vacuously) true if p has no in-neighbors. Otherwise, the critical step
is immediately true. The second conjunct is also immediately (and vacuously) true if p has no in-neighbors. Otherwise, the critical step  it is followed in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) by the steps that search the in-neighbors of p. Since the matching backtracking step
it is followed in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) by the steps that search the in-neighbors of p. Since the matching backtracking step  does eventually happen, we know that the search of every in-neighbor \(y_b\) is completed, hence \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the corresponding concluding backtracking step
does eventually happen, we know that the search of every in-neighbor \(y_b\) is completed, hence \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the corresponding concluding backtracking step  . Overall,
. Overall,  holds.
holds.
\([\Leftarrow ]\) Suppose  holds. Since the step
holds. Since the step  is non-critical (i.e., the counter at (p, k) is either already zero or nonzero and remains so after decrement), we know the search immediately backtracks to \(x_d\). Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain
is non-critical (i.e., the counter at (p, k) is either already zero or nonzero and remains so after decrement), we know the search immediately backtracks to \(x_d\). Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain  .
.
Now suppose  holds. Since the step
holds. Since the step  is critical (i.e., it zeroes the counter at (p, k)), it is followed by a search of the in-neighbors of p. If p has no in-neighbors, then this search is (vacuously and) immediately complete, causing a direct backtracking, so \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the backtracking step
is critical (i.e., it zeroes the counter at (p, k)), it is followed by a search of the in-neighbors of p. If p has no in-neighbors, then this search is (vacuously and) immediately complete, causing a direct backtracking, so \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the backtracking step  . Otherwise, let \(y_b\) be the last in-neighbor of p. By
. Otherwise, let \(y_b\) be the last in-neighbor of p. By  , \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the backtracking step
, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the backtracking step  . Clearly, this step is directly followed by a backtracking step from p to the out-neighbor which caused the critical step that initiated the search of all in-neighbors, namely to \(x_d\). Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) again contains the step
. Clearly, this step is directly followed by a backtracking step from p to the out-neighbor which caused the critical step that initiated the search of all in-neighbors, namely to \(x_d\). Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) again contains the step  .
.
(12) Proof of  , when p is existential (Fig. 7a).
, when p is existential (Fig. 7a).
Since p is existential, the initial value of the counter of (p, k) is 1.
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the advancing instep  and this step is critical, namely the one that zeroes the counter of (p, k), namely the earliest instep to (p, k) (since the counter starts at 1). Since \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step, it does begin with a walk that ends with
and this step is critical, namely the one that zeroes the counter of (p, k), namely the earliest instep to (p, k) (since the counter starts at 1). Since \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step, it does begin with a walk that ends with  . Since the step is the earliest into (p, k), the prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) strictly before
. Since the step is the earliest into (p, k), the prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) strictly before  contains no instep
contains no instep  from another out-neighbor \(y_b\ne x_d\) of p —neither, of course, from \(x_d\) itself (by Lemma 6).
from another out-neighbor \(y_b\ne x_d\) of p —neither, of course, from \(x_d\) itself (by Lemma 6).
\([\Leftarrow ]\) Suppose that, for every out-neighbor \(y_b\) of p, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) begins with a walk that ends with the instep  and contains no strictly earlier instep
and contains no strictly earlier instep  . For \(y_b=x_d\), this implies that \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the instep
. For \(y_b=x_d\), this implies that \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the instep  . For \(y_b\ne x_d\), it implies that
. For \(y_b\ne x_d\), it implies that  is the earliest advancing step into p. Since the counter of (p, k) starts at 1, this very first advancing instep zeroes it. Therefore, the step
is the earliest advancing step into p. Since the counter of (p, k) starts at 1, this very first advancing instep zeroes it. Therefore, the step  is critical.
is critical.
(13) Proof of  , when p is universal (Fig. 7b).
, when p is universal (Fig. 7b).
Since p is universal, the initial value of the counter of (p, k) is the number \(m:=|\delta (p,w_k)|\) of out-neighbors of (p, k).
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the advancing step  and this step is critical, namely it zeroes the counter of (p, k). So, when
and this step is critical, namely it zeroes the counter of (p, k). So, when  happens, there have already been \(m{-}1\) other decrements, and thus \(m{-}1\) other insteps
happens, there have already been \(m{-}1\) other decrements, and thus \(m{-}1\) other insteps  , one from each out-neighbor \(y_b\ne x_d\). Now pick any out-neighbor \(y_b\) and let us see whether \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk from
, one from each out-neighbor \(y_b\ne x_d\). Now pick any out-neighbor \(y_b\) and let us see whether \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk from  to
to  .
.
-
If \(y_b\ne x_d\), then (as just argued) \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains both steps
 and
and  and in this order; so, the part between these two steps is the desired walk.
and in this order; so, the part between these two steps is the desired walk. -
If \(y_b=x_d\), then the desired walk is just the step
 , and we know is in \({\widetilde{{\scriptstyle \mathcal {W}}}}\).
, and we know is in \({\widetilde{{\scriptstyle \mathcal {W}}}}\).
Thus, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk of the desired form for all out-neighbors \(y_b\). So,  holds.
holds.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk from  to
to  , for every single one of the m out-neighbors \(y_b\) of p. By the special case \(y_b=x_d\), where that walk reduces to a single step, we know \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step
, for every single one of the m out-neighbors \(y_b\) of p. By the special case \(y_b=x_d\), where that walk reduces to a single step, we know \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step  . Consider the time t when this step occurs. Pick any other out-neighbor \(y_b\ne x_d\) of p. Since \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk from
. Consider the time t when this step occurs. Pick any other out-neighbor \(y_b\ne x_d\) of p. Since \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk from  to
to  , the step
, the step  has already happened at least once by time t, and thus exactly once (Lemma 6). Therefore, by time t, the counter of (p, k) has been decremented exactly \(m{-}1\) times. Hence, the decrement caused by the step
has already happened at least once by time t, and thus exactly once (Lemma 6). Therefore, by time t, the counter of (p, k) has been decremented exactly \(m{-}1\) times. Hence, the decrement caused by the step  zeroes the counter. So, the step is critical. Overall, (P5) holds.
zeroes the counter. So, the step is critical. Overall, (P5) holds.
(14) Proof of  , when p is existential (Fig. 7c).
, when p is existential (Fig. 7c).
\([\Rightarrow ]\) Suppose the advancing step  occurs in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) and is non-critical, namely it does not decrement the counter of (p, k) from its initial value 1 to zero. Hence, it is not the earliest advancing step into p. That is, at least one other advancing step
occurs in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) and is non-critical, namely it does not decrement the counter of (p, k) from its initial value 1 to zero. Hence, it is not the earliest advancing step into p. That is, at least one other advancing step  precedes it, where \(y_b\ne x_d\) is an out-neighbor of p. Then the part of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) between these two insteps is a walk of the form described in
precedes it, where \(y_b\ne x_d\) is an out-neighbor of p. Then the part of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) between these two insteps is a walk of the form described in  .
.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk that starts with  and ends with
and ends with  , for some out-neighbor \(y_b\ne x_d\) of p. Then
, for some out-neighbor \(y_b\ne x_d\) of p. Then  does appear in \({\widetilde{{\scriptstyle \mathcal {W}}}}\); and it certainly cannot be critical, because the earlier instep
does appear in \({\widetilde{{\scriptstyle \mathcal {W}}}}\); and it certainly cannot be critical, because the earlier instep  is advancing (since \(y_b\) is an out-neighbor of p) and thus the counter of (p, k) has already been zeroed by either it or an earlier advancing step into p.
is advancing (since \(y_b\) is an out-neighbor of p) and thus the counter of (p, k) has already been zeroed by either it or an earlier advancing step into p.
(15) Proof of  , when p is universal (Fig. 7d).
, when p is universal (Fig. 7d).
Let \(m:=|\delta (p,w_k)|\) be the initial value of the counter of (p, k).
\([\Rightarrow ]\) Suppose the advancing step  occurs in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) and is non-critical, namely it does not zero the counter of (p, k). Hence, the number of advancing steps into p that precede
occurs in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) and is non-critical, namely it does not zero the counter of (p, k). Hence, the number of advancing steps into p that precede  in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) is strictly less than \(m{-}1\). Therefore, at least one out-neighbor \(y_b\ne x_d\) of p is such that the step
in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) is strictly less than \(m{-}1\). Therefore, at least one out-neighbor \(y_b\ne x_d\) of p is such that the step  does not appear in the prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) up to
does not appear in the prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) up to  . So, this prefix is the walk described in
. So, this prefix is the walk described in  .
.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) starts with a prefix that ends in the step  and fails to contain the step
and fails to contain the step  , for some out-neighbor \(y_b\ne x_d\) of p. By where the prefix ends, we know
, for some out-neighbor \(y_b\ne x_d\) of p. By where the prefix ends, we know  appears in \({\widetilde{{\scriptstyle \mathcal {W}}}}\). Moreover, the number of earlier advancing steps into p is strictly less than \(m{-}1\) (as they do not include
appears in \({\widetilde{{\scriptstyle \mathcal {W}}}}\). Moreover, the number of earlier advancing steps into p is strictly less than \(m{-}1\) (as they do not include  ), so the value of the counter of (p, k) at the time of
), so the value of the counter of (p, k) at the time of  is strictly more than \(m-(m{-}1)=1\). Therefore,
is strictly more than \(m-(m{-}1)=1\). Therefore,  does not zero the counter and is thus non-critical.
does not zero the counter and is thus non-critical.
(16) Proof of  , given \(p\rightarrow x_d=y_d\) and some \(z_c\rightarrow p\) (Fig. 8a).
, given \(p\rightarrow x_d=y_d\) and some \(z_c\rightarrow p\) (Fig. 8a).
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the successive steps  . Since \(x_d\) is an out-neighbor of p, the first of these two steps is advancing. Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the advancing instep
. Since \(x_d\) is an out-neighbor of p, the first of these two steps is advancing. Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the advancing instep  , and we only need to show that it is non-critical. Toward a contradiction, suppose it is critical. Then it is followed by a further advancing step, to the first of the (one or more, as we know) in-neighbors \(z_c\) of p. Since the next step is
, and we only need to show that it is non-critical. Toward a contradiction, suppose it is critical. Then it is followed by a further advancing step, to the first of the (one or more, as we know) in-neighbors \(z_c\) of p. Since the next step is  , we must conclude that \(x_d\) is also an in-neighbor of p, contradicting the fact that A is asymmetric.
, we must conclude that \(x_d\) is also an in-neighbor of p, contradicting the fact that A is asymmetric.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the non-critical advancing step  . Since the step is non-critical, it is followed by the matching backtracking outstep
. Since the step is non-critical, it is followed by the matching backtracking outstep  . Therefore, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the successive steps
. Therefore, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the successive steps  .
.
(17) Proof of  , given \(p\rightarrow x_d=y_d\) and no \(z\rightarrow p\) (Fig. 8a).
, given \(p\rightarrow x_d=y_d\) and no \(z\rightarrow p\) (Fig. 8a).
\([\Rightarrow ]\) Obvious. \([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the instep  . Since \(x_d\) is an out-neighbor of p, this is an advancing instep. If it is non-critical, then it is immediately followed by the matching backtracking step
. Since \(x_d\) is an out-neighbor of p, this is an advancing instep. If it is non-critical, then it is immediately followed by the matching backtracking step  , and we are done. If it is critical, then it initiates a search of all in-neighbors of p. Since p has no in-neighbors, this search is immediately complete, and followed by a backtracking step from p to the initiating out-neighbor \(x_d\), namely by the outstep
, and we are done. If it is critical, then it initiates a search of all in-neighbors of p. Since p has no in-neighbors, this search is immediately complete, and followed by a backtracking step from p to the initiating out-neighbor \(x_d\), namely by the outstep  , as desired.
, as desired.
(18) Proof of  , given \(y_b\rightarrow p\rightarrow x_d\) (Fig. 8b).
, given \(y_b\rightarrow p\rightarrow x_d\) (Fig. 8b).
\([\Leftarrow ]\) Obvious. \([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the successive steps  . Since \(x_d\) is an out-neighbor of p, the first step is advancing. So \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the advancing instep
. Since \(x_d\) is an out-neighbor of p, the first step is advancing. So \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain the advancing instep  . If this instep is non-critical, then the second step
. If this instep is non-critical, then the second step  is the matching backtracking step
is the matching backtracking step  ; hence, \(x_d=y_b\) and thus G contains the arrows \(x_d\rightarrow p\rightarrow x_d\), contradicting the fact that A is asymmetric. Therefore,
; hence, \(x_d=y_b\) and thus G contains the arrows \(x_d\rightarrow p\rightarrow x_d\), contradicting the fact that A is asymmetric. Therefore,  is critical. Hence, the second step
is critical. Hence, the second step  is the advancing step to the first in-neighbor of p. So, \(y_b\) is indeed the first in-neighbor.
is the advancing step to the first in-neighbor of p. So, \(y_b\) is indeed the first in-neighbor.
(19) Proof of  , given \(x_d\rightarrow p\rightarrow y_b\) (Fig. 8c).
, given \(x_d\rightarrow p\rightarrow y_b\) (Fig. 8c).
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the successive steps  . Then indeed \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the instep
. Then indeed \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the instep  . Since \(x_d\) is an in-neighbor of p, this instep is a backtracking one. If \(x_d\) is not the last in-neighbor, then the next step
. Since \(x_d\) is an in-neighbor of p, this instep is a backtracking one. If \(x_d\) is not the last in-neighbor, then the next step  is advancing to the in-neighbor after it, so \(y_b\) is an in-neighbor; so, G contains both arrows \(y_b\rightarrow p\rightarrow y_b\), and A is not asymmetric —contradiction. So, \(x_d\) is the last in-neighbor of p. Therefore, the next step
is advancing to the in-neighbor after it, so \(y_b\) is an in-neighbor; so, G contains both arrows \(y_b\rightarrow p\rightarrow y_b\), and A is not asymmetric —contradiction. So, \(x_d\) is the last in-neighbor of p. Therefore, the next step  is backtracking to the out-neighbor that caused the critical step which initiated the search of all in-neighbors of p, and thus that out-neighbor is \(y_b\). Therefore, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the critical advancing step
is backtracking to the out-neighbor that caused the critical step which initiated the search of all in-neighbors of p, and thus that out-neighbor is \(y_b\). Therefore, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the critical advancing step  .
.
\([\Leftarrow ]\) Suppose  . By the last two conjuncts, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the backtracking step
. By the last two conjuncts, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the backtracking step  from the last in-neighbor \(x_d\) of p. Clearly, this step is followed by a further backtracking step, to the out-neighbor of p that caused the critical step which initiated the search of all in-neighbors. By the first conjunct of
from the last in-neighbor \(x_d\) of p. Clearly, this step is followed by a further backtracking step, to the out-neighbor of p that caused the critical step which initiated the search of all in-neighbors. By the first conjunct of  , that out-neighbor is \(y_b\). So,
, that out-neighbor is \(y_b\). So,  is immediately followed by
is immediately followed by  , as desired.
, as desired.
(20) Proof of  , given successive \(x_d,y_b\rightarrow p\) (Fig. 8d).
, given successive \(x_d,y_b\rightarrow p\) (Fig. 8d).
\([\Rightarrow ]\) Obvious. \([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the instep  . Since \(x_d\) is an in-neighbor of p, this instep is backtracking. Since \(x_d\) is not the last in-neighbor, the next step is advancing from p to its in-neighbor immediately after \(x_d\). Namely, the next step is
. Since \(x_d\) is an in-neighbor of p, this instep is backtracking. Since \(x_d\) is not the last in-neighbor, the next step is advancing from p to its in-neighbor immediately after \(x_d\). Namely, the next step is  , as desired.
, as desired.
(21) Proof of  (Fig. 9a, b).
(Fig. 9a, b).
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk \({\scriptstyle \mathcal {W}}\) from  to
to  . If \({\scriptstyle \mathcal {W}}\) is express, then
. If \({\scriptstyle \mathcal {W}}\) is express, then  holds, and we are done. Otherwise, \({\scriptstyle \mathcal {W}}\) contains stopovers. Let
holds, and we are done. Otherwise, \({\scriptstyle \mathcal {W}}\) contains stopovers. Let  be a step in \({\scriptstyle \mathcal {W}}\) that creates the last stopover. This occurs strictly between
be a step in \({\scriptstyle \mathcal {W}}\) that creates the last stopover. This occurs strictly between  and
and  (since its pivot is a stopover), and is thus distinct from both (by Lemma 6). Let \({\scriptstyle \mathcal {W}}_1\) be the prefix of \({\scriptstyle \mathcal {W}}\) up to
(since its pivot is a stopover), and is thus distinct from both (by Lemma 6). Let \({\scriptstyle \mathcal {W}}_1\) be the prefix of \({\scriptstyle \mathcal {W}}\) up to  , and \({\scriptstyle \mathcal {W}}_2\) the suffix from
, and \({\scriptstyle \mathcal {W}}_2\) the suffix from  onward. Then \({\scriptstyle \mathcal {W}}_1\) is a walk as in the first conjunct of
onward. Then \({\scriptstyle \mathcal {W}}_1\) is a walk as in the first conjunct of
 ; and \({\scriptstyle \mathcal {W}}_2\) is a walk as in the second conjunct. Overall,
; and \({\scriptstyle \mathcal {W}}_2\) is a walk as in the second conjunct. Overall,  holds, and we are done again.
holds, and we are done again.
\([\Leftarrow ]\) If
 holds, then clearly (P8) holds. So, suppose
holds, then clearly (P8) holds. So, suppose  holds. Then \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk \({\scriptstyle \mathcal {W}}_1\) from
holds. Then \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk \({\scriptstyle \mathcal {W}}_1\) from  to
to  and a walk \({\scriptstyle \mathcal {W}}_2\) from
and a walk \({\scriptstyle \mathcal {W}}_2\) from  to
to  . By Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2\), which is a walk that starts with
. By Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2\), which is a walk that starts with  and ends with
and ends with  . Hence, (P8) holds again.
. Hence, (P8) holds again.
(22) Proof of  , when \((x_d,p)=(y_b,q)\) (Fig. 9c).
, when \((x_d,p)=(y_b,q)\) (Fig. 9c).
\([\Rightarrow ]\) Obvious. \([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the instep  . Consider the single-step walk \({\scriptstyle \mathcal {W}}\) consisting of only this step. This is a walk from
. Consider the single-step walk \({\scriptstyle \mathcal {W}}\) consisting of only this step. This is a walk from  (which is the same as
(which is the same as  ) to
) to  ; is contained in \({\widetilde{{\scriptstyle \mathcal {W}}}}\); and is express (trivially, since it contains no internal configurations).
; is contained in \({\widetilde{{\scriptstyle \mathcal {W}}}}\); and is express (trivially, since it contains no internal configurations).
(23) Proof of  , when \((x_d,p)\ne (y_b,q)\). (Fig. 9d.)
, when \((x_d,p)\ne (y_b,q)\). (Fig. 9d.)
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains an express walk \({\scriptstyle \mathcal {W}}\) from  to
to  . Since the two steps are distinct, \({\scriptstyle \mathcal {W}}\) has length at least 2. Let
. Since the two steps are distinct, \({\scriptstyle \mathcal {W}}\) has length at least 2. Let  be its second step. Then \(z_c\) is on the same side of the current cell as \(y_b\), namely \(c=b\in \{\textsc {l} {,}\textsc {i} {,}\textsc {r} \}\) (shown below). Hence, \({\scriptstyle \mathcal {W}}\) starts with the two steps
be its second step. Then \(z_c\) is on the same side of the current cell as \(y_b\), namely \(c=b\in \{\textsc {l} {,}\textsc {i} {,}\textsc {r} \}\) (shown below). Hence, \({\scriptstyle \mathcal {W}}\) starts with the two steps  , hence the first conjunct of
, hence the first conjunct of  holds. Moreover, the suffix \({\scriptstyle \mathcal {W}}'\) of \({\scriptstyle \mathcal {W}}\) from
holds. Moreover, the suffix \({\scriptstyle \mathcal {W}}'\) of \({\scriptstyle \mathcal {W}}\) from  onward is an express walk (since \({\scriptstyle \mathcal {W}}\) is), exactly as required by the second conjunct. Hence,
onward is an express walk (since \({\scriptstyle \mathcal {W}}\) is), exactly as required by the second conjunct. Hence,  holds.
holds.
To show \(c=b\), we assume the contrary (\(c\ne b\)) and take cases on b.
If \(b=\textsc {i} \), then \(y_b\) is on the current cell. If the steps  and
and  coincide, then \(z_c=q_\textsc {i} \), and thus \(c=\textsc {i} =b\), contradicting our assumption. Hence, the steps do not coincide. Therefore, \(y_b\) is an internal configuration of \({\scriptstyle \mathcal {W}}\), and thus a stopover, contradicting the fact that \({\scriptstyle \mathcal {W}}\) is express.
coincide, then \(z_c=q_\textsc {i} \), and thus \(c=\textsc {i} =b\), contradicting our assumption. Hence, the steps do not coincide. Therefore, \(y_b\) is an internal configuration of \({\scriptstyle \mathcal {W}}\), and thus a stopover, contradicting the fact that \({\scriptstyle \mathcal {W}}\) is express.
If \(b=\textsc {l} \), then the steps  and
and  do not coincide (since the first one starts on the current cell, but the second one does not). Hence, \(z_c\) is an internal configuration of \({\scriptstyle \mathcal {W}}\). If \(c=\textsc {i} \), then \(z_c\) is a stopover. If \(z_c=\textsc {r} \), then \({\scriptstyle \mathcal {W}}\) crosses from the right to the left side of the current cell, so it contains at least one stopover. Either way, \({\scriptstyle \mathcal {W}}\) is not express, contradiction.
do not coincide (since the first one starts on the current cell, but the second one does not). Hence, \(z_c\) is an internal configuration of \({\scriptstyle \mathcal {W}}\). If \(c=\textsc {i} \), then \(z_c\) is a stopover. If \(z_c=\textsc {r} \), then \({\scriptstyle \mathcal {W}}\) crosses from the right to the left side of the current cell, so it contains at least one stopover. Either way, \({\scriptstyle \mathcal {W}}\) is not express, contradiction.
If \(b=\textsc {r} \), then we apply an analysis symmetric to the case \(b=\textsc {l} \).
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk \( {\scriptstyle \mathcal {W}}_1\) consisting of the two steps  and an express walk \({\scriptstyle \mathcal {W}}_2\) from
and an express walk \({\scriptstyle \mathcal {W}}_2\) from  to
to  . By Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2\), which is indeed a walk from
. By Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2\), which is indeed a walk from  to
to  , and an express one (since any stopover would have to lie strictly between (p, k) and (q, k), so it would also be a stopover in the express walk \({\scriptstyle \mathcal {W}}_2\) —contradiction).
, and an express one (since any stopover would have to lie strictly between (p, k) and (q, k), so it would also be a stopover in the express walk \({\scriptstyle \mathcal {W}}_2\) —contradiction).
(24) Proof of  , when the walk is not express. (Fig. 10b.)
, when the walk is not express. (Fig. 10b.)
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a non-express left-sided walk \({\scriptstyle \mathcal {W}}\) from  to
to  . Let
. Let  be the step of \({\scriptstyle \mathcal {W}}\) that creates the last stopover, and
be the step of \({\scriptstyle \mathcal {W}}\) that creates the last stopover, and  the step immediately after it. Since the common pivot (r, k) of these two steps is strictly between the pivots (p, k) and (q, k) of the steps
the step immediately after it. Since the common pivot (r, k) of these two steps is strictly between the pivots (p, k) and (q, k) of the steps  and
and  , we know
, we know  (resp.,
(resp.,  ) occurs strictly before
) occurs strictly before  (resp., strictly after
(resp., strictly after  ), and is thus distinct from it (Lemma 6). Let \({\scriptstyle \mathcal {W}}_1,{\scriptstyle \mathcal {W}}_2,{\scriptstyle \mathcal {W}}_3\) be, respectively: the prefix of \({\scriptstyle \mathcal {W}}\) up to
), and is thus distinct from it (Lemma 6). Let \({\scriptstyle \mathcal {W}}_1,{\scriptstyle \mathcal {W}}_2,{\scriptstyle \mathcal {W}}_3\) be, respectively: the prefix of \({\scriptstyle \mathcal {W}}\) up to  ; the two-step infix
; the two-step infix  ; and the suffix from
; and the suffix from  onward. Then \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains all three of these walks; and \({\scriptstyle \mathcal {W}}_1,{\scriptstyle \mathcal {W}}_3\) are left-sided (as the entire \({\scriptstyle \mathcal {W}}\) is); and \({\scriptstyle \mathcal {W}}_3\) is express (since
onward. Then \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains all three of these walks; and \({\scriptstyle \mathcal {W}}_1,{\scriptstyle \mathcal {W}}_3\) are left-sided (as the entire \({\scriptstyle \mathcal {W}}\) is); and \({\scriptstyle \mathcal {W}}_3\) is express (since  creates the last stopover). So,
creates the last stopover). So,  holds.
holds.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a left-sided walk \({\scriptstyle \mathcal {W}}_1\) from  to
to  ; a walk \({\scriptstyle \mathcal {W}}_2\) consisting of the two steps
; a walk \({\scriptstyle \mathcal {W}}_2\) consisting of the two steps  ; and a left-sided express walk \({\scriptstyle \mathcal {W}}_3\) from
; and a left-sided express walk \({\scriptstyle \mathcal {W}}_3\) from  to
to  . By two applications of Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2{\scriptstyle \mathcal {W}}_3\). Clearly, \({\scriptstyle \mathcal {W}}\) is from
. By two applications of Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2{\scriptstyle \mathcal {W}}_3\). Clearly, \({\scriptstyle \mathcal {W}}\) is from  to
to  and is left-sided (because \({\scriptstyle \mathcal {W}}_1\) and \({\scriptstyle \mathcal {W}}_3\) are). Hence, (P10) holds.
and is left-sided (because \({\scriptstyle \mathcal {W}}_1\) and \({\scriptstyle \mathcal {W}}_3\) are). Hence, (P10) holds.
(25) Proof of  , when \((p_\textsc {i} ,x_d)=(y_b,q_\textsc {i} )\). (Fig. 10a.)
, when \((p_\textsc {i} ,x_d)=(y_b,q_\textsc {i} )\). (Fig. 10a.)
\([\Rightarrow ]\) Obvious. \([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the instep  . This can also be viewed as the outstep
. This can also be viewed as the outstep  ; and also as the single-step walk \({\scriptstyle \mathcal {W}}\) from the outstep
; and also as the single-step walk \({\scriptstyle \mathcal {W}}\) from the outstep  to the instep
to the instep  . Clearly, this \({\scriptstyle \mathcal {W}}\) contains no internal configurations, so it is (vacuously) both express and left-sided.
. Clearly, this \({\scriptstyle \mathcal {W}}\) contains no internal configurations, so it is (vacuously) both express and left-sided.
(26) Proof of  , when length is 2, \(x=y\), and \(d=b=\textsc {l} \). (Fig. 10c.)
, when length is 2, \(x=y\), and \(d=b=\textsc {l} \). (Fig. 10c.)
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains an express left-sided 2-long walk \({\scriptstyle \mathcal {W}}\) from  to
to  . Then clearly the two occurrences of \(y_\textsc {l} \) refer to the same one configuration occurrence in \({\scriptstyle \mathcal {W}}\). So, \({\scriptstyle \mathcal {W}}\) contains only the successive steps
. Then clearly the two occurrences of \(y_\textsc {l} \) refer to the same one configuration occurrence in \({\scriptstyle \mathcal {W}}\). So, \({\scriptstyle \mathcal {W}}\) contains only the successive steps  . From the perspective of cell \(k{-}1\), these are the steps
. From the perspective of cell \(k{-}1\), these are the steps  .
.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the successive steps  , from the perspective of cell \(k{-}1\). From the perspective of cell k, these are the steps
, from the perspective of cell \(k{-}1\). From the perspective of cell k, these are the steps  , which are clearly an express left-sided walk from
, which are clearly an express left-sided walk from  to
to  of length 2.
of length 2.
(27) Proof of  , when length is at least 3 and \(d=b=\textsc {l} \). (Fig. 10c.)
, when length is at least 3 and \(d=b=\textsc {l} \). (Fig. 10c.)
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains an express left-sided walk \({\scriptstyle \mathcal {W}}\) from  to
to  , of length at least 3. Relative to cell \(k{-}1\), let
, of length at least 3. Relative to cell \(k{-}1\), let  and
and  be the second and second-but-last steps of \({\scriptstyle \mathcal {W}}\) (which exist, since the length is at least 3). Then \(c,a\ne \textsc {r} \) (or else \({\scriptstyle \mathcal {W}}\) is not express), and the first and last conjuncts of
be the second and second-but-last steps of \({\scriptstyle \mathcal {W}}\) (which exist, since the length is at least 3). Then \(c,a\ne \textsc {r} \) (or else \({\scriptstyle \mathcal {W}}\) is not express), and the first and last conjuncts of  are immediately true. For the middle conjunct, we let \({\scriptstyle \mathcal {W}}'\) be the infix of \({\scriptstyle \mathcal {W}}\) from
are immediately true. For the middle conjunct, we let \({\scriptstyle \mathcal {W}}'\) be the infix of \({\scriptstyle \mathcal {W}}\) from  to
to  . Clearly, this contains no visits to cell k (since \({\scriptstyle \mathcal {W}}\) is express). So, it is left-sided relative to cell \(k{-}1\), as required.
. Clearly, this contains no visits to cell k (since \({\scriptstyle \mathcal {W}}\) is express). So, it is left-sided relative to cell \(k{-}1\), as required.
\([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains a walk \({\scriptstyle \mathcal {W}}_1\) with only the steps  ; a left-sided walk \({\scriptstyle \mathcal {W}}_2\) from
; a left-sided walk \({\scriptstyle \mathcal {W}}_2\) from  to
to  ; and a walk \({\scriptstyle \mathcal {W}}_3\) with only the steps
; and a walk \({\scriptstyle \mathcal {W}}_3\) with only the steps  (all relative to cell \(k{-}1\)). By two applications of Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2{\scriptstyle \mathcal {W}}_3\). Since \({\scriptstyle \mathcal {W}}_2\) is left-sided relative to cell \(k{-}1\), the only configurations of \({\scriptstyle \mathcal {W}}\) on cell k are the pivots (p, k) and (q, k) of the starting outstep and the ending instep. So, relative to cell k, \({\scriptstyle \mathcal {W}}\) is an express left-sided walk from
(all relative to cell \(k{-}1\)). By two applications of Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2{\scriptstyle \mathcal {W}}_3\). Since \({\scriptstyle \mathcal {W}}_2\) is left-sided relative to cell \(k{-}1\), the only configurations of \({\scriptstyle \mathcal {W}}\) on cell k are the pivots (p, k) and (q, k) of the starting outstep and the ending instep. So, relative to cell k, \({\scriptstyle \mathcal {W}}\) is an express left-sided walk from  to
to  .
.
(28) The full code of function outstep instep r :

(29) The full code of function outstep instep rx :

(30) Proof of  , when \((x_d,p)=(y_b,q)\).
, when \((x_d,p)=(y_b,q)\).
\([\Rightarrow ]\) Obvious. \([\Leftarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step  . Pick any occurrence of the step in \({\widetilde{{\scriptstyle \mathcal {W}}}}\). By Lemma 6, this occurrence is the only one. In particular, no earlier occurrence exists. Therefore, (P14) holds.
. Pick any occurrence of the step in \({\widetilde{{\scriptstyle \mathcal {W}}}}\). By Lemma 6, this occurrence is the only one. In particular, no earlier occurrence exists. Therefore, (P14) holds.
(31) Proof of  , when \((x_d,p)\ne (y_b,q)\). (Fig. 11a, b.)
, when \((x_d,p)\ne (y_b,q)\). (Fig. 11a, b.)
\([\Rightarrow ]\) Suppose \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains  with no strictly earlier occurrence of
with no strictly earlier occurrence of  . If
. If  is the earliest step into the current cell (Fig. 11a), then
is the earliest step into the current cell (Fig. 11a), then  holds and we are done. Otherwise, let
holds and we are done. Otherwise, let  be the latest step of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) into the current cell that strictly precedes
be the latest step of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) into the current cell that strictly precedes  (Fig. 11b). Then \((z_c,r)\ne (x_d,p)\) (by Lemma 6); and \((z_c,r)\ne (y_b,q)\) (since
(Fig. 11b). Then \((z_c,r)\ne (x_d,p)\) (by Lemma 6); and \((z_c,r)\ne (y_b,q)\) (since  does not appear strictly before
does not appear strictly before  ); and the prefix \({\scriptstyle \mathcal {W}}\) of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) up to
); and the prefix \({\scriptstyle \mathcal {W}}\) of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) up to  is the concatenation of two walks: the prefix \({\scriptstyle \mathcal {W}}_1\) up to
is the concatenation of two walks: the prefix \({\scriptstyle \mathcal {W}}_1\) up to  , and the walk \({\scriptstyle \mathcal {W}}_2\) from
, and the walk \({\scriptstyle \mathcal {W}}_2\) from  to
to  . Clearly, \({\scriptstyle \mathcal {W}}_1\) avoids
. Clearly, \({\scriptstyle \mathcal {W}}_1\) avoids  (since \({\scriptstyle \mathcal {W}}\) does); and \({\scriptstyle \mathcal {W}}_2\) uses no stopovers on the current cell (by the selection of
(since \({\scriptstyle \mathcal {W}}\) does); and \({\scriptstyle \mathcal {W}}_2\) uses no stopovers on the current cell (by the selection of  ). Overall,
). Overall,  holds, as the chosen
holds, as the chosen  differs from both other steps and satisfies both the first conjunct (by the properties of \({\scriptstyle \mathcal {W}}_1\)) and the second conjunct (by the properties of \({\scriptstyle \mathcal {W}}_2\)).
differs from both other steps and satisfies both the first conjunct (by the properties of \({\scriptstyle \mathcal {W}}_1\)) and the second conjunct (by the properties of \({\scriptstyle \mathcal {W}}_2\)).
\([\Leftarrow ]\) Suppose  holds. (Fig. 11a.) Then \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step
holds. (Fig. 11a.) Then \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step  . If it also contains
. If it also contains  strictly earlier, then (q, k) would be a visit to the current cell strictly earlier than (p, k), a contradiction. Therefore, (P14) holds.
strictly earlier, then (q, k) would be a visit to the current cell strictly earlier than (p, k), a contradiction. Therefore, (P14) holds.
Now suppose  holds, because of certain \(z_c,r\). (Fig. 11b.) By the first conjunct and since \((z_c,r)\ne (y_b,q)\), we know \({\widetilde{{\scriptstyle \mathcal {W}}}}\) starts with a prefix \({\scriptstyle \mathcal {W}}_1\) which ends with
holds, because of certain \(z_c,r\). (Fig. 11b.) By the first conjunct and since \((z_c,r)\ne (y_b,q)\), we know \({\widetilde{{\scriptstyle \mathcal {W}}}}\) starts with a prefix \({\scriptstyle \mathcal {W}}_1\) which ends with  and does not contain
and does not contain  . By the second conjunct, we know \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains a walk \({\scriptstyle \mathcal {W}}_2\) which starts with
. By the second conjunct, we know \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains a walk \({\scriptstyle \mathcal {W}}_2\) which starts with  , ends with
, ends with  , and includes no stopovers. Hence,
, and includes no stopovers. Hence,  can be nowhere in \({\scriptstyle \mathcal {W}}_2\) either: not at the start, since \((z_c,r)\ne (y_b,q)\) (given explicitly by
can be nowhere in \({\scriptstyle \mathcal {W}}_2\) either: not at the start, since \((z_c,r)\ne (y_b,q)\) (given explicitly by  ); not at the end, since \((x_d,p)\ne (y_b,q)\) (by our starting assumption); and not in between, since there are no stopovers. Now, by Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2\). By the properties of \({\scriptstyle \mathcal {W}}_1,{\scriptstyle \mathcal {W}}_2\), we know \({\scriptstyle \mathcal {W}}\) ends with
); not at the end, since \((x_d,p)\ne (y_b,q)\) (by our starting assumption); and not in between, since there are no stopovers. Now, by Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2\). By the properties of \({\scriptstyle \mathcal {W}}_1,{\scriptstyle \mathcal {W}}_2\), we know \({\scriptstyle \mathcal {W}}\) ends with  and avoids
and avoids  . Moreover, since \({\scriptstyle \mathcal {W}}\) starts with the step
. Moreover, since \({\scriptstyle \mathcal {W}}\) starts with the step  (because \({\scriptstyle \mathcal {W}}_1\) does, as a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\)), we know \({\scriptstyle \mathcal {W}}\) is actually a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) (by Lemma 6). Hence, (P14) holds.
(because \({\scriptstyle \mathcal {W}}_1\) does, as a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\)), we know \({\scriptstyle \mathcal {W}}\) is actually a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) (by Lemma 6). Hence, (P14) holds.
(32) Proof of  , when \(k<n{+}1\). (Fig. 11c, d.)
, when \(k<n{+}1\). (Fig. 11c, d.)
\([\Rightarrow ]\) Suppose (P15) holds and let the reference cell be cell \(k{+}1\). Then \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the step  and this is the first step into cell k. Let \({\scriptstyle \mathcal {W}}\) be the prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) up to that step. Let
and this is the first step into cell k. Let \({\scriptstyle \mathcal {W}}\) be the prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) up to that step. Let  be the earliest step of \({\scriptstyle \mathcal {W}}\) into cell \(k{+}1\) (this clearly exists, as \({\scriptstyle \mathcal {W}}\) starts with a step into cell \(n{+}1\) and \(k{+}1\le n{+}1\)). Let \({\scriptstyle \mathcal {W}}_1\) be the prefix of \({\scriptstyle \mathcal {W}}\) up to that step, and \({\scriptstyle \mathcal {W}}_2\) the suffix from then on, i.e., from
be the earliest step of \({\scriptstyle \mathcal {W}}\) into cell \(k{+}1\) (this clearly exists, as \({\scriptstyle \mathcal {W}}\) starts with a step into cell \(n{+}1\) and \(k{+}1\le n{+}1\)). Let \({\scriptstyle \mathcal {W}}_1\) be the prefix of \({\scriptstyle \mathcal {W}}\) up to that step, and \({\scriptstyle \mathcal {W}}_2\) the suffix from then on, i.e., from  to
to  .
.
If \({\scriptstyle \mathcal {W}}_2\) has length 2 (Fig. 11c), then it consists of just these two steps: the first ends where the second starts (\(f=x\)) and \({\scriptstyle \mathcal {W}}_2\) is exactly  . So, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains these successive steps. Overall, disjunct (i) holds and we are done.
. So, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains these successive steps. Overall, disjunct (i) holds and we are done.
If \({\scriptstyle \mathcal {W}}_2\) has length at least 3 (Fig. 11d), then \({\scriptstyle \mathcal {W}}_2\) contains one or more steps strictly between  and
and  . Let
. Let  and
and  be the first and the last such steps, respectively. Then \({\scriptstyle \mathcal {W}}_2\) has the form
be the first and the last such steps, respectively. Then \({\scriptstyle \mathcal {W}}_2\) has the form

where only the last configuration is on cell k. So, \(b,c\ne \textsc {l} \) and the walk from  to
to  is right-sided. Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains both desired pairs of successive steps and the desired right-sided walk. So, disjunct (ii) holds, and we are done again.
is right-sided. Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains both desired pairs of successive steps and the desired right-sided walk. So, disjunct (ii) holds, and we are done again.
\([\Leftarrow ]\) Suppose  holds for some u, f and let the reference cell be cell \(k{+}1\). Then the step
holds for some u, f and let the reference cell be cell \(k{+}1\). Then the step  appears in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) and is the earliest one into cell \(k{+}1\). Let \({\scriptstyle \mathcal {W}}_1\) be the prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) up to that step. Clearly, no configuration in \({\scriptstyle \mathcal {W}}_1\) is on cell k. We take cases as to which of the disjuncts (i) and (ii) of
appears in \({\widetilde{{\scriptstyle \mathcal {W}}}}\) and is the earliest one into cell \(k{+}1\). Let \({\scriptstyle \mathcal {W}}_1\) be the prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) up to that step. Clearly, no configuration in \({\scriptstyle \mathcal {W}}_1\) is on cell k. We take cases as to which of the disjuncts (i) and (ii) of  holds.
holds.
If (i) holds (Fig. 11c), then \(x=f\) and \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains the walk \({\scriptstyle \mathcal {W}}_2\) consisting of the two successive steps  . In particular, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains
. In particular, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains  , as required. Now, since \(x=f\), the first of these steps equals the last step of \({\scriptstyle \mathcal {W}}_1\). By Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2\). Since no configuration in \({\scriptstyle \mathcal {W}}_1\) is on cell k, it follows that
, as required. Now, since \(x=f\), the first of these steps equals the last step of \({\scriptstyle \mathcal {W}}_1\). By Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2\). Since no configuration in \({\scriptstyle \mathcal {W}}_1\) is on cell k, it follows that  is indeed the earliest step of \({\scriptstyle \mathcal {W}}\) into cell k. Moreover, since \({\scriptstyle \mathcal {W}}\) starts with the step
is indeed the earliest step of \({\scriptstyle \mathcal {W}}\) into cell k. Moreover, since \({\scriptstyle \mathcal {W}}\) starts with the step  (because \({\scriptstyle \mathcal {W}}_1\) does, as a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\)), we know \({\scriptstyle \mathcal {W}}\) is actually a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) (by Lemma 6). Hence,
(because \({\scriptstyle \mathcal {W}}_1\) does, as a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\)), we know \({\scriptstyle \mathcal {W}}\) is actually a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) (by Lemma 6). Hence,  is also the earliest step into cell k for in the entire \({\widetilde{{\scriptstyle \mathcal {W}}}}\), as required.
is also the earliest step into cell k for in the entire \({\widetilde{{\scriptstyle \mathcal {W}}}}\), as required.
If (ii) holds for some \(y_b,z_c\) (Fig. 11d), then \({\widetilde{{\scriptstyle \mathcal {W}}}}\) contains all of the following: a walk \({\scriptstyle \mathcal {W}}_2\) with only the steps  ; a right-sided walk \({\scriptstyle \mathcal {W}}_3\) from
; a right-sided walk \({\scriptstyle \mathcal {W}}_3\) from  to
to  ; and a walk \({\scriptstyle \mathcal {W}}_4\) with only the steps
; and a walk \({\scriptstyle \mathcal {W}}_4\) with only the steps  . Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain
. Hence, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) does contain  , as required. Now, by three applications of Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2{\scriptstyle \mathcal {W}}_3{\scriptstyle \mathcal {W}}_4\). Since no configuration in \({\scriptstyle \mathcal {W}}_1\) or \({\scriptstyle \mathcal {W}}_3\) is on cell k, it follows that
, as required. Now, by three applications of Corollary 3, \({\widetilde{{\scriptstyle \mathcal {W}}}}\) also contains the concatenation \({\scriptstyle \mathcal {W}}:={\scriptstyle \mathcal {W}}_1{\scriptstyle \mathcal {W}}_2{\scriptstyle \mathcal {W}}_3{\scriptstyle \mathcal {W}}_4\). Since no configuration in \({\scriptstyle \mathcal {W}}_1\) or \({\scriptstyle \mathcal {W}}_3\) is on cell k, it follows that  is indeed the earliest step of \({\scriptstyle \mathcal {W}}\) into cell k. But \({\scriptstyle \mathcal {W}}\) is also a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) (since \({\scriptstyle \mathcal {W}}_1\) is, by the same reasoning as earlier). Hence,
is indeed the earliest step of \({\scriptstyle \mathcal {W}}\) into cell k. But \({\scriptstyle \mathcal {W}}\) is also a prefix of \({\widetilde{{\scriptstyle \mathcal {W}}}}\) (since \({\scriptstyle \mathcal {W}}_1\) is, by the same reasoning as earlier). Hence,  is also the earliest step into cell k for the entire \({\widetilde{{\scriptstyle \mathcal {W}}}}\), as required.
is also the earliest step into cell k for the entire \({\widetilde{{\scriptstyle \mathcal {W}}}}\), as required.
(33) This is obvious for all accepting call configurations, except possibly for those of the form \(c=\bigl ((\textsc {crit-instep},1,x_d,p),k\bigr )\). There, we should note that not all branches spawned in l:2 end up accepting in l:3: for \(y_b=x_d\), the test of l:3 certainly fails, since we are already past l:1 and thus the outarrow \(p\rightarrow x_d\) exists. Hence, at least one branch in an accepting run from c will need to proceed to a call in l:5 or l:7, raising the call height of c to at least 2.
Rights and permissions
About this article
Cite this article
Geffert, V., Kapoutsis, C.A. & Zakzok, M. Improved complement for two-way alternating automata. Acta Informatica 59, 619–669 (2022). https://doi.org/10.1007/s00236-021-00414-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-021-00414-w





 and
and  and in this order; so, the part between these two steps is the desired walk.
and in this order; so, the part between these two steps is the desired walk.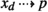 , and we know is in
, and we know is in