Bullwhip and inventory variance in a closed loop supply chain

Abstract

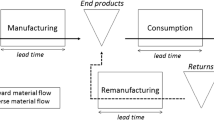
A simple dynamic model of a hybrid manufacturing/remanufacturing system is investigated. In particular we study an infinite horizon, continuous time, APIOBPCS (Automatic Pipeline Inventory and Order Based Production Control System) model. We use Åström’s method to quantify variance ratios in the closed loop supply chain. Specifically we highlight the effect of a combined “in-use” and remanufacturing lead-time and the return rate on the inventory variance and bullwhip produced by the ordering policy. Our results clearly show that a larger return rate leads to less bullwhip and less inventory variance in the plant producing new components. Thus returns can be used to absorb demand fluctuations to some extent. Longer remanufacturing and “in-use” lead-times have less impact at reducing inventory variance and bullwhip than shorter lead-times. We find that, within our specified system, that inventory variance and bullwhip is always less in supply chains with returns than supply chains without returns. We conclude by separating out the remanufacturing lead-time from the “in-use” lead-time and investigating its impact on our findings. We find that short remanufacturing lead-times do not qualitatively change our results.

Appendix A

Theorem

If the customer demand is drawn from an independently and identically distributed (i.i.d.) random distribution, then the following equation holds.

$$\frac{{\sigma ^{2}_{y} }}{{\sigma ^{2}_{x} }} = {\int_0^{ + \infty } {{\left[ {g{\left( t \right)}} \right]}} }^{2} dt = {\int_0^{ + \infty } {{\left[ {L^{{ - 1}} G{\left( s \right)}} \right]}^{2} dt} }$$

where g(t) is the time domain response and G(s) is its Laplace transform in the complex frequency domain. L ⁻¹ G(s)=g(t). y is the system’s output, that is, the order rate or the inventory levels. x is the input, the customer demand.

Proof

From the definition of Bullwhip, we have

$$VR = \frac{{\sigma ^{2}_{y} }}{{\sigma ^{2}_{x} }}$$

(A1)

.

The definition of σ ² is well known to be

$$\sigma ^{2}_{y} = E{\left[ {y{\left( t \right)} - E{\left[ {y{\left( t \right)}} \right]}} \right]}^{2} = E{\left[ {y{\left( t \right)}^{2} } \right]} - {\left[ {E{\left[ {y{\left( t \right)}} \right]}} \right]}^{2} {\text{ and}}$$

(A2)

$$\sigma ^{2}_{x} = E{\left[ {x{\left( t \right)} - E{\left[ {x{\left( t \right)}} \right]}} \right]}^{2} = E{\left[ {x{\left( t \right)}^{2} } \right]} - {\left[ {E{\left[ {x{\left( t \right)}} \right]}} \right]}^{2} $$

(A3)

where E[y(t)] and E[x(t)] are the mean values of a process’s output and input respectively, denoted as μ(y) and μ(x). So

$$\begin{array}{*{20}l} {{E{\left[ {y{\left( t \right)}} \right]} = \mu {\left( y \right)} = {\mathop {\lim }\limits_{T \to \infty } }\frac{1}{{2T}}{\int_{ - T}^{ + T} {y{\left( t \right)}dt} }} \hfill} & {{and} \hfill} & {{E{\left[ {x{\left( t \right)}} \right]}} \hfill} \\ \end{array} = \mu {\left( x \right)} = {\mathop {\lim }\limits_{T \to \infty } }\frac{1}{{2T}}{\int_{ - T}^{ + T} {x{\left( t \right)}dt} }$$

(A4)

.

Suppose that the system is linear and the demand is at stationary process thus μ(y)=μ(x). (A1) can therefore be expressed by

$$VR = \frac{{\sigma ^{2}_{y} }}{{\sigma ^{2}_{x} }} = \frac{{E{\left[ {y{\left( t \right)}^{2} } \right]}}}{{E{\left[ {x{\left( t \right)}^{2} } \right]}}}$$

(A5)

.

We know that $y{\left( t \right)} = {\int_{ - \infty }^{ + \infty } {g{\left( t \right)} \otimes } }\,x{\left( t \right)}dt$where ⊗ denotes the convolution operator, then Eq. (A5) becomes

$$\begin{aligned} & \frac{{E{\left[ {y{\left( t \right)}^{2} } \right]}}}{{E{\left[ {x{\left( t \right)}^{2} } \right]}}} = \frac{{{\mathop {\lim }\limits_{T \to \infty } }\frac{1}{{2T}}{\int_{ - T}^{ + T} {y{\left( t \right)}^{2} dt} }}}{{{\mathop {\lim }\limits_{T \to \infty } }\frac{1}{{2T}}{\int_{ - T}^{ + T} {x{\left( t \right)}^{2} dt} }}} = \frac{{{\mathop {\lim }\limits_{T \to \infty } }{\int_{ - T}^{ + T} {dt} }{\int_{ - \infty }^{ + \infty } {{\left[ {g{\left( t \right)}x{\left( t \right)}} \right]}^{2} dt} }}}{{{\mathop {\lim }\limits_{T \to \infty } }{\int_{ - T}^{ + T} {x{\left( t \right)}^{2} dt} }}} \\ & = \frac{{{\mathop {\lim }\limits_{T \to \infty } }{\int_{ - T}^{ + T} {x{\left( t \right)}^{2} dt} }{\int_{ - \infty }^{ + \infty } {g{\left( t \right)}} }^{2} dt}}{{{\mathop {\lim }\limits_{T \to \infty } }{\int_{ - T}^{ + T} {x{\left( t \right)}^{2} dt} }}} = {\int_{ - \infty }^{ + \infty } {g{\left( t \right)}^{2} dt} } = {\int_{ - \infty }^{ + \infty } {{\left[ {L^{{ - 1}} G{\left( s \right)}} \right]}^{2} dt} } \\ \end{aligned} $$

(A6)

Furthermore, we notice that ${\int_{ - \infty }^0 {g{\left( t \right)}} }dt = 0$. This result shows that

$$\frac{{\sigma ^{2}_{{OUT}} }}{{\sigma ^{2}_{{IN}} }} = {\int_0^{ + \infty } {g{\left( t \right)}^{2} dt = {\int_0^{ + \infty } {{\left[ {L^{{ - 1}} G{\left( s \right)}} \right]}^{2} dt} }} }$$

(A7)