Risk–incentives trade-off and outside options

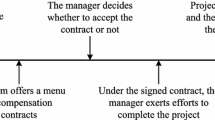
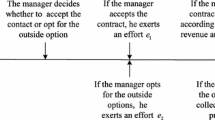
Abstract

Despite the prominence of the risk–incentives trade-off in the agency theory, empirical evidence provides at best a mixed result. In this paper, we argue that these mixed results may be attributed to the heterogeneity of risk aversion magnitude among the agents and the outside options available on the market. We show that when an increase in the uncertainty amplifies the riskiness of principal’s internal project more than the agent’s outside option, a positive risk–incentives relationship can be predicted when the internal project is sufficiently risky. On the other hand, when an uncertainty increase amplifies the riskiness of outside option more than the internal project, this positive risk–incentives relationship occurs if the internal project is of limited risk. These results hold irrespective of whether the agent’s risk aversion magnitude is publicly observable or privately known. Our analysis leads to a more fine-tuned empirical validation of agency theory and some testable hypotheses on the interactions between internal and external uncertainties.

Appendix: Proofs

Proof of Proposition 1

From the optimization problem, the principal’s objective is decreasing in the fixed payment $\alpha$. As the agent’s certainty equivalent CE is increasing in $\alpha$, at optimality the constraint should be binding: CE = CE$_{\text{ o}}$. Recalling that ${\text{ CE}}=\alpha +\beta +\frac{1}{2}\beta ^{2}(1-r\sigma ^{2})$ and ${\text{ CE}}_{\text{ o}}=\frac{1}{2}(1-rv^{2})$, we can rewrite the fixed payment as

$$\begin{aligned} \alpha =-\frac{1}{2}\beta ^{2}(1-r\sigma ^{2})+\frac{1}{2}(1-rv^{2}). \end{aligned}$$

Replacing $\alpha$ by $-\frac{1}{2}\beta ^{2}(1-r\sigma ^{2})+\frac{1}{2} (1-rv^{2})$, the principal’s objective becomes

$$\begin{aligned} \max _{\beta \ge 0} \left\{ (1-\beta )\beta -\alpha \right\}&= \max _{\beta \ge 0} \left\{ \beta -\frac{1}{2}\beta ^{2}(1+r\sigma ^{2})-\frac{1}{2}(1-rv^{2})\right\} \\&= \frac{1}{2}\left\{ \frac{1}{1+r\sigma ^{2}}-(1-rv^{2})\right\} , \end{aligned}$$

and the corresponding optimal commission rate is $\beta _{\sigma }(r)=\frac{1 }{1+r\sigma ^{2}}$. Note that the principal is willing to keep the agent within the firm if and only if she receives a positive payoff. Therefore, she offers a contract to the agent whenever $\frac{1}{2}\{ \frac{1}{1+r\sigma ^{2}}-(1-rv^{2})\} \ge 0$, i.e., whenever $r\ge \frac{1}{v^{2}}-\frac{1}{\sigma ^{2}}$. Together with the positivity of $r$, we obtain the cutoff level $\max \{\frac{1}{v^{2}}-\frac{1}{\sigma ^{2}},0\}$. The optimal fixed payment and the induced effort level follow immediately from $\beta _{\sigma }(r)$. $\square$

 

Proof of Proposition 2

It suffices to consider the cutoff level. Let $A(\sigma )=\frac{1}{v^{2}}-\frac{1}{\sigma ^{2}}$. Its derivative can be expressed as follows: $A^{\prime }(\sigma )=2(\frac{1}{\sigma ^{3}}-\frac{1}{v^{3}}v^{\prime }(\sigma ))$, which is negative if and only if $v^{\prime }(\sigma )>\frac{v^{3}}{\sigma ^{3}}$. When $0<b<1, v^{\prime }(\sigma )=bc\sigma ^{b-1}$ and $\frac{v^{3}}{\sigma ^{3}}=c^{3}\sigma ^{3(b-1)}$. Thus, if $\sigma ^{2(1-b)}>\frac{c^{2}}{b}, v^{\prime }(\sigma )>\frac{v^{3}}{\sigma ^{3}}$ and therefore $A(\sigma )$ is decreasing in $\sigma$. Furthermore, since $\frac{1}{v^{2}}-\frac{1}{ \sigma ^{2}}=\frac{1}{c^{2}\sigma ^{2}}(\sigma ^{2(1-b)}-c^{2})$, when $\sigma ^{2(1-b)}>\frac{c^{2}}{b}>c^{2}, A(\sigma )>0,$ and consequently the cutoff level is determined by $A(\sigma )$. Thus, from the fact that $A(\sigma )$ is decreasing in $\sigma$, if $\sigma _{1}>\sigma _{2}$ and $\sigma _{1}$ and $\sigma _{2}$ both satisfy $\sigma ^{2(1-b)}>\frac{c^{2}}{b }$, there exists a $r\in (r_{\sigma _{1}},r_{\sigma _{2}})$ such that $\beta _{\sigma _{1}}(r)>\beta _{\sigma _{2}}(r)=0$.

Now consider the case when $b>1$. In this case, $A(\sigma )=\frac{1}{v^{2}}-\frac{1}{\sigma ^{2}}>0$ if and only if $\sigma ^{2(b-1)}<\frac{1}{c^{2}}.$ Under this condition, we know that

$$\begin{aligned} \sigma ^{2(b-1)}<\frac{b}{c^{2}}\Leftrightarrow v^{\prime }(\sigma )=bc\sigma ^{b-1}>c^{3}\sigma ^{3(b-1)}=\frac{v^{3}}{\sigma ^{3}}, \end{aligned}$$

and therefore $A(\sigma )$ is decreasing in $\sigma .$ Since $A(\sigma )$ determines the cutoff level $r_{\sigma }$ when $\sigma ^{2(b-1)}<\frac{1}{ c^{2}}$, if $\sigma _{1}>\sigma _{2}$ and $\sigma _{1}$ and $\sigma _{2}$ both satisfy $\sigma ^{2(b-1)}<\frac{1}{c^{2}}$, there exists a $r\in (r_{\sigma _{1}},r_{\sigma _{2}})$ such that $\beta _{\sigma _{1}}(r)>\beta _{\sigma _{2}}(r)=0$. $\square$

 

Proof of Proposition 3

Define $A(\sigma )=\frac{1}{v^{2}}-\frac{1}{\sigma ^{2}}$ and $A^{\prime }(\sigma )=2(\frac{1}{\sigma ^{3}}-\frac{1}{v^{3}}v^{\prime }(\sigma ))<0$ if and only if $v^{\prime }(\sigma )>\frac{v^{3}}{\sigma ^{3}}$. When $b\le 0, v^{\prime }(\sigma )\le 0<\frac{v^{3}}{\sigma ^{3}}$ and thus $A(\sigma )$ is increasing in $\sigma$. Given that both $A(\sigma )$ and $\frac{1}{1+r\sigma ^{2}}$ are decreasing in $\sigma$, the optimal commission rate $\beta _{\sigma }(r)$ is decreasing in $\sigma$ for any $r$. Now consider the case when $b=1$. In this case, $v^{\prime }(\sigma )=c$ and $\frac{v^{3}}{\sigma ^{3}}=c^{3}$. Therefore, $A^{\prime }(\sigma )<0$ if and only if $c>1,$ in which case $A(\sigma )=\frac{1}{v^{2}}-\frac{1}{\sigma ^{2}}<0$. But then this implies that when $c>1$, the cutoff level is determined by $\max \{A(\sigma ),0\}=0$ and does not depend on $A(\sigma )$. Thus, as $\frac{1}{1+r\sigma ^{2}}$ is decreasing in $\sigma , \beta _{\sigma }(r)$ is decreasing in $\sigma$ for any $r$. The last two cases $0<b<1$ and $b>1$ follow immediately from Proposition 2. $\square$

 

Proof of Proposition 4

Our strategy is to first assume that every type of agent would be offered a contract, and then characterize the optimal menu of contracts. In the end, the principal can decide whether to include the agent, depending on whether the principal can extract a positive revenue from the agent. Note that following our notation, an exclusion of the agent can be conveniently incorporated by assuming that $(\alpha (r),\beta (r))=(0,0)$.

• (1) Formulation: Consider first the scenario in which the agent chooses a contract offered by the principal. Suppose that the agent’s true type is $r$ but he takes the contract $(\alpha (\tilde{r}),\beta (\tilde{r}))$ (by reporting to be type-$\tilde{r}$). The agent’s expected utility given $\alpha (\tilde{r})$ and $\beta (\tilde{r})$ is $\mathbb E _{\epsilon }[ -{\text{ e}}^{-r(\alpha (\tilde{r})+\beta (\tilde{r})(a+\epsilon )-\frac{1}{2}a^{2})}] =-{\text{ e}}^{-r{\text{ CE}}(a| \tilde{r},r)},$ where ${\text{ CE}}(a|\tilde{r},r)\equiv \alpha (\tilde{r})+\beta (\tilde{r})a-\frac{1}{2}a^{2}-\frac{1}{2}r\sigma ^{2}\beta ^{2}(\tilde{r}).$ Thus, the optimal effort is $a(\tilde{r},r)\equiv \arg \max _{a\ge 0}{\text{ CE}}(a| \tilde{r},r)=\beta (\tilde{r})$, and the agent’s certainty equivalent under this effort level is

  $$\begin{aligned} {\text{ CE}}(\tilde{r},r)\equiv \max _{a\ge 0}{\text{ CE}}(a|\tilde{r},r)=\alpha (\tilde{r})+\frac{1}{2}\beta ^{2}(\tilde{r})(1-r\sigma ^{2}). \end{aligned}$$

  Let ${\text{ CE}}(r)\equiv {\text{ CE}}(r,r)$. We now turn to the principal’s problem. The optimal linear menu is the solution to the following problem:

  $$\begin{aligned} \text{(P)}\ \max _{\left\{ \alpha (r)\text{ arbitrary}, \beta (r)\ge 0\right\} }&\mathbb E _{r}\left\{ (1-\beta (r))\beta (r)-\alpha (r)\right\} \end{aligned}$$

  (4)
  $$\begin{aligned} \text{ s.t.} {\text{ CE}}(r)&\ge {\text{ CE}}(\tilde{r},r),\forall \tilde{r},r, \end{aligned}$$

  (5)
  $$\begin{aligned} \ {\text{ CE}}(r)&\ge {\text{ CE}}_\mathrm{o}(r),\forall r. \end{aligned}$$

  (6)

  The incentive compatibility (IC) constraint (5) ensures that choosing the intended contract $(\alpha (r),\beta (r))$ is in the best interest of the type-$r$ agent.

• (2) Reduced program: In the sequel, we follow the optimal control theoretic approach by Maggi and Rodriguez-Clare (1995) to characterize the optimal menu of contracts. Define $U(\tilde{r},r)\equiv {\text{ CE}}(\tilde{r},r)-{\text{ CE}}_\mathrm{o}(r)$ as the “surplus”(information rent) a type-$r$ agent receives if he reports to be type-$\tilde{r}$. From the definitions of ${\text{ CE}}(\tilde{r},r)$ and ${\text{ CE}}_\mathrm{o}(r)$, we have

  $$\begin{aligned} U(\tilde{r},r)=\alpha (\tilde{r})+\frac{1}{2}(1-r\sigma ^{2})[\beta (\tilde{r })]^{2}-\frac{1}{2}(1-rv^{2}). \end{aligned}$$

  (7)

  Further define $U(r)\equiv U(r,r)$. Note that the certainty equivalent of the reservation utility, ${\text{ CE}}_{o}(r)= \frac{1}{2}(1-rv^{2})$, is weakly convex (linear) in type $r$. Thus, in the following we follow closely (Maggi and Rodriguez-Clare 1995, Section 4.1) to characterize the optimal menu. From the envelope theorem, the first-order necessary condition of the (IC) constraint gives rise to

  $$\begin{aligned} U^{^{\prime }}(r)=\frac{1}{2}[v^{2}-\sigma ^{2}(\beta (r))^{2}],\forall r. \end{aligned}$$

  Moreover, from the definition of $U(r)$, we have that

  $$\begin{aligned} -\alpha (r)=\frac{1}{2}(1-r\sigma ^{2})[\beta (r)]^{2}-\frac{1}{2} (1-rv^{2})-U(r), \end{aligned}$$

  and consequently the principal’s payoff (the objective function) can be rewritten as

  $$\begin{aligned} \mathbb E _{r}\left\{ (1\!-\!\beta (r))\beta (r)\!-\!\alpha (r)\right\} \!=\!\mathbb E _{r}\left\{ \beta (r)\!-\!\frac{1}{2}(1\!+\!r\sigma ^{2})\beta ^{2}(r)\!-\!\frac{1}{2} (1\!-\!rv^{2})\!-\!U(r)\right\} . \end{aligned}$$

  The optimization problem (P) can then be rewritten as follows:

  $$\begin{aligned} \ \ \text{(P1)}\ \max _{\left\{ \beta (r)\ge 0,U(r)\right\} }&\mathbb E _{r}\left\{ \beta (r)-\frac{1}{2}(1+r\sigma ^{2})\beta ^{2}(r)-\frac{1}{2} (1-rv^{2})-U(r)\right\} \\ \text{ s.t.} U^{^{\prime }}(r)&= \frac{1}{2}[v^{2}-\sigma ^{2}(\beta (r))^{2}],\forall r, \\ \ U(r)&\ge 0,\forall r. \end{aligned}$$

• (3) Candidate solution: In the sequel, $\beta$ denotes the control variable, $U$ denotes the state variable, and $\mu$ denotes the costate variable. We can then write down the Hamiltonian of (P1) as follows:

  $$\begin{aligned} \mathcal H (U,\beta ,\mu ,r)\equiv [\beta \!-\!\frac{1}{2}(1\!+\!r\sigma ^{2})\beta ^{2}\!-\!\frac{1}{2}(1\!-\!rv^{2})\!-\!U]f(r)\!+\!\frac{1}{2}\mu [v^{2}\!-\!\sigma ^{2}\beta ^{2}], \end{aligned}$$

  and the Lagrangian is $L=\mathcal H +\tau U.$ Following Maggi and Rodriguez-Clare (1995), the optimal solution of (P1) can be obtained via the following conditions:

  $$\begin{aligned} \frac{\partial \mathcal H }{\partial \beta }&= 1-(1+r\sigma ^{2})\beta f(r)+\mu (r)\sigma ^{2}\beta =0,\\ \frac{\mathrm{d}\mu }{\mathrm{d}r}&= -\frac{\partial L}{\partial U}=-f(r)-\tau (r),\\ \frac{\mathrm{d}U}{\mathrm{d}r}&= \frac{1}{2}[v^{2}-\sigma ^{2}(\beta (r))^{2}],\\ \tau (r)U(r)&= 0,\tau (r)\ge 0,U(r)\ge 0,\\ \mu (\underline{\mathrm{r}})U(\underline{\mathrm{r}})&= 0,\mu (\underline{\mathrm{r}})\le 0,\mu (\bar{r} )U(\bar{r})=0,\mu (\bar{r})\ge 0, \\&\quad \text{(transversality} \text{ conditions),} \end{aligned}$$

  which correspond to equations (1)–(5) in Maggi and Rodriguez-Clare (1995), pp. 248–249. The above conditions are both necessary and sufficient since $\mathcal H$ is concave in $\beta$. The crucial step now is to construct the right solution for the costate variable $\mu (r)$. According to Maggi and Rodriguez-Clare (1995), we should first find a function $\hat{\mu }(r)$ such that $U^{^{\prime }}(r)=0$ if the costate variable is $\hat{\mu }(r)$. Afterwards, we can decompose the costate variable $\mu (r)$ into three parts:

  $$\begin{aligned} \mu (r)=\left\{ \begin{array}{l@{\quad }l} F(r),&F(r)<\hat{\mu }(r) \\ \hat{\mu }(r),&F(r)-1\le \hat{\mu }(r)\le F(r) \\ F(r)-1,&\hat{\mu }(r)>F(r)-1 \end{array} \right.\!. \end{aligned}$$

  When $F(r)<\hat{\mu }(r), \mu (r)=F(r).$ Substituting this in the first-order condition, we obtain that

  $$\begin{aligned} \frac{\partial \mathcal H }{\partial \beta }&= 1-(1+r\sigma ^{2})\beta f(r)+F(r)\sigma ^{2}\beta =0, \\&\Rightarrow \beta (r)=\frac{1}{1+\sigma ^{2}(r+F(r)/f(r))}=\frac{1}{ 1+\sigma ^{2}(r+h(r))}. \end{aligned}$$

  In this region, the agent’s information rent is decreasing in $r$ since $\frac{\mathrm{d}U}{\mathrm{d}r}=\frac{1}{2}[v^{2}-\sigma ^{2}(\beta (r))^{2}]<0$. When $F(r)-1\le \hat{\mu }(r)\le F(r), \mu (r)=\hat{\mu }(r)$, and the corresponding control variable is obtained via

  $$\begin{aligned} \frac{\mathrm{d}U}{\mathrm{d}r}=\frac{1}{2}[v^{2}-\sigma ^{2}(\beta (r))^{2}]=0\Rightarrow \beta (r)=\frac{v}{\sigma }. \end{aligned}$$

  In this region, the agent’s information rent is a constant $(\frac{\mathrm{d}U}{\mathrm{d}r}=0)$. Finally, when $\hat{\mu }(r)>F(r)-1, \mu (r)=F(r)-1.$ Substituting this in the first-order condition, we obtain that

  $$\begin{aligned} \beta (r)=\frac{1}{1+\sigma ^{2}(r+\frac{1-F(r)}{f(r)})}=\frac{1}{1+\sigma ^{2}(r+H(r))}. \end{aligned}$$

  Collectively,

  $$\begin{aligned} \beta (r)=\left\{ \begin{array}{l@{\quad }l} \frac{1}{1+\sigma ^{2}(r+h(r))},&F(r)<\hat{\mu }(r)\\ \frac{v}{\sigma },&F(r)-1\le \hat{\mu }(r)\le F(r)\\ \frac{1}{1+\sigma ^{2}(r-H(r))},&\hat{\mu }(r)>F(r)-1 \end{array}\right.. \end{aligned}$$

  (8)

  Define $r_{1}$ and $r_{2}$ as the thresholds that separate these three regions. (IC) requires the monotonicity condition on $\beta (r)$ in each region, which is guaranteed by the regularity condition. The boundary points $r_{1}$ and $r_{2}$ are determined by the unique solutions to $\frac{1}{1+\sigma ^{2}(r+h(r))}=\frac{v}{\sigma }$ and to $\frac{1}{1+\sigma ^{2}(r-H(r))}=\frac{v}{\sigma };$ the uniqueness follows from the monotonicity of $h(r)$ and $H(r)$.

• (4) Characterization: To obtain the optimal commission rate, we should check if the solution in (8) is indeed feasible and yields a positive payoff for the principal. In the following, we divide the analysis into three cases: (1) $r<r_{1}$, (2) $r_{1}\le r\le r_{2}$, and (3) $r>r_{2}$. Define $I(r)\equiv r+h(r)$. Consider the first case $r<r_{1}.$ In the case, after substituting $\beta (r)$ by $\frac{1}{1+\sigma ^{2}(r+h(r))}$, the corresponding integrand of the principal’s objective is $f(r)[ \frac{1}{2[1+\sigma ^{2}I(r)]}+\frac{1}{2}(v^{2}I(r)-1)],$ which is positive if and only if $I(r)\ge \frac{\sigma ^{2}-v^{2}}{\sigma ^{2}v^{2}}$. Moreover, when $r<r_{1}$, from the monotonicity of $I(\cdot )$, we have $I(r)<I(r_{1})=\frac{\sigma -v}{\sigma ^{2}v},$ where the equality follows from $\frac{1}{1+\sigma ^{2}I(r_{1})}=\frac{v}{\sigma }.$ Note that when $\sigma <v$, the region degenerates since $I(\cdot )$ is strictly positive. Thus, it suffices to consider the situation in which $\sigma >v$. But then

  $$\begin{aligned} \frac{\sigma ^{2}-v^{2}}{\sigma ^{2}v^{2}}=\frac{\sigma -v}{\sigma ^{2}v} \frac{\sigma +v}{\sigma }>\frac{\sigma -v}{\sigma ^{2}v}=I(r_{1})>I(r). \end{aligned}$$

  This implies that in this region the integrand is never positive. Thus, this region vanishes in the optimal solution. Now consider the case $r_{1}\le r<r_{2}$. In this case, after substituting $\beta (r)$ by $\frac{v}{\sigma }$, the integrand of the principal’s objective is

  $$\begin{aligned} f(r)\left[ \frac{v}{\sigma }-\frac{1}{2}(1+r\sigma ^{2})\frac{v^{2}}{\sigma ^{2}}-\frac{1}{2}(1-rv^{2})\right] =-\frac{1}{2}f(r)(\frac{v}{\sigma }-1)^{2}\le 0. \end{aligned}$$

  Consequently, it is optimal for the principal not to include this region. Therefore, the only possibility is $r\ge r_{2}$. Recall that $J(r)\equiv r-H(r)$. The corresponding maximum integrand is $\frac{1}{2} f(r)[ \frac{1}{1+\sigma ^{2}J(r)}+v^{2}J(r)-1].$ Note that in this region $J(r)\ge J(r_{2})=\frac{\sigma ^{2}-v^{2}}{\sigma ^{2}v^{2}}$. It can be verified that if $\sigma >v$, the integrand $\frac{1}{2}f(r)[ \frac{1}{1+\sigma ^{2}J(r)}-(1-v^{2}J(r))] \ge 0$ is positive if and only if $J(r)\ge \frac{\sigma ^{2}-v^{2}}{\sigma ^{2}v^{2}}$; when $\sigma <v, \frac{1}{2}f(r)[ \frac{1}{1+\sigma ^{2}J(r)}-(1-v^{2}J(r))] \ge 0$ if and only if $J(r)\ge 0$. To summarize, the optimal commission rate is

  $$\begin{aligned} \beta _{\sigma }(r)=\left\{ \begin{array}{l@{\quad }l} \frac{1}{1+\sigma ^{2}J(r)},&J(r)\ge \max \{\frac{\sigma ^{2}-v^{2}}{ \sigma ^{2}v^{2}},0\} \\ 0,&\text{ otherwise} \end{array} .\right. \end{aligned}$$

  We can further construct the optimal fixed payment $\alpha _{\sigma }^{*}(r)$:

  $$\begin{aligned} \alpha _{\sigma }(r)\!=\!\left\{ \begin{array}{l@{\quad }l} \frac{1}{2}\int _{r_{\sigma }}^{r}(v^{2}\!-\!\sigma ^{2}\beta _{\sigma }^{2}(y))\mathrm{d}y\!-\!\frac{1}{2}(1-r\sigma ^{2})\beta _{\sigma }^{2}(r)\!+\!\frac{1}{2} (1-rv^{2}),&r\!\ge \! r_{\sigma } \\ 0,&\text{ otherwise} \end{array} \right.\!\!. \end{aligned}$$

  Note that at the boundary, $\alpha _{\sigma }(r_{\sigma })= \frac{1}{2}(1-r_{\sigma }v^{2})$ in order to induce the agent’s participation. The solution $\{\alpha _{\sigma }(\cdot ), \beta _{\sigma }(\cdot )\}$ constructed above yields an upper bound on the maximum objective value of ( 4) and satisfies (IR). To show that $\{\alpha _{\sigma }(\cdot )$ , $\beta _{\sigma }(\cdot )\}$ indeed solves the principal’s optimization problem (4)–(6), it suffices to verify that $\{\alpha _{\sigma }(\cdot ), \beta _{\sigma }(\cdot )\}$ satisfies (IC) i.e.,

  $$\begin{aligned} {\text{ CE}}(r)\ge {\text{ CE}}(\tilde{r},r),\forall \tilde{r},r\in [r_{\sigma },\bar{r}]. \end{aligned}$$

  (9)

  This follows the standard approach and thus is omitted. $\square$

 

Proof of Proposition 5

Given the compensation $T(x)$, the agent intends to find an effort $a$ that solves the following:

$$\begin{aligned} \max _{a\ge 0}\left\{ -{\text{ e}}^{-r(T(a+\epsilon )-\frac{1}{2}a^{2})}\right\} \equiv \max _{a\ge 0}\left\{ T(a+\epsilon )-\frac{1}{2}a^{2}\right\} . \end{aligned}$$

Let $a^{*}$ denote the optimal (target) effort. The agent’s incentive constraint gives rise to the following optimality condition: $T^{^{\prime }}(a^{*}+\epsilon )-a^{*}=0, \forall \epsilon .$ Integrating over $\epsilon$, we obtain that

$$\begin{aligned} T(a^{*}+\epsilon )=a^{*}(a^{*}+\epsilon )+K=a^{*}x+K, \end{aligned}$$

where $K$ is the constant that induces the agent to participate.

Therefore, the optimal contract $T(x)$ turns out to be linear. Accordingly, the agent’s utility upon participation is

$$\begin{aligned} \mathbb E _{\epsilon }\left[ \left\{ -{\text{ e}}^{-r(a^{*}+\epsilon -\frac{1}{2} \left(a^{*}\right) ^{2}+K)}\right\} \right] =\mathbb E _{\epsilon } \left[ \left\{ -{\text{ e}}^{-r(a^{*}+\epsilon -\frac{1}{2}\left(a^{*}\right) ^{2}+K)}\right\} \right]. \end{aligned}$$

and its certainty equivalent is ${\text{ CE}}=a^{*}-\frac{1}{2}(a^{*})^{2}+K-\frac{1}{2}r\sigma ^{2}.$ On the other hand, the agent’s reservation utility is now:

$$\begin{aligned} \mathbb E _{\xi }\left[ \max _{a\ge 0}\left\{ -{\text{ e}}^{-r(a+\xi -\frac{1}{2} a^{2})}\right\} \right] =\mathbb E _{\xi }\left[ -{\text{ e}}^{-r(\xi +\frac{1}{2})}\right], \end{aligned}$$

i.e., ${\text{ CE}}_\mathrm{o}=\frac{1}{2}(1-rv^{2}).$ The constant $K$ can be obtained as follows:

$$\begin{aligned} a^{*}\!-\!\frac{1}{2}\left(a^{*}\right) ^{2}\!+\!K\!-\!\frac{1}{2}r\sigma ^{2}\!=\! \frac{1}{2}(1\!-\!rv^{2})\Leftrightarrow K\!=\!\frac{1}{2}r\sigma ^{2}\!+\!\frac{1}{2} (1-rv^{2})-a^{*}+\frac{1}{2}\left(a^{*}\right) ^{2}. \end{aligned}$$

Now we return to the first stage wherein the principal decides the target effort $a^{*}$. Her goal is to maximize the following:

$$\begin{aligned}&\max _{a^{*}\ge 0}\left\{ \mathbb E _{\epsilon }\left[ a^{*}+\epsilon -T(a^{*}+\epsilon )\right] \right\} \\&\quad =\max _{a^{*}\ge 0}\left\{ \mathbb E _{\epsilon }\left[ a^{*}+\epsilon -a^{*}(a^{*}+\epsilon )-K\right] \right\} \\&\quad =\max _{a^{*}\ge 0}\left\{ a^{*}-\left(a^{*}\right) ^{2}+a^{*}-\frac{1}{2}\left(a^{*}\right) ^{2}-\frac{1}{2}r\sigma ^{2}-\frac{1}{2}(1-rv^{2})\right\} \\&\quad =\frac{1}{6}+\frac{1}{2}r(v^{2}-\sigma ^{2}), \end{aligned}$$

where $a^{*}+\epsilon$ corresponds to the principal’s gross benefit from the project and $T(a^{*}+\epsilon )$ is the compensation she pays to the agent. The second equality follows as we substitute $K.$ In the third equality, we find that the objective is a concave quadratic function of $a^{*}$; thus, at optimality $a^{*}=2/3$ if the principal would like to keep the agent within the firm. From the last expression, we again observe that if the external uncertainty is higher than the internal one, the principal is more likely to keep the agent. Additionally, when the agent is more risk-averse, he is more likely to work for the principal. $\square$