Existence and Stability of Traveling Pulses in a Reaction–Diffusion-Mechanics System

Abstract

In this article, we analyze traveling waves in a reaction–diffusion-mechanics (RDM) system. The system consists of a modified FitzHugh–Nagumo equation, also known as the Aliev–Panfilov model, coupled bidirectionally with an elasticity equation for a deformable medium. In one direction, contraction and expansion of the elastic medium decreases and increases, respectively, the ionic currents and also alters the diffusivity. In the other direction, the dynamics of the R–D components directly influence the deformation of the medium. We demonstrate the existence of traveling waves on the real line using geometric singular perturbation theory. We also establish the linear stability of these traveling waves using the theory of exponential dichotomies.

Appendices

Appendix A: Center Manifold Computation

We augment the traveling wave equation with an equation for ϵ. Then the knee,

$$(u,v,w,\epsilon)= (u_{\mathrm{knee}},0,w_{\mathrm{knee}},0 ), $$

is a center-unstable fixed point with one positive eigenvalue and three zero eigenvalues. The positive eigenvalue is cF ²(w _knee). The corresponding eigenvector is w _c =〈1,cF(w _knee),0,0〉. As an eigenvalue, zero has geometric multiplicity one (algebraic multiplicity three), with eigenvector w ₀=〈1,0,0,0〉 and generalized eigenvector w ₁=〈0,1,F _W (w _knee)f(u _knee,w _knee)+F(w _knee)u _knee,0〉, and w ₂=〈0,0,ku _knee−w _knee,c(F _W (w _knee)f(u _knee,w _knee)+F(w _knee)u _knee)²〉. For ease of notation, we denote the values of u and w at the knee by

To compute the center manifold approximation, we suppose

In order to proceed, we first expand

$$F(w)=F_0+F_1(w-w_{\mathrm{knee}})+\cdots, $$

where

The center manifold approximation requires us to express the nonlinearity in terms of local coordinates at the knee,

The linear terms in (u−u _knee) drop out since

$$F_0 \bigl(3ku_{\mathrm{knee}}^2-2k(1+a)u_{\mathrm {knee}}+ka+w_{\mathrm{knee}} \bigr)=0. $$

We now insert the center manifold ansatz into the differential equation for v. Working order by order, the coefficients in the center manifold expansion are computed to be

The reduced dynamics on the center manifold are then given to leading order by

Appendix B: Proof of Lemma 3.4: Corner Estimates

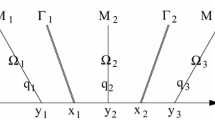
A crucial feature of our approach is the ability to divide the domain, ℝ into pieces over which the dynamics are effectively described as a perturbation of the front, back, left slow manifold, right slow manifold, or near the knee. Within these domains, the solution is either characterized as being pointwise close (in ξ) to the singular solution (front, back, knee) or as evolving at an $\mathcal{O}(\epsilon )$ rate (slow manifolds).

The purpose of this Appendix is to explain the tools that we use to justify this decomposition. We review this material in order for the article to be self-contained.

For $\mathcal{O}(1)$ timescales along the front, the true solution remains $\mathcal{O} (\epsilon)$ close to the singular solution. We seek the optimal time scale over which the solution “turns a corner” from evolving pointwise close to the singular solution along the front to evolving at an $\mathcal {O}(\epsilon)$ rate, or equivalently being $\mathcal{O}(\epsilon)$ close to the slow manifold. Hence, the term corner estimates. For entry and exit to the slow manifold at normally hyperbolic points, this question has been answered by a theorem in Eszter (1999). We state it and repeat the proof here for completeness and for motivation for the case when the exit from the slow manifold does not occur at a normally hyperbolic point.

2.1 B.1 Corner Estimates—Normally Hyperbolic Points

Before stating the theorem, we note that the theorem relies on the use of Fenichel normal form to describe a neighborhood of the slow manifold. For convenience, we will assume that we are working with the entry to the right slow manifold. The corner estimates for the entry and exit points for the left slow manifold are similar. Here, we assume a transformation has been performed which places the system in Fenichel normal form; see Fenichel (1971/1972), Jones (1995). The Fenichel normal form is

The matrix Λ has spectrum in the right-half plane, while the spectrum of Γ lies in the left-half plane, with both bounds being strict and independent of ϵ. The slow manifold is represented by the set (a,b,y)=(0,0,y). Consider a box D surrounding the slow manifold and define two manifolds of entry and exit points,

We assume for all ϵ>0 and sufficiently small, there exists a solution entering the slow manifold at time ξ ₁ through N ₁ and then passing through N ₂ at some later time ξ ₂(ϵ), which is $\mathcal{O}(\epsilon^{-1})$. We further assume that this solution satisfies lim _ϵ→0 y(ξ ₁)=y ₀. The dynamics as one enters through N ₁ describe the fast layer problem, while as the solution passes through N ₂ the leading order the dynamics are given by the slow manifold. We will define a corner function Ξ(ϵ) that will describe the transition between these two regimes.

Theorem 5

(Eszter 1999)

Let Ξ(ϵ) satisfy lim _ϵ→0 Ξ(ϵ)=∞ and lim _ϵ→0 ϵΞ(ϵ)=0. Then we have that

$$\lim_{\epsilon\to0}(a,b,y) \bigl(\varXi(\epsilon),\epsilon \bigr)=(0,0,y_0). $$

Moreover, if Ξ=−θlog(ϵ) for some θ>0 and if $\|y(\xi_{1},\epsilon)-y_{0}\|=\mathcal{O}(\epsilon)$, then there exists K>0 for which

$$\frac{1}{\epsilon}\bigl\|(a,b,y) \bigl(\varXi(\epsilon),\epsilon \bigr)-(0,0,y_0)\bigr\| \leq K\varXi(\epsilon), $$

as ϵ→0.

Proof

The proof of this theorem can be found in Eszter (1999). However, for completeness we will reproduce it here. We will assume that both a and b are one dimensional, which is sufficient for the purposes of this work, but the result is true more generally; see Eszter (1999). We assume there exists local constants α _± and β _± such that on the box D for sufficiently small ϵ we have

We find that if ξ>ξ ₁, then

$$\bigl|a(\xi)\bigr|\geq\bigl|a(\xi_1)\bigr|\mathrm{e}^{\alpha_-(\xi-\xi_1)}. $$

Since a(ξ ₂)∈N ₂, we have

$$\bigl|a(\xi_1)\bigr|\leq\varDelta \mathrm{e}^{-\alpha_-(\xi_2-\xi_1)}. $$

Using the upper bound on Λ, we find in a similar fashion that

$$\bigl|a \bigl(\varXi(\epsilon) \bigr)\bigr|\leq\varDelta \mathrm{e}^{-\alpha_-\xi _2+\alpha_+\varXi(\epsilon) -(\alpha_+-\alpha_-)\xi_1}=K_1\mathrm{e}^{-\frac{\alpha_-K_2}{\epsilon}}, $$

where K ₁ and K ₂ are positive constants. We therefore have that as ϵ→0 then a(Ξ(ϵ))→0, as well.

For b, the result is more immediate, as we have

$$\bigl|b(\xi)\bigr|\leq\bigl|b(\xi_1)\bigr|\mathrm{e}^{\beta_+(\xi-\xi_1)} \leq\varDelta \mathrm{e}^{\beta_+(\xi-\xi_1)}. $$

This implies that

$$\bigl|b \bigl(\varXi(\epsilon) \bigr)\bigr|\leq\varDelta \mathrm{e}^{\beta_+(\varXi (\epsilon)-\xi_1)}, $$

and by hypothesis on Ξ(ϵ) we find that this also goes to zero in the limit as ϵ→0. The solution to the slow component may be written in the implicit form

$$y \bigl(\varXi(\epsilon),\epsilon \bigr)=y_1(\xi_1, \epsilon )+\epsilon\int_{\xi_1}^{\varXi(\epsilon)} g \bigl(a(\sigma, \epsilon),b(\sigma ,\epsilon),y( \sigma,\epsilon),\epsilon \bigr) \,\mathrm{d}\sigma. $$

Since the box D is compact, we may take the supremum over D and arrive at

$$\bigl\|y \bigl(\varXi(\epsilon),\epsilon \bigr)-y_1(\xi_1, \epsilon )\bigr\|\leq\epsilon \bigl( \varXi(\epsilon)-\xi_1 \bigr)L. $$

By the hypothesis on Ξ(ϵ) and y ₁, we arrive at the desired result. Since the convergence to zero of a and b is exponential, we find that the second part of the result follows, as well. □

2.2 B.2 Corner Estimates—The Flow Near the Knee

At nonhyperbolic points, a Fenichel normal form does not exist and, therefore, the techniques in Lemma 5 do not apply directly. Instead, we will use the normal form for a fold point derived in Krupa and Szmolyan (2001) to divide the domain into three pieces: one where the solution evolves at an $\mathcal{O}(\epsilon)$ rate, a second where the solution is pointwise $\mathcal{O}(\epsilon^{1/3})$ close to the nonhyperbolic knee, and a third where the solution is pointwise $\mathcal{O}(\epsilon^{1/3})$ close to the singular solution along the back. In fact, this decomposition has already been done in Krupa and Szmolyan (2001) in terms of various coordinate charts, so our task will be to confirm that their decomposition satisfies the properties that we are interested in.

We recall from the existence proof the normal form for a fold point presented in Krupa and Szmolyan (2001),

(B.1)

This system was analyzed using geometric desingularization techniques. The approach is to introduce a change of coordinates,

$$x=\bar{r}\bar{x},\qquad y=\bar{r}^2\bar{y}, \qquad\epsilon=\bar {r}^3\bar{\epsilon}, $$

where $\bar{x}^{2}+\bar{y}^{2}+\bar{\epsilon}^{2}=1$. In this way, the degenerate point at the origin is blown-up to a sphere. Instead of analyzing the system in these coordinates, it is convenient to work in various coordinate charts. The three charts K ₁,K ₂, and K ₃ are introduced in Krupa and Szmolyan (2001) and are described using the local coordinates

Recall the definition of the entry and exit subsections for some value of ρ>0,

Definition 3

For ρ>0 and δ>0, both small but $\mathcal{O}(1)$ with respect to ϵ, we define entry and exit subsections for the charts defined above.

The flow from the entry subsection Δ ⁱⁿ to Δ ^out is described with the aid of transition maps $\varPi_{1}:\varSigma_{1}^{\mathrm{in}}\to\varSigma_{1}^{\mathrm {out}}$, $\varPi_{2}:\varSigma_{2}^{\mathrm{in}}\to\varSigma_{2}^{\mathrm{out}}$ and $\varPi_{3}:\varSigma_{3}^{\mathrm{in}}\to\varSigma_{3}^{\mathrm{out}}$.

The following facts are shown in Krupa and Szmolyan (2001).

Theorem 6

(Krupa and Szmolyan 2001)

There exists constants ρ>0 and δ>0, both $\mathcal {O}(1)$ for which the trajectory entering Δ ⁱⁿ, exponentially close to the slow manifold has the following properties:

• 1. The derivative of any trajectory that stays $\mathcal {O}(\epsilon)$ close to the slow manifold in chart K ₁ has a derivative bounded by $\mathcal{O}(\epsilon)$.

• 2. While in chart K ₂, the tracked trajectory is $\mathcal {O}(\epsilon^{1/3})$ close to the fold point.

• 3. While in chart K ₃, the tracked slow manifold is $\mathcal {O}(\epsilon^{1/3})$ pointwise close in χ to the flow for the reduced (ϵ=0) system along the back.

The proofs of 1 and 2 follow from Krupa and Szmolyan (2001). We will establish 3 in the following lemma.

Lemma B.11

Consider the fold-point normal form (B.1). There exists a function Ξ(ϵ) such that if x(0,ϵ)=ρ, $y(0,\epsilon )=\mathcal{O}(\epsilon^{2/3})$ then there exist a K>0 for which

$$\bigl|(x,y) (t,\epsilon)- \bigl(x(t),0 \bigr)\bigr|<K\epsilon^{1/3}. $$

Proof

We desingularize as in Krupa and Szmolyan (2001). Let x=σ, y=σ ² y ₃, and ϵ=σ ³ ϵ ₃. Then (B.1) is transformed to

$$ \everymath{\displaystyle} \begin{array}{@{}rcl} \sigma'&=&\sigma^2 F(\sigma, y_3, \epsilon_3), \\[2mm] y_3'&=& \epsilon_3\sigma \bigl(-1+ \mathcal{O}(\sigma) \bigr)-2y_3\sigma F(\sigma,y_3, \epsilon_3), \\[2mm] \epsilon_3'&=& -3\epsilon_3\sigma F( \sigma,y_3,\epsilon_3), \end{array} $$

(B.2)

where $F=1-y_{3}+\mathcal{O}(\sigma)$. We consider initial conditions of the form,

$$x(0)=\rho,\qquad y(0)=\kappa\epsilon^{2/3}, $$

which transform to the initial conditions,

$$\sigma(0)=\rho, \qquad y_3(0)=\kappa\frac{\epsilon^{2/3}}{\rho^2},\qquad \epsilon_3(0) =\frac{\epsilon}{\rho^3}. $$

The vector field in (B.2) may be desingularized by defining a new time scale,

$$ \tau=\int_0^t \sigma (s)F\bigl(\sigma (s),y_3(s),e_3(s)\bigr)\,\mathrm{d}s. $$

(B.3)

Provided that F≠0, this rescaling of the independent variable serves only to change the time parameterization of solutions. In the new variables, we have

The nonlinear term $\frac{\epsilon_{3}}{1-y_{3}}$ is nonresonant and can therefore be transformed away using a smooth change of coordinates. This system is (in new coordinate $\tilde{y}_{3}$)

This system may be solved implicitly as

$$ \everymath{\displaystyle} \begin{array}{@{}rcl} \sigma(\tau)&=&\mathrm{e}^\tau\sigma(0), \\[2mm] \tilde{y}_3(\tau)&=&\mathrm{e}^{-2\tau}\tilde{y}_3(0)+ \epsilon_3(0)\mathrm{e}^{-2\tau } \bigl(\mathrm{e}^{-\tau}-1 \bigr) \\[2mm] &&{}+ \sigma(0) \epsilon_3(0)\mathrm{e}^{-2\tau} \int_0^\tau H \bigl(\sigma(s),\tilde{y}_3(s),\epsilon_3(s) \bigr)\,\mathrm{d}s, \\[4mm] \epsilon_3(\tau)&=&\mathrm{e}^{-3\tau}\epsilon_3(0). \end{array} $$

(B.4)

A contraction mapping argument and the fact that H is at least C ¹ in y ₃ shows that there exists a unique y ₃ solving (B.4) so long as (σ,y ₃,ϵ ₃) stays in the compact set

$$D:= \bigl\{ (\sigma,y_3,\epsilon_3) | \sigma\in[0,\rho], y_3\in[-\beta_3,\beta_3], \epsilon_3 \in[0,\delta] \bigr\}. $$

Noting the initial conditions, we see that the solution is defined on the interval $(\tilde{\varXi},0)$ with $\tilde{\varXi}=\frac{1}{3}\log(\frac{\epsilon_{3}(0)}{\delta})$.

Note first that $(\sigma(\tilde{\varXi}),y_{3}(\tilde{\varXi }),\epsilon_{3}(\tilde{\varXi}))\in\varSigma_{3}^{\mathrm{in}}$. Also, we have σ(0)=ρ, $y_{3}(0)=\kappa\frac{\epsilon^{2/3}}{\rho^{2}}$ and $\epsilon_{3}(0)=\frac{\epsilon}{\rho^{3}}$. Reverting to original variables, we have

with $\tilde{\varXi}=\frac{1}{3}\log(\frac{\epsilon}{\delta\rho^{3}})$. This gives the transition time between $\varSigma_{3}^{\mathrm{in}}$ and $\varSigma_{3}^{\mathrm{out}}$ in terms of the τ timescale. Let Ξ be the transition time in the t timescale. Then (B.3) provides

$$\tilde{\varXi}=\int_0^\varXi\sigma(\sigma)F \bigl( \sigma(s),y_3(s),\epsilon_3(s) \bigr)\,\mathrm{d}s. $$

To compute the leading order description of Ξ, we note that $\sigma(s)= \mathcal{O}(-1/s)$ as s→−∞. Using the fact that $F=1-y_{3}+\mathcal{O}(\sigma)$, we derive

$$\tilde{\varXi}\sim-\int_\varXi^{\mathcal{O}(1)} \frac{-C}{s}\,\mathrm{d}s. $$

This implies that

$$\varXi\sim-C \mathrm{e}^{-\tilde{\varXi}}\sim\mathcal{O} \bigl(\epsilon^{-1/3} \bigr). $$

An easy computation shows that this solution remains pointwise close to the ϵ=0, y=0 solution on the interval $(\tilde{\varXi},0)$. □

Appendix C: Brief Review of Roughness of Dichotomy Results

The existence of the exponential dichotomies on each subinterval will follow from various roughness of dichotomy results. For completeness, we list those results here.

Theorem 7

(Proposition 4.1 in Coppel (1978))

Let x∈ℝⁿ and suppose that the linear system x′=A(ξ)x has an exponential dichotomy on J. Then the linear system x′=(A(ξ)+B(ξ))x also has an exponential dichotomy on J provided that |B(ξ)|<δ for all ξ∈J, for some δ sufficiently small.

Note that the decay rates of the exponential dichotomy will be altered by $\mathcal{O}(\delta)$ amounts. A stronger result is provided by the following theorem.

Theorem 8

(Chapter 4 of Coppel 1965)

Suppose that x′=Ax has an exponential dichotomy on J. Suppose that

$$\int_{J} \bigl|B(\xi) \bigr|\,\mathrm{d}\xi<\infty, $$

then the system x′=(A+B(ξ))x also has an exponential dichotomy on J with the same decay rates as the original exponential dichotomy.

A final result will be useful for the analysis along the slow manifolds.

Theorem 9

(Proposition 6.1 in Coppel 1978)

Suppose that the n×n matrix A(ξ) is bounded and hyperbolic for all ξ∈J with k eigenvalues with real part less than −α<0 and n−k eigenvalues with real part greater than β>0. In addition, suppose that A(ξ) is continuously differentiable and there exists a δ>0 such that |A′(ξ)|<δ for all ξ∈J. Then the linear system x′=A(ξ)x has an exponential dichotomy on J.