Abstract
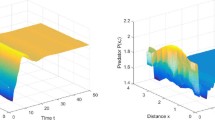
Prey-taxis is the process that predators move preferentially toward patches with highest density of prey. It is well known to have an important role in biological control and the maintenance of biodiversity. To model the coexistence and spatial distributions of predator and prey species, this paper concerns nonconstant positive steady states of a wide class of prey-taxis systems with general functional responses over 1D domain. Linearized stability of the positive equilibrium is analyzed to show that prey-taxis destabilizes prey–predator homogeneity when prey repulsion (e.g., due to volume-filling effect in predator species or group defense in prey species) is present, and prey-taxis stabilizes the homogeneity otherwise. Then, we investigate the existence and stability of nonconstant positive steady states to the system through rigorous bifurcation analysis. Moreover, we provide detailed and thorough calculations to determine properties such as pitchfork and turning direction of the local branches. Our stability results also provide a stable wave mode selection mechanism for thee reaction–advection–diffusion systems including prey-taxis models considered in this paper. Finally, we provide numerical studies of prey-taxis systems with Holling–Tanner kinetics to illustrate and support our theoretical findings. Our numerical simulations demonstrate that the \(2\times 2\) prey-taxis system is able to model the formation and evolution of various striking patterns, such as spikes, periodic oscillations, and coarsening even when the domain is one-dimensional. These dynamics can model the coexistence and spatial distributions of interacting prey and predator species. We also give some insights on how system parameters influence pattern formation in these models.








Similar content being viewed by others
References
Abrams, P., Matsuda, H.: Effects of adaptive predatory and anti-predator behaviour in a two-prey–one-predator system. Evol. Ecol. 7, 312–326 (1993)
Ainseba, B.E., Bendahmane, M., Noussair, A.: A reaction–diffusion system modeling predator–prey with prey-taxis. Nonlinear Anal. RWA 9, 2086–2105 (2008)
Braza, P.: The bifurcation structure of the Holling–Tanner model for predator–prey interactions using two-timing. SIAM J. Appl. Math. 63, 889–904 (2003)
Chen, S., Shi, J.: Global stability in a diffusive Holling–Tanner predator–prey model. Appl. Math. Lett. 25, 614–618 (2012)
Chen, S., Shi, J., Wei, J.: Global stability and Hopf bifurcation in a delayed diffusive Leslie–Gower predator–prey system. Int. J. Bifurc. Chaos Appl. Sci. Eng. 22, 11 (2012)
Crandall, M.G., Rabinowitz, P.H.: Bifurcation from simple eigenvalues. J. Funct. Anal. 8, 321–340 (1971)
Crandall, M.G., Rabinowitz, P.H.: Bifurcation, perturbation of simple eigenvalues, and linearized stability. Arch. Ration. Mech. Anal. 52, 161–180 (1973)
Du, Y., Hsu, S.-B.: A diffusive predator–prey model in heterogeneous environment. J. Differ. Equ. 203, 331–364 (2004)
Ghazaryan, A., Manukian, V., Schecter, S.: Travelling waves in the Holling–Tanner model with weak diffusion. Proc. Roy. Soc. London Ser. A. 471, 20150045 (2015)
Gliwicz, Z.M., Maszczyk, P., Jablonski, J., Wrzosek, D.: Patch exploitation by planktivorous fish and the concept of aggregation as an antipredation defense in zooplankton. Limnol. Oceanogr. 58, 1621–1639 (2013)
He, X., Zheng, S.: Global boundedness of solutions in a reaction–diffusion system of predator–prey model with prey-taxis. Appl. Math. Lett. 49, 73–77 (2015)
Hillen, T., Painter, K.J.: Global existence for a parabolic chemotaxis model with prevention of overcrowding. Adv. Appl. Math. 26, 280–301 (2001)
Hillen, T., Painter, K.J.: A user’s guidance to PDE models for chemotaxis. J. Math. Biol. 58, 183–217 (2009)
Holling, C.S.: The functional response of invertebrate predators to prey density. Mem. Entomol. Soc. Can. 45, 3–60 (1965)
Horstmann, D.: From 1970 until now: The Keller–Segel model in chemotaxis and its consequences I. Jahresber. DMV 105(2003), 103–165 (1970)
Hsiao, L., De Mottoni, P.: Persistence in reacting–diffusing systems: interaction of two predators and one prey. Nonlinear Anal. TMA 11, 367–536 (1987)
Hsu, S.-B., Huang, T.-W.: Global stability for a class of predator–prey systems. SIAM J. Appl. Math. 55, 763–783 (1995)
Hsu, S.-B., Huang, T.-W.: Uniqueness of limit cycles for a predator–prey system of Holling and Leslie type. Can. Appl. Math. Q. 6, 91–117 (1998)
Kareiva, P., Odell, G.: Swarms of predators exhibit “preytaxis” if individual predators use area-restricted search. Am. Nat. 130, 233–270 (1987)
Kuto, K.: Stability of steady-state solutions to a prey–predator system with cross-diffusion. J. Differ. Equ. 197, 293–314 (2004)
Kuto, K., Yamada, Y.: Multiple coexistence states for a prey–predator system with cross-diffusion. J. Differ. Equ. 197, 315–348 (2004)
Lee, J.M., Hilllen, T., Lewis, M.A.: Continuous traveling waves for prey-taxis. Bull. Math. Biol. 70, 654–676 (2008)
Lee, J.M., Hilllen, T., Lewis, M.A.: Pattern formation in prey-taxis systems. J. Biol. Dyn. 3, 551–573 (2009)
Li, X., Jiang, W.H., Shi, J.-P.: Hopf bifurcation and turing instability in the reaction–diffusion Holling–Tanner predator–prey model. IMA J. Appl. Math. 78, 287–306 (2013)
Lin, J.-J., Wang, W., Zhao, C., Yang, T.-H.: Global dynamics and traveling wave solutions of two predators–one prey models. Discrete Contin. Dyn. Syst. Ser. B 20, 1135–1154 (2015)
Loladze, I., Kuang, Y., Elser, J.-J., Fagan, W.-F.: Competition and stoichiometry: coexistence of two predators on one prey. Theor. Popul. Biol. 65, 1–15 (2004)
Ma, Z.-P., Li, W.-T.: Bifurcation analysis on a diffusive Holling–Tanner predator–prey model. Appl. Math. Model. 37, 4371–4384 (2013)
May, R.M.: Stability and complexity in model ecosystems, 2nd edn. Princeton University Press, Princeton (1974)
Painter, K., Hillen, T.: Volume-filling and quorum-sensing in models for chemosensitive movement. Can. Appl. Math. Q. 10, 501–543 (2002)
Painter, K., Hillen, T.: Spatio-temporal chaos in a chemotaxis model. Phys. D 240, 363–375 (2011)
Peng, R., Shi, J.: Non-existence of non-constant positive steady states of two Holling type-II predator–prey systems: strong interaction case. J. Differ. Equ. 247, 866–886 (2009)
Peng, R., Wang, M.-X.: Positive steady states of the Holling–Tanner prey–predator model with diffusion. Proc. R. Soc. Edinb. Sect. A 135, 149–164 (2005)
Peng, R., Wang, M.-X.: Global stability of the equilibrium of a diffusive Holling–Tanner prey–predator model. Appl. Math. Lett. 20, 664–670 (2007)
Peng, R., Wang, M.-X., Yang, G.-Y.: Stationary patterns of the Holling–Tanner prey–predator model with diffusion and cross-diffusion. Appl. Math. Comput. 196, 570–577 (2008)
Potapov, A.B., Hillen, T.: Metastability in chemotaxis models. J. Dyn. Differ. Equ. 17, 293–330 (2005)
Sáez, E., González-Olivares, E.: Dynamics of a predator–prey model. SIAM J. Appl. Math. 59, 1867–1878 (1999)
Sapoukhina, N., Tyutyunov, Y., Arditi, R.: The role of prey taxis in biological control: a spatial theoretical model. Am. Nat. 162, 61–76 (2003)
Shi, H.-B., Ruan, S.: Spatial, temporal and spatiotemporal patterns of diffusive predator–prey models with mutual interference. IMA J. Appl. Math. 80, 1534–1568 (2015)
Shi, H.-B., Li, W.-T., Lina, G.: Positive steady states of a diffusive predator–prey system with modified Holling–Tanner functional response. Nonlinear Anal. RWA 11, 3711–3721 (2010)
Shi, J., Wang, X.: On global bifurcation for quasilinear elliptic systems on bounded domains. J. Differ. Equ. 246, 2788–2812 (2009)
Tanner, J.T.: The stability and the intrinsic growth rates of prey and predator populations. Ecology 56, 855–867 (1975)
Tao, Y.: Global existence of classical solutions to a predator–prey model with nonlinear prey-taxis. Nonlinear Anal. RWA 11, 2056–2064 (2010)
Tello, J.I., Winkler, M.: Stabilization in a two-species chemotaxis system with a logistic source. Nonlinearity 25, 1413–1425 (2012)
Ton, T., Hieu, N.: Dynamics of species in a model with two predators and one prey. Nonlinear Anal. TMA 74, 4868–4881 (2011)
Wang, K., Wang, Q., Yu, F.: Stationary and time periodic patterns of two-predator and one-prey systems with prey-taxis (2015) (preprint). arxiv:1508.03909
Wang, Q., Gai, C., Yan, J.: Qualitative analysis of a Lotka–Volterra competition system with advection. Discrete Contin. Dyn. Syst. 35, 1239–1284 (2015)
Wang, Q., Yang, J., Zhang, L.: Time periodic and stable patterns of a two-competing-species Keller–Segel chemotaxis model effect of cellular growth (2015) (preprint). arxiv:1505.06463
Wang, Q., Zhang, L., Yang, J., Hu, J.: Global existence and steady states of a two competing species Keller–Segel chemotaxis model. Kinet. Relat. Models 8, 777–807 (2015)
Wang, X., Wang, W., Zhang, G.: Global bifurcation of solutions for a predator–prey model with prey-taxis. Math. Methods Appl. Sci. 38, 431–443 (2015)
Wang, Y.-X., Li, W.-T.: Spatial patterns of the Holling–Tanner predator–prey model with nonlinear diffusion effects. Appl. Anal. 92, 2168–2181 (2013)
Wollkind, D.J., Collings, J.B., Logan, J.: Metastability in a temperature-dependent model system for predator–prey mite outbreak interactions on fruit trees. Bull. Math. Biol. 50, 379–409 (1988)
Zhou, J., Kim, C.-G., Shi, J.: Positive steady state solutions of a diffusive Leslie–Gower predator–prey model with Holling type II functional response and cross-diffusion. Discrete Contin. Dyn. Syst. 34, 3875–3899 (2014)
Acknowledgments
Qi Wang is partially supported by NSF-China (Grant No. 11501460) and the Project (No. 15ZA0382) from Department of Education, Sichuan China.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Michael Ward.
Appendix
Appendix
In this Appendix, we determine the direction of the pitchfork branch \(\Gamma _{k}(s)\) for system (3.1) with general population kinetics. According to Theorem 4.2 and Corollary 1, the only stable local branch must be \(\Gamma _{k_0}(s)\), \(s\in (-\delta ,\delta )\), and its stability is determined by the turning direction, while all the rest are always unstable. We see that each bifurcation branch \(\Gamma _{k}\) turns to the right if \(\mathcal K_2>0\) and it turns to the left if \(\mathcal K_2<0\). Therefore, we shall need to evaluate the sign of \(\mathcal K_2\) in order to determine the stability of the stationary solution to (1.1).
Our calculations apply for each \(k\in \mathbb N^+\), and in order to evaluate \(\mathcal {K}_2\), we proceed as follows. By the asymptotic expansions (4.1)–(4.4), we equate \(s^3\)-terms in the second equation of (3.1)
In order to obtain closed formula of \(\mathcal K_2\), we collect the following identities which can be easily obtained through straightforward calculations,
and
Multiplying (6.1) by \(\cos \frac{k\pi x}{L}\) and integrating it over (0, L) by parts, we conclude from (6.2)–(6.4) that
where we denote
and
Equating \(s^3\)-terms in the first equation of (3.1), we have that
Multiplying (6.6) by \(\cos \frac{k\pi x}{L}\) and integrating it over (0, L) lead us to
where
On the other hand, since \((\varphi _2,\psi _2)\in \mathcal {Z}\) as defined in (3.14), we have that
Combining (6.7) and (6.8) gives
and solving (6.9) gives
where
Finally, we need to evaluate \(\int _0^L\varphi _1\hbox {d}x\), \(\int _0^L\psi _1\hbox {d}x\), \(\int _0^L\varphi _1\cos \frac{2k\pi x}{L}\hbox {d}x\), and \(\int _0^L\psi _1\cos \frac{2k\pi x}{L}\hbox {d}x\).
Integrating (4.5) and (4.7) over (0, L), we have that
Solving (6.11) gives us
where
Multiplying (4.5) and (4.7) by \(\cos \frac{2k\pi x}{L}\) and then integrating them over (0, L) by part, we have that
where
Solving (6.13) gives us
where
and
We point out that \(E_0\) is always nonzero thanks to (3.12).
In light of (6.10), (6.12), and (6.14), we are able to represent \(\mathcal K_2\) in (6.5) in terms of system parameters.
Rights and permissions
About this article
Cite this article
Wang, Q., Song, Y. & Shao, L. Nonconstant Positive Steady States and Pattern Formation of 1D Prey-Taxis Systems. J Nonlinear Sci 27, 71–97 (2017). https://doi.org/10.1007/s00332-016-9326-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-016-9326-5