Rigorous Statistical Bounds in Uncertainty Quantification for One-Layer Turbulent Geophysical Flows

Abstract

Statistical bounds controlling the total fluctuations in mean and variance about a basic steady-state solution are developed for the truncated barotropic flow over topography. Statistical ensemble prediction is an important topic in weather and climate research. Here, the evolution of an ensemble of trajectories is considered using statistical instability analysis and is compared and contrasted with the classical deterministic instability for the growth of perturbations in one pointwise trajectory. The maximum growth of the total statistics in fluctuations is derived relying on the statistical conservation principle of the pseudo-energy. The saturation bound of the statistical mean fluctuation and variance in the unstable regimes with non-positive-definite pseudo-energy is achieved by linking with a class of stable reference states and minimizing the stable statistical energy. Two cases with dependence on initial statistical uncertainty and on external forcing and dissipation are compared and unified under a consistent statistical stability framework. The flow structures and statistical stability bounds are illustrated and verified by numerical simulations among a wide range of dynamical regimes, where subtle transient statistical instability exists in general with positive short-time exponential growth in the covariance even when the pseudo-energy is positive-definite. Among the various scenarios in this paper, there exist strong forward and backward energy exchanges between different scales which are estimated by the rigorous statistical bounds.

A Transient Statistical Instability of the Barotropic System with Topography

In this appendix, we illustrate the transient statistical instability existing generally in the topographic barotropic flows from the linearized statistical equations. It can be seen that the system contains strong internal growth of uncertainty among a wide parameter regimes despite the saturated statistical stability bounds achieved in the main text. In the transient statistical stability analysis, we calculate the maximum growth rate in the covariance equation near a statistically steady-state solution. The positive growth rate characterizes the increase in uncertainty represented by the ensemble variance. Typically, this can illustrate the exponential growth of the ensemble ‘spread’ in the transient state with a Gaussian initial distribution assigned to the group of particles.

In the barotropic flow with topography, the instability is mainly due to the energy transfer between the large-scale flow U and the small-scale eddies $\omega$. For simplicity, in analysis it is useful to consider the layered topographic modes (Majda and Wang 2006) only along x-direction

$$\begin{aligned} h=\sum _{k=-N}^{N}\hat{h}_{k}\mathrm{e}^{ikx},\qquad \omega =\sum _{k=-N}^{N}\hat{\omega }_{k}\mathrm{e}^{ikx}. \end{aligned}$$

The above layered modes with wavenumbers $\mathbf {k}=\left( k,0\right)$ form a closed system. The quadratic nonlinear interactions in (2.7) between small-scale layered modes, $\nabla ^{\bot }\psi \cdot \nabla \omega$ and $\nabla ^{\bot }\varPsi \cdot \nabla \left( \omega -\mu \psi \right)$, are eliminated since all the wavenumbers are along the same direction. This simplification enables us to focus on the interactions between the large mean flow and small-scale modes due to topographic stress and beta-effect. Therefore, the original fluctuation equation can be effectively simplified in the spectral domain as

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}\hat{\omega }_{k}}{\mathrm{d}t}&=i\beta \frac{\mu +k^{2}}{\mu k}\hat{\omega }_{k}-i\frac{\mu k}{\mu +k^{2}}\hat{h}_{k}U\left( t\right) -ik\hat{\omega }_{k}U\left( t\right) ,\\ \frac{\mathrm{d}U}{\mathrm{d}t}&=\sum _{k=-N}^{N}\frac{\hat{h}_{k}^{*}}{ik}\hat{\omega }_{k}. \end{aligned} \end{aligned}$$

(A.1)

Notice that the state variables $\left( U,\omega \right)$ in (A.1) are already the fluctuation components about the steady-state solution $\left( V_{\mu },Q_{\mu }\right)$ defined in (2.4). The nonlinear coupling between the mean flow and vortical modes is from the last term in the first equation. The chaotic dynamics with deterministic instability in the layered model is discussed in Chapter 5 of Majda and Wang (2006). Next, we consider the statistical growth rate in the transient state from an Gaussian initial distribution due to the instability from topography using the layered model (A.1).

1.1 A.1 Transient Statistical Instability in the Layered Model

We investigate the statistical instability from the statistical formulation of the layered system (A.1), where no nonlinear interactions between small-scale modes are included. Thus, the only source of instability is from the interaction between large and small scales due to the topographic stress h. For a better formulation of the linearized system, we decompose the complex spectral modes into the real and imaginary parts

$$\begin{aligned} \hat{\omega }_{k}=a_{k}+ib_{k},\quad \hat{h}_{k}=h_{k}^{r}+ih_{k}^{i},\qquad k=1,\cdots ,N, \end{aligned}$$

with $\hat{\omega }_{-k}=\hat{\omega }_{k}^{*},\hat{h}_{-k}=\hat{h}_{k}^{*}$. Thus, the state variables of interest form the vector $\mathbf {u}=\left( a_{1},b_{1},\cdots ,a_{N},b_{N},U\right) ^\mathrm{T}$ of length $2N+1$. From the layered equation (A.1), the deterministic dynamics of each wavenumber k can be written as

$$\begin{aligned} \frac{\mathrm{d}a_{k}}{\mathrm{d}t}= & {} -\beta \frac{\mu +k^{2}}{\mu k}b_{k}+\frac{\mu k}{\mu +k^{2}}h_{k}^{i}U+kb_{k}U,\nonumber \\ \frac{\mathrm{d}b_{k}}{\mathrm{d}t}= & {} \beta \frac{\mu +k^{2}}{\mu k}a_{k}-\frac{\mu k}{\mu +k^{2}}h_{k}^{r}U-ka_{k}U, \nonumber \\ \frac{\mathrm{d}U}{\mathrm{d}t}= & {} 2\sum _{k=1}^{N}k^{-1}\left( h_{k}^{r}b_{k}-h_{k}^{i}a_{k}\right) . \end{aligned}$$

(A.2)

The small-scale spectral modes $\left( a_{k},b_{k}\right)$ are decoupled with each other in (A.2), while the mean flow U combines all the feedbacks from small scales through the topographic stress. The only nonlinearity of the above system comes from the mean flow and vortical modes interactions, $\left( a_{k}U,b_{k}U\right)$.

To consider the statistical evolution of uncertainty in the system (A.2), it is useful to derive the dynamical equation of the covariance matrix $R=\left\langle \mathbf {u}^{\prime }\mathbf {u}^{\prime T}\right\rangle$ for fluctuations $\mathbf {u}^{\prime }$ away from a statistically steady mean state $\bar{\mathbf {u}}_{k}=\left( \bar{a}_{k},\bar{b}_{k},\bar{U}\right)$. The exponential growth rate of the linearized covariance R illustrates how the uncertainty from the initial data grows due to the instability in the system; and the statistical mean state is the fixed point that a steady-state solution can be reached. The linearized part of the covariance dynamics for R can be written abstractly as

$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}=L_{\bar{\mathbf {u}}}R+RL_{\bar{\mathbf {u}}}^\mathrm{T}+h.o.t.,\quad R=R^\mathrm{T}=\begin{bmatrix}\ddots&&\vdots \\&\begin{array}{cc} \overline{a_{k}^{\prime 2}} &{} \overline{a_{k}^{\prime }b_{k}^{\prime }}\\ \overline{b_{k}^{\prime }a_{k}^{\prime }} &{} \overline{b_{k}^{\prime 2}} \end{array}&\cdots&\begin{array}{c} \overline{a_{k}^{\prime }U^{\prime }}\\ \overline{b_{k}^{\prime }U^{\prime }} \end{array}\\&\vdots&\ddots&\vdots \\ \cdots&\begin{array}{cc} \overline{U^{\prime }a_{k}^{\prime }}&\overline{U^{\prime }b_{k}^{\prime }}\end{array}&\cdots&\overline{U^{\prime 2}} \end{bmatrix}_{\left( 2N+1\right) \times \left( 2N+1\right) }. \end{aligned}$$

Above h.o.t. represents the third-order moment feedbacks to the covariance (see details as in Majda and Qi 2016, 2017a). In the linear statistical stability analysis, we assume a Gaussian distribution in the initial ensemble so the third-order moments are zero initially, and observe the growth in the covariance matrix in the transient state. Thus, the effects of higher-order moments are small in the beginning time. The linearized coefficient $L_{\bar{\mathbf {u}}}$ related to the statistical mean state $\bar{\mathbf {u}}$ can be written in a block-diagonal structure in the small-scale modes

$$\begin{aligned} L_{\bar{\mathbf {u}}}=\begin{bmatrix}\ddots&0&\vdots \\&\begin{array}{cc} 0 &{} -\beta \frac{\mu +k^{2}}{\mu k}+k\bar{U}\\ \beta \frac{\mu +k^{2}}{\mu k}-k\bar{U} &{} 0 \end{array}&\cdots&\begin{array}{c} \frac{\mu k}{\mu +k^{2}}h_{k}^{i}+k\bar{b}_{k}\\ -\frac{\mu k}{\mu +k^{2}}h_{k}^{r}-k\bar{a}_{k} \end{array}\\ 0&\vdots&\ddots&\vdots \\ \cdots&\begin{array}{cc} -2k^{-1}h_{k}^{i}&2k^{-1}h_{k}^{r}\end{array}&\cdots&0 \end{bmatrix}_{\left( 2N+1\right) \times \left( 2N+1\right) }. \end{aligned}$$

(A.3)

Therefore, the linear instability can be characterized by the positive eigenvalues of the linearized coefficient matrix $L_{\bar{\mathbf {u}}}$. The positive eigenvalues illustrate the exponential growth rate of the uncertainty in covariance from the initial Gaussian ensemble around the presumed steady-state statistical mean $\bar{\mathbf {u}}=\left( \bar{a}_{k},\bar{b}_{k},\bar{U}\right)$. (A relation in the mean states is proposed next based on the steady-state mean equations.) Large growth rate implies that the growing uncertainty in variances may drive the system to diverge from the original statistical mean $\bar{\mathbf {u}}$. Especially, if we set zero mean state $\bar{a}_{k}=\bar{b}_{k}=\bar{U}=0$, the eigenvalues of the above matrix $L_{\bar{\mathbf {u}}}$ are the same with the local Lyapunov exponents of the original linearized system (A.2) that characterize the separation rate of two trajectories with close initial states.

1.1.1 A.1.1 Transient Growth Rate in Single-Mode Interaction

We begin with the simple setup that there is one single nonzero topographic mode $\hat{h}_{k}$ and small-scale mode $\left( a_{k},b_{k}\right)$ interacting with the mean flow U. Then, all the other modes $\left( a_{l},b_{l}\right)$ with $l\ne k$ remain zero for all the time from the decoupled dynamics in (A.2) (see Chapter 5 of Majda and Wang 2006). Therefore, the linearized coefficient matrix $L_{\bar{\mathbf {u}},k}$ becomes just a $3\times 3$ matrix

$$\begin{aligned} L_{\bar{\mathbf {u}},k}=\begin{bmatrix}0&-\beta \frac{\mu +k^{2}}{\mu k}+k\bar{U}&\frac{\mu k}{\mu +k^{2}}h_{k}^{i}+k\bar{b}_{k}\\ \beta \frac{\mu +k^{2}}{\mu k}-k\bar{U}&0&-\frac{\mu k}{\mu +k^{2}}h_{k}^{r}-k\bar{a}_{k}\\ -2k^{-1}h_{k}^{i}&2k^{-1}h_{k}^{r}&0 \end{bmatrix}. \end{aligned}$$

Furthermore, we consider a special form of topography with only nonzero imaginary part

$$\begin{aligned} h_{k}^{r}\equiv 0,\;h_{k}^{i}=H\;\Rightarrow \;\bar{a}_{k}\equiv 0,\;\bar{b}_{k}=\frac{\frac{\mu k}{\mu +k^{2}}\bar{U}}{\frac{\beta }{\mu }\frac{\mu +k^{2}}{k}-k\bar{U}}H. \end{aligned}$$

The coefficient matrix $L_{\bar{\mathbf {u}},k}$ first has one zero eigenvalue $\lambda =0$, and the other two eigenvalues can be solved by

$$\begin{aligned} \begin{aligned} \lambda ^{2}&=-\left( \frac{\beta }{\mu }\frac{k^{2}+\mu }{k}-k\bar{U}\right) ^{2}-2H\left( \frac{\mu }{k^{2}+\mu }H+\bar{b}_{k}\right) \\&=2H^{2}\left[ k^{2}\bar{U}/\beta -\left( 1+\mu ^{-1}k^{2}\right) \right] ^{-1}-\left( \frac{\beta }{\mu }\frac{k^{2}+\mu }{k}-k\bar{U}\right) ^{2}. \end{aligned} \end{aligned}$$

(A.4)

Statistical instability takes place when the right hand side above is positive. We can first find an immediate result that a necessary condition for the existence of linear instability occurs when

$$\begin{aligned} k^{2}\bar{U}/\beta -\left( 1+\mu ^{-1}k^{2}\right)>0\;\Leftrightarrow \;\bar{U}+V_{\mu }>\beta k^{-2}, \end{aligned}$$

in the northern hemisphere $\beta >0$. This shows a lower bound for the total mean flow $\bar{U}+V_{\mu }$ to induce instability. The growth rate with single-mode interaction will also be illustrated through numerical results next.

As one specific example, we consider the case with zero steady mean state, $\bar{a}_{k}=\bar{b}_{k}=\bar{U}=0$. The eigenvalues (Lyapunov exponents) in (A.4) can be simplified as

$$\begin{aligned} \lambda ^{2}=-\frac{2H^{2}}{1+\mu ^{-1}k^{2}}-\beta ^{2}\left( \frac{k}{\mu }+\frac{1}{k}\right) ^{2}. \end{aligned}$$

Explicitly, we can calculate the regime of linear instability among the values of

$$\begin{aligned} -k^{2}<\mu <-\left[ \left( \frac{2H^{2}}{\beta ^{2}}\right) ^{\frac{1}{3}}k^{-4/3}+k^{-2}\right] ^{-1}\equiv \mu _{c}. \end{aligned}$$

(A.5)

The growth rate $\lambda \rightarrow \infty$ as $\mu \rightarrow -k^{2}$; and the growth rate $\lambda \rightarrow 0$ as $\mu \rightarrow \mu _{c}$. Obviously the beta-effect works as a stabilizing effect so that larger value of $\beta$ makes smaller regime of instability. On the other hand, the larger values of the topographic strength H will induce stronger instability into the system when the system becomes unstable. (A.5) is consistent with the deterministic linear instability discussed in Chapter 5 of (Majda and Wang 2006).

1.1.2 A.1.2 Relations in the Statistical Steady Mean State

Here, we propose a special set of values in the statistical mean $\left( \bar{a}_{k},\bar{b}_{k},\bar{U}\right)$ for calculating the transient growth rate from the steady-state solution of the mean equations. The statistical mean dynamics can be derived by taking ensemble average about the original equations (A.2) so that

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}\bar{a}_{k}}{\mathrm{d}t}&=-\beta \frac{\mu +k^{2}}{\mu k}\bar{b}_{k}+\frac{\mu k}{\mu +k^{2}}h_{k}^{i}\bar{U}+k\bar{b}_{k}\bar{U}+k\overline{b_{k}^{\prime }U^{\prime }},\\ \frac{\mathrm{d}\bar{b}_{k}}{\mathrm{d}t}&=\beta \frac{\mu +k^{2}}{\mu k}\bar{a}_{k}-\frac{\mu k}{\mu +k^{2}}h_{k}^{r}\bar{U}-k\bar{a}_{k}\bar{U}-k\overline{a_{k}^{\prime }U^{\prime }},\\ \frac{\mathrm{d}\bar{U}}{\mathrm{d}t}&=2\sum _{k=1}^{N}k^{-1}\left( h_{k}^{r}\bar{b}_{k}-h_{k}^{i}\bar{a}_{k}\right) . \end{aligned} \end{aligned}$$

In statistical steady state, the time derivatives on the left hand side vanish. Especially, we assume a statistical steady state under the homogeneous assumption that there is no cross-covariance in the steady state and the mean flow dynamics vanish at each mode

$$\begin{aligned} h_{k}^{i}\bar{a}_{k}=h_{k}^{r}\bar{b}_{k},\quad \overline{a_{k}^{\prime }U^{\prime }}=\overline{b_{k}^{\prime }U^{\prime }}=0, \end{aligned}$$

which can also be guaranteed automatically from the initial setup. The above relations assume a homogeneous steady state without cross-covariances between modes in different scales. With the assumptions, the statistical mean of each small-scale mode can be determined by the large-scale flow mean $\bar{U}$,

$$\begin{aligned} \bar{a}_{k}=\frac{\frac{\mu k}{\mu +k^{2}}\bar{U}}{\frac{\beta }{\mu }\frac{\mu +k^{2}}{k}-k\bar{U}}h_{k}^{r},\quad \bar{b}_{k}=\frac{\frac{\mu k}{\mu +k^{2}}\bar{U}}{\frac{\beta }{\mu }\frac{\mu +k^{2}}{k}-k\bar{U}}h_{k}^{i}, \end{aligned}$$

(A.6)

The group of steady-state means (A.6) from the homogeneous assumption may not be unique. We adopt this kind of solutions to illustrate the instability features of the system as a typical example.

Fig. 14

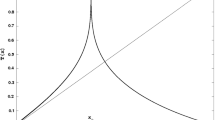
Transient growth rate from the largest positive eigenvalue of the linearized coefficient matrix in the covariance equation with $\beta =1,\bar{U}=0$. The four solid lines are the growth rates from single-mode interaction with wavenumber $k=1,2,3,4$ separately as in (A.4). The dotted-dashed line is from the combined interaction of the full matrix (A.3) of all first four modes. The right panel shows results with different values of $\beta =0,0.1,0.5,1,5$

1.2 A.2 Numerical Illustration of the Statistical Instability with Exponential Growth Rate

In this part, we further illustrate the transient statistical instability analyzed above with simple numerical results. We compare the exponential growth rates from both the single topography interaction and the full linearized coefficient matrix $L_{\bar{\mathbf {u}}}$ in (A.3) where mean flow interaction with multiple small-scale spectral modes is included.

Fig. 15

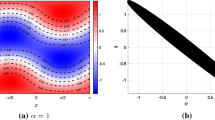
Transient growth rates from the largest positive eigenvalue of the linearized coefficient matrix in the covariance equation with changing $\bar{U}=-\,1,0,1,1.5,2$. The second row shows the exponential growth rates with changing steady mean state $\bar{U}$ and parameter $\mu$ with $\beta =1$. The interactions with first two wavenumbers $k=1,2$ are shown separately. a Transient growth rates with first four modes interacting with different $\bar{U}=-\,1,0,1,1.5,2$. b Transient growth rates with changing steady mean state ${\bar{U}}$ and parameter $\mu$

1.2.1 A.2.1 Transient Growth Rate with Zero Mean Fluctuation

First, we consider the case with zero steady mean fluctuation, $\bar{a}_{k}=\bar{b}_{k}=\bar{U}=0$. The exponential growth here illustrates the increase in the variance from an initial Gaussian distribution with no bias in the mean. Figure 14 shows the exponential growth rates from interactions with the leading four wavenumbers $k=1,2,3,4$. The layered topographic is taken as $\hat{h}_{k}=Hk^{-2}\mathrm{e}^{-i\theta _{k}}$ in each spectral mode with uniform phase shift $\theta _{k}=\frac{\pi }{4}$ in the same zonal structure as in the main text. In the single-mode interaction case, consistent with the analysis result in (A.5), large exponential growth will be induced when the parameter $\mu$ reaches the resonance points $-\,k^{2}$, and instability vanishes after the critical value $\mu _{c}$. Also notice that there exists overlap between the unstable regimes of different wavenumbers.

We also compute the maximum eigenvalue directly from the full linearized coefficient matrix (A.3) in the dotted-dashed line in Fig. 14. In this case, the feedbacks to the mean flow from each small-scale mode are combined together. Again the growth rate becomes large near the resonance points $\mu =-k^{2}$. And the growth rate gets reduced among the overlapped regimes of different single-mode instability. In the regime $-\,1<\mu <0$ interactions with other smaller-scale modes have little effect on the final growth rate with single-mode interaction. Especially, note that the unbounded growth rate is one-sided. Positive growth rate only appears when $\mu$ approaches $-\,k^{2}$ from the right side, while weaker instability is generated from the left side. Similar phenomena can be observed from the model simulations for statistical instability in the main text.

The effect with different values of $\beta$ in the linear stability is shown in the right panel in Fig. 14. Here, we test different values $\beta =0,0.1,0.5,1,5$. Consistent with the results before, the beta-effect can serve as a stabilizing factor. As the value of $\beta$ increases, the size of the unstable regime with a positive growth rate gets reduced, while the entire regime $-\,1<\mu <0$ is unstable when $\beta =0$.

1.2.2 A.2.2 Transient Growth rate with Nonzero Mean Fluctuation

Further, we show the statistical growth rate with nonzero mean state $\bar{U}\ne 0$. In Fig. 15a, as a further comparison, we show the exponential growth rate of multiple modes interaction with dependence on steady-state mean flow value $\bar{U}$. Compared with the previous case with zero mean state $\bar{U}=0$, positive exponential growth rates are also induced in the statistically nonlinear stable regime $\mu >0$. The various regimes of positive growth rates show the large instability existing with the topographic barotropic flow in the general sense.

Further in Fig. 15b, we plot the regimes of unstable growth rates with different steady mean values $\bar{U}$ and parameter $\mu$. As the wavenumber k increases, the unstable regime becomes narrower. As the steady mean state $\left| \bar{U}\right|$ increases, the instability reduces and finally vanishes. And especially in regime $\bar{U}>0$, there exist two separated regimes for $\mu >0$ and $\mu <0$ with positive growth rates. Compared with the single mode $k=1$ case, the unstable regime with positive exponential growth rate gets narrowed down by including multiple small-scale mode interactions. Still the two branches of transient statistical unstable regimes exist.