Distributions of the budget sets: an axiomatic analysis

Abstract

Economic systems generate various distributions of opportunity sets for individuals to choose consumption bundles. This paper presents an axiomatic analysis of distributions of opportunity sets. We introduce three properties for distributions of opportunity sets, and show that they axiomatically characterize the distributions of the budget sets in the market economy. We also axiomatically characterize the distribution of equal-income budget sets by considering two equity properties.

Appendix

To prove Theorem 1, it is useful to introduce the following property:

Tightness A distribution of opportunity sets $(S_1, \ldots ,S_n) \in \mathcal {S}^n$ is tight if for every $i \in N$, and every $x_i \in \partial ^+ S_i$, there exists $x_{-i} \in \Pi _{j\ne i} \partial ^+ S_j$ such that $\sum _{h\in N} x_h = \omega$.

Notice that Tightness implies Freedom of Choice under Inter-dependence.

The proof of Theorems 1 relies on the following sequence of lemmas.

Lemma 1

If $(S_1,\ldots ,S_n)\in \mathcal S^n$ satisfies Freedom of Choice under Inter-dependence and Omnipresent Freedom of Choice, then it satisfies Tightness.

Proof

Suppose that $(S_1,\ldots ,S_n)\in \mathcal S^n$ satisfies Freedom of Choice under Inter-dependence and Omnipresent Freedom of Choice, but violates Tightness. Then, there exist $i\in N$ and $x_i \in \partial ^+S_i$ such that for all $x_{-i} \in \Pi _{j\ne i} \partial ^+S_j$, $x_i +\sum _{j\ne i}x_j \ne \omega .$ By Freedom of Choice under Inter-dependence, however, there exists $y_{-i} \in \Pi _{j\ne i} \partial ^+S_j$ with $x_i+\sum _{j\ne i}y_j < \omega .$ Define $z \in \mathbb R_+^{nk}$ by $z_i :=x_i+\frac{1}{n}(\omega -x_i-\sum _{j\ne i}y_j) >x_i$ and $z_j :=y_j+\frac{1}{n}(\omega -x_i-\sum _{j\ne i}y_j) >y_j$. Then, z is a feasible allocation, but for all $h\in N$, $z_h \notin S_h$. This contradicts the supposition that the given distribution of opportunity sets satisfies Omnipresent Freedom of Choice. $\square$

For each $x_i \in \mathbb R_+^k$ and each $\varepsilon >0$, define $V(x_i,\varepsilon ) := \{ y_i \in \mathbb R_+^k \mid |y_{i\ell }-x_{i\ell } | < \varepsilon \text{ for } \text{ every } \ell \in K \}$. Recollect that $\Omega = \{ a \in \mathbb R_+^k \mid a \le \omega \}$.

Lemma 2

Suppose that $(S_1,\ldots ,S_n)\in \mathcal S^n$ satisfies Freedom of Choice under Inter-dependence and Omnipresent Freedom of Choice. For every $i\in N$ and every $x_i \in S_i$, if

$$\begin{aligned} V(x_i,\varepsilon ) \cap (\mathbb R_+^k {\setminus } S_i) \cap \Omega \ne \emptyset \end{aligned}$$

for every $\varepsilon >0$, then $x_i \in \partial ^+ S_i$.

Proof

Suppose that $(S_1,\ldots ,S_n)\in \mathcal S^n$ satisfies Freedom of Choice under Inter-dependence and Omnipresent Freedom of Choice. Since the distribution of opportunity sets is feasible, $S_i \subseteq \Omega$ for every $i\in N$. By Lemma 1, the distribution satisfies Tightness. Suppose, on the contrary, that there exist $i\in N$ and $x_i \in S_i$ such that $V(x_i,\varepsilon ) \cap (\mathbb R_+^k {\setminus } S_i) \cap \Omega \ne \emptyset ,$ for every $\varepsilon >0$, and yet $x_i \notin \partial ^+ S_i$. Then, there exists $z_i \in \partial ^+S_i$ with $z_i >x_i$. By Tightness, there is $z_{-i} \in \Pi _{j\ne i} \partial ^+S_j$ such that $z_i+\sum _{j\ne i}z_j=\omega$.

Define the allocation $t\in \mathbb R_+^{nk}$ by $t_i:=x_i$ and $t_j:= z_j+\frac{1}{n-1}(z_i-x_i) > z_j$ for every $j\ne i$. Then, t is a feasible allocation and $t_j \notin S_j$ for every $j\ne i$.

Let $K(x_i) := \{ \ell \in K \mid \omega _\ell > x_{i\ell } \}$. If $K(x_i) = \emptyset$, then $x_{i\ell } =\omega _\ell$ for every $\ell \in K$, and comprehensiveness of $S_i$ implies $S_i = \Omega$. Hence, we have $(\mathbb R_+^k {\setminus } S_i) \cap \Omega = \emptyset$, which is a contradiction. Thus, $K(x_i) \ne \emptyset$. For each $\varepsilon >0$, define the consumption bundle $x_i(\varepsilon ) \in \mathbb R_+^k$ by

$$\begin{aligned} x_{i\ell }(\varepsilon ) = \left\{ \begin{array}{ll} x_{i\ell } +\varepsilon &{}\, \text{ if } \ell \in K(x_i) \\ x_{i\ell } &{}\, \text{ otherwise. } \end{array} \right. \end{aligned}$$

Claim: $x_i(\varepsilon ) \notin S_i$ for every $\varepsilon >0$. Suppose, on the contrary, that $x_i(\varepsilon ) \in S_i$ for some $\varepsilon >0$. Let $y_i \in V(x_i,\varepsilon ).$ If $y_{i\ell } > \omega _{\ell }$ for some $\ell \in K$, then $y_i \notin \Omega$. Otherwise, $y_{i\ell } \le \omega _{\ell }$ for all $\ell \in K$. Then, $y_i \le x_i(\varepsilon ) \in S_i$. It follows from comprehensiveness of $S_i$ that $y_i \in S_i$ and hence $y_i \notin (\mathbb R_+^k {\setminus } S_i)$. Therefore, we have $V(x_i,\varepsilon ) \cap (\mathbb R_+^k {\setminus } S_i) \cap \Omega = \emptyset$, which is a contradiction. Thus, the claim has been proven.

For each $\ell \in K(x_i)$, define $J(\ell ) := \{ j\in N{\setminus } \{i\} \mid t_{j\ell } >0\}$. Since $\ell \in K(x_i)$, we have $t_{i\ell } = x_{i\ell } < \omega _{\ell }$. Together with $\sum _{h\in N} t_{h\ell } = \omega _\ell$, it follows that $J(\ell ) \ne \emptyset$. Let $\varepsilon _{\ell } >0$ be such that $t_{j\ell } - \varepsilon _{\ell } \ge 0$ for every $j \in J(\ell )$.

For every $j \in N{\setminus } \{i\}$, since $S_j$ is closed and $t_j \notin S_j$, it follows that there exists $\varepsilon _j >0$ such that $V(t_j,\varepsilon _j) \cap S_j = \emptyset .$

Let

$$\begin{aligned} \varepsilon ^* := \min \left\{ \min _{\ell \in K(x_i)} \varepsilon _{\ell }, \min _{j\in N{\setminus } \{i\} } \varepsilon _j \right\} . \end{aligned}$$

Define the allocation $v \in \mathbb R_+^{nk}$ by

$$\begin{aligned} v_{i\ell }= & {} \left\{ \begin{array}{ll} x_{i\ell } +|J(\ell )| \frac{\varepsilon ^*}{2} &{} \text{ if } \ell \in K(x_i) \\ x_{i\ell } &{} \text{ otherwise } \end{array} \right. \\ \text{ and } \text{ for } \text{ every } j \ne i, \\ v_{j\ell }= & {} \left\{ \begin{array}{ll} t_{j\ell } - \frac{\varepsilon ^*}{2} &{} \text{ if } \ell \in K(x_i) \text{ and } j\in J(\ell ) \\ t_{j\ell } &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

Then, v is a feasible allocation. By the above claim, we have $v_i \notin S_i$. For every $j \in N{\setminus } \{i\}$, because $\frac{\varepsilon ^*}{2} < \varepsilon ^* \le \varepsilon _j$ and $V(t_j,\varepsilon _j) \cap S_j = \emptyset$, it follows that $v_j \notin S_j$. This contradicts the supposition that the given distribution $(S_1, \ldots , S_n)$ satisfies Omnipresent Freedom of Choice. $\square$

At this point, it may be noted that the property, No Opportunity-Freedom Enhancing Coordination, implies the following statement which will be useful in proving the subsequent lemmas:

For every $M \subseteq N$, if $x_i \in \partial ^+ S_i$ for all $i \in M$, then there exists no $(y_i)_{i\in M} \in \Pi _{i\in M} S_i$ such that $\sum _{i\in M} y_i > \sum _{i\in M} x_i$.

The proof of this implication is straightforward and we omit it.

Lemma 3

If $(S_1,\ldots ,S_n)\in \mathcal S^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination, then $S_i$ is convex for all $i\in N$.

Proof

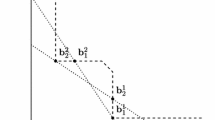
Assume that $(S_1,\ldots , S_n) \in \mathcal {S}^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination. By Lemma 1, $(S_1,\ldots ,S_n)$ satisfies Tightness. Suppose, on the contrary, that $S_i$ is not convex for some $i\in N$. Then, there exist $x_i, y_i \in \partial ^+ S_i$ such that $z_i:=\frac{1}{2}(x_i+y_i) \notin S_i$. Since $x_i, y_i \in S_i$ and S is feasible, it follows that $x_i, y_i \in \Omega$ and hence $z_i \in \Omega$ as well. Let $\alpha := \max \{ \alpha ' \in \mathbb R \mid \alpha ' z_i \in S_i \}$. Because $S_i$ is compact and comprehensive, such $\alpha$ exists and $0\le \alpha <1$. Let $v_i := \alpha z_i$. It is clear that for every $\varepsilon >0$, $V(v_i,\varepsilon ) \cap (\mathbb R_+^k {\setminus } S_i) \cap \Omega \ne \emptyset$. By Lemma 2, $v_i \in \partial ^+ S_i$. It follows from Tightness that there exist $x_{-i}, y_{-i}, v_{-i} \in \Pi _{j\ne i} \partial ^+S_j$ such that

$$\begin{aligned} x_i+\sum _{ j\ne i} x_j= & {} \omega \\ y_i+\sum _{ j\ne i} y_j= & {} \omega \\ v_i+\sum _{ j\ne i} v_j= & {} \omega . \end{aligned}$$

Since $v_i < \frac{1}{2}(x_i+y_i)$, we have $\sum _{j\ne i} v_j =\omega -v_i > \omega - \frac{1}{2}(x_i+y_i)$. Then, we have

$$\begin{aligned} v_i+ \sum _{ j\ne i} x_j< & {} \frac{1}{2}(x_i+y_i)+\sum _{ j\ne i} x_j \\= & {} x_i+\sum _{ j\ne i} x_j -\frac{1}{2}x_i+\frac{1}{2}y_i \\= & {} \omega -\frac{1}{2}x_i+\frac{1}{2}y_i \\ y_i +\sum _{ j\ne i} v_j> & {} y_i+\omega - \frac{1}{2}(x_i+y_i) \\= & {} \omega -\frac{1}{2}x_i+\frac{1}{2}y_i \end{aligned}$$

Hence,

$$\begin{aligned} y_i + \sum _{ j\ne i} v_j > v_i+ \sum _{ j\ne i} x_j. \end{aligned}$$

Therefore, $(v_i, x_{-i}) \notin \partial ^+ (\sum _{h\in N}S_h)$. But this means that $(S_1,\ldots ,S_n)$ does not satisfy No Opportunity-Freedom Enhancing Coordination, which is a contradiction. $\square$

Lemma 4

If $(S_1, \ldots , S_n) \in \mathcal {S}^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination, then for all $i\in N$, there exist $p^i \in \mathbb {R}_{+}^k{\setminus }\{0\}$ and $m_i \in \mathbb {R}_+$ such that $\partial ^+ S_i \subseteq B^*(p^i,m_i) \cap \Omega$.

Proof

Assume that $(S_1,\ldots , S_n) \in \mathcal {S}^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination. By Lemma 1, $(S_1,\ldots ,S_n)$ satisfies Tightness. It follows from Lemma 3 that $S_i$ is convex for every $i \in N$. Let $i\in N$. By Freedom of Choice under Inter-dependence, $\partial ^+S_i \subset \Omega$. Define $T_i : = \sum _{j\in N{\setminus }\{i\}}S_j$ and $V_i : = \{\omega \}-T_i := \{x_i\in \mathbb {R}^k_+ \mid \exists z_i \in T_i, x_i = \omega -z_i \}$. Since $S_j$ is convex for all $j \in N{\setminus }\{i\}$, $T_i$ is convex, and so is $(-T_i)$. Hence, $V_i$ is convex.

By No Opportunity-Freedom Enhancing Coordination,

$$\begin{aligned} \sum _{j\in N{\setminus }\{i\}}\partial ^+ S_j \subseteq \partial ^+ T_i. \end{aligned}$$

(1)

It follows from Tightness and (1) that

(A) for all $y_i \in \partial ^+ S_i$, there exists $z_i \in \partial ^+ T_i$ such that $y_i + z_i = \omega$.

In order to show that

$$\begin{aligned} V_i \cap \text{ int }S_i = \emptyset , \end{aligned}$$

(2)

suppose, to the contrary, that there exists $x_i \in V_i \cap \text{ int }S_i$. Since $x_i \in \text{ int } S_i$, there exists $x'_i \in \partial ^+S_i$ with $x'_i > x_i$. From (A), there exists $z_i \in \partial ^+ T_i$ such that $x'_i +z_i=\omega$. On the other hand, since $x_i \in V_i$, there exists $z'_i \in T_i$ with $x_i =\omega - z'_i$. Together we have $z'_i = \omega -x_i > \omega -x'_i =z_i$, which contradicts $z_i \in \partial ^+ T_i$. Thus, (2) must hold true.

By the separating hyperplane theorem, there exist $p^i \in \mathbb {R}^k, p^i \ne 0$ and $m_i \in \mathbb {R}$ such that $S_i \subseteq \{ x_i \in \mathbb {R}_+^k \mid p^i\cdot x_i \le m_i\}$ and $V_i \subseteq \{ x_i \in \mathbb {R}_+^k \mid p^i\cdot x_i \ge m_i\}.$ Since $S_i$ is comprehensive, it follows that $p^i > 0$. To complete the proof, we need to show that

$$\begin{aligned} \partial ^+ S_i \subseteq \{ x_i \in \mathbb {R}_+^k \mid p^i\cdot x_i = m_i\} \end{aligned}$$

(3)

Suppose, to the contrary, that there exists $s_i \in \partial ^+ S_i$ such that $p^i \cdot s_i < m_i$. From (A) above, there exists $t_i \in \partial ^+ T_i$ with $s_i + t_i = \omega$. Then, $p\cdot (\omega -t_i) = p\cdot s_i < m_i$. But since $\omega -t_i \in V_i$, we have $p\cdot (\omega -t_i) \ge m_i$. This is a contradiction. Thus, the relation (3) must hold true. $\square$

Lemma 5

If $(S_1, \ldots , S_n) \in \mathcal {S}^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination, then, for all $i\in N$, there exist $p^i \in \mathbb {R}_{++}^k$ and $m_i \in \mathbb {R}_+$ such that $S_i = B(p^i,m_i) \cap \Omega$.

Proof

Assume that $(S_1,\ldots , S_n) \in \mathcal {S}^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination. By Lemma 1, $(S_1,\ldots ,S_n)$ satisfies Tightness. Let $N^0 := \{ i\in N \mid S_i =\{0\} \}$ and $N^* := N{\setminus } N^0$. By Tightness, $N^* \ne \emptyset$. If $i\in N^0$, then it is obvious that $S_i = B(p^i,0) \cap \Omega$ for any $p^i \in \mathbb {R}_{++}^k$. If $N^*=\{i\}$, then Tightness implies that $S_i=\Omega$. Then, it is clear that for any $p^i \in \mathbb {R}_{++}^k$, $S_i = B(p^i,m_i) \cap \Omega$ with $m_i = p^i \cdot \omega$.

In the rest of the proof, we assume that $|N^*| \ge 2$. Let $i\in N^*$. By Lemma 4, there exists $p^i \in \mathbb {R}_{+}^k$ and $m_i \in \mathbb {R}_+$ such that $\partial ^+ S_i \subseteq B^*(p^i,m_i) \cap \Omega$.

Step 1: $m_i >0$.

Suppose, to the contrary, that $m_i=0$. Let $M:= N^* {\setminus } \{i\} \ne \emptyset$. We will show that $\sum _{j\in M}S_j \supseteq \Omega$. Suppose, to the contrary, that there exists $y_0 \in \mathbb {R}_+^k$ such that $y_0 \le \omega$, but $y_0 \notin \sum _{j\in M}S_j$. Since $\sum _{j\in M}S_j$ is closed, there exists $z_0 \in \mathbb {R}_+^k$ with $z_0 \ll \omega$ and $z_0 \notin \sum _{j\in M}S_j$. For each $j \in M$, define $\lambda _j \in \mathbb {R}_+$ by

$$\begin{aligned} \lambda _j := \max \{ \lambda \in \mathbb {R}_+ \mid \lambda z_0 \in S_j \}. \end{aligned}$$

By definition, $\sum _{j \in M} \lambda _j z_0 = (\sum _{j \in M} \lambda _j) z_0 \in \sum _{j\in M}S_j$. Since $z_0 \notin \sum _{j\in M}S_j$, we must have $\sum _{j \in M} \lambda _j <1$. Define

$$\begin{aligned} \varepsilon := \frac{1-\sum _{j \in M} \lambda _j}{|N^*|-1} >0. \end{aligned}$$

Define an allocation $z \in \mathbb {R}_+^{nk}$ by $z_j := (\lambda _j +\varepsilon )z_0$ for each $j \in M$, and $z_{j'} := (\omega -z_0)/|N{\setminus } M|$ for each $j' \in N{\setminus } M$ (note that $\omega -z_0 \gg 0$ and that $|N{\setminus } M| \ge 1$). Then, $\sum _{j\in N} z_j=\omega$. However, from the definition of $\lambda _j$, we have $z_j \notin S_j$ for all $j \in M$. Because $S_i \subseteq B(p,0)$ and $p^i >0$, it follows that $z_i \notin S_i$. This is a contradiction with Omnipresent Freedom of Choice of S. Thus, we have shown that $\sum _{j\in M}S_j \supseteq \Omega$. By No Opportunity-Freedom Enhancing Coordination, $\partial ^+ \sum _{j\in M}S_j \supseteq \sum _{j\in M} \partial ^+ S_j$. Therefore, there exists no $(y_j)_{j\in M} \in \Pi _{j\in M} \partial ^+ S_j$ such that $\sum _{j\in M}y_j < \omega$. On the other hand, since $i \notin N^0$, there exists $x_i \in \partial ^+ S_i$ with $x_i > 0$. By Tightness, there exists $(y'_j)_{j\in M} \in \Pi _{j\in M} \partial ^+ S_j$ such that $x_i + \sum _{j\in M} y'_j = \omega$, and hence $\sum _{j\in M} y'_j =\omega -x_i < \omega$. This is a contradiction.

Step 2: $S_i = B(p^i,m_i) \cap \Omega$.

From the proof of Lemma 4, it is enough to show that $S_i \supseteq B(p^i,m_i) \cap X(\omega )$. Suppose, to the contrary, that there exists $x_i \in \mathbb {R}_+^k$ such that $x_i \in B(p^i,m_i) \cap \Omega$ but $x_i \notin S_i$. Since $S_i$ is comprehensive, for all $x'_i \in \mathbb {R}_+^k$ with $x'_i \ge x_i$, $x'_i \notin S_i$. From Step 1, $m_i >0$. Hence one can find $x'_i \in B(p^i,m_i) \cap \Omega$ such that $x'_i \notin S_i$ and $p^i \cdot x'_i >0$. Because $S_i$ is closed in $\mathbb {R}_+^k$, there exists $x_i^* \in \mathbb {R}_+^k$ such that $x_i^* \notin S_i$ and

$$\begin{aligned} p^i \cdot x_i^* < p^i \cdot x'_i \le m_i. \end{aligned}$$

(4)

Next we will show that $(\omega -x_i^*) \notin \sum _{j\in M} S_j$. Suppose, to the contrary, that $(\omega -x_i^*) \in \sum _{j\in M} S_j$. Since $\{ \omega \} -\sum _{j\in M} S_j \subseteq \{ x_0 \in \mathbb R_+^k \mid p^i \cdot x_0 \ge m_i \}$ from the proof of Lemma 4, we have $p^i \cdot [ \omega - (\omega -x_i^*)] \ge m_i$. Hence, $p^i \cdot x_i^* \ge m_i$, which is in contradiction with (4). Thus, it must be true that $(\omega -x_i^*) \notin \sum _{j\in M} S_j$. Then, by a similar argument to the proof of Step 1, we can find a feasible allocation $z \in \mathbb {R}_+^{nk}$ such that $z_h \notin S_h$ for all $h \in N$. This is a contradiction with Omnipresent Freedom of Choice of $(S_1,\ldots ,S_n)$.

Step 3: $p^i \gg 0$.

Suppose that for some good $\ell \in \{ 1,\ldots ,k\}$, $p^i_{\ell }=0$. Then, for all $x_i \in \partial ^+S_i$, $x_{i\ell }=\omega _{\ell }.$ By Tightness,

(B) for all $j \in N^*$ with $j\ne i$, and all $x_j \in \partial ^+S_j$, $x_{j\ell }=0$.

On the other hand, by applying Steps 1 and 2 to each $j\in N^*$ with $j\ne i$, we obtain that for all $j\in N^*$ with $j\ne i$, there exist $p^j \in \mathbb R_+^k$ and $m_j >0$ such that $S_j = B(p^j,m_j) \cap \Omega$. Since $m_j >0$, there exists $x_j \gg 0$ such that $p^j \cdot x_j \le m_j$, and hence $x_j \in S_j$. But then, there exists $x'_j \in \partial ^+S_j$ with $x'_j \ge x_j \gg 0$. This contradicts (B). Thus, it must be true that $p^i \gg 0$. This completes the proof. $\square$

Lemma 6

If $(S_1,\ldots , S_n) \in \mathcal {S}^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination, then there exist $p \in \mathbb {R}_{++}^k$ and $(m_1, \ldots ,m_n) \in \mathbb {R}_+^n$ such that $S_i = B(p,m_i) \cap \Omega$ for all $i\in N$, and $\sum _{i\in N} m_i = p\cdot \omega$.

Proof

Assume that $(S_1,\ldots , S_n) \in \mathcal {S}^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination. By Lemma 1, S satisfies Tightness. Let $N^0 := \{ i\in N \mid S_i =\{0\} \}$ and $N^* := N{\setminus } N^0$. By Tightness, $N^* \ne \emptyset$. It follows from Lemma 5 that for each $i \in N^*$, there exist $p^i \in \mathbb {R}_{++}^k$ and $m_i \in \mathbb R_{++}$ such that $S_i = B(p^i,m_i) \cap \Omega$.

Claim: for all $i, j\in N^*$, and all $s, t \in K$,

$$\begin{aligned} \frac{p^i_s}{p^i_t} = \frac{p^j_s}{p^j_t}. \end{aligned}$$

Suppose, on the contrary, that $\frac{p^i_s}{p^i_t} \ne \frac{p^j_s}{p^j_t}$ for some $i,j\in N^*$ and some $s,t\in K$. Without loss of generality, let $\frac{p^i_s}{p^i_t} > \frac{p^j_s}{p^j_t}$. Since $p^i, p^j \gg 0$, $m_i, m_j >0$, and $p^i \cdot \omega > m_i$, there exist $\varepsilon > 0$, $a_i \in \partial ^+ S_i$ and $b_j \in \partial ^+ S_j$ such that $a'_i : =(a_{i1}, \ldots , a_{is}-\varepsilon , \ldots , a_{it} + \frac{p^i_s}{p^i_t} \varepsilon , \ldots , a_{in}) \in \partial ^+ S_i$ and $b'_j := (b_{j1}, \ldots , b_{js}+\varepsilon , \ldots , b_{jt} - \frac{p^j_s}{p^j_t} \varepsilon , \ldots , b_{jn}) \in \partial ^+ S_j$. Since S satisfies No Opportunity-Freedom Enhancing Coordination, it follows that $a_i + b_j \in \partial ^+(S_i+S_j)$. On the other hand, because $a'_i \in S_i$ and $b'_j \in S_j$, we have $a'_i + b'_j \in (S_i + S_j)$. Observe that $a'_{ir} + b'_{jr} = a_{ir} + b_{jr}$ for all $r \ne t$, and $a'_{it} + b'_{jt} = a_{it} + b_{jt} + [\frac{p^i_s}{p^i_t}-\frac{p^j_s}{p^j_t})] \varepsilon > a_{it} + b_{jt}$. Therefore, $a_i + b_j \not \in \partial ^+(S_i+S_j)$, which contradicts No Opportunity-Freedom Enhancing Coordination. Thus, it must be true that $\frac{p^i_s}{p^i_t} = \frac{p^j_s}{p^j_t}$ for all $i, j\in N^*$, and all $s, t \in K$.

Choose $i\in N^*$, and define $p := (1, \frac{p^i_2}{p^i_1}, \ldots ,\frac{p^i_n}{p^i_1} )\in \mathbb R_{++}^k$. Then, it follows from the above claim that $p^j =p^j_1p$ for all $j \in N^*$. For each $j\in N^*$, define $m'_i := m_i/p^j_1$. Then, we have $S_j=B(p,m'_i) \cap \Omega$ for all $j\in N^*$. For all $j\in N^0$, let $m'_j = 0$. Then, it is clear that for all $j\in N^0$, $S_j=\{ 0\}=B(p,m'_j) \cap \Omega$.

Let $i\in N^*$, and $x_i \in \partial ^+S_i$. From the proof of Lemma 1, there exist $(x_j)_{j\in N{\setminus } \{i \}} \in \Pi _{j\in N{\setminus } \{i \}} \partial ^+ S_j$ such that $\sum _{h\in N} x_h = \omega$. For all $h\in N$, since $\partial ^+S_h=B^*(p,m'_h) \cap \Omega$, it follows that $p\cdot x_h =m'_h$. Then,

$$\begin{aligned} \sum _{h\in N} m'_h= & {} \sum _{h\in N} p\cdot x_h\\= & {} p\cdot \sum _{h\in N} x_h \\= & {} p\cdot \omega . \end{aligned}$$

This completes the proof. $\square$

Lemma 7

Every distribution of budget sets with positive prices satisfies Freedom of Choice under Inter-dependence, No Opportunity-Freedom Enhancing Coordination, and Omnipresent Freedom of Choice.

Proof

Let $(S_1, \ldots , S_n) \in \mathcal{S}^n$ be a distribution of budget sets with positive prices. Let $p \in \mathbb {R}_{++}^k$ and $(m_1, \ldots , m_n) \in \mathbb {R}_{+}^n$ be such that $S_i =\{ x_i \in \mathbb R_+^k \mid p\cdot x_i \le m_i \text{ and } x_i \le \omega \}$ for every $i \in N$, and $\sum _{i\in N} m_i = p\cdot \omega$.

Freedom of Choice under Inter-dependence: Let $i\in N$ and $x_i \in \partial ^+ S_i$ be given. Then, $p\cdot x_i =m_i$. Define $v :=\omega -x_i$. Notice that $v \ge 0$. If $v = 0$, then $S_j = \{ 0\}$ for all $j \ne i$, and $S_i = X( \omega )$. Clearly, this distribution of opportunity sets is feasible. Consider $v > 0$ next. For every $j\in N$ with $j\ne i$, let $\alpha _j \in \mathbb R_+$ be such that $p\cdot (\alpha _j v) =m_j$, and define $x_j := \alpha _j v$. Then, $x_j \in \partial ^+ S_j$ for every $j\in N$. On the other hand, we have $p\cdot v =p\cdot (\omega -x_i) =\sum _{h\in N} m_h -m_i =\sum _{j\ne i} m_j = \sum _{j\ne i} p\cdot (\alpha _j v)$. Hence, $(1-\sum _{j\ne i} \alpha _j) p\cdot v =0$. Since $p\cdot v >0$, it follows that $\sum _{j\ne i} \alpha _j=1$. Therefore, $\sum _{h\in N} x_h=x_i+\sum _{j\ne i} x_j =x_i +\sum _{j\ne i} \alpha _j v =x_i+v=\omega$. Thus, we have proven that $(S_1, \ldots , S_n)$ satisfies Freedom of Choice under Inter-dependence.

Omnipresent Freedom of Choice: Suppose, on the contrary, that there exists a feasible allocation $x \in Z$ such that for every $i\in N$, $x_i \notin S_i$. Then, for every $i\in N$, $p\cdot x_i > m_i$. Hence, $\sum _{i\in N} p \cdot x_i > \sum _{i\in N} m_i = p\cdot \omega$. However, since $\sum _{i\in N} x_i \le \omega$ and $p\gg 0$, we must have $\sum _{i\in N} p \cdot x_i \le p\cdot \omega$, which is a contradiction. Thus, for every $x\in Z$, there exists $i\in N$ such that $x_i \in S_i$.

No Opportunity-Freedom Enhancing Coordination: Let $M\subseteq N$ be given. For every $y \in \sum _{j\in M} S_j$, there exists $(x_j)_{j\in M} \in \Pi _{j\in M} S_j$ such that $y=\sum _{j\in M} x_j$, and hence $p\cdot y=\sum _{j\in M} p\cdot x_j \le \sum _{j\in M} m_j$. Let $z \in \sum _{j\in M} \partial ^+ S_j$. Obviously, $z \in \sum _{j\in M} S_j$. There exists $(w_j)_{j\in M} \in \Pi _{j\in M} \partial ^+S_j$ such that $z=\sum _{j\in M} w_j$, and thus $p\cdot z=\sum _{j\in M} p\cdot w_j =\sum _{j\in M} m_j$. Since $p \gg 0$, there cannot exist $y \in \sum _{j\in M} S_j$ with $y > z$. Therefore, $z \in \partial ^+ (\sum _{j\in M} S_j)$. We have shown that $\sum _{j\in M} \partial ^+ S_j \subseteq \partial ^+ (\sum _{j\in M} S_j)$. $\square$

Proof of Theorem 1

By Lemma 7, every distribution of budget sets with positive prices satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination. It follows from Lemma 6 that if a distribution of opportunity sets $(S_1, \ldots , S_n) \in \mathcal {S}^n$ satisfies Freedom of Choice under Inter-dependence, Omnipresent Freedom of Choice, and No Opportunity-Freedom Enhancing Coordination, then it is a distribution of budget sets with positive prices. $\square$