Abstract
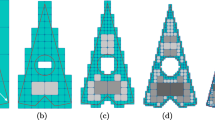
We present a tetrahedral mesh generation algorithm designed for the Lagrangian simulation of deformable bodies. The algorithm’s input is a level set (i.e., a signed distance function on a Cartesian grid or octree). First a bounding box of the object is covered with a uniform lattice of subdivision-invariant tetrahedra. The level set is then used to guide a red green adaptive subdivision procedure that is based on both the local curvature and the proximity to the object boundary. The final topology is carefully chosen so that the connectivity is suitable for large deformation and the mesh approximates the desired shape. Finally, this candidate mesh is compressed to match the object boundary. To maintain element quality during this compression phase we relax the positions of the nodes using finite elements, masses and springs, or an optimization procedure. The resulting mesh is well suited for simulation since it is highly structured, has topology chosen specifically for large deformations, and is readily refined if required during subsequent simulation. We then use this algorithm to generate meshes for the simulation of skeletal muscle from level set representations of the anatomy. The geometric complexity of biological materials makes it very difficult to generate these models procedurally and as a result we obtain most if not all data from an actual human subject. Our current method involves using voxelized data from the Visible Male [1] to create level set representations of muscle and bone geometries. Given this representation, we use simple level set operations to rebuild and repair errors in the segmented data as well as to smooth aliasing inherent in the voxelized data.













Similar content being viewed by others
References
U.S. National Library of Medicine (1994) The Visible Human Project. http://www.nlm.nih.gov/research/visible/
Martins J, Pires E, Salvado R, Dinis P (1998) A numerical model of passive and active behavior of skeletal muscles. Comput Meth Appl Mech Eng 151:419–433
Hirota G, Fisher S, State A, Lee C, Fuchs H (2001) An implicit finite element method for elastic solids in contact. Comput Anim
Cotin S, Delingette H, Ayache N (1996) Real-time volumetric deformable models for surgery simulation. Proc of Vis in Biomed Comput, pp 535–540
Ganovelli F, Cignoni P, Montani C, Scopigno R (2000) A multiresolution model for soft objects supporting interactive cuts and lacerations. Eurographics, pp 271–282
Bro-Nielsen M, Cotin S (1996) Real-time volumetric deformable models for surgery simulation using finite elements and condensation. Comput Graph Forum 15(3):57–66
Fleishmann P, Kosik R, Selberherr S (1999) Simple mesh examples to illustrate specific finite element mesh requirements. In: 8th international meshing roundtable, pp 241–246
Marcum DL (1995) Generation of unstructured grids for viscous flow applications. AIAA
Garimella R, Shephard M (1998) Boundary layer meshing for viscous flows in complex domains. In: 7th international meshing roundtable, pp 107–118
Lohner R, Cebral J (1999) Generation of non-isotropic unstructured grids via directional enrichment. In: 2nd symposium on trends in unstructured mesh generation
Burns G, Glazer AM (1990) Space groups for solid state scientists, 2nd edn. Academic, New York
Osher S, Sethian J (1988) fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. J Comp Phys 79:12–49
Weatherill NP, Hassan O (1994) Efficient three-dimensional delaunay triangulation with automatic point creation and imposed boundary constraints. Int J Numer Meth Eng 37:2005–2039
Shewchuk J (1998) Tetrahedral mesh generation by delaunay refinement. In: Procedings of the 14th annual symposium on computer and geomics, pp 86–95
Cheng SW, Dey TK, Edelsbrunner H, Facello MA, Teng SH (2000) Sliver exudation. J ACM 47(5):883–904
Edelsbrunner H, Guoy D (2002) An experimental study of sliver exudation. Eng Comput 18(3):229–240
Shewchuk J (2002) Constrained Delaunay tetrahedralizations and provably good boundary recovery. In: 11th international meshing roundtable
Schöberl J (1997) NETGEN - an advancing front 2D/3D mesh generator based on abstract rules. Comput Vis Sci 1:41–52
Möller P, Hansbo P (1995) On advancing front mesh generation in three dimensions. Int J Numer Meth Eng 38:3551–3569
Lo SH (1991) Volume Discretization into tetrahedra - I, Verification and orientation of boundary surfaces. Comput Struct 39(5):493–500
Lo SH (1991) Volume discretization into tetrahedra - II, 3D triangulation by advancing front approach. Comput Struct 39(5):501–511
Mavriplis DJ (1995) An advancing front delaunay triangulation algorithm designed for robustness. J Comp Phys 117:90–101
Radovitzky RA, Ortiz M (2000) Tetrahedral mesh generation based in node insertion in crystal lattice arrangements and advancing-front Delaunay triangulation. Comput Meth Appl Mech Eng 187:543–569
Fuchs A (1998) Automatic grid generation with almost regular Delaunay tetrahedra. In: 7th international meshing roundtable, pp 133–148
Shimada K, Gossard D (1995) Bubble mesh: automated triangular meshing of non-manifold geometry by sphere packing. ACM 3rd symposium on solid model and application, pp 409–419
Yamakawa S, Shimada K (2000) High quality anisotropic tetrahedral mesh generation via packing ellipsoidal bubbles. In: 9th international meshing roundtable, pp 263–273
Yamakawa S, Shimada K (2003) Anisotropic tetrahedral meshing via bubble packing and advancing front. Int J Numer Meth Eng 57:1923–1942
Li X, Teng S, Üngör A (1999) Biting spheres in 3D. In: 8th international meshing roundtable, pp 85–95
Li X, Teng S, Üngör A (1999) Biting ellipses to generate anisotropic mesh. In: 8th international meshing roundtable, pp 97–108
Kass M, Witkin A, Terzopoulos D (1987) Snakes: active contour models. Int J Comput Vis, pp 321–331
Miller J, Breen D, Lorensen W, O’Bara R, Wozny M (1991) Geometrically deformed models: a method for extracting closed geometric models from volume data. Comput Graph (SIGGRAPH Proc.), pp 217–226
Sadarjoen IA, Post FH (1997) Deformable surface techniques for field visualization. Eurographics, pp 109–116
Neugebauer P, Klein K (1997) Adaptive triangulation of objects reconstructed from multiple range images. Vis
Grosskopf S, Neugebauer PJ (1998) Fitting geometrical deformable models to registered range images. European Workshop on 3D structure from multiple images of large-scale environments (SMILE), pp 266–274
Kobbelt LP, Vorsatz J, Labsik U, Seidel HP (1999) A shrink wrapping approach to remeshing polygonal surfaces. Eurographics, pp 119–130
Wood Z, Desbrun M, Schröder P, Breen D (2000) Semi-regular mesh extraction from volumes. Vis. pp 275–282
Ohtake Y, Belyaev AG (2002) Dual/primal mesh optimization for polygonized implicit surfaces. In: Proceedings of the 7th ACM Symposium on Solid Model Appl, ACM, New York, pp 171–178
de Figueiredo LH, Gomes J, Terzopoulos D, Velho L (1992) Physically-based methods for polygonization of implicit surfaces. In: Proceedings of the conference on graphic interface, pp 250–257
Velho L, Gomes J, Terzopoulos D (1997) Implicit manifolds, triangulations and dynamics. J Neural Parallel Scientif Comput 15(1–2):103–120
Gloth O, Vilsmeier R (2000) Level Sets as Input for Hybrid Mesh Generation. In: 9th international meshing roundtable, pp 137–146
Arnold A, Salinas S, Asakawa D, Delp S (2000) accuracy of muscle moment arms estimated from MRI-based musculoskeletal models of the lower extremity. Comput Aided Surg 5:108–119
Garner B, Pandy M (1999) A kinematic model of the upper limb based on the visible human project (VHP) image dataset. Comput Meth Biomech Biomed Eng 2:107–124
Garner B, Pandy M (2001) Musculoskeletal model of the upper limb based on the visible human male dataset. Comput Meth Biomech Biomed Eng 4:93–126
Arnold A, Blemker S, Delp S (2001) Evaluation of a deformable musculoskeletal model for estimating muscle-tendon lengths during crouch gait. Comput Aided Surg 29:263–274
Üngör A (2001) Tiling 3D euclidean space with acute tetrahedra. In: Proceedings of the canadian conference on Computer Geomics, pp 169–172
Yerry MA, Shephard MS (1984) Automatic three-dimensional mesh generation by the modified Octree technique. Int J Numer Meth Eng 20:1965–1990
Shephard MS, Georges MK (1991) Automatic three-dimensional mesh generation by the finite Octree technique. Int J Numer Meth Eng 32:709–739
Bey J (1995) Tetrahedral grid refinement. Computing 55:355–378
Grosso R, Lürig C, Ertl T (1997) The multilevel finite element method for adaptive mesh optimization and visualization of volume data. Visualization, pp 387–394
de Cougny HL, Shephard MS (1999) Parallel refinement and coarsening of tetrahedral meshes. Int J Numer Meth Eng 46:1101–1125
Bessette G, Becker E, Taylor L, Littlefield D (2003) Modeling of impact problems using an H-adaptive, explicit lagrangian finite element method in three dimensions. Comput Meth Appl Mech Eng 192:1649–1679
Tsitsiklis J (1995) Efficient algorithms for globally optimal trajectories. IEEE Trans Automat Control 40:1528–1538
Sethian J (1996) A fast marching level set method for monotonically advancing fronts. Proc Natl Acad Sci 93:1591–1595
Zhao HK, Osher S, Fedkiw R (2001) Fast surface reconstruction using the level set method. In: 1st IEEE Wrkshp on Variational and Level Set Methods 8th Int Conf on Comput Vis, pp 194–202
Osher S, Fedkiw R (2002) Level set methods and dynamic implicit surfaces. Springer, Berlin Heidelberg New York
Strain J (1999) Fast tree-based redistancing for level set computations. J Comput Phys 152:664–686
Strain J (1999) Tree methods for moving interfaces. J Comput Phys 151:616–648
Westermann R, Kobbelt L, Ertl T (1999) Real-time exploration of regular volume data by adaptive reconstruction of isosurfaces. The Vis Comput 15(2):100–111
Ambrosio L, Soner HM (1996) Level set approach to mean curvature flow in arbitrary codimension. J Diff Geom 43:693–737
Hughes T (1987) The finite element method: linear static and dynamic finite element analysis. Prentice Hall, Englewoodcliff
Bridson R, Marino S, Fedkiw R (2003) Simulation of clothing with folds and wrinkles. In: Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Comput Anim, pp 28–36
Bridson R, Fedkiw R, Anderson J (2002) Robust treatment of collisions, contact and friction for cloth animation. ACM Trans Graph (SIGGRAPH Proc) 21:594–603
Gnoffo P (1982) A vectorized, finite-volume, adaptive-grid algorithm for Navier-stokes calculations. Num Grid Generat, pp 819–835
Gnoffo P (1982) A finite-volume, adaptive grid algorithm applied to planetary entry flowfields. AIAA
Lohner R, Morgan K, Zienkiewicz OC (1986) Adaptive grid refinement for compressible euler equations. Wiley, New York, pp 281–297
Nakahashi K, Deiwert GS (1987) Self-adaptive-grid method with application to airfoil flow. AIAA 25(4):513–520
Dompierre J, Vallet M, Fortin M, Habashi WG, Aït-Ali-Yahia D, Boivin S, Bourgault Y, Tam A (1995) Edge-based mesh adaptation for CFD. In: Conference on Numerical Methods for the Euler and Navier-Stokes Equations
Vallet M, Dompierre J, Bourgault Y, Fortin M, Habashi WG (1996) Coupling flow solvers and grids through an edge-based adaptive grid method. Fluids Engineering Div Conference, vol 3
Fortin M, Vallet M, Dompierre J, Bourgault Y, Habashi WG (1996) Anisotropic mesh adaptation: theory, validation, and applications. Comput Fluid Dynamics
Bossen FJ, Heckbert PS (1996) A pliant method for anisotropic mesh generation. In: Proceedings of the 5th international meshing roundtable, pp 63–76
Palmerio B (1994) An attraction-repulsion mesh adaption model for flow solution on unstructured grids. Comput Fluids 23(3):487–506
Bourguignon D, Cani MP (2000) Controlling anisotropy in mass-spring systems. Eurographics, Eurographics Assoc, pp 113–123
Cooper L, Maddock S (1997) Preventing collapse within mass-spring-damper models of deformable objects. In: Proceedings of the 5th international conference in central europe on computer graphics and vision
Bonet J, Wood R (1997) Nonlinear continuum mechanics for finite element analysis. Cambridge University Press, Cambridge
Teran J, Blemker S, Ng V, Fedkiw R (2003) Finite volume methods for the simulation of skeletal muscle. In: Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on computer Animation, pp 68–74
Freitag L, Ollivier-Gooch C (1997) Tetrahedral mesh improvement using swapping and smoothing. Int J Num Meth Eng 40:3979–4002
Torczon V (1997) On the convergence of pattern search algorithms. SIAM J Opt 7(1):1–25
Fung YC (1981) Biomechanics: mechanical properties of living tissues. Springer, Berlin Heidelberg New York
Yucesoy CA, Koopman BH, Huijing PA, Grootenboer HJ (2002) Three-dimensional finite element modeling of skeletal muscle using a two-domain approach: linked fiber-matrix mesh model. J Biomech 35:1253–1262
Weiss J, Maker B, Govindjee S (1996) Finite-element impementation of incompressible, transversely isotropic hyperelasticity. Comput Meth Appl Mech Eng 135:107–128
Zajac F (1989) Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng 17(4):359–411
Ng-Thow-Hing V, Fiume E (1997) Interactive display and animation of B-spline solids as muscle shape primitives. In: Thalmann D, van de Panne M (eds) Proceedings of the eurographics workshop on computer animation and sim. Springer, Berlin Heidelberg New York
Ng-Thow-Hing V, Fiume E (2002) Application-specific muscle representations. In: Sturzlinger W, McCool M (eds) Proc of Gr Inter Canadian Information Processing Society, pp 107–115
Crowninshield R (1978) Use of optimization techniques to predict muscle forces. Trans ASME 100:88–92
Bridson R (2003) Computational aspects of dynamic surfaces. PhD thesis, Stanford University
Acknowledgements
Research supported in part by an ONR YIP award and PECASE award (ONR N00014-01-1-0620), a Packard Foundation Fellowship, a Sloan Research Fellowship, ONR N00014-03-1-0071, ONR N00014-02-1-0720, ARO DAAD19-03-1-0331, NSF ITR-0121288, NSF ACI-0205671, NSF DMS-0106694, NSF ACI-0323866 and NSF IIS-0326388. In addition, N. M. and R. B. were supported in part by a Stanford Graduate Fellowships, and J. T. was supported in part by an NSF Graduate Research Fellowship.
Author information
Authors and Affiliations
Corresponding authors
Appendix
Appendix
Consider the tetrahedron defined by the points x 1,x 2,x 3,x 4 and the altitude spring from x 4 to the triangle x 1,x 2,x 3. The Cauchy stress in the tetrahedron due to this spring is
where f is the scalar force in an altitude spring (see Sect. 6), A 4 is the area of the triangle x 1,x 2,x 3 and n 4 is the outward pointing normal of the tetrahedron on face x 1,x 2,x 3.
This can be shown by considering the results of [75]. A finite volume interpretation of the constant strain tetrahedron finite element forces shows that the nodal force response to an internal Cauchy stress σ can be written as
Using this result, the force on x 4 due to σ alt is
A simple geometric argument shows that −(A 1 n T4 n 1)/A 4 is the ratio of the projected area of the face x 2,x 3,x 4 on the plane through x 1,x 2,x 3 with A 4. This is the barycentric weight of x 4 in the plane x 1,x 2,x 3 on the point x 1. Defining the barycentric weight as w 1, we can similarly derive
Therefore, the force on x 4 is
Similarly,
which are precisely the altitude spring forces.
Rights and permissions
About this article
Cite this article
Teran, J., Molino, N., Fedkiw, R. et al. Adaptive physics based tetrahedral mesh generation using level sets. Engineering with Computers 21, 2–18 (2005). https://doi.org/10.1007/s00366-005-0308-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-005-0308-8