Skip to main content
SpringerLink
Log in

Fractional-order Fibonacci-hybrid functions approach for solving fractional delay differential equations

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

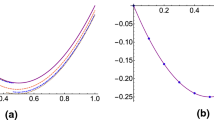
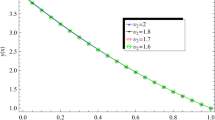
Abstract

The aim of the current paper is to propose an efficient method for finding the approximate solution of fractional delay differential equations. This technique is based on hybrid functions of block-pulse and fractional-order Fibonacci polynomials. First, we define fractional-order Fibonacci polynomials. Next, using Fibonacci polynomials of fractional-order, we introduce a new set of basis functions. These new functions are called fractional-order Fibonacci-hybrid functions (FFHFs) which are appropriate for the approximation of smooth and piecewise smooth functions. The Riemann–Liouville integral operational matrix and delay operational matrix of the FFHFs are obtained. Then, using these matrices and collocation method, the problem is reduced to a system of algebraic equations. Using Newton’s iterative method, we solve this system. Some examples are proposed to test the efficiency and effectiveness of the present method. Given the application of these kinds of fractional equations in the modeling of many phenomena, a numerical example of this work includes the Hutchinson model which describes the rate of population growth.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Zhang T, Meng X, Zhang T (2014) SVEIRS: a new epidemic disease model with time delays and impulsive effects. Abstr Appl Anal 2014:15

    MathSciNet  MATH  Google Scholar 

  2. Sipahi R, Niculescu SI (2009) Deterministic time-delayed traffic flow models: a survey. In: Atay F (ed) Complex time-delay systems. understanding complex systems. Springer, Berlin, Heidelberg

    Google Scholar 

  3. Myshkis AD (1949) General theory of differential equations with a retarded argument. Uspehi Mat. Nauk 22 (134), (in Russian). Amer. Math. soc. transl. no. 55, 1951, pp 21–57

  4. Krasovskii NN (1963) Stability of motion. Standford University Press, Standford

    MATH  Google Scholar 

  5. Bellman R, Cooke KL (1963) Differential-difference equation. Academic, New York

    MATH  Google Scholar 

  6. El’sgol’c LE, Norkin SB (1973) Introduction to the theory of differential equations with deviating argument, 2th edn. Nauka, Moscov (in Russian), 1971. Mathematics in science and Eng., vol 105. Academic Press, New York

  7. Hale JK (1977) Theory of functional differential equations. Springer, New York

    MATH  Google Scholar 

  8. Khosravian-Arab H, Dehghan M, Eslahchi MR (2015) Fractional SturmLiouville boundary value problems in unbounded domains: theory and applications. J Comput Phys 299:526–560

    MathSciNet  MATH  Google Scholar 

  9. Singh J (2019) A new analysis for fractional rumor spreading dynamical model in a social network with Mittag-Leffler law. Chaos Interdiscip J Nonlinear Sci 29(1):013137

    MathSciNet  MATH  Google Scholar 

  10. Kumar D, Singh J, Baleanu D (2018) Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Phys A Stat Mech Appl 492:155–167

    MathSciNet  Google Scholar 

  11. Loverro A (2004) Fractional calculus: history, definitions and applications for the engineer. Department of Aerospace and Mechanical Engineering, Rapport technique, Univeristy of Notre Dame, Notre Dame, pp 1–28

    Google Scholar 

  12. Atangana A, Secer A (2013) A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstract and applied analysis, vol 2013. Hindawi, Cairo

    MATH  Google Scholar 

  13. Dumitru B, Kai D, Enrico S (2012) Fractional calculus: models and numerical methods, vol 3. World Scientific, Singapore

    MATH  Google Scholar 

  14. Kumar D, Singh J, Baleanu D (2018) A new analysis of the Fornberg-Whitham equation pertaining to a fractional derivative with Mittag-Leffler-type kernel. Eur Phys J Plus 133(2):70. https://doi.org/10.1140/epjp/i2018-11934-y

    Article  Google Scholar 

  15. Singh J, Kumar D, Baleanu D (2018) On the analysis of fractional diabetes model with exponential law. Adv Differ Equ 2018(1):231. https://doi.org/10.1186/s13662-018-1680-1

    Article  MathSciNet  MATH  Google Scholar 

  16. Sabermahani S, Ordokhani Y, Yousefi SA (2017) Numerical approach based on fractional-order Lagrange polynomials for solving a class of fractional differential equations. Comput Appl Math 2017:1–23. https://doi.org/10.1007/s40314-017-0547-5

    Article  MATH  Google Scholar 

  17. Kazem S, Abbasbandy S, Kumar S (2013) Fractional-order Legendre functions for solving fractional-order differential equations. Appl Math Model 37(7):5498–5510

    MathSciNet  MATH  Google Scholar 

  18. Krishnasamy VS, Razzaghi M (2016) The numerical solution of the Bagley-Torvik equation with fractional Taylor method. J Comput Nonlinear Dyn 11(5):051010-051010–6

    Google Scholar 

  19. Kumar D, Singh J, Baleanu D, Rathore S (2018) Analysis of a fractional model of the Ambartsumian equation. Eur Phys J Plus 133(7):259. https://doi.org/10.1140/epjp/i2018-12081-3

    Article  Google Scholar 

  20. Singh J, Secer A, Swroop R, Kumar D (2018) A reliable analytical approach for a fractional model of advection-dispersion equation. Nonlinear Engineering. https://doi.org/10.1515/nleng-2018-0027

    Google Scholar 

  21. Assari P, Cuomo S (2018) The numerical solution of fractional differential equations using the Volterra integral equation method based on thin plate splines. Eng Comput. https://doi.org/10.1007/s00366-018-0671-x

    Google Scholar 

  22. Dehghan M, Manafian J, Saadatmandi A (2010) Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer Methods Partial Differ Equ Int J 26(2):448–479

    MathSciNet  MATH  Google Scholar 

  23. Saadatmandi A, Dehghan M (2010) A new operational matrix for solving fractional-order differential equations. Comput Math Appl 59(3):1326–1336

    MathSciNet  MATH  Google Scholar 

  24. Singh J, Kumar D, Baleanu D, Rathore S (2018) An efficient numerical algorithm for the fractional Drinfeld–Sokolov–Wilson equation. Appl Math Comput 335:12–24

    MathSciNet  MATH  Google Scholar 

  25. Sadeghi Hafshejani M, Karimi Vanani S, Sedighi Hafshejani J (2011) Numerical solution of delay differential equations using Legendre wavelet method. World Appl Sci 13:27–33

    Google Scholar 

  26. Sedaghat S, Ordokhani Y, Dehghan M (2012) Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun Nonlinear Sci Numer Simul 17:4815–4830

    MathSciNet  MATH  Google Scholar 

  27. Rahimkhani P, Ordokhani Y, Babolian E (2017) Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet. Comput Appl Math 309:493–510

    MathSciNet  MATH  Google Scholar 

  28. Rahimkhani P, Ordokhani Y, Babolian E (2017) A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations. Numer Algor. 74:223–245

    MathSciNet  MATH  Google Scholar 

  29. Seong HY, Majid ZA (2014) Fifth order predictor-corrector methods for solving third order delay differential equations. AIP Conf Proc 1635(1):94–98

    Google Scholar 

  30. Dehghan M, Abbaszadeh M (2018) A Legendre spectral element method (SEM) based on the modified bases for solving neutral delay distributed-order fractional damped diffusion-wave equation. Math Methods Appl Sci 41(9):3476–3494

    MathSciNet  MATH  Google Scholar 

  31. Dehghan M, Abbaszadeh M (2018) An efficient technique based on finite difference/finite element method for solution of two-dimensional space/multi-time fractional Bloch-Torrey equations. Appl Numer Math 131:190–206

    MathSciNet  MATH  Google Scholar 

  32. Baleanu D, Magin RL, Bhalekar S, Daftardar-Gejji V (2015) Chaos in the fractional order nonlinear Bloch equation with delay. Commun Nonlinear Sci Numer Simulat 25(1–3):41–49

    MathSciNet  MATH  Google Scholar 

  33. Moghaddam BP, Yaghoobi S, Machado JT (2016) An extended predictorcorrector algorithm for variable-order fractional delay differential equations. J Comput Nonlinear Dyn 11(6):061001. https://doi.org/10.1115/1.4032574

    Article  Google Scholar 

  34. Ohira T, Milton J (2009) Delayed random walks: Investigating the interplay between delay and noise. Delay differential equations. Springer, Boston, pp 1–31

    Google Scholar 

  35. Huang C, Guo Z, Yang Z, Chen Y, Wen F (2015) Dynamics of delay differential equations with its applications 2014. Abstract and applied analysis. Hindawi, Cairo

    Google Scholar 

  36. an der Heiden U (1979) Delays in physiological systems. J Math Biol 8:345–364

    MathSciNet  MATH  Google Scholar 

  37. an der Heiden U, Mackey MC, Walther HO (1981) Complex oscillations in a simple deterministic neuronal network. In: Hoppensteadt F (ed) Mathematical aspects of physiology. American Mathematical Society, Providence, pp 355–360

    Google Scholar 

  38. Radziunas M (2016) New multi-mode delay differential equation model for lasers with optical feedback. Opt Quant Electron 48:470. https://doi.org/10.1007/s11082-016-0736-2

    Article  Google Scholar 

  39. Mashayekhi S, Razzaghi M (2016) Numerical solution of distributed order fractional differential equations by hybrid functions. J Comput Phys 315(15):169–181

    MathSciNet  MATH  Google Scholar 

  40. Youssri YH, Abd-Elhameed WM (2017) Spectral solutions for multi-term fractional initial value problems using a new Fibonacci operational matrix of fractional integration. Progr Fract Differ Appl 2(2):141–151

    Google Scholar 

  41. Razzaghi M, Marzban HR (2000) A hybrid analysis direct method in the calculus of variations. Int J Comput Math 75(3):259–269

    MathSciNet  MATH  Google Scholar 

  42. Tavassoli Kajani M, Hadi Vencheh A (2005) Solving second kind integral equations with Hybrid Chebyshev and Block-Pulse functions. Appl Math Comput 163:71–77

    MathSciNet  MATH  Google Scholar 

  43. Behroozifar M (2013) Numerical solution of delay differential equations via operational matrices of hybrid of block-pulse functions and Bernstein polynomials. Comput Methods Differ Equ 2(1):78–95

    MATH  Google Scholar 

  44. Marzban HR, Razzaghi M (2006) Solution of multi-delay systems using hybrid of block-pulse functions and Taylor series. J Sound Vib 292(3):954–963

    MathSciNet  MATH  Google Scholar 

  45. Odibat Z, Shawagfeh NT (2007) Generalized Taylor’s formula. Appl Math Comput 186(1):286–293

    MathSciNet  MATH  Google Scholar 

  46. Falcon S, Plaza A (2007) The k-Fibonacci sequence and the Pascal 2-triangle. Chaos Solitons Fract 33(1):38–49

    MathSciNet  MATH  Google Scholar 

  47. Falcon S, Plaza A (2009) On k-Fibonacci sequences and polynomials and their derivatives. Chaos Solitons Fract 39:1005–1019

    MathSciNet  MATH  Google Scholar 

  48. Rabiei K, Ordokhani Y, Babolian E (2017) Fractional-order Boubaker functions and their applications in solving delay fractional optimal control problems. J Vib Control 24:1–14

    MathSciNet  MATH  Google Scholar 

  49. Kreyszig E (1978) Introductory functional analysis with applications. Wiley, New York

    MATH  Google Scholar 

  50. Saeed U, Rehman MU (2014) Hermite wavelet method for fractional delay differential equations. J Differ Equ 2014:1–8

    Google Scholar 

  51. Fowler AC (2005) Asymptotic methods for delay equations. J Eng Math 53(3–4):271–290

    MathSciNet  MATH  Google Scholar 

  52. Moghaddam BP, Mostaghim ZS (2013) A numerical method based on finite difference for solving fractional delay differential equations. J Taibah Univ Sci 7(3):120–127

    Google Scholar 

Download references

Acknowledgements

The authors wish to express their sincere thanks to referees for their valuable suggestions that improved the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran

    Sedigheh Sabermahani & Yadollah Ordokhani

  2. Department of Mathematics, Faculty of Mathematical Sciences, Shahid Beheshti University, Tehran, Iran

    Sohrab-Ali Yousefi

Authors
  1. Sedigheh Sabermahani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yadollah Ordokhani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sohrab-Ali Yousefi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yadollah Ordokhani.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sabermahani, S., Ordokhani, Y. & Yousefi, SA. Fractional-order Fibonacci-hybrid functions approach for solving fractional delay differential equations. Engineering with Computers 36, 795–806 (2020). https://doi.org/10.1007/s00366-019-00730-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-019-00730-3

Keywords

Search

Navigation