Skip to main content
SpringerLink
Log in

Novel solution for heat and mass transfer of a MHD micropolar fluid flow on a moving plate with suction and injection

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

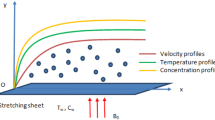
Two new functions on the semi-infinite interval, namely Rational Gegenbauer (R) and Exponential Gegenbauer (E) functions are proposed to solve the heat transfer problem. The considered problem is flow of MHD micropolar over a moving plate with suction and injection boundary conditions. For applying Tau method efficiently, two matrices of derivative and product for both of rational and exponential Gegenbauer whose enable us to solve a system of nonlinear algebraic equations on the semi-infinite interval were introduced, and an error bound of these functions approximation was estimated which led to have an exponential convergence rate in this method. Moreover, the influence of the important physical parameters on heat and mass transfer phenomena are studied with details. Comparing the results of Rational Gegenbauer Tau and Exponential Gegenbauer Tau methods with available analytical and numerical solutions shows that the present methods are efficient and have fast convergence rate and high accuracy. This method can solve a set of coupled nonlinear and high-order differential equations on a semi-infinite domain by converting to a set of linear equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

b :

Constant

\(B_0\) :

Uniform transverse magnetic field

\(c_\mathrm{f}\) :

Skin-friction coefficient

\(c_p\) :

Specific heat at constant pressure

Ec:

Eckert number

f :

Dimensionless velocity

G :

Microrotation parameter

g :

Dimensionless microrotation

\(G_1\) :

Microrotation constant

K :

Coupling constant parameter

\(k^*\) :

Mean absorption coefficient

M :

Magnetic field parameter

N :

Components of microrotation

Nu:

Nusselt number

Pr:

Prandtl number

\(q_\mathrm{r}\) :

Radiative heat flux

\(q_\mathrm{w}\) :

Surface heat flux

R :

Thermal radiation parameter

Re:

Reynolds number

s :

Constant characteristic of the fluid

T :

Temperature of fluid

u, v :

Velocity components along x and y directions, respectively

x, y :

Cartesian coordinates along the plate and normal to it, respectively

\(\eta\) :

Similarity variable

\(\gamma\) :

Constant

\(\kappa\) :

Thermal conductivity

\(\mu\) :

Dynamic viscosity

\(\nu\) :

Kinematic viscosity

\(\rho\) :

Density of the fluid

\(\sigma\) :

Electrical conductivity

\(\sigma ^*\) :

Stefan–Boltzmann

\(\tau\) :

Skin friction

\(\theta\) :

Dimensionless temperature

\(\varphi\) :

Stream function

\(\infty\) :

Ambient condition

w:

Condition of the wall

References

  1. Canuto C, Hussaini MY, Quarteroni A, Zang TA (1986) Spectral methods in fluid dynamics. Prentice-Hall, Englewood Cliffs

    MATH  Google Scholar 

  2. Assari P, Dehghan M (2017) The numerical solution of two-dimensional logarithmic integral equations on normal domains using radial basis functions with polynomial precision. Eng Comput 33(4):853–870

    Google Scholar 

  3. Khalil H, Khan RA, Baleanu D, Rashidi MM (2019) Some new operational matrices and its application to fractional order Poisson equations with integral type boundary constrains. Comput Math Appl 78(6):1826–1837

    MathSciNet  MATH  Google Scholar 

  4. Hosseininia M, Heydari MH, Ghaini FMM, Avazzadeh Z (2019) A wavelet method to solve nonlinear variable-order time fractional 2D Klein–Gordon equation. Comput Math Appl 78(12):3713–3730

    MathSciNet  MATH  Google Scholar 

  5. Lanczos C (1938) Trigonometric interpolation of empirical and analytical functions. J Math Phys 17:123–199

    MATH  Google Scholar 

  6. Tajvidi T, Razzaghi M, Dehghan M (2008) Modified rational Legendre approach to laminar viscous flow over a semi-infinite flat plate. Chaos Solitons Fractals 35:59–66

    MathSciNet  MATH  Google Scholar 

  7. El-Daou MK (2011) Exponentially weighted Legendre–Gauss Tau methods for linear second-order differential equations. Comput Math Appl 62:51–64

    MathSciNet  MATH  Google Scholar 

  8. Saadatmandi A, Dehghan M (2011) A Tau approach for solution of the space fractional diffusion equation. Comput Math Appl 62:1135–1142

    MathSciNet  MATH  Google Scholar 

  9. Doha EH, Bhrawy AH, Ezz-Eldien SS (2011) Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations. Appl Math Model 35:5662–5672

    MathSciNet  MATH  Google Scholar 

  10. Coulaud O, Funaro D, Kavian O (1990) Laguerre spectral approximation of elliptic problems in exterior domains. Comput Method Appl Mech Eng 80:451–458

    MathSciNet  MATH  Google Scholar 

  11. Funaro D, Kavian O (1991) Approximation of some diffusion evolution equations in unbounded domains by Hermite functions. Math Comput 57:597–619

    MathSciNet  MATH  Google Scholar 

  12. Liu C, Zhub S (2015) Laguerre pseudospectral approximation to the Thomas–Fermi equation. J Comput Appl Math 282:251–261

    MathSciNet  Google Scholar 

  13. Alıcı H, Taşeli H (2015) The Laguerre pseudospectral method for the radial Schrödinger equation. Appl Numer Math 87:87–99

    MathSciNet  MATH  Google Scholar 

  14. Guo BY (2000) Jacobi spectral approximation and its applications to differential equations on the half line. J Comput Math 18:95–112

    MathSciNet  MATH  Google Scholar 

  15. Guo BY (2001) Gegenbauer approximation and its applications to differential equations with rough asymptotic behaviors at infinity. Appl Numer Math 38:403–425

    MathSciNet  MATH  Google Scholar 

  16. Boyd JP (2000) Chebyshev and Fourier spectral methods, 2nd edn. Dover, New York

    Google Scholar 

  17. Christov CI (1982) A complete orthogonal system of functions in \(L^2(-\infty,\infty )\) space. SIAM J Appl Math 42:1337–1344

    MathSciNet  MATH  Google Scholar 

  18. Boyd JP (1987) Orthogonal rational functions on a semi-infinite interval. J Comput Phys 70:63–88

    MathSciNet  MATH  Google Scholar 

  19. Boyd JP (1987) Spectral methods using rational basis functions on an infinite interval. J Comput Phys 69:112–142

    MathSciNet  MATH  Google Scholar 

  20. Guo BY, Shen J, Wang ZQ (2000) A rational approximation and its applications to differential equations on the half line. J Sci Comput 15:117–147

    MathSciNet  MATH  Google Scholar 

  21. Boyd JP, Rangan C, Bucksbaum PH (2003) Pseudospectral methods on a semi-infinite interval with application to the Hydrogen atom: a comparison of the mapped Fourier-sine method with Laguerre series and rational Chebyshev expansions. J Comput Phys 188:56–74

    MATH  Google Scholar 

  22. Parand K, Razzaghi M (2004) Rational Chebyshev Tau method for solving higher-order ordinary differential equations. Int J Comput Math 81:73–80

    MathSciNet  MATH  Google Scholar 

  23. Parand K, Razzaghi M (2004) Rational Chebyshev Tau method for solving Volterra’s population model. Appl Math Comput 149:893–900

    MathSciNet  MATH  Google Scholar 

  24. Parand K, Dehghan M, Rezaei AR, Ghaderi SM (2010) An approximational algorithm for the solution of the nonlinear Lane–Emden type equations arising in astrophysics using Hermite functions collocation method. Comput Phys Commun 181:1096–1108

    MATH  Google Scholar 

  25. Parand K, Dehghan M, Taghavi A (2010) Modified generalized Laguerre function Tau method for solving laminar viscous flow: the Blasius equation. Int J Numer Methods Heat Fluid Flow 20:728–743

    MathSciNet  Google Scholar 

  26. Parand K, Nikarya M, Rad JA, Baharifard F (2012) A new reliable numerical algorithm based on the first kind of Bessel functions to solve Prandtl–Blasius laminar viscous flow over a semi-infinite flat plate. Z Naturforsch A 67:665–673

    Google Scholar 

  27. Parand K, Dehghan M, Baharifard F (2013) Solving a laminar boundary layer equation with the rational Gegenbauer functions. Appl Math Model 37:851–863

    MathSciNet  MATH  Google Scholar 

  28. Baharifard F, Kazem S, Parand K (2015) Rational and exponential legendre Tau method on steady flow of a third grade fluid in a porous half space. Int J Appl Comput Math 67:1–20

    MATH  Google Scholar 

  29. Rabiei K, Parand K (2019) Collocation method to solve inequality-constrained optimal control problems of arbitrary order. Eng Comput 36:1–11

    Google Scholar 

  30. Gudi T, Majumder P (2019) Conforming and discontinuous Galerkin FEM in space for solving parabolic obstacle problem. Comput Math Appl 78(12):3896–3915

    MathSciNet  MATH  Google Scholar 

  31. Modather M, Chamkha AJ (2010) An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium. Turk J Eng Environ Sci 33(4):245–258

    Google Scholar 

  32. Damseh RA, Al-Odat MQ, Chamkha AJ, Shannak BA (2009) Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface. Int J Therm Sci 48(8):1658–1663

    Google Scholar 

  33. Eringen AC (1966) Theory of micropolar fluids. J Math Mech 16:1–18

    MathSciNet  Google Scholar 

  34. Eringen AC (2001) Microcontinuum field theories: II. Fluent media. Springer, New York

    MATH  Google Scholar 

  35. Łukaszewicz G (1999) Micropolar fluids, theory and applications, modeling and simulation in science, engineering and technology. Birkhäuser, Boston

    MATH  Google Scholar 

  36. Ariman T, Turk MA, Sylvester ND (1974) Microcontinuum fluid mechanics—a review. Int J Eng Sci 12:273–293

    MATH  Google Scholar 

  37. Sakiadis BC (1961) Boundary layer behavior on continuous solid surface; the boundary layer on a continuous flat surface. Am Inst Chem Eng J 7:221–225

    Google Scholar 

  38. Soundalgekar VM, Takhar HS (1983) Boundary layer flow of a micropolar fluid on a continuous moving plate. Int J Eng Sci 21:961–965

    Google Scholar 

  39. Crane LJ (1970) Flow past a stretching plate. Z Angew Math Phys 21:645–647

    Google Scholar 

  40. Abolbashari MH, Freidoonimehr N, Nazari F, Rashidi MM (2014) Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol 267:256–267

    Google Scholar 

  41. Freidoonimehr N, Rashidi MM, Mahmud S (2015) Unsteady MHD free convective flow past a permeable stretching vertical surface in a nano-fluid. Int J Threm Sci 87:136–145

    Google Scholar 

  42. Chamkha AJ, Aly AM, Mansour MA (2010) Similarity solution for unsteady heat and mass transfer from a stretching surface embedded in a porous medium with suction/injection and chemical reaction effects. Chem Eng Commun 197(6):846–858

    Google Scholar 

  43. Rees DAS, Bassom AP (1996) The Blasius boundary-layer flow of a micropolar fluid. Int J Eng Sci 34:113–124

    MathSciNet  MATH  Google Scholar 

  44. Gupta P, Gupta A (1977) Heat and mass transfer on a stretching sheet with suction or blowing. Can J Chem Eng 55:744–746

    Google Scholar 

  45. Hassanien IA, Gorla RSR (1990) Heat transfer to a micropolar fluid from a nonisothermal stretching sheet with suction and blowing. Acta Mech 84:191–203

    Google Scholar 

  46. Hady FM (1996) On the solution of heat transfer to micropolar fluid from a nonisothermal stretching sheet with injection. Int J Numer Meth Heat Fluid Flow 6:99–104

    MATH  Google Scholar 

  47. Perdikis C, Raptis A (1996) Heat transfer of a micropolar fluid by the presence of radiation. Heat Mass Transf 31:381–382

    Google Scholar 

  48. Raptis A (1998) Flow of a micropolar fluid past a continuously moving plate by the presence of radiation. Int J Heat Mass Transf 41:2865–2866

    MATH  Google Scholar 

  49. Chamkha AJ (2002) Fully developed free convection of a micropolar fluid in a vertical channel. Int Commun Heat Mass Transf 29:1119–1127

    Google Scholar 

  50. Rahman MM, Uddin MJ, Aziz A (2009) Effects of variable electric conductivity and non-uniform heat source (or sink) on convective micropolar fluid flow along an inclined flat plate with surface heat flux. Int J Therm Sci 48:2331–2340

    Google Scholar 

  51. Zhang J-K, Li B-W, Hu Z-M (2013) Effects of optical parameters on fluid flow and heat transfer of participating magnetic fluid. Int J Heat Mass Transf 59:126–136

    Google Scholar 

  52. Magyari E, Chamkha AJ (2008) Exact analytical results for the thermosolutal MHD Marangoni boundary layers. Int J Therm Sci 47(7):848–857

    Google Scholar 

  53. Takhar HS, Chamkha AJ, Nath G (2002) MHD flow over a moving plate in a rotating fluid with magnetic field, Hall currents and free stream velocity. Int J Eng 40(13):1511–152

    MATH  Google Scholar 

  54. Takhar HS, Chamkha AJ, Nath G (1999) Unsteady flow and heat transfer on a semi-infinite flat plate with an aligned magnetic field. Int J Eng 37(13):1723–1736

    Google Scholar 

  55. Chamkha AJ, Aly AM (2010) MHD free convection flow of a nanofluid past a vertical plate in the presence of heat generation or absorption effects. Chem Eng Commun 198(3):425–441

    Google Scholar 

  56. Seddeek MA (2003) Flow of a magneto-micropolar fluid past a continuously moving plate. Phys Lett A 306:255–257

    Google Scholar 

  57. Seddeek MA, Odda SN, Akl MY, Abdelmeguid MS (2009) Analytical solution for the effect of radiation on flow of a magneto-micropolar fluid past a continuously moving plate with suction and blowing. Comput Mater Sci 45:423–428

    Google Scholar 

  58. Khedr MEM, Chamkha AJ, Bayomi M (2009) MHD flow of a micropolar fluid past a stretched permeable surface with heat generation or absorption. Nonlinear Anal Model 14(1):27–40

    MATH  Google Scholar 

  59. Chamkha AJ, Mohamed RA, Ahmed SE (2011) Unsteady MHD natural convection from a heated vertical porous plate in a micropolar fluid with Joule heating, chemical reaction and radiation effects. Meccanica 46(2):399–411

    MathSciNet  MATH  Google Scholar 

  60. Bhargava R, Bég OA, Sharma S, Zueco J (2010) Finite element study of nonlinear two-dimensional deoxygenated biomagnetic micropolar flow. Commun Nonlinear Sci 15(5):1210–1223

    MathSciNet  MATH  Google Scholar 

  61. Aslani KE, Benos L, Tzirtzilakis E, Sarris IE (2020) Micromagnetorotation of MHD micropolar flows. Symmetry 12:1

    Google Scholar 

  62. Rashidi MM, Erfani E (2012) Analytical method for solving steady MHD convective and slip flow due to a rotating disk with viscous dissipation and ohmic heating. Eng Comput 6:562–579

    Google Scholar 

  63. Rashidi MM, Momoniat E, Rostami B (2012) Analytic approximate solutions for MHD boundary-layer viscoelastic fluid flow over continuously moving stretching surface by homotopy analysis method with two auxiliary parameters. J Appl Math 2012:1–19

    MathSciNet  MATH  Google Scholar 

  64. Raptis A, Perdikis C, Takhar HS (2004) Effect of thermal radiation on MHD flow. Appl Math Comput 153:645–649

    MathSciNet  MATH  Google Scholar 

  65. Szegö G (1975) Orthogonal polynomials, 4th edn. AMS Coll Publ, New York

    MATH  Google Scholar 

  66. Stegun I, Abramowitz M (1968) Handbook of mathematical functions. Dover, New York

    MATH  Google Scholar 

  67. Boyd JP (1982) The optimzation of convergence for Chebyshev polynomial methods in an unbounded domain. J Comput Phys 45:43–79

    MathSciNet  MATH  Google Scholar 

  68. Kim DS, Kim T, Rim SH (2012) Some identities involving Gegenbauer polynomials. Adv Differ Equ 2012:219

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to both reviewers for carefully reading this paper and for their comments and suggestions which have improved the paper.

Author information

Authors and Affiliations

  1. School of Computer Science, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran

    F. Baharifard

  2. Department of Computer Sciences, Faculty of Mathematical Sciences, Shahid Beheshti University, G. C., Tehran, Iran

    K. Parand

  3. Department of Cognitive Modeling, Institute for Cognitive and Brain Sciences, Shahid Beheshti University, G. C., Tehran, Iran

    K. Parand

  4. Department of Statistics and Actuarial Science, University of Waterloo, Waterloo, Canada

    K. Parand

  5. Shanghai Key Lab of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Tongji University, 4800 Cao An Rd., Jiading, 201804, Shanghai, China

    M. M. Rashidi

Authors
  1. F. Baharifard
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Parand
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. M. Rashidi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. Baharifard.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Baharifard, F., Parand, K. & Rashidi, M.M. Novel solution for heat and mass transfer of a MHD micropolar fluid flow on a moving plate with suction and injection. Engineering with Computers 38, 13–30 (2022). https://doi.org/10.1007/s00366-020-01026-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01026-7

Keywords

Mathematics Subject Classification

Search

Navigation