Pan-H-Linked Graphs

Abstract

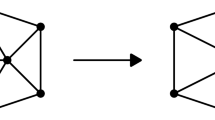
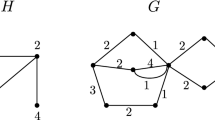
Let H be a multigraph, possibly containing loops. An H-subdivision is any simple graph obtained by replacing the edges of H with paths of arbitrary length. Let H be an arbitrary multigraph of order k, size m, n ₀(H) isolated vertices and n ₁(H) vertices of degree one. In Gould and Whalen (Graphs Comb. 23:165–182, 2007) it was shown that if G is a simple graph of order n containing an H-subdivision ${\mathcal{H}}$ and ${\delta(G) \ge \frac{n+m-k+n_1(H)+2n_0(H)}{2}}$, then G contains a spanning H-subdivision with the same ground set as ${\mathcal{H}}$ . As a corollary to this result, the authors were able to obtain Dirac’s famed theorem on hamiltonian graphs; namely that if G is a graph of order n ≥ 3 with ${\delta(G)\ge\frac{n}{2}}$ , then G is hamiltonian. Bondy (J. Comb. Theory Ser. B 11:80–84, 1971) extended Dirac’s theorem by showing that if G satisfied the condition ${\delta(G) \ge \frac{n}{2}}$ then G was either pancyclic or a complete bipartite graph. In this paper, we extend the result from Gould and Whalen (Graphs Comb. 23:165–182, 2007) in a similar manner. An H-subdivision ${\mathcal{H}}$ in G is 1-extendible if there exists an H-subdivision ${\mathcal{H}^{*}}$ with the same ground set as ${\mathcal{H}}$ and ${|\mathcal{H}^{*}| = |\mathcal{H}| + 1}$ . If every H-subdivision in G is 1-extendible, then G is pan-H-linked. We demonstrate that if H is sufficiently dense and G is a graph of large enough order n such that ${\delta(G) \ge \frac{n+m-k+n_1(H)+2n_0(H)}{2}}$ , then G is pan-H-linked. This result is sharp.