The Cyclomatic Number of a Graph and its Independence Polynomial at −1

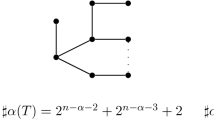
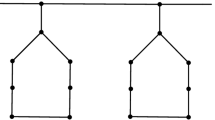
Abstract

If by s _k is denoted the number of independent sets of cardinality k in a graph G, then ${I(G;x)=s_{0}+s_{1}x+\cdots+s_{\alpha}x^{\alpha}}$ is the independence polynomial of G (Gutman and Harary in Utilitas Mathematica 24:97–106, 1983), where α = α(G) is the size of a maximum independent set. The inequality |I (G; −1)| ≤ 2^ν(G), where ν(G) is the cyclomatic number of G, is due to (Engström in Eur. J. Comb. 30:429–438, 2009) and (Levit and Mandrescu in Discret. Math. 311:1204–1206, 2011). For ν(G) ≤ 1 it means that ${I(G;-1)\in\{-2,-1,0,1,2\}.}$ In this paper we prove that if G is a unicyclic well-covered graph different from C ₃, then ${I(G;-1)\in\{-1,0,1\},}$ while if G is a connected well-covered graph of girth ≥ 6, non-isomorphic to C ₇ or K ₂ (e.g., every well-covered tree ≠ K ₂), then I (G; −1) = 0. Further, we demonstrate that the bounds {−2^ν(G), 2^ν(G)} are sharp for I (G; −1), and investigate other values of I (G; −1) belonging to the interval [−2^ν(G), 2^ν(G)].